Skip to main content
SpringerLink
Log in

Meshless Method with Domain Decomposition for Submerged Porous Breakwaters in Waves

  • Published:
Journal of Ocean University of China Aims and scope Submit manuscript

Abstract

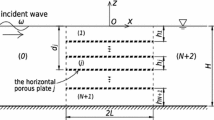
Based on the improved version of the meshless singular boundary method (ISBM) in multi domain (MD), a numerical method is proposed in this paper to study the interaction of submerged permeable breakwaters and regular waves at normal incidence. To account for fluid flow inside the porous breakwaters, the conventional model of Sollitt and Cross for porous media is adopted. Both single and dual trapezoidal breakwaters are examined. The physical problem is formulated in the context of the linear potential wave theory. The domain decomposition method (DDM) is employed, in which the full computational domain is decomposed into separate domains, that is, the fluid domain and the domains of the breakwaters. Respectively, appropriate mixed type boundary and continuity conditions are applied for each subdomain and at the interfaces between domains. The solution is approximated in each subdomain by the ISBM. The discretized algebraic equations are combined, resulting in an overdetermined full system that is solved using a least-square solution procedure. The numerical results are presented in terms of the hydrodynamic quantities of reflection, transmission, and wave-energy dissipation. The relevance of the results of the present numerical procedure is first validated against data of previous studies, and then selected computations are discussed for various structural conditions. The proposed method is demonstrated to be highly accurate and computationally efficient.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Abul-Azm, A. G., 1994. Diffraction through wide submerged breakwaters under oblique waves. Ocean Engineering, 21 (7): 683–706.

    Article  Google Scholar 

  • Bakhti, Y., Chioukh, N., Hamoudi, B., and Boukhari, M., 2017. A multi-domain boundary element method to analyze the reflection and transmission of oblique waves from double porous thin walls. Journal of Marine Science and Application, 16 (3): 276–285.

    Article  Google Scholar 

  • Brebbia, C. A., and Dominguez, J., 1992. Boundary elements: An introductory course. Computational Mechanics Publications. WIT Press, Southampton and Boston, 55–57.

    Google Scholar 

  • Chen, C. W., Fan, C. M., Young, D. L., Murugesan, K., and Tsai, C. C., 2005. Eigenanalysis for membranes with stringers using the methods of fundamental solutions and domain decomposition. Computer Modeling in Engineering and Sciences, 8 (1): 29–44.

    Google Scholar 

  • Chen, K. H., Lu, M. C., and Hsu, H. M., 2011. Regularized meshless method analysis of the problem of obliquely incident water wave. Engineering Analysis with Boundary Elements, 35 (3): 355–362.

    Article  Google Scholar 

  • Chen, W., Zhang, J. Y., and Fu, Z. J., 2014. Singular boundary method for modified Helmholtz equations. Engineering Analysis with Boundary Elements, 44: 112–119.

    Article  Google Scholar 

  • Chioukh, N., Boukhari, M., Yüksel, Y., and Hamoudi, B., 2016. Performance of porous marine structures of single and double perforated seawalls in regular oblique waves. Proceedings of the 35th International Conference on Coastal Engineering, ASCE, Antalya, Turkey, 35: waves.8.

    Google Scholar 

  • Chioukh, N., Çevik, E., and Yüksel, Y., 2017. Reflection and transmission of regular waves from/through single and double perforated thin walls. China Ocean Engineering, 31 (4): 466–475.

    Article  Google Scholar 

  • Chioukh, N., Ouazzane, K., Yüksel, Y., Hamoudi, B., and Çevik, E., 2019. Meshless method for analysis of permeable breakwaters in the proximity of a vertical wall. China Ocean Engineering, 33: 148–159.

    Article  Google Scholar 

  • Cho, Y. S., Lee, J. I., and Kim, Y. T., 2004. Experimental study of strong reflection of regular water waves over submerged breakwaters in tandem. Ocean Engineering, 31 (10): 1325–1335.

    Article  Google Scholar 

  • Dattatri, J., Raman, H., and Shankar, N. J., 1978. Performance characteristics of submerged breakwaters. Proceedings of the 16th International Conference on Coastal Engineering, ASCE, Hamburg, Germany, 16: 2153–2171.

    Google Scholar 

  • Fairweather, G., and Karageorghis, A., 1998. The method of fundamental solutions for elliptic boundary value problems. Advances in Computational Mathematics, 9: 69–95.

    Article  Google Scholar 

  • Fu, Z. J., Chen, W., Lin, J., and Cheng, A. H. D., 2015. Singular boundary method for various exterior wave applications. International Journal of Computational Methods, 12 (2): 1550011.

    Article  Google Scholar 

  • Gu, Y., and Chen, W., 2013. Infinite domain potential problems by a new formulation of singular boundary method. Applied Mathematical Modelling, 37 (4): 1638–1651.

    Article  Google Scholar 

  • Gu, Y., and Chen, W., 2014. Recent advances in singular boundary method for ultra-thin structural problems. WIT Transactions on Modelling and Simulation, Boundary Elements and other Mesh Reduction Methods XXXVI, 56: 233–243.

    Google Scholar 

  • Gu, Y., Chen, W., and He, X. Q., 2012a. Domain-decomposition singular boundary method for stress analysis in multi-layered elastic materials. Computers, Materials and Continua, 29 (2): 129–154.

    Google Scholar 

  • Gu, Y., Chen, W., and Zhang, J. Y., 2012b. Investigation on near-boundary solutions by singular boundary method. Engineering Analysis with Boundary Elements, 36 (8): 1173–1182.

    Article  Google Scholar 

  • Hsu, T. W., Chang, H. K., and Hsieh, C. M., 2002. Bragg reflection of waves by different shapes of artificial bars. China Ocean Engineering, 16 (3): 21–30.

    Google Scholar 

  • Htike, H., Chen, W., and Gu, Y., 2011. Singular boundary method for heat conduction in layered materials. Computers, Materials and Continua, 24 (1): 1–14.

    Google Scholar 

  • Koley, S., 2019. Wave transmission through multilayered porous breakwater under regular and irregular incident waves. Engineering Analysis with Boundary Elements, 108: 393–401.

    Article  Google Scholar 

  • Koley, S., Behera, H., and Sahoo, T., 2015a. Oblique wave trapping by porous structures near a wall. Journal of Engineering Mechanics, ASCE, 141 (3): 04014122.

    Article  Google Scholar 

  • Koley, S., Sarkar, A., and Sahoo, T., 2015b. Interaction of gravity waves with bottom-standing submerged structures having perforated outer-layer placed on a sloping bed. Applied Ocean Research, 52: 245–260.

    Article  Google Scholar 

  • Li, J., Fu, Z., and Chen, W., 2016. Numerical investigation on the obliquely incident water wave passing through the submerged breakwater by singular boundary method. Computers and Mathematics with Applications, 71 (1): 381–390.

    Article  Google Scholar 

  • Liu, Y., and Li, H. J., 2013. Hydrodynamic performance of a composite breakwater with an upper horizontal porous plate and a lower rubble mound. Ocean Systems Engineering, 3 (1): 55–70.

    Article  Google Scholar 

  • Liu, Y., and Li, H. J., 2014. Analysis of wave performance through pile-rock breakwaters. Proceedings of the Institution of Mechanical Engineers, Part M: Journal of Engineering for the Maritime Environment, 228 (3): 284–292.

    Google Scholar 

  • Lokesha, K. N. B., Sannasiraj, S. A., Sundar, V., and Schlurmann, T., 2015. Experimental investigations on wave transmission at submerged breakwater with smooth and stepped slopes. Procedia Engineering, 116: 713–719.

    Article  Google Scholar 

  • Ouyang, H. T., Chen, K. H., and Tsai, C. M., 2016. Wave characteristics of Bragg reflections from a train of submerged bottom breakwaters. Journal of Hydro-Environment Research, 11: 91–100.

    Article  Google Scholar 

  • Qiu, L., Wang, F., and Lin, J., 2019. A meshless singular boundary method for transient heat conduction problems in layered materials. Computers and Mathematics with Applications, 78: 3544–3562.

    Article  Google Scholar 

  • Sasikumar, A., Kamath, A., and Bihs, H., 2020. Modeling porous coastal structures using a level set method based VRANS-solver on staggered grids. Coastal Engineering Journal, 62 (2): 198–216.

    Article  Google Scholar 

  • Senouci, F., Chioukh, N., and Dris, M. E. A., 2019. Performance evaluation of bottom-standing submerged breakwaters in regular waves using the meshless singular boundary method. Journal of Ocean University of China, 18 (4): 823–833.

    Article  Google Scholar 

  • Sollitt, C. K., and Cross, R. H., 1972. Wave transmission through permeable breakwaters. Proceedings of the 13th International Conference on Coastal Engineering, ASCE, Vancouver, 13: 1827–1846.

    Google Scholar 

  • Srineash, V. K., Kamath, A., Murali, K., and Bihs, H., 2020. Numerical simulation of wave Interaction with submerged porous structures and application for coastal resilience. Journal of Coastal Research, 36 (4): 752–770.

    Article  Google Scholar 

  • Sulisz, W., 1985. Wave reflection and transmission at permeable breakwaters of arbitrary cross-section. Coastal Engineering, 9 (4): 371–386.

    Article  Google Scholar 

  • Tsai, C. H., and Young, D. L., 2011. The method of fundamental solutions for water-wave diffraction by thin porous breakwater. Journal of Mechanics, 27 (1): 149–155.

    Article  Google Scholar 

  • Twu, S. W., and Liu, C. C., 2004. Interaction of non-breaking regular waves with a periodic array of artificial porous bars. Coastal Engineering, 51 (3): 223–236.

    Article  Google Scholar 

  • Twu, S. W., Liu, C. C., and Hsu, W. H., 2001. Wave damping characteristics of deeply submerged breakwaters. Journal of Waterway, Port, Coastal and Ocean Engineering. ASCE, 127 (2): 97–105.

    Article  Google Scholar 

  • Venkateswarlu, V., and Karmakar, D., 2019. Wave scattering by vertical porous block placed over flat and elevated seabed. Marine Systems and Ocean Technology, 14 (2–3): 85–109.

    Article  Google Scholar 

  • Young, D. L., Chen, K. H., and Lee, C. W., 2005. Novel meshless method for solving the potential problems with arbitrary domains. Journal of Computational Physics, 209 (1): 290–321.

    Article  Google Scholar 

  • Young, D. L., Fan, C. M., Tsai, C. C., and Chen, C. W., 2006. The method of fundamental solutions and domain decomposition method for degenerate seepage flownet problems. Journal of the Chinese Institute of Engineers, 29 (1): 63–73.

    Article  Google Scholar 

  • Zhao, Y., Li, H. J., and Liu, Y., 2017. Oblique wave scattering by a submerged porous breakwater with a partially reflecting sidewall. Journal of Marine Science and Technology, 25 (4): 383–392.

    Google Scholar 

Download references

Acknowledgement

This paper is supported by the Ministry of Higher Education and Scientific Research of Algeria (grant PRFU number A01L06UN310220200002).

Author information

Authors and Affiliations

  1. Department of Hydraulics, University of Sidi Bel-Abbes, Sidi Bel-Abbes, 22000, Algeria

    Nadji Chioukh

  2. Laboratory of Civil Engineering and Environment, University of Sidi Bel-Abbes, Sidi Bel-Abbes, 22000, Algeria

    Nadji Chioukh

  3. Laboratory of Hydraulics and Coastal Engineering, Yildiz Technical University, Esenler-Istanbul, 34220, Turkey

    Yalçın Yüksel

Authors
  1. Nadji Chioukh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yalçın Yüksel
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nadji Chioukh.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chioukh, N., Yüksel, Y. Meshless Method with Domain Decomposition for Submerged Porous Breakwaters in Waves. J. Ocean Univ. China 20, 1325–1340 (2021). https://doi.org/10.1007/s11802-021-4563-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11802-021-4563-0

Key words

Search

Navigation