Abstract
The paper develops a set of quantified temporal alethic boulesic doxastic systems. Every system in this set consists of five parts: a ‘quantified’ part, a temporal part, a modal (alethic) part, a boulesic part and a doxastic part. There are no systems in the literature that combine all of these branches of logic. Hence, all systems in this paper are new. Every system is defined both semantically and proof-theoretically. The semantic apparatus consists of a kind of \(T \times W\) models, and the proof-theoretical apparatus of semantic tableaux. The ‘quantified part’ of the systems includes relational predicates and the identity symbol. The quantifiers are, in effect, a kind of possibilist quantifiers that vary over every object in the domain. The tableaux rules are classical. The alethic part contains two types of modal operators for absolute and historical necessity and possibility. According to ‘boulesic logic’ (the logic of the will), ‘willing’ (‘consenting’, ‘rejecting’, ‘indifference’ and ‘non-indifference’) is a kind of modal operator. Doxastic logic is the logic of beliefs; it treats ‘believing’ (and ‘conceiving’) as a kind of modal operator. I will explore some possible relationships between these different parts, and investigate some principles that include more than one type of logical expression. I will show that every tableau system in the paper is sound and complete with respect to its semantics. Finally, I consider an example of a valid argument and an example of an invalid sentence. I show how one can use semantic tableaux to establish validity and invalidity and read off countermodels. These examples illustrate the philosophical usefulness of the systems that are introduced in this paper.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The purpose of this paper is to develop a set of quantified temporal alethic boulesic doxastic systems. Every system is semantically defined by some class of \(T \times W\) models. According to a \(T \times W\) model, both worlds and times are basic and truth is relativised to world-moment pairs. Hence, a sentence may be true at some world-moment pairs and false at others. For more on the \(T \times W\) approach, see, for example [113, 115]. Our proof theory is built on semantic tableaux. I will introduce a set of semantic tableau systems and prove that they are sound and complete with respect to their semantics. Every quantified temporal alethic boulesic doxastic system includes five parts: a ‘quantified’ part, a temporal part, a modal (alethic) part, a boulesic part and a doxastic part. The quantified, temporal and modal parts are well-known. The doxastic part of the systems is quite different from standard doxastic logic, while boulesic logic is a ‘new’ kind of logic that deals with ‘boulesic’ expressions, such as ‘wants’ and ‘consents’. Some interactions between the different parts of the systems have been investigated, for example between alethic and temporal logic, and between predicate and modal logic (see below for references). Still, as far as I know, there are no systems in the literature that combine all these different parts. Consequently, all systems in this paper are new. Since most of the different parts are well-known, I will focus on the combination of the various components.Footnote 1
The ‘quantified part’ of the systems in this paper consists of relational predicate logic with identity. The quantifiers are, in effect, a kind of ‘possibilist’ quantifiers that varies over every entity in the domain. The domain of entities is the same in every world-moment pair even though different things can exist in different world-moment pairs. Each system includes a universal quantifier, \(\Pi \) (‘everything’), and a particular quantifier, \(\Sigma \) (‘something’). In every system, it is possible to define a pair of ‘actualist’ quantifiers in terms of the possibilist quantifiers and an existence predicate. In every world-moment pair the actualist quantifiers vary over everything that exists in this pair, so to speak. For introductions to predicate logic, see, for example [19, 26, 32, 59, 96].
Every system contains several temporal operators, for example \({\mathbb {A}}\) (always), \({\mathbb {S}}\) (sometimes), \({\mathbb {G}}\) (always in the future), \({\mathbb {F}}\) (sometime in the future), \({\mathbb {H}}\) (always in the past) and \({\mathbb {P}}\) (sometime in the past). See [14, 22, 35, 44, 65, 80, 85, 86] for some introductions to temporal logic.
The modal part of our systems includes two types of modal operators for absolute and historical necessity and possibility: \(U\) (absolute necessity), \(M\) (absolute possibility),  (historical necessity) and
(historical necessity) and  (historical possibility). For more on modal logic, see, for example [16, 17, 25, 34, 36, 38, 41, 56, 57, 64, 69, 93, 104, 105, 107, 121].
(historical possibility). For more on modal logic, see, for example [16, 17, 25, 34, 36, 38, 41, 56, 57, 64, 69, 93, 104, 105, 107, 121].
Every system includes a doxastic part. Doxastic logic is ‘the logic of belief’; it deals with ‘doxastic’ attitudes such as believing and conceiving or imagining. However, the kind of doxastic logic that is used in this paper is quite different from standard systems that can be found in the literature. Every system in this paper includes two doxastic operators: \({\mathcal {B}}\) (believing) and \({\mathcal {C}}\) (conceiving). \({\mathcal {B}}\) and \({\mathcal {C}}\) are two sentential operators that take individual terms and formulas as arguments and generate formulas as values. The expression \({\mathcal {B}}_{d}A\) reads as ‘individual d believes that it is the case that A’, while the expression \({\mathcal {C}}_{d}A\) reads as ‘it is conceivable to d that A’ or ‘it is imaginable to d that A’. For more information on ordinary doxastic (and epistemic) logic and many relevant references, see, for example [2, 7, 33, 39, 43, 47, 48, 51, 66,67,68, 76, 87, 106, 109, 111, 112]. The history of this branch of logic is discussed in [18, 63], and [6, 43, 61, 97] include information about the relationship between knowledge and belief. I focus on the concept of belief in this paper. For reasons why this approach to doxastic logic is attractive, see [89].
Boulesic logic, ‘the logic of the will’, is a new kind of logic. It is introduced by [91] and deals with ‘boulesic’ attitudes such as wanting and accepting or consenting. Every system includes five boulesic operators \({\mathcal {W}}\), \({\mathcal {A}}\), \({\mathcal {R}}\), \({\mathcal {I}}\) and \({\mathcal {N}}\), five sentential operators that take individual terms and formulas as arguments and generate formulas as values. The expression \({\mathcal {W}}_{d}B\) reads as ‘individual d wants it to be the case that B’, the expression \({\mathcal {A}}_{d}B\) reads as ‘d accepts that (it is the case that) B’ or ‘d consents to the state of affairs (the idea) that B’, the expression \({\mathcal {R}}_{d}B\) reads as ‘d rejects (disapproves, objects to, condemns) (the state of affairs that) B’, the expression \({\mathcal {I}}_{d}B\) reads as ‘d is indifferent towards (the state of affairs that) B’, and the expression \({\mathcal {N}}_{d}B\) reads as ‘d is non-indifferent towards (the state of affairs that) B’. There are some similarities between boulesic logic and so-called ‘intentional logic’, which deals with people’s intentions. For more on intentional logic, see, for example [20, 21, 28, 72, 74, 94]. See [42] (Chapter 10), [62, 73] for some other vaguely similar ideas. However, there are also many important differences. According to boulesic logic, almost nothing of interest follows from the proposition that someone wants something (or has some other boulesic attitude towards something), unless we assume that this individual is (perfectly) rational or wise. Nevertheless, we can derive all sorts of interesting consequences from the statement that an individual wants something (or has some other boulesic attitude towards something) if we assume that this individual is (perfectly) rational or wise. Different interpretations of the concept of rationality entail different consequences. Exactly what follows depend on what conditions we choose to impose on the so-called boulesic accessibility relation in our semantic models (see Sect. 3.3). For an introduction to various philosophical views on rationality, see, for example [75]. For reasons why we should be interested in boulesic logic, see [91].
As I have already mentioned, the various parts of the systems in this paper have been investigated before, as have some possible relations between them. Logicians have, for example developed systems that combine temporal logic and modal logic, epistemic (doxastic) logic and temporal logic, predicate logic and modal logic, and predicate logic and epistemic (doxastic) logic. Various attempts to combine modal logic and temporal logic can be found in, for example [27, 31, 103, 122]. For more on how to incorporate time in epistemic and doxastic logic, see, for example [33] (Section 4.3 and Chapter 8) and [76] (Section 2.14), and for some different approaches to temporal epistemic logic, see, for example [1, 45, 47, 52, 58, 60, 77, 92, 108]. For some ideas on how to combine modal logic and predicate logic, see, for example [13, 23, 29, 36, 40, 41, 50, 56, 57, 70, 71, 82, 84, 98,99,100]. Short introductions to first-order epistemic logic can be found in [33, pp. 80–91] and [76, pp. 225–229].Footnote 2 However, there are many interesting connections that have not been studied at all and, as far as I know, there are no systems in the literature that combine all the different parts explored in this paper. All the systems we will introduce are, therefore, new. Consequently, there are good logical reasons to be interested in the formal parts of this paper. There are also many philosophical reasons to explore the systems that I will introduce. I cannot discuss all these reasons, but I will mention three of the most striking ones.
Reason 1. We seem to need quantified temporal alethic boulesic doxastic logic to be able to adequately symbolise and evaluate many philosophically interesting principles. Consider the following example:
Principle 1. For every individual x, if x is perfectly rational then x wants it to be the case that A sometime in the future only if x believes that it is possible that it will be the case that A sometime in the future.
This principle can be symbolised in the following way in our systems:  .
.  is a theorem in every system that includes \(T-{\mathcal {W}}{\mathcal {B}}D\) and is valid in every model that satisfies \(C-{\mathcal {W}}{\mathcal {B}}D\). It is an instance of the following schema
is a theorem in every system that includes \(T-{\mathcal {W}}{\mathcal {B}}D\) and is valid in every model that satisfies \(C-{\mathcal {W}}{\mathcal {B}}D\). It is an instance of the following schema  (\({\mathcal {W}}{\mathcal {B}}D\)). Note that Principle 1 includes a quantifier expression (‘For every individual x’), a boulesic expression (‘x wants it to be the case that’), a temporal expression (‘sometime in the future’), a doxastic expression (‘x believes that’) and a modal (alethic) expression (‘it is possible that’). So, we need a system of the kind introduced in this paper to adequately symbolise it.
(\({\mathcal {W}}{\mathcal {B}}D\)). Note that Principle 1 includes a quantifier expression (‘For every individual x’), a boulesic expression (‘x wants it to be the case that’), a temporal expression (‘sometime in the future’), a doxastic expression (‘x believes that’) and a modal (alethic) expression (‘it is possible that’). So, we need a system of the kind introduced in this paper to adequately symbolise it.
Here is another example:
Principle 2. For every individual x, if x is perfectly rational then x wants it to be the case that B sometime in the future if x wants it to be the case that A sometime in the future and x believes that it is necessary that it is always going to be the case that A implies B.
Principle 2 can be symbolised in the following way in our systems:  . This principle is a theorem in every system that includes \(T-{\mathcal {B}}N{\mathcal {W}}\) and is valid in every model that satisfies \(C-{\mathcal {B}}N{\mathcal {W}}\).
. This principle is a theorem in every system that includes \(T-{\mathcal {B}}N{\mathcal {W}}\) and is valid in every model that satisfies \(C-{\mathcal {B}}N{\mathcal {W}}\).  is similar to the following principle,
is similar to the following principle,  , which is one version of the so-called hypothetical imperative (see Sect. 3.3 for more on this). Again, note that Principle 2 includes a quantifier expression (‘For every individual x’), a boulesic expression (‘x wants it to be the case that’), two temporal expressions (‘sometime in the future’ and ‘it is always going to be the case that’), a doxastic expression (‘x believes that’) and a modal (alethic) expression (‘it is necessary that’). Hence, we need a system of the kind introduced in this paper to adequately symbolise Principle 2.
, which is one version of the so-called hypothetical imperative (see Sect. 3.3 for more on this). Again, note that Principle 2 includes a quantifier expression (‘For every individual x’), a boulesic expression (‘x wants it to be the case that’), two temporal expressions (‘sometime in the future’ and ‘it is always going to be the case that’), a doxastic expression (‘x believes that’) and a modal (alethic) expression (‘it is necessary that’). Hence, we need a system of the kind introduced in this paper to adequately symbolise Principle 2.
Reason 2. We can use the systems in this paper to find countermodels to some propositions that are intuitively invalid. Consider the following sentence:
The bar exam. For every individual x, if x wants to become a lawyer sometime in the future and x believes that it is necessary that x will become a lawyer sometime in the future only if x will pass the bar exam sometime in the future, then x wants to pass the bar exam sometime in the future.
‘The bar exam’ is a proposition that can be symbolised in the following way in our systems:  , where the interpretation of the predicates should be obvious. Even though
, where the interpretation of the predicates should be obvious. Even though  is a theorem (in some systems),
is a theorem (in some systems),  is not a theorem in any system in this paper and is not valid in any class of models we consider. If someone is not perfectly rational, she may want A even though she does not want everything that she believes is a necessary means to A. So, this is intuitively plausible. In Sect. 7, I will show how we can prove that
is not a theorem in any system in this paper and is not valid in any class of models we consider. If someone is not perfectly rational, she may want A even though she does not want everything that she believes is a necessary means to A. So, this is intuitively plausible. In Sect. 7, I will show how we can prove that  is invalid in the class of all models and how one can use semantic tableaux to construct countermodels to invalid sentences. Again, we need all parts of our systems to adequately symbolise ‘The bar exam’. This is a good reason to be interested in the systems in this paper.
is invalid in the class of all models and how one can use semantic tableaux to construct countermodels to invalid sentences. Again, we need all parts of our systems to adequately symbolise ‘The bar exam’. This is a good reason to be interested in the systems in this paper.
Reason 3. We appear to need systems of the kind in this paper to prove that certain intuitively valid arguments are valid.
Consider the following example:
The perpetuum mobile argument
P1. John believes that it is necessary that it is always going to be the case that he will not build a perpetuum mobile.
P2. For every x, if x is perfectly rational, then x wants to build a perpetuum mobile sometime in the future only if x believes that it is possible that x will build a perpetuum mobile sometime in the future.
P3. For every x, if x is perfectly rational, then if x believes that it is possible that x will build a perpetuum mobile sometime in the future, then x does not believe that it is impossible that x will build a perpetuum mobile sometime in the future.
Hence,
C. If John is perfectly rational, he accepts the fact that he will never build a perpetuum mobile sometime in the future.
Intuitively, this argument is valid. It appears to be necessary that if the premises are true then the conclusion is true. That an argument is valid does not necessarily mean that it is sound; a valid argument can have false premises. So, I am not primarily interested in the soundness of the argument. However, (P2) and (P3) are theorems in some systems in this paper (see Sect. 7). So, given certain assumptions, we can prove that at least (P2) and (P3) are true. (P2) is an instance of Principle 1 above. (P3) follows from the proposition that no perfectly rational individual believes both A and not-A (at one and the same time), which is an intuitively plausible principle. Note that the argument includes a doxastic expression (‘believes’), a modal expression (‘it is necessary that’), two temporal expressions (‘it is always going to be the case that’ and ‘sometime in the future’), a quantifier expression (‘For every x’) and two boulesic expressions (‘wants’ and ‘accepts’). Consequently, to prove that the argument is valid we need a system that includes all of these parts. Since there are no systems of this kind in the literature, this is a good reason to be interested in the results in this paper. In Sect. 7, I will show how we can use a semantic tableau to prove that the perpetuum mobile argument is valid in the class of all models.
I conclude that we have very good philosophical reasons to be interested in the systems in this paper.
The paper is divided into seven main sections. Section 2 deals with the syntax and Sect. 3 with the semantics of our systems. Section 4 describes the proof theory of our logics, while Sect. 5 includes some examples of theorems. Section 6 establishes the soundness and completeness of every system in the paper. Finally, in Sect. 7, I consider some examples of valid and invalid sentences and arguments.
2 Syntax
2.1 Alphabet
Terms: (i) A set of variables \(x_{1}\), \(x_{2}\), \(x_{3}\) \(\ldots \). (ii) A set of constants (rigid designators) \(k_{d_{1}}\), \(k_{d_{2}}\), \(k_{d_{3}}\), \(\ldots \). Predicates: (iii) For every natural number \(n > 0\), n-place predicate symbols \(P^{1}_{n}\), \(P^{2}_{n}\), \(P^{3}_{n}\) \(\ldots \). (iv) The monadic existence predicate E, and the monadic rationality predicate R. (v) The dyadic identity predicate (necessary identity) \(=\). Connectives: (vi) The primitive truth-functional connectives \(\lnot \) (negation), \(\wedge \) (conjunction), \(\vee \) (disjunction), \(\rightarrow \) (material implication) and \(\leftrightarrow \) (material equivalence). Operators: (vii) The alethic operators \(U\), \(M\),  and
and  . (viii) The temporal operators \({\mathbb {A}}\), \({\mathbb {S}}\), \({\mathbb {G}}\), \({\mathbb {F}}\), \({\mathbb {H}}\) and \({\mathbb {P}}\). (ix) The boulesic operators \({\mathcal {W}}\), \({\mathcal {A}}\), \({\mathcal {R}}\), \({\mathcal {I}}\) and \({\mathcal {N}}\). (x) The doxastic operators \({\mathcal {B}}\) and \({\mathcal {C}}\). Quantifiers: (xi) The (possibilist) quantifiers \(\Pi \) and \(\Sigma \). Parentheses: (xii) The brackets ) and (.
. (viii) The temporal operators \({\mathbb {A}}\), \({\mathbb {S}}\), \({\mathbb {G}}\), \({\mathbb {F}}\), \({\mathbb {H}}\) and \({\mathbb {P}}\). (ix) The boulesic operators \({\mathcal {W}}\), \({\mathcal {A}}\), \({\mathcal {R}}\), \({\mathcal {I}}\) and \({\mathcal {N}}\). (x) The doxastic operators \({\mathcal {B}}\) and \({\mathcal {C}}\). Quantifiers: (xi) The (possibilist) quantifiers \(\Pi \) and \(\Sigma \). Parentheses: (xii) The brackets ) and (.
x, y and z \(\ldots \) stand for arbitrary variables, a, b, c \(\ldots \) for arbitrary constants, and s and t for arbitrary terms (with or without primes or subscripts). For more on the set of constants, see Sect. 3.1. I will use \(F_{n}\), \(G_{n}\), \(H_{n}\) \(\ldots \) for arbitrary n-place predicates and I will omit the subscript if it can be read off from the context.
2.2 Language
The language \({\mathcal {L}}\) is defined in the following way: (i) Any constant or variable is a term. (ii) If \(t_{1},\ldots ,t_{n}\) are any terms and P is any n-place predicate, \(Pt_{1}\ldots t_{n}\) is an atomic formula. (iii) If t is a term, Et (‘t exists’) is an atomic formula and Rt (‘t is perfectly rational’) is an atomic formula. (iv) If s and t are terms, then \(s = t\) (‘s is identical with t’) is an atomic formula. (v) If A and B are formulas, so are \(\lnot A\), \((A\wedge B)\), \((A\vee B)\), \((A\rightarrow B)\) and \((A\leftrightarrow B)\). (vi) If A is a formula, so are \(UA\) (‘it is universally [or absolutely] necessary that A’), \(MA\) (‘it is universally [or absolutely] possible that A’),  (‘it is [historically] necessary that A’) and
(‘it is [historically] necessary that A’) and  (‘it is [historically] possible that A’). (vii) If B is a formula, so are \({\mathbb {A}}B\) (it is always the case that B), \({\mathbb {S}}B\) (it is sometimes the case that B), \({\mathbb {G}}B\) (it is always going to be the case that B), \({\mathbb {F}}B\) (it will some time [in the future] be the case that B), \({\mathbb {H}}B\) (it has always been the case that B) and \({\mathbb {P}}B\) (it was some time [in the past] the case that B). (viii) If D is any formula and t is any term, then \({\mathcal {W}}_{t}D\) (‘t wants it to be the case that (desires that) D’), \({\mathcal {A}}_{t}D\) (‘t accepts that (consents to the idea that, approves that, tolerates that, is willing that) (it is the case that) D’), \({\mathcal {R}}_{t}D\) (‘t rejects (disapproves, objects to, condemns) (the state of affairs that) D’), \({\mathcal {I}}_{t}D\) (‘t is indifferent towards (the state of affairs that) D’), \({\mathcal {N}}_{t}D\) (‘t is non-indifferent towards (the state of affairs that) D’), \({\mathcal {B}}_{t}D\) (‘t believes that D’), and \({\mathcal {C}}_{t}D\) (‘it is conceivable (doxastically possible) for t that D’) are formulas. (ix) If A is any formula and x is any variable, then \(\Pi xA\) (‘for every [possible] x: A’) and \(\Sigma xA\) (‘for some [possible] x: A’) are formulas. (x) Nothing else is a formula.
(‘it is [historically] possible that A’). (vii) If B is a formula, so are \({\mathbb {A}}B\) (it is always the case that B), \({\mathbb {S}}B\) (it is sometimes the case that B), \({\mathbb {G}}B\) (it is always going to be the case that B), \({\mathbb {F}}B\) (it will some time [in the future] be the case that B), \({\mathbb {H}}B\) (it has always been the case that B) and \({\mathbb {P}}B\) (it was some time [in the past] the case that B). (viii) If D is any formula and t is any term, then \({\mathcal {W}}_{t}D\) (‘t wants it to be the case that (desires that) D’), \({\mathcal {A}}_{t}D\) (‘t accepts that (consents to the idea that, approves that, tolerates that, is willing that) (it is the case that) D’), \({\mathcal {R}}_{t}D\) (‘t rejects (disapproves, objects to, condemns) (the state of affairs that) D’), \({\mathcal {I}}_{t}D\) (‘t is indifferent towards (the state of affairs that) D’), \({\mathcal {N}}_{t}D\) (‘t is non-indifferent towards (the state of affairs that) D’), \({\mathcal {B}}_{t}D\) (‘t believes that D’), and \({\mathcal {C}}_{t}D\) (‘it is conceivable (doxastically possible) for t that D’) are formulas. (ix) If A is any formula and x is any variable, then \(\Pi xA\) (‘for every [possible] x: A’) and \(\Sigma xA\) (‘for some [possible] x: A’) are formulas. (x) Nothing else is a formula.
The concepts of bound and free variables, and open and closed formulas, are defined in the usual way. A, B, C \(\ldots \) stand for arbitrary formulas, and \(\Gamma \), \(\Phi \) \(\ldots \) for finite sets of closed formulas. \(A[a_{1}, \ldots , a_{n}/x_{1}, \ldots , x_{n}]\) is the result of replacing every free occurrence of \(x_{1}\) by \(a_{1}\), and \(\ldots \), and every free occurrence of \(x_{n}\) by \(a_{n}\) in A. \(A[a_{1}, \ldots , a_{n}/x_{1}, \ldots , x_{n}]\) will be abbreviated as \(A[a_{1}, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}]\). A[t/x] is the formula obtained by substituting t for every free occurrence of x in A. The definitions are standard. Brackets around formulas are usually dropped if the result is not ambiguous.
Definition 1
(Operators and quantifiers) Temporal operators: \(\underline{{\mathbb {G}}} A\) (‘it is and it is always going to be the case that A’) \(=_{df}\) \((A \wedge {\mathbb {G}} A)\); \(\underline{{\mathbb {H}}} A\) (‘it is and it has always been the case that A’) \(=_{df}\) \((A \wedge {\mathbb {H}} A)\); \(\underline{{\mathbb {F}}} A\) (‘it is or it will some time in the future be the case that A’) \(=_{df}\) \((A \vee {\mathbb {F}} A)\); \(\underline{{\mathbb {P}}} A\) (‘it is or it has some time in the past been the case that A’) \(=_{df}\) \((A \vee {\mathbb {P}} A)\). Actualist quantifiers: \(\forall xA\) (‘for every existing x A’) \(=_{df}\) \(\Pi x(Ex\rightarrow A)\) and \(\exists xA\) (‘for some existing x \(A') =_{df} \Sigma x(Ex\wedge A)\).
3 Semantics
3.1 Models
Definition 2
(Models) A model \({\mathcal {M}}\) is a relational structure \(\left\langle D, W, T, <, {\mathfrak {R}}, {\mathfrak {A}}, {\mathfrak {D}}, v\right\rangle \), where D is a non-empty set of individuals (the domain), W is a non-empty set of possible worlds, T is a non-empty set of times, < is a binary relation on T (< is a subset of \(T \times T\)), \({\mathfrak {R}}\) is a ternary alethic accessibility relation (\({\mathfrak {R}}\) is a subset of \(W \times W \times T\)), \({\mathfrak {A}}\) is a four-place boulesic accessibility relation (\({\mathfrak {A}}\) is a subset of \(D \times W \times W \times T\)), \({\mathfrak {D}}\) is a four-place doxastic accessibility relation (\({\mathfrak {D}}\) is a subset of \(D \times W \times W \times T\)), and v is an interpretation function.
\({\mathfrak {R}}\) is used in the definition of the truth conditions for sentences that begin with the alethic operators  and
and  , \({\mathfrak {A}}\) is used in the definition of the truth conditions for sentences that begin with the boulesic operators \({\mathcal {W}}\), \({\mathcal {A}}\), \({\mathcal {R}}\), \({\mathcal {I}}\) and \({\mathcal {N}}\), \({\mathfrak {D}}\) is used in the definition of the truth conditions for sentences that begin with the doxastic operators \({\mathcal {B}}\) and \({\mathcal {C}}\), and < is used to define the truth conditions for sentences that begin with the temporal operators. Intuitively, \(\tau < \tau '\) says that the time \(\tau \) is before the time \(\tau '\), \({\mathfrak {R}}\omega \omega '\tau \) says that the possible world \(\omega '\) is alethically (historically) accessible from the possible world \(\omega \) at the time \(\tau \), \({\mathfrak {A}}\delta \omega \omega '\tau \) says that the possible world \(\omega '\) is boulesically accessible (acceptable) to the individual \(\delta \) in (or relative to) the possible world \(\omega \) at the time \(\tau \), or that \(\delta \) accepts \(\omega '\) in (or relative to) \(\omega \) at \(\tau \), and \({\mathfrak {D}}\delta \omega \omega '\tau \) says that the possible world \(\omega '\) is doxastically accessible (conceivable) to the individual \(\delta \) in (or relative to) the possible world \(\omega \) at the time \(\tau \).
, \({\mathfrak {A}}\) is used in the definition of the truth conditions for sentences that begin with the boulesic operators \({\mathcal {W}}\), \({\mathcal {A}}\), \({\mathcal {R}}\), \({\mathcal {I}}\) and \({\mathcal {N}}\), \({\mathfrak {D}}\) is used in the definition of the truth conditions for sentences that begin with the doxastic operators \({\mathcal {B}}\) and \({\mathcal {C}}\), and < is used to define the truth conditions for sentences that begin with the temporal operators. Intuitively, \(\tau < \tau '\) says that the time \(\tau \) is before the time \(\tau '\), \({\mathfrak {R}}\omega \omega '\tau \) says that the possible world \(\omega '\) is alethically (historically) accessible from the possible world \(\omega \) at the time \(\tau \), \({\mathfrak {A}}\delta \omega \omega '\tau \) says that the possible world \(\omega '\) is boulesically accessible (acceptable) to the individual \(\delta \) in (or relative to) the possible world \(\omega \) at the time \(\tau \), or that \(\delta \) accepts \(\omega '\) in (or relative to) \(\omega \) at \(\tau \), and \({\mathfrak {D}}\delta \omega \omega '\tau \) says that the possible world \(\omega '\) is doxastically accessible (conceivable) to the individual \(\delta \) in (or relative to) the possible world \(\omega \) at the time \(\tau \).
The valuation function v assigns every constant c in \({\mathcal {L}}\) an element v(c) of D, and each world-moment pair, \(\left\langle \omega , \tau \right\rangle \), and n-place predicate, P, in \({\mathcal {L}}\) a subset, \(v_{\omega \tau }(P)\), of \(D^{n}\). That is, \(v_{\omega \tau }(P)\) (the extension of P in \(\omega \) at \(\tau \)) is the set of n-tuples that satisfy P in the world \(\omega \) at time \(\tau \) (in the world-moment pair \(\left\langle \omega , \tau \right\rangle \)). Accordingly, every constant is a ‘rigid designator’: it refers to the same individual in every world-moment pair. Note, however, that the extension of a predicate may change from world-moment pair to world-moment pair and that it may be empty in a world-moment pair. The language of the model \({\mathcal {M}}\), \(\mathcal {L(M)}\), is obtained by adding a constant \(k_{d}\), such that \(v(k_{d}) = d\), to the language for every member \(d \in D\). It follows that every object in the domain of a model has at least one name in our language and that several different constants may refer to one and the same object.
The predicate R in \({\mathcal {L}}\) is special. Intuitively, ‘Rc’ says that the individual c is perfectly rational, perfectly reasonable or perfectly wise. If v(c) is in the extension of R in the world-moment pair \(\left\langle \omega , \tau \right\rangle \), then v(c) is perfectly rational, reasonable or wise in the world \(\omega \) at the time \(\tau \), that is, in the world-moment pair \(\left\langle \omega , \tau \right\rangle \). Exactly what this entails will depend on the conditions we impose on the boulesic accessibility relation \({\mathfrak {A}}\) and the doxastic accessibility relation \({\mathfrak {D}}\) (Sect. 3.3). R functions as an ordinary predicate. Accordingly, an individual \(\delta \) may be in R’s extension in one world-moment pair even though \(\delta \) is not in R’s extension in every world-moment pair. It follows that the fact that an individual \(\delta \) is perfectly rational, reasonable or wise in one world-moment pair does not entail that \(\delta \) is perfectly rational, reasonable or wise in every world-moment pair. It is possible to add the assumption that every perfectly rational individual is necessarily perfectly rational to every system in this paper (the semantic condition \(C-UR\) guarantees that this is the case: see Table 16 in Sect. 3.3), but this assumption is not built into any system. We will see that R plays an important role in the definitions of the truth conditions for sentences of the forms \({\mathcal {W}}_{a}D\), \({\mathcal {A}}_{a}D\), \({\mathcal {R}}_{a}D\), \({\mathcal {I}}_{a}D\), \({\mathcal {N}}_{a}D\), \({\mathcal {B}}_{a}D\) and \({\mathcal {C}}_{a}D\) (see Sect. 3.2). Consequently, R is an important element in our systems in this paper.
Let A be a closed boulesic or doxastic formula of the form \({\mathcal {W}}_{a}D\), \({\mathcal {A}}_{a}D\), \({\mathcal {R}}_{a}D\), \({\mathcal {I}}_{a}D\), \({\mathcal {N}}_{a}D\), \({\mathcal {B}}_{a}D\) or \({\mathcal {C}}_{a}D\). Then, the matrix of A is constructed in the following way. Let m be the least number greater than every n such that \(x_{n}\) occurs bound in D. Replace every occurrence of an individual constant with \(x_{m}\), \(x_{m + 1}\), etc. (move from left to right). The result is the formula’s matrix. Here are some examples: the matrix of \({\mathcal {W}}_{a}Pcd\) is \({\mathcal {W}}_{x_{1}}Px_{2}x_{3}\); the matrix of \({\mathcal {B}}_{c}Paa\) is \({\mathcal {B}}_{x_{1}}Px_{2}x_{3}\); the matrix of \({\mathcal {W}}_{a}(Fa \leftrightarrow Gbc)\) is \({\mathcal {W}}_{x_{1}}(Fx_{2} \leftrightarrow Gx_{3}x_{4})\); the matrix of \({\mathcal {B}}_{a}{\mathcal {A}}_{b}\Pi x_{1}(Fx_{1} \vee Gc)\) is \({\mathcal {B}}_{x_{2}}{\mathcal {A}}_{x_{3}}\Pi x_{1}(Fx_{1} \vee Gx_{4})\); the matrix of \({\mathcal {W}}_{c}{\mathcal {W}}_{d}\Pi x_{2}(Fx_{2} \rightarrow \Sigma x_{3}Px_{3})\) is \({\mathcal {W}}_{x_{4}}{\mathcal {W}}_{x_{5}}\Pi x_{2}(Fx_{2} \rightarrow \Sigma x_{3}Px_{3})\), etc. For each world-moment pair, \(\left\langle \omega , \tau \right\rangle \), and n-place matrix M (of this kind) the valuation function v assigns a subset, \(v_{\omega \tau }(M)\), of \(D^{n}\). That is, if M is any matrix of the form \({\mathcal {W}}_{t}D\), \({\mathcal {A}}_{t}D\), \({\mathcal {R}}_{t}D\), \({\mathcal {I}}_{t}D\), \({\mathcal {N}}_{t}D\), \({\mathcal {B}}_{t}D\) or \({\mathcal {C}}_{t}D\) with free variables \(x_{1}, \ldots , x_{n}\), then \(v_{\omega \tau }(M) \subseteq D^{n}\). Note that M always contains at least one free variable. Let M be a matrix where \(x_{m}\) is the first free variable in M and \(a_{m}\) is the constant in \(M[a_{1}, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}]\) that replaces \(x_{m}\). Then, the truth conditions for closed boulesic and doxastic formulas of the form \(M[a_{1}, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}]\), when \(v_{\omega \tau }(Ra_{m}) = 0\), are defined in terms of the extension of M in \(\omega \) at \(\tau \) (see condition 2 in Sect. 3.2 below).Footnote 3
The extension of the identity predicate is the same in every possible world at every moment in time (in a model). It follows that all identities (and non-identities) are both absolutely and historically necessary, as well as eternal. The existence predicate E functions as other predicates in \({\mathcal {L}}\). The extension of this predicate can vary from one world-moment pair to another. ‘Ec’ is true in a world-moment pair just in case v(c) exists in this world-moment pair.
3.2 Truth Conditions and Some Semantic Concepts
Let \(\omega \in W\), \(\tau \in T\) in a model \({\mathcal {M}}\) \(=\) \(\left\langle D, W, T, <, {\mathfrak {R}}, {\mathfrak {A}}, {\mathfrak {D}}, v\right\rangle \) and let A be a well-formed sentence in \({\mathcal {L}}\). Then, \({\mathcal {M}}, \omega , \tau \Vdash A\) stands for ‘A is true in \(\omega \) at \(\tau \) in \({\mathcal {M}}\)’ (or ‘A is true in the pair \(\left\langle \omega , \tau \right\rangle \) in \({\mathcal {M}}\)’). \({\mathcal {M}}, \omega , \tau \nVdash A\) iff it is not true that \({\mathcal {M}}, \omega , \tau \Vdash A\), that is, \({\mathcal {M}}, \omega , \tau \nVdash A\) iff \({\mathcal {M}}, \omega , \tau \Vdash \lnot A\). ‘\(\forall \omega ' \in W\)’ is read as ‘for all possible worlds \(\omega '\) in W’; and ‘\(\exists \omega ' \in W\)’ is read as ‘for some possible world \(\omega '\) in W’, etc. Now, the truth conditions for various sentences in \({\mathcal {L}}\) can be defined in the following way (the truth conditions for the omitted formulas are straightforward):
-
1.
\({\mathcal {M}}, \omega , \tau \Vdash Pa_{1}\ldots a_{n}\) iff \(\left\langle v(a_{1}), \ldots , v(a_{n})\right\rangle \in v_{\omega \tau }(P)\).
-
2.
Let M be a matrix where \(x_{m}\) is the first free variable in M and \(a_{m}\) is the constant in \(M[a_{1}, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}]\) that replaces \(x_{m}\).
Then the truth conditions for closed boulesic and doxastic formulas of the form \(M[a_{1}, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}]\), when \(v(a_{m})\) is not an element in \(v_{\omega \tau }(R)\), are as follows:
\({\mathcal {M}}, \omega , \tau \Vdash M[a_{1}, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}]\) iff \(\left\langle v(a_{1}), \ldots , v(a_{n})\right\rangle \in v_{\omega \tau }(M)\).
-
3.
\({\mathcal {M}}, \omega , \tau \Vdash A \wedge B\) iff \({\mathcal {M}}, \omega , \tau \Vdash A\) and \({\mathcal {M}}, \omega , \tau \Vdash B\).
-
4.
\({\mathcal {M}}, \omega , \tau \Vdash UA\) iff \(\forall \omega ' \in W\) and \(\forall \tau ' \in T\): \({\mathcal {M}}, \omega ', \tau ' \Vdash A\).
-
5.
\({\mathcal {M}}, \omega , \tau \Vdash MA\) iff \(\exists \omega ' \in W\) and \(\exists \tau ' \in T\): \({\mathcal {M}}, \omega ', \tau ' \Vdash A\).
-
6.
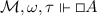 iff \(\forall \omega ' \in W\) s.t. \({\mathfrak {R}}\omega \omega '\tau \): \({\mathcal {M}}, \omega ', \tau \Vdash A\).
iff \(\forall \omega ' \in W\) s.t. \({\mathfrak {R}}\omega \omega '\tau \): \({\mathcal {M}}, \omega ', \tau \Vdash A\). -
7.
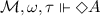 iff \(\exists \omega ' \in W\) s.t. \({\mathfrak {R}}\omega \omega '\tau \): \({\mathcal {M}}, \omega ', \tau \Vdash A\).
iff \(\exists \omega ' \in W\) s.t. \({\mathfrak {R}}\omega \omega '\tau \): \({\mathcal {M}}, \omega ', \tau \Vdash A\). -
8.
\({\mathcal {M}}, \omega , \tau \Vdash {\mathbb {A}}B\) iff \(\forall \tau ' \in T\): \({\mathcal {M}}, \omega , \tau ' \Vdash B\).
-
9.
\({\mathcal {M}}, \omega , \tau \Vdash {\mathbb {S}}B\) iff \(\exists \tau ' \in T\): \({\mathcal {M}}, \omega , \tau ' \Vdash B\).
-
10.
\({\mathcal {M}}, \omega , \tau \Vdash {\mathbb {G}}B\) iff \(\forall \tau ' \in T\) s.t. \(\tau < \tau '\): \({\mathcal {M}}, \omega , \tau ' \Vdash B\).
-
11.
\({\mathcal {M}}, \omega , \tau \Vdash {\mathbb {F}}B\) iff \(\exists \tau ' \in T\) s.t. \(\tau < \tau '\): \({\mathcal {M}}, \omega , \tau ' \Vdash B\).
-
12.
\({\mathcal {M}}, \omega , \tau \Vdash {\mathbb {H}}B\) iff \(\forall \tau ' \in T\) s.t. \(\tau ' < \tau \): \({\mathcal {M}}, \omega , \tau ' \Vdash B\).
-
13.
\({\mathcal {M}}, \omega , \tau \Vdash {\mathbb {P}}B\) iff \(\exists \tau ' \in T\) s.t. \(\tau ' < \tau \): \({\mathcal {M}}, \omega , \tau ' \Vdash B\).
-
14.
\({\mathcal {M}}, \omega , \tau \Vdash \Pi xA\) iff for all \(k_{d} \in \mathcal {L(M)}, {\mathcal {M}}, \omega , \tau \Vdash A[k_{d}/x]\).
-
15.
\({\mathcal {M}}, \omega , \tau \Vdash \Sigma xA\) iff for some \(k_{d} \in \mathcal {L(M)}, {\mathcal {M}}, \omega , \tau \Vdash A[k_{d}/x]\).
-
16.
\({\mathcal {M}}, \omega , \tau \Vdash {\mathcal {W}}_{a}D\) iff for all \(\omega '\) such that \({\mathfrak {A}}v(a)\omega \omega '\tau \): \({\mathcal {M}}, \omega ', \tau \Vdash D\), given that v(a) is an element in \(v_{\omega \tau }(R)\), if v(a) is not an element in \(v_{\omega \tau }(R)\), then \({\mathcal {W}}_{a}D\) is assigned a truth value in \(\omega \) at \(\tau \) in a way that does not depend on the value of D (see condition 2 above).
-
17.
\({\mathcal {M}}, \omega , \tau \Vdash {\mathcal {A}}_{a}D\) iff for at least one \(\omega '\) such that \({\mathfrak {A}}v(a)\omega \omega '\tau \): \({\mathcal {M}}, \omega ', \tau \Vdash D\), given that v(a) is an element in \(v_{\omega \tau }(R)\), if v(a) is not an element in \(v_{\omega \tau }(R)\), then \({\mathcal {A}}_{a}D\) is assigned a truth value in \(\omega \) at \(\tau \) in a way that does not depend on the value of D (see condition 2 above).
-
18.
\({\mathcal {M}}, \omega , \tau \Vdash {\mathcal {R}}_{a}D\) iff for all \(\omega '\) such that \({\mathfrak {A}}v(a)\omega \omega '\tau \): \({\mathcal {M}}, \omega ', \tau \Vdash \lnot D\), given that v(a) is an element in \(v_{\omega \tau }(R)\), if v(a) is not an element in \(v_{\omega \tau }(R)\), then \({\mathcal {R}}_{a}D\) is assigned a truth value in \(\omega \) at \(\tau \) in a way that does not depend on the value of D (see condition 2 above).
-
19.
\({\mathcal {M}}, \omega , \tau \Vdash {\mathcal {I}}_{a}D\) iff for at least one \(\omega '\) such that \({\mathfrak {A}}v(a)\omega \omega '\tau \): \({\mathcal {M}}, \omega ', \tau \Vdash D\) and for at least one \(\omega '\) such that \({\mathfrak {A}}v(a)\omega \omega '\tau \): \({\mathcal {M}}, \omega ', \tau \Vdash \lnot D\), given that v(a) is an element in \(v_{\omega \tau }(R)\), if v(a) is not an element in \(v_{\omega \tau }(R)\), then \({\mathcal {I}}_{a}D\) is assigned a truth value in \(\omega \) at \(\tau \) in a way that does not depend on the value of D (see condition 2 above).
-
20.
\({\mathcal {M}}, \omega , \tau \Vdash {\mathcal {N}}_{a}D\) iff for all \(\omega '\) such that \({\mathfrak {A}}v(a)\omega \omega '\tau \): \({\mathcal {M}}, \omega ', \tau \Vdash D\) or for all \(\omega '\) such that \({\mathfrak {A}}v(a)\omega \omega '\tau \): \({\mathcal {M}}, \omega ', \tau \Vdash \lnot D\), given that v(a) is an element in \(v_{\omega \tau }(R)\), if v(a) is not an element in \(v_{\omega \tau }(R)\), then \({\mathcal {N}}_{a}D\) is assigned a truth value in \(\omega \) at \(\tau \) in a way that does not depend on the value of D (see condition 2 above).
-
21.
\({\mathcal {M}}, \omega , \tau \Vdash {\mathcal {B}}_{a}D\) iff for all \(\omega '\) such that \({\mathfrak {D}}v(a)\omega \omega '\tau \): \({\mathcal {M}}, \omega ', \tau \Vdash D\), given that v(a) is an element in \(v_{\omega \tau }(R)\), if v(a) is not an element in \(v_{\omega \tau }(R)\), then \({\mathcal {B}}_{a}D\) is assigned a truth value in \(\omega \) at \(\tau \) in a way that does not depend on the value of D (see condition 2 above).
-
22.
\({\mathcal {M}}, \omega , \tau \Vdash {\mathcal {C}}_{a}D\) iff for at least one \(\omega '\) such that \({\mathfrak {D}}v(a)\omega \omega '\tau \): \({\mathcal {M}}, \omega ', \tau \Vdash D\), given that v(a) is an element in \(v_{\omega \tau }(R)\), if v(a) is not an element in \(v_{\omega \tau }(R)\), then \({\mathcal {C}}_{a}D\) is assigned a truth value in \(\omega \) at \(\tau \) in a way that does not depend on the value of D (see condition 2 above).
\(\Pi \) and \(\Sigma \) are ‘substitutional’, ‘possibilist’ quantifiers; they vary over every object in the domain since the domain is the same in every possible world and every object in the domain has a name (see Sect. 3.1).
Intuitively speaking, conditions 16–22 are interpreted in the following way. If v(a) is not perfectly rational in a world-moment pair, \({\mathcal {W}}_{a}D\), \({\mathcal {A}}_{a}D\), \({\mathcal {R}}_{a}D\), \({\mathcal {I}}_{a}D\), \({\mathcal {N}}_{a}D\), \({\mathcal {B}}_{a}D\) and \({\mathcal {C}}_{a}D\) behave as ordinary predicates in this world at this time; and if v(a) is perfectly rational in a world-moment pair, \({\mathcal {W}}_{a}D\), \({\mathcal {A}}_{a}D\), \({\mathcal {R}}_{a}D\), \({\mathcal {B}}_{a}D\) and \({\mathcal {C}}_{a}D\) behave as ordinary modal operators in this world at this time. If v(a) is perfectly rational in a world-moment pair, then \({\mathcal {I}}_{a}D\) is equivalent with \({\mathcal {A}}_{a}D \wedge {\mathcal {A}}_{a}\lnot D\) and \({\mathcal {N}}_{a}D\) is equivalent with \({\mathcal {W}}_{a}D \vee {\mathcal {W}}_{a}\lnot D\) in this world-moment pair.
We are now in a position to define some important semantic concepts.
Definition 3
(Semantic concepts) Satisfiability in a model: A set of sentences \(\Gamma \) is satisfiable in a model \({\mathcal {M}}\) iff there is a possible world \(\omega \) and moment in time \(\tau \) in \({\mathcal {M}}\) such that every sentence in \(\Gamma \) is true in \(\omega \) at \(\tau \). Validity in a class of models: A sentence A is valid in a class of models \({{\varvec{M}}}\) iff A is true in every world at every moment of time in every model in \({{\varvec{M}}}\). Logical consequence in a class of models: A sentence B is a logical consequence of a set of sentences \(\Gamma \) in a class of models \({{\varvec{M}}}\) (\({{\varvec{M}}}, \Gamma \Vdash B\)) iff for every model \({\mathcal {M}}\) in \({{\varvec{M}}}\) and world-moment pair \(\left\langle \omega , \tau \right\rangle \) in \({\mathcal {M}}\), if all elements of \(\Gamma \) are true in \(\left\langle \omega , \tau \right\rangle \) (in \(\omega \) at \(\tau \)) in \({\mathcal {M}}\), then B is true in \(\left\langle \omega , \tau \right\rangle \) (in \(\omega \) at \(\tau \)) in \({\mathcal {M}}\). If \({{\varvec{M}}}, \Gamma \Vdash B\), then \(\Gamma \) entails B in \({{\varvec{M}}}\) and the argument from \(\Gamma \) to B is valid in \({{\varvec{M}}}\). An argument is invalid (in \({{\varvec{M}}}\)) iff it is not valid (in \({{\varvec{M}}}\)).
3.3 Conditions on Models, Systems of Classes of Models and Logical Systems
A logical system can be defined as a set of sentences valid in a class of models. So, by imposing various constraints on the accessibility relations in a model, we can define a large set of classes of models that can be used to generate various logical systems. In this section, I will introduce some constraints of this kind. I will consider some formal properties of the accessibility relations, and I will mention some conditions that deal with some possible relationships between the various accessibility relations and with some possible relationships between the accessibility relations and the valuation function. Since our models include four different accessibility relations, there are sixteen possible types of interactions between these relations. It is not possible to consider all possible constraints, but I will consider some of the conditions that seem most interesting. It is not obvious exactly which conditions we should accept. It might be the case that different constraints are plausible for different purposes. The choice will depend on our interpretation of the concept of rationality (or wisdom). Some conditions might generate systems that include theorems that are philosophically or intuitively implausible. So, it is not necessarily the case that we should accept all constraints. Still, all conditions in this section are interesting and they are worth exploring further.
The conditions in this section are more or less self-explanatory. Nevertheless, I have added a few comments about some of the new clauses and I mention some formulas that are valid in various classes of models. There are many interesting relationships between the different constraints that I will not investigate in this paper. However, I will mention some interesting connections.
Table 1 includes information about some formal properties that might be imposed on the alethic accessibility relation. In normal modal logic, the alethic accessibility relation is a binary relation (see, for example [16, 25, 36, 41, 84]). In this paper, \({\mathfrak {R}}\) is treated as a 3-place relation. Intuitively, this means that the ordinary alethic accessibility relation is relativised to particular moments in time. A possible world \(\omega '\) can be alethically accessible from a possible world \(\omega \) at one moment in time, even though \(\omega '\) is not alethically accessible from \(\omega \) at another moment in time. ‘C’ in ‘\(C-aT\)’ is an abbreviation of ‘condition’ and ‘a’ stands for for ‘alethic’. \(C-aT\) is a 3-place version of the well-known condition T in ordinary modal logic. According to \(C-aD\), the alethic accessibility relation \({\mathfrak {R}}\) is serial at every moment in time; according to \(C-a4\), \({\mathfrak {R}}\) is transitive at every moment in time, etc. If it is clear from the context that we are talking about a semantic condition and not, for example a tableau rule, I will often omit the initial C. It is normally binary relations that are called serial, transitive, Euclidean, etc. However, in this section, I will extend these concepts to 3-place and 4-place relations. If \({\mathfrak {R}}\) satisfies \(C-aT\), I will call \({\mathfrak {R}}\) reflexive, and so on.
The conditions in Table 2 are well-known. They mention some possible restrictions on the temporal relation ‘earlier than’, <, in a model. ‘PD’ is an abbreviation of ‘past D’, ‘FD’ of ‘future D’, ‘DE’ of ‘dense’, ‘FC’ of ‘future convergence’, ‘PC’ of ‘past convergence’, ‘C’ of ‘comparability’, ‘UB’ of ‘upper bounds’, and ‘LB’ of ‘lower bounds’. According to \(C-t4\), time is transitive; according to \(C-C\) time is ‘comparable’, etc. Most introductions to temporal logic mention the conditions in Table 2 (see, for example [14, 22, 35, 44, 65, 80, 85, 86]). Therefore, I will not discuss them any further in this paper.
The conditions in Table 3 deal with the boulesic accessibility relation (‘b’ stands for ‘boulesic’). \({\mathfrak {A}}\) is a 4-place relation; intuitively, \({\mathfrak {A}}\delta \omega \omega '\tau \) says that the possible world \(\omega '\) is boulesically accessible from the possible world \(\omega \) to the individual \(\delta \) at the time \(\tau \). We can think of this as a 2-place boulesic accessibility relation that is relativised to individuals and moments in time. A possible world \(\omega '\) can be boulesically accessible from a possible world \(\omega \) to individual \(\delta \) at one moment in time even though \(\omega '\) is not boulesically accessible from \(\omega \) to \(\delta \) at every moment in time. And (if we do not impose any restrictions on the boulesic accessibility relation), \(\omega '\) can be boulesically accessible from \(\omega \) to individual \(\delta \) at a moment in time \(\tau \) even though \(\omega '\) is not boulesically accessible from \(\omega \) to another individual \(\delta '\) at \(\tau \).
According to condition \(C-bD\), it is true that for every (individual) \(\delta \), for every (moment in time) \(\tau \) and for every (possible world) \(\omega \) there is a (possible world) \(\omega '\) such that \(\delta \) accepts \(\omega '\) in \(\omega \) at \(\tau \). In other words, according to this condition, every individual always accepts at least one possible world at every moment in time, no matter what situation she is in. In every model that satisfies this condition, the following schema is valid: \(\Pi x (Rx \rightarrow \lnot ({\mathcal {W}}_{x} B \wedge {\mathcal {W}}_{x} \lnot B))\). Intuitively, this formula says that someone is perfectly rational only if she has no contradictory wants. More precisely, the formula says that if an individual x is perfectly rational, then it is not the case that x wants it to be the case that B at the same time that x wants it to be the case that not-B. This principle is intuitively reasonable.
Let \({\mathcal {M}}\) be a model that satisfies \(C-UR\), or  and \(C-FT\) or \(C-FTR\) (see Tables 5, 16). Then, if \({\mathcal {M}}\) satisfies \(C-b4\), \(\Pi x (Rx \rightarrow ({\mathcal {W}}_{x} B \rightarrow {\mathcal {W}}_{x} {\mathcal {W}}_{x} B))\) is valid in \({\mathcal {M}}\); if \({\mathcal {M}}\) satisfies \(C-b5\), \(\Pi x (Rx \rightarrow ({\mathcal {A}}_{x} B \rightarrow {\mathcal {W}}_{x} {\mathcal {A}}_{x} B))\) and \(\Pi x (Rx \rightarrow (\lnot {\mathcal {W}}_{x} B \rightarrow {\mathcal {W}}_{x} \lnot {\mathcal {W}}_{x} B))\) are valid in \({\mathcal {M}}\); if \({\mathcal {M}}\) satisfies \(C-{\mathcal {W}}bT\), \(\Pi x (Rx \rightarrow {\mathcal {W}}_{x}({\mathcal {W}}_{x} B \rightarrow B))\) is valid in \({\mathcal {M}}\); if \({\mathcal {M}}\) satisfies \(C-{\mathcal {W}}bD\), \(\Pi x (Rx \rightarrow {\mathcal {W}}_{x}({\mathcal {W}}_{x} B \rightarrow \lnot {\mathcal {W}}_{x} \lnot B))\) is valid in \({\mathcal {M}}\); and if \({\mathcal {M}}\) satisfies \(C-{\mathcal {W}}bB\), \(\Pi x (Rx \rightarrow {\mathcal {W}}_{x}(B \rightarrow {\mathcal {W}}_{x} {\mathcal {A}}_{x} B))\) is valid in \({\mathcal {M}}\). \(\Pi x (Rx \rightarrow ({\mathcal {W}}_{x} B \rightarrow {\mathcal {W}}_{x} {\mathcal {W}}_{x} B))\) says that if x is perfectly rational, then if x wants it to be the case that B then x wants it to be the case that x wants it to be the case that B. So, according to this formula, a perfectly rational individual does not want to ‘get rid’ of any of her wants. \(\Pi x (Rx \rightarrow (\lnot {\mathcal {W}}_{x} B \rightarrow {\mathcal {W}}_{x} \lnot {\mathcal {W}}_{x} B))\) says that if x is perfectly rational, then if x does not want it to be the case that B then x wants it to be the case that x does not want it to be the case that B. Hence, according to this formula, a perfectly rational individual does not want to ‘add’ any new wants to the set of all her wants. Of course, \(\Pi x (Rx \rightarrow ({\mathcal {W}}_{x} B \rightarrow {\mathcal {W}}_{x} {\mathcal {W}}_{x} B))\) is compatible with the claim that a perfectly rational individual wants to get rid of some wants in the future, and \(\Pi x (Rx \rightarrow (\lnot {\mathcal {W}}_{x} B \rightarrow {\mathcal {W}}_{x} \lnot {\mathcal {W}}_{x} B))\) is compatible with the proposition that a perfectly rational individual wants to add wants to the set of all her wants in the future. However, at the moment when a perfectly rational individual wants something she wants to want it according to \(\Pi x (Rx \rightarrow ({\mathcal {W}}_{x} B \rightarrow {\mathcal {W}}_{x} {\mathcal {W}}_{x} B))\); and at the moment when a perfectly rational individual does not want something she wants it to be the case that she does not want it according to \(\Pi x (Rx \rightarrow (\lnot {\mathcal {W}}_{x} B \rightarrow {\mathcal {W}}_{x} \lnot {\mathcal {W}}_{x} B))\).
and \(C-FT\) or \(C-FTR\) (see Tables 5, 16). Then, if \({\mathcal {M}}\) satisfies \(C-b4\), \(\Pi x (Rx \rightarrow ({\mathcal {W}}_{x} B \rightarrow {\mathcal {W}}_{x} {\mathcal {W}}_{x} B))\) is valid in \({\mathcal {M}}\); if \({\mathcal {M}}\) satisfies \(C-b5\), \(\Pi x (Rx \rightarrow ({\mathcal {A}}_{x} B \rightarrow {\mathcal {W}}_{x} {\mathcal {A}}_{x} B))\) and \(\Pi x (Rx \rightarrow (\lnot {\mathcal {W}}_{x} B \rightarrow {\mathcal {W}}_{x} \lnot {\mathcal {W}}_{x} B))\) are valid in \({\mathcal {M}}\); if \({\mathcal {M}}\) satisfies \(C-{\mathcal {W}}bT\), \(\Pi x (Rx \rightarrow {\mathcal {W}}_{x}({\mathcal {W}}_{x} B \rightarrow B))\) is valid in \({\mathcal {M}}\); if \({\mathcal {M}}\) satisfies \(C-{\mathcal {W}}bD\), \(\Pi x (Rx \rightarrow {\mathcal {W}}_{x}({\mathcal {W}}_{x} B \rightarrow \lnot {\mathcal {W}}_{x} \lnot B))\) is valid in \({\mathcal {M}}\); and if \({\mathcal {M}}\) satisfies \(C-{\mathcal {W}}bB\), \(\Pi x (Rx \rightarrow {\mathcal {W}}_{x}(B \rightarrow {\mathcal {W}}_{x} {\mathcal {A}}_{x} B))\) is valid in \({\mathcal {M}}\). \(\Pi x (Rx \rightarrow ({\mathcal {W}}_{x} B \rightarrow {\mathcal {W}}_{x} {\mathcal {W}}_{x} B))\) says that if x is perfectly rational, then if x wants it to be the case that B then x wants it to be the case that x wants it to be the case that B. So, according to this formula, a perfectly rational individual does not want to ‘get rid’ of any of her wants. \(\Pi x (Rx \rightarrow (\lnot {\mathcal {W}}_{x} B \rightarrow {\mathcal {W}}_{x} \lnot {\mathcal {W}}_{x} B))\) says that if x is perfectly rational, then if x does not want it to be the case that B then x wants it to be the case that x does not want it to be the case that B. Hence, according to this formula, a perfectly rational individual does not want to ‘add’ any new wants to the set of all her wants. Of course, \(\Pi x (Rx \rightarrow ({\mathcal {W}}_{x} B \rightarrow {\mathcal {W}}_{x} {\mathcal {W}}_{x} B))\) is compatible with the claim that a perfectly rational individual wants to get rid of some wants in the future, and \(\Pi x (Rx \rightarrow (\lnot {\mathcal {W}}_{x} B \rightarrow {\mathcal {W}}_{x} \lnot {\mathcal {W}}_{x} B))\) is compatible with the proposition that a perfectly rational individual wants to add wants to the set of all her wants in the future. However, at the moment when a perfectly rational individual wants something she wants to want it according to \(\Pi x (Rx \rightarrow ({\mathcal {W}}_{x} B \rightarrow {\mathcal {W}}_{x} {\mathcal {W}}_{x} B))\); and at the moment when a perfectly rational individual does not want something she wants it to be the case that she does not want it according to \(\Pi x (Rx \rightarrow (\lnot {\mathcal {W}}_{x} B \rightarrow {\mathcal {W}}_{x} \lnot {\mathcal {W}}_{x} B))\).
The conditions in Table 4 are concerned with some possible restrictions on the doxastic accessibility relation (‘d’ stands for ‘doxastic’). In standard doxastic logic, the doxastic accessibility relation is usually treated as a 2-place relation (see, for example [33, 76]; however, see also [37, 89]). In this paper, \({\mathfrak {D}}\) is a 4-place relation. We can think of this as a relativisation of the ordinary binary doxastic accessibility relation to individuals and moments in time. Intuitively, \({\mathfrak {D}}\delta \omega \omega '\tau \) says that the possible world \(\omega '\) is doxastically accessible from the possible world \(\omega \) to the individual \(\delta \) at time \(\tau \). So, a possible world \(\omega '\) can be doxastically accessible from a possible world \(\omega \) at a time \(\tau \) to individual \(\delta \) even though \(\omega '\) is not doxastically accessible from \(\omega \) to \(\delta \) at another time \(\tau '\), and \(\omega '\) can be doxastically accessible from \(\omega \) at \(\tau \) to \(\delta \) even though \(\omega '\) is not doxastically accessible from \(\omega \) at \(\tau \) to another individual \(\delta '\) (given that we do not impose some conditions on our accessibility relations that exclude such models).
In the class of all models that satisfy \(C-dO\), the following formula is valid: \(\Pi x(Rx\rightarrow (A\rightarrow {\mathcal {B}}_{x}A))\). Therefore, we will call this condition the condition of doxastic omniscience. \(C-dO\) does not entail that absolutely everyone is doxastically omniscient; it speaks about everyone who is perfectly rational. In the class of all models that satisfy \(C-dT\), \(\Pi x(Rx\rightarrow ({\mathcal {B}}_{x}A\rightarrow A))\) is valid. Consequently, we will call this condition the condition of doxastic infallibility. \(C-dT\) does not entail that absolutely everyone is infallible; it is restricted to everyone who is perfectly rational. In the class of all models that satisfy \(C-dD\), the principle of (doxastic) consistency is valid: \(\Pi x (Rx \rightarrow \lnot ({\mathcal {B}}_{x} A \wedge {\mathcal {B}}_{x} \lnot A))\). According to this formula, someone is perfectly rational only if she has no contradictory beliefs. Accordingly, we shall call \(C-dD\) the condition of (doxastic) consistency.
\(C-d4\) is called the condition of positive introspection. If a model \({\mathcal {M}}\) satisfies \(C-d4\) and \(C-UR\), or  and \(C-FT\) or \(C-FTR\) (see Tables 6, 16), then \(\Pi x(Rx\rightarrow ({\mathcal {B}}_{x} A\rightarrow {\mathcal {B}}_{x} {\mathcal {B}}_{x} A))\) is valid in \({\mathcal {M}}\). \(C-d5\) is called the condition of negative introspection. If a model \({\mathcal {M}}\) satisfies \(C-d5\) and \(C-UR\), or
and \(C-FT\) or \(C-FTR\) (see Tables 6, 16), then \(\Pi x(Rx\rightarrow ({\mathcal {B}}_{x} A\rightarrow {\mathcal {B}}_{x} {\mathcal {B}}_{x} A))\) is valid in \({\mathcal {M}}\). \(C-d5\) is called the condition of negative introspection. If a model \({\mathcal {M}}\) satisfies \(C-d5\) and \(C-UR\), or  and \(C-FT\) or \(C-FTR\) (see Tables 6, 16), then \(\Pi x(Rx\rightarrow (\lnot {\mathcal {B}}_{x} A\rightarrow {\mathcal {B}}_{x} \lnot {\mathcal {B}}_{x} A))\) is valid in \({\mathcal {M}}\). Intuitively, \(\Pi x(Rx\rightarrow ({\mathcal {B}}_{x} A\rightarrow {\mathcal {B}}_{x} {\mathcal {B}}_{x} A))\) says that every perfectly rational individual is aware of all her beliefs, and \(\Pi x(Rx\rightarrow (\lnot {\mathcal {B}}_{x} A\rightarrow {\mathcal {B}}_{x} \lnot {\mathcal {B}}_{x} A))\) says that every perfectly rational individual is aware of all her ‘non-beliefs’.
and \(C-FT\) or \(C-FTR\) (see Tables 6, 16), then \(\Pi x(Rx\rightarrow (\lnot {\mathcal {B}}_{x} A\rightarrow {\mathcal {B}}_{x} \lnot {\mathcal {B}}_{x} A))\) is valid in \({\mathcal {M}}\). Intuitively, \(\Pi x(Rx\rightarrow ({\mathcal {B}}_{x} A\rightarrow {\mathcal {B}}_{x} {\mathcal {B}}_{x} A))\) says that every perfectly rational individual is aware of all her beliefs, and \(\Pi x(Rx\rightarrow (\lnot {\mathcal {B}}_{x} A\rightarrow {\mathcal {B}}_{x} \lnot {\mathcal {B}}_{x} A))\) says that every perfectly rational individual is aware of all her ‘non-beliefs’.
\(C-dO\) is stronger than \(C-{\mathcal {B}}dO\), \(C-dT\) is stronger than \(C-{\mathcal {B}}dT\), etc., that is, \(C-dO\) entails \(C-{\mathcal {B}}dO\) but not vice versa, \(C-dT\) entails \(C-{\mathcal {B}}dT\) but not vice versa, etc. In the class of all models that satisfy \(C-{\mathcal {B}}dT\) (and \(C-UR\)) but not \(C-dT\), for example we can show that \(\Pi x(Rx\rightarrow {\mathcal {B}}_{x}({\mathcal {B}}_{x}A\rightarrow A))\) is valid but not that \(\Pi x(Rx\rightarrow ({\mathcal {B}}_{x}A\rightarrow A))\) is valid. In other words, in this class of models, we can show that every perfectly rational individual believes that she is infallible but not that she is infallible. Similar relations hold between \(C-dO\) and \(C-{\mathcal {B}}dO\), between \(C-dD\) and \(C-{\mathcal {B}}dD\), etc.
So far, we have considered some formal properties of single accessibility relations. Now, let us turn to some possible connections between two different accessibility relations.
The conditions in Table 5 are concerned with some possible relationships between the alethic accessibility relation and the boulesic accessibility relation. According to  , the possible world \(\omega '\) is alethically accessible from the possible world \(\omega \) at time \(\tau \) if \(\omega '\) is boulesically accessible from \(\omega \) to individual \(\delta \) at \(\tau \). In the class of all models that satisfy this condition, the following formulas are valid:
, the possible world \(\omega '\) is alethically accessible from the possible world \(\omega \) at time \(\tau \) if \(\omega '\) is boulesically accessible from \(\omega \) to individual \(\delta \) at \(\tau \). In the class of all models that satisfy this condition, the following formulas are valid:  and
and  . The latter formula is a version of the so-called hypothetical imperative, which says that if x is perfectly rational, then if x wants A to be the case and it is necessary that if A then B then x wants B to be the case (for more on this principle, see below).
. The latter formula is a version of the so-called hypothetical imperative, which says that if x is perfectly rational, then if x wants A to be the case and it is necessary that if A then B then x wants B to be the case (for more on this principle, see below).
According to  , in every possible world, at every moment in time, every individual accepts at least one possible world that is alethically accessible at that time. This condition is stronger than the condition \(C-bD\) (Table 3). \(C-bD\) is derivable from
, in every possible world, at every moment in time, every individual accepts at least one possible world that is alethically accessible at that time. This condition is stronger than the condition \(C-bD\) (Table 3). \(C-bD\) is derivable from  , but \(C-bD\) (in itself) does not entail
, but \(C-bD\) (in itself) does not entail  . In the class of all models that satisfy this condition, the following formula is valid:
. In the class of all models that satisfy this condition, the following formula is valid:  , which says that if an individual x is perfectly rational, then x wants it to be the case that A only if A is possible.
, which says that if an individual x is perfectly rational, then x wants it to be the case that A only if A is possible.
 is stronger than
is stronger than  , and
, and  is stronger than
is stronger than  .
.  is valid in every model that satisfies
is valid in every model that satisfies  (and \(C-UR\)), and
(and \(C-UR\)), and  is valid in every model that satisfies
is valid in every model that satisfies  (and \(C-UR\), or
(and \(C-UR\), or  and \(C-FT\) or \(C-FTR\)).
and \(C-FT\) or \(C-FTR\)).
Suppose a model satisfies \(C-ba4\). Then  is valid in this model. Suppose it satisfies \(C-ba5\). Then
is valid in this model. Suppose it satisfies \(C-ba5\). Then  is valid in this model.
is valid in this model.  is valid in every model that satisfies \(C-ab4\) (and \(C-UR\), \(C-FT\) or \(C-FTR\)); and
is valid in every model that satisfies \(C-ab4\) (and \(C-UR\), \(C-FT\) or \(C-FTR\)); and  is valid in every model that satisfies \(C-ab5\) (and \(C-UR\), \(C-FT\) or \(C-FTR\)).
is valid in every model that satisfies \(C-ab5\) (and \(C-UR\), \(C-FT\) or \(C-FTR\)).
In every model that satisfies  (and \(C-UR\), \(C-FT\) or \(C-FTR\)),
(and \(C-UR\), \(C-FT\) or \(C-FTR\)),  is valid. In every model that satisfies
is valid. In every model that satisfies  (and \(C-UR\), \(C-FT\) or \(C-FTR\)),
(and \(C-UR\), \(C-FT\) or \(C-FTR\)),  is valid. If a model satisfies
is valid. If a model satisfies  (and \(C-UR\), \(C-FT\) or \(C-FTR\)), we can show that
(and \(C-UR\), \(C-FT\) or \(C-FTR\)), we can show that  is valid in this model.
is valid in this model.
The conditions in Table 6 describe some possible relationships between the alethic accessibility relation and the doxastic accessibility relation.
In the class of all models that satisfy  ,
,  is valid. Intuitively, this formula says that every perfectly wise individual believes every historically necessary truth. Hence, we shall call this condition the condition of (doxastic) necessity-omniscience. Similarly, if a model satisfies
is valid. Intuitively, this formula says that every perfectly wise individual believes every historically necessary truth. Hence, we shall call this condition the condition of (doxastic) necessity-omniscience. Similarly, if a model satisfies  ,
,  is valid in this model. Intuitively, this formula says that a perfectly rational individual believes something only if it is historically settled. Therefore, we can call this condition the condition of doxastic necessity-restriction. In the class of all models that satisfy
is valid in this model. Intuitively, this formula says that a perfectly rational individual believes something only if it is historically settled. Therefore, we can call this condition the condition of doxastic necessity-restriction. In the class of all models that satisfy  ,
,  is valid. Intuitively, this formula says that a perfectly rational individual only believes something if it is possible. Accordingly, we shall call this condition the condition of possibility-infallibility.
is valid. Intuitively, this formula says that a perfectly rational individual only believes something if it is possible. Accordingly, we shall call this condition the condition of possibility-infallibility.
Suppose a model satisfies \(C-da4\). Then  is valid in this model. Suppose it satisfies \(C-da5\). Then
is valid in this model. Suppose it satisfies \(C-da5\). Then  is valid in this model. If a model satisfies \(C-ad4\) (and \(C-UR\) in Table 16), then
is valid in this model. If a model satisfies \(C-ad4\) (and \(C-UR\) in Table 16), then  is valid in this model. According to this formula, if a perfectly wise individual believes something, it is (historically) necessary that she believes it. Consequently, we can call this condition the condition of the necessity of beliefs. Similarly, if a model satisfies \(C-ad5\) (and \(C-UR\)), the following formula is valid:
is valid in this model. According to this formula, if a perfectly wise individual believes something, it is (historically) necessary that she believes it. Consequently, we can call this condition the condition of the necessity of beliefs. Similarly, if a model satisfies \(C-ad5\) (and \(C-UR\)), the following formula is valid:  . Intuitively, this formula says that if a perfectly rational individual does not believe something, it is historically necessary that she does not believe it. Accordingly, we can call this condition the condition of the necessity of non-beliefs.
. Intuitively, this formula says that if a perfectly rational individual does not believe something, it is historically necessary that she does not believe it. Accordingly, we can call this condition the condition of the necessity of non-beliefs.
 is valid in the class of all models that satisfy
is valid in the class of all models that satisfy  (and \(C-UR\)).
(and \(C-UR\)).  is valid in the class of all models that satisfy
is valid in the class of all models that satisfy  (and \(C-UR\)).
(and \(C-UR\)).  is valid in the class of all models that satisfy
is valid in the class of all models that satisfy  (and \(C-UR\)).
(and \(C-UR\)).
 is stronger than
is stronger than  ,
,  is stronger than
is stronger than  and
and  is stronger than
is stronger than  .
.  is valid in the class of all models that satisfy
is valid in the class of all models that satisfy  (and \(C-UR\));
(and \(C-UR\));  is valid in the class of all models that satisfy
is valid in the class of all models that satisfy  (and \(C-UR\)); and
(and \(C-UR\)); and  is valid in the class of all models that satisfy
is valid in the class of all models that satisfy  (and \(C-UR\)).
(and \(C-UR\)).
The conditions in Table 7 are concerned with some possible relationships between the boulesic accessibility relation and the doxastic accessibility relation.
\(C-{\mathcal {W}}{\mathcal {B}}\) is a condition that is theoretically interesting but intuitively problematic. In every model that satisfies this condition, the following formula is valid: \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x} A \rightarrow {\mathcal {B}}_{x}A))\), which says that if a perfectly rational individual wants something she believes that it is true. But it seems possible to conceive of many instances of this schema that are false. Consider, for example the following scenario. Suppose that \(\delta \) is perfectly rational and wants it to be the case that there is peace everywhere in the world. Does it follow that \(\delta \) believes that there is peace everywhere in the world? Is it not possible for someone who is perfectly rational to want something even though she does not believe it to be true?
\(C-{\mathcal {B}}{\mathcal {W}}\) is the ‘converse’ of \(C-{\mathcal {W}}{\mathcal {B}}\). This constraint is also theoretically interesting but intuitively problematic. In every model that satisfies this condition, the following formula is valid: \(\Pi x(Rx \rightarrow ({\mathcal {B}}_{x} A \rightarrow {\mathcal {W}}_{x}A))\), which says that if a perfectly rational individual believes something she wants it to be true. This condition also appears to have many problematic instances. Suppose, for example that someone is perfectly rational and believes that there is a lot of suffering in the world. Does it follow that she wants it to be the case that there is a lot of suffering in the world? It seems to be absurd to assert this. Notwithstanding such instances, there might be good reasons to accept \(C-{\mathcal {B}}{\mathcal {W}}\), for \(C-{\mathcal {B}}{\mathcal {W}}\) follows from  and
and  , which are two conditions we might want to accept. If a perfectly rational individual only believes something if it is historically settled, and she wants all historically settled facts to be true, then if she believes something, she also wants it to be true. Suppose we accept these constraints. Then, a perfectly rational individual believes that there is a lot of suffering in the world only if it is historically settled that there is a lot of suffering in the world. And if this is the case, she accepts this state of affairs and even wants it to obtain. This is compatible with the proposition that she wants this state of affairs to change in the future; she might want it to be the case that there will not be a lot of suffering in the world in the future. So, even though \(C-{\mathcal {B}}{\mathcal {W}}\) is intuitively problematic, it is not certain that we should reject it.
, which are two conditions we might want to accept. If a perfectly rational individual only believes something if it is historically settled, and she wants all historically settled facts to be true, then if she believes something, she also wants it to be true. Suppose we accept these constraints. Then, a perfectly rational individual believes that there is a lot of suffering in the world only if it is historically settled that there is a lot of suffering in the world. And if this is the case, she accepts this state of affairs and even wants it to obtain. This is compatible with the proposition that she wants this state of affairs to change in the future; she might want it to be the case that there will not be a lot of suffering in the world in the future. So, even though \(C-{\mathcal {B}}{\mathcal {W}}\) is intuitively problematic, it is not certain that we should reject it.
Note that \(C-{\mathcal {W}}{\mathcal {C}}\) and \(C-{\mathcal {B}}{\mathcal {A}}\) are logically equivalent. In the class of all models that satisfy \(C-{\mathcal {W}}{\mathcal {C}}\) or \(C-{\mathcal {B}}{\mathcal {A}}\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}D \rightarrow {\mathcal {C}}_{x}D))\) and \(\Pi x(Rx \rightarrow ({\mathcal {B}}_{x}D \rightarrow {\mathcal {A}}_{x}D))\) are valid. Intuitively, \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}D \rightarrow {\mathcal {C}}_{x}D))\) says that a perfectly rational individual wants something only if it is conceivable to her, and \(\Pi x(Rx \rightarrow ({\mathcal {B}}_{x}D \rightarrow {\mathcal {A}}_{x}D))\) says that a perfectly rational individual accepts everything she believes to be true. Even though a perfectly rational individual accepts the world (as she believes it to be) according to the latter formula, this does not necessarily entail that she does not want it to change in the future.
Let \({\mathcal {M}}\) be a model. Then, if \({\mathcal {M}}\) satisfies \({\mathcal {W}}dO\) and (UR or  and FTR), then \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}(A \rightarrow {\mathcal {B}}_{x}A))\) and \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}A \rightarrow {\mathcal {W}}_{x}{\mathcal {B}}_{x}A))\) are valid in \({\mathcal {M}}\). Intuitively, \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}(A \rightarrow {\mathcal {B}}_{x}A))\) says that a perfectly rational individual wants to be doxastically omniscient. This is compatible with the proposition that she is not doxastically omniscient. If \({\mathcal {M}}\) satisfies \({\mathcal {W}}dT\) (and UR or
and FTR), then \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}(A \rightarrow {\mathcal {B}}_{x}A))\) and \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}A \rightarrow {\mathcal {W}}_{x}{\mathcal {B}}_{x}A))\) are valid in \({\mathcal {M}}\). Intuitively, \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}(A \rightarrow {\mathcal {B}}_{x}A))\) says that a perfectly rational individual wants to be doxastically omniscient. This is compatible with the proposition that she is not doxastically omniscient. If \({\mathcal {M}}\) satisfies \({\mathcal {W}}dT\) (and UR or  and FTR), then \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}({\mathcal {B}}_{x} A \rightarrow A))\) and \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}{\mathcal {B}}_{x} A \rightarrow {\mathcal {W}}_{x}A))\) are valid in \({\mathcal {M}}\). Intuitively, \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}({\mathcal {B}}_{x} A \rightarrow A))\) says that every perfectly rational individual wants to be infallible, that is, she wants to believe something only if it is true. This does not necessarily entail that she is infallible. If \({\mathcal {M}}\) satisfies \({\mathcal {W}}dB\) (and UR or
and FTR), then \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}({\mathcal {B}}_{x} A \rightarrow A))\) and \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}{\mathcal {B}}_{x} A \rightarrow {\mathcal {W}}_{x}A))\) are valid in \({\mathcal {M}}\). Intuitively, \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}({\mathcal {B}}_{x} A \rightarrow A))\) says that every perfectly rational individual wants to be infallible, that is, she wants to believe something only if it is true. This does not necessarily entail that she is infallible. If \({\mathcal {M}}\) satisfies \({\mathcal {W}}dB\) (and UR or  and FTR), then \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}(A \rightarrow {\mathcal {B}}_{x} {\mathcal {C}}_{x} A))\) and \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}(A \rightarrow {\mathcal {B}}_{x} \lnot {\mathcal {B}}_{x} \lnot A))\) are valid in \({\mathcal {M}}\). If \({\mathcal {M}}\) satisfies \({\mathcal {W}}dD\) (and UR or
and FTR), then \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}(A \rightarrow {\mathcal {B}}_{x} {\mathcal {C}}_{x} A))\) and \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}(A \rightarrow {\mathcal {B}}_{x} \lnot {\mathcal {B}}_{x} \lnot A))\) are valid in \({\mathcal {M}}\). If \({\mathcal {M}}\) satisfies \({\mathcal {W}}dD\) (and UR or  and FTR), then \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}({\mathcal {B}}_{x} A \rightarrow \lnot {\mathcal {B}}_{x} \lnot A))\) is valid in \({\mathcal {M}}\). Intuitively, \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}({\mathcal {B}}_{x} A \rightarrow \lnot {\mathcal {B}}_{x} \lnot A))\) says that every perfectly rational individual wants to have consistent beliefs, that is, she wants it to be the case that she does not believe both A and not-A. This condition, in itself, does not exclude the possibility that a perfectly rational individual has beliefs that are inconsistent.
and FTR), then \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}({\mathcal {B}}_{x} A \rightarrow \lnot {\mathcal {B}}_{x} \lnot A))\) is valid in \({\mathcal {M}}\). Intuitively, \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}({\mathcal {B}}_{x} A \rightarrow \lnot {\mathcal {B}}_{x} \lnot A))\) says that every perfectly rational individual wants to have consistent beliefs, that is, she wants it to be the case that she does not believe both A and not-A. This condition, in itself, does not exclude the possibility that a perfectly rational individual has beliefs that are inconsistent.
\(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}({\mathcal {B}}_{x}A \rightarrow {\mathcal {B}}_{x}{\mathcal {B}}_{x}A))\) is valid in every model that satisfies \({\mathcal {W}}d4\) (and UR). Intuitively, this formula says that if someone is perfectly rational then she wants to be aware of all her beliefs. This constraint is compatible with the proposition that it is not the case that every perfectly rational individual is aware of all her beliefs.
\(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}(\lnot {\mathcal {B}}_{x}A \rightarrow {\mathcal {B}}_{x}\lnot {\mathcal {B}}_{x}A))\) is valid in every model that satisfies \({\mathcal {W}}d5\) (and UR). Intuitively, this formula says that if someone is perfectly rational then she wants to be aware of all her non-beliefs. This condition is compatible with the proposition that it is not the case that every perfectly rational individual is aware of all her non-beliefs.
If \({\mathcal {M}}\) satisfies db4 (and UR or  and FTR), then \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x} D \rightarrow {\mathcal {B}}_{x} {\mathcal {W}}_{x}D))\) is a valid in \({\mathcal {M}}\). Intuitively, \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x} D \rightarrow {\mathcal {B}}_{x} {\mathcal {W}}_{x}D))\) says that a perfectly rational individual is aware of all her wants. More precisely, the formula says that if x is perfectly rational then if x wants it to be the case that A then x believes that x wants it to be the case that A. If \({\mathcal {M}}\) satisfies db5 (and UR or
and FTR), then \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x} D \rightarrow {\mathcal {B}}_{x} {\mathcal {W}}_{x}D))\) is a valid in \({\mathcal {M}}\). Intuitively, \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x} D \rightarrow {\mathcal {B}}_{x} {\mathcal {W}}_{x}D))\) says that a perfectly rational individual is aware of all her wants. More precisely, the formula says that if x is perfectly rational then if x wants it to be the case that A then x believes that x wants it to be the case that A. If \({\mathcal {M}}\) satisfies db5 (and UR or  and FTR), then \(\Pi x(Rx \rightarrow ({\mathcal {A}}_{x} D \rightarrow {\mathcal {B}}_{x} {\mathcal {A}}_{x}D))\) and \(\Pi x(Rx \rightarrow (\lnot {\mathcal {W}}_{x} D \rightarrow {\mathcal {B}}_{x} \lnot {\mathcal {W}}_{x}D))\) are valid in \({\mathcal {M}}\). Intuitively, \(\Pi x(Rx \rightarrow ({\mathcal {A}}_{x} D \rightarrow {\mathcal {B}}_{x} {\mathcal {A}}_{x}D))\) says that a perfectly rational individual is aware of everything she accepts, and \(\Pi x(Rx \rightarrow (\lnot {\mathcal {W}}_{x} D \rightarrow {\mathcal {B}}_{x} \lnot {\mathcal {W}}_{x}D))\) says that she is aware of everything she does not want, that is, if she does not want something, she believes that she does not want it. If \({\mathcal {M}}\) satisfies bd4 (and UR or
and FTR), then \(\Pi x(Rx \rightarrow ({\mathcal {A}}_{x} D \rightarrow {\mathcal {B}}_{x} {\mathcal {A}}_{x}D))\) and \(\Pi x(Rx \rightarrow (\lnot {\mathcal {W}}_{x} D \rightarrow {\mathcal {B}}_{x} \lnot {\mathcal {W}}_{x}D))\) are valid in \({\mathcal {M}}\). Intuitively, \(\Pi x(Rx \rightarrow ({\mathcal {A}}_{x} D \rightarrow {\mathcal {B}}_{x} {\mathcal {A}}_{x}D))\) says that a perfectly rational individual is aware of everything she accepts, and \(\Pi x(Rx \rightarrow (\lnot {\mathcal {W}}_{x} D \rightarrow {\mathcal {B}}_{x} \lnot {\mathcal {W}}_{x}D))\) says that she is aware of everything she does not want, that is, if she does not want something, she believes that she does not want it. If \({\mathcal {M}}\) satisfies bd4 (and UR or  and FTR), then \(\Pi x(Rx \rightarrow ({\mathcal {B}}_{x} D \rightarrow {\mathcal {W}}_{x} {\mathcal {B}}_{x}D))\) is a valid in \({\mathcal {M}}\). Intuitively, \(\Pi x(Rx \rightarrow ({\mathcal {B}}_{x} D \rightarrow {\mathcal {W}}_{x} {\mathcal {B}}_{x}D))\) says that if a perfectly rational individual believes something, she wants to believe it. This is, of course, compatible with the possibility that she wants to change her beliefs in the future. If \({\mathcal {M}}\) satisfies bd5 (and UR or
and FTR), then \(\Pi x(Rx \rightarrow ({\mathcal {B}}_{x} D \rightarrow {\mathcal {W}}_{x} {\mathcal {B}}_{x}D))\) is a valid in \({\mathcal {M}}\). Intuitively, \(\Pi x(Rx \rightarrow ({\mathcal {B}}_{x} D \rightarrow {\mathcal {W}}_{x} {\mathcal {B}}_{x}D))\) says that if a perfectly rational individual believes something, she wants to believe it. This is, of course, compatible with the possibility that she wants to change her beliefs in the future. If \({\mathcal {M}}\) satisfies bd5 (and UR or  and FTR), then \(\Pi x(Rx \rightarrow ({\mathcal {C}}_{x} D \rightarrow {\mathcal {W}}_{x} {\mathcal {C}}_{x}D))\) and \(\Pi x(Rx \rightarrow (\lnot {\mathcal {B}}_{x} D \rightarrow {\mathcal {W}}_{x} \lnot {\mathcal {B}}_{x}D))\) are valid in \({\mathcal {M}}\). Intuitively, \(\Pi x(Rx \rightarrow (\lnot {\mathcal {B}}_{x} D \rightarrow {\mathcal {W}}_{x} \lnot {\mathcal {B}}_{x}D))\) says that if a perfectly rational individual does not believe something, she wants it to be the case that she does not believe it. Again, this condition is consistent with the possibility that a perfectly rational individual wants to change her beliefs in the future.
and FTR), then \(\Pi x(Rx \rightarrow ({\mathcal {C}}_{x} D \rightarrow {\mathcal {W}}_{x} {\mathcal {C}}_{x}D))\) and \(\Pi x(Rx \rightarrow (\lnot {\mathcal {B}}_{x} D \rightarrow {\mathcal {W}}_{x} \lnot {\mathcal {B}}_{x}D))\) are valid in \({\mathcal {M}}\). Intuitively, \(\Pi x(Rx \rightarrow (\lnot {\mathcal {B}}_{x} D \rightarrow {\mathcal {W}}_{x} \lnot {\mathcal {B}}_{x}D))\) says that if a perfectly rational individual does not believe something, she wants it to be the case that she does not believe it. Again, this condition is consistent with the possibility that a perfectly rational individual wants to change her beliefs in the future.
Note that \(C-{\mathcal {A}}{\mathcal {B}}P\) and \(C-{\mathcal {C}}{\mathcal {W}}P\) are logically equivalent. Hence, both \(\Pi x(Rx \rightarrow ({\mathcal {A}}_{x}{\mathcal {B}}_{x} D \rightarrow {\mathcal {B}}_{x} {\mathcal {A}}_{x}D))\) and \(\Pi x(Rx \rightarrow ({\mathcal {C}}_{x}{\mathcal {W}}_{x} D \rightarrow {\mathcal {W}}_{x} {\mathcal {C}}_{x}D))\) are valid in every model that satisfies \({\mathcal {A}}{\mathcal {B}}P\) or \({\mathcal {C}}{\mathcal {W}}P\) and UR or  and
and  and FTR. \(\Pi x(Rx \rightarrow ({\mathcal {B}}_{x}{\mathcal {W}}_{x} D \rightarrow {\mathcal {W}}_{x} {\mathcal {B}}_{x}D))\) is valid in every model that satisfies \({\mathcal {B}}{\mathcal {W}}P\) and UR or
and FTR. \(\Pi x(Rx \rightarrow ({\mathcal {B}}_{x}{\mathcal {W}}_{x} D \rightarrow {\mathcal {W}}_{x} {\mathcal {B}}_{x}D))\) is valid in every model that satisfies \({\mathcal {B}}{\mathcal {W}}P\) and UR or  and
and  and FTR. \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}{\mathcal {B}}_{x} D \rightarrow {\mathcal {B}}_{x} {\mathcal {W}}_{x}D))\) is valid in every model that satisfies \({\mathcal {W}}{\mathcal {B}}P\) and UR or
and FTR. \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}{\mathcal {B}}_{x} D \rightarrow {\mathcal {B}}_{x} {\mathcal {W}}_{x}D))\) is valid in every model that satisfies \({\mathcal {W}}{\mathcal {B}}P\) and UR or  and
and  and FTR.
and FTR.
The constraints in Table 8 are concerned with some possible relationships between the alethic, the boulesic and the doxastic accessibility relations.
If a model satisfies  and UR or FTR and
and UR or FTR and  , then
, then  is valid in this model. If a model satisfies
is valid in this model. If a model satisfies  and UR or FTR and
and UR or FTR and  , then
, then  is valid in this model. If a model satisfies
is valid in this model. If a model satisfies  and UR or FTR and
and UR or FTR and  , then
, then  is valid in this model. If a model satisfies
is valid in this model. If a model satisfies  and UR or FTR and
and UR or FTR and  , then
, then  is valid in this model. If a model satisfies
is valid in this model. If a model satisfies  and UR or FTR and
and UR or FTR and  , then
, then  is valid in this model.
is valid in this model.
 is valid in every model that satisfies \(C-{\mathcal {W}}{\mathcal {B}}D\); and
is valid in every model that satisfies \(C-{\mathcal {W}}{\mathcal {B}}D\); and  is valid in every model that satisfies \(C-{\mathcal {B}}N {\mathcal {W}}\).
is valid in every model that satisfies \(C-{\mathcal {B}}N {\mathcal {W}}\).  says that a perfectly rational individual wants something only if she believes that it is possible. It also follows from this condition that no perfectly rational individual wants a state of affairs to obtain at the same time that she does not believe that it is possible that this state of affairs obtains. So, \(C-{\mathcal {W}}{\mathcal {B}}D\) is a philosophically quite interesting condition. Note the difference between
says that a perfectly rational individual wants something only if she believes that it is possible. It also follows from this condition that no perfectly rational individual wants a state of affairs to obtain at the same time that she does not believe that it is possible that this state of affairs obtains. So, \(C-{\mathcal {W}}{\mathcal {B}}D\) is a philosophically quite interesting condition. Note the difference between  and
and  (that is valid in every model that satisfies
(that is valid in every model that satisfies  ). According to
). According to  , a perfectly rational individual wants something only if it is possible and according to
, a perfectly rational individual wants something only if it is possible and according to  a perfectly rational individual wants something only if she believes that it is possible.
a perfectly rational individual wants something only if she believes that it is possible.  is not valid in every model that satisfies
is not valid in every model that satisfies  and
and  is not valid in every model that satisfies \(C-{\mathcal {W}}{\mathcal {B}}D\).
is not valid in every model that satisfies \(C-{\mathcal {W}}{\mathcal {B}}D\).
 says that if a perfectly rational individual believes that it is necessary that A, she wants A to be the case. In every model that satisfies \(C-{\mathcal {B}}N {\mathcal {W}}\), we can also show that the following version of the so-called hypothetical imperative is valid:
says that if a perfectly rational individual believes that it is necessary that A, she wants A to be the case. In every model that satisfies \(C-{\mathcal {B}}N {\mathcal {W}}\), we can also show that the following version of the so-called hypothetical imperative is valid:  , which says that if x is perfectly rational, then if x wants it to be the case that A and believes that it is necessary that A implies B, then x also wants it to be the case that B. So, this is also a philosophically quite interesting condition. We have observed that
, which says that if x is perfectly rational, then if x wants it to be the case that A and believes that it is necessary that A implies B, then x also wants it to be the case that B. So, this is also a philosophically quite interesting condition. We have observed that  is valid in every model that satisfies
is valid in every model that satisfies  (see Table 5). Note the difference between
(see Table 5). Note the difference between  and
and  in these different versions of the hypothetical imperative. ‘
in these different versions of the hypothetical imperative. ‘ ’ says that x believes that it is necessary that A implies B and ‘
’ says that x believes that it is necessary that A implies B and ‘ ’ says that it is necessary that A implies B.
’ says that it is necessary that A implies B.  is not valid in every model that satisfies
is not valid in every model that satisfies  and
and  is not valid in every model that satisfies \(C-{\mathcal {B}}N {\mathcal {W}}\).Footnote 4
is not valid in every model that satisfies \(C-{\mathcal {B}}N {\mathcal {W}}\).Footnote 4
The conditions in Table 9 concern some possible interactions between the alethic accessibility relation \({\mathfrak {R}}\) and the temporal accessibility relation <. ‘ASP’ is an abbreviation of ‘alethic shared past’ and ‘AR’ of ‘alethic ramification’.
If a possible world \(\omega '\) is alethically accessible from a possible world \(\omega \) at time \(\tau '\), then \(\omega '\) is alethically accessible from \(\omega \) at every moment \(\tau \) that is earlier than \(\tau '\) according to \(C-ASP\).
The following formulas are valid in every model that satisfies \(C-ASP\):  ,
,  ,
,  and
and  .
.
Note that \(C-ASP\) and \(C-a4\) entail \(C-AR\).
In every model that satisfies \(C-AR\), we can show that  is valid.
is valid.
The conditions in Table 10 are concerned with some possible connections between the boulesic accessibility relation \({\mathfrak {A}}\) and the temporal accessibility relation <. In every model that satisfies \(C-{\mathcal {W}}{\mathbb {G}}bT\) (and UR), \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}({\mathcal {W}}_{x}B \rightarrow B))\) is valid. In every model that satisfies \(C-{\mathcal {W}}{\mathbb {G}}bD\) (and UR),  is valid. In every model that satisfies \(C-{\mathcal {W}}{\mathbb {G}}bB\) (and UR), \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}(B \rightarrow {\mathcal {W}}_{x}{\mathcal {A}}_{x}B))\) is valid. If a model satisfies \(C-BR\) (‘boulesic ramification’) (and \(C-UR\)), then \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x} {\mathbb {G}} B \rightarrow {\mathcal {W}}_{x} {\mathbb {G}} {\mathcal {W}}_{x} B))\) is valid in this model.
is valid. In every model that satisfies \(C-{\mathcal {W}}{\mathbb {G}}bB\) (and UR), \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}(B \rightarrow {\mathcal {W}}_{x}{\mathcal {A}}_{x}B))\) is valid. If a model satisfies \(C-BR\) (‘boulesic ramification’) (and \(C-UR\)), then \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x} {\mathbb {G}} B \rightarrow {\mathcal {W}}_{x} {\mathbb {G}} {\mathcal {W}}_{x} B))\) is valid in this model.
In every model that satisfies both \(C-{\mathcal {W}}{\mathbb {G}}bT\) and \(C-{\mathcal {W}}bT\) (and \(C-UR\)), \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}\underline{{\mathbb {G}}} ({\mathcal {W}}_{x}B \rightarrow B))\) is valid. According to this formula, it is true that if x is perfectly rational, then x wants it to be the case that it is and that it is always going to be the case that if x wants it to be the case that B then B. \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}\underline{{\mathbb {G}}} ({\mathcal {W}}_{x}B \rightarrow B))\) is equivalent with \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}(({\mathcal {W}}_{x}B \rightarrow B) \wedge {\mathbb {G}} ({\mathcal {W}}_{x}B \rightarrow B)))\). Similarly, in every model that satisfies both \(C-{\mathcal {W}}{\mathbb {G}}bB\) and \(C-{\mathcal {W}}bB\) (and \(C-UR\)), \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}\underline{{\mathbb {G}}} (B \rightarrow {\mathcal {W}}_{x}{\mathcal {A}}_{x}B))\) is valid. \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}\underline{{\mathbb {G}}} (B \rightarrow {\mathcal {W}}_{x}{\mathcal {A}}_{x}B))\) is equivalent with \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}((B \rightarrow {\mathcal {W}}_{x}{\mathcal {A}}_{x}B) \wedge {\mathbb {G}} (B \rightarrow {\mathcal {W}}_{x}{\mathcal {A}}_{x}B)))\).
The conditions in Table 11 are similar to the conditions in Table 10. However, the constraints in Table 11 are concerned with some possible connections between the doxastic accessibility relation \({\mathfrak {D}}\) and the temporal accessibility relation <. In every model that satisfies \(C-{\mathcal {B}}{\mathbb {G}}dT\) (and \(C-UR\)), for example \(\Pi x(Rx \rightarrow {\mathcal {B}}_{x}{\mathbb {G}}({\mathcal {B}}_{x} A \rightarrow A))\) is valid. According to this formula, if x is perfectly rational, then x believes that it is always going to be the case that if x believes A then A is true. In other words, every perfectly rational individual believes that she is always going to be infallible according to this condition. In every model that satisfies both \(C-{\mathcal {B}}{\mathbb {G}}bT\) and \(C-{\mathcal {B}}bT\) (and \(C-UR\)), \(\Pi x(Rx \rightarrow {\mathcal {B}}_{x}\underline{{\mathbb {G}}} ({\mathcal {B}}_{x}A \rightarrow A))\) is valid, which is equivalent with \(\Pi x(Rx \rightarrow {\mathcal {B}}_{x}(({\mathcal {B}}_{x}A \rightarrow A) \wedge {\mathbb {G}} ({\mathcal {B}}_{x}A \rightarrow A)))\). \(\Pi x(Rx \rightarrow {\mathcal {B}}_{x}{\mathbb {G}}(A \rightarrow {\mathcal {B}}_{x} A))\) is valid in every model that satisfies \(C-{\mathcal {B}}{\mathbb {G}}dO\) (and \(C-UR\)). If a model satisfies both \(C-{\mathcal {B}}{\mathbb {G}}dO\) and \(C-{\mathcal {B}}dO\) (and \(C-UR\)) \(\Pi x(Rx \rightarrow {\mathcal {B}}_{x}\underline{{\mathbb {G}}}(A \rightarrow {\mathcal {B}}_{x} A))\) is valid in this model, etc.
So far, we have investigated some possible properties of single accessibility relations, such as transitivity, and some possible connections between two different accessibility relations, such as inclusion. Now, we will turn to some possible relationships that involve three different accessibility relations.
The conditions in Table 12 deal with some possible connections between the boulesic accessibility relation \({\mathfrak {A}}\), the doxastic accessibility relation \({\mathfrak {D}}\) and the temporal accessibility relation <. The conditions in this table are similar to the six last conditions in Table 7.
\(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}(A \rightarrow {\mathcal {B}}_{x}A))\) and \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}{\mathbb {G}}A \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}{\mathcal {B}}_{x}A))\) are valid in every model that satisfies \({\mathcal {W}}{\mathbb {G}}dO\) and UR. If a model satisfies \({\mathcal {W}}{\mathbb {G}}dT\) and UR, then \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}({\mathcal {B}}_{x} A \rightarrow A))\) and \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}{\mathbb {G}}{\mathcal {B}}_{x} A \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}A))\) are valid in this model. If a model satisfies \({\mathcal {W}}{\mathbb {G}}dB\) and UR, then \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}(A \rightarrow {\mathcal {B}}_{x} {\mathcal {C}}_{x} A))\) and \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}(A \rightarrow {\mathcal {B}}_{x} \lnot {\mathcal {B}}_{x} \lnot A))\) are valid in this model. If a model satisfies \({\mathcal {W}}{\mathbb {G}}dD\) and UR, then \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}({\mathcal {B}}_{x} A \rightarrow \lnot {\mathcal {B}}_{x} \lnot A))\) is valid in this model. Intuitively, \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}({\mathcal {B}}_{x} A \rightarrow A))\) says that every perfectly rational individual wants it to be the case that it is always going to be the case that she believes something only if it is true; \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}({\mathcal {B}}_{x} A \rightarrow \lnot {\mathcal {B}}_{x} \lnot A))\) says that every perfectly rational individual wants it to be the case that she is always going to have consistent beliefs, etc.
\(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}({\mathcal {B}}_{x}A \rightarrow {\mathcal {B}}_{x}{\mathcal {B}}_{x}A))\) is valid in every model that satisfies \({\mathcal {W}}{\mathbb {G}}d4\) (and UR). Intuitively, this formula says that if someone is perfectly rational then this individual wants it to be the case that it is always going to be the case that she is aware of all her beliefs.
\(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}(\lnot {\mathcal {B}}_{x}A \rightarrow {\mathcal {B}}_{x}\lnot {\mathcal {B}}_{x}A))\) is valid in every model that satisfies \({\mathcal {W}}{\mathbb {G}}d5\) (and UR). Intuitively, this formula says that if someone is perfectly rational then this individual wants it to be the case that it is always going to be the case that she is aware of all her non-beliefs.
If a model satisfies \({\mathcal {W}}dO\), \({\mathcal {W}}{\mathbb {G}}dO\) and UR, then \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}\underline{{\mathbb {G}}}(A \rightarrow {\mathcal {B}}_{x}A))\) is valid in this model. If a model satisfies \({\mathcal {W}}dT\), \({\mathcal {W}}{\mathbb {G}}dT\) and UR, then \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}\underline{{\mathbb {G}}}({\mathcal {B}}_{x} A \rightarrow A))\) is valid in this model. If a model satisfies \({\mathcal {W}}dB\), \({\mathcal {W}}{\mathbb {G}}dB\) and UR, then \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}\underline{{\mathbb {G}}}(A \rightarrow {\mathcal {B}}_{x} {\mathcal {C}}_{x} A))\) is valid in this model. If a model satisfies \({\mathcal {W}}dD\), \({\mathcal {W}}{\mathbb {G}}dD\) and UR, then \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}\underline{{\mathbb {G}}}({\mathcal {B}}_{x} A \rightarrow \lnot {\mathcal {B}}_{x} \lnot A))\) is valid in this model. \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}\underline{{\mathbb {G}}}({\mathcal {B}}_{x}A \rightarrow {\mathcal {B}}_{x}{\mathcal {B}}_{x}A))\) is valid in every model that satisfies \({\mathcal {W}}d4\), \({\mathcal {W}}{\mathbb {G}}d4\) and UR, and \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}\underline{{\mathbb {G}}}(\lnot {\mathcal {B}}_{x}A \rightarrow {\mathcal {B}}_{x}\lnot {\mathcal {B}}_{x}A))\) is valid in every model that satisfies \({\mathcal {W}}d5\), \({\mathcal {W}}{\mathbb {G}}d5\) and UR.
The constraints in Table 13 concern two possible connections between the alethic accessibility relation \({\mathfrak {R}}\), the boulesic accessibility relation \({\mathfrak {A}}\) and the temporal accessibility relation <.  is valid in every model that satisfies
is valid in every model that satisfies  (and \(C-UR\)), and
(and \(C-UR\)), and  is valid in every model that satisfies
is valid in every model that satisfies  (and \(C-UR\)). Suppose that a model satisfies
(and \(C-UR\)). Suppose that a model satisfies  and
and  (and \(C-UR\)). Then
(and \(C-UR\)). Then  is valid in this model.
is valid in this model.  is valid in every model that satisfies
is valid in every model that satisfies  and
and  (and \(C-UR\)). The informal interpretations of these formulas should be obvious.
(and \(C-UR\)). The informal interpretations of these formulas should be obvious.  , for example says that if x is perfectly rational, then x wants it to be the case that it is always going to be the case that x wants A only if A is possible.
, for example says that if x is perfectly rational, then x wants it to be the case that it is always going to be the case that x wants A only if A is possible.
The conditions in Table 14 are formally similar to the conditions in Table 13; they concern three possible connections between the alethic accessibility relation \({\mathfrak {R}}\), the doxastic accessibility relation \({\mathfrak {D}}\) and the temporal accessibility relation <.  is valid in every model that satisfies
is valid in every model that satisfies  (and \(C-UR\)),
(and \(C-UR\)),  is valid in every model that satisfies
is valid in every model that satisfies  (and \(C-UR\)), and
(and \(C-UR\)), and  is valid in every model that satisfies
is valid in every model that satisfies  (and \(C-UR\)). If a model satisfies
(and \(C-UR\)). If a model satisfies  and
and  (and \(C-UR\)), then
(and \(C-UR\)), then  is valid in this model. If a model satisfies
is valid in this model. If a model satisfies  and
and  (and \(C-UR\)), then
(and \(C-UR\)), then  is valid in this model.
is valid in this model.  is valid in every model that satisfies
is valid in every model that satisfies  ,
,  (and \(C-UR\)). Again, the informal interpretations of these formulas should be obvious.
(and \(C-UR\)). Again, the informal interpretations of these formulas should be obvious.  , for example says that if x is perfectly rational, then x believes that it is always going to be the case that x believes A only if A is possible.
, for example says that if x is perfectly rational, then x believes that it is always going to be the case that x believes A only if A is possible.
Finally, I will mention some possible connections that involve all four accessibility relations (see Table 15).
 is valid in every model that satisfies
is valid in every model that satisfies  (and \(C-UR\)), and
(and \(C-UR\)), and  is valid in every model that satisfies
is valid in every model that satisfies  (and \(C-UR\)). If a model satisfies
(and \(C-UR\)). If a model satisfies  (and \(C-UR\)), then
(and \(C-UR\)), then  is valid in this model. If a model satisfies
is valid in this model. If a model satisfies  (and \(C-UR\)), then
(and \(C-UR\)), then  is valid in this model. If a model satisfies
is valid in this model. If a model satisfies  (and \(C-UR\)), then
(and \(C-UR\)), then  is valid in this model.
is valid in this model.  is valid in every model that satisfies
is valid in every model that satisfies  and
and  (and \(C-UR\)), and
(and \(C-UR\)), and  is valid in every model that satisfies
is valid in every model that satisfies  and
and  (and \(C-UR\)). If a model satisfies
(and \(C-UR\)). If a model satisfies  and
and  (and \(C-UR\)), then
(and \(C-UR\)), then  is valid in this model. If a model satisfies
is valid in this model. If a model satisfies  and
and  (and \(C-UR\)), then
(and \(C-UR\)), then  is valid in this model. If a model satisfies
is valid in this model. If a model satisfies  and
and  (and \(C-UR\)), then
(and \(C-UR\)), then  is valid in this model.
is valid in this model.
Again, the informal interpretations of these formulas should be obvious.  , for example says that if x is perfectly rational, then x wants it to be the case that it is always going to be the case that x believes A only if A is possible.
, for example says that if x is perfectly rational, then x wants it to be the case that it is always going to be the case that x believes A only if A is possible.
We have now investigated some possible interactions between the different accessibility relations in our models. Let us turn to four constraints that involve the valuation function v.
The conditions in Table 16 concern some possible connections between the alethic accessibility relation \({\mathfrak {R}}\) and the valuation function v. ‘FT’ is an abbreviation of ‘forward transfer’, ‘BT’ of ‘backward transfer’, ‘R’ of ‘rationality’ and ‘U’ of ‘universal’. \(\Pi x(Rx \rightarrow U Rx)\) is valid in every model that satisfies \(C-UR\). \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x} Rx)\) is valid in every model that satisfies \(C-FTR\) (and  , and \(\Pi x(Rx \rightarrow {\mathcal {B}}_{x} Rx)\) is valid in every model that satisfies \(C-FTR\) (and
, and \(\Pi x(Rx \rightarrow {\mathcal {B}}_{x} Rx)\) is valid in every model that satisfies \(C-FTR\) (and  .
.
According to \(C-FT\), every atomic formula (and every sentence of the form \({\mathcal {W}}_{c}D\), \({\mathcal {A}}_{c}D\), \({\mathcal {R}}_{c}D\), \({\mathcal {I}}_{c}D\), \({\mathcal {N}}_{c}D\), \({\mathcal {B}}_{c}D\) or \({\mathcal {C}}_{c}D\), given that \(\lnot Rc\) is true) is historically settled. Suppose that \(C-FT\) is true. Then, if A is atomic then  holds at every world-moment pair; and if A is of the form \({\mathcal {W}}_{c}D\), \({\mathcal {A}}_{c}D\), \({\mathcal {R}}_{c}D\), \({\mathcal {I}}_{c}D\), \({\mathcal {N}}_{c}D\), \({\mathcal {B}}_{c}D\) or \({\mathcal {C}}_{c}D\),
holds at every world-moment pair; and if A is of the form \({\mathcal {W}}_{c}D\), \({\mathcal {A}}_{c}D\), \({\mathcal {R}}_{c}D\), \({\mathcal {I}}_{c}D\), \({\mathcal {N}}_{c}D\), \({\mathcal {B}}_{c}D\) or \({\mathcal {C}}_{c}D\),  holds at every world-moment pair. According to \(C-BT\), every atomic formula (and every sentence of the form \({\mathcal {W}}_{c}D\), \({\mathcal {A}}_{c}D\), \({\mathcal {R}}_{c}D\), \({\mathcal {I}}_{c}D\), \({\mathcal {N}}_{c}D\), \({\mathcal {B}}_{c}D\) or \({\mathcal {C}}_{c}D\), given that \(\lnot Rc\) is true) that is historically possible is true. Suppose that \(C-BT\) is true. Then, if A is atomic then
holds at every world-moment pair. According to \(C-BT\), every atomic formula (and every sentence of the form \({\mathcal {W}}_{c}D\), \({\mathcal {A}}_{c}D\), \({\mathcal {R}}_{c}D\), \({\mathcal {I}}_{c}D\), \({\mathcal {N}}_{c}D\), \({\mathcal {B}}_{c}D\) or \({\mathcal {C}}_{c}D\), given that \(\lnot Rc\) is true) that is historically possible is true. Suppose that \(C-BT\) is true. Then, if A is atomic then  holds at every world-moment pair; and if A is of the form \({\mathcal {W}}_{c}D\), \({\mathcal {A}}_{c}D\), \({\mathcal {R}}_{c}D\), \({\mathcal {I}}_{c}D\), \({\mathcal {N}}_{c}D\), \({\mathcal {B}}_{c}D\) or \({\mathcal {C}}_{c}D\),
holds at every world-moment pair; and if A is of the form \({\mathcal {W}}_{c}D\), \({\mathcal {A}}_{c}D\), \({\mathcal {R}}_{c}D\), \({\mathcal {I}}_{c}D\), \({\mathcal {N}}_{c}D\), \({\mathcal {B}}_{c}D\) or \({\mathcal {C}}_{c}D\),  holds at every world-moment pair. Note that \(C-FT\) and \(C-BT\) do not entail that every sentence is historically necessary, nor that every sentence that is historically possible is true. Various ‘future-directed sentences’, such as \({\mathbb {G}}Fc\) and \({\mathbb {F}}Rc\), are, for example not necessarily historically settled even if we assume that \(C-FT\) and \(C-BT\) hold.
holds at every world-moment pair. Note that \(C-FT\) and \(C-BT\) do not entail that every sentence is historically necessary, nor that every sentence that is historically possible is true. Various ‘future-directed sentences’, such as \({\mathbb {G}}Fc\) and \({\mathbb {F}}Rc\), are, for example not necessarily historically settled even if we assume that \(C-FT\) and \(C-BT\) hold.
The conditions in this section can be used to divide the class of all models into various subsets. Let \({\mathcal {M}}(C_{1}, \ldots , C_{n})\) be the class of models that satisfy the conditions \(C_{1}, \ldots , C_{n}\). Then, for example \({\mathcal {M}}(C-bD, C-dD, C-d4, C-d5)\) is the class of models that satisfy the conditions \(C-bD\), \(C-dD\), \(C-d4\) and \(C-d5\), etc. We are now in a position to define the concept of a system of a class of models.
Definition 4
(System of a class of models) The (logical) system of \({{\mathcal {M}}}\), or the logic of \({{\mathcal {M}}}\), \({\mathcal {S}}({{\mathcal {M}}})\), is the set of all sentences in the language \({\mathcal {L}}\) that are valid in the class of models \({{\mathcal {M}}}\).
By imposing different conditions on our models it is possible to generate many non-equivalent logical systems. \({\mathcal {S}}({\mathcal {M}}(C-bD, C-dD, C-d4, C-d5))\) (the system of \({\mathcal {M}}(C-bD, C-dD, C-d4, C-d5)\)) is, for example the class of sentences in \({\mathcal {L}}\) that are valid in the class of models that satisfy the conditions \(C-bD\), \(C-dD\), \(C-d4\) and \(C-d5\).
4 Proof Theory
In this section, I will introduce several tableau rules that can be used to define a set of tableau systems. Every tableau system is an extension of propositional logic. Every system also includes a modal part, a temporal part, a boulesic part, a doxastic part and rules for a pair of (possibilist) quantifiers. For more information on the tableau technique, see, for example [30, 36, 59, 84, 96].
4.1 Tableau Rules
The informal interpretation of most of the rules in this section is straightforward. For example according to the box-rule ( ) (Table 18), we may add \(A, w_{j}t_{k}\) to any open branch in a tree that includes
) (Table 18), we may add \(A, w_{j}t_{k}\) to any open branch in a tree that includes  and \(Rw_{i}w_{j}t_{k}\); according to the rule for material implication (\(\rightarrow \)), we may extend the tip of any open branch in a tree on which \(A\rightarrow B, w_{i}t_{k}\) occurs into two new branches, with \(\lnot A, w_{i}t_{k}\) at the tip of one new branch and \(B, w_{i}t_{k}\) at the other, etc. Nevertheless, I will say a few words about some of the rules that might need some explanation. The tableau rules in this section correspond to the semantic conditions in Sect. 3.3.
and \(Rw_{i}w_{j}t_{k}\); according to the rule for material implication (\(\rightarrow \)), we may extend the tip of any open branch in a tree on which \(A\rightarrow B, w_{i}t_{k}\) occurs into two new branches, with \(\lnot A, w_{i}t_{k}\) at the tip of one new branch and \(B, w_{i}t_{k}\) at the other, etc. Nevertheless, I will say a few words about some of the rules that might need some explanation. The tableau rules in this section correspond to the semantic conditions in Sect. 3.3.
Consider the rules in Tables 20, 21 and 22. Intuitively, ‘\(Rc, w_{i}t_{k}\)’ says that the individual denoted by ‘c’ is perfectly rational in the possible world denoted by ‘\(w_{i}\)’ at the time denoted by ‘\(t_{k}\)’, ‘\(Acw_{i}w_{j}t_{k}\)’ says that the possible world referred to by ‘\(w_{j}\)’ is boulesically accessible (acceptable) to the individual denoted by ‘c’ in the possible world denoted by ‘\(w_{i}\)’ at the time denoted by ‘\(t_{k}\)’ and ‘\(Dcw_{i}w_{j}t_{k}\)’ says that the possible world referred to by ‘\(w_{j}\)’ is doxastically accessible to the individual denoted by ‘c’ in the possible world denoted by ‘\(w_{i}\)’ at the time denoted by ‘\(t_{k}\)’. Note that c can be replaced by any constant in the rules in Tables 20, 21 and 22 and similar rules in this section.
The terms a and c in the quantifier rules in (Table 23) are constants (not variables); a is any constant that occurs on the branch (or a new one if there are no constants on the branch) and c is a constant that is new to the branch, that is, that does not already occur on the branch.
The CUT rule in (Table 24) is often useful in practice. It can, for example be used to establish many new derived rules and to simplify various derivations. In this rule, A can be replaced by any sentence. In the completeness proofs, I will use a weaker rule, CUTR, and not CUT. In CUTR, A is of the form Rc, where c is a constant that occurs as an index to some boulesic operator on the branch.
In (\(T-TIi\)) (Table 24), \(A(t_{i})\) is a line in a tableau that includes ‘\(t_{i}\)’, and \(A(t_{j})\) is like \(A(t_{i})\) except that ‘\(t_{i}\)’ is replaced by ‘\(t_{j}\)’. For example if \(A(t_{i})\) is \(A, w_{k}t_{i}\), then \(A(t_{j})\) is \(A, w_{k}t_{j}\); if \(A(t_{i})\) is \(Rw_{k}w_{l}t_{i}\), then \(A(t_{j})\) is \(Rw_{k}w_{l}t_{j}\); if \(A(t_{i})\) is \(t_{i} = t_{k}\), then \(A(t_{j})\) is \(t_{j} = t_{k}\), etc. If \(A(t_{i})\) is \(A, w_{k}t_{i}\), we only apply the rule when A is atomic or of the form \({\mathcal {W}}_{t}D\), \({\mathcal {A}}_{t}D\), \({\mathcal {R}}_{t}D\), \({\mathcal {I}}_{t}D\), \({\mathcal {N}}_{t}D\), \({\mathcal {B}}_{t}D\) or \({\mathcal {C}}_{t}D\) given that \(\lnot Rt, w_{k}t_{i}\) is on the branch. \(T-Ii\) (and TIii) is redundant in any system that does not include \(T-FC\), \(T-PC\) or \(T-C\) (see Table 27). \(T-TIii\), \(T-AIi\) and \(T-AIii\) are interpreted similarly. \(T-AIi\) and \(T-AIii\) are redundant in every system that does not include \(T-dO\), \(T-{\mathcal {B}}dO\), \(T-{\mathcal {W}}dO\), \(T-{\mathcal {B}}{\mathbb {G}}dO\) or \(T-{\mathcal {W}}{\mathbb {G}}dO\).
Consider the ‘identity rules’ in Table 25. ‘R’ in (\(T-R=\)) is an abbreviation of ‘reflexive’, ‘S’ in (\(T-S=\)) of ‘substitution (of identities)’, ‘N’ in (\(T-N=\)) of ‘necessary identity’, ‘A’ in (\(T-A=\)) of ‘(boulesic) accessibility’ and ‘D’ in (\(T-D=\)) of ‘(doxastic) accessibility’. (\(T-R=\)) has no premises; \(t = t, w_{i}t_{k}\) can be added to any open branch in a tree. (\(T-S=\)) can be applied to any atomic formula. Substitutions of the following kind are also allowed. Let M be a matrix where \(x_{m}\) is the first free variable in M and \(a_{m}\) is the constant in \(M[a_{1}, \ldots , a, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}]\) that replaces \(x_{m}\). Moreover, assume that we have \(a = b, w_{i}t_{k}\), \(M[a_{1}, \ldots , a, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}], w_{i}t_{k}\) and \(\lnot Ra_{m}, w_{i}t_{k}\) on the branch. Then, we may apply (\(T-S=\)) to construct an extension of the branch that includes \(M[a_{1}, \ldots , b, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}], w_{i}t_{k}\).
Table 32 contains some boulesic doxastic accessibility rules. Note that \(T-{\mathcal {W}}{\mathcal {C}}\) is ‘equivalent’ to \(T-{\mathcal {B}}{\mathcal {A}}\) and that \(T-{\mathcal {A}}{\mathcal {B}}P\) is ‘equivalent’ to \(T-{\mathcal {C}}{\mathcal {W}}P\). Every sentence that is a theorem in a system that includes \(T-{\mathcal {W}}{\mathcal {C}}\) is also a theorem in a system that includes \(T-{\mathcal {B}}{\mathcal {A}}\), and vice versa, and similarly for \(T-{\mathcal {A}}{\mathcal {B}}P\) and \(T-{\mathcal {C}}{\mathcal {W}}P\). If a system includes \(T-{\mathcal {W}}{\mathcal {C}}\) or \(T-{\mathcal {B}}{\mathcal {A}}\), we can prove that both \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}D \rightarrow {\mathcal {C}}_{x}D))\) and \(\Pi x(Rx \rightarrow ({\mathcal {B}}_{x}D \rightarrow {\mathcal {A}}_{x}D))\) are theorems in this system. If a system includes \(T-{\mathcal {A}}{\mathcal {B}}P\) or \(T-{\mathcal {C}}{\mathcal {W}}P\) (and \(T-UR)\), we can prove that both \(\Pi x(Rx \rightarrow ({\mathcal {A}}_{x}{\mathcal {B}}_{x}D \rightarrow {\mathcal {B}}_{x}{\mathcal {A}}_{x}D))\) and \(\Pi x(Rx \rightarrow ({\mathcal {C}}_{x}{\mathcal {W}}_{x}D \rightarrow {\mathcal {W}}_{x}{\mathcal {C}}_{x}D))\) are theorems in this system.
Table 42 includes some ‘transfer rules’. ‘FT’ in ‘\(T-FT\)’ and ‘\(T-FTR\)’ is an abbreviation of ‘Forward Transfer’, ‘BT’ in ‘\(T-BT\)’ of ‘Backward Transfer’, and ‘R’ in ‘\(T-FTR\)’ and ‘\(T-UR\)’ of ‘Rationality’. Note that A in \(T-FT\) and \(T-BT\) is atomic or of the form \({\mathcal {W}}_{c}D\), \({\mathcal {A}}_{c}D\), \({\mathcal {R}}_{c}D\), \({\mathcal {I}}_{c}D\), \({\mathcal {N}}_{c}D\), \({\mathcal {B}}_{c}D\) or \({\mathcal {C}}_{c}D\) given that \(\lnot Rc, w_{i}t_{l}\) (\(\lnot Rc, w_{j}t_{l}\)) is on the branch. \(T-FTR\) is weaker than \(T-FT\); \(T-FTR\) is derivable in every system that includes \(T-FT\).
In every system that includes \(T-UR\), we can show that the following formula is provable: \(\Pi x(Rx \rightarrow URx)\). \(\Pi x(Rx \rightarrow URx)\) says that every perfectly rational individual is necessarily perfectly rational. Intuitively, it is not obvious whether or not this principle is true and whether or not the transfer rules in Table 42 should be added to our systems. Individuals that are perfectly rational but not necessarily perfectly rational are conceivable and appear to be (logically) possible. Hence, it is a good thing that not all systems assume that this principle is true. \(T-FT\) and \(T-BT\) appear to be plausible if we think of reality as a tree like structure that branches towards the future but is determined in the past (and the present). For some applications, we may want to exclude them.
4.2 Some Important Proof-Theoretical Concepts
Let us now introduce some important proof-theoretical concepts. I will define what we mean by a tableau system, a proof in a system, a theorem in a system, a derivation in a system and the logic of a (tableau) system, etc. First, we will consider the concept of a tableau.
A tree is a structure whose elements consists of a set of nodes ordered by a successor relation. A root is a node that is not a successor of any node. Every tree has exactly one root. All other nodes in a tree are successors of the root. A node without any successor is a tip or a leaf. A path from the root to a tip is a branch. For more on the concept of a tree, see, for example [95, 96, pp. 3–4].
A (semantic) tableau is a tree where the nodes have the following form: \(A, w_{i}t_{j}\), where A is a formula in \({\mathcal {L}}\) and i, j \(\in \) \(\left\{ 0, 1, 2, 3,\ldots \right\} \), or \(Rw_{i}w_{j}t_{k}\), \(Acw_{i}w_{j}t_{k}\), \(Dcw_{i}w_{j}t_{k}\), \(t_{i} < t_{j}\), \(w_{i} = w_{j}\) or \(t_{i} = t_{j}\) where i, j, k \(\in \) \(\left\{ 0, 1, 2, 3,\ldots \right\} \) and c is a constant in \({\mathcal {L}}\).
A branch in a tableau is closed iff \(A, w_{i}t_{j}\) and \(\lnot A, w_{i}t_{j}\) occur on the branch (for some A, \(w_{i}\) and \(t_{j}\)); it is open iff it is not closed. Intuitively, this means that a branch is closed iff it contains a contradiction and it is open just in case it does not contain any contradiction. A tableau is closed iff every branch in it is closed and it is open iff it is not closed.
Definition 5
(Tableau systems) Tableau system: A tableau system is a set of tableau rules. Quantified temporal alethic boulesic doxastic tableau system: a quantified temporal alethic boulesic doxastic tableau system is a tableau system that includes all propositional rules, all basic temporal rules, all basic alethic rules, all basic boulesic rules, all basic doxastic rules, the quantifier rules, the CUT-rule (or CUTR) and all the identity rules (including the temporal and alethic identity rules).
Let us call the smallest quantified temporal alethic boulesic doxastic tableau system \({\mathcal {Q}}\). It is possible to generate a large class of quantified temporal alethic boulesic doxastic tableau systems by adding various tableau rules to \({\mathcal {Q}}\). The name of a quantified temporal alethic boulesic doxastic tableau system consists of a list of the names of the (non-basic) rules that the system contains. The initial ‘T’ in a tableau rule will often be omitted. Hence, ‘aTbDdD’, for example is the name of the quantified temporal alethic boulesic doxastic tableau system that includes all the rules that are included in \({\mathcal {Q}}\) and the rules \(T-aT\), \(T-bD\) and \(T-dD\), etc.
Definition 6
(Proof-theoretical concepts) ‘S’ below stands for a (quantified temporal alethic boulesic doxastic) tableau system and an S-tableau is a tableau generated in accordance with the rules in S. Proof in a system: A proof of a sentence A in S is a closed S-tableau for \(\lnot A, w_{0}t_{0}\), that is, a closed S-tableau whose root consists of \(\lnot A, w_{0}t_{0}\). Theorem in a system: A sentence A is a theorem in S (is provable in S) iff there is a proof of A in S, that is, iff there is a closed S-tableau whose root consists of \(\lnot A, w_{0}t_{0}\). Derivation in a system: A derivation (deduction) of a sentence B from a set of sentences \(\Gamma \) in S is a closed S-tableau that starts with \(A, w_{0}t_{0}\) for every \(A \in \Gamma \) and \(\lnot B, w_{0}t_{0}\). The sentences in \(\Gamma \) are the premises and B the conclusion of the derivation. Proof-theoretic consequence in a system: The sentence B is a proof-theoretic consequence of the set of sentences \(\Gamma \) in S (B is derivable (deducible) from \(\Gamma \) in S, \(\Gamma \vdash {_{S}}\; B\)) iff there is a derivation of B from \(\Gamma \) in S, that is, iff there is a closed S-tableau that starts with \(A, w_{0}t_{0}\) for every \(A \in \Gamma \) and \(\lnot B, w_{0}t_{0}\).
Definition 7
(The logic of a tableau system) The logic L(S) of a tableau system S is the class of all sentences in our language (\({\mathcal {L}}\)) that are theorems in this system.
For example L(aTbDdD), the logic of aTbDdD, is the class of all sentences in \({\mathcal {L}}\) that are provable in aTbDdD, that is, in the quantified temporal alethic boulesic doxastic tableau system that includes all the rules that every system of this kind contains and the rules \(T-aT\), \(T-bD\) and \(T-dD\).
5 Examples of Theorems
In this section, I will mention some interesting formulas that are theorems in some tableau systems. The proofs are usually straightforward and are omitted.
(1) Some ‘boulesic’ sentences that are theorems in every system. All the following sentences (schemas) are theorems in every system in this paper: \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}B \leftrightarrow \lnot {\mathcal {A}}_{x} \lnot B))\), \(\Pi x(Rx \rightarrow (\lnot {\mathcal {W}}_{x}B \leftrightarrow {\mathcal {A}}_{x} \lnot B))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x} \lnot B \leftrightarrow \lnot {\mathcal {A}}_{x}B))\), \(\Pi x(Rx \rightarrow ({\mathcal {A}}_{x}B \leftrightarrow \lnot {\mathcal {W}}_{x} \lnot B))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \wedge B) \leftrightarrow ({\mathcal {W}}_{x}A \wedge {\mathcal {W}}_{x}B)))\), \(\Pi x(Rx \rightarrow (({\mathcal {W}}_{x}A \vee {\mathcal {W}}_{x}B) \rightarrow {\mathcal {W}}_{x}(A \vee B)))\), \(\Pi x(Rx \rightarrow ({\mathcal {A}}_{x}(A \wedge B) \rightarrow ({\mathcal {A}}_{x}A \wedge {\mathcal {A}}_{x}B)))\), \(\Pi x(Rx \rightarrow ({\mathcal {A}}_{x}(A \vee B) \leftrightarrow ({\mathcal {A}}_{x}A \vee {\mathcal {A}}_{x}B)))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \rightarrow B) \rightarrow ({\mathcal {W}}_{x}A \rightarrow {\mathcal {W}}_{x}B)))\), \(\Pi x(Rx \rightarrow (({\mathcal {W}}_{x}A \wedge {\mathcal {W}}_{x}(A \rightarrow B)) \rightarrow {\mathcal {W}}_{x}B))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \rightarrow B) \rightarrow (\lnot {\mathcal {W}}_{x} B \rightarrow \lnot {\mathcal {W}}_{x}A)))\), \(\Pi x(Rx \rightarrow ((\lnot {\mathcal {W}}_{x}B \wedge {\mathcal {W}}_{x}(A \rightarrow B)) \rightarrow \lnot {\mathcal {W}}_{x}A))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \rightarrow B) \rightarrow ({\mathcal {W}}_{x}\lnot B \rightarrow {\mathcal {W}}_{x}\lnot A)))\), \(\Pi x(Rx \rightarrow (({\mathcal {W}}_{x}\lnot B \wedge {\mathcal {W}}_{x}(A \rightarrow B)) \rightarrow {\mathcal {W}}_{x}\lnot A))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \rightarrow B) \rightarrow ({\mathcal {A}}_{x}A \rightarrow {\mathcal {A}}_{x}B)))\), \(\Pi x(Rx \rightarrow (({\mathcal {A}}_{x}A \wedge {\mathcal {W}}_{x}(A \rightarrow B)) \rightarrow {\mathcal {A}}_{x}B))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \rightarrow B) \rightarrow (\lnot {\mathcal {A}}_{x} B \rightarrow \lnot {\mathcal {A}}_{x}A)))\), \(\Pi x(Rx \rightarrow ((\lnot {\mathcal {A}}_{x}B \wedge {\mathcal {W}}_{x}(A \rightarrow B)) \rightarrow \lnot {\mathcal {A}}_{x}A))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \rightarrow B) \rightarrow ({\mathcal {A}}_{x}\lnot B \rightarrow {\mathcal {A}}_{x}\lnot A)))\), \(\Pi x(Rx \rightarrow (({\mathcal {A}}_{x}\lnot B \wedge {\mathcal {W}}_{x}(A \rightarrow B)) \rightarrow {\mathcal {A}}_{x}\lnot A))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \leftrightarrow B) \rightarrow ({\mathcal {W}}_{x}A \leftrightarrow {\mathcal {W}}_{x}B)))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \leftrightarrow B) \rightarrow (\lnot {\mathcal {W}}_{x}A \leftrightarrow \lnot {\mathcal {W}}_{x}B)))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \leftrightarrow B) \rightarrow ({\mathcal {W}}_{x}\lnot A \leftrightarrow {\mathcal {W}}_{x}\lnot B)))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \leftrightarrow B) \rightarrow ({\mathcal {A}}_{x}A \leftrightarrow {\mathcal {A}}_{x}B)))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \leftrightarrow B) \rightarrow (\lnot {\mathcal {A}}_{x}A \leftrightarrow \lnot {\mathcal {A}}_{x}B)))\) and \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \leftrightarrow B) \rightarrow ({\mathcal {A}}_{x}\lnot A \leftrightarrow {\mathcal {A}}_{x}\lnot B)))\).
(2) Some ‘doxastic’ sentences that are theorems in every system. Let S be a sentence in (1) above and let \(S'\) be the sentence that is the result of replacing every occurrence of \({\mathcal {W}}_{x}\) by an occurrence of \({\mathcal {B}}_{x}\) and every occurrence of \({\mathcal {A}}_{x}\) by an occurrence of \({\mathcal {C}}_{x}\). Then if S is a theorem in every system, then \(S'\) is a theorem in every system. For example if \(S =\) \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}B \leftrightarrow \lnot {\mathcal {A}}_{x} \lnot B))\), then \(S' =\) \(\Pi x(Rx \rightarrow ({\mathcal {B}}_{x}B \leftrightarrow \lnot {\mathcal {C}}_{x} \lnot B))\). Since \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}B \leftrightarrow \lnot {\mathcal {A}}_{x} \lnot B))\) is a theorem in every system, \(\Pi x(Rx \rightarrow ({\mathcal {B}}_{x}B \leftrightarrow \lnot {\mathcal {C}}_{x} \lnot B))\) is a theorem in every system, etc.
(3) Some other ‘boulesic’ sentences that are theorems in every system. \(\Pi x(Rx \rightarrow ({\mathcal {R}}_{x}B \leftrightarrow \lnot {\mathcal {A}}_{x} B))\), \(\Pi x(Rx \rightarrow ({\mathcal {R}}_{x}B \leftrightarrow {\mathcal {W}}_{x} \lnot B))\), \(\Pi x(Rx \rightarrow ({\mathcal {N}}_{x}B \leftrightarrow \lnot {\mathcal {I}}_{x} B))\), \(\Pi x(Rx \rightarrow ({\mathcal {I}}_{x}B \leftrightarrow ({\mathcal {A}}_{x} B \wedge {\mathcal {A}}_{x} \lnot B)))\), \(\Pi x(Rx \rightarrow ({\mathcal {N}}_{x}B \leftrightarrow ({\mathcal {W}}_{x} B \vee {\mathcal {W}}_{x} \lnot B)))\), \(\Pi x(Rx \rightarrow ({\mathcal {I}}_{x}B \leftrightarrow {\mathcal {I}}_{x} \lnot B))\), \(\Pi x(Rx \rightarrow ({\mathcal {N}}_{x}B \leftrightarrow {\mathcal {N}}_{x} \lnot B))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \rightarrow B) \rightarrow ({\mathcal {R}}_{x} B \rightarrow {\mathcal {R}}_{x} A)))\), \(\Pi x(Rx \rightarrow (({\mathcal {R}}_{x} B \wedge {\mathcal {W}}_{x}(A \rightarrow B)) \rightarrow {\mathcal {R}}_{x} A))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \rightarrow B) \rightarrow (\lnot {\mathcal {R}}_{x} A \rightarrow \lnot {\mathcal {R}}_{x}B)))\), \(\Pi x(Rx \rightarrow ((\lnot {\mathcal {R}}_{x}A \wedge {\mathcal {W}}_{x}(A \rightarrow B)) \rightarrow \lnot {\mathcal {R}}_{x}B))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \rightarrow B) \rightarrow ({\mathcal {R}}_{x}\lnot A \rightarrow {\mathcal {R}}_{x}\lnot B)))\), \(\Pi x(Rx \rightarrow (({\mathcal {R}}_{x}\lnot A \wedge {\mathcal {W}}_{x}(A \rightarrow B)) \rightarrow {\mathcal {R}}_{x}\lnot B))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \leftrightarrow B) \rightarrow ({\mathcal {R}}_{x}A \leftrightarrow {\mathcal {R}}_{x}B)))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \leftrightarrow B) \rightarrow (\lnot {\mathcal {R}}_{x}A \leftrightarrow \lnot {\mathcal {R}}_{x}B)))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \leftrightarrow B) \rightarrow ({\mathcal {R}}_{x}\lnot A \leftrightarrow {\mathcal {R}}_{x}\lnot B)))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \leftrightarrow B) \rightarrow ({\mathcal {I}}_{x}A \leftrightarrow {\mathcal {I}}_{x}B)))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \leftrightarrow B) \rightarrow (\lnot {\mathcal {I}}_{x}A \leftrightarrow \lnot {\mathcal {I}}_{x}B)))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \leftrightarrow B) \rightarrow ({\mathcal {I}}_{x}\lnot A \leftrightarrow {\mathcal {I}}_{x}\lnot B)))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \leftrightarrow B) \rightarrow ({\mathcal {N}}_{x}A \leftrightarrow {\mathcal {N}}_{x}B)))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \leftrightarrow B) \rightarrow (\lnot {\mathcal {N}}_{x}A \leftrightarrow \lnot {\mathcal {N}}_{x}B)))\) and \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \leftrightarrow B) \rightarrow ({\mathcal {N}}_{x}\lnot A \leftrightarrow {\mathcal {N}}_{x}\lnot B)))\).
(4) Some sentences that include one type of operator that can be proved in every system. The dual of \(U\) is \(M\), the dual of  is
is  , the dual of \({\mathbb {A}}\) is \({\mathbb {S}}\), the dual of \({\mathbb {G}}\) is \({\mathbb {F}}\), the dual of \({\mathbb {H}}\) is \({\mathbb {P}}\), the dual of \(\mathbf{O }\) is \(\mathbf{P }\), the dual of \(\underline{{\mathbb {G}}}\) is \(\underline{{\mathbb {F}}}\), and the dual of \(\underline{{\mathbb {H}}}\) is \(\underline{{\mathbb {P}}}\). Let
, the dual of \({\mathbb {A}}\) is \({\mathbb {S}}\), the dual of \({\mathbb {G}}\) is \({\mathbb {F}}\), the dual of \({\mathbb {H}}\) is \({\mathbb {P}}\), the dual of \(\mathbf{O }\) is \(\mathbf{P }\), the dual of \(\underline{{\mathbb {G}}}\) is \(\underline{{\mathbb {F}}}\), and the dual of \(\underline{{\mathbb {H}}}\) is \(\underline{{\mathbb {P}}}\). Let  be \(U\),
be \(U\),  , \({\mathbb {A}}\), \({\mathbb {G}}\), \({\mathbb {H}}\), \(\mathbf{O }\), \(\underline{{\mathbb {G}}}\) or \(\underline{{\mathbb {H}}}\), and let
, \({\mathbb {A}}\), \({\mathbb {G}}\), \({\mathbb {H}}\), \(\mathbf{O }\), \(\underline{{\mathbb {G}}}\) or \(\underline{{\mathbb {H}}}\), and let  be the dual of
be the dual of  . Then, all of the following formulas are theorems in every system in this paper:
. Then, all of the following formulas are theorems in every system in this paper:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  and
and  .
.
(5) Some ‘boulesic’ sentences that are theorems in every bD-system. All the following sentences (schemas) can be proved in every system in this paper that includes bD: \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}B \rightarrow {\mathcal {A}}_{x}B))\), \(\Pi x(Rx \rightarrow \lnot ({\mathcal {W}}_{x}B \wedge {\mathcal {W}}_{x}\lnot B))\), \(\Pi x(Rx \rightarrow ({\mathcal {A}}_{x}B \vee {\mathcal {A}}_{x}\lnot B))\), \(\Pi x(Rx \rightarrow \lnot ({\mathcal {W}}_{x}(A \vee B) \wedge ({\mathcal {W}}_{x}\lnot A \wedge {\mathcal {W}}_{x}\lnot B)))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \rightarrow B) \rightarrow ({\mathcal {W}}_{x}A \rightarrow {\mathcal {A}}_{x}B)))\), \(\Pi x(Rx \rightarrow (({\mathcal {W}}_{x}A \wedge {\mathcal {W}}_{x}(A \rightarrow B)) \rightarrow {\mathcal {A}}_{x}B))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \rightarrow B) \rightarrow (\lnot {\mathcal {A}}_{x}B \rightarrow \lnot {\mathcal {W}}_{x}A)))\), \(\Pi x(Rx \rightarrow ((\lnot {\mathcal {A}}_{x}B \wedge {\mathcal {W}}_{x}(A \rightarrow B)) \rightarrow \lnot {\mathcal {W}}_{x}A))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \rightarrow B) \rightarrow ({\mathcal {W}}_{x}\lnot B \rightarrow \lnot {\mathcal {W}}_{x}A)))\) and \(\Pi x(Rx \rightarrow (({\mathcal {W}}_{x}\lnot B \wedge {\mathcal {W}}_{x}(A \rightarrow B)) \rightarrow \lnot {\mathcal {W}}_{x}A))\).
(6) Some ‘doxastic’ sentences that are theorems in every dD -system. Let S be a sentence in (5) above and let \(S'\) be the sentence that is the result of replacing every occurrence of \({\mathcal {W}}_{x}\) by an occurrence of \({\mathcal {B}}_{x}\) and every occurrence of \({\mathcal {A}}_{x}\) by an occurrence of \({\mathcal {C}}_{x}\). Then if S is a theorem in every bD-system, then \(S'\) is a theorem in every dD-system.
(7) Some other ‘boulesic’ sentences that are theorems in every bD -system. We can also establish the following sentences in every bD-system: \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}B \rightarrow \lnot {\mathcal {R}}_{x}B))\), \(\Pi x(Rx \rightarrow ({\mathcal {R}}_{x}B \rightarrow \lnot {\mathcal {W}}_{x}B))\), \(\Pi x(Rx \rightarrow \lnot ({\mathcal {R}}_{x}B \wedge {\mathcal {R}}_{x}\lnot B))\), \(\Pi x(Rx \rightarrow \lnot ({\mathcal {W}}_{x}B \wedge {\mathcal {R}}_{x} B))\), \(\Pi x(Rx \rightarrow \lnot ( {\mathcal {W}}_{x}(A \vee B) \wedge ({\mathcal {R}}_{x} A \wedge {\mathcal {R}}_{x} B)))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \rightarrow B) \rightarrow ({\mathcal {W}}_{x}A \rightarrow \lnot {\mathcal {R}}_{x}B)))\), \(\Pi x(Rx \rightarrow (({\mathcal {W}}_{x}A \wedge {\mathcal {W}}_{x}(A \rightarrow B)) \rightarrow \lnot {\mathcal {R}}_{x}B))\), \(\Pi x(Rx \rightarrow ({\mathcal {W}}_{x}(A \rightarrow B) \rightarrow ({\mathcal {R}}_{x}B \rightarrow \lnot {\mathcal {W}}_{x}A)))\) and \(\Pi x(Rx \rightarrow (({\mathcal {R}}_{x}B \wedge {\mathcal {W}}_{x}(A \rightarrow B)) \rightarrow \lnot {\mathcal {W}}_{x}A))\).
(8) Some ‘alethic-boulesic’ sentences that are theorems in every  -system. All the following formulas (schemas) are theorems in every
-system. All the following formulas (schemas) are theorems in every  -system in this paper:
-system in this paper:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  and
and  .
.
(9) Some ‘alethic-doxastic’ sentences that are theorems in every  -system. Let S be a sentence in (8) above and let \(S'\) be the sentence that is the result of replacing every occurrence of \({\mathcal {W}}_{x}\) by an occurrence of \({\mathcal {B}}_{x}\) and every occurrence of \({\mathcal {A}}_{x}\) by an occurrence of \({\mathcal {C}}_{x}\). Then if S is a theorem in every
-system. Let S be a sentence in (8) above and let \(S'\) be the sentence that is the result of replacing every occurrence of \({\mathcal {W}}_{x}\) by an occurrence of \({\mathcal {B}}_{x}\) and every occurrence of \({\mathcal {A}}_{x}\) by an occurrence of \({\mathcal {C}}_{x}\). Then if S is a theorem in every  -system, then \(S'\) is a theorem in every
-system, then \(S'\) is a theorem in every  -system.
-system.
(10) Some other ‘alethic-boulesic’ sentences that are theorems in every  -system.
-system.  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
(11) Some ‘alethic-boulesic’ sentences that are theorems in every system that includes  and bD (or
and bD (or  ).
).  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
(12) Some ‘alethic-doxastic’ sentences that are theorems in every system that includes  and dD (or
and dD (or  ).
).  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
(13) Some other ‘alethic-boulesic’ sentences that are theorems in every system that includes  and bD (or
and bD (or  ).
).  ,
,  ,
,  ,
,  ,
,  .
.
(14) Barcan-like formulas. The following Barcan-like formulas are theorems in every system in this paper:
\(\Pi x(Rx \rightarrow (\Pi y {\mathcal {W}}_{x} D \leftrightarrow {\mathcal {W}}_{x}\Pi y D))\), \(\Pi x(Rx \rightarrow (\Sigma y{\mathcal {A}}_{x} D \leftrightarrow {\mathcal {A}}_{x} \Sigma y D))\), \(\Pi x(Rx \rightarrow ({\mathcal {A}}_{x} \Pi y D \rightarrow \Pi y {\mathcal {A}}_{x} D))\), \(\Pi x(Rx \rightarrow (\Sigma y {\mathcal {W}}_{x} D \rightarrow {\mathcal {W}}_{x} \Sigma y D))\), \(\Pi x(Rx \rightarrow (\Pi y {\mathcal {B}}_{x} D \leftrightarrow {\mathcal {B}}_{x}\Pi y D))\), \(\Pi x(Rx \rightarrow (\Sigma y{\mathcal {C}}_{x} D \leftrightarrow {\mathcal {C}}_{x} \Sigma y D))\), \(\Pi x(Rx \rightarrow ({\mathcal {C}}_{x} \Pi y D \rightarrow \Pi y {\mathcal {C}}_{x} D))\) and \(\Pi x(Rx \rightarrow (\Sigma y {\mathcal {B}}_{x} D \rightarrow {\mathcal {B}}_{x} \Sigma y D))\). Let  be \(U\),
be \(U\),  , \({\mathbb {A}}\), \({\mathbb {G}}\), \({\mathbb {H}}\), \(\mathbf{O }\), \({\underline{\mathbb {G}}}\) or \({\underline{\mathbb {H}}}\), and let
, \({\mathbb {A}}\), \({\mathbb {G}}\), \({\mathbb {H}}\), \(\mathbf{O }\), \({\underline{\mathbb {G}}}\) or \({\underline{\mathbb {H}}}\), and let  be the dual of
be the dual of  . Then, all of the following sentences can be proved in every system in this paper:
. Then, all of the following sentences can be proved in every system in this paper:  ,
,  ,
,  , and
, and  .
.
(15) Some theorems that can be proved in systems that include the transfer rules. In every system that includes \(T-UR\) or \(T-FTR\) and  , we can prove that the following sentence is a theorem: \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x} Rx)\), which says that everyone who is perfectly rational wants to be perfectly rational. In every system that includes \(T-UR\) or \(T-FTR\) and
, we can prove that the following sentence is a theorem: \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x} Rx)\), which says that everyone who is perfectly rational wants to be perfectly rational. In every system that includes \(T-UR\) or \(T-FTR\) and  , we can prove that the following sentence is a theorem: \(\Pi x(Rx \rightarrow {\mathcal {B}}_{x} Rx)\), which says that everyone who is perfectly rational believes that she is perfectly rational. In every system that includes \(T-UR\) or \(T-FTR\) and
, we can prove that the following sentence is a theorem: \(\Pi x(Rx \rightarrow {\mathcal {B}}_{x} Rx)\), which says that everyone who is perfectly rational believes that she is perfectly rational. In every system that includes \(T-UR\) or \(T-FTR\) and  , and \(T-bD\), we can prove that the following sentence is a theorem: \(\Pi x(Rx \rightarrow {\mathcal {A}}_{x} Rx)\), which says that everyone who is perfectly rational accepts that she is perfectly rational. Similarly, in every system that includes \(T-UR\) or \(T-FTR\) and
, and \(T-bD\), we can prove that the following sentence is a theorem: \(\Pi x(Rx \rightarrow {\mathcal {A}}_{x} Rx)\), which says that everyone who is perfectly rational accepts that she is perfectly rational. Similarly, in every system that includes \(T-UR\) or \(T-FTR\) and  , and \(T-dD\), we can prove that the following sentence is a theorem: \(\Pi x(Rx \rightarrow {\mathcal {C}}_{x} Rx)\). In every system that includes \(T-UR\), we can prove the following sentence: \(\Pi x(Rx \rightarrow URx)\), which says that every perfectly rational individual is necessarily perfectly rational.
, and \(T-dD\), we can prove that the following sentence is a theorem: \(\Pi x(Rx \rightarrow {\mathcal {C}}_{x} Rx)\). In every system that includes \(T-UR\), we can prove the following sentence: \(\Pi x(Rx \rightarrow URx)\), which says that every perfectly rational individual is necessarily perfectly rational.
(16) Some theorems that include the identity sign. If a system includes (\(T-S=\)) and (\(T-A=\)), we can establish the following theorems in this system: \(({\mathcal {W}}_{c} D \wedge c = d) \rightarrow {\mathcal {W}}_{d} D\), \(({\mathcal {A}}_{c} D \wedge c = d) \rightarrow {\mathcal {A}}_{d} D\), \(({\mathcal {R}}_{c} D \wedge c = d) \rightarrow {\mathcal {R}}_{d} D\), \(({\mathcal {I}}_{c} D \wedge c = d) \rightarrow {\mathcal {I}}_{d} D\), \(({\mathcal {N}}_{c} D \wedge c = d) \rightarrow {\mathcal {N}}_{d} D\), \(\Pi x \Pi y (({\mathcal {W}}_{x} D \wedge x = y) \rightarrow {\mathcal {W}}_{y} D)\), \(\Pi x \Pi y(({\mathcal {A}}_{x} D \wedge x = y) \rightarrow {\mathcal {A}}_{y} D)\), \(\Pi x \Pi y (({\mathcal {R}}_{x} D \wedge x = y) \rightarrow {\mathcal {R}}_{y} D)\), \(\Pi x \Pi y (({\mathcal {I}}_{x} D \wedge x = y) \rightarrow {\mathcal {I}}_{y} D)\) and \(\Pi x \Pi y (({\mathcal {N}}_{x} D \wedge x = y) \rightarrow {\mathcal {N}}_{y} D)\). If a system includes (\(T-S=\)) and (\(T-D=\)), we can prove the following theorems in this system: \(({\mathcal {B}}_{c} D \wedge c = d) \rightarrow {\mathcal {B}}_{d} D\), \(({\mathcal {C}}_{c} D \wedge c = d) \rightarrow {\mathcal {C}}_{d} D\), \(\Pi x \Pi y (({\mathcal {B}}_{x} D \wedge x = y) \rightarrow {\mathcal {B}}_{y} D)\) and \(\Pi x \Pi y(({\mathcal {C}}_{x} D \wedge x = y) \rightarrow {\mathcal {C}}_{y} D)\). By using (\(T-N=\)), we can show that all identities and non-identities are (absolutely and historically) necessary and eternal, that is, we can prove all of the following theorems: \(\Pi x \Pi y (x = y \rightarrow U x = y)\),  , \(\Pi x \Pi y (\lnot x = y \rightarrow U \lnot x = y)\),
, \(\Pi x \Pi y (\lnot x = y \rightarrow U \lnot x = y)\),  , \(\Pi x \Pi y (x = y \rightarrow {\mathbb {A}} x = y)\) and \(\Pi x \Pi y (\lnot x = y \rightarrow {\mathbb {A}} \lnot x = y)\). Since every constant is treated as a rigid designator in this paper, this is plausible.
, \(\Pi x \Pi y (x = y \rightarrow {\mathbb {A}} x = y)\) and \(\Pi x \Pi y (\lnot x = y \rightarrow {\mathbb {A}} \lnot x = y)\). Since every constant is treated as a rigid designator in this paper, this is plausible.
(17) Some ‘boulesic’ and ‘alethic boulesic’ sentences that are theorems in various systems. If a system includes \(T-b4\), then \(\Pi x((Rx \wedge {\mathcal {W}}_{x}Rx) \rightarrow ({\mathcal {W}}_{x}B \rightarrow {\mathcal {W}}_{x}{\mathcal {W}}_{x}B))\) is a theorem in this system. If a system includes \(T-b5\), then \(\Pi x((Rx \wedge {\mathcal {W}}_{x}Rx) \rightarrow ({\mathcal {A}}_{x}B \rightarrow {\mathcal {W}}_{x}{\mathcal {A}}_{x}B))\) is a theorem in this system. In every system that includes \(T-{\mathcal {W}}bT\), \(\Pi x((Rx \wedge {\mathcal {W}}_{x}Rx) \rightarrow {\mathcal {W}}_{x}({\mathcal {W}}_{x}A \rightarrow A))\) is provable. In every system that includes \(T-{\mathcal {W}}bB\) and b4, \(\Pi x((Rx \wedge {\mathcal {W}}_{x}Rx) \rightarrow {\mathcal {W}}_{x}({\mathcal {A}}_{x}{\mathcal {W}}_{x}A \rightarrow A))\) is a theorem.  is provable in every system that includes
is provable in every system that includes  and
and  is provable in every system that includes
is provable in every system that includes  .
.
(18) Some ‘doxastic’ and ‘alethic doxastic’ sentences that are theorems in various systems. In every system that includes \(T-d4\), \(\Pi x((Rx \wedge {\mathcal {B}}_{x}Rx) \rightarrow ({\mathcal {B}}_{x}D \rightarrow {\mathcal {B}}_{x}{\mathcal {B}}_{x}D))\) is a theorem. In every system that includes \(T-d5\), \(\Pi x((Rx \wedge {\mathcal {B}}_{x}Rx) \rightarrow ({\mathcal {C}}_{x}D \rightarrow {\mathcal {B}}_{x}{\mathcal {C}}_{x}D))\) is provable. If a system includes \(T-{\mathcal {W}}dT\), then \(\Pi x((Rx \wedge {\mathcal {B}}_{x}Rx) \rightarrow {\mathcal {B}}_{x}({\mathcal {B}}_{x}A \rightarrow A))\) is a theorem in this system. In every system that includes \(T-{\mathcal {W}}dB\) and b4, \(\Pi x((Rx \wedge {\mathcal {B}}_{x}Rx) \rightarrow {\mathcal {B}}_{x}({\mathcal {C}}_{x}{\mathcal {B}}_{x}A \rightarrow A))\) is a theorem.  is a theorem in every system that includes
is a theorem in every system that includes  and
and  is a theorem in every system that includes
is a theorem in every system that includes  .
.
(19) Some theorems that include temporal and boulesic operators. In every system that includes \(T-{\mathcal {W}}{\mathbb {G}}bT\), \(\Pi x((Rx\wedge {\mathcal {W}}_{x}{\mathbb {G}}Rx) \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}({\mathcal {W}}_{x}A \rightarrow A))\) is a theorem and \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}({\mathcal {W}}_{x}A \rightarrow A))\) can be proved in every system that includes \(T-{\mathcal {W}}{\mathbb {G}}bT\) and \(T-UR\). In every system that includes \(T-{\mathcal {W}}{\mathbb {G}}bD\), \(\Pi x((Rx\wedge {\mathcal {W}}_{x}{\mathbb {G}}Rx) \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}({\mathcal {W}}_{x}A \rightarrow {\mathcal {A}}_{x}A))\) is a theorem and \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}({\mathcal {W}}_{x}A \rightarrow {\mathcal {A}}_{x}A))\) can be proved in every system that includes \(T-{\mathcal {W}}{\mathbb {G}}bD\) and \(T-UR\). \(\Pi x((Rx\wedge {\mathcal {W}}_{x}{\mathbb {G}}Rx \wedge {\mathcal {W}}_{x}{\mathbb {G}}{\mathcal {W}}_{x}Rx) \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}(B \rightarrow {\mathcal {W}}_{x}{\mathcal {A}}_{x}B))\) is a theorem in every system that contains \(T-{\mathcal {W}}{\mathbb {G}}bB\) and \(\Pi x(Rx \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}(B \rightarrow {\mathcal {W}}_{x}{\mathcal {A}}_{x}B))\) is a theorem in every system that contains \(T-{\mathcal {W}}{\mathbb {G}}bB\) and \(T-UR\). \(\Pi x((Rx\wedge {\mathcal {W}}_{x}{\mathbb {G}}Rx) \rightarrow ({\mathcal {W}}_{x}{\mathbb {G}}A \rightarrow {\mathcal {W}}_{x}{\mathbb {G}}{\mathcal {W}}_{x}A))\) can be proved in every system that includes \(T-BR\).
(20) Some theorems that include temporal and doxastic operators. In every system that includes \(T-{\mathcal {B}}{\mathbb {G}}dO\), \(\Pi x((Rx\wedge {\mathcal {B}}_{x}{\mathbb {G}}Rx) \rightarrow {\mathcal {B}}_{x}{\mathbb {G}}(A \rightarrow {\mathcal {B}}_{x}A))\) is a theorem and \(\Pi x(Rx \rightarrow {\mathcal {B}}_{x}{\mathbb {G}}(A \rightarrow {\mathcal {B}}_{x}A))\) can be proved in every system that includes \(T-{\mathcal {B}}{\mathbb {G}}dO\) and \(T-UR\). In every system that contains \(T-{\mathcal {B}}{\mathbb {G}}dT\), \(\Pi x((Rx\wedge {\mathcal {B}}_{x}{\mathbb {G}}Rx) \rightarrow {\mathcal {B}}_{x}{\mathbb {G}}({\mathcal {B}}_{x}A \rightarrow A))\) is a theorem and \(\Pi x(Rx \rightarrow {\mathcal {B}}_{x}{\mathbb {G}}({\mathcal {B}}_{x}A \rightarrow A))\) can be established in every system that contains \(T-{\mathcal {B}}{\mathbb {G}}dT\) and \(T-UR\). In every system that includes \(T-{\mathcal {B}}{\mathbb {G}}dD\), \(\Pi x((Rx\wedge {\mathcal {B}}_{x}{\mathbb {G}}Rx) \rightarrow {\mathcal {B}}_{x}{\mathbb {G}}({\mathcal {B}}_{x}A \rightarrow {\mathcal {C}}_{x}A))\) is a theorem and \(\Pi x(Rx \rightarrow {\mathcal {B}}_{x}{\mathbb {G}}({\mathcal {B}}_{x}A \rightarrow {\mathcal {C}}_{x}A))\) can be proved in every system that includes \(T-{\mathcal {B}}{\mathbb {G}}dD\) and \(T-UR\). \(\Pi x((Rx\wedge {\mathcal {B}}_{x}{\mathbb {G}}Rx \wedge {\mathcal {B}}_{x}{\mathbb {G}}{\mathcal {B}}_{x}Rx) \rightarrow {\mathcal {B}}_{x}{\mathbb {G}}(B \rightarrow {\mathcal {B}}_{x}{\mathcal {C}}_{x}B))\) is a theorem in every system that contains \(T-{\mathcal {B}}{\mathbb {G}}dB\) and \(\Pi x(Rx \rightarrow {\mathcal {B}}_{x}{\mathbb {G}}(B \rightarrow {\mathcal {B}}_{x}{\mathcal {C}}_{x}B))\) is a theorem in every system that contains \(T-{\mathcal {B}}{\mathbb {G}}dB\) and \(T-UR\). In every system that includes \(T-DR\), we can show that \(\Pi x((Rx\wedge {\mathcal {B}}_{x}{\mathbb {G}}Rx) \rightarrow ({\mathcal {B}}_{x}{\mathbb {G}}A \rightarrow {\mathcal {B}}_{x}{\mathbb {G}}{\mathcal {B}}_{x}A))\) is a theorem.
(21) Some theorems in various systems. We have already mentioned many interesting principles in Sect. 3.3. We have seen that some of them are valid in various classes of models. We can also show that they are theorems in the ‘corresponding’ tableau systems. Let A be a formula in Sect. 3.3. Then if A is valid in every model that satisfies the semantic conditions \(C-X_{1}\), \(\ldots \), \(C-X_{n}\), then A is a theorem in every quantified temporal alethic boulesic doxastic tableau system that includes the tableau rules \(T-X_{1}\), \(\ldots \), \(T-X_{n}\). This follows from the completeness results in Sect. 6.
We have seen that  is valid in every model that satisfies \(C-{\mathcal {W}}{\mathcal {B}}D\) and that
is valid in every model that satisfies \(C-{\mathcal {W}}{\mathcal {B}}D\) and that  is valid in every model that satisfies \(C-{\mathcal {B}}N {\mathcal {W}}\). Hence,
is valid in every model that satisfies \(C-{\mathcal {B}}N {\mathcal {W}}\). Hence,  is a theorem in every system that includes \(T-{\mathcal {W}}{\mathcal {B}}D\) and
is a theorem in every system that includes \(T-{\mathcal {W}}{\mathcal {B}}D\) and  is a theorem in every system that includes \(T-{\mathcal {B}}N {\mathcal {W}}\). We have seen that the following version of the hypothetical imperative is valid in every model that satisfies \(C-{\mathcal {B}}N {\mathcal {W}}\):
is a theorem in every system that includes \(T-{\mathcal {B}}N {\mathcal {W}}\). We have seen that the following version of the hypothetical imperative is valid in every model that satisfies \(C-{\mathcal {B}}N {\mathcal {W}}\):  . Hence,
. Hence,  is a theorem in every system that includes \(T-{\mathcal {B}}N {\mathcal {W}}\). We have seen that if a model satisfies
is a theorem in every system that includes \(T-{\mathcal {B}}N {\mathcal {W}}\). We have seen that if a model satisfies  ,
,  and \(C-UR\), then
and \(C-UR\), then  is valid in this model. Accordingly,
is valid in this model. Accordingly,  is a theorem in every system that includes
is a theorem in every system that includes  ,
,  and \(T-UR\). We have seen that if a model satisfies
and \(T-UR\). We have seen that if a model satisfies  ,
,  and \(C-UR\), then
and \(C-UR\), then  is valid in this model. Consequently,
is valid in this model. Consequently,  is a theorem in every system that includes
is a theorem in every system that includes  ,
,  and \(T-UR\). Etc. Since this is the case, I will not discuss these principles in this section too.
and \(T-UR\). Etc. Since this is the case, I will not discuss these principles in this section too.
6 Soundness and Completeness Theorems
In this section, I will show that every system in this paper is sound and complete with respect to its semantics. The concepts of soundness and completeness are defined as usual.
Definition 8
(Soundness and completeness) Let \(S = T-A_{1}, ..., T-A_{n}\) be a quantified temporal alethic boulesic doxastic tableau system (see the definitions in Sect. 4.2), where \(T-A_{1}, ..., T-A_{n}\) are the non-basic tableau rules in S. We shall say that the class of models, \({{\varvec{M}}}\), corresponds to S iff \({{\varvec{M}}} = {{\varvec{M}}}(C-A_{1}, ..., C-A_{n})\). Let \({{\varvec{M}}}\) correspond to S. Then, S is sound with respect to \({{\varvec{M}}}\) iff \(\Gamma \vdash _{S} A\) entails \({{\varvec{M}}}, \Gamma \Vdash A\), and S is complete with respect to \({{\varvec{M}}}\) iff \({{\varvec{M}}}, \Gamma \Vdash A\) entails \(\Gamma \vdash _{S} A\).
Lemma 1
(Locality) Let \({\mathcal {M}}_{1} = \langle D, W, T, <,{\mathfrak {R}}, {\mathfrak {A}}, {\mathfrak {D}}, v_{1}\rangle \) and \({\mathcal {M}}_{2} = \left\langle D, W, T, <, \right. \) \(\left. {\mathfrak {R}}, {\mathfrak {A}}, {\mathfrak {D}}, v_{2}\right\rangle \) be two models. The language of \({\mathcal {M}}_{1}\) is the same as the language of \({\mathcal {M}}_{2}\), for \({\mathcal {M}}_{1}\) and \({\mathcal {M}}_{2}\) have the same domain. We shall call this language \({\mathcal {L}}\). Furthermore, let A be any closed formula of \({\mathcal {L}}\) such that \(v_{1}\) and \(v_{2}\) agree on the denotations of all the predicates, constants and matrices in it. Then, \({\mathcal {M}}_{1}, \omega , \tau \Vdash A\) iff \({\mathcal {M}}_{2}, \omega , \tau \Vdash A\) (for all \(\omega \in W\) and \(\tau \in T\)).
Proof
By induction on the formulas in the language \({\mathcal {L}}\) (‘the IH’ stands for ‘the induction hypothesis’).
Atomic formulas. \({\mathcal {M}}_{1}, \omega , \tau \Vdash Pa_{1}\ldots a_{n}\) iff \(\left\langle v_{1}(a_{1}),\ldots ,v_{1}(a_{n})\right\rangle \in v_{1\omega \tau }(P)\) iff \(\left\langle v_{2}(a_{1}),\ldots ,v_{2}(a_{n})\right\rangle \in v_{2\omega \tau }(P)\) iff \({\mathcal {M}}_{2}, \omega , \tau \Vdash Pa_{1}\ldots a_{n}\).
Assume that \({\mathcal {M}}_{1}, \omega , \tau \nVdash Ra_{m}\), that M is a matrix where \(x_{m}\) is the first free variable in M and that \(a_{m}\) is the constant in \(M[a_{1}, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}]\) that replaces \(x_{m}\). Then: \({\mathcal {M}}_{2}, \omega , \tau \nVdash Ra_{m}\) and \({\mathcal {M}}_{1}, \omega , \tau \Vdash M[a_{1}, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}]\) iff \(\left\langle v_{1}(a_{1}), \ldots , v_{1}(a_{n})\right\rangle \in v_{1\omega \tau }(M)\) iff \(\left\langle v_{2}(a_{1}), \ldots , v_{2}(a_{n})\right\rangle \in v_{2\omega \tau }(M)\) iff \({\mathcal {M}}_{2}, \omega , \tau \Vdash M[a_{1}, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}]\).
Conjunctions, disjunctions and other truth-functional connectives.
Straightforward.
( ).
).  iff for some \(\omega '\) such that \({\mathfrak {R}}\omega \omega '\tau \), \({\mathcal {M}}_{1}, \omega ', \tau \Vdash B\) iff for some \(\omega '\) such that \({\mathfrak {R}}\omega \omega '\tau \), \({\mathcal {M}}_{2}, \omega ', \tau \Vdash B\) [the IH] iff
iff for some \(\omega '\) such that \({\mathfrak {R}}\omega \omega '\tau \), \({\mathcal {M}}_{1}, \omega ', \tau \Vdash B\) iff for some \(\omega '\) such that \({\mathfrak {R}}\omega \omega '\tau \), \({\mathcal {M}}_{2}, \omega ', \tau \Vdash B\) [the IH] iff  .
.
(\({\mathbb {G}}\)). \({\mathcal {M}}_{1}, \omega , \tau \Vdash {\mathbb {G}} B\) iff for all \(\tau '\) such that \(\tau < \tau '\), \({\mathcal {M}}_{1}, \omega , \tau ' \Vdash B\) iff for all \(\tau '\) such that \(\tau < \tau '\), \({\mathcal {M}}_{2}, \omega , \tau ' \Vdash B\) [the IH] iff \({\mathcal {M}}_{2}, \omega , \tau \Vdash {\mathbb {G}}B\).
The cases for the other alethic and temporal operators are similar.
(\({\mathcal {W}}_{c}D\)). A is of the form \({\mathcal {W}}_{c}D\). Suppose that \({\mathcal {M}}_{1}, \omega , \tau \Vdash {\mathcal {W}}_{c}D\). There are two cases: \({\mathcal {M}}_{1}, \omega , \tau \nVdash Rc\) or \({\mathcal {M}}_{1}, \omega , \tau \Vdash Rc\). Assume \({\mathcal {M}}_{1}, \omega , \tau \nVdash Rc\). Then \({\mathcal {M}}_{2}, \omega , \tau \nVdash Rc\). Hence, \({\mathcal {M}}_{2}, \omega , \tau \Vdash {\mathcal {W}}_{c}D\). And vice versa. Suppose \({\mathcal {M}}_{1}, \omega , \tau \Vdash Rc\). Then for all \(\omega '\) such that \({\mathfrak {A}}v_{1}(c)\omega \omega '\tau \): \({\mathcal {M}}_{1}, \omega ', \tau \Vdash D\). Consequently, for all \(\omega '\) such that \({\mathfrak {A}}v_{2}(c)\omega \omega '\tau \): \({\mathcal {M}}_{2}, \omega ', \tau \Vdash D\) [by assumption and the IH]. Furthermore, \({\mathcal {M}}_{2}, \omega , \tau \Vdash Rc\). Hence, \({\mathcal {M}}_{2}, \omega , \tau \Vdash {\mathcal {W}}_{c}D\). And vice versa. It follows that \({\mathcal {M}}_{1}, \omega , \tau \Vdash {\mathcal {W}}_{c}D\) iff \({\mathcal {M}}_{2}, \omega , \tau \Vdash {\mathcal {W}}_{c}D\).
(\({\mathcal {A}}_{c}D\)). A is of the form \({\mathcal {A}}_{c}D\). Assume that \({\mathcal {M}}_{1}, \omega , \tau \Vdash {\mathcal {A}}_{c}D\). There are two cases: \({\mathcal {M}}_{1}, \omega , \tau \nVdash Rc\) or \({\mathcal {M}}_{1}, \omega , \tau \Vdash Rc\). Suppose that \({\mathcal {M}}_{1}, \omega , \tau \nVdash Rc\). Then \({\mathcal {M}}_{2}, \omega , \tau \nVdash Rc\). Accordingly, \({\mathcal {M}}_{2}, \omega , \tau \Vdash {\mathcal {A}}_{c}D\). And vice versa. Assume that \({\mathcal {M}}_{1}, \omega , \tau \Vdash Rc\). Then for some \(\omega '\) such that \({\mathfrak {A}}v_{1}(c)\omega \omega '\tau \): \({\mathcal {M}}_{1}, \omega ', \tau \Vdash D\). It follows that for some \(\omega '\) such that \({\mathfrak {A}}v_{2}(c)\omega \omega '\tau \): \({\mathcal {M}}_{2}, \omega ', \tau \Vdash D\) [by assumption and the IH]. Furthermore, \({\mathcal {M}}_{2}, \omega , \tau \Vdash Rc\). Consequently, \({\mathcal {M}}_{2}, \omega , \tau \Vdash {\mathcal {A}}_{c}D\). And vice versa. In conclusion, \({\mathcal {M}}_{1}, \omega , \tau \Vdash {\mathcal {A}}_{c}D\) iff \({\mathcal {M}}_{2}, \omega , \tau \Vdash {\mathcal {A}}_{c}D\).
Other boulesic and doxastic operators. Similar.
(\(\Pi \)). \({\mathcal {M}}_{1}, \omega , \tau \Vdash \Pi xB\) iff for all \(k_{d} \in {\mathcal {L}}\), \({\mathcal {M}}_{1}, \omega , \tau \Vdash B[k_{d}/x]\) iff for all \(k_{d} \in {\mathcal {L}}\), \({\mathcal {M}}_{2}, \omega , \tau \Vdash B[k_{d}/x]\) [by the IH, and the fact that \(v_{1\omega \tau }(k_{d}) = v_{2\omega \tau }(k_{d}) = d\)] iff \({\mathcal {M}}_{2}, \omega , \tau \Vdash \Pi xB\).
The particular quantifier (\(\Sigma \)). Similar. \(\square \)
Lemma 2
(Denotation) Let \({\mathcal {M}} = \left\langle D, W, T, <, {\mathfrak {R}}, {\mathfrak {A}}, {\mathfrak {D}}, v\right\rangle \) be any model, let A be a formula of the language of \({\mathcal {M}}\) with at most one free variable, x, and let a and b be any two constants such that \(v(a) = v(b)\). Then for any \(\omega \in W\) and \(\tau \in T\): \({\mathcal {M}}, \omega , \tau \Vdash A[a/x]\) iff \({\mathcal {M}}, \omega , \tau \Vdash A[b/x]\).
Proof
The proof is by induction on the sentences in our language \({\mathcal {L}}\).
Atomic formulas. (Suppose that the formula has one occurrence of ‘a’ distinct from each \(a_{i}\) for the sake of illustration.)
\({\mathcal {M}}, \omega , \tau \Vdash Pa_{1}\ldots a\ldots a_{n}\) iff \(\left\langle v(a_{1}),\ldots ,v(a),\ldots ,v(a_{n})\right\rangle \in v_{\omega \tau }(P)\)
iff \(\left\langle v(a_{1}),\ldots ,v(b),\ldots ,v(a_{n})\right\rangle \in v_{\omega \tau }(P)\) iff \({\mathcal {M}}, \omega , \tau \Vdash Pa_{1}\ldots b\ldots a_{n}\).
Assume that \({\mathcal {M}}, \omega , \tau \nVdash Ra_{m}\), that M is a matrix where \(x_{m}\) is the first free variable in M and that \(a_{m}\) is the constant in \(M[a_{1}, \ldots , a, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}]\) (\(M[a_{1}, \ldots , b, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}]\)) that replaces \(x_{m}\). (Suppose that the formula has one occurrence of ‘a’ distinct from each \(a_{i}\) and that \(a_{m}\) is not a (b) for the sake of illustration.)
Then, \({\mathcal {M}}, \omega , \tau \Vdash M[a_{1}, \ldots , a, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}]\) iff \(\left\langle v(a_{1}), \ldots , v(a), \ldots , v(a_{n})\right\rangle \in v_{\omega \tau }(M)\) iff \(\left\langle v(a_{1}), \ldots , v(b), \ldots , v(a_{n})\right\rangle \in v_{\omega \tau }(M)\) iff \({\mathcal {M}}, \omega , \tau \) \(\Vdash \) \(M[a_{1}, \ldots , b, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}]\).
Conjunctions, disjunctions and other truth-functional connectives.
Straightforward.
( ).
).  iff for all \(\omega '\) such that \({\mathfrak {R}}\omega \omega '\tau \), \({\mathcal {M}}, \omega ', \tau \Vdash B[a/x]\) iff for all \(\omega '\) such that \({\mathfrak {R}}\omega \omega '\tau \), \({\mathcal {M}}, \omega ', \tau \Vdash B[b/x]\) [the IH] iff
iff for all \(\omega '\) such that \({\mathfrak {R}}\omega \omega '\tau \), \({\mathcal {M}}, \omega ', \tau \Vdash B[a/x]\) iff for all \(\omega '\) such that \({\mathfrak {R}}\omega \omega '\tau \), \({\mathcal {M}}, \omega ', \tau \Vdash B[b/x]\) [the IH] iff  .
.
(\(U\)). \({\mathcal {M}}, \omega , \tau \Vdash UB[a/x]\) iff for all \(\omega '\) and \(\tau '\), \({\mathcal {M}}, \omega ', \tau ' \Vdash B[a/x]\) iff for all \(\omega '\) and \(\tau '\), \({\mathcal {M}}, \omega ', \tau ' \Vdash B[b/x]\) [the IH] iff \({\mathcal {M}}, \omega , \tau \Vdash U B[b/x]\).
Other alethic and temporal operators. Similar.
(\({\mathcal {W}}_{t}\)). Either \({\mathcal {M}}, \omega , \tau \Vdash Rt\) or \({\mathcal {M}}, \omega , \tau \nVdash Rt\). We have already established the result in the latter case. Hence, suppose that \({\mathcal {M}}, \omega , \tau \Vdash Rt\). The term t cannot be a variable distinct from x, for x is the only free variable. Accordingly, t is either x or a constant. Suppose that t is x. Then \({\mathcal {M}}, \omega , \tau \Vdash {\mathcal {W}}_{x}D[a/x]\) iff \({\mathcal {M}}, \omega , \tau \Vdash {\mathcal {W}}_{a}D[a/x]\) iff for all \(\omega '\) such that \({\mathfrak {A}}v(a)\omega \omega '\tau \), \({\mathcal {M}}, \omega ', \tau \) \(\Vdash D[a/x]\) iff for all \(\omega '\) such that \({\mathfrak {A}}v(b)\omega \omega '\tau \), \({\mathcal {M}}, \omega ', \tau \Vdash D[b/x]\) [by the fact that \(v(a) = v(b)\) and the IH] iff \({\mathcal {M}}, \omega , \tau \Vdash {\mathcal {W}}_{b}D[b/x]\) iff \({\mathcal {M}}, \omega , \tau \Vdash {\mathcal {W}}_{x}D[b/x]\). Suppose that t is a constant, say c. Then \({\mathcal {M}}, \omega , \tau \Vdash {\mathcal {W}}_{c}D[a/x]\) iff for all \(\omega '\) such that \({\mathfrak {A}}v(c)\omega \omega '\tau \), \({\mathcal {M}}, \omega ', \tau \Vdash D[a/x]\) iff for all \(\omega '\) such that \({\mathfrak {A}}v(c)\omega \omega '\tau \), \({\mathcal {M}}, \omega ', \tau \Vdash D[b/x]\) [by the IH] iff \({\mathcal {M}}, \omega , \tau \Vdash {\mathcal {W}}_{c}D[b/x]\).
(\({\mathcal {C}}_{t}\)). Either \({\mathcal {M}}, \omega , \tau \Vdash Rt\) or \({\mathcal {M}}, \omega , \tau \nVdash Rt\). We have seen that the result holds in the latter case. So, suppose that \({\mathcal {M}}, \omega , \tau \Vdash Rt\). The term t cannot be a variable distinct from x, for x is the only free variable. Hence, t is either x or a constant. Suppose that t is x. Then \({\mathcal {M}}, \omega , \tau \Vdash {\mathcal {C}}_{x}D[a/x]\) iff \({\mathcal {M}}, \omega , \tau \Vdash {\mathcal {C}}_{a}D[a/x]\) iff for some \(\omega '\) such that \({\mathfrak {D}}v(a)\omega \omega '\tau \), \({\mathcal {M}}, \omega ', \tau \Vdash D[a/x]\) iff for some \(\omega '\) such that \({\mathfrak {D}}v(b)\omega \omega '\tau \), \({\mathcal {M}}, \omega ', \tau \Vdash D[b/x]\) [by the fact that \(v(a) = v(b)\) and the IH] iff \({\mathcal {M}}, \omega , \tau \Vdash {\mathcal {C}}_{b}D[b/x]\) iff \({\mathcal {M}}, \omega , \tau \Vdash {\mathcal {C}}_{x}D[b/x]\). Assume that t is a constant, say c. Then \({\mathcal {M}}, \omega , \tau \Vdash {\mathcal {C}}_{c}D[a/x]\) iff for some \(\omega '\) such that \({\mathfrak {D}}v(c)\omega \omega '\tau \), \({\mathcal {M}}, \omega ', \tau \Vdash D[a/x]\) iff for some \(\omega '\) such that \({\mathfrak {D}}v(c)\omega \omega '\tau \), \({\mathcal {M}}, \omega ', \tau \Vdash D[b/x]\) [by the IH] iff \({\mathcal {M}}, \omega , \tau \Vdash {\mathcal {C}}_{c}D[b/x]\).
Other boulesic and doxastic operators. Similar.
(\(\Pi \)). Let A be of the form \(\Pi yB\). If \(x = y\), then \(A[a/x] = A[b/x] = A\); so the result is trivial. Thus, suppose that x and y are distinct. Then, \((\Pi yB)[b/x] = \Pi y(B[b/x])\) and \((B[b/x])[a/y] = (B[a/y])[b/x]\). \({\mathcal {M}}, \omega , \tau \Vdash (\Pi yB)[a/x]\) iff \({\mathcal {M}}, \omega , \tau \Vdash \Pi y(B[a/x])\) iff for all \(k_{d} \in \mathcal {L(M)}\), \({\mathcal {M}}, \omega , \tau \Vdash (B[a/x])[k_{d}/y]\) iff for all \(k_{d} \in \mathcal {L(M)}\), \({\mathcal {M}}, \omega , \tau \Vdash (B[k_{d}/y])[a/x]\) iff for all \(k_{d} \in \mathcal {L(M)}\), \({\mathcal {M}}, \omega , \tau \Vdash (B[k_{d}/y])[b/x]\) [the IH] iff for all \(k_{d} \in \mathcal {L(M)}\), \({\mathcal {M}}, \omega , \tau \Vdash (B[b/x])[k_{d}/y]\) iff \({\mathcal {M}}, \omega , \tau \Vdash \Pi y(B[b/x])\) iff \({\mathcal {M}}, \omega , \tau \Vdash (\Pi yB)[b/x]\).
The particular quantifier (\(\Sigma \)). Similar. \(\square \)
6.1 Soundness Theorem
Let \({\mathcal {M}}\) \(=\) \(\left\langle D, W, T, <, {\mathfrak {R}}, {\mathfrak {A}}, {\mathfrak {D}}, v\right\rangle \) be a model and let \({\mathcal {B}}\) be a branch of a tableau. Then \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\) iff there is a function f from \(w_{0}, w_{1}, w_{2}, \ldots \) to W, and a function g from \(t_{0}, t_{1}, t_{2}, \ldots \) to T such that
-
(i)
A is true in \(f(w_{i})\) at \(g(t_{j})\) in \({\mathcal {M}}\), for every node \(A, w_{i}t_{j}\) on \({\mathcal {B}}\);
-
(ii)
if \(Rw_{i}w_{j}t_{k}\) is on \({\mathcal {B}}\), then \({\mathfrak {R}}f(w_{i})f(w_{j})g(t_{k})\) in \({\mathcal {M}}\);
-
(iii)
if \(Acw_{i}w_{j}t_{k}\) is on \({\mathcal {B}}\), then \({\mathfrak {A}}v(c)f(w_{i})f(w_{j})g(t_{k})\) in \({\mathcal {M}}\);
-
(iv)
if \(Dcw_{i}w_{j}t_{k}\) is on \({\mathcal {B}}\), then \({\mathfrak {D}}v(c)f(w_{i})f(w_{j})g(t_{k})\) in \({\mathcal {M}}\);
-
(v)
if \(t_{i} < t_{j}\) is on \({\mathcal {B}}\), then \(g(t_{i}) < g(t_{j})\) in \({\mathcal {M}}\);
-
(vi)
if \(t_{i} = t_{j}\) is on \({\mathcal {B}}\), then \(g(t_{i}) = g(t_{j})\) in \({\mathcal {M}}\).
-
(vii)
if \(w_{i} = w_{j}\) is on \({\mathcal {B}}\), then \(f(w_{i}) = f(w_{j})\) in \({\mathcal {M}}\);
We shall say that f and g show that \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\) if these conditions are fulfilled.
Lemma 3
(Soundness Lemma) Let \({\mathcal {B}}\) be a branch of a tableau and let \({\mathcal {M}}\) be a model. If \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\) and a tableau rule is applied to it, then there is a model \({\mathcal {M}}'\) and an extension of \({\mathcal {B}}\), \({\mathcal {B}}'\), such that \({\mathcal {B}}'\) is satisfiable in \({\mathcal {M}}'\).
Proof
The proof is by induction on the height of the deduction. Let f and g be functions that show that the branch \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\).
Connectives and modal and temporal operators. Straightforward.
(\({\mathcal {W}}\)). Suppose that \(Rc, w_{i}t_{k}\), \({\mathcal {W}}_{c}D, w_{i}t_{k}\), and \(Acw_{i}w_{j}t_{k}\) are on \({\mathcal {B}}\), and that we apply the \({\mathcal {W}}\)-rule to give an extended branch containing \(D, w_{j}t_{k}\). Since \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\), \({\mathcal {W}}_{c}D\) and Rc are true in \(f(w_{i})\) at \(g(t_{k})\). Moreover, for any \(w_{i}\) and \(w_{j}\) such that \(Acw_{i}w_{j}t_{k}\) is on \({\mathcal {B}}\), \({\mathfrak {A}}v(c)f(w_{i})f(w_{j})g(t_{k})\). Thus by the truth conditions for \({\mathcal {W}}_{c}D\), D is true in \(f(w_{j})\) at \(g(t_{k})\).
(\({\mathcal {C}}\)). Suppose that \(Rc, w_{i}t_{k}\), \({\mathcal {C}}_{c}A, w_{i}t_{k}\) are on \({\mathcal {B}}\) and that we apply the \({\mathcal {C}}\)-rule to extend the branch with \(Dcw_{i}w_{j}t_{k}\) and \(A, w_{j}t_{k}\). Since \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\), \({\mathcal {C}}_{c}A\) and Rc are true in \(f(w_{i})\) at \(g(t_{k})\). Accordingly, for some \(\omega \) in W, \({\mathfrak {A}}v(c)f(w_{i})\omega g(t_{k})\) and A is true in \(\omega \) at \(g(t_{k})\) [by the truth conditions for \({\mathcal {C}}_{c}A\) and the fact that Rc is true in \(f(w_{i})\) at \(g(t_{k})\)]. Let \(f'\) be the same as f except that \(f'(w_{j}) = \omega \). Since f and \(f'\) differ only at \(w_{j}\), \(f'\) and g show that \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\). By definition \({\mathfrak {A}}v(c)f'(w_{i})f'(w_{j})g(t_{k})\), and A is true in \(f'(w_{j})\) at \(g(t_{k})\).
Other boulesic and doxastic rules. Similar.
(\(\Pi \)). Assume that \(\Pi xA, w_{i}t_{j}\) is on \({\mathcal {B}}\) and that we apply the \(\Pi \)-rule to give an extended branch that includes a node of the form \(A[a/x], w_{i}t_{j}\). Since \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\), \({\mathcal {M}}\) makes \(\Pi xA\) true in \(f(w_{i})\) at \(g(t_{j})\). Accordingly, \(A[k_{d}/x]\) is true in \(f(w_{i})\) at \(g(t_{j})\) in \({\mathcal {M}}\), for all \(k_{d} \in \mathcal {L(M)}\). Let d be such that \(v(a) = v(k_{d})\). By the Denotation Lemma, A[a/x] is true in \(f(w_{i})\) at \(g(t_{j})\) in \({\mathcal {M}}\). Consequently, we can take \({\mathcal {M}}'\) to be \({\mathcal {M}}\).
(\(\Sigma \)). Suppose that \(\Sigma xA, w_{i}t_{j}\) is on \({\mathcal {B}}\) and that we apply the \(\Sigma \)-rule to extend the branch with \(A[c/x], w_{i}t_{j}\) (where c is new). \(\Sigma xA\) is true in \(f(w_{i})\) at \(g(t_{j})\) in \({\mathcal {M}}\), for \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\). So, there is some \(k_{d} \in \mathcal {L(M)}\) such that \({\mathcal {M}}\) makes \(A[k_{d}/x]\) true in \(f(w_{i})\) at \(g(t_{j})\). Let \({\mathcal {M}}' = \left\langle D, W, T, <, {\mathfrak {R}}, {\mathfrak {A}}, {\mathfrak {D}}, v'\right\rangle \) be the same as \({\mathcal {M}}\) except that \(v'(c) = d\). Since c does not occur in \(A[k_{d}/x]\), \(A[k_{d}/x]\) is true in \(f(w_{i})\) at \(g(t_{j})\) in \({\mathcal {M}}'\), by the Locality Lemma. Consequently, A[c/x] is true in \(f(w_{i})\) at \(g(t_{j})\) in \({\mathcal {M}}'\) by the Denotation Lemma and the fact that \(v'(c) = d = v'(k_{d})\). Furthermore, \({\mathcal {M}}'\) makes all other formulas on the branch true at their respective world-moment pairs as well, by the Locality Lemma. For c does not occur in any other formula on the branch.
The cases for (\(\lnot \Pi \)) and (\(\lnot \Sigma \)) are similar.
Accessibility rules. Let us consider three examples for the sake of illustration.
( ). Suppose that \(Acw_{i}w_{j}t_{l}\) is on \({\mathcal {B}}\), and that we apply (
). Suppose that \(Acw_{i}w_{j}t_{l}\) is on \({\mathcal {B}}\), and that we apply ( ) to give an extended branch containing \(Dcw_{j}w_{k}t_{l}\) and \(Rw_{j}w_{k}t_{l}\), where \(w_{k}\) is new. Since \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\), \({\mathfrak {R}}f(w_{i})f(w_{j})g(t_{l})\). Hence, for some \(\omega \) in W, \({\mathfrak {D}}v(c)f(w_{j})\omega g(t_{l})\) and \({\mathfrak {R}}f(w_{j})\omega g(t_{l})\) since \({\mathcal {M}}\) satisfies condition
) to give an extended branch containing \(Dcw_{j}w_{k}t_{l}\) and \(Rw_{j}w_{k}t_{l}\), where \(w_{k}\) is new. Since \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\), \({\mathfrak {R}}f(w_{i})f(w_{j})g(t_{l})\). Hence, for some \(\omega \) in W, \({\mathfrak {D}}v(c)f(w_{j})\omega g(t_{l})\) and \({\mathfrak {R}}f(w_{j})\omega g(t_{l})\) since \({\mathcal {M}}\) satisfies condition  . Let \(f'\) be the same as f except that \(f'(w_{k}) = \omega \). Since \(w_{k}\) does not occur on \({\mathcal {B}}\), \(f'\) and g show that \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\). Moreover, \({\mathfrak {D}}v(c)f(w_{j})f(w_{k})g(t_{l})\) and \({\mathfrak {R}}f(w_{j})f(w_{k})g(t_{l})\) by construction. Consequently, \(f'\) and g show that the extension of \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\).
. Let \(f'\) be the same as f except that \(f'(w_{k}) = \omega \). Since \(w_{k}\) does not occur on \({\mathcal {B}}\), \(f'\) and g show that \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\). Moreover, \({\mathfrak {D}}v(c)f(w_{j})f(w_{k})g(t_{l})\) and \({\mathfrak {R}}f(w_{j})f(w_{k})g(t_{l})\) by construction. Consequently, \(f'\) and g show that the extension of \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\).
(\(T-{\mathcal {W}}{\mathbb {G}}dD\)). Suppose that \(Acw_{i}w_{j}t_{l}\) and \(t_{l} < t_{m}\) are on \({\mathcal {B}}\), and that we apply (\(T-{\mathcal {W}}{\mathbb {G}}dD\)) to give an extended branch containing \(Dcw_{j}w_{k}t_{m}\), where \(w_{k}\) is new. Since \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\), \({\mathfrak {A}}v(c)f(w_{i})f(w_{j})g(t_{l})\) and \(g(t_{l}) < g(t_{m})\). Accordingly, for some \(\omega \) in W, \({\mathfrak {D}}v(c)f(w_{j})\omega g(t_{m})\) since \({\mathcal {M}}\) satisfies condition \(C-{\mathcal {W}}{\mathbb {G}}dD\). Let \(f'\) be the same as f except that \(f'(w_{k}) = \omega \). Since \(w_{k}\) does not occur on \({\mathcal {B}}\), \(f'\) and g show that \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\). Then, by construction \({\mathfrak {D}}v(c)f(w_{j})f(w_{k})g(t_{m})\). Consequently, \(f'\) and g show that the extension of \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\).
( ). Suppose that \(Acw_{i}w_{j}t_{l}\), \(t_{l} < t_{m}\) and \(Dcw_{j}w_{k}t_{m}\) are on \({\mathcal {B}}\), and that we apply (
). Suppose that \(Acw_{i}w_{j}t_{l}\), \(t_{l} < t_{m}\) and \(Dcw_{j}w_{k}t_{m}\) are on \({\mathcal {B}}\), and that we apply ( ) to give an extended branch containing \(Rw_{j}w_{k}t_{m}\). Since \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\), \({\mathfrak {A}}v(c)f(w_{i})f(w_{j})g(t_{l})\), \(g(t_{l}) < g(t_{m})\) and \({\mathfrak {D}}v(c)f(w_{j})f(w_{k})g(t_{m})\). Accordingly, \({\mathfrak {R}}f(w_{j})f(w_{k})g(t_{m})\), for \({\mathcal {M}}\) satisfies condition
) to give an extended branch containing \(Rw_{j}w_{k}t_{m}\). Since \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\), \({\mathfrak {A}}v(c)f(w_{i})f(w_{j})g(t_{l})\), \(g(t_{l}) < g(t_{m})\) and \({\mathfrak {D}}v(c)f(w_{j})f(w_{k})g(t_{m})\). Accordingly, \({\mathfrak {R}}f(w_{j})f(w_{k})g(t_{m})\), for \({\mathcal {M}}\) satisfies condition  . It follows that the extension of \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\). \(\square \)
. It follows that the extension of \({\mathcal {B}}\) is satisfiable in \({\mathcal {M}}\). \(\square \)
Theorem 1
(Soundness Theorem) Every system S in this paper is sound with respect to its semantics.
Proof
Let \({{\varvec{M}}}\) be the class of models that corresponds to S and assume that B does not follow from \(\Gamma \) in \({{\varvec{M}}}\). Then there is some possible world \(\omega \) and some moment in time \(\tau \) in some model \({\mathcal {M}}\) in \({{\varvec{M}}}\) such that every premise in \(\Gamma \) is true in \(\omega \) at \(\tau \) and the conclusion B is false in \(\omega \) at \(\tau \). Consider an S-tableau whose initial list consists of \(A, w_{0}t_{0}\) for every \(A \in \Gamma \) and \(\lnot B, w_{0}t_{0}\), where ‘\(w_{0}\)’ refers to \(\omega \) and ‘\(t_{0}\)’ refers to \(\tau \). Then the initial list is satisfiable in \({\mathcal {M}}\). Every time we apply a rule to this list it produces at least one extension that is satisfiable in a model \({\mathcal {M}}'\) in \({{\varvec{M}}}\) (by the Soundness Lemma). So, we can find a whole branch such that every initial section of this branch is satisfiable in some model \({\mathcal {M}}''\) in \({{\varvec{M}}}\). If this branch is closed, then some sentence is both true and false in some possible world at some time in \({\mathcal {M}}''\). Nevertheless, this is impossible. Hence, the tableau is open. Accordingly, B is not derivable from \(\Gamma \) in S. Therefore, if B is derivable from \(\Gamma \) in S, then B follows from \(\Gamma \) in \({{\varvec{M}}}\). \(\square \)
6.2 Completeness Theorem
We now turn to our completeness theorems. This section establishes that every system in this paper is complete with respect to its semantics. However, before we consider the actual proofs, we will introduce some new concepts.
Intuitively, a complete tableau as a tableau where every rule that can be applied has been applied. Different systems contain different tableau rules. So, a tableau that is complete in one systems is not necessarily complete in another system. There can also be several different (complete) tableaux for the same sentence or set of sentences in one and the same system since the tableau rules can be applied in different orders. We shall use the following method to produce a complete tableau.Footnote 5 (1) For every open branch in turn, begin at its root and move towards its tip. Apply any rule that produces something new to the branch. If a rule has multiple applications (such as \(U\) and \(\Pi \)), then make all possible applications at once. (2) When we have done this for all open branches in the tableau, we repeat the process. Some rules, such as \(T-bD\) and  (\(T-FD\)), introduce new ‘possible worlds’ (moments in time). Every rule of this kind is applied once at the tip of every open branch at the end of every cycle (given that it produces something new). If a system includes more than one rule of this kind (R1, R2 \(\ldots \)), we apply R1 the first time, R2 the second time, etc. Before we conclude a cycle in this procedure we split the end of every open branch in the tree and add \(Rc, w_{i}t_{j}\) to the left node and \(\lnot Rc, w_{i}t_{j}\) to the right node, for every constant c (that occurs as an index to some boulesic or doxastic operator on the tree), \(w_{i}\) and \(t_{j}\) on the branch. If there is still something to do according to this ‘algorithm’, the tableau is incomplete; if not, it is complete.
(\(T-FD\)), introduce new ‘possible worlds’ (moments in time). Every rule of this kind is applied once at the tip of every open branch at the end of every cycle (given that it produces something new). If a system includes more than one rule of this kind (R1, R2 \(\ldots \)), we apply R1 the first time, R2 the second time, etc. Before we conclude a cycle in this procedure we split the end of every open branch in the tree and add \(Rc, w_{i}t_{j}\) to the left node and \(\lnot Rc, w_{i}t_{j}\) to the right node, for every constant c (that occurs as an index to some boulesic or doxastic operator on the tree), \(w_{i}\) and \(t_{j}\) on the branch. If there is still something to do according to this ‘algorithm’, the tableau is incomplete; if not, it is complete.
Definition 9
(Induced Model) Suppose that \({\mathcal {B}}\) is an open branch in a complete tableau and that I is the set of numbers on \({\mathcal {B}}\) immediately preceded by a ‘t’. Let \(i \rightleftharpoons j\) iff \(i = j\), or ‘\(t_{i} = t_{j}\)’ or ‘\(t_{j} = t_{i}\)’ is on \({\mathcal {B}}\). \(\rightleftharpoons \) is an equivalence relation and [i] is the equivalence class of i. Moreover, let K be the set of numbers on \({\mathcal {B}}\) immediately preceded by a ‘w’. We shall say that \(k \approx l\) just in case \(k = l\), or ‘\(w_{k} = w_{l}\)’ or ‘\(w_{l} = w_{k}\)’ occurs on \({\mathcal {B}}\). \(\approx \) is an equivalence relation and [k] is the equivalence class of k. Furthermore, let C be the set of all constants on \({\mathcal {B}}\). We shall say that \(a \sim b\) iff \(a = b, w_{0}t_{0}\) occurs on the branch; \(a \sim b\) is an equivalence relation and [a] is the equivalence class of a under \(\sim \). The model \({\mathcal {M}} = \left\langle D, W, T, <, {\mathfrak {R}}, {\mathfrak {A}}, {\mathfrak {D}}, v\right\rangle \) induced by \({\mathcal {B}}\) is defined in the following way. \(D = \left\{ [a]: a \in C\right\} \) (or, if \(C = \emptyset \), \(D = \left\{ o\right\} \) for an arbitrary o). \(W = \left\{ \omega _{[k]}: k \in K \right\} \), \(T = \left\{ \tau _{[i]}: i \in I\right\} \), \(\tau _{[i]} < \tau _{[j]}\) iff \(t_{i} < t_{j}\) occurs on \({\mathcal {B}}\), \({\mathfrak {R}}\omega _{[i]}\omega _{[j]}\tau _{[k]}\) iff \(Rw_{i}w_{j}t_{k}\) occurs on \({\mathcal {B}}\), \({\mathfrak {A}}v(a)\omega _{[i]}\omega _{[j]}\tau _{[k]}\) iff \(Aaw_{i}w_{j}t_{k}\) occurs on \({\mathcal {B}}\) and \({\mathfrak {D}}v(a)\omega _{[i]}\omega _{[j]}\tau _{[k]}\) iff \(Daw_{i}w_{j}t_{k}\) occurs on \({\mathcal {B}}\). \(v(a) = [a]\), and \(\left\langle [a_{1}],\ldots ,[a_{n}]\right\rangle \in v_{\omega _{[i]}\tau _{[j]}}(P)\) iff \(Pa_{1}\ldots a_{n}, w_{i}t_{j}\) is on \({\mathcal {B}}\), given that P is any n-place predicate other than identity. (o is not in the extension of anything.) If \(\lnot Ra_{m}, w_{i}t_{j}\) occurs on \({\mathcal {B}}\) and M is an n-place matrix with instantiations on the branch (where \(x_{m}\) is the first free variable in M and \(a_{m}\) is the constant in \(M[a_{1}, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}]\) that replaces \(x_{m}\)), then \(\left\langle [a_{1}], \ldots , [a_{n}]\right\rangle \) \(\in \) \(v_{\omega _{[i]}\tau _{[j]}}(M)\) iff \(M[a_{1}, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}], w_{i}t_{j}\) is on \({\mathcal {B}}\). (This is well defined thanks to the identity rules.)
If our tableau system does not contain \(T-FC\), \(T-PC\) or \(T-C\), \(\rightleftharpoons \) is reduced to identity and \([i] = \left\{ i\right\} \). Therefore, we may take T to be \(\left\{ \tau _{i}: t_{i} \; occurs \; on \; {\mathcal {B}}\right\} \) in such systems and dispense with the equivalence classes. Moreover, if our tableau system does not include any ‘world identity’ rules, \(\approx \) is reduced to identity and \([k] = \left\{ k\right\} \).Footnote 6 Accordingly, in such systems, we may take W to be \(\left\{ \omega _{i}: w_{i} \; occurs \; on \; b\right\} \) and dispense with the equivalence classes.
Lemma 4
(Completeness Lemma) Suppose that \({\mathcal {B}}\) is an open branch in a complete tableau and that \({\mathcal {M}}\) is a model induced by \({\mathcal {B}}\). Then, for every formula A:
-
(i)
if \(A, w_{i}t_{j}\) is on \({\mathcal {B}}\), then \({\mathcal {M}}, \omega _{[i]}, \tau _{[j]} \Vdash A\), and
-
(ii)
if \(\lnot A, w_{i}t_{j}\) is on \({\mathcal {B}}\), then \({\mathcal {M}}, \omega _{[i]}, \tau _{[j]} \nVdash A\).
Proof
The lemma is established by induction on the complexity of A.
(i) Atomic formulas.
\(Pa_{1}\ldots a_{n}, w_{i}t_{j}\) is on \({\mathcal {B}}\) \(\Rightarrow \) \(\left\langle [a_{1}],\ldots ,[a_{n}]\right\rangle \in v_{\omega _{[i]}\tau _{[j]}}(P)\) \(\Rightarrow \)
\(\left\langle v(a_{1}),\ldots ,v(a_{n})\right\rangle \) \(\in \) \(v_{\omega _{[i]}\tau _{[j]}}(P)\) \(\Rightarrow \) \({\mathcal {M}}, \omega _{[i]}, \tau _{[j]} \Vdash Pa_{1}\ldots a_{n}\).
\(a = b, w_{i}t_{j}\) is on \({\mathcal {B}}\) \(\Rightarrow \) \(a \sim b\) (\(T-N=\)) \(\Rightarrow \) \([a] = [b]\) \(\Rightarrow \) \(v(a) = v(b)\) \(\Rightarrow \) \({\mathcal {M}}, \omega _{[i]}, \tau _{[j]} \Vdash a = b\).
Suppose that M is a matrix where \(x_{m}\) is the first free variable and \(a_{m}\) is the constant in \(M[a_{1}, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}]\) that replaces \(x_{m}\) and that \({\mathcal {M}}, \omega _{[i]}, \tau _{[j]} \nVdash Ra_{m}\).
Then: \(M[a_{1}, \ldots , a_{n} / {\mathop {x}\limits ^{\rightarrow }}], w_{i}t_{j}\) occurs on \({\mathcal {B}}\) \(\Rightarrow \) \(\left\langle [a_{1}], \ldots , [a_{n}]\right\rangle \) \(\in \) \(v_{\omega _{[i]}\tau _{[j]}}(M)\)
\(\Rightarrow \) \(\left\langle v(a_{1}), \ldots , v(a_{n})\right\rangle \) \(\in \) \(v_{\omega _{[i]}\tau _{[j]}}(M)\) \(\Rightarrow \) \({\mathcal {M}}, \omega _{[i]}, \tau _{[j]} \Vdash M[a_{1}, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}]\).
Other truth-functional connectives and modal and temporal operators. Straightforward.
Boulesic operators. (\({\mathcal {W}}\)). Suppose \({\mathcal {W}}_{c}D, w_{i}t_{k}\) is on \({\mathcal {B}}\). Moreover, suppose that \(Rc, w_{i}t_{k}\) is not on \({\mathcal {B}}\). Then \(\lnot Rc, w_{i}t_{k}\) is on \({\mathcal {B}}\) [by CUTR]. Hence, \({\mathcal {W}}_{c}D\) is true in \(\omega _{[i]}\) at \(\tau _{[k]}\) by definition and previous steps. Suppose \(Rc, w_{i}t_{k}\) is on \({\mathcal {B}}\). Then since the tableau is complete, the \({\mathcal {W}}\)-rule has been applied and for every \(w_{j}\) such that \(Acw_{i}w_{j}t_{k}\) is on \({\mathcal {B}}\), \(D, w_{j}t_{k}\) is on \({\mathcal {B}}\). By the induction hypothesis, D is true in every \(\omega _{[j]}\) at \(\tau _{[k]}\) such that \({\mathfrak {A}}v(c)\omega _{[i]}\omega _{[j]}\tau _{[k]}\). Since \(Rc, w_{i}t_{k}\) is on \({\mathcal {B}}\), v(c) is perfectly rational in \(\omega _{[i]}\) at \(\tau _{[k]}\). It follows that \({\mathcal {W}}_{c}D\) is true in \(\omega _{[i]}\) at \(\tau _{[k]}\), as required.
Other boulesic operators. Similar.
Doxastic operators. (\({\mathcal {C}}\)). Suppose \({\mathcal {C}}_{a}D, w_{i}t_{k}\) is on \({\mathcal {B}}\). Furthermore, assume that \(Ra, w_{i}t_{k}\) is not on \({\mathcal {B}}\). Then \(\lnot Ra, w_{i}t_{k}\) is on \({\mathcal {B}}\) [by CUTR]. Accordingly, \({\mathcal {C}}_{a}D\) is true in \(\omega _{[i]}\) at \(\tau _{[k]}\) by definition and previous steps. Suppose \(Ra, w_{i}t_{k}\) is on \({\mathcal {B}}\). Then the \({\mathcal {C}}\)-rule has been applied to \({\mathcal {C}}_{a}D, w_{i}t_{k}\), since the tableau is complete. Hence, for some new \(w_{j}\), \(Daw_{i}w_{j}t_{k}\) and \(D, w_{j}t_{k}\) occur on \({\mathcal {B}}\). By the induction hypothesis, \({\mathfrak {D}}v(a)\omega _{[i]}\omega _{[j]}\tau _{[k]}\), and D is true in \(\omega _{[j]}\) at \(\tau _{[k]}\). Since \(Ra, w_{i}t_{k}\) is on \({\mathcal {B}}\), v(a) is perfectly rational in \(\omega _{[i]}\) at \(\tau _{[k]}\). Hence, \({\mathcal {C}}_{a}D\) is true in \(\omega _{[i]}\) at \(\tau _{[k]}\), as required.
The case for (\({\mathcal {B}}\)) is similar.
Quantifiers. (\(\Pi \)). Suppose that \(\Pi xD, w_{i}t_{j}\) is on the branch. Since the tableau is complete, (\(\Pi \)) has been applied. Hence, for all \(c \in C\), \(D[c/x], w_{i}t_{j}\) is on the branch. Consequently, \({\mathcal {M}}, \omega _{[i]}, \tau _{[j]} \Vdash D[c/x]\) for all \(c \in C\) [by the induction hypothesis]. If \(k_{d} \in \mathcal {L(M)}\), then for some \(c \in C\), \(v(c) = v(k_{d})\). By the Denotation Lemma, for all \(k_{d} \in \mathcal {L(M)}\), \({\mathcal {M}}, \omega _{[i]}, \tau _{[j]} \Vdash D[k_{d}/x]\). Consequently, \({\mathcal {M}}, \omega _{[i]}, \tau _{[j]} \Vdash \Pi xD\).
The case for \(\Sigma \) is similar.
(ii) Atomic formulas.
\(\lnot Pa_{1}\ldots a_{n}, w_{i}t_{j}\) is on \({\mathcal {B}}\) \(\Rightarrow \) \(Pa_{1}\ldots a_{n}, w_{i}t_{j}\) is not on \({\mathcal {B}}\) (\({\mathcal {B}}\) open) \(\Rightarrow \) \(\left\langle [a_{1}],\ldots ,[a_{n}]\right\rangle \notin v_{\omega _{[i]}\tau _{[j]}}(P)\) \(\Rightarrow \) \(\left\langle v(a_{1}),\ldots ,v(a_{n})\right\rangle \notin v_{\omega _{[i]}\tau _{[j]}}(P)\) \(\Rightarrow \) \({\mathcal {M}}, \omega _{[i]}, \tau _{[j]}\) \(\nVdash Pa_{1}\ldots a_{n}\).
\(\lnot a = b, w_{i}t_{j}\) is on \({\mathcal {B}}\) \(\Rightarrow \) \(a = b, w_{0}t_{0}\) is not on \({\mathcal {B}}\) (\({\mathcal {B}}\) open) \(\Rightarrow \) it is not the case that \(a \sim b\) \(\Rightarrow \) \([a] \ne [b]\) \(\Rightarrow \) \(v(a) \ne v(b)\) \(\Rightarrow \) \({\mathcal {M}}, \omega _{[i]}, \tau _{[j]} \nVdash a = b\).
Suppose that M is a matrix where \(x_{m}\) is the first free variable and \(a_{m}\) is the constant in \(M[a_{1}, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}]\) that replaces \(x_{m}\) and that \({\mathcal {M}}, \omega _{[i]}, \tau _{[j]} \nVdash Ra_{m}\). Then: \(\lnot M[a_{1}, \ldots , a_{n} /{\mathop {x}\limits ^{\rightarrow }}], w_{i}t_{j}\) occurs on \({\mathcal {B}}\) \(\Rightarrow \) \(M[a_{1}, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}], w_{i}t_{j}\) is not on \({\mathcal {B}}\) (\({\mathcal {B}}\) open) \(\Rightarrow \) \(\left\langle [a_{1}], \ldots , [a_{n}]\right\rangle \) \(\notin \) \(v_{\omega _{[i]}\tau _{[j]}}(M)\) \(\Rightarrow \) \(\left\langle v(a_{1}), \ldots , v(a_{n})\right\rangle \) \(\notin \) \(v_{\omega _{[i]}\tau _{[j]}}(M)\) \(\Rightarrow \) \({\mathcal {M}}, \omega _{[i]}, \tau _{[j]} \nVdash M[a_{1}, \ldots , a_{n}/{\mathop {x}\limits ^{\rightarrow }}]\).
Other truth-functional connectives and modal and temporal operators. Straightforward.
Boulesic operators. (\(\lnot {\mathcal {W}}\)). Suppose \(\lnot {\mathcal {W}}_{c}D, w_{i}t_{k}\) is on \({\mathcal {B}}\). Furthermore, suppose that \(Rc, w_{i}t_{k}\) is not on \({\mathcal {B}}\). Then \(\lnot Rc, w_{i}t_{k}\) is on \({\mathcal {B}}\) [by CUTR]. Hence, \({\mathcal {W}}_{c}D\) is false in \(\omega _{[i]}\) at \(\tau _{[k]}\) by definition and previous steps. Suppose \(Rc, w_{i}t_{k}\) is on \({\mathcal {B}}\). Then the \(\lnot {\mathcal {W}}\)-rule has been applied to \(\lnot {\mathcal {W}}_{c}D, w_{i}t_{k}\) and we have \({\mathcal {A}}_{c}\lnot D, w_{i}t_{k}\) on \({\mathcal {B}}\). For the branch is complete. Then the \({\mathcal {A}}\)-rule has been applied to \({\mathcal {A}}_{c}\lnot D, w_{i}t_{k}\), since the branch is complete. Hence, for some new \(w_{j}\), \(Acw_{i}w_{j}t_{k}\) and \(\lnot D, w_{j}t_{k}\) occur on \({\mathcal {B}}\). By the induction hypothesis, \({\mathfrak {A}}v(c)\omega _{[i]}\omega _{[j]}\tau _{[k]}\), and D is false in \(\omega _{[j]}\) at \(\tau _{[k]}\). Since \(Rc, w_{i}t_{k}\) is on \({\mathcal {B}}\), v(c) is perfectly rational in \(\omega _{[i]}\) at \(\tau _{[k]}\). Consequently, \({\mathcal {W}}_{c}D\) is false in \(\omega _{[i]}\) at \(\tau _{[k]}\), as required.
Other boulesic operators. Similar.
Doxastic operators. (\(\lnot {\mathcal {C}}\)). Suppose \(\lnot {\mathcal {C}}_{a}D, w_{i}t_{k}\) is on \({\mathcal {B}}\). Moreover, assume that \(Ra, w_{i}t_{k}\) is not on \({\mathcal {B}}\). Then \(\lnot Ra, w_{i}t_{k}\) is on \({\mathcal {B}}\) [by CUTR]. Therefore, \({\mathcal {C}}_{a}D\) is false in \(\omega _{[i]}\) at \(\tau _{[k]}\) by definition and previous steps. Suppose \(Ra, w_{i}t_{k}\) occurs on \({\mathcal {B}}\). Then (\(\lnot {\mathcal {C}}\)) has been applied to \(\lnot {\mathcal {C}}_{a}D, w_{i}t_{k}\) and we have \({\mathcal {B}}_{a}\lnot D, w_{i}t_{k}\) on \({\mathcal {B}}\), for the branch is complete. Again, since the tableau is complete, the \({\mathcal {B}}\)-rule has been applied and for every \(w_{j}\) such that \(Daw_{i}w_{j}t_{k}\) is on \({\mathcal {B}}\), \(\lnot D, w_{j}t_{k}\) is on \({\mathcal {B}}\). Consequently, D is false in every \(\omega _{[j]}\) at \(\tau _{[k]}\) such that \({\mathfrak {D}}v(a)\omega _{[i]}\omega _{[j]}\tau _{[k]}\) (by the induction hypothesis). Since \(Ra, w_{i}t_{k}\) is on \({\mathcal {B}}\), v(a) is perfectly rational in \(\omega _{[i]}\) at \(\tau _{[k]}\). It follows that \({\mathcal {C}}_{a}D\) is false in \(\omega _{[i]}\) at \(\tau _{[k]}\), as required.
(\(\lnot {\mathcal {B}}\)). Similar.
Quantifiers.
(\(\lnot \Pi \)). Suppose that \(\lnot \Pi xD, w_{i}t_{j}\) is on the branch. Since the tableau is complete, (\(\lnot \Pi \)) has been applied. Hence, \(\Sigma x\lnot D, w_{i}t_{j}\) is on the branch. Again, since the tableau is complete (\(\Sigma \)) has been applied. Accordingly, for some c, \(\lnot D[c/x], w_{i}t_{j}\) is on the branch. Hence, \({\mathcal {M}}, \omega _{[i]}, \tau _{[j]} \nVdash D[c/x]\), by (IH). For some \(k_{d} \in \mathcal {L(M)}\), \(v(c) = d\), and \(v(k_{d}) = d\). Consequently, \({\mathcal {M}}, \omega _{[i]}, \tau _{[j]} \nVdash D[k_{d}/x]\), by the Denotation Lemma. It follows that \({\mathcal {M}}, \omega _{[i]}, \tau _{[j]} \nVdash \Pi xD\).
(\(\lnot \Sigma \)). Straightforward.
Theorem 2
(Completeness Theorem) Each system in this paper is complete with respect to its semantics.
Proof
First we prove that the theorem holds for our weakest system \({\mathcal {Q}}\). Then we extend the theorem to all stronger systems. Let \({{\varvec{M}}}\) be the class of models that corresponds to \({\mathcal {Q}}\).
Suppose that B is not derivable from \(\Gamma \) in \({\mathcal {Q}}\): then it is not the case that there is a closed \({\mathcal {Q}}\)-tableau whose initial list comprises \(A, w_{0}t_{0}\) for every A in \(\Gamma \) and \(\lnot B, w_{0}t_{0}\). Let t be a complete \({\mathcal {Q}}\)-tableau whose initial list starts with \(A, w_{0}t_{0}\) for every A in \(\Gamma \) and \(\lnot B, w_{0}t_{0}\). Then t is not closed|in other words, it is open. Hence, there is at least one open branch in t. Let \({\mathcal {B}}\) be an open branch in t. The model induced by \({\mathcal {B}}\) makes all the premises in \(\Gamma \) true and B false in \(\omega _{[0]}\) at \(\tau _{[0]}\). Accordingly, it is not the case that B follows from \(\Gamma \) in \({{\varvec{M}}}\). In conclusion, if B follows from \(\Gamma \) in \({{\varvec{M}}}\), then B is derivable from \(\Gamma \) in \({\mathcal {Q}}\).
To prove that all extensions of \({\mathcal {Q}}\) are complete with respect to their semantics, we have to check that the model induced by the open branch \({\mathcal {B}}\) is of the right kind. To do this we first check that this is true for every single semantic condition. Then we combine each of the individual arguments. I will go through some steps to illustrate the method.
\(C-AR\). Suppose that \({\mathfrak {R}}\omega _{[i]}\omega _{[j]}\tau _{[l]}\), \(\tau _{[l]} < \tau _{[m]}\) and \({\mathfrak {R}}\omega _{[j]}\omega _{[k]}\tau _{[m]}\). Then \(Rw_{i}w_{j}t_{l}\), \(t_{l} < t_{m}\) and \(Rw_{j}w_{k}t_{m}\) occur on \({\mathcal {B}}\) [by the definition of an induced model]. Since \({\mathcal {B}}\) is complete (\(T-AR\)) has been applied. Hence, \(Rw_{i}w_{k}t_{l}\) is on \({\mathcal {B}}\). Accordingly, \({\mathfrak {R}}\omega _{[i]}\omega _{[k]}\tau _{[l]}\), as required [by the definition of an induced model].
\(C-{\mathcal {W}}dO\). Suppose that \({\mathfrak {A}}v(c)\omega _{[i]}\omega _{[j]}\tau _{[l]}\) and \({\mathfrak {D}}v(c)\omega _{[j]}\omega _{[k]}\tau _{[l]}\). Then \(Acw_{i}w_{j}t_{l}\) and \(Dcw_{j}w_{k}t_{l}\) occur on \({\mathcal {B}}\) [by the definition of an induced model]. Since \({\mathcal {B}}\) is complete (\(T-{\mathcal {W}}dO\)) has been applied. Hence, \(w_{j} = w_{k}\) is on \({\mathcal {B}}\). So, \(j \approx k\). Therefore, \([j] = [k]\) and \(\omega _{[j]} = \omega _{[k]}\), as required [by the definition of an induced model].
\(C-{\mathcal {W}}{\mathbb {G}}bT\). Suppose that \({\mathfrak {A}}v(c)\omega _{[i]}\omega _{[j]}\tau _{[l]}\) and \(\tau _{[l]} < \tau _{[m]}\). Then \(Acw_{i}w_{j}t_{l}\) and \(t_{l} < t_{m}\) occur on \({\mathcal {B}}\) [by the definition of an induced model]. Since \({\mathcal {B}}\) is complete (\(T-{\mathcal {W}}{\mathbb {G}}bT\)) has been applied. Hence, \(Acw_{j}w_{j}t_{m}\) is on \({\mathcal {B}}\). Consequently, \({\mathfrak {A}}v(c)\omega _{[j]}\omega _{[j]}\tau _{[m]}\), as required [by the definition of an induced model].
 . Assume that \({\mathfrak {A}}v(c)\omega _{[i]}\omega _{[j]}\tau _{[l]}\) and \(\tau _{[l]} < \tau _{[m]}\). Then \(Acw_{i}w_{j}t_{l}\) and \(t_{l} < t_{m}\) occur on \({\mathcal {B}}\) [by the definition of an induced model]. \({\mathcal {B}}\) is complete. Hence, (
. Assume that \({\mathfrak {A}}v(c)\omega _{[i]}\omega _{[j]}\tau _{[l]}\) and \(\tau _{[l]} < \tau _{[m]}\). Then \(Acw_{i}w_{j}t_{l}\) and \(t_{l} < t_{m}\) occur on \({\mathcal {B}}\) [by the definition of an induced model]. \({\mathcal {B}}\) is complete. Hence, ( ) has been applied. So, for some \(w_{k}\), \(Rw_{j}w_{k}t_{m}\) and \(Dcw_{j}w_{k}t_{m}\) are on \({\mathcal {B}}\). In conclusion, for some \(\omega _{[k]}\), \({\mathfrak {R}}\omega _{[j]}\omega _{[k]}\tau _{[m]}\) and \({\mathfrak {D}}v(c)\omega _{[j]}\omega _{[k]}\tau _{[m]}\), as required [by the definition of an induced model].
) has been applied. So, for some \(w_{k}\), \(Rw_{j}w_{k}t_{m}\) and \(Dcw_{j}w_{k}t_{m}\) are on \({\mathcal {B}}\). In conclusion, for some \(\omega _{[k]}\), \({\mathfrak {R}}\omega _{[j]}\omega _{[k]}\tau _{[m]}\) and \({\mathfrak {D}}v(c)\omega _{[j]}\omega _{[k]}\tau _{[m]}\), as required [by the definition of an induced model].
 . Suppose that \({\mathfrak {A}}v(c)\omega _{[i]}\omega _{[j]}\tau _{[l]}\), \(\tau _{[l]} < \tau _{[m]}\) and \({\mathfrak {D}}v(c)\omega _{[j]}\omega _{[k]}\tau _{[m]}\). Then \(Acw_{i}w_{j}t_{l}\), \(t_{l} < t_{m}\) and \(Dcw_{j}w_{k}t_{m}\) occur on \({\mathcal {B}}\) [by the definition of an induced model]. Since \({\mathcal {B}}\) is complete (
. Suppose that \({\mathfrak {A}}v(c)\omega _{[i]}\omega _{[j]}\tau _{[l]}\), \(\tau _{[l]} < \tau _{[m]}\) and \({\mathfrak {D}}v(c)\omega _{[j]}\omega _{[k]}\tau _{[m]}\). Then \(Acw_{i}w_{j}t_{l}\), \(t_{l} < t_{m}\) and \(Dcw_{j}w_{k}t_{m}\) occur on \({\mathcal {B}}\) [by the definition of an induced model]. Since \({\mathcal {B}}\) is complete ( ) has been applied. Accordingly, \(Rw_{j}w_{k}t_{m}\) occurs on \({\mathcal {B}}\). It follows that \({\mathfrak {R}}\omega _{[j]}\omega _{[k]}\tau _{[m]}\), as required [by the definition of an induced model]. \(\square \)
) has been applied. Accordingly, \(Rw_{j}w_{k}t_{m}\) occurs on \({\mathcal {B}}\). It follows that \({\mathfrak {R}}\omega _{[j]}\omega _{[k]}\tau _{[m]}\), as required [by the definition of an induced model]. \(\square \)
7 Examples
In this section, I will consider one example of a valid argument, the perpetuum mobile argument, and one example of an invalid formula, the bar exam, which were mentioned in the introduction. These examples will illustrate how one can use semantic tableaux to construct derivations and proofs and how one can read off countermodels from open and complete trees.
7.1 Example 1: The Perpetuum Mobile Argument (A Valid Argument)
I will now show that the conclusion in the perpetuum mobile argument is derivable from the premises in every system in this paper. By the soundness theorem in Sect. 6, it follows that the perpetuum mobile argument is valid in the class of all models; in other words, the conclusion is a logical consequence of the premises in the class of all models.
The argument can be symbolised in the following way in our language \({\mathcal {L}}\):
P1.  . John believes that it is necessary that it is always going to be the case that he will not build a perpetuum mobile.
. John believes that it is necessary that it is always going to be the case that he will not build a perpetuum mobile.
P2.  . For every x, if x is perfectly rational, then x wants to build a perpetuum mobile sometime in the future only if x believes that it is possible that x will build a perpetuum mobile sometime in the future.
. For every x, if x is perfectly rational, then x wants to build a perpetuum mobile sometime in the future only if x believes that it is possible that x will build a perpetuum mobile sometime in the future.
P3.  . For every x, if x is perfectly rational, then if x believes that it is possible that x will build a perpetuum mobile sometime in the future, then x does not believe that it is impossible that x will build a perpetuum mobile sometime in the future.
. For every x, if x is perfectly rational, then if x believes that it is possible that x will build a perpetuum mobile sometime in the future, then x does not believe that it is impossible that x will build a perpetuum mobile sometime in the future.
Hence,
C. \(Rj \rightarrow {\mathcal {A}}_{j}\lnot {\mathbb {F}} Pj\). If John is perfectly rational, he accepts the fact that he will never build a perpetuum mobile sometime in the future.
To show that the conclusion (C) is derivable from the premises (P1)–(P3) in every system in this paper, we construct a closed tableau that starts with all premises and the negation of the conclusion. More precisely, we construct a closed tableau that starts with \(P1, w_{0}t_{0}\), \(P2, w_{0}t_{0}\), \(P3, w_{0}t_{0}\) and \(\lnot C, w_{0}t_{0}\). We will not use any special tableau rules in the tree; hence, the conclusion is derivable from the premises in our weakest system \({\mathcal {Q}}\). Accordingly, it is derivable in every system. It follows that the argument is valid in the class of all models [by the soundness theorem in Sect. 6]. This establishes the desired result.
Here is the tableau derivation:

At this stage, all branches in the tableau are closed. Hence, the whole tableau is closed. Accordingly, the tableau constitutes a derivation from the premises to the conclusion in \({\mathcal {Q}}\), and so, the conclusion is derivable from the premises in \({\mathcal {Q}}\), as required. ‘MP’ is an abbreviation of ‘Modus Ponens’. MP is a derived rule in our systems.
Note that (P2) [ ] is a theorem in every system that includes \(T-{\mathcal {W}}{\mathcal {B}}D\), and that (P3) [
] is a theorem in every system that includes \(T-{\mathcal {W}}{\mathcal {B}}D\), and that (P3) [ ] is a theorem in every system that includes \(T-dD\). It follows that (P2) is valid in the class of models that satisfy \(C-{\mathcal {W}}{\mathcal {B}}D\) and that (P3) is valid in the class of models that satisfy \(C-dD\) (by the soundness results in Sect. 6). Furthermore, both (P2) and (P3) are theorems in every system that includes \(T-{\mathcal {W}}{\mathcal {B}}D\) and \(T-dD\). Hence, in every system that includes \(T-{\mathcal {W}}{\mathcal {B}}D\) and \(T-dD\), (P2) and (P3) are ‘redundant’; the conclusion (C) is directly derivable from (P1) alone. By the soundness theorem in Sect. 6, (C) is a logical consequence of (P1) in the class of all models that satisfy \(C-{\mathcal {W}}{\mathcal {B}}D\) and \(C-dD\). (It is left to the reader to verify the claims in this paragraph.)
] is a theorem in every system that includes \(T-dD\). It follows that (P2) is valid in the class of models that satisfy \(C-{\mathcal {W}}{\mathcal {B}}D\) and that (P3) is valid in the class of models that satisfy \(C-dD\) (by the soundness results in Sect. 6). Furthermore, both (P2) and (P3) are theorems in every system that includes \(T-{\mathcal {W}}{\mathcal {B}}D\) and \(T-dD\). Hence, in every system that includes \(T-{\mathcal {W}}{\mathcal {B}}D\) and \(T-dD\), (P2) and (P3) are ‘redundant’; the conclusion (C) is directly derivable from (P1) alone. By the soundness theorem in Sect. 6, (C) is a logical consequence of (P1) in the class of all models that satisfy \(C-{\mathcal {W}}{\mathcal {B}}D\) and \(C-dD\). (It is left to the reader to verify the claims in this paragraph.)
7.2 Example 2: The Bar Exam (An Invalid Sentence and a Countermodel)
In this section, I will show that ‘the bar exam’ (see the introduction) is not valid in the class of all models. To establish this, I will show that the sentence is not a theorem in the system \({\mathcal {Q}}\). By the completeness theorems in Sect. 6, it follows that the formula is not valid in the class of all models. I will use an open branch in a complete tree for the sentence to read off a countermodel and I will verify that this model is a countermodel to the formula. It is possible to prove that the sentence is not a theorem in any system in this paper. Hence, it is possible to show that the sentence is not valid in any class of models (that we are interested in). It is left to the reader to verify this claim.
The ‘bar exam’ can be symbolised in the following way:
The bar exam.  , where the interpretation of the predicates should be obvious. For every individual x, if x wants to become a lawyer sometime in the future and x believes that it is necessary that x will become a lawyer sometime in the future only if x will pass the bar exam sometime in the future, then x wants to pass the bar exam sometime in the future.
, where the interpretation of the predicates should be obvious. For every individual x, if x wants to become a lawyer sometime in the future and x believes that it is necessary that x will become a lawyer sometime in the future only if x will pass the bar exam sometime in the future, then x wants to pass the bar exam sometime in the future.
To show that a sentence A is not valid in a class of models \(\mathbf{M }\) we construct an open complete S-tableau for the negation of this sentence (where S is complete with respect to \(\mathbf{M }\)). More precisely, we construct an open complete S-tableau that begins with \(\lnot A, w_{0}t_{0}\). Then we use an open branch in the tree to read off a countermodel. Here is our tableau:

The left branch in this tree can be extended. Nevertheless, at this stage we cannot apply any more rules to the right branch, which is open (and complete). Accordingly, the whole tableau is open (and complete). Hence,  is not a theorem in our weakest system \({\mathcal {Q}}\). Consequently, the formula is not valid in the class of all models (by the completeness results in Sect. 6).
is not a theorem in our weakest system \({\mathcal {Q}}\). Consequently, the formula is not valid in the class of all models (by the completeness results in Sect. 6).
Let us verify this conclusion. We can use the right branch to read off a countermodel \({\mathcal {M}}\) since the right branch in the tree is open and complete. The matrix of \({\mathcal {W}}_{c}{\mathbb {F}}Lc\) is \({\mathcal {W}}_{x_{1}}{\mathbb {F}}Lx_{2}\), the matrix of \({\mathcal {W}}_{c}{\mathbb {F}}Pc\) is \({\mathcal {W}}_{x_{1}}{\mathbb {F}}Px_{2}\) and the matrix of  is
is  . \(W = \left\{ \omega _{0}\right\} \), \(T =\left\{ \tau _{0}\right\} \), \(D = \left\{ [c]\right\} \), \(v(c) = [c]\), and the extensions of L and P are empty in \(\omega _{0}\) at \(\tau _{0}\). <, \({\mathfrak {R}}\), \({\mathfrak {A}}\) and \({\mathfrak {D}}\) are empty. \(v_{\omega _{0}\tau _{0}}({\mathcal {W}}_{x_{1}}{\mathbb {F}}Lx_{2})\) is the extension of \({\mathcal {W}}_{x_{1}}{\mathbb {F}}Lx_{2}\) in \(\omega _{0}\) at \(\tau _{0}\), \(v_{\omega _{0}\tau _{0}}({\mathcal {W}}_{x_{1}}{\mathbb {F}}Px_{2})\) is the extension of \({\mathcal {W}}_{x_{1}}{\mathbb {F}}Px_{2}\) in \(\omega _{0}\) at \(\tau _{0}\) and
. \(W = \left\{ \omega _{0}\right\} \), \(T =\left\{ \tau _{0}\right\} \), \(D = \left\{ [c]\right\} \), \(v(c) = [c]\), and the extensions of L and P are empty in \(\omega _{0}\) at \(\tau _{0}\). <, \({\mathfrak {R}}\), \({\mathfrak {A}}\) and \({\mathfrak {D}}\) are empty. \(v_{\omega _{0}\tau _{0}}({\mathcal {W}}_{x_{1}}{\mathbb {F}}Lx_{2})\) is the extension of \({\mathcal {W}}_{x_{1}}{\mathbb {F}}Lx_{2}\) in \(\omega _{0}\) at \(\tau _{0}\), \(v_{\omega _{0}\tau _{0}}({\mathcal {W}}_{x_{1}}{\mathbb {F}}Px_{2})\) is the extension of \({\mathcal {W}}_{x_{1}}{\mathbb {F}}Px_{2}\) in \(\omega _{0}\) at \(\tau _{0}\) and  is the extension of
is the extension of  in \(\omega _{0}\) at \(\tau _{0}\).
in \(\omega _{0}\) at \(\tau _{0}\).
If \(\lnot Ra_{m}, w_{i}t_{j}\) is on the branch \({\mathcal {B}}\) and M is an n-place matrix with instantiations on the branch (where \(x_{m}\) is the first free variable in M and \(a_{m}\) is the constant in \(M[a_{1}, \ldots , a_{n}/x_{1}, \ldots , x_{n}]\) that replaces \(x_{m}\)), then \(\left\langle [a_{1}],\ldots , [a_{n}]\right\rangle \) is an element of \(v_{\omega _{i}\tau _{j}}(M)\) iff \(M[a_{1}, \ldots , a_{n}/x_{1}, \ldots , x_{n}], w_{i}t_{j}\) occurs on \({\mathcal {B}}\).
\(\lnot Rc, w_{0}t_{0}\) is on the branch, while \({\mathcal {W}}_{x_{1}}{\mathbb {F}}Px_{2}[c, c/x_{1}, x_{2}], w_{0}t_{0}\) (that is, \({\mathcal {W}}_{c}{\mathbb {F}}Pc, w_{0}t_{0}\)) does not occur on the branch. \(x_{1}\) is the first free variable in \({\mathcal {W}}_{x_{1}}{\mathbb {F}}Px_{2}\) and c is the constant in \({\mathcal {W}}_{x_{1}}{\mathbb {F}}Px_{2}[c, c/x_{1}, x_{2}]\) that replaces \(x_{1}\). Hence, \(\left\langle [c], [c]\right\rangle \) is not an element in \(v_{\omega _{0}\tau _{0}}({\mathcal {W}}_{x_{1}}{\mathbb {F}}Px_{2})\) (\(v_{\omega _{0}\tau _{0}}({\mathcal {W}}_{x_{1}}{\mathbb {F}}Px_{2})\) is empty). Since \(\lnot Rc, w_{0}t_{0}\) is on \({\mathcal {B}}\), Rc is false in \(\omega _{0}\) at \(\tau _{0}\). If \({\mathcal {M}}, \omega _{0}, \tau _{0} \nVdash Rc\), then \({\mathcal {M}}, \omega _{0}, \tau _{0} \Vdash {\mathcal {W}}_{x_{1}}{\mathbb {F}}Px_{2}[c, c/x_{1}, x_{2}]\) iff \(\left\langle v(c), v(c)\right\rangle \) is in \(v_{\omega _{0}\tau _{0}}({\mathcal {W}}_{x_{1}}{\mathbb {F}}Px_{2})\). So, \({\mathcal {M}}, \omega _{0}, \tau _{0} \Vdash {\mathcal {W}}_{x_{1}}{\mathbb {F}}Px_{2}[c, c/x_{1}, x_{2}]\) iff \(\left\langle v(c), v(c)\right\rangle \) is in \(v_{\omega _{0}\tau _{0}}({\mathcal {W}}_{x_{1}}{\mathbb {F}}Px_{2})\). \(\left\langle v(c), v(c)\right\rangle \) is not in \(v_{\omega _{0}\tau _{0}}({\mathcal {W}}_{x_{1}}{\mathbb {F}}Px_{2})\). Hence, it is not the case that \({\mathcal {M}}, \omega _{0}, \tau _{0}\) \(\Vdash {\mathcal {W}}_{x_{1}}{\mathbb {F}}Px_{2}[c, c/x_{1}, x_{2}]\). It follows that it is not the case that \({\mathcal {M}}, \omega _{0}, \tau _{0} \Vdash {\mathcal {W}}_{c}{\mathbb {F}}Pc\), that is, \({\mathcal {W}}_{c}{\mathbb {F}}Pc\) is false in \(\omega _{0}\) at \(\tau _{0}\), for \({\mathcal {W}}_{x_{1}}{\mathbb {F}}Px_{2}[c, c/x_{1}, x_{2}]\) \(=\) \({\mathcal {W}}_{c}{\mathbb {F}}Pc\).
\({\mathcal {W}}_{x_{1}}{\mathbb {F}}Lx_{2}[c, c/x_{1}, x_{2}], w_{0}t_{0}\) (that is, \({\mathcal {W}}_{c}{\mathbb {F}}Lc, w_{0}t_{0})\) occurs on the branch. Note that \(x_{1}\) is the first free variable in \({\mathcal {W}}_{x_{1}}{\mathbb {F}}Lx_{2}\) and that c is the constant in \({\mathcal {W}}_{x_{1}}{\mathbb {F}}Lx_{2}[c, c/x_{1}, x_{2}]\) that replaces \(x_{1}\). Accordingly, \(\left\langle [c], [c]\right\rangle \) is an element in \(v_{\omega _{0}\tau _{0}}({\mathcal {W}}_{x_{1}}{\mathbb {F}}Lx_{2})\). If \({\mathcal {M}}, \omega _{0}, \tau _{0} \nVdash Rc\), then \({\mathcal {M}}, \omega _{0}, \tau _{0} \Vdash {\mathcal {W}}_{x_{1}}{\mathbb {F}}Lx_{2}[c, c/x_{1}, x_{2}]\) iff \(\left\langle v(c), v(c)\right\rangle \) is in \(v_{\omega _{0}\tau _{0}}({\mathcal {W}}_{x_{1}}{\mathbb {F}}Lx_{2})\). Hence, \({\mathcal {M}}, \omega _{0}, \tau _{0} \Vdash {\mathcal {W}}_{x_{1}}{\mathbb {F}}Lx_{2}[c, c/x_{1}, x_{2}]\) iff \(\left\langle v(c), v(c)\right\rangle \) is in \(v_{\omega _{0}\tau _{0}}({\mathcal {W}}_{x_{1}}{\mathbb {F}}Lx_{2})\). \(\left\langle v(c), v(c)\right\rangle \) is in \(v_{\omega _{0}\tau _{0}}({\mathcal {W}}_{x_{1}}{\mathbb {F}}Lx_{2})\). Consequently, \({\mathcal {M}}, \omega _{0}, \tau _{0} \Vdash {\mathcal {W}}_{x_{1}}{\mathbb {F}}Lx_{2}[c, c/x_{1}, x_{2}]\). Since \({\mathcal {W}}_{x_{1}}{\mathbb {F}}Lx_{2}[c, c/x_{1}, x_{2}] ={\mathcal {W}}_{c}{\mathbb {F}}Lc\), it follows that \({\mathcal {M}}, \omega _{0}, \tau _{0} \Vdash {\mathcal {W}}_{c}{\mathbb {F}}Lc\). In other words, \({\mathcal {W}}_{c}{\mathbb {F}}Lc\) is true in \(\omega _{0}\) at \(\tau _{0}\).
 (
( occurs on the branch. \(x_{1}\) is the first free variable in
occurs on the branch. \(x_{1}\) is the first free variable in  and c is the constant in
and c is the constant in  that replaces \(x_{1}\). Hence, \(\left\langle [c], [c], [c]\right\rangle \) is an element in
that replaces \(x_{1}\). Hence, \(\left\langle [c], [c], [c]\right\rangle \) is an element in  . If \({\mathcal {M}}, \omega _{0}, \tau _{0} \nVdash Rc\), then
. If \({\mathcal {M}}, \omega _{0}, \tau _{0} \nVdash Rc\), then  iff \(\left\langle v(c), v(c), v(c)\right\rangle \) is in
iff \(\left\langle v(c), v(c), v(c)\right\rangle \) is in  . Therefore,
. Therefore,  iff \(\left\langle v(c), v(c), v(c)\right\rangle \) is in
iff \(\left\langle v(c), v(c), v(c)\right\rangle \) is in  . Since \(\left\langle v(c), v(c), v(c)\right\rangle \) is in
. Since \(\left\langle v(c), v(c), v(c)\right\rangle \) is in  , we can deduce that
, we can deduce that  . So,
. So,  , for
, for  \(=\)
\(=\)  . In other words,
. In other words,  is true in \(\omega _{0}\) at \(\tau _{0}\).
is true in \(\omega _{0}\) at \(\tau _{0}\).
We have shown that \({\mathcal {W}}_{c}{\mathbb {F}}Lc\) is true in \(\omega _{0}\) at \(\tau _{0}\) and that  is true in \(\omega _{0}\) at \(\tau _{0}\). Hence,
is true in \(\omega _{0}\) at \(\tau _{0}\). Hence,  is true in \(\omega _{0}\) at \(\tau _{0}\). Moreover, we have established that \({\mathcal {W}}_{c}{\mathbb {F}}Pc\) is false in \(\omega _{0}\) at \(\tau _{0}\). It follows that
is true in \(\omega _{0}\) at \(\tau _{0}\). Moreover, we have established that \({\mathcal {W}}_{c}{\mathbb {F}}Pc\) is false in \(\omega _{0}\) at \(\tau _{0}\). It follows that  is false in \(\omega _{0}\) at \(\tau _{0}\). Since [c] is an object in the domain, we conclude that
is false in \(\omega _{0}\) at \(\tau _{0}\). Since [c] is an object in the domain, we conclude that  is false in \(\omega _{0}\) at \(\tau _{0}\). Consequently, this sentence is not valid in the class of all models.
is false in \(\omega _{0}\) at \(\tau _{0}\). Consequently, this sentence is not valid in the class of all models.
 is not a theorem in any system in this paper, but
is not a theorem in any system in this paper, but  is provable in several systems, for example in every system that includes \(T-{\mathcal {B}}N{\mathcal {W}}\). Hence, this sentence is valid in every model that satisfies \(C-{\mathcal {B}}N{\mathcal {W}}\).
is provable in several systems, for example in every system that includes \(T-{\mathcal {B}}N{\mathcal {W}}\). Hence, this sentence is valid in every model that satisfies \(C-{\mathcal {B}}N{\mathcal {W}}\).
Notes
Note also that many philosophers and logicians have developed logical systems that include temporal, alethic and deontic elements, see, for example [4, 5, 8,9,10,11, 24, 101, 102, 110]. Systems that combine modal and temporal logic with a kind of action logic have been explored by researchers within the stit-paradigm. Sometimes these systems also include a deontic part. For more information on stit-logic, see, for example [12, 15, 49, 53,54,55, 79, 81, 94, 116,117,118,119,120]. See [78] for an early attempt to combine various systems. For an introduction to various multiagent systems, see [114].
For more on matrices, see [83], Chapters 1–2.
For more on the hypothetical imperative, see, for example [91] and the references in this paper.
Note that this method is often not the most ‘efficient’ one; it is often possible to construct shorter proofs or derivations by using some more ‘intuitive’ procedure instead.
The following rules are world identity rules: \(T-dO\), \(T-{\mathcal {B}}dO\), \(T-{\mathcal {W}}dO\), \(T-{\mathcal {B}}{\mathbb {G}}dO\) and \(T-{\mathcal {W}}{\mathbb {G}}dO\).
References
Ågotnes, T.: Action and knowledge in alternating-time temporal logic (Knowledge, rationality and action). Synthese 149(2), 375–407 (2006)
Alechina, N., Logan, B.: Belief ascription under bounded resources. Synthese 173(2), 179–197 (2013)
Åqvist, L.: The logic of historical necessity as founded on two-dimensional modal tense logic. J. Philos. Log. 28, 329–369 (1999)
Åqvist, L.: Combinations of tense and deontic modality: on the RT approach to temporal logic with historical necessity and conditional obligation. J. Appl. Log. 3, 421–460 (2005)
Åqvist, L., Hoepelman, J.: Some theorems about a “tree” system of deontic tense logic. In: Hilpinen, R. (ed.) New Studies in Deontic Logic: Norms, Actions, and the Foundation of Ethics, pp. 187–221. D. Reidel Publishing Company, Dordrecht (1981)
Askounis, D., Koutras, C.D., Zikos, Y.: Knowledge means ‘all’, belief means ‘most’. J. Appl. Non-Class. Log. 26(3), 173–192 (2016)
Bacharach, M.O.L., Gérard-Varet, L.-A., Mongin, P., Shin, H.S. (eds.): Epistemic Logic and the Theory of Games and Decisions. Springer, Dordrecht (1997)
Bailhache, P.: Les normes dans le temps et sur l’action. Essai de logique déontique. Université de Nantes, Nantes (1986)
Bailhache, P.: Essai de logique déontique. Librarie Philosophique, Vrin, Collection Mathesis, Paris (1991)
Bailhache, P.: The deontic branching time: two related conceptions. Log. Anal. 36, 159–175 (1993)
Bailhache, P.: Canonical models for temporal deontic logic. Log. Anal. 149, 3–21 (1997)
Balbiani, P., Herzig, A., Troquard, N.: Alternative axiomatics and complexity of deliberative STIT theories. J. Philos. Log. 37, 387–406 (2008)
Barcan, R.C.: A functional calculus of first order based on strict implication. J. Symb. Log. 11, 1–16 (1946)
Barringer, H., Fisher, M., Gabbay, D., Gough, G. (eds.): Advances in Temporal Logic. Springer, Berlin (2000)
Belnap, N., Perloff, M., Xu, M.: Facing the Future: Agents and Choices in Our Indeterminist World. Oxford University Press, Oxford (2001)
Blackburn, P., de Rijke, M., Venema, Y.: Modal Logic. Cambridge University Press, Cambridge (2001)
Blackburn, P., van Benthem, J., Wolter, F. (eds.): Handbook of Modal Logic. Elsevier, Amsterdam (2007)
Boh, I.: Epistemic Logic in the Middle Ages. Routledge, Abingdon (1993)
Bostock, D.: Intermediate Logic. Clarendon Press, Oxford (1997)
Broersen, J.M.: Making a start with the stit logic analysis of intentional action. J. Philos. Log. 40(4), 499–530 (2011)
Broersen, J.M., Dastani, M., van der Torre, L.: Resolving conflicts between beliefs, obligations, intentions, and desires. In: Benferhat, S., Besnard, P. (eds.) Symbolic and Quantitative Approaches to Reasoning with Uncertainty, pp. 568–579. Springer, Berlin (2001)
Burgess, J.P.: Basic tense logic. In: Gabbay, D., Guenthner, F. (eds.) Handbook of Philosophical Logic, vol. 2, pp. 89–133. Reidel, Dordrecht (1984)
Carnap, R.: Modalities and quantification. J. Symb. Log. 11(2), 33–64 (1946)
Chellas, B.F.: The Logical Form of Imperatives. Perry Lane Press, Stanford (1969)
Chellas, B.F.: Modal Logic: An Introduction. Cambridge University Press, Cambridge (1980)
Church, A.: Introduction to Mathematical Logic. Princeton University Press, Princeton (1996)
Ciuni, R., Zanardo, A.: Completeness of a branching-time logic with possible choices. Stud. Log. 96, 393–420 (2010)
Cohen, P.R., Levesque, H.J.: Intention is choice with commitment. Artif. Intell. 42, 213–261 (1990)
Corsi, G.: A unified completeness theorem for quantified modal logics. J. Symb. Log. 67(4), 1483–1510 (2002)
D’Agostino, M., Gabbay, D.M., Hähnle, R., Posegga, J. (eds.): Handbook of Tableau Methods. Kluwer Academic Publishers, Dordrecht (1999)
DiMaio, M.C., Zanardo, A.: A Gabbay-Rule free axiomatization of T \(\times \) W validity. J. Philos. Log. 27, 435–487 (1998)
Epstein, R.L.: Classical Mathematical Logic. Princeton University Press, Princeton (2006)
Fagin, R., Halpern, J.Y., Moses, Y., Vardi, M.Y.: Reasoning About Knowledge. The MIT Press, Cambridge (1995)
Fine, K.: Modality and Tense. Oxford University Press, Oxford (2005)
Finger, M., Gabbay, D., Reynolds, M.: Advanced tense logic. In: Gabbay, D., Guenther, F. (eds.) Handbook of Philosophical Logic, vol. 7, pp. 43–203. Kluwer Academic Publishers, Dordrecht (2002)
Fitting, M., Mendelsohn, R.L.: First-Order Modal Logic. Kluwer Academic Publishers, Dordrecht (1998)
Fitting, M., Thalmann, L., Voronkov, A.: Term-modal logics. Stud. Log. 69, 133–169 (2001)
Gabbay, D.M.: Investigations in Modal and Tense Logics with Applications to Problems in Philosophy and Linguistics. Reidel, Dordrecht (1976)
Galeazzi, P., Lorini, E.: Epistemic logic meets epistemic game theory: a comparison between multi-agent Kripke models and type spaces. Synthese 193, 2097–2127 (2016)
Garson, J.W.: Quantification in modal logic. In: Gabbay, D.M., Guenthner, F. (eds.) Handbook of Philosophical Logic, 2nd edn. Springer, Dordrecht (1984)
Garson, J.W.: Modal Logic for Philosophers. Cambridge University Press, New York (2006)
Gensler, H.J.: Introduction to Logic. Routledge, London (2002)
Gochet, P., Gribomont, P.: Epistemic logic. In: Gabbay, D.M., Woods, J. (eds.) Handbook of the History of Logic, vol. 7, pp. 99–195. North-Holland, Amsterdam (2006)
Goldblatt, R.: Logics of Time and Computation. CSLI, Stanford (1992)
Goranko, V., Jamroga, W.: Comparing semantics of logics for multi-agent systems (Knowledge, rationality and action). Synthese 139(2), 241–280 (2004)
Hendricks, V.F.: Active agents (Special issue on connecting the different faces of information). J. Log. Lang. Inf. 12(4), 469–495 (2003)
Hendricks, V.F., Jørgensen, K.F., Pedersen, S.A. (eds.): Knowledge Contributors. Synthese Library, vol. 322. Kluwer Academic Publishers, Dordrecht (2003)
Hendricks, V.F.: Mainstream and Formal Epistemology. Cambridge University Press, New York (2005)
Herzig, A., Lorini, E.: A dynamic logic of agency I: STIT, capabilities and powers. J. Log. Lang. Inf. 19(1), 89–121 (2010)
Hintikka, J.: Modality and quantification. Theoria 27, 117–128 (1961)
Hintikka, J.: Knowledge and Belief: An Introduction to the Logic of the Two Notions. Cornell University Press, Ithaca. Reprinted 2005, King’s College London Publications (1962)
Hoshi, T., Yap, A.: Dynamic epistemic logic with branching temporal structures (Knowledge, rationality and action. Logics of intelligent interaction). Synthese 169(2), 259–281 (2009)
Horty, J.F.: Agency and obligation. Synthese 108, 269–307 (1996)
Horty, J.F.: Agency and deontic logic. Oxford University Press, Oxford (2001)
Horty, J.F., Belnap, N.: The deliberative stit: a study of action, omission, ability, and obligation. J. Philos. Log. 24, 583–644 (1995)
Hughes, G.E., Cresswell, M.J.: An Introduction to Modal Logic. Routledge, London (1968)
Hughes, G.E., Cresswell, M.J.: A New Introduction to Modal Logic. Routledge, London (1996)
Isaac, A., Hoshi, T.: Synchronizing diachronic uncertainty. J. Log. Lang. Inf. 20(2), 137–159 (2011)
Jeffrey, R.C.: Formal Logic: Its Scope and Limits. McGraw-Hill, New York (1967)
Kacprzak, M., Penczek, W.: A sat-based approach to unbounded model checking for alternating-time temporal epistemic logic (Knowledge, rationality and action). Synthese 142(2), 203–227 (2004)
Kraus, S., Lehmann, D.: Knowledge, belief and time. Theor. Comput. Sci. 58, 155–174 (1988)
Knuuttila, S.: Emotions in Ancient and Medieval Philosophy. Oxford University Press, Oxford (2004)
Knuuttila, S.: Medieval modal theories and modal logic. In: Gabbay, D., Woods, J. (eds.) Handbook of the History of Logic: Mediaeval and Renaissance Logic, vol. 2, pp. 505–578. North-Holland, Amsterdam (2008)
Kracht, M.: Tools and Techniques in Modal Logic. Studies in Logic, vol. 142. Elsevier, Amsterdam (1999)
Kröger, F., Merz, S.: Temporal Logic and State Systems. Springer, Berlin (2008)
Lenzen, W.: Recent work in epistemic logic. Acta Philos. Fenn. 30, 1–219 (1978)
Lenzen, W.: Glauben. Wissen und Wahrscheinlichkeit. Springer, Vienna (1980)
Lenzen, W.: Epistemic Logic. In: Niiniluoto, I., Sintonen, M., Woleński, J. (eds.) Handbook of Epistemology, pp. 963–983. Kluwer Academic Publishers, Dordrecht (2004)
Lewis, C.I., Langford, C.H.: Symbolic Logic. The Century Company, New York (1932)
Lindström, S.: On the proper treatment of quantification in contexts of logical and metaphysical modalities. In: Lagerlund, H., Lindström, S., Sliwinski, R. (eds.) Modality Matters: Twenty-Five Essays in Honour of Krister Segerberg. Uppsala Philosophical Studies, vol. 53. Uppsala (2006)
Lindström, S., Segerberg, K.: Modal logic and philosophy. In: Blackburn, P., van Benthem, J., Wolter, F. (eds.) Handbook of Modal Logic. Studies in Logic and Practical Reasoning, vol. 3, pp. 1149–1215. Elsevier, Amsterdam (2007)
Lorini, E., Herzig, A.: A Logic of intention and attempt (Knowledge, rationality and action). Synthese 163(1), 45–77 (2008)
Mally, E.: Grundgesetze des Sollens: Elemente der Logik des Willens. Leuschner and Lubensky (1926)
Marra, A., Klein, D.: Logic and ethics: an integrated model for norms, intentions and actions. In: van der Hoek, W., Holliday, W.H., Wang, W. (eds.) International Workshop on Logic, Rationality and Interaction, pp. 268–281. Springer, Berlin (2015)
Mele, A.R.: The Oxford Handbook of Rationality. Oxford University Press, Oxford (2004)
Meyer, J.J.C., van der Hoek, W.: Epistemic Logic for AI and Computer Science. Cambridge University Press, Cambridge (1995)
Mohalik, S., Ramanujam, R.: Automata for epistemic temporal logic with synchronous communication (Temporal logics of agency). J. Log. Lang. Inf. 19(4), 451–484 (2010)
Montague, R.: Logical necessity, physical necessity, ethics and quantifiers. Inquiry 4, 259–269 (1960)
Müller, T. (ed.): Nuel Belnap on Indeterminism and Free Action. Springer, Berlin (2014)
Øhrstrøm, P., Hasle, P.F.V.: Temporal Logic: From Ancient Ideas to Artificial Intelligence. Kluwer Academic Publishers, Dordrecht (1995)
Olkhovikov, G.K., Wansing, H.: An axiomatic system and a tableau calculus for STIT imagination logic. J. Philos. Log. 47, 259–279 (2018)
Parks, Z.: Investigations into quantified modal logic-I. Stud. Log. 35, 109–125 (1976)
Priest, G.: Towards Non-Being. Oxford University Press, Oxford (2005)
Priest, G.: An Introduction to Non-Classical Logic. Cambridge University Press, Cambridge (2008)
Prior, A.: Past, Present and Future. Clarendon, Oxford (1967)
Rescher, N., Urquhart, A.: Temporal Logic. Springer, Wien (1971)
Rescher, N.: Epistemic Logic: Survey of the Logic of Knowledge. University of Pittsburgh Press, Pittsburgh (2005)
Rönnedal, D.: Temporal Alethic-Deontic Logic and Semantic Tableaux. J. Appl. Log. 10, 219–237 (2012)
Rönnedal, D.: Doxastic logic: a new approach. J. Appl. Non-class. Log. 28(4), 313–347 (2018)
Rönnedal, D.: Boulesic-doxastic logic. Australas. J. Log. 16(3), 83–132 (2019)
Rönnedal, D.: Boulesic logic, deontic logic and the structure of a perfectly rational will. Organon F 27(2), 187–262 (2020)
Sack, J.: Temporal languages for epistemic programs. J. Log. Lang. Inf. 17(2), 183–216 (2008)
Segerberg, K.: An Essay in Classical Modal Logic, vol. 3. University of Uppsala, Uppsala (1971)
Semmling, C., Wansing, H.: From BDI and stit to bdi-stit logic. Log. Log. Philos. 17, 185–207 (2008)
Smullyan, R.M.: Trees and nest structures. J. Symb. Log. 31, 303–321 (1966)
Smullyan, R.M.: First-Order Logic. Springer, Heidelberg (1968)
Stalnaker, R.: On logics of knowledge and belief. Philos. Stud. 128, 169–199 (2006)
Stalnaker, R., Thomason, R.: Abstraction in first-order modal logic. Theoria 34, 203–207 (1968)
Thomason, R., Stalnaker, R.: Modality and reference. Noûs 2(4), 359–372 (1968)
Thomason, R.: Some completeness results for modal predicate calculi. In: Lambert, K. (ed.) Philosophical Problems in Logic. D. Reidel, Dordrecht (1970)
Thomason, R.: Deontic logic as founded on tense logic. In: Hilpinen, R. (ed.) New Studies in Deontic Logic: Norms, Actions, and the Foundation of Ethics, pp. 165–176. D. Reidel Publishing Company, Dordrecht (1981)
Thomason, R.: Deontic logic and the role of freedom in moral deliberation. In: Hilpinen, R. (ed.) New Studies in Deontic Logic: Norms, Actions, and the Foundation of Ethics, pp. 177–186. D. Reidel Publishing Company, Dordrecht (1981)
Thomason, R.: Combinations of tense and modality. In: Gabbay, D.M., Guenthner, F. (eds.) Handbook of Philosophical Logic, 2nd edn, pp. 135–165. Springer, Dordrecht (1984). (2nd edn, pp. 205–234, 2002)
van Benthem, J.: Modal Logic and Classical Logic. Bibliopolis, Naples (1983)
van Benthem, J.: A Manual of Intensional Logic. CSLI Publications, Stanford (1985)
van Benthem, J.: Epistemic logic and epistemology: the state of their affairs. Philos. Stud. 128, 49–76 (2006)
van Benthem, J.: Modal Logic for Open Minds. CSLI Publications, Stanford (2010)
van der Hoek, W., Wooldridge, M.: Cooperation, knowledge, and time: alternating-time temporal epistemic logic and its applications (The dynamics of knowledge). Stud. Log. 75(1), 125–157 (2003)
van Ditmarsch, H., van der Hoek, W., Kooi, B.: Dynamic Epistemic Logic. Springer, Berlin (2008)
van Eck, J.E.: A System of Temporally Relative Modal and Deontic Predicate Logic and its Philosophical Applications. University of Groningen, Groningen, Department of Philosophy (1981)
von Kutschera, F.: Einführung in die intensionale Semantik. de Gruyter, Berlin (1976)
von Kutschera, F.: Grundfragen der Erkenntnistheorie. de Gruyter, Berlin (1981)
von Kutschera, F.: T \(\times \) W completeness. J. Philos. Log. 26, 241–250 (1997)
Wooldridge, M.: An Introduction to Multiagent Systems. Wiley, Chichester (2002)
Wölfl, S.: Combinations of tense and modality for predicate logic. J. Philos. Log. 28, 371–398 (1999)
Xu, M.: Decidability of stit theory with a single agent and refref equivalence. Stud. Log. 53, 259–298 (1994)
Xu, M.: Doing and refraining from refraining. J. Philos. Log. 23, 621–632 (1994)
Xu, M.: Busy choice sequences, refraining formulas, and modalities. Stud. Log. 54, 267–301 (1995)
Xu, M.: Axioms for deliberative stit. J. Philos. Log. 27(5), 505–552 (1998)
Xu, M.: Combinations of stit with ought and know. J. Philos. Log. 44, 851–877 (2015)
Zakharyaschev, M., Segerberg, K., de Rijke, W.H. (eds.): Advances in Modal Logic, vol. 2. CSLI Publications, Stanford (2001)
Zanardo, A.: Branching-time logic with quantification over branches: the point of view of modal logic. J. Symb. Log. 61(1), 1–39 (1996)
Funding
Open access funding provided by Stockholm University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The first version of this paper was finished in 2018. I would like to thank everyone who has commented on the text since then. Thanks also to the editor Jean-Yves Béziau for helpful guidance.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rönnedal, D. Quantified Temporal Alethic Boulesic Doxastic Logic. Log. Univers. 15, 1–65 (2021). https://doi.org/10.1007/s11787-020-00264-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11787-020-00264-z





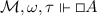 iff
iff 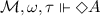 iff
iff