Abstract
This paper is dedicated to weighted composition semigroups on spaces of continuous functions and their subspaces. We consider semigroups induced by semiflows and semicocycles on Banach spaces \(\mathcal {F}(\Omega )\) of continuous functions on a Hausdorff space \(\Omega \) such that the norm-topology is stronger than the compact-open topology like the Hardy spaces, the weighted Bergman spaces, the Dirichlet space, the Bloch type spaces, the space of bounded Dirichlet series and weighted spaces of continuous or holomorphic functions. It was shown by Gallardo-Gutiérrez, Siskakis and Yakubovich that there are no non-trivial norm-strongly continuous weighted composition semigroups on Banach spaces \(\mathcal {F}(\mathbb {D})\) of holomorphic functions on the open unit disc \(\mathbb {D}\) such that \(H^{\infty }\subset \mathcal {F}(\mathbb {D})\subset \mathcal {B}_{1}\) where \(H^{\infty }\) is the Hardy space of bounded holomorphic functions on \(\mathbb {D}\) and \(\mathcal {B}_{1}\) the Bloch space. However, we show that there are non-trivial weighted composition semigroups on such spaces which are strongly continuous w.r.t. the mixed topology between the norm-topology and the compact-open topology. We study such weighted composition semigroups in the general setting of Banach spaces of continuous functions and derive necessary and sufficient conditions on the spaces involved, the semiflows and semicocycles for strong continuity w.r.t. the mixed topology and as a byproduct for norm-strong continuity as well. Moreover, we give several characterisations of their generator and their space of norm-strong continuity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \((\mathcal {F}(\Omega ),\Vert \cdot \Vert )\) be a Banach space of scalar-valued continuous functions on a Hausdorff space \(\Omega \) such that the \(\Vert \cdot \Vert \)-topology is stronger than the compact-open topology \(\tau _{{\text {co}}}\) on \(\mathcal {F}(\Omega )\). Suppose that \(\varphi :=(\varphi _{t})_{t\ge 0}\) is a semiflow and \(m:=(m_{t})_{t\ge 0}\) an associated semicocycle on \(\Omega \) such that the induced weighted composition semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) given by \(C_{m,\varphi }(t)f:=m_{t}\cdot (f\circ \varphi _{t})\) for all \(t\ge 0\) and \(f\in \mathcal {F}(\Omega )\) is a well-defined semigroup of linear maps from \(\mathcal {F}(\Omega )\) to \(\mathcal {F}(\Omega )\).
In the case that \(\Omega =\mathbb {D}\subset \mathbb {C}\) is the open unit disc, \(\varphi \) a jointly continuous holomorphic semiflow and \(\mathcal {F}(\mathbb {D})\) a space of holomorphic functions on \(\mathbb {D}\) such semigroups are well-studied in the unweighted case, i.e. \(m_{t}(z)=1\) for all \(t\ge 0\) and \(z\in \mathbb {D}\), on the Hardy spaces \(H^{p}\) for \(1\le p<\infty \) in [10], on the weighted Bergman spaces \(A_{\alpha }^{p}\) for \(\alpha >-1\) and \(1\le p<\infty \) in [69], on the Dirichlet space \(\mathcal {D}\) in [70] and on more general spaces \(\mathcal {F}(\mathbb {D})\) in [4, 12, 23, 38, 71]. In particular, they are always \(\Vert \cdot \Vert \)-strongly continuous on \(H^{p}\), \(A_{\alpha }^{p}\) and \(\mathcal {D}\).
The weighted case, where m is a jointly continuous holomorphic semicocycle, is more complicated and got more attention recently [5, 11, 17, 18, 39, 63, 77]. However, to the best of our knowledge from the spaces mentioned above only for the Hardy spaces \(H^{p}\), \(1\le p<\infty \), and the weighted Bergman spaces \(A_{\alpha }^{p}\), \(1\le p<\infty \) and \(\alpha >-1\), sufficient (non-trivial) conditions on general m are known such that the weighted composition semigroup becomes \(\Vert \cdot \Vert \)-strongly continuous [47, 63, 68, 71, 77]. In [5] non-trivial sufficient conditions for \(\Vert \cdot \Vert \)-strong continuity are given for Banach spaces \(\mathcal {F}(\mathbb {D})\) of holomorphic functions in which the polynomials are dense in the case that \(m_{t}=\varphi _{t}'\) for all \(t\ge 0\).
Considering the Hardy space for \(p=\infty \), it is shown in [39] that the only \(\Vert \cdot \Vert \)-strongly continuous weighted composition semigroups on \(\mathcal {F}(\mathbb {D})\) such that \(H^{\infty }\subset \mathcal {F}(\mathbb {D})\subset \mathcal {B}_{1}\) are the trivial ones, i.e. \(\varphi _{t}={{\,\textrm{id}\,}}\) for all \(t\ge 0\). Here, \(\mathcal {B}_{1}\) stands for the Bloch space. In the unweighted case this has already been observed in [3, 38]. Similarly, it is shown in [21, Theorem 7.1, p. 34] that there no non-trivial \(\Vert \cdot \Vert \)-strongly continuous composition semigroups on the space \(\mathscr {H}^{\infty }\) of bounded Dirichlet series on the open right half-plane. Nevertheless, there are non-trivial weighted composition semigroups on such spaces \(\mathcal {F}(\mathbb {D})\) resp. \(\mathscr {H}^{\infty }\) as well and it is said in [38, p. 494] that it would be desirable to substitute the \(\Vert \cdot \Vert \)-strong continuity by a weaker property so that the description of the generator of a (weighted) composition semigroup given in [38, Main theorem, p. 490] ([39, Theorems 2.1, 3.1, pp. 68–69] in the weighted case) remains valid. This is one of the problems we solve in the present paper. We substitute the \(\Vert \cdot \Vert \)-strong continuity by \(\gamma \)-strong continuity where \(\gamma :=\gamma (\Vert \cdot \Vert ,\tau _{{\text {co}}})\) is the mixed topology between the \(\Vert \cdot \Vert \)-topology and \(\tau _{{\text {co}}}\), which was introduced in [76] and is a Hausdorff locally convex topology.
Let us outline the content of our paper. In Sect. 2 we recall the notions of a Saks space \((X,\Vert \cdot \Vert ,\tau )\), where \((X,\Vert \cdot \Vert )\) is a normed space and \(\tau \) a coarser norming Hausdorff locally convex topology on X, the mixed topology \(\gamma :=\gamma (\Vert \cdot \Vert ,\tau )\), some background on semigroups on Hausdorff locally convex spaces and in Theorem 2.7 how \(\gamma \)-strongly continuous, locally \(\gamma \)-equicontinuous semigroups are related to the concept of a \(\tau \)-bi-continuous semigroup, which was introduced in [54, 55]. We then give several examples of Saks spaces of the form \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\), which include among others the Hardy spaces \(H^{p}\) for \(1\le p< \infty \), the weighted Bergman spaces \(A_{\alpha }^{p}\) for \(1\le p<\infty \) and \(\alpha >-1\), and the Dirichlet space \(\mathcal {D}\) in Example 2.9, the v-Bloch spaces w.r.t. a continuous weight v in Example 2.10, especially the Bloch type spaces \(\mathcal {B}_{\alpha }\) for \(\alpha >0\), as well as weighted spaces of continuous resp. holomorphic functions, especially, the Hardy space \(H^{\infty }\) and the space \(\mathscr {H}^{\infty }\) of bounded Dirichlet series in Examples 2.11, 2.12 and 2.13.
In Sect. 3 we recap the notions of a semiflow \(\varphi \), a semicocycle m for \(\varphi \) and introduce the notion of a co-semiflow \((m,\varphi )\). We give equivalent characterisations of their joint continuity depending on the topological properties of \(\Omega \), present several examples and generalise the concept of a generator of a semiflow, which was introduced in [10] for jointly continuous holomorphic semiflows.
In Sect. 4 we use the concepts and results of the preceding sections to prove one of our main results Proposition 4.5, which generalises [36, Proposition 2.10, p. 5] and [50, Corollary 4.3, p. 20], that the weighted composition semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) on a Saks space \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) is \(\gamma \)-strongly continuous and locally \(\gamma \)-equicontinuous if the semigroup is locally bounded (w.r.t. the operator norm) and the co-semiflow \((m,\varphi )\) is jointly continuous. Then we derive sufficient conditions depending on \((m,\varphi )\) for the local boundedness of the semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) for the Saks spaces mentioned above, in particular in the case \(\mathcal {F}(\Omega )=\mathscr {H}^{\infty }\) in Theorem 4.16.
In Sect. 5 we turn to the generator (A, D(A)) of locally bounded, \(\gamma \)-strongly continuous weighted composition semigroups and show in Proposition 5.4 that it coincides with the Lie generator, i.e. the pointwise generator, if the Saks space \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) is sequentially complete (w.r.t. the mixed topology \(\gamma \)) and the co-semiflow \((m,\varphi )\) is jointly continuous. This generalises [36, Proposition 2.12, p. 6] and [26, Proposition 2.4, p. 118] where \(\mathcal {F}(\Omega )=\mathcal {C}_{b}(\Omega )\) is the space of bounded continuous functions on a completely regular Hausdorff k-space resp. Polish space \(\Omega \) and m trivial. The connection to \(\tau \)-bi-continuous semigroups from Sect. 2 also allows us to deduce in Proposition 5.3 that on sequentially complete Saks spaces \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) such semigroups are \(\Vert \cdot \Vert \)-strongly continuous if \((\mathcal {F}(\Omega ),\Vert \cdot \Vert )\) is reflexive, and to show that the space of \(\Vert \cdot \Vert \)-strong continuity coincides with the \(\Vert \cdot \Vert \)-closure of D(A). In Theorem 5.11 we turn to the special case that \(\Omega \subset \mathbb {C}\) is open, the jointly continuous co-semiflow \((m,\varphi )\) continuously differentiable w.r.t. t and \(\mathcal {F}(\Omega )\) for instance a space of holomorphic functions, which results in the representation
of the generator, where  and
and  denote the derivatives w.r.t. t of \(\varphi \) and m in \(t=0\), respectively. In Theorem 5.10 we also handle the more complicated case where \(\Omega \subset \mathbb {R}\) is open and the space \(\mathcal {F}(\Omega )\) need not be a space of continuously differentiable or holomorphic functions, for example \(\mathcal {F}(\Omega )=\mathcal {C}_{b}(\Omega )\).
denote the derivatives w.r.t. t of \(\varphi \) and m in \(t=0\), respectively. In Theorem 5.10 we also handle the more complicated case where \(\Omega \subset \mathbb {R}\) is open and the space \(\mathcal {F}(\Omega )\) need not be a space of continuously differentiable or holomorphic functions, for example \(\mathcal {F}(\Omega )=\mathcal {C}_{b}(\Omega )\).
Section 6 is dedicated to the converse of (1) in the sense that a \(\gamma \)-strongly continuous semigroup with such a generator for some holomorphic functions G and g on \(\Omega \) must be a weighted composition semigroup w.r.t. some jointly continuous holomorphic co-semiflow \((m,\varphi )\) at least if \(\Omega =\mathbb {D}\), \((\mathcal {F}(\mathbb {D}),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) is a sequentially complete Saks space of holomorphic functions and the embedding \(\mathcal {H}(\overline{\mathbb {D}})\hookrightarrow (\mathcal {F}(\mathbb {D}),\Vert \cdot \Vert )\) continuous where \(\mathcal {H}(\overline{\mathbb {D}})\) denotes the space of holomorphic germs near \(\overline{\mathbb {D}}\) with its inductive limit topology (see Theorem 6.1). In Example 6.2 we show that this embedding condition is fulfilled for the spaces like \(H^{p}\) for \(1\le p\le \infty \), \(A_{\alpha }^{p}\) for \(\alpha >-1\) and \(1\le p<\infty \), \(\mathcal {D}\) and \(\mathcal {B}_{\alpha }\) for \(\alpha >0\). Theorem 6.1 in combination with Theorem 5.11 (see also Theorem 7.4) is the counterpart of [38, Main theorem, p. 490] and [39, Theorems 2.1, 3.1, pp. 68–69] we were searching for.
In the closing Sect. 7 we generalise in Proposition 7.1 results from [25, 26] on unweighted composition semigroups on \(\mathcal {C}_{b}(\mathbb {R})\) to the more general setting of weighted composition semigroups on weighted spaces of continuous functions. Further, Theorem 7.2 gives us necessary and sufficient conditions for a weighted composition semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) on a sequentially complete Saks space \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) of holomorphic functions on an open connected set \(\Omega \subset \mathbb {C}\) to be \(\Vert \cdot \Vert \)-strongly continuous resp. \(\gamma \)-strongly continuous. In combination with Theorem 4.14 we obtain sufficient conditions on \((m,\varphi )\) so that \((C_{m,\varphi }(t))_{t\ge 0}\) is \(\Vert \cdot \Vert \)-strongly continuous on the Hardy spaces \(H^{p}\) for \(1<p<\infty \), the weighted Bergman spaces \(A_{\alpha }^{p}\) for \(\alpha >-1\) and \(1< p<\infty \) and on the Dirichlet space \(\mathcal {D}\). For the first two spaces we get back the conditions from [63, 77] by a different proof and they improve the already known ones from [47, 68, 71]. In combination with Theorems 4.15 and 4.17 we obtain sufficient conditions on \((m,\varphi )\) so that \((C_{m,\varphi }(t))_{t\ge 0}\) is \(\gamma \)-strongly continuous on the Hardy space \(H^{\infty }\) and the Bloch type spaces \(\mathcal {B}_{\alpha }\) for \(\alpha >0\).
2 Background on Semigroups on Saks Spaces
In this section we recall some basic notions and results in the context of semigroups on Hausdorff locally convex spaces, bi-continuous semigroups, the mixed topology and Saks spaces to keep this work practically self-contained. We refer the interested reader for more detailed information to [22, 45, 46, 54, 79]. For a Hausdorff locally convex space \((X,\tau )\) over the field \(\mathbb {K}=\mathbb {R}\) or \(\mathbb {C}\) we use the symbol \(\mathcal {L}(X,\tau )\) for the space of continuous linear operators from \((X,\tau )\) to \((X,\tau )\). If \((X,\Vert \cdot \Vert )\) is a normed space, we just write \(\mathcal {L}(X):=\mathcal {L}(X,\tau _{\Vert \cdot \Vert })\) where \(\tau _{\Vert \cdot \Vert }\) is the \(\Vert \cdot \Vert \)-topology. First, we recall the notions of strong continuity and equicontinuity.
2.1 Definition
Let \((X,\tau )\) be a Hausdorff locally convex space, I a set and \((T(t))_{t\in I}\) a family of linear maps \(X\rightarrow X\).
-
(a)
Let I be a Hausdorff space. \((T(t))_{t\in I}\) is called \(\tau \)-strongly continuous if \(T(t)\in \mathcal {L}(X,\tau )\) for every \(t\in I\) and the map \(T_{x}:I\rightarrow (X,\tau )\), \(T_{x}(t):=T(t)x\), is continuous for every \(x\in X\).
-
(b)
Let \(\sigma \) be an additional Hausdorff locally convex topology on X. \((T(t))_{t\in I}\) is called \(\sigma \)-\(\tau \)-equicontinuous if
$$\begin{aligned} \forall \;p\in \Gamma _{\tau }\;\exists \;\widetilde{p}\in \Gamma _{\sigma },\;C\ge 0\; \forall \;t\in I,\,x\in X:\;p(T(t)x)\le C\widetilde{p}(x) \end{aligned}$$where \(\Gamma _{\tau }\) and \(\Gamma _{\sigma }\) are directed systems of continuous seminorms that generate \(\tau \) and \(\sigma \), respectively. If \(\tau =\sigma \), we just write \(\tau \)-equicontinuous instead of \(\tau \)-\(\tau \)-equicontinuous.
In the context of semigroups of linear maps there are different degrees of equicontinuity and boundedness. In the following definition we use the symbol \({{\,\textrm{id}\,}}\) for the identity map on a set X, i.e. the map \({{\,\textrm{id}\,}}:X\rightarrow X\), \({{\,\textrm{id}\,}}(x):=x\).
2.2 Definition
Let X be a linear space and \((T(t))_{t\ge 0}\) a family of linear maps \(X\rightarrow X\).
-
(a)
\((T(t))_{t\ge 0}\) is called a semigroup if \(T(0)={{\,\textrm{id}\,}}\) and \(T(t+s)=T(t)T(s)\) for all \(t,s\ge 0\).
-
(b)
Let \((X,\tau )\) be a Hausdorff locally convex space. \((T(t))_{t\ge 0}\) is called locally \(\tau \)-equicontinuous if \((T(t))_{t\in [0,t_{0}]}\) is \(\tau \)-equicontinuous for all \(t_{0}\ge 0\). \((T(t))_{t\ge 0}\) is called quasi-\(\tau \)-equicontinuous if there exists \(\omega \in \mathbb {R}\) such that \((\textrm{e}^{-\omega t}T(t))_{t\ge 0}\) is \(\tau \)-equicontinuous.
-
(c)
Let \((X,\Vert \cdot \Vert )\) be a normed space. \((T(t))_{t\ge 0}\) is called locally bounded if for all \(t_{0}\ge 0\) it holds that
$$\begin{aligned} \sup _{t\in [0,t_{0}]}\Vert T(t)\Vert _{\mathcal {L}(X)}<\infty \end{aligned}$$where \(\Vert T(t)\Vert _{\mathcal {L}(X)}:=\sup _{x\in X,\,\Vert x\Vert \le 1}\Vert T(t)x\Vert \). \((T(t))_{t\ge 0}\) is called exponentially bounded if there exist \(M\ge 1\) and \(\omega \in \mathbb {R}\) such that \(\Vert T(t)\Vert _{\mathcal {L}(X)}\le M\textrm{e}^{\omega t}\) for all \(t\ge 0\).
Since local boundedness of semigroups of linear maps on normed spaces will be an essential condition in our work, we give the following characterisation, which carries over from the case of norm-strongly continuous semigroups on Banach spaces in [33, Chap. I, 5.5 Proposition, p. 39] and whose simple proof we omit.
2.3 Proposition
Let \((X,\Vert \cdot \Vert )\) be a normed space and \((T(t))_{t\ge 0}\) a semigroup of linear maps \(X\rightarrow X\). Then the following assertions are equivalent.
-
(a)
\((T(t))_{t\ge 0}\) is exponentially bounded.
-
(b)
\((T(t))_{t\ge 0}\) is locally bounded.
-
(c)
There exists \(t_{0}>0\) such that \(\sup _{t\in [0,t_{0}]}\Vert T(t)\Vert _{\mathcal {L}(X)}<\infty \).
If \((X,\Vert \cdot \Vert )\) is complete, then each of the preceding assertions is equivalent to:
-
(d)
There exists \(t_{0}>0\) such that \(\sup _{t\in [0,t_{0}]}\Vert T(t)x\Vert <\infty \) for all \(x\in X\) and \(T(t)\in \mathcal {L}(X)\) for all \(t\in [0,t_{0}]\).
Let us recall the definition of the mixed topology, [76, Section 2.1], and the notion of a Saks space, [22, I.3.2 Definition, p. 27–28], which will be important for the rest of the paper.
2.4 Definition
[49, 2.1 Definition, pp. 3–4] Let \((X,\Vert \cdot \Vert )\) be a normed space and \(\tau \) a Hausdorff locally convex topology on X that is coarser than the \(\Vert \cdot \Vert \)-topology \(\tau _{\Vert \cdot \Vert }\). Then
-
(a)
the mixed topology \(\gamma :=\gamma (\Vert \cdot \Vert ,\tau )\) is the finest linear topology on X that coincides with \(\tau \) on \(\Vert \cdot \Vert \)-bounded sets and such that \(\tau \subset \gamma \subset \tau _{\Vert \cdot \Vert }\);
-
(b)
the triple \((X,\Vert \cdot \Vert ,\tau )\) is called a Saks space if there exists a directed system of continuous seminorms \(\Gamma _{\tau }\) that generates the topology \(\tau \) such that
$$\begin{aligned} \Vert x\Vert =\sup _{p\in \Gamma _{\tau }} p(x), \quad x\in X. \end{aligned}$$(2)
The mixed topology is actually Hausdorff locally convex and the definition given above is equivalent to the one introduced by Wiweger [76, Section 2.1] due to [76, Lemmas 2.2.1, 2.2.2, p. 51].
2.5 Definition
[51, Definitions 2.2, 5.7, pp. 423, 433], [49, 2.4 Definition, pp. 4–5] Let \((X,\Vert \cdot \Vert ,\tau )\) be a Saks space.
-
(a)
We call \((X,\Vert \cdot \Vert ,\tau )\) (sequentially) complete if \((X,\gamma )\) is (sequentially) complete.
-
(b)
We call \((X,\Vert \cdot \Vert ,\tau )\) semi-Montel if \((X,\gamma )\) is a semi-Montel space.
-
(c)
We call \((X,\Vert \cdot \Vert ,\tau )\) C-sequential if \((X,\gamma )\) is C-sequential, i.e. every convex sequentially open subset of \((X,\gamma )\) is already open (see [72, p. 273]).
A Saks space is complete if and only if the \(\Vert \cdot \Vert \)-closed unit ball \(B_{\Vert \cdot \Vert }:=\{x\in X\;|\; \Vert x\Vert \le 1\}\) is \(\tau \)-complete by [22, I.1.14 Proposition, p. 11]. The definition of the mixed topology given in Definition 2.4 (a) is a bit abstract but sometimes the mixed topology coincides with a more concrete topology whose origin is [76, Theorem 3.1.1, p. 62], see for instance [22, 49, 76] for such cases. This happens for example if \((X,\Vert \cdot \Vert ,\tau )\) is a semi-Montel Saks space. It is semi-Montel if and only if \(B_{\Vert \cdot \Vert }:=\{x\in X\;|\; \Vert x\Vert \le 1\}\) is \(\tau \)-compact by [22, I.1.13 Proposition, p. 11]. Since the space \((X,\gamma )\) is usually not barrelled by [22, I.1.15 Proposition, p. 12], one cannot apply automatic local equicontinuity results like [46, Proposition 1.1, p. 259] to \(\gamma \)-strongly continuous semigroups. A way to circumvent this problem is the condition that the space is C-sequential. A sufficient condition that guarantees that \((X,\Vert \cdot \Vert ,\tau )\) is C-sequential is that \(\tau \) is metrisable on \(B_{\Vert \cdot \Vert }\) by [53, Proposition 5.7, p. 2681–2682].
2.6 Remark
If \((X,\Vert \cdot \Vert ,\tau )\) is a sequentially complete Saks space, then the normed space \((X,\Vert \cdot \Vert )\) is complete because \(\gamma \) is a coarser topology than the norm \(\Vert \cdot \Vert \)-topology and completeness of a normed space is equivalent to sequential completeness.
On sequentially complete Saks spaces \((X,\Vert \cdot \Vert ,\tau )\) there is another notion of strongly continuous semigroups, namely, so-called \(\tau \)-bi-continuous semigroups which were introduced in [54, Definition 1.3, p. 6–7] (cf. [55, Definition 3, p. 207]). Due to [52, 2.9 Remark (b)] (cf. [34, Proposition A.1.3, p. 73]) and the comments after [51, Definition 2.2, p. 423], a semigroup \((T(t))_{t\ge 0}\) of linear maps \(X\rightarrow X\) is \(\tau \)-bi-continuous if and only if it is locally sequentially \(\gamma \)-equicontinuous and the map \(T_{x}:[0,\infty )\rightarrow (X,\gamma )\), \(T_{x}(t)=T(t)x\), is continuous for every \(x\in X\) (we note that in contrast to Definition 2.1 (a) the definition of \(\gamma \)-strong continuity in [52] does not include the condition that \(T(t)\in \mathcal {L}(X,\gamma )\) for every \(t\ge 0\)). Hence every \(\gamma \)-strongly continuous and locally \(\gamma \)-equicontinuous semigroup on a sequentially complete Saks space is \(\tau \)-bi-continuous and the converse is not true in general by [35, Example 4.1, p. 320]. However, on sequentially complete C-sequential Saks spaces the converse is also true by [48, Theorem 7.4, p. 180] and [75, Theorem 7.4, p. 52], even more, every \(\tau \)-bi-continuous semigroup is \(\gamma \)-strongly continuous and quasi-\(\gamma \)-equicontinuous by [50, Theorem 3.17, p. 13]. Summarising, we have the following theorem.
2.7 Theorem
Let \((X,\Vert \cdot \Vert ,\tau )\) be a sequentially complete C-sequential Saks space and \((T(t))_{t\ge 0}\) a semigroup of linear maps \(X\rightarrow X\). Then the following assertions are equivalent.
-
(a)
\((T(t))_{t\ge 0}\) is \(\tau \)-bi-continuous.
-
(b)
\((T(t))_{t\ge 0}\) is \(\gamma \)-strongly continuous and locally \(\gamma \)-equicontinuous.
-
(c)
\((T(t))_{t\ge 0}\) is \(\gamma \)-strongly continuous and quasi-\(\gamma \)-equicontinuous.
We close this section with some examples of Saks spaces and a convention we will use throughout the paper. We denote by \(\mathcal {C}(\Omega )\) the space of \(\mathbb {K}\)-valued continuous functions on a Hausdorff space \(\Omega \) and by \(\tau _{{\text {co}}}\) the compact-open topology on \(\mathcal {C}(\Omega )\), i.e. the topology of uniform convergence on compact subsets of \(\Omega \).
2.8 Convention
Let \(\Omega \) be a Hausdorff space and \((\mathcal {F}(\Omega ),\Vert \cdot \Vert )\) a normed space such that \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\). Then \(\mathcal {C}(\Omega )\) induces the relative compact-open topology \({\tau _{{\text {co}}}}_{\mid \mathcal {F}(\Omega )}\) on \(\mathcal {F}(\Omega )\) and we get a Saks space \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,{\tau _{{\text {co}}}}_{\mid \mathcal {F}(\Omega )})\) if and only if
-
(i)
for every compact set \(K\subset \Omega \) there is \(C\ge 0\) such that
$$\begin{aligned} \sup _{x\in K}|f(x)|\le C\Vert f\Vert ,\quad f\in \mathcal {F}(\Omega ), \end{aligned}$$which is equivalent to the inclusion \(I:(\mathcal {F}(\Omega ),\Vert \cdot \Vert ) \rightarrow (\mathcal {C}(\Omega ),\tau _{{\text {co}}})\), \(I(f):=f\), being continuous, and
-
(ii)
there exists a directed system of continuous seminorms \(\Gamma _{{\tau _{{\text {co}}}}_{\mid \mathcal {F}(\Omega )}}\) that generates the topology \({\tau _{{\text {co}}}}_{\mid \mathcal {F}(\Omega )}\) such that
$$\begin{aligned} \Vert f\Vert =\sup _{p\in \Gamma _{{\tau _{{\text {co}}}}_{\mid \mathcal {F}(\Omega )}}} p(f), \quad f\in \mathcal {F}(\Omega ). \end{aligned}$$
If this is fulfilled, we write that \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}}):=(\mathcal {F}(\Omega ),\Vert \cdot \Vert ,{\tau _{{\text {co}}}}_{\mid \mathcal {F}(\Omega )})\) is a Saks space.
Further, we denote by \(\mathcal {H}(\Omega ):=\mathcal {C}^{1}_{\mathbb {C}}(\Omega )\) the space of holomorphic functions on an open set \(\Omega \subset \mathbb {C}\) and set \(\mathbb {D}:=\{z\in \mathbb {C}\;|\;|z|< 1\}\). Moreover, we write \(\mathcal {C}^{1}(\Omega ):=\mathcal {C}^{1}_{\mathbb {R}}(\Omega )\) for the space of continuously differentiable functions on an open set \(\Omega \subset \mathbb {R}\). Due to [49, 3.5 Corollary, p. 9–10] and [81, Theorems 4.25, 9.8, p. 81, 260] we have the following result.
2.9 Example
For the following spaces \((\mathcal {F}(\mathbb {D}),\Vert \cdot \Vert )\) the triples \((\mathcal {F}(\mathbb {D}),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) are complete semi-Montel C-sequential Saks spaces and \(\mathcal {F}(\mathbb {D})\subset \mathcal {H}(\mathbb {D})\):
-
(a)
The Hardy spaces \((H^{p},\Vert \cdot \Vert _{p})\) given by
$$\begin{aligned} H^{p}:=\Bigl \{f\in \mathcal {H}(\mathbb {D})\;|\; \Vert f\Vert _{p}^{p}:=\sup _{0<r<1}\frac{1}{2\pi }\int _{0}^{2\pi }|f(r\textrm{e}^{\textrm{i}\theta })|^{p}\textrm{d}\theta <\infty \Bigr \}. \end{aligned}$$ -
(b)
The weighted Bergman spaces \((A_{\alpha }^{p},\Vert \cdot \Vert _{\alpha ,p})\) for \(\alpha >-1\) and \(1\le p<\infty \) given by
$$\begin{aligned} A_{\alpha }^{p}:=\Bigl \{f\in \mathcal {H}(\mathbb {D})\;|\; \Vert f\Vert _{\alpha ,p}^{p}:=\frac{\alpha +1}{\pi }\int _{\mathbb {D}}|f(z)|^{p}(1-|z|^2)^{\alpha }\textrm{d}z<\infty \Bigr \}. \end{aligned}$$ -
(c)
The Dirichlet space \((\mathcal {D},\Vert \cdot \Vert _{\mathcal {D}})\) given by
$$\begin{aligned} \mathcal {D}:=\Bigl \{f\in \mathcal {H}(\mathbb {D})\;|\; \Vert f\Vert _{\mathcal {D}}^2:=|f(0)|^2+\frac{1}{\pi }\int _{\mathbb {D}}|f'(z)|^2\textrm{d}z<\infty \Bigr \} \end{aligned}$$with the inner product
$$\begin{aligned} \langle f, g\rangle :=f(0)\overline{g(0)}+\frac{1}{\pi }\int _{\mathbb {D}}f'(z)\overline{g'(z)}\textrm{d}z,\quad f,g\in \mathcal {D}. \end{aligned}$$
Moreover, the spaces in (a) for \(1<p<\infty \), in (b) for \(\alpha >-1\) and \(1<p<\infty \), and in (c) are reflexive.
Our next example is the Bloch space w.r.t. a weight v.
2.10 Example
([49, 4.10 Corollary, p. 19]) For a continuous function \(v:\mathbb {D}\rightarrow (0,\infty )\) we define the v-Bloch space
Then \((\mathcal {B}v(\mathbb {D}),\Vert \cdot \Vert _{\mathcal {B}v(\mathbb {D})},\tau _{{\text {co}}})\) is a complete semi-Montel C-sequential Saks space.
For \(\alpha >0\) we get with \(v_{\alpha }(z):=(1-|z|^2)^{\alpha }\), \(z\in \mathbb {D}\), the usual Bloch type space \(\mathcal {B}_{\alpha }:=\mathcal {B}v_{\alpha }(\mathbb {D})\) (see [80, p. 1144]).
The case \(p=\infty \) in Example 2.9 (a) can also be covered, namely, we have the following result for weighted \(H^{\infty }\)-spaces.
2.11 Example
[49, 4.6 Corollary, p. 17–18] For an open set \(\Omega \subset \mathbb {C}\) and a continuous function \(v:\Omega \rightarrow (0,\infty )\) we set
Then \((\mathcal {H}v(\Omega ),\Vert \cdot \Vert _{v},\tau _{{\text {co}}})\) is a complete semi-Montel C-sequential Saks space.
If \(v=\mathbb {1}\), we set \(H^{\infty }(\Omega ):=\mathcal {H}v(\Omega )\) and \(H^{\infty }:=H^{\infty }(\mathbb {D})\), which is the Hardy space of bounded holomorphic functions on \(\mathbb {D}\) (see [81, p. 253]). Here, \(\mathbb {1}\) denotes the map \(\mathbb {1}:\Omega \rightarrow \mathbb {K}\), \(\mathbb {1}(x):=1\), on a set \(\Omega \subset \mathbb {K}\). In our following example we consider the space of bounded Dirichlet series which is a topological subspace of \(H^{\infty }(\mathbb {C}_{+})\) where \(\mathbb {C}_{+}:=\{z\in \mathbb {C}\;|\;{{\,\textrm{Re}\,}}z >0\}\) is the open right half-plane, see e.g. [21, p. 27].
2.12 Example
We define the space \(\mathscr {H}^{\infty }\) of bounded Dirichlet series as the topological subspace of \(H^{\infty }(\mathbb {C}_{+})\) consisting of bounded holomorphic functions on \(\mathbb {C}_{+}\) that can be written as a Dirichlet series on some half-plane contained in \(\mathbb {C}_{+}\). Further, we denote by \(\Vert \cdot \Vert _{\mathscr {H}^{\infty }}\) the restriction of the norm \(\Vert \cdot \Vert _{\mathbb {1}}\) of \(H^{\infty }(\mathbb {C}_{+})\) to \(\mathscr {H}^{\infty }\). Then \((\mathscr {H}^{\infty },\Vert \cdot \Vert _{\mathscr {H}^{\infty }},\tau _{{\text {co}}})\) is a complete semi-Montel C-sequential Saks space.
Proof
Due to [7, Lemma 18, p. 227] the unit ball \(B_{\Vert \cdot \Vert _{\mathscr {H}^{\infty }}}\) of \(\mathscr {H}^{\infty }\) is \(\tau _{{\text {co}}}\)-compact. Therefore \((\mathscr {H}^{\infty },\Vert \cdot \Vert _{\mathscr {H}^{\infty }},\tau _{{\text {co}}})\) is a complete semi-Montel Saks space by [22, I.3.1 Lemma, p. 27] and [22, I.1.14, I.1.13 Propositions, p. 11]. Moreover, the topology \(\tau _{{\text {co}}}\) is metrisable on \(\mathscr {H}^{\infty }\) and thus \((\mathscr {H}^{\infty },\Vert \cdot \Vert _{\mathscr {H}^{\infty }},\tau _{{\text {co}}})\) is C-sequential by [53, Proposition 5.7, p. 2681–2682]. \(\square \)
For our last example of this section we recall that a completely regular Hausdorff space \(\Omega \) is called a \(k_{\mathbb {R}}\)-space if any map \(f:\Omega \rightarrow \mathbb {R}\) whose restriction to each compact \(K\subset \Omega \) is continuous, is already continuous on \(\Omega \) (see [59, p. 487]). In particular, Polish spaces and locally compact Hausdorff spaces are \(k_{\mathbb {R}}\)-spaces. Due to [49, 4.5 Corollary, p. 15–16] and [50, Remark 3.19 (a), p. 14] we have the following result.
2.13 Example
For a completely regular Hausdorff space \(\Omega \) and a continuous function \(v:\Omega \rightarrow (0,\infty )\) we set
Then \((\mathcal {C}v(\Omega ),\Vert \cdot \Vert _{v},\tau _{{\text {co}}})\) is a Saks space, which is complete if \(\Omega \) is a \(k_{\mathbb {R}}\)-space. It is C-sequential if \(\Omega \) is a hemicompact Hausdorff \(k_{\mathbb {R}}\)-space or a Polish space.
If \(\Omega \subset \mathbb {C}\) is open, then \(\mathcal {H}v(\Omega )\) from Example 2.11 is a subspace of \(\mathcal {C}v(\Omega )\) and the mixed topologies are compatible, i.e.
by [22, I.4.6 Lemma, p. 44]. If \(v=\mathbb {1}\), then we get the space of bounded continuous functions \(\mathcal {C}_{b}(\Omega )=\mathcal {C}v(\Omega )\) on \(\Omega \) and \(\Vert \cdot \Vert _{v}=\Vert \cdot \Vert _{\infty }\) is the supremum norm. Further examples of Saks spaces may be found, for instance, in [22, 49, 50, 52, 54].
3 Semiflows, Semicocycles and Semicoboundaries
In this section we recall the notions and properties of semiflows, associated semicoclyes and of semicoboundaries, which form a special class of semicocycles.
3.1 Definition
Let I, \(\Omega \) and Y be Hausdorff spaces and \(\varphi :=(\varphi _{t})_{t\in I}\) a family of functions \(\varphi _{t}:\Omega \rightarrow Y\).
-
(a)
We call \(\varphi \) separately continuous if \(\varphi _{t}\) and \(\varphi _{(\cdot )}(x):I\rightarrow Y\) are continuous for all \(t\in I\) and \(x\in \Omega \).
-
(b)
We call \(\varphi \) jointly continuous if the map \(I\times \Omega \rightarrow Y\), \((t,x)\mapsto \varphi _{t}(x)\), is continuous where \(I\times \Omega \) is equipped with the product topology.
-
(c)
Let \(I:=[0,\infty )\). We say that \(\varphi _{(\cdot )}(x)\in \mathcal {C}^{1}[0,\infty )\) for \(x\in \Omega \) if \(\varphi _{(\cdot )}(x)\) is continuously differentiable on \([0,\infty )\) where differentiability in \(t=0\) means right-differentiability in \(t=0\). Further, we set
 for all \(t_{0}\in [0,\infty )\).
for all \(t_{0}\in [0,\infty )\). -
(d)
Let \(\Omega \subset \mathbb {K}\) be open. If \(\varphi _{t}\in \mathcal {C}_{\mathbb {K}}^{1}(\Omega )\) for \(t\in I\), we set \(\varphi _{t}'(x_{0}):=(\frac{\partial }{\partial x}\varphi _{t})(x_{0})\) for all \(x_{0}\in \Omega \).
Let us come to semiflows.
3.2 Definition
Let \(\Omega \) be a Hausdorff space. A family \(\varphi :=(\varphi _{t})_{t\ge 0}\) of continuous functions \(\varphi _{t}:\Omega \rightarrow \Omega \) is called a semiflow if
-
(i)
\(\varphi _{0}(x)=x\) for all \(x\in \Omega \), and
-
(ii)
\(\varphi _{t+s}(x)=(\varphi _{t}\circ \varphi _{s})(x)\) for all \(t,s\ge 0\) and \(x\in \Omega \).
We call a semiflow \(\varphi \) trivial and write \(\varphi ={{\,\textrm{id}\,}}\) if \(\varphi _{t}={{\,\textrm{id}\,}}\) for all \(t\ge 0\). We call a semiflow \(\varphi \) a \(C_{0}\)-semiflow if  for all \(x\in \Omega \). If \(\Omega \subset \mathbb {C}\) is open, we call a semiflow \(\varphi \) holomorphic if \(\varphi _{t}\in \mathcal {H}(\Omega )\) for all \(t\ge 0\).
for all \(x\in \Omega \). If \(\Omega \subset \mathbb {C}\) is open, we call a semiflow \(\varphi \) holomorphic if \(\varphi _{t}\in \mathcal {H}(\Omega )\) for all \(t\ge 0\).
A lot of examples of jointly continuous holomorphic semiflows and their whole classification are given in [71, p. 4–5] for \(\Omega =\mathbb {D}\), in [1, Proposition 1.4.26, p. 98] for \(\Omega =\mathbb {C}\), in [1, Proposition 1.4.27, p. 98] for \(\Omega =\mathbb {C}{\setminus }\{0\}\), in [1, Proposition 1.4.29, p. 99] for \(\Omega =\{z\in \mathbb {C}\;|\;r<|z|<1\}\), \(0<r<1\), and in [1, Proposition 1.4.30, p. 99] for \(\Omega =\mathbb {D}{\setminus }\{0\}\). Further examples may be found in [13, Chap. 8] and also in the following sections of our paper.
3.3 Proposition
([24, Theorems 2.2, 2.3, p. 692], [20, 2., p. 318–319]) Let \(\varphi \) be a semiflow on a locally compact Hausdorff space \(\Omega \).
-
(a)
Let \(\Omega \) be \(\sigma \)-compact. Then \(\varphi \) is jointly continuous if and only if \(\varphi \) is \(C_{0}\).
-
(b)
Let \(\Omega \) be metrisable. Then \(\varphi \) is jointly continuous if and only if \(\varphi \) is separately continuous.
An important concept for semiflows is their generator.
3.4 Definition
Let \(\varphi \) be a semiflow on a Hausdorff space \(\Omega \) such that \(\varphi _{(\cdot )}(x)\in \mathcal {C}^{1}[0,\infty )\) for all \(x\in \Omega \). A continuous function \(G:\Omega \rightarrow \Omega \) is called the generator of \(\varphi \) if  for all \(t\ge 0\) and \(x\in \Omega \).
for all \(t\ge 0\) and \(x\in \Omega \).
3.5 Remark
If existing, the generator of \(\varphi \) is uniquely determined because we have  for all \(x\in \Omega \).
for all \(x\in \Omega \).
The generator is also called the speed of the semiflow (see [6, p. 210] where the symbol \(\lambda \) is used for G). For a separately continuous semiflow \(\varphi \) the existence of the generator is equivalent to right-differentiability in \(t=0\) and continuity of  .
.
3.6 Proposition
Let \(\Omega \) be a Hausdorff space and \(\varphi \) a separately continuous semiflow on \(\Omega \). Then \(\varphi _{(\cdot )}(x)\in \mathcal {C}^{1}[0,\infty )\) for all \(x\in \Omega \) and  for all \(t\ge 0\) if and only if \(\varphi _{(\cdot )}(x)\) is right-differentiable in \(t=0\) for all \(x\in \Omega \) and
for all \(t\ge 0\) if and only if \(\varphi _{(\cdot )}(x)\) is right-differentiable in \(t=0\) for all \(x\in \Omega \) and  . In this case
. In this case  for all \(t\ge 0\) and \(x\in \Omega \), and
for all \(t\ge 0\) and \(x\in \Omega \), and  is the generator of \(\varphi \).
is the generator of \(\varphi \).
Proof
We only need to prove the implication \(\Leftarrow \). Let \(\varphi _{(\cdot )}(x)\) be right-differentiable in \(t=0\) for all \(x\in \Omega \) and  .
For \(x\in \Omega \) we claim that \(\varphi _{(\cdot )}(x)\) is continuously right-differentiable on \([0,\infty )\) with right-derivative
.
For \(x\in \Omega \) we claim that \(\varphi _{(\cdot )}(x)\) is continuously right-differentiable on \([0,\infty )\) with right-derivative  for all \(t\ge 0\). Indeed, we have
for all \(t\ge 0\). Indeed, we have

for all \(t\ge 0\). Thus \(\varphi _{(\cdot )}(x)\) is right-differentiable on \([0,\infty )\) and the right-derivative is continuous (in t) because  and \(\varphi \) is separately continuous. It follows that the continuous function \(\varphi _{(\cdot )}(x)\) is continuously differentiable on \([0,\infty )\) with
and \(\varphi \) is separately continuous. It follows that the continuous function \(\varphi _{(\cdot )}(x)\) is continuously differentiable on \([0,\infty )\) with  for all \(t\ge 0\) (see e.g. [62, Chap. 2, Corollary 1.2, p. 43]). \(\square \)
for all \(t\ge 0\) (see e.g. [62, Chap. 2, Corollary 1.2, p. 43]). \(\square \)
Further sufficient and necessary conditions for a given continuous function \(G:\mathbb {R}\rightarrow \mathbb {R}\) to be the generator of a jointly continuous flow on \(\mathbb {R}\) are contained in [6, Lemma 2.2, p. 212]. The notion of a generator in the case of a jointly continuous holomorphic semiflow was introduced in [10, p. 103]. In this case the generator always exists and is not only continuous but even holomorphic.
3.7 Theorem
[10, (1.1) Theorem, p. 101–102] Let \(\Omega \subset \mathbb {C}\) be open and \(\varphi \) a jointly continuous holomorphic semiflow on \(\Omega \). Then \(\varphi _{(\cdot )}(z)\in \mathcal {C}^{1}[0,\infty )\) for all \(z\in \Omega \) and there is \(G\in \mathcal {H}(\Omega )\) such that  for all \(t\ge 0\) and \(z\in \Omega \).
for all \(t\ge 0\) and \(z\in \Omega \).
We also have the following generalisation of [13, Proposition 10.1.8 (1), p. 276–277] where \(\mathbb {K}=\mathbb {C}\) and \(\Omega =\mathbb {D}\).
3.8 Proposition
Let \(\varphi \) be a semiflow on an open set \(\Omega \subset \mathbb {K}\) such that \(\varphi _{(\cdot )}(x)\in \mathcal {C}^{1}[0,\infty )\) for all \(x\in \Omega \) and \(\varphi _{t}\in \mathcal {C}^{1}_{\mathbb {K}}(\Omega )\) for all \(t\ge 0\). Then

If in addition \(\varphi \) has a generator G, then

Proof
For all \(s,t\ge 0\) and \(x\in \Omega \) we have \(\varphi _{s}(\varphi _{t}(x))=\varphi _{t+s}(x)=(\varphi _{t}\circ \varphi _{s})(x)\). By differentiating w.r.t. s we get

for all \(s,t\ge 0\) and \(x\in \Omega \), which yields  for \(s=0\). The rest of the statement follows from the definition of a generator and Remark 3.5. \(\square \)
for \(s=0\). The rest of the statement follows from the definition of a generator and Remark 3.5. \(\square \)
Next, let us recall the notion of a semicocycle for a semiflow.
3.9 Definition
Let \(\varphi :=(\varphi _{t})_{t\ge 0}\) be a semiflow on a Hausdorff space \(\Omega \). A family \(m:=(m_{t})_{t\ge 0}\) of continuous functions \(m_{t}:\Omega \rightarrow \mathbb {K}\) is called a multiplicative semicocycle for \(\varphi \) if
-
(i)
\(m_{0}(x)=1\) for all \(x\in \Omega \), and
-
(ii)
\(m_{t+s}(x)=m_{t}(x)m_{s}(\varphi _{t}(x))\) for all \(t,s\ge 0\) and \(x\in \Omega \).
We call a semicocycle m trivial and write \(m=\mathbb {1}\) if \(m_{t}=\mathbb {1}\) for all \(t\ge 0\). We call a semicocycle m a \(C_{0}\)-semicocycle if  for all \(x\in \Omega \). If \(\Omega \subset \mathbb {C}\) is open, we call a semicocycle m holomorphic if \(m_{t}\in \mathcal {H}(\Omega )\) for all \(t\ge 0\).
for all \(x\in \Omega \). If \(\Omega \subset \mathbb {C}\) is open, we call a semicocycle m holomorphic if \(m_{t}\in \mathcal {H}(\Omega )\) for all \(t\ge 0\).
If \(\varphi \) is a holomorphic semiflow on an open set \(\Omega \subset \mathbb {C}\), then a simple example of a holomorphic semicocycle m for \(\varphi \) is given by the complex derivatives \(m_{t}:=\varphi _{t}'\) for \(t\ge 0\) by the chain rule. There is an analogon of Proposition 2.3 for semicocycles due to König [47] which will be important later on. The similarity to Proposition 2.3 is not a coincidence because they use the same ideas, which can be found in the proofs of [27, VIII.1.4 Lemma, VIII.1.5 Corollary, p. 618–619].
3.10 Proposition
Let \(\varphi \) be a semiflow on a Hausdorff space \(\Omega \) and m a semicocycle for \(\varphi \). Then the following assertions are equivalent.
-
(a)
There exist \(M\ge 1\) and \(\omega \in \mathbb {R}\) such that \(\Vert m_{t}\Vert _{\infty }\le M\textrm{e}^{\omega t}\) for all \(t\ge 0\).
-
(b)
It holds that \(\sup _{t\in [0,t_{0}]}\Vert m_{t}\Vert _{\infty }<\infty \) for all \(t_{0}\ge 0\).
-
(c)
There exists \(t_{0}>0\) such that \(\sup _{t\in [0,t_{0}]}\Vert m_{t}\Vert _{\infty }<\infty \).
-
(d)
It holds that \(\Vert m_{t}\Vert _{\infty }<\infty \) for all \(t\ge 0\).
-
(e)
It holds that
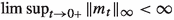 .
.
Proof
The implications (d)\(\Rightarrow \)(a)\(\Rightarrow \)(e)\(\Rightarrow \)(c)\(\Rightarrow \)(d) follow from the proof of [47, Lemma 2.1 (a), p. 472] (we note that it is not relevant for the proof that \((h_{t})_{t\ge 0}:=m\) in the cited lemma is assumed to be holomorphic and \(\Omega \) to be equal to \(\mathbb {D}\)). Moreover, the implications (a)\(\Rightarrow \)(b)\(\Rightarrow \)(c) clearly hold. \(\square \)
3.11 Definition
Let \(\varphi \) be a semiflow on a Hausdorff space \(\Omega \) and m a semicocycle for \(\varphi \). We call the tuple \((m,\varphi )\) a co-semiflow on \(\Omega \). We call a co-semiflow \((m,\varphi )\) jointly continuous (separately continuous, \(C_{0}\), holomorphic) if \(\varphi \) and m are both jointly continuous (separately continuous, \(C_{0}\), holomorphic).
3.12 Proposition
Let \((m,\varphi )\) be a co-semiflow on an open subset \(\Omega \) of a metric space and \(\varphi \) jointly continuous. Then m is jointly continuous if and only if m is \(C_{0}\).
Proof
The implication \(\Rightarrow \) clearly holds. The other implication follows from [31, Definition 3.1, p. 1203], the proof of [31, Theorem 3.1, p. 1204] with \(\mathcal {D}:=\Omega \) and \(\mathcal {A}:=\mathbb {C}\), and the observation that the assumption that \(\mathcal {D}\) is an open connected subset of a Banach space (see [31, p. 1200]) is not needed in the proof of [31, Theorem 3.1, p. 1204]. \(\square \)
Analogously to Proposition 3.6 we have the following result for semicocycles.
3.13 Proposition
Let \(\Omega \) be a Hausdorff space and \((m,\varphi )\) a separately continuous co-semiflow on \(\Omega \). Then \(m_{(\cdot )}(x)\in \mathcal {C}^{1}[0,\infty )\) for all \(x\in \Omega \) and  for all \(t\ge 0\) if and only if \(m_{(\cdot )}(x)\) is right-differentiable in \(t=0\) for all \(x\in \Omega \) and
for all \(t\ge 0\) if and only if \(m_{(\cdot )}(x)\) is right-differentiable in \(t=0\) for all \(x\in \Omega \) and  . In this case
. In this case  and
and  for all \(t\ge 0\) and \(x\in \Omega \).
for all \(t\ge 0\) and \(x\in \Omega \).
Proof
We only need to prove the implication \(\Leftarrow \). Let \(m_{(\cdot )}(x)\) be right-differentiable in \(t=0\) for all \(x\in \Omega \) and  . For \(x\in \Omega \) we claim that \(m_{(\cdot )}(x)\) is continuously right-differentiable on \([0,\infty )\) with right-derivative
. For \(x\in \Omega \) we claim that \(m_{(\cdot )}(x)\) is continuously right-differentiable on \([0,\infty )\) with right-derivative  for all \(t\ge 0\). Indeed, we have
for all \(t\ge 0\). Indeed, we have

for all \(t\ge 0\). Thus \(m_{(\cdot )}(x)\) is right-differentiable on \([0,\infty )\) and the right-derivative is continuous (in t) because  and \((m,\varphi )\) is separately continuous. It follows from [62, Chap. 2, Corollary 1.2, p. 43] that the continuous function \(m_{(\cdot )}(x)\) is continuously differentiable on \([0,\infty )\) with
and \((m,\varphi )\) is separately continuous. It follows from [62, Chap. 2, Corollary 1.2, p. 43] that the continuous function \(m_{(\cdot )}(x)\) is continuously differentiable on \([0,\infty )\) with  for all \(t\ge 0\). Thus for \(x\in \Omega \) we know that the map \(t\mapsto m_{t}(x)\) solves the initial value problem
for all \(t\ge 0\). Thus for \(x\in \Omega \) we know that the map \(t\mapsto m_{t}(x)\) solves the initial value problem

with  . Another solution of this initial value problem is given by the map
. Another solution of this initial value problem is given by the map  . Since the solution of this initial value problem is unique (e.g. by [42, Chap. 1, Theorem 3, p. 7]), we get that
. Since the solution of this initial value problem is unique (e.g. by [42, Chap. 1, Theorem 3, p. 7]), we get that  for all \(t\ge 0\). \(\square \)
for all \(t\ge 0\). \(\square \)
We have the following construction of a semicocycle given a jointly continuous semiflow and a continuous function on a locally compact metric space.
3.14 Proposition
Let \(\varphi \) be a jointly continuous semiflow on a locally compact metric space \(\Omega \) and \(g\in \mathcal {C}(\Omega )\). Then the following assertions hold.
-
(a)
The family \(m:=(m_{t})_{t\ge 0}\) given by \(m_{t}(x):=\exp (\int _{0}^{t}g(\varphi _{s}(x))\textrm{d}s)\) for all \(t\ge 0\) and \(x\in \Omega \) is a jointly continuous semicocycle for \(\varphi \). In particular, \(m_{(\cdot )}(x)\in \mathcal {C}^{1}[0,\infty )\),
 ,
,  and \(m_{t}(x)\ne 0\) for all \(t\ge 0\) and \(x\in \Omega \).
and \(m_{t}(x)\ne 0\) for all \(t\ge 0\) and \(x\in \Omega \). -
(b)
If \(\Omega \subset \mathbb {K}\) is open and \(\varphi _{t},g\in \mathcal {C}^{1}_{\mathbb {K}}(\Omega )\) for all \(t\ge 0\), then \(m_{t}\in \mathcal {C}^{1}_{\mathbb {K}}(\Omega )\) for all \(t\ge 0\) with m from part (a).
Proof
(a) Let \(t\ge 0\). We note that \(g\circ \varphi _{t}\in \mathcal {C}(\Omega )\) and the map \(g(\varphi _{(\cdot )}(x))\) is continuous and therefore integrable on [0, t]. For every \(x_{0}\in \Omega \) there is a compact neighbourhood \(U\subset \Omega \) of \(x_{0}\) such that \(|g(\varphi _{(\cdot )}(x))|\le \sup \{|g(\varphi _{s}(w))|\;|\;(s,w)\in [0,t]\times U\}<\infty \) on [0, t] for all \(x\in U\) because \(\Omega \) is locally compact, \(g\in \mathcal {C}(\Omega )\) and \(\varphi \) jointly continuous. Setting \(F_{t}:\Omega \rightarrow \mathbb {K}\), \(F_{t}(x):=\int _{0}^{t}g(\varphi _{s}(x))\textrm{d}s\), we deduce that \(F_{t}\) is continuous on the metric space \(\Omega \) by [32, 5.6 Satz, p. 147] and thus \(m_{t}=\exp \circ F_{t}\) as well. From here it is easy to check that m is a \(C_{0}\)-semicocycle for \(\varphi \) and so jointly continuous by Proposition 3.12. The rest of statement (a) follows from the integral form of \(m_{t}(x)\) and Proposition 3.13.
(b) In the case \(\mathbb {K}=\mathbb {R}\) the statement follows from [32, 5.7 Satz, p. 147–148] and in the case \(\mathbb {K}=\mathbb {C}\) from [32, 5.8 Satz, p. 148]. \(\square \)
On connected proper subsets of \(\mathbb {C}\) every jointly continuous holomorphic semicocycle of a jointly continuous holomorphic semiflow is actually of the integral form in Proposition 3.14 (a).
3.15 Proposition
Let \(\Omega \subset \mathbb {C}\) be open and connected, and \((m,\varphi )\) a jointly continuous holomorphic co-semiflow on \(\Omega \). Then it holds \(m_{(\cdot )}(z)\in \mathcal {C}^{1}[0,\infty )\),  and
and  for all \(t\ge 0\) and \(z\in \Omega \).
for all \(t\ge 0\) and \(z\in \Omega \).
Proof
Due to [44, Theorem 4, p. 3392] we have \(m_{(\cdot )}(z)\in \mathcal {C}^{1}[0,\infty )\) for all \(z\in \Omega \) and  for all \(t\ge 0\). Then it follows from Proposition 3.13 that
for all \(t\ge 0\). Then it follows from Proposition 3.13 that  for all \(t\ge 0\) and \(z\in \Omega \). \(\square \)
for all \(t\ge 0\) and \(z\in \Omega \). \(\square \)
Proposition 3.15 improves [44, Theorem 3, p. 3392] with  from simply connected open \(\Omega \subset \mathbb {C}\) to just connected open \(\Omega \subset \mathbb {C}\). Moreover, Proposition 3.15 implies [47, Lemma 2.1 (b), p. 472]. There is another way to construct semicocycles for a semiflow apart from the one in Proposition 3.14, namely, so-called (semi)coboundaries, see e.g. [43, p. 240], [47, p. 469–470] and [61, p. 513]. For that construction we need the notion of a fixed point of a semiflow.
from simply connected open \(\Omega \subset \mathbb {C}\) to just connected open \(\Omega \subset \mathbb {C}\). Moreover, Proposition 3.15 implies [47, Lemma 2.1 (b), p. 472]. There is another way to construct semicocycles for a semiflow apart from the one in Proposition 3.14, namely, so-called (semi)coboundaries, see e.g. [43, p. 240], [47, p. 469–470] and [61, p. 513]. For that construction we need the notion of a fixed point of a semiflow.
3.16 Definition
Let \(\Omega \) be a Hausdorff space and \(\varphi \) a semiflow on \(\Omega \). We call \(x\in \Omega \) a fixed point of \(\varphi \) if it is a common fixed point of all \(\varphi _{t}\), i.e. \(\varphi _{t}(x)=x\) for all \(t\ge 0\). We denote the set of all fixed points of \(\varphi \) by \({\text {Fix}}(\varphi ):=\{x\in \Omega \;|\;\forall \;t\ge 0:\;\varphi _{t}(x)=x\}\).
Let \(\Omega \) be a Hausdorff space and \(\varphi \) a semiflow on \(\Omega \). Let \(\omega \in \mathcal {C}(\Omega )\), \(\omega \ne 0\), such that its set of zeros \(N_{\omega }:=\{x\in \Omega \;|\;\omega (x)=0\}\) fulfils that \(N_{\omega }\subset {\text {Fix}}(\varphi )\), and that \(\Omega {\setminus } N_{\omega }\) is dense in \(\Omega \). We set
and note that \(m_{t}^{\omega }:\Omega {{\setminus }} N_{\omega }\rightarrow \mathbb {K}\) is continuous for all \(t\ge 0\). Moreover,
If \(N_{\omega }\ne \varnothing \), suppose additionally that \(m_{t}^{\omega }\) is continuously extendable on \(\Omega \) for all \(t\ge 0\) and denote the (unique) extension by \(m_{t}^{\omega }\) as well. Then (3) also holds for \(x\in N_{\omega }\) by continuity and the density of \(\Omega {\setminus } N_{\omega }\) in \(\Omega \). Thus \(m^{\omega }:=(m_{t}^{\omega })_{t\ge 0}\) is a semicocycle for \(\varphi \) under this assumption.
3.17 Definition
Let \(\Omega \) be a Hausdorff space and \(\varphi \) a semiflow on \(\Omega \). A semicocycle m for \(\varphi \) is called a semicoboundary for \(\varphi \) if there is \(\omega \in \mathcal {C}(\Omega )\), \(\omega \ne 0\), such that \(N_{\omega }\subset {\text {Fix}}(\varphi )\), the set \(\Omega {\setminus } N_{\omega }\) is dense in \(\Omega \), and \(m=m^{\omega }\).
3.18 Example
Let \(\Omega \subset \mathbb {C}\) be open and connected, \(\varphi \) a holomorpic semiflow on \(\Omega \) and \(\omega \in \mathcal {H}(\Omega )\), \(\omega \ne 0\), such that \(N_{\omega }\subset {\text {Fix}}(\varphi )\). Then the semicoboundary \(m^{\omega }\) for \(\varphi \) satisfies
and \(m_{t}^{\omega }\in \mathcal {H}(\Omega )\) for all \(t\ge 0\) where \({\text {ord}}_{\omega }(z)\in \mathbb {N}\) is the order of the zero \(z\in N_{\omega }\) of \(\omega \). If \(\varphi \) is additionally jointly continuous, then \(m^{\omega }\) is jointly continuous.
Proof
First, we note that \(\Omega {\setminus } N_{\omega }\) is dense in \(\Omega \) since \(N_{\omega }\) is discrete in \(\Omega \). For \(b\in N_{\omega }\) there is \(\psi \in \mathcal {H}(\Omega )\) such that \(\psi (b)\ne 0\) and \(\omega (z)=(z-b)^{n}\psi (z)\) for all \(z\in \Omega \) with \(n:={\text {ord}}_{\omega }(b)\). Let \(t\ge 0\). Then we have for all \(z\in \Omega {\setminus } N_{\omega }\)
because \(N_{\omega }\subset {\text {Fix}}(\varphi )\). Therefore \(m_{t}^{\omega }\) is continuously extendable on \(\Omega \) and this extension is holomorphic on \(\Omega \) by Riemann’s removable singularity theorem.
Now, if \(\varphi \) is additionally jointly continuous, then we have  for all \(z\in \Omega {\setminus } N_{\omega }\). Furthermore, the map \([0,\infty )\rightarrow \mathbb {C}\), \(t\mapsto \varphi _{t}'(z)\), is continuous for every \(z\in \Omega \) by [43, Lemma 2.1, p. 242] with connected \(G:=\Omega \). Hence we have
for all \(z\in \Omega {\setminus } N_{\omega }\). Furthermore, the map \([0,\infty )\rightarrow \mathbb {C}\), \(t\mapsto \varphi _{t}'(z)\), is continuous for every \(z\in \Omega \) by [43, Lemma 2.1, p. 242] with connected \(G:=\Omega \). Hence we have  for all \(z\in N_{\omega }\). We conclude that \(m_{t}^{\omega }\) is \(C_{0}\) and thus jointly continuous by Proposition 3.12. \(\square \)
for all \(z\in N_{\omega }\). We conclude that \(m_{t}^{\omega }\) is \(C_{0}\) and thus jointly continuous by Proposition 3.12. \(\square \)
For \(\Omega =\mathbb {D}\) the previous example is already contained in [68, p. 361–362]. We already observed that \((\varphi _{t}')_{t\ge 0}\) is a simple example of a semicocycle of a holomorphic semiflow \(\varphi \) on an open set \(\Omega \subset \mathbb {C}\). If \(\Omega \) is also connected, then it holds \({\text {Fix}}(\varphi )=N_{G}\) with the generator G of \(\varphi \) by [1, Proposition 1.4.13 (i), p. 89]. Thus \((\varphi _{t}')_{t\ge 0}\) is even a semicoboundary by Theorem 3.7 and Proposition 3.8, which is jointly continuous by the arguments in the example above.
3.19 Example
Let \(\Omega \subset \mathbb {C}\) be open and connected, and \(\varphi \) a jointly continuous holomorphic semiflow on \(\Omega \) with generator \(G\ne 0\). Then \(m_{t}^{G}(z)=\varphi _{t}'(z)\) for all \(t\ge 0\) and \(z\in \Omega \), and \(m^{G}\) is jointly continuous.
For \(\Omega =\mathbb {D}\) the previous example is also contained in [71, Example 7.4, p. 247–248]. The relation between semicoboundaries and the semicocycles from Proposition 3.14 of a jointly continuous holomorphic semiflow on \(\Omega =\mathbb {D}\) is given in [47, Lemma 2.2, p. 472].
4 Semigroups of Weighted Composition Operators
Before introducing weighted composition semigroups induced by a co-semiflow \((m,\varphi )\), we start this section with weighted composition families induced by a tuple \((m,\varphi )\) which need not be a co-semiflow. First, we generalise a part of [41, Proposition 1, p. 307].
4.1 Proposition
Let \(\Omega \) be a Hausdorff space and \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) a Saks space such that \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\). Let I be a set, \(\varphi :=(\varphi _{t})_{t\in I}\) and \(m:=(m_{t})_{t\in I}\) be families of functions \(\varphi _{t}:\Omega \rightarrow \Omega \) and \(m_{t}:\Omega \rightarrow \mathbb {K}\) such that
-
(i)
\(C_{m,\varphi }(t)f:=m_{t}\cdot (f\circ \varphi _{t})\in \mathcal {F}(\Omega )\) for all \(t\in I\) and \(f\in \mathcal {F}(\Omega )\), and
-
(ii)
\(\varphi _{I}(K):=\bigcup _{t\in I}\varphi _{t}(K)\) is relatively compact in \(\Omega \) and \(m_{I}(K):=\bigcup _{t\in I}m_{t}(K)\) is bounded in \(\mathbb {K}\) for all compact \(K\subset \Omega \).
Then \((C_{m,\varphi }(t))_{t\in I}\) is \(\tau _{{\text {co}}}\)-equicontinuous. If in addition \(\sup _{t\in I}\Vert C_{m,\varphi }(t)\Vert _{\mathcal {L}(\mathcal {F}(\Omega ))}<\infty \), then \((C_{m,\varphi }(t))_{t\in I}\) is \(\gamma \)-equicontinuous.
Proof
First, we observe that \((C_{m,\varphi }(t))_{t\in I}\) is a well-defined family of linear maps \(\mathcal {F}(\Omega )\rightarrow \mathcal {F}(\Omega )\) by condition (i). Second, for compact \(K\subset \Omega \) we note that
for all \(t\in I\) and \(f\in \mathcal {F}(\Omega )\), implying that \((C_{m,\varphi }(t))_{t\in I}\) is \(\tau _{{\text {co}}}\)-equicontinuous by condition (ii) and the continuity of the functions in \(\mathcal {F}(\Omega )\).
Now, suppose that \(\sup _{t\in I}\Vert C_{m,\varphi }(t)\Vert _{\mathcal {L}(\mathcal {F}(\Omega ))}<\infty \). Since \(\tau _{{\text {co}}}\) is a coarser topology than \(\gamma \), we obtain from the part above that the family \((C_{m,\varphi }(t))_{t\in I}\) is \(\gamma \)-\(\tau _{{\text {co}}}\)-equicontinuous. It follows from [50, 3.16 Proposition, (f)\(\Leftrightarrow \)(g), p. 12–13] that \((C_{m,\varphi }(t))_{t\in I}\) is even \(\gamma \)-equicontinuous. \(\square \)
4.2 Remark
Let \(\Omega \) be a Hausdorff space, I a compact Hausdorff space, \(\varphi :=(\varphi _{t})_{t\in I}\) and \(m:=(m_{t})_{t\in I}\) families of functions \(\varphi _{t}:\Omega \rightarrow \Omega \) and \(m_{t}:\Omega \rightarrow \mathbb {K}\). If \(\varphi \) and m are both jointly continuous, then condition (ii) of Proposition 4.1 is fulfilled since \(\varphi _{I}(K)\) and \(m_{I}(K)\) are compact for all compact \(K\subset \Omega \).
Our next goal is to derive necessary and sufficient conditions for the weighted composition family \((C_{m,\varphi }(t))_{t\in I}\) to be \(\gamma \)-strongly continuous. For the necessary condition we need the following definition.
4.3 Definition
Let \(\Omega \) and I be Hausdorff spaces, \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\) a linear space, and \(\varphi :=(\varphi _{t})_{t\in I}\) a family of functions \(\varphi _{t}:\Omega \rightarrow \Omega \). We say that the topology of \(\Omega \) is initial-like w.r.t. \((\varphi ,\mathcal {F}(\Omega ))\) if for every compact set \(K\subset \Omega \) the continuity of the map \(I\times K\rightarrow \mathbb {K}\), \((t,x)\mapsto f(\varphi _{t}(x))\), for all \(f\in \mathcal {F}(\Omega )\) implies the continuity of the map \(I\times K\rightarrow \Omega \), \((t,x)\mapsto \varphi _{t}(x)\).
4.4 Remark
-
(a)
Obviously, if \(\Omega \) carries the initial topology induced by \(\mathcal {F}(\Omega )\), then the topology of \(\Omega \) is initial-like w.r.t. \((\varphi ,\mathcal {F}(\Omega ))\) for any family of functions \(\varphi :=(\varphi _{t})_{t\in I}\) with \(\varphi _{t}:\Omega \rightarrow \Omega \). For instance, a completely regular Hausdorff space \(\Omega \) carries the initial topology induced by the space \(\mathcal {C}_{b}(\Omega )\) of bounded continuous functions on \(\Omega \) (see [2, 2.55 Theorem, p. 49] and [2, 2.56 Corollary, p. 50]).
-
(b)
If \(\Omega \subset \mathbb {K}\) and the identity \({\text {id}}:\Omega \rightarrow \Omega \), \(x\mapsto x\), belongs to \(\mathcal {F}(\Omega )\), then the topology of \(\Omega \) is initial-like w.r.t. \((\varphi ,\mathcal {F}(\Omega ))\) for any family of functions \(\varphi :=(\varphi _{t})_{t\in I}\) with \(\varphi _{t}:\Omega \rightarrow \Omega \).
Now, we use the ideas of the proofs of [36, Proposition 2.10, p. 5] (see also [66, Theorem 4.5, p. 51–52]) and [50, Corollary 4.3 (a), (b), p. 20] where \(\mathcal {F}(\Omega )=\mathcal {C}_{b}(\Omega )\) is the space of bounded continuous functions on a completely regular Hausdorff space \(\Omega \), \(I=[0,\infty )\) and \(m=\mathbb {1}\).
4.5 Proposition
Let \(\Omega \) be a Hausdorff space and \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) a Saks space such that \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\). Let I be a metric space, \(\varphi :=(\varphi _{t})_{t\in I}\) and \(m:=(m_{t})_{t\in I}\) be families of continuous functions \(\varphi _{t}:\Omega \rightarrow \Omega \) and \(m_{t}:\Omega \rightarrow \mathbb {K}\) such that \(C_{m,\varphi }(t)f:=m_{t}\cdot (f\circ \varphi _{t})\in \mathcal {F}(\Omega )\) for all \(t\in I\) and \(f\in \mathcal {F}(\Omega )\). Further, suppose that \(\sup _{t\in I}\Vert C_{m,\varphi }(t)\Vert _{\mathcal {L}(\mathcal {F}(\Omega ))}<\infty \). Then the following assertions hold.
-
(a)
If \(\varphi \) and m are jointly continuous, then \((C_{m,\varphi }(t))_{t\in I}\) is \(\gamma \)-strongly continuous.
-
(b)
If \(\Omega \) is a \(k_{\mathbb {R}}\)-space whose topology is initial-like w.r.t. \((\varphi ,\mathcal {F}(\Omega ))\), \(\mathbb {1}\in \mathcal {F}(\Omega )\), I is locally compact, \(m_{t}(x)\ne 0\) for all \((t,x)\in I\times \Omega \) and \((C_{m,\varphi }(t))_{t\in I}\) is \(\gamma \)-strongly continuous, then \(\varphi \) and m are jointly continuous.
Proof
First, we observe that \(C_{m,\varphi }(t)\) is linear and \(\gamma \)-continuous, thus \(C_{m,\varphi }(t)\in \mathcal {L}(\mathcal {F}(\Omega ),\gamma )\), for every \(t\in I\) due to Proposition 4.1 and Remark 4.2 applied to the singleton \(I_{t}:=\{t\}\) and the continuity of \(\varphi _{t}\) and \(m_{t}\).
Since I is a metric space and \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\), the family \((C_{m,\varphi }(t))_{t\in I}\) is \(\gamma \)-strongly continuous if and only if the map
is continuous for every compact \(K\subset \Omega \) and \(f\in \mathcal {F}(\Omega )\) by [22, I.1.10 Proposition, p. 9] and the assumption \(\sup _{t\in I}\Vert C_{m,\varphi }(t)\Vert _{\mathcal {L}(\mathcal {F}(\Omega ))}<\infty \). It follows from [30, Lemma 4.16, p. 56] that this is equivalent to the continuity of the map
for every compact \(K\subset \Omega \) and \(f\in \mathcal {F}(\Omega )\).
(a) If \(\varphi \) and m are jointly continuous, then the map (4) is clearly continuous for every compact \(K\subset \Omega \) and \(f\in \mathcal {F}(\Omega )\).
(b) Since \(\mathbb {1}\in \mathcal {F}(\Omega )\), the continuity of the map (4) implies the continuity of the map
for every compact \(K\subset \Omega \). The continuity of the maps (4) and (5), that \(m_{t}(x)\ne 0\) for all \((t,x)\in I\times \Omega \) and that the topology of \(\Omega \) is initial-like w.r.t. \((\varphi ,\mathcal {F}(\Omega ))\) yield the continuity of the map
for every compact \(K\subset \Omega \). Conversely, the continuity of the maps (5) and (6) clearly implies the continuity of the map (4) for every compact \(K\subset \Omega \) and \(f\in \mathcal {F}(\Omega )\). Hence the continuity of the map (4) for every compact \(K\subset \Omega \) and \(f\in \mathcal {F}(\Omega )\) is equivalent to the continuity of the maps (5) and (6) for every compact \(K\subset \Omega \). Now, if I is locally compact and \(\Omega \) a \(k_{\mathbb {R}}\)-space, then \(I\times \Omega \) is also a \(k_{\mathbb {R}}\)-space by a comment after the proof of [15, Théorème (2.1), p. 54–55]. Thus the \(\gamma \)-strong continuity of \((C_{m,\varphi }(t))_{t\in I}\) implies the continuity of the maps (5) and (6) for every compact \(K\subset \Omega \), which then implies the joint continuity of \(\varphi \) and m because \(I\times \Omega \) is a \(k_{\mathbb {R}}\)-space. \(\square \)
4.6 Remark
Looking at the proof, we see that we can drop the condition that \(\mathbb {1}\in \mathcal {F}(\Omega )\) in Proposition 4.5 (b) if \(m_{t}=\mathbb {1}\) for all \(t\in I\).
From now on we restrict to the case that \((m,\varphi )\) is a co-semiflow on a Hausdorff space \(\Omega \). If \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\) is a linear space and \(C_{m,\varphi }(t)f:=m_{t}\cdot (f\circ \varphi _{t})\in \mathcal {F}(\Omega )\) for all \(t\ge 0\) and \(f\in \mathcal {F}(\Omega )\), then a simple computation shows that \((C_{m,\varphi }(t))_{t\ge 0}\) is a semigroup of linear operators on \(\mathcal {F}(\Omega )\), i.e. \(C_{m,\varphi }(t):\mathcal {F}(\Omega )\rightarrow \mathcal {F}(\Omega )\) is linear and \(C_{m,\varphi }(t+s)=C_{m,\varphi }(t)C_{m,\varphi }(s)\) for all \(t,s\ge 0\).
4.7 Definition
Let \((m,\varphi )\) be a co-semiflow on a Hausdorff space \(\Omega \) and \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\) a linear space. The tuple \((m,\varphi )\) is called a co-semiflow for \(\mathcal {F}(\Omega )\) if \(C_{m,\varphi }(t)f:=m_{t}\cdot (f\circ \varphi _{t})\in \mathcal {F}(\Omega )\) for all \(t\ge 0\) and \(f\in \mathcal {F}(\Omega )\). In this case \((C_{m,\varphi }(t))_{t\ge 0}\) is called the weighted composition semigroup on \(\mathcal {F}(\Omega )\) w.r.t. the co-semiflow \((m,\varphi )\).
4.8 Remark
Let \(\Omega \) be a Hausdorff space, \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\) a linear space and \((m,\varphi )\) a co-semiflow for \(\mathcal {F}(\Omega )\).
-
(a)
If \(\mathbb {1}\in \mathcal {F}(\Omega )\), then \(m_{t}=C_{m,\varphi }(t)\mathbb {1}\in \mathcal {F}(\Omega )\) for all \(t\ge 0\).
-
(b)
If \({{\,\textrm{id}\,}}\in \mathcal {F}(\Omega )\), then \(m_{t}\varphi _{t}=C_{m,\varphi }(t){{\,\textrm{id}\,}}\in \mathcal {F}(\Omega )\) for all \(t\ge 0\).
If the semicocycle is actually a semicoboundary, then the weighted composition semigroup may have a quite simple structure.
4.9 Remark
Let \(\Omega \) be a Hausdorff space, \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\) a linear space and \((m,\varphi )\) a co-semiflow for \(\mathcal {F}(\Omega )\) such that there is \(\omega \in \mathcal {C}(\Omega )\) with \(N_{\omega }=\varnothing \) and \(m=m^{\omega }\). Then a direct calculation shows that
for all \(t\ge 0\) where \(M_{\omega }f:=\omega f\) and \(M_{\frac{1}{\omega }}f:=\frac{1}{\omega }f\) for all \(f\in \mathcal {F}(\Omega )\). This means that \(C_{m,\varphi }(t)\) and \(C_{\mathbb {1},\varphi }(t)\) are similar as linear operators on \(\mathcal {F}(\Omega )\) for all \(t\ge 0\) if \((\mathbb {1},\varphi )\) is also a co-semiflow for \(\mathcal {F}(\Omega )\) (cf. [39, p. 67] in the case \(\Omega =\mathbb {D}\) and \(\mathcal {F}(\mathbb {D})\) being a space of holomorphic functions).
Sufficient and necessary conditions for the existence of \(\omega \) in Remark 4.9 are given in [44, Theorem 5, p. 3393] in the case that \((m,\varphi )\) is a jointly continuous holomorphic co-semiflow on an open simply connected subset \(\Omega \) of \(\mathbb {C}\). The question which tuples \((m,\varphi )\) are co-semiflows for a given space \(\mathcal {F}(\Omega )\) is difficult on its own. Using Proposition 4.1 and Proposition 4.5 (a), we obtain the following generalisation of [36, Proposition 2.10, p. 5] and [50, Corollary 4.3, p. 20].
4.10 Theorem
Let \(\Omega \) be a Hausdorff space, \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) a Saks space such that \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\) and \((C_{m,\varphi }(t))_{t\ge 0}\) a locally bounded weighted composition semigroup on \(\mathcal {F}(\Omega )\) w.r.t. a jointly continuous co-semiflow \((m,\varphi )\). Then the following assertions hold.
-
(a)
\((C_{m,\varphi }(t))_{t\ge 0}\) is \(\gamma \)-strongly continuous, locally \(\tau _{{\text {co}}}\)-equicontinuous and locally \(\gamma \)-equicontinuous.
-
(b)
If \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) is a sequentially complete Saks space, then \((C_{m,\varphi }(t))_{t\ge 0}\) is a \(\tau _{{\text {co}}}\)-bi-continuous semigroup on \(\mathcal {F}(\Omega )\).
-
(c)
If \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) is a sequentially complete C-sequential Saks space, then \((C_{m,\varphi }(t))_{t\ge 0}\) is quasi-\(\gamma \)-equicontinuous.
Proof
(a) The \(\gamma \)-strong continuity follows from Proposition 4.5 (a) and the local boundedness with \(I:=[0,t_{0}]\) for every \(t_{0}\ge 0\). The local \(\tau _{{\text {co}}}\)-equicontinuity and local \(\gamma \)-equicontinuity are a consequence of Proposition 4.1, Remark 4.2 and the local boundedness with \(I:=[0,t_{0}]\) for every \(t_{0}\ge 0\).
(b)+(c) The remaining parts follow from Theorem 2.7 and the comments before it. \(\square \)
We note that \((\mathcal {C}_{b}(\mathbb {R}),\Vert \cdot \Vert _{\infty },\tau _{{\text {co}}})\) is a sequentially complete C-sequential Saks space and the left translation semigroup on \(\mathcal {C}_{b}(\mathbb {R})\), i.e. the (un)weighted composition semigroup \((C_{\mathbb {1},\varphi }(t))_{t\ge 0}\) w.r.t. the jointly continuous co-semiflow \((\mathbb {1},\varphi )\) where \(\varphi _{t}(x):=t+x\) for all \(t\ge 0\), \(x\in \mathbb {R}\), is exponentially bounded, locally \(\tau _{{\text {co}}}\)-equicontinuous and quasi-\(\gamma \)-equicontinuous by (the proof of) [50, Theorem 4.1, p. 19] and [50, Example 4.2 (a), p. 19] (or by Theorem 4.10), but not quasi-\(\tau _{{\text {co}}}\)-equicontinuous by [56, Example 3.2, p. 549]. This shows that Theorem 4.10 is sharp in the sense that we cannot expect quasi-\(\tau _{{\text {co}}}\)-equicontinuity of weighted composition semigroups in general.
Looking at Theorem 4.10, we see that the local boundedness of \((C_{m,\varphi }(t))_{t\ge 0}\) is a crucial ingredient. The rest of this section is dedicated to deriving sufficient conditions on \((m,\varphi )\) and \(\mathcal {F}(\Omega )\) such that \((C_{m,\varphi }(t))_{t\ge 0}\) becomes locally bounded. Our strategy can be described as follows. Let \(\Omega \) be a Hausdorff space, \((m,\varphi )\) a co-semiflow on \(\Omega \) and \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) a Saks space such that \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\). We decompose \(C_{m,\varphi }=C_{m,{{\,\textrm{id}\,}}}C_{\mathbb {1},\varphi }\) and see that \((m,\varphi )\) is a co-semiflow for \(\mathcal {F}(\Omega )\) if \((m,{{\,\textrm{id}\,}})\) and \((\mathbb {1},\varphi )\) are co-semiflows for \(\mathcal {F}(\Omega )\). In this case we have the estimate
for all \(t\ge 0\). Therefore the semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) is locally bounded if \((m,{{\,\textrm{id}\,}})\) and \((\mathbb {1},\varphi )\) are co-semiflows for \(\mathcal {F}(\Omega )\), and the multiplication semigroup \((C_{m,{{\,\textrm{id}\,}}}(t))_{t\ge 0}\) as well as the unweighted composition semigroup \((C_{\mathbb {1},\varphi }(t))_{t\ge 0}\) are locally bounded. This strategy might not be optimal but gives rather simple, more applicable, sufficient conditions that guarantee the local boundedness of \((C_{m,\varphi }(t))_{t\ge 0}\).
4.11 Remark
-
(a)
If \(\varphi \) is a holomorphic semiflow on \(\mathbb {D}\) and \(1\le p<\infty \), then \((\mathbb {1},\varphi )\) is a co-semiflow for \(H^{p}\) and \(C_{\mathbb {1},\varphi }(t)\in \mathcal {L}(H^{p})\) for all \(t\ge 0\) by [28, Corollary, p. 29].
-
(b)
If \(\varphi \) is a holomorphic semiflow on \(\mathbb {D}\), \(\alpha >-1\) and \(1\le p<\infty \), then \((\mathbb {1},\varphi )\) is a co-semiflow for \(A_{\alpha }^{p}\) and \(C_{\mathbb {1},\varphi }(t)\in \mathcal {L}(A_{\alpha }^{p})\) for all \(t\ge 0\) by [57, 3.4 Proposition, p. 884].
-
(c)
If \(\varphi \) is a holomorphic semiflow on \(\mathbb {D}\), then \((\mathbb {1},\varphi )\) is a co-semiflow for \(\mathcal {D}\) and \(C_{\mathbb {1},\varphi }(t)\in \mathcal {L}(\mathcal {D})\) for all \(t\ge 0\) by [70, p. 166].
-
(d)
Let \(v_{0}:[0,1]\rightarrow [0,\infty )\) be a continuous non-increasing function such that \(v_{0}(x)\ne 0\) for all \(x\in [0,1)\), \(v_{0}(1)=0\) and set \(v:\overline{\mathbb {D}}\rightarrow [0,\infty )\), \(v(z):=v_{0}(|z|)\) (see [60, p. 873]). Let \(\varphi \) be a holomorphic semiflow on \(\mathbb {D}\). Then there is a necessary and sufficient condition such that \((\mathbb {1},\varphi )\) is a co-semiflow for \(\mathcal {B}v(\mathbb {D})\) and \(C_{\mathbb {1},\varphi }(t)\in \mathcal {L}(\mathcal {B}v(\mathbb {D}))\) for all \(t\ge 0\) given in [60, Theorem 2.3, p. 876].
-
(e)
Let \(\Omega \) be a completely regular Hausdorff space, \(v:\Omega \rightarrow (0,\infty )\) continuous and \(\varphi \) a semiflow on \(\Omega \). Suppose that for every \(x\in \Omega \) there is \(f\in \mathcal {C}(\Omega )\) such that \(vf\in \mathcal {C}_{0}(\Omega )\) and \(f(x)\ne 0\). This condition is for instance fulfilled if \(\Omega \) is locally compact. Then \((\mathbb {1},\varphi )\) is a co-semiflow for \(\mathcal {C}v(\Omega )\) and \(C_{\mathbb {1},\varphi }(t)\in \mathcal {L}(\mathcal {C}v(\Omega ))\) for all \(t\ge 0\) if and only if for every \(t\ge 0\) there is \(K_{t}\ge 0\) such that \(v(x)\le K_{t}v(\varphi _{t}(x))\) for all \(x\in \Omega \) by [67, 2.2 Theorem, p. 307].
-
(f)
Let \(\Omega \subset \mathbb {C}\) be open, \(v:\Omega \rightarrow (0,\infty )\) continuous and and \(\varphi \) a holomorphic semiflow on \(\Omega \). Then \((\mathbb {1},\varphi )\) is a co-semiflow for \(\mathcal {H}v(\Omega )\) and \(C_{\mathbb {1},\varphi }(t)\in \mathcal {L}(\mathcal {H}v(\Omega ))\) for all \(t\ge 0\) if for every \(t\ge 0\) there is \(K_{t}\ge 0\) such that \(v(z)\le K_{t}v(\varphi _{t}(z))\) for all \(z\in \Omega \) by [67, 2.2 Theorem, p. 307].
Let \(\Omega \) be a Hausdorff space and \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\) a linear space. We define the multiplier space \(\mathcal {M}(\mathcal {F}(\Omega ))\) of continuous multipliers of \(\mathcal {F}(\Omega )\) by \(\mathcal {M}(\mathcal {F}(\Omega )):=\{g\in \mathcal {C}(\Omega )\;|\;\forall \;f\in \mathcal {F}(\Omega ):\;gf\in \mathcal {F}(\Omega )\}\).Footnote 1
4.12 Proposition
Let \(\Omega \) be a Hausdorff space, \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) a sequentially complete Saks space such that \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\) and suppose that for every \(x\in \Omega \) there is \(f\in \mathcal {F}(\Omega )\) such that \(f(x)\ne 0\). Then we have \(\mathcal {M}(\mathcal {F}(\Omega ))\subset \mathcal {C}_{b}(\Omega )\). Further, \(C_{m,{{\,\textrm{id}\,}}}(t)\in \mathcal {L}(\mathcal {F}(\Omega ))\) for all \(t\ge 0\) if \((m,{{\,\textrm{id}\,}})\) is a co-semiflow on \(\Omega \) and \(m_{t}\in \mathcal {M}(\mathcal {F}(\Omega ))\) for all \(t\ge 0\).
Proof
Due to our assumption, Remark 2.6 and Convention 2.8\((\mathcal {F}(\Omega ),\Vert \cdot \Vert )\) is a functional Banach space in the sense of [29, p. 57] and thus our statement follows from [29, Lemma 11, p. 57]. \(\square \)
4.13 Proposition
-
(a)
\(\mathcal {M}(H^{p})=\mathcal {M}(A_{\alpha }^{p})=H^{\infty }\) for \(\alpha >-1\) and \(1\le p<\infty \).
-
(b)
\(\mathcal {M}(\mathcal {B}_{\alpha })=H^{\infty }\) for \(\alpha >1\), \(\mathcal {M}(\mathcal {B}_{\alpha })=\mathcal {B}_{\alpha }\) for \(0<\alpha <1\) and \(\mathcal {M}(\mathcal {B}_{1})=\{f\in H^{\infty }\;|\;\sup _{z\in \mathbb {D}}|f'(z)|(1-|z|^2)\ln ((1-|z|^{2})^{-1})<\infty \}\).
-
(c)
\(\mathcal {M}(\mathcal {C}v(\Omega ))=\mathcal {C}_{b}(\Omega )\) for all locally compact Hausdorff spaces \(\Omega \) and continuous \(v:\Omega \rightarrow (0,\infty )\).
-
(d)
\(\mathcal {M}(\mathcal {H}v(\Omega ))=H^{\infty }(\Omega )\) for all open sets \(\Omega \subset \mathbb {C}\) and continuous \(v:\Omega \rightarrow (0,\infty )\) if \(\mathbb {1}\in \mathcal {H}v(\Omega )\).
Proof
In (a) we have \(H^{\infty }\subset \mathcal {M}(H^{p})\) and \(H^{\infty }\subset \mathcal {M}(A_{\alpha }^{p})\), in (c) we have \(\mathcal {C}_{b}(\Omega )\subset \mathcal {M}(\mathcal {C}v(\Omega ))\), and in (d) we have \(H^{\infty }(\Omega )\subset \mathcal {M}(\mathcal {H}v(\Omega ))\). Therefore the statements in part (a), (c) and (d) follow from Proposition 4.12 and Examples 2.9, 2.11, 2.13 since in (a) \(\mathbb {1}\in H^{p}, A_{\alpha }^{p}\) and since in (c) for every \(x\in \Omega \) there is \(f\in \mathcal {F}(\Omega )\) such that \(f(x)\ne 0\) because \(\Omega \) is a locally compact Hausdorff space. Part (b) is [80, Theorem 27, p. 1170]. \(\square \)
The multiplier space \(\mathcal {M}(\mathcal {D})\) of the Dirichlet space is more complicated and its elements can be described in terms of the Carleson measure by [73, Theorems 1.1 (c), 2.3, 2.7, p. 115, 122, 125] with \(\alpha =\frac{1}{2}\). From Proposition 4.12 and \(\mathbb {1}\in \mathcal {D}\) it follows that \(\mathcal {M}(\mathcal {D})\subset (\mathcal {D}\cap H^{\infty })\).
4.14 Theorem
Let \((m,\varphi )\) be a holomorphic co-semiflow on \(\mathbb {D}\) such that \(\varphi \) is jointly continuous. Then \((m,\varphi )\) is a co-semiflow for \(\mathcal {F}(\mathbb {D})\) and the weighted composition semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) on \(\mathcal {F}(\mathbb {D})\) is locally bounded in each of the following cases if
-
(a)
\(\mathcal {F}(\mathbb {D})=H^{p}\) for \(1\le p<\infty \) and
 ,
, -
(b)
\(\mathcal {F}(\mathbb {D})=A_{\alpha }^{p}\) for \(\alpha >-1\) and \(1\le p<\infty \) and
 ,
, -
(c)
\(\mathcal {F}(\mathbb {D})=\mathcal {D}\) and \(m_{t}\in \mathcal {M}(\mathcal {D})\) for all \(t\ge 0\).
Proof
The condition  in (a) and (b) yields that \(m_{t}\in H^{\infty }\) for all \(t\ge 0\) by Proposition 3.10, which is also true in (c) because \(\mathcal {M}(\mathcal {D})\subset H^{\infty }\). Hence in all the cases \((\mathbb {1},\varphi )\), \((m,{{\,\textrm{id}\,}})\) and \((m,\varphi )\) are co-semiflows for \(\mathcal {F}(\mathbb {D})\) by Remark 4.11 and Proposition 4.13.
in (a) and (b) yields that \(m_{t}\in H^{\infty }\) for all \(t\ge 0\) by Proposition 3.10, which is also true in (c) because \(\mathcal {M}(\mathcal {D})\subset H^{\infty }\). Hence in all the cases \((\mathbb {1},\varphi )\), \((m,{{\,\textrm{id}\,}})\) and \((m,\varphi )\) are co-semiflows for \(\mathcal {F}(\mathbb {D})\) by Remark 4.11 and Proposition 4.13.
(a) We have
for all \(t\ge 0\) and \(f\in H^{p}\) by [28, Corollary, p. 29], yielding
for all \(t\ge 0\). Further, we note that \(\Vert C_{m,{{\,\textrm{id}\,}}}(t)\Vert _{\mathcal {L}(H^{p})}\le \Vert m_{t}\Vert _{\infty }\) for all \(t\ge 0\).
(b) Due to [13, Theorem 8.1.15, p. 211] and [13, Proposition 10.1.7 (1)\(\Leftrightarrow \)(2), p. 275] there is \(t_{0}>0\) such that \(\Vert \varphi _{t}-{{\,\textrm{id}\,}}\Vert _{\infty }\le 1\) for all \(t\in [0,t_{0}]\) since \(\varphi \) is jointly continuous, which implies that \(\Vert \varphi _{t}\Vert _{\infty }\le 2\) for all \(t\in [0,t_{0}]\). Therefore we obtain
for all \(t\in [0,t_{0}]\) by [69, Lemma 1, p. 399] where \(K(\varphi _{t}):=1\) if \(\alpha \ge 0\), and \(K(\varphi _{t}):=(\Vert \varphi _{t}\Vert _{\infty }+|\varphi _{t}(0)|)^{\alpha /p}(\Vert \varphi _{t}\Vert _{\infty }+3|\varphi _{t}(0)|)^{-\alpha /p}\) if \(-1<\alpha <0\). Furthermore, we note that \(\Vert C_{m,{{\,\textrm{id}\,}}}(t)\Vert _{\mathcal {L}(A_{\alpha }^{p})}\le \Vert m_{t}\Vert _{\infty }\) for all \(t\ge 0\).
(c) Due to [58, Theorem 2 (a), p. 26] and [1, Proposition 1.4.6, p. 85] we have
for all \(t\ge 0\) where \(L(\varphi _{t}):=-\ln (1-|\varphi _{t}(0)|^{2})\). By [81, Proposition 5.1, p. 101] we have \(H^{\infty }\subset \mathcal {B}_{1}\) and
for all \(g\in H^{\infty }\). By [73, p. 114] with \(\alpha =\frac{1}{2}\) there is \(M>0\) such that
for all \(f\in \mathcal {D}\). We deduce that
for all \(t\ge 0\) and \(f\in \mathcal {D}\), which implies \(\Vert C_{m,{{\,\textrm{id}\,}}}(t)\Vert _{\mathcal {L}(\mathcal {D})}^{2}\le 2(1+M)\Vert m_{t}\Vert _{\infty }^{2}\) for all \(t\ge 0\).
Therefore we derive in (a), (b) and (c) from the joint continuity of \(\varphi \) that \((C_{\mathbb {1},\varphi }(t))_{t\ge 0}\) is locally bounded. Proposition 3.10 yields that \((C_{m,{{\,\textrm{id}\,}}}(t))_{t\ge 0}\) is locally bounded and thus \((C_{m,\varphi }(t))_{t\ge 0}\) is locally bounded, too. \(\square \)
Any semiflow \(\varphi \) on \(\mathbb {D}\) given in [71, p. 4–5] is holomorphic and \(C_{0}\), thus jointly continuous by Proposition 3.3 (a). For any such \(\varphi \) take the semicocycle m given by \(m_{t}:\mathbb {D}\rightarrow \mathbb {C}\), \(m_{t}(z):=\exp (\int _{0}^{t}g(\varphi _{s}(z))\textrm{d}s)\), for all \(t\ge 0\) for some \(g\in \mathcal {H}(\mathbb {D})\) (see Proposition 3.14 (a)). If \(M:=\sup _{z\in \mathbb {D}}{{\,\textrm{Re}\,}}(g(z))<\infty \), then \( \Vert m_{t}\Vert _{\infty }\le \textrm{e}^{tM} \) for all \(t\ge 0\) and so  (cf. [47, p. 474]). Hence \((C_{m,\varphi }(t))_{t\ge 0}\) is a locally bounded semigroup on \(\mathcal {F}(\mathbb {D})\) in case (a) and (b) of Theorem 4.14.
(cf. [47, p. 474]). Hence \((C_{m,\varphi }(t))_{t\ge 0}\) is a locally bounded semigroup on \(\mathcal {F}(\mathbb {D})\) in case (a) and (b) of Theorem 4.14.
An example in case (c) of the Dirichlet space \(\mathcal {D}\) is the jointly continuous holomorphic co-semiflow \((\varphi ',\varphi )\) on \(\mathbb {D}\) given by \(\varphi _{t}:\mathbb {D}\rightarrow \mathbb {D}\), \(\varphi _{t}(z):=\textrm{e}^{-ct}z\), for all \(t\ge 0\) for some \(c\in \mathbb {C}\) with \({{\,\textrm{Re}\,}}(c)\ge 0\) since \(\varphi _{t}'(z)=\textrm{e}^{-ct}\) for all \(t\ge 0\) and \(z\in \mathbb {D}\), which implies \(m_{t}:=\varphi _{t}'\in \mathcal {D}\) for all \(t\ge 0\). The same is true if we choose \(\varphi _{t}(z):=\textrm{e}^{-t}z+1-\textrm{e}^{-t}\) for all \(t\ge 0\) and \(z\in \mathbb {D}\). Thus \((C_{\varphi ',\varphi }(t))_{t\ge 0}\) is a locally bounded semigroup on \(\mathcal {D}\) by Theorem 4.14 (c) in both cases.
4.15 Theorem
Let \((m,\varphi )\) be a holomorphic co-semiflow on \(\mathbb {D}\) and \(\alpha >0\). Then \((m,\varphi )\) is a co-semiflow for \(\mathcal {B}_{\alpha }\) and the weighted composition semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) on \(\mathcal {B}_{\alpha }\) is locally bounded if
for all \(t\ge 0\), there exists \(t_{0}>0\) such that \(\sup _{t\in [0,t_{0}]}K_{\alpha }(\varphi _{t})<\infty \) and
-
(a)
for \(\alpha >1\) if
 ,
, -
(b)
for \(\alpha =1\) if
 and $$\begin{aligned} \sup _{t\in [0,t_{0}]}\sup _{z\in \mathbb {D}}|m_{t}'(z)|(1-|z|^{2})\ln ((1-|z|^{2})^{-1})<\infty , \end{aligned}$$
and $$\begin{aligned} \sup _{t\in [0,t_{0}]}\sup _{z\in \mathbb {D}}|m_{t}'(z)|(1-|z|^{2})\ln ((1-|z|^{2})^{-1})<\infty , \end{aligned}$$ -
(c)
for \(0<\alpha <1\) if \(m_{t}\in \mathcal {B}_{\alpha }\) for all \(t\ge 0\) and \( \sup _{t\in [0,t_{0}]}\Vert m_{t}\Vert _{\mathcal {B}_{\alpha }}<\infty . \)
Proof
By the proof of [78, Theorem 2.2 (i), p. 115] we have
for all \(t\ge 0\) and \(f\in \mathcal {B}_{\alpha }\), yielding \(f\circ \varphi _{t}\in \mathcal {B}_{\alpha }\) and that \((\mathbb {1},\varphi )\) is a co-semiflow for \(\mathcal {B}_{\alpha }\). In addition, the existence of \(t_{0}>0\) such that \(\sup _{t\in [0,t_{0}]}K_{\alpha }(\varphi _{t})<\infty \) gives that \((C_{\mathbb {1},\varphi }(t))_{t\ge 0}\) is a locally bounded semigroup.
Moreover, the conditions in (a), (b) and (c) guarantee that \(m_{t}\in \mathcal {M}(\mathcal {B}_{\alpha })\) for all \(t\ge 0\) by Proposition 3.10 and Proposition 4.13 (b). Hence in all the cases \((m,{{\,\textrm{id}\,}})\) and so \((m,\varphi )\) are co-semiflows for \(\mathcal {B}_{\alpha }\).
(a) For \(\alpha >1\) we have by the proof of [80, Proposition 7, p. 1147] that there is \(L_{\alpha }>0\) such that
for all \(z\in \mathbb {D}\) and \(f\in \mathcal {B}_{\alpha }\). It follows that
for all \(t\ge 0\) and \(f\in \mathcal {B}_{\alpha }\).
(b) For \(\alpha =1\) we get as in the proof of [80, Proposition 7, p. 1147], using [80, Proposition 7 3), p. 1146] with \(t=\alpha -1=0\) and \(s=0\), that there is \(L_{1}>0\) such that
for all \(z\in \mathbb {D}\) and \(f\in \mathcal {B}_{1}\). It follows that
for all \(t\ge 0\) and \(f\in \mathcal {B}_{1}\).
(c) Again, for \(0<\alpha <1\) we get as in the proof of [80, Proposition 7, p. 1147], using [80, Proposition 7 1), p. 1146] with \(t=\alpha -1<0\) and \(s=0\), that there is \(L_{\alpha }>0\) such that
for all \(z\in \mathbb {D}\) and \(f\in \mathcal {B}_{\alpha }\). This implies \(\mathcal {B}_{\alpha }\subset H^{\infty }\) and \(\Vert g\Vert _{\infty }\le (1+L_{\alpha })\Vert g\Vert _{\mathcal {B}_{\alpha }}\) for all \(g\in \mathcal {B}_{\alpha }\) and \(0<\alpha <1\). It follows that
for all \(t\ge 0\) and \(f\in \mathcal {B}_{\alpha }\).
Hence our conditions in (a) and (b) combined with Proposition 3.10, and in (c) guarantee that \((C_{m,{{\,\textrm{id}\,}}}(t))_{t\ge 0}\) is a locally bounded semigroup and thus \((C_{m,\varphi }(t))_{t\ge 0}\) as well. \(\square \)
The jointly continuous holomorphic co-semiflow \((\varphi ',\varphi )\) on \(\mathbb {D}\) given by \(\varphi _{t}:\mathbb {D}\rightarrow \mathbb {D}\), \(\varphi _{t}(z):=\textrm{e}^{-ct}z\), for all \(t\ge 0\) for some \(c\in \mathbb {C}\) with \({{\,\textrm{Re}\,}}(c)\ge 0\), fulfils \(m_{t}(z):=\varphi _{t}'(z)=\textrm{e}^{-ct}\),
and \(\Vert \varphi _{t}'\Vert _{\infty }=\textrm{e}^{-{{\,\textrm{Re}\,}}(c)t}\) as well as \(m_{t}'(z)=\varphi _{t}''(z)=0\) and \(\Vert m_{t}\Vert _{\mathcal {B}_{\alpha }}=|\varphi _{t}'(0)|=\textrm{e}^{-{{\,\textrm{Re}\,}}(c)t}\) for all \(t\ge 0\) and \(z\in \mathbb {D}\). Thus \((C_{\varphi ',\varphi }(t))_{t\ge 0}\) is a locally bounded semigroup on \(\mathcal {B}_{\alpha }\) for all \(\alpha >0\) by Theorem 4.15.
Let us turn to the space of bounded Dirichlet series. We say that a holomorphic function \(\varphi :\mathbb {C}_{+}\rightarrow \mathbb {C}_{+}\) belongs to the class \(\mathscr {G}_{\infty }\) if there exist \(c_{\varphi }\in \mathbb {N}_{0}\) and a Dirichlet series \(\rho _{\varphi }\) which converges on some open half-plane and extends holomorphically to \(\mathbb {C}_{+}\) such that \(\varphi (z)=c_{\varphi }z+\rho _{\varphi }(z)\) for all \(z\in \mathbb {C}_{+}\) (see [21, Definition 2.6, p. 9]).
4.16 Theorem
Let \((m,\varphi )\) be a holomorphic co-semiflow on \(\mathbb {C}_{+}\). Then \((m,\varphi )\) is a co-semiflow for \(\mathscr {H}^{\infty }\) and the weighted composition semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) on \(\mathscr {H}^{\infty }\) is locally bounded if \(\varphi _{t}\in \mathscr {G}_{\infty }\), \(m_{t}\in \mathscr {H}^{\infty }\) for all \(t\ge 0\) and  . The converse is true if \(\inf _{z\in \mathbb {C}_{+}}|m_{t}(z)|>0\) for all \(t\ge 0\).
. The converse is true if \(\inf _{z\in \mathbb {C}_{+}}|m_{t}(z)|>0\) for all \(t\ge 0\).
Proof
By [8, Proposition 2, p. 219] \((\mathbb {1},\varphi )\) is a co-semiflow for \(\mathscr {H}^{\infty }\) if and only \(\varphi _{t}\in \mathscr {G}_{\infty }\) for all \(t\ge 0\). Further, we observe that \(\Vert {C_{\mathbb {1},\varphi }(t)f}\Vert _{\mathscr {H}^{\infty }}\le \Vert f\Vert _{\mathscr {H}^{\infty }}\) for all \(f\in \mathscr {H}^{\infty }\) if \(\varphi _{t}\in \mathscr {G}_{\infty }\) for \(t\ge 0\). Due to [74, Theorem 7 a), p. 9–10] we have \(\mathcal {M}(\mathscr {H}^{\infty })=\mathscr {H}^{\infty }\), which implies that \((m,{{\,\textrm{id}\,}})\) is a co-semiflow for \(\mathscr {H}^{\infty }\) if and only if \(m_{t}\in \mathscr {H}^{\infty }\) for all \(t\ge 0\). We note that \(\Vert C_{m,{{\,\textrm{id}\,}}}(t)f\Vert _{\mathscr {H}^{\infty }}\le \Vert m_{t}\Vert _{\infty }\Vert f\Vert _{\mathscr {H}^{\infty }}\) for all \(f\in \mathscr {H}^{\infty }\) if \(m_{t}\in \mathscr {H}^{\infty }\) for \(t\ge 0\).
Now, the first implication follows from our considerations above and Proposition 3.10. Let us consider the converse implication. The properties \(m_{t}\in \mathscr {H}^{\infty }\) for all \(t\ge 0\) and  follow from the local boundedness of the weighted composition semigroup and the observation that \(\mathbb {1}\in \mathscr {H}^{\infty }\) since \(\Vert m_{t}\Vert _{\infty }=\Vert m_{t}\Vert _{\mathscr {H}^{\infty }}=\Vert C_{m,\varphi }(t)\mathbb {1}\Vert _{\mathscr {H}^{\infty }}\) for all \(t\ge 0\). The property \(\varphi _{t}\in \mathscr {G}_{\infty }\) for all \(t\ge 0\) follows from our first observation of the proof, writing \(C_{\mathbb {1},\varphi }(t)=(1/m_{t})C_{m,\varphi }(t)\) and noting that \(1/m_{t}\) belongs to the Banach algebra \(\mathscr {H}^{\infty }\) by [64, Theorem 6.2.1, p. 147] if and only if \(\inf _{z\in \mathbb {C}_{+}}|m_{t}(z)|>0\). \(\square \)
follow from the local boundedness of the weighted composition semigroup and the observation that \(\mathbb {1}\in \mathscr {H}^{\infty }\) since \(\Vert m_{t}\Vert _{\infty }=\Vert m_{t}\Vert _{\mathscr {H}^{\infty }}=\Vert C_{m,\varphi }(t)\mathbb {1}\Vert _{\mathscr {H}^{\infty }}\) for all \(t\ge 0\). The property \(\varphi _{t}\in \mathscr {G}_{\infty }\) for all \(t\ge 0\) follows from our first observation of the proof, writing \(C_{\mathbb {1},\varphi }(t)=(1/m_{t})C_{m,\varphi }(t)\) and noting that \(1/m_{t}\) belongs to the Banach algebra \(\mathscr {H}^{\infty }\) by [64, Theorem 6.2.1, p. 147] if and only if \(\inf _{z\in \mathbb {C}_{+}}|m_{t}(z)|>0\). \(\square \)
The jointly continuous holomorphic co-semiflow \((\mathbb {1},\varphi )\) on \(\mathbb {C}_{+}\) given by \(\varphi _{t}:\mathbb {C}_{+}\rightarrow \mathbb {C}_{+}\), \(\varphi _{t}(z):=z+t\), for all \(t\ge 0\) fulfils with \(m_{t}(z):=1\) for all \(t\ge 0\) and \(z\in \mathbb {C}_{+}\) that \(\varphi _{t}\in \mathscr {G}_{\infty }\), \(m_{t}\in \mathscr {H}^{\infty }\) for all \(t\ge 0\) and  . Thus \((C_{\mathbb {1},\varphi }(t))_{t\ge 0}\) is a locally bounded semigroup on \(\mathscr {H}^{\infty }\) by Theorem 4.16.
. Thus \((C_{\mathbb {1},\varphi }(t))_{t\ge 0}\) is a locally bounded semigroup on \(\mathscr {H}^{\infty }\) by Theorem 4.16.
4.17 Theorem
Let \(\Omega \subset \mathbb {C}\) be open, \(v:\Omega \rightarrow (0,\infty )\) continuous, \(\mathbb {1}\in \mathcal {H}v(\Omega )\) and \((m,\varphi )\) a holomorphic co-semiflow on \(\Omega \). If  ,
,
for all \(t\ge 0\) and there exists \(t_{0}>0\) such that \(\sup _{t\in [0,t_{0}]}K(\varphi _{t})<\infty \), then \((m,\varphi )\) is a co-semiflow for \(\mathcal {H}v(\Omega )\) and the weighted composition semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) on \(\mathcal {H}v(\Omega )\) is locally bounded. If \(v=\mathbb {1}\), then the converse holds as well.
Proof
We deduce from Remark 4.11 (f) and Proposition 4.13 (d) that \((m,{{\,\textrm{id}\,}})\), \((\mathbb {1},\varphi )\) and so \((m,\varphi )\) are co-semiflows for \(\mathcal {H}v(\Omega )\). We observe that
for all \(t\ge 0\) and \(f\in \mathcal {H}v(\Omega )\), yielding \(\Vert C_{\mathbb {1},\varphi }(t)\Vert _{\mathcal {L}(\mathcal {H}v(\Omega ))}\le K(\varphi _{t})\).
Moreover, we note that
for all \(t\ge 0\) and \(f\in \mathcal {H}v(\Omega )\), yielding \(\Vert C_{m,{{\,\textrm{id}\,}}}(t)\Vert _{\mathcal {L}(\mathcal {H}v(\Omega ))}\le \Vert m_{t}\Vert _{\infty }\). Therefore \((C_{m,{{\,\textrm{id}\,}}}(t))_{t\ge 0}\) is locally bounded by Proposition 3.10. The same is true for the semigroup \((C_{\mathbb {1},\varphi }(t))_{t\ge 0}\) by the existence of \(t_{0}>0\) and so \((C_{m,\varphi }(t))_{t\ge 0}\) is locally bounded as well.
If \(v=\mathbb {1}\), then the converse holds as well by Proposition 3.10 since then \(K(\varphi _{t})=1\) and \(\Vert m_{t}\Vert _{\infty }=\Vert m_{t}\Vert _{v}=\Vert C_{m,\varphi }(t)\mathbb {1}\Vert _{v}\) for all \(t\ge 0\). \(\square \)
Analogously we obtain the corresponding result for \(\mathcal {C}v(\Omega )\) by using Remark 4.11 (e) and Proposition 4.13 (c).
4.18 Theorem
Let \(\Omega \) be a locally compact Hausdorff space, \(v:\Omega \rightarrow (0,\infty )\) continuous and \((m,\varphi )\) a co-semiflow on \(\Omega \). If  ,
,
for all \(t\ge 0\) and there exists \(t_{0}>0\) such that \(\sup _{t\in [0,t_{0}]}K(\varphi _{t})<\infty \), then \((m,\varphi )\) is a co-semiflow for \(\mathcal {C}v(\Omega )\) and the weighted composition semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) on \(\mathcal {C}v(\Omega )\) is locally bounded. If \(\mathbb {1}\in \mathcal {C}v(\Omega )\) and \(v=\mathbb {1}\), then the converse holds as well.
Apart from the weight \(v=\mathbb {1}\) there are other weights that fulfil the conditions of Theorem 4.17 and Theorem 4.18. For instance, take the left-translation semiflow \(\varphi \) given by \(\varphi _{t}:\mathbb {K}\rightarrow \mathbb {K}\), \(\varphi _{t}(x):=x+t\), for \(t\ge 0\) and set \(v:\mathbb {K}\rightarrow (0,\infty )\), \(v(x):=\textrm{e}^{-|x|}\). Then \(K(\varphi _{t})\le \textrm{e}^{t}\) for all \(t\ge 0\) and we can choose any \(t_{0}>0\) (cf. [67, (i), p. 310]). Taking now any (holomorphic) semicocycle m for \(\varphi \) such that  , we get a locally bounded semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) on \(\mathcal {H}v(\mathbb {C})\) (if \(\mathbb {K}=\mathbb {C}\) and \(\mathbb {1}\in \mathcal {H}v(\mathbb {C})\)) resp. \(\mathcal {C}v(\mathbb {K})\) by Theorem 4.17 resp. Theorem 4.18.
, we get a locally bounded semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) on \(\mathcal {H}v(\mathbb {C})\) (if \(\mathbb {K}=\mathbb {C}\) and \(\mathbb {1}\in \mathcal {H}v(\mathbb {C})\)) resp. \(\mathcal {C}v(\mathbb {K})\) by Theorem 4.17 resp. Theorem 4.18.
5 Generators of Weighted Composition Semigroups
In this section we give several characterisations of the generator of a \(\gamma \)-strongly continuous weighted composition semigroup on a Saks space. Let \((X,\Vert \cdot \Vert ,\tau )\) be a Saks space and \((T(t))_{t\ge 0}\) a \(\gamma \)-strongly continuous semigroup on X. We define the generator (A, D(A)) of \((T(t))_{t\ge 0}\) according to [46, p. 260] by

and

If \((X,\Vert \cdot \Vert ,\tau )\) is sequentially complete, then D(A) is \(\gamma \)-dense in X by [46, Proposition 1.3, p. 261]. The bi-generator \((A_{\Vert \cdot \Vert ,\tau },D(A_{\Vert \cdot \Vert ,\tau }))\) of \((T(t))_{t\ge 0}\) is given by

and

In the context of \(\tau \)-bi-continuous semigroups their generators are actually defined as bi-generators (see [34, Definition 1.2.6, p. 7]). The notion of the bi-generator was originally introduced in [54, 55] (and corrected in [34]).
5.1 Proposition
Let \((X,\Vert \cdot \Vert ,\tau )\) be a Saks space and \((T(t))_{t\ge 0}\) a \(\gamma \)-strongly continuous, locally bounded semigroup on X. Then we have
Proof
The inclusion \(D(A_{\Vert \cdot \Vert ,\tau })\subset D(A)\) follows from [22, I.1.10 Proposition, p. 9], which says that a sequence in X is \(\gamma \)-convergent if and only if it is \(\tau \)-convergent and \(\Vert \cdot \Vert \)-bounded. Further, \(Af=A_{\Vert \cdot \Vert ,\tau }f\) for \(f\in D(A)\) because \(\tau \) is coarser than \(\gamma \).
Conversely, suppose that there is \(x\in D(A)\) such that \(\sup _{t\in (0,1]}\tfrac{\Vert T(t)x-x\Vert }{t}=\infty \). Due to the local boundedness of \((T(t))_{t\ge 0}\) this implies that there is a sequence \((t_{n})_{n\in \mathbb {N}}\) in (0, 1] such that  and \(\sup _{n\in \mathbb {N}}\tfrac{\Vert T(t_{n})x-x\Vert }{t_{n}}=\infty \). Since \(\gamma \text {-}\lim _{n\rightarrow \infty }\frac{T(t_{n})x-x}{t_{n}}\) exists in X, this is a contradiction because \(\gamma \)-convergent sequences are \(\Vert \cdot \Vert \)-bounded by [22, I.1.10 Proposition, p. 9]. \(\square \)
and \(\sup _{n\in \mathbb {N}}\tfrac{\Vert T(t_{n})x-x\Vert }{t_{n}}=\infty \). Since \(\gamma \text {-}\lim _{n\rightarrow \infty }\frac{T(t_{n})x-x}{t_{n}}\) exists in X, this is a contradiction because \(\gamma \)-convergent sequences are \(\Vert \cdot \Vert \)-bounded by [22, I.1.10 Proposition, p. 9]. \(\square \)
Due to Theorem 4.10 (a) and (b) we directly get the following corollary of Proposition 5.1.
5.2 Corollary
Let \(\Omega \) be a Hausdorff space, \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) a Saks space such that \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\) and (A, D(A)) the generator of a locally bounded weighted composition semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) on \(\mathcal {F}(\Omega )\) w.r.t. a jointly continuous co-semiflow \((m,\varphi )\). Then we have
For our next observation we recall the definition of the generator of a norm-strongly continuous semigroup on a Banach space. Let \((X,\Vert \cdot \Vert )\) be a Banach space and \((T(t))_{t\ge 0}\) a \(\Vert \cdot \Vert \)-strongly continuous semigroup on X. We define the norm-generator \((A_{\Vert \cdot \Vert },D(A_{\Vert \cdot \Vert }))\) of \((T(t))_{t\ge 0}\) according to [33, Chap. 2, 1.2 Definition, p. 49] by

and

5.3 Proposition
Let \(\Omega \) be a Hausdorff space, \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) a sequentially complete Saks space such that \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\) and (A, D(A)) the generator of the weighted composition semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) on \(\mathcal {F}(\Omega )\) w.r.t. a jointly continuous co-semiflow \((m,\varphi )\). Then the following assertions hold.
-
(a)
If \((C_{m,\varphi }(t))_{t\ge 0}\) is \(\Vert \cdot \Vert \)-strongly continuous, then
$$\begin{aligned} D(A)=D(A_{\Vert \cdot \Vert })\quad \text {and}\quad A=A_{\Vert \cdot \Vert }. \end{aligned}$$ -
(b)
If \((\mathcal {F}(\Omega ),\Vert \cdot \Vert )\) is reflexive and \((C_{m,\varphi }(t))_{t\ge 0}\) locally bounded, then the semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) is \(\Vert \cdot \Vert \)-strongly continuous.
-
(c)
Let \(\bigl [(m,\varphi ),\mathcal {F}(\Omega )\bigr ]\) denote the space of \(\Vert \cdot \Vert \)-strong continuity of \((C_{m,\varphi }(t))_{t\ge 0}\), i.e.

If \((C_{m,\varphi }(t))_{t\ge 0}\) is locally bounded, then we have
$$\begin{aligned} \bigl [(m,\varphi ),\mathcal {F}(\Omega )\bigr ]=\overline{D(A)}^{\Vert \cdot \Vert } \end{aligned}$$where \(\overline{D(A)}^{\Vert \cdot \Vert }\) denotes the closure of D(A) w.r.t. the \(\Vert \cdot \Vert \)-topology.
Proof
Due to [33, Chap. I, 5.5 Proposition, p. 39] a \(\Vert \cdot \Vert \)-strongly continuous semigroup is exponentially bounded and thus locally bounded. Hence part (a) follows from Theorem 4.10 (b) and [53, Lemma 5.15, p. 2684]. Parts (b) and (c) are a consequence of Theorem 4.10 (b) and [54, Corollary 1.25, p. 26] resp. [16, Theorem 5.6, p. 340]. \(\square \)
Let \(\Omega \) be a Hausdorff space, \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\) a linear space and \((m,\varphi )\) a co-semiflow for \(\mathcal {F}(\Omega )\). Then the Lie generator of the co-semiflow \((m,\varphi )\) is given by

and

In other words, the Lie generator is the generator of the weighted composition semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) w.r.t. the topology of pointwise convergence. The Lie generator was introduced in [26, p. 115] for the space \(\mathcal {F}(\Omega )=\mathcal {C}_{b}(\Omega )\) of bounded continuous functions on a Polish space \(\Omega \), equipped with the supremum norm \(\Vert \cdot \Vert =\Vert \cdot \Vert _{\infty }\), and a jointly continuous co-semiflow \((\mathbb {1},\varphi )\). The following proposition generalises [36, Proposition 2.12, p. 6] and [26, Proposition 2.4, p. 118] where \(\mathcal {F}(\Omega )=\mathcal {C}_{b}(\Omega )\) and \(\Omega \) a completely regular Hausdorff k-space resp. Polish space.
5.4 Proposition
Let \(\Omega \) be a Hausdorff space, \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) a sequentially complete Saks space such that \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\) and (A, D(A)) the generator of a locally bounded weighted composition semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) on \(\mathcal {F}(\Omega )\) w.r.t. a jointly continuous co-semiflow \((m,\varphi )\). Then we have
Proof
Since \(\gamma \) is stronger than \(\tau _{{\text {co}}}\) and thus stronger than the topology of pointwise convergence, we only need to prove the inclusion \(D(A_{m,\varphi })\subset D(A)\). Let \(f\in D(A_{m,\varphi })\) and set \(g:=A_{m,\varphi }f\). Since \(g\in \mathcal {F}(\Omega )\) and \((C_{m,\varphi }(t))_{t\ge 0}\) is \(\gamma \)-strongly continuous by Theorem 4.10 (a), the \(\gamma \)-Riemann integral \(\int _{0}^{t}C_{m,\varphi }(s)g\textrm{d}s\) exists in \(\mathcal {F}(\Omega )\) for every \(t\ge 0\) by [45, Proposition 1.1, p. 232] because \((\mathcal {F}(\Omega ),\gamma )\) is sequentially complete. Now, the function \(f_{x}:[0,\infty )\rightarrow \mathbb {K}\), \(s\mapsto m_{s}(x)f(\varphi _{s}(x))\), is right-differentiable with right-derivative \(g_{x}:[0,\infty )\rightarrow \mathbb {K}\), \(s\mapsto m_{s}(x)g(\varphi _{s}(x))\), because \(f\in D(A_{m,\varphi })\) and

for every \(s\ge 0\) and \(x\in \Omega \). The right-derivative \(g_{x}\) is continuous for every \(x\in \Omega \) as \(g\in \mathcal {F}(\Omega )\) and \((m,\varphi )\) is jointly continuous. Hence \(f_{x}\in \mathcal {C}^{1}[0,\infty )\) with derivative \(g_{x}\) by [62, Chap. 2, Corollary 1.2, p. 43] and
for every \(t\ge 0\) and \(x\in \Omega \) by the fundamental theorem of calculus. In combination with the existence of the \(\gamma \)-Riemann integral \(\int _{0}^{t}C_{m,\varphi }(s)g\textrm{d}s\) in \(\mathcal {F}(\Omega )\) for every \(t\ge 0\) this yields
for every \(t\ge 0\), implying our statement by [46, Proposition 1.2 (2), p. 260]. \(\square \)
5.5 Remark
Let \(\Omega \) be a Hausdorff space, \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) a sequentially complete Saks space such that \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\) and (A, D(A)) the generator of a locally bounded weighted composition semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) on \(\mathcal {F}(\Omega )\) w.r.t. a jointly continuous co-semiflow \((m,\varphi )\). We may also define the \(\tau _{{\text {co}}}\)-generator \((A_{\tau _{{\text {co}}}},D(A_{\tau _{{\text {co}}}}))\) by

and

Then it follows from \(\tau _{{\text {co}}}\) being coarser than \(\gamma \) and Proposition 5.4 that
If we have more information on the co-semiflow than just joint continuity, then we may give a simpler characterisation of the generator of a weighted composition semigroup.
5.6 Proposition
Let \(\Omega \) be a Hausdorff space, \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) a sequentially complete Saks space such that \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\) and (A, D(A)) the generator of a locally bounded weighted composition semigroup \((C_{m,{{\,\textrm{id}\,}}}(t))_{t\ge 0}\) on \(\mathcal {F}(\Omega )\) w.r.t. a jointly continuous co-semiflow \((m,{{\,\textrm{id}\,}})\). If \(m_{(\cdot )}(x)\) is right-differentiable in \(t=0\) for all \(x\in \Omega \), then

Proof
For \(f\in \mathcal {F}(\Omega )\) we have

for all \(x\in \Omega \), yielding our statement by Proposition 5.4. \(\square \)
5.7 Proposition
Let \(\Omega \subset \mathbb {K}\) be open, \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) a sequentially complete Saks space such that \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\) and (A, D(A)) the generator of a locally bounded weighted composition semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) on \(\mathcal {F}(\Omega )\) w.r.t. a jointly continuous co-semiflow \((m,\varphi )\).
-
(a)
If
-
(i)
\(m_{(\cdot )}(x)\in \mathcal {C}^{1}[0,\infty )\) and \(\varphi _{(\cdot )}(x)\in \mathcal {C}^{1}[0,\infty )\) for all \(x\in \Omega \),
then

and
 for all \(f\in D_{0}\).
for all \(f\in D_{0}\). -
(i)
-
(b)
Let \(\omega \subset \Omega \) be open. If condition (i) is fulfilled and
-
(ii)
\(\varphi \) has a generator G, i.e. there is a function \(G\in \mathcal {C}(\Omega )\) such that
 for all \(t\ge 0\) and \(x\in \Omega \), and
for all \(t\ge 0\) and \(x\in \Omega \), and -
(iii)
\(t_{x}:=\inf \{t>0\;|\;\exists \; y\in \Omega {\setminus }\omega ,\,y\ne x:\; \varphi _{t}(x)=y\}>0\) for all \(x\in \Omega {\setminus }\omega \),
then

and
 for all \(f\in D_{1}\), where
for all \(f\in D_{1}\), where  in the definition of \(D_{1}\) means that there is an extension \(g\in \mathcal {F}(\Omega )\) of the map
in the definition of \(D_{1}\) means that there is an extension \(g\in \mathcal {F}(\Omega )\) of the map  .
. -
(ii)
Proof
(a) Let \(f\in \mathcal {C}^{1}_{\mathbb {K}}(\Omega )\cap \mathcal {F}(\Omega )\) and \(x\in \Omega \). Fix \(\widetilde{t}>0\). We note that the map \(h_{x}:[0,\widetilde{t}\,]\rightarrow \mathbb {K}\),  , is continuous by condition (i), the continuity of \(f'\) and the joint continuity of \((m,\varphi )\). Then we have
, is continuous by condition (i), the continuity of \(f'\) and the joint continuity of \((m,\varphi )\). Then we have

for every \(0<t\le \widetilde{t}\) by (i) and the fundamental theorem of calculus. This implies

for every \(0<t\le \widetilde{t}\). Further, we observe that

by the continuity of \(h_{x}\). Due to the Heine–Cantor theorem the continuous function \(h_{x}\) is even uniformly continuous on the compact interval \([0,\widetilde{t}\,]\). Thus for every \(\varepsilon >0\) there is \(0<\delta \le \widetilde{t}\) such that for all \(s\ge 0\) with \(|s|=|s-0|<\delta \) we have

for all \(0<t<\delta \). We deduce that

The rest of the statement follows from (13) and Proposition 5.4.
(b) Let \(f\in \mathcal {C}^{1}_{\mathbb {K}}(\omega )\cap \mathcal {F}(\Omega )\) and \(x\in \Omega \). First, we consider the case that \(x\in \omega \). Since \(\omega \) is open, \(\varphi _{0}(x)=x\in \omega \), and \(\varphi _{(\cdot )}(x)\) is continuous, there is \(\delta _{x}>0\) such that \(\varphi _{t}(x)\in \omega \) for all \(t\in [0,\delta _{x}]\). It follows that the map \(h_{x}:[0,\widetilde{t}\,]\rightarrow \mathbb {K}\) from part (a) is still a well-defined continuous function for the choice \(\widetilde{t}:=\delta _{x}\) and the rest of the proof carries over.
Let us turn to the case \(x\in \Omega {\setminus }\omega \). Now, we need the restriction that  . We set \(p(x):=\inf \{t>0\;|\;\varphi _{t}(x)=x\}\). If \(p(x)=0\), then x is a fixed point of \(\varphi \), and thus
. We set \(p(x):=\inf \{t>0\;|\;\varphi _{t}(x)=x\}\). If \(p(x)=0\), then x is a fixed point of \(\varphi \), and thus

Suppose that \(p(x)>0\). Setting \(t(x):=\min \{p(x),t_{x}\}\), we observe that \(t(x)>0\) by condition (iii). Hence the map \(h_{x}:(0,\widetilde{t}\,]\rightarrow \mathbb {K}\) from part (a) is still a well-defined continuous function for the choice \(\widetilde{t}:=t(x)\). Next, we show that \(h_{x}\) is continuously extendable in \(s=0\). We denote by \(g\in \mathcal {F}(\Omega )\) the extension of  and note that g as an element of \(\mathcal {F}(\Omega )\) is continuous on \(\Omega \). Then
and note that g as an element of \(\mathcal {F}(\Omega )\) is continuous on \(\Omega \). Then  is a continuous extension of
is a continuous extension of  on \(\Omega \). For \(0<s<t(x)\) we have by condition (ii) and Remark 3.5 that
on \(\Omega \). For \(0<s<t(x)\) we have by condition (ii) and Remark 3.5 that

and thus

We derive that

since \(\widetilde{g}\) is continuous in x and \((m,\varphi )\) is a \(C_{0}\)-co-semiflow. Hence \(h_{x}\) is continuously extendable in \(s=0\) by setting  . From here the rest of the proof of part (a) carries over with
. From here the rest of the proof of part (a) carries over with  replaced by g(x). \(\square \)
replaced by g(x). \(\square \)
The expression \(p(x)=\inf \{t>0\;|\;\varphi _{t}(x)=x\}\) in the proof of part (b) is also called the period of \(x\in \Omega \) w.r.t. \(\varphi \) (see [65, p. 660]). For the proof of the converse inclusion in Proposition 5.7 in the case that \(\mathcal {F}(\Omega )\) is not a subspace of \(\mathcal {C}^{1}_{\mathbb {K}}(\Omega )\) we need to know what happens with \(\varphi _{t}\) and \(m_{t}\) to the left of \(t=0\), meaning we consider flows and cocycles instead of just semiflows and semicocycles.
5.8 Definition
Let \(\Omega \) be a Hausdorff space. A family \(\varphi :=(\varphi _{t})_{t\in \mathbb {R}}\) of continuous functions \(\varphi _{t}:\Omega \rightarrow \Omega \) is called a flow if
-
(i)
\(\varphi _{0}(x)=x\) for all \(x\in \Omega \), and
-
(ii)
\(\varphi _{t+s}(x)=(\varphi _{t}\circ \varphi _{s})(x)\) for all \(t,s\in \mathbb {R}\) and \(x\in \Omega \).
We call a flow trivial and write \(\varphi ={{\,\textrm{id}\,}}\) if \(\varphi _{t}={{\,\textrm{id}\,}}\) for all \(t\in \mathbb {R}\). We call a flow \(\varphi \) a \(C_{0}\)-flow if \(\lim _{t\rightarrow 0}\varphi _{t}(x)=x\) for all \(x\in \Omega \). A family \(m:=(m_{t})_{t\in \mathbb {R}}\) of continuous functions \(m_{t}:\Omega \rightarrow \mathbb {K}\) is called a multiplicative cocycle for a flow \(\varphi \) if
-
(i)
\(m_{0}(x)=1\) for all \(x\in \Omega \), and
-
(ii)
\(m_{t+s}(x)=m_{t}(x)m_{s}(\varphi _{t}(x))\) for all \(t,s\in \mathbb {R}\) and \(x\in \Omega \).
We call a cocycle m trivial and write \(m=\mathbb {1}\) if \(m_{t}=\mathbb {1}\) for all \(t\in \mathbb {R}\). We call a cocycle m a \(C_{0}\)-cocycle if \(\lim _{t\rightarrow 0}m_{t}(x)=1\) for all \(x\in \Omega \). We call the tuple \((m,\varphi )\) a co-flow on \(\Omega \). We call a co-flow \((m,\varphi )\) jointly continuous (separately continuous, \(C_{0}\)) if \(\varphi \) and m are both jointly continuous (separately continuous, \(C_{0}\)).
We have the following characterisation of joint continuity of flows and cocycles on certain Hausdorff spaces \(\Omega \).
5.9 Proposition
Let \((m,\varphi )\) be a co-flow on a Hausdorff space \(\Omega \).
-
(a)
Let \(\Omega \) be locally compact and \(\sigma \)-compact. Then \(\varphi \) is jointly continuous if and only if \(\varphi \) is \(C_{0}\).
-
(b)
Let \(\Omega \) be an open subset of a metric space and \(\varphi \) jointly continuous. Then m is jointly continuous if and only if m is \(C_{0}\).
Proof
(a) We only need to prove the implication \(\Leftarrow \). We define \(\psi :=(\psi _{t})_{t\ge 0}\) by \(\psi _{t}(x):=\varphi _{-t}(x)\) for all \(t\ge 0\) and \(x\in \Omega \). Then it is easily checked that \(\psi \) is a semiflow. Further, we have

for all \(x\in \Omega \). It follows from Proposition 3.3 that \(\psi \) is jointly continuous and \((\varphi _{t})_{t\ge 0}\) as well. Since \(\psi _{0}(x)=x=\varphi _{0}(x)\) for all \(x\in \Omega \), we get that \(\varphi \) is jointly continuous. The proof of part (b) is analogous and we only need to use Proposition 3.12 instead of Proposition 3.3. \(\square \)
5.10 Theorem
Let \(\Omega \subset \mathbb {R}\) be open, \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) a sequentially complete Saks space such that \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\) and (A, D(A)) the generator of a locally bounded weighted composition semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) on \(\mathcal {F}(\Omega )\) w.r.t. a \(C_{0}\)-co-flow \((m,\varphi )\) such that \(m_{(\cdot )}(x)\in \mathcal {C}^{1}(\mathbb {R})\) and \(\varphi _{(\cdot )}(x)\in \mathcal {C}^{1}(\mathbb {R})\) for all \(x\in \Omega \), and \(m_{t}(x)\ne 0\) for all \((t,x)\in \mathbb {R}\times \Omega \).
-
(a)
If the map \(V_{\varphi }\rightarrow \Omega \), \((t,x)\mapsto \varphi _{t}(x)\), is surjective, where
 , then
, then 
and
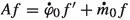 for all \(f\in D(A)\).
for all \(f\in D(A)\). -
(b)
If
-
(i)
\((\varphi _{t})_{t\ge 0}\) has a generator G, and
-
(ii)
\(t_{x}:=\inf \{t>0\;|\;\exists \; y\in N_{G},\,y\ne x:\; \varphi _{t}(x)=y\}>0\) for all \(x\in N_{G}\), where \(N_{G}=\{z\in \Omega \;|\;G(z)=0\}\),
then

and
 for all \(f\in D(A)\).
for all \(f\in D(A)\). -
(i)
Proof
(a) Due to Proposition 5.7 (a) we only need to show that \(D(A)\subset D_{0}\). Let \(f\in D(A)\) and \(x\in \Omega \). By assumption there is \((t_{0},x_{0})\in V_{\varphi }\) such that \(x=\varphi _{t_{0}}(x_{0})\). The arguments in the proof of Proposition 5.4 in combination with Proposition 5.9 applied to the \(C_{0}\)-co-flow \((m,\varphi )\) show that \(f_{x_{0}}:\mathbb {R}\rightarrow \mathbb {R}\), \(s\mapsto m_{s}(x_{0})f(\varphi _{s}(x_{0}))\), is continuously differentiable. We deduce that \(f\circ \varphi _{(\cdot )}(x_{0})\) is continuously differentiable on \(\mathbb {R}\) since
for all \(t\in \mathbb {R}\), \(m_{(\cdot )}(x_{0})\in \mathcal {C}^{1}(\mathbb {R})\) and \(f_{x_{0}}\in \mathcal {C}^{1}(\mathbb {R})\). By assumption we know that \(\varphi _{(\cdot )}(x_{0})\in \mathcal {C}^{1}(\mathbb {R})\) with  . By the inverse function theorem there is an open neighbourhood \(U:=U(t_{0})\subset \mathbb {R}\) of \(t_{0}\) such that \(\varphi _{(\cdot )}(x_{0})\) is invertible on U and the inverse is continuously differentiable on the open neighbourhood \(W:=\varphi _{U}(x_{0})\subset \Omega \) of \(x=\varphi _{t_{0}}(x_{0})\). Noting that
. By the inverse function theorem there is an open neighbourhood \(U:=U(t_{0})\subset \mathbb {R}\) of \(t_{0}\) such that \(\varphi _{(\cdot )}(x_{0})\) is invertible on U and the inverse is continuously differentiable on the open neighbourhood \(W:=\varphi _{U}(x_{0})\subset \Omega \) of \(x=\varphi _{t_{0}}(x_{0})\). Noting that
for all \(y\in W\), we conclude that f is continuously differentiable in \(x=\varphi _{t_{0}}(x_{0})\in W\), yielding \(f\in \mathcal {C}^{1}(\Omega )\cap \mathcal {F}(\Omega )\). Using (13) and Proposition 5.4, finishes the proof of part (a).
(b) Due to Proposition 5.7 (b) with \(\omega :=\Omega {\setminus } N_{G}\) we only need to show that \(D(A)\subset D_{1}\). Let \(f\in D(A)\). Since \(\varphi _{0}(x)=x\) and

for every \(x\in \Omega {\setminus } N_{G}\), we obtain that the map \(V_{\varphi }\rightarrow \Omega {{\setminus }} N_{G}\), \((t,x)\mapsto \varphi _{t}(x)\), is surjective. Hence the proof of part (a) shows that f is continuously differentiable in every \(x\in \Omega {\setminus } N_{G}\). The first part of the proof of Proposition 5.7 (b) yields that

holds for all \(x\in \Omega {\setminus } N_{G}\). The left-hand side g of this equation belongs to \(\mathcal {F}(\Omega )\) as \(f\in D(A)\), yielding \(f\in D_{1}\). \(\square \)
Looking at the proof of Theorem 5.10 (b), we see that part (a) is a special case of (b) if there is a generator G such that \(N_{G}=\varnothing \). If \((\varphi _{t})_{t\ge 0}\) is the restriction of a jointly continuous holomorphic semiflow \(\psi \) on an open set \(\widetilde{\Omega }\subset \mathbb {C}\), i.e. \(\varphi _{t}=\psi _{t}\) on \(\Omega :=\widetilde{\Omega }\cap \mathbb {R}\) for all \(t\ge 0\), then the generator G of \((\varphi _{t})_{t\ge 0}\) exists by Theorem 3.7, namely, it is the restriction of the generator of \(\psi \) to \(\Omega \). So condition (i) of Theorem 5.10 (b) is fulfilled in this case. If in addition \(\psi \) is non-trivial, \(\widetilde{\Omega }\) simply connected and \(\widetilde{\Omega }\ne \mathbb {C}\), then \(|N_{G}|\le |{\text {Fix}}(\psi )|\le 1\) by [13, Remark 10.1.6, p. 275] combined with the Riemann mapping theorem and thus \(t_{x}=\inf \varnothing =\infty \) for all \(x\in N_{G}\), yielding that condition (ii) of Theorem 5.10 (b) is also fulfilled.
Now, we will see that the proof of the converse inclusion in Proposition 5.7 is much simpler if \(\mathcal {F}(\Omega )\) is a subspace of \(\mathcal {C}^{1}_{\mathbb {K}}(\Omega )\).
5.11 Theorem
Let \(\Omega \subset \mathbb {K}\) be open, \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) a sequentially complete Saks space such that \(\mathcal {F}(\Omega )\subset \mathcal {C}^{1}_{\mathbb {K}}(\Omega )\) and (A, D(A)) the generator of a locally bounded weighted composition semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) on \(\mathcal {F}(\Omega )\) w.r.t. a jointly continuous co-semiflow \((m,\varphi )\). If \(m_{(\cdot )}(x)\in \mathcal {C}^{1}[0,\infty )\) and \(\varphi _{(\cdot )}(x)\in \mathcal {C}^{1}[0,\infty )\) for all \(x\in \Omega \), then

and  for all \(f\in D(A)\).
for all \(f\in D(A)\).
Proof
By Proposition 5.7 (a) and the assumption \(\mathcal {F}(\Omega )\subset \mathcal {C}^{1}_{\mathbb {K}}(\Omega )\), we have

and  for all \(f\in D_{0}\). The converse inclusion holds by \(\mathcal {F}(\Omega )\subset \mathcal {C}^{1}_{\mathbb {K}}(\Omega )\), (13) and Proposition 5.4. \(\square \)
for all \(f\in D_{0}\). The converse inclusion holds by \(\mathcal {F}(\Omega )\subset \mathcal {C}^{1}_{\mathbb {K}}(\Omega )\), (13) and Proposition 5.4. \(\square \)
Now, we may use the theory on weighted composition semigroups developed so far to show (in combination with Proposition 4.5) that the condition that \(m_{(\cdot )}(x)\in \mathcal {C}^{1}[0,\infty )\) for all \(x\in \Omega \) is quite often a necessary condition for \(\gamma \)-strong continuity of the induced weighted composition semigroup. The underlying idea of the proof comes from the proof of [47, Theorem 1, p. 470].
5.12 Proposition
Let \(\Omega \subset \mathbb {K}\) be open, \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) a sequentially complete Saks space such that \(\mathcal {F}(\Omega )\subset \mathcal {C}^{1}_{\mathbb {K}}(\Omega )\) and
If \((m,\varphi )\) is a jointly continuous co-semiflow for \(\mathcal {F}(\Omega )\), \((C_{m,\varphi }(t))_{t\ge 0}\) locally bounded and \(\varphi \) has a generator G, then \(m_{(\cdot )}(x)\in \mathcal {C}^{1}[0,\infty )\),  and
and  for all \(t\ge 0\) and \(x\in \Omega \). If in addition \(\mathbb {K}=\mathbb {C}\) and \(G\in \mathcal {H}(\Omega )\), then
for all \(t\ge 0\) and \(x\in \Omega \). If in addition \(\mathbb {K}=\mathbb {C}\) and \(G\in \mathcal {H}(\Omega )\), then  .
.
Proof
Let (A, D(A)) be the generator of the \(\gamma \)-strongly continuous weighted composition semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) on \(\mathcal {F}(\Omega )\). We fix \(x\in \Omega \). By (14) there is \(F\in \mathcal {F}(\Omega )\) such that \(F(x)\ne 0\). Since F is continuous on \(\Omega \), there is a compact neighbourhood \(U\subset \Omega \) of x such that \(F(z)\ne 0\) for all \(z\in U\). Due to Theorem 4.10 (a) \((C_{m,\varphi }(t))_{t\ge 0}\) is \(\gamma \)-strongly continuous on the sequentially complete space \((X,\gamma )\), impying that D(A) is \(\gamma \)-dense in \(\mathcal {F}(\Omega )\) by [46, Proposition 1.3, p. 261]. Thus there is \(f\in D(A)\) such that \(f(z)\ne 0\) for all \(z\in U\) since \(\gamma \) is stronger than the topology \(\tau _{{\text {co}}}\) and U compact. Using that \(\varphi _{0}(x)=x\) and the joint continuity of \(\varphi \), we deduce that there are \(t_{0}>0\) and a neighbourhood \(U_{0}\) of x such that \(\varphi _{s}(\zeta )\in U\) for all \(s\in [0,t_{0}]\) and \(\zeta \in U_{0}\). In particular, \(f(\varphi _{s}(\zeta ))\ne 0\) for all \(s\in [0,t_{0}]\) and \(\zeta \in U_{0}\). Further, we have
for all \(0<s\le t_{0}\) and

for all \(\zeta \in U_{0}\). Therefore  for all \(\zeta \in U_0\), yielding that
for all \(\zeta \in U_0\), yielding that  is continuous on \(\Omega \) because x is arbitrary. If in addition \(\mathbb {K}=\mathbb {C}\) and \(G\in \mathcal {H}(\Omega )\), then we also get
is continuous on \(\Omega \) because x is arbitrary. If in addition \(\mathbb {K}=\mathbb {C}\) and \(G\in \mathcal {H}(\Omega )\), then we also get  . The continuous differentiability of \(m_{(\cdot )}(x)\) on \([0,\infty )\) and
. The continuous differentiability of \(m_{(\cdot )}(x)\) on \([0,\infty )\) and  for all \(t\ge 0\) and \(x\in \Omega \) follow from Proposition 3.13. \(\square \)
for all \(t\ge 0\) and \(x\in \Omega \) follow from Proposition 3.13. \(\square \)
We note that we may replace the condition \(\mathcal {F}(\Omega )\subset \mathcal {C}^{1}_{\mathbb {K}}(\Omega )\) by the condition \(D(A)\subset \mathcal {C}^{1}_{\mathbb {K}}(\Omega )\) because we only need it for the function \(f\in D(A)\) in the proof of Proposition 5.12. Condition (14) is for example fulfilled if \(\mathbb {1}\in \mathcal {F}(\Omega )\).
5.13 Corollary
Let \(\Omega \subset \mathbb {C}\) be open, \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) a sequentially complete Saks space such that \(\mathcal {F}(\Omega )\subset \mathcal {H}(\Omega )\) and \(\mathbb {1}\in \mathcal {F}(\Omega )\). If \((m,\varphi )\) is a jointly continuous holomorphic co-semiflow for \(\mathcal {F}(\Omega )\) and \((C_{m,\varphi }(t))_{t\ge 0}\) locally bounded, then \(m_{(\cdot )}(z)\in \mathcal {C}^{1}[0,\infty )\),  and
and  for all \(t\ge 0\) and \(z\in \Omega \).
for all \(t\ge 0\) and \(z\in \Omega \).
Proof
Our statement follows from Proposition 5.12 since (14) is fulfilled as \(\mathbb {1}\in \mathcal {F}(\Omega )\) and \(\varphi \) has a generator \(G\in \mathcal {H}(\Omega )\) by Theorem 3.7. \(\square \)
Due to [33, Chap. I, 5.5 Proposition, p. 39] and Corollary 5.13 we get back [47, Theorem 1, p. 470] as a special case where \(\Omega =\mathbb {D}\) and \(\mathcal {F}(\mathbb {D})=H^{p}\), \(1\le p<\infty \), is the Hardy space on \(\mathbb {D}\). Moreover, in contrast to Proposition 3.15, where \(\Omega \subset \mathbb {C}\) is connected, Corollary 5.13 allows arbitrary open sets \(\Omega \) but for the cost of more assumptions on \((m,\varphi )\). For example the condition \(\mathbb {1}\in \mathcal {F}(\Omega )\) in Corollary 5.13 implies that \(m_{t}\in \mathcal {F}(\Omega )\) for all \(t\ge 0\) (see Remark 4.8).
6 Converse of the Holomorphic Generation Theorem
Let \(\Omega \subset \mathbb {C}\) be open, \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) a sequentially complete Saks space such that \(\mathcal {F}(\Omega )\subset \mathcal {H}(\Omega )\). Suppose that \(\Omega \) is connected or that \(\mathbb {1}\in \mathcal {F}(\Omega )\). Due to Theorem 3.7, Theorem 5.11, and Proposition 3.15 or Corollary 5.13 we know that the generator (A, D(A)) of a locally bounded weighted composition semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) on \(\mathcal {F}(\Omega )\) w.r.t. a jointly continuous holomorphic co-semiflow \((m,\varphi )\) is given by
where \(G\in \mathcal {H}(\Omega )\) is the generator of \(\varphi \) and  .
.
In this section we want to prove the converse statement, namely, if we know that the domain of a \(\gamma \)-strongly continuous semigroup \((T(t))_{t\ge 0}\) on \(\mathcal {F}(\Omega )\) is given by (15), we want to show, under suitable conditions, that this semigroup is a weighted composition semigroup whose semiflow has G as a generator and whose semicocycle m is given by \(m_{t}(z):=\exp (\int _{0}^{t}g(\varphi _{s}(z))\textrm{d}s)\) for all \(t\ge 0\) and \(z\in \Omega \).
Our main result in this direction is an analogon of [38, Main theorem, p. 490] (\(g=0\)) and [39, Theorem 3.1, p. 69] where \(\Omega =\mathbb {D}\) and \((T(t))_{t\ge 0}\) is a \(\Vert \cdot \Vert \)-strongly continuous semigroup. We define the space of holomorphic germs near the closed unit disc \(\overline{\mathbb {D}}\) by the inductive limit
equipped with its inductive limit topology (see e.g. [9, p. 81–82]). For \(n\in \mathbb {N}_{0}\) set \(e_{n}:\mathbb {C}\rightarrow \mathbb {C}\), \(e_{n}(z):=z^{n}\). Then \(e_{n}\in \mathcal {H}(\overline{\mathbb {D}})\) for all \(n\in \mathbb {N}_{0}\). Hence the assumption that \(\mathcal {H}(\overline{\mathbb {D}})\hookrightarrow (\mathcal {F}(\mathbb {D}),\Vert \cdot \Vert )\) embeds continuously implies that \(e_{n}\in \mathcal {F}(\mathbb {D})\) for all \(n\in \mathbb {N}_{0}\).
6.1 Theorem
Let \((\mathcal {F}(\mathbb {D}),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) be a sequentially complete Saks space such that \(\mathcal {F}(\mathbb {D})\subset \mathcal {H}(\mathbb {D})\), and \(\mathcal {H}(\overline{\mathbb {D}})\hookrightarrow (\mathcal {F}(\mathbb {D}),\Vert \cdot \Vert )\) embeds continuously. If \((T(t))_{t\ge 0}\) is a \(\gamma \)-strongly continuous semigroup on \(\mathcal {F}(\mathbb {D})\) with generator (A, D(A)) of the form
for some \(G,g\in \mathcal {H}(\mathbb {D})\), then there is a jointly continuous holomorphic co-semiflow \((m,\varphi )\) for \(\mathcal {F}(\mathbb {D})\) such that G is the generator of \(\varphi \), \(m_{t}(z)=\exp (\int _{0}^{t}g(\varphi _{s}(z))\textrm{d}s)\) for all \(t\ge 0\), \(z\in \mathbb {D}\), and \((T(t))_{t\ge 0}=(C_{m,\varphi }(t))_{t\ge 0}\).
Proof
The proof of [39, Theorem 3.1, p. 69] carries over to our setting. We only have to adjust the proof in three instances. First, we have to use that \(Af=\frac{\textrm{d}}{\textrm{d}t}T(t)f\) for all \(t\ge 0\) and \(f \in D(A)\) by [46, Proposition 1.2 (1), p. 260] in the proof of [39, Claim 1, p. 70]. Second, D(A) is \(\gamma \)-dense in \(\mathcal {F}(\mathbb {D})\) by [46, Proposition 1.3, p. 261]. Thus for every \(f\in \mathcal {F}(\mathbb {D})\) there is a net \((f_{\iota })_{\iota \in I}\), I a directed set, which is \(\gamma \)-convergent to f. Since T(t) is \(\gamma \)-continuous for every \(t\ge 0\), this implies that \((T(t)f_{\iota })_{\iota \in I}\) is \(\gamma \)-convergent to T(t)f for every \(t\ge 0\). This proves the validity of [39, Eq. (3.6), p. 71] because \(\gamma \) is finer than \(\tau _{{\text {co}}}\). Third, we note that \(\delta _{z}\in (\mathcal {F}(\mathbb {D}),\gamma )'\) and \(\delta _{z}\in (\mathcal {F}(\mathbb {D}),\Vert \cdot \Vert )'\) for all \(z\in \mathbb {D}\), where \(\delta _{z}(f):=f(z)\) for all \(f\in \mathcal {F}(\mathbb {D})\), because \(\delta _{z}\in (\mathcal {F}(\mathbb {D}),\tau _{{\text {co}}})'\) and \(\gamma \) and the \(\Vert \cdot \Vert \)-topology are finer than \(\tau _{{\text {co}}}\). We now get by [39, Eq. (3.10), p. 72] that
for all \(z\in \mathbb {D}\), \(n\in \mathbb {N}\) and \(0\le t<t_{0}\) with \(t_{0}>0\) from [39, p. 69]. Let \(\Gamma _{\gamma }\) denote a directed system of continuous seminorms that generates \(\gamma \). Since \(\delta _{z}\in (\mathcal {F}(\mathbb {D}),\gamma )'\), \(T(t)\in \mathcal {L}(\mathcal {F}(\mathbb {D}),\gamma )\) and the \(\Vert \cdot \Vert \)-topology is finer than \(\gamma \), there are \(p=p_{z,t}\in \Gamma _{\gamma }\), \(K_{1}=K_{1}(z,t)\ge 0\) and \(K_{2}=K_{2}(p)\ge 0\) such that
for all \(z\in \mathbb {D}\), \(n\in \mathbb {N}\) and \(0\le t<t_{0}\). This implies that there is \(0<t_{1}\le t_{0}\) such that \(|\varphi _{t}(z)|<1\) for all \(z\in \mathbb {D}\) and \(0\le t<t_{1}\) like in the proof of [38, Claim 2, p. 492]. This is all we have to change in the proof of [39, Theorem 3.1, p. 69]. Moreover, we note that the joint continuity of \(\varphi \) follows from [39, p. 65] and Proposition 3.3 (b), and the joint continuity of m from Proposition 3.14 (a). \(\square \)
We note that Theorem 6.1 implies [39, Theorem 3.1, p. 69] if \((T(t))_{t\ge 0}\) is \(\Vert \cdot \Vert \)-strongly continuous and \(T(t)\in \mathcal {L}(X,\gamma )\) for all \(t\ge 0\) because then \((T(t))_{t\ge 0}\) is also \(\gamma \)-strongly continuous. The semicocycle m in Theorem 6.1 is given by \(m_{t}=T(t)\mathbb {1}=T(t)e_{0}\) and the semiflow \(\varphi \) by \(\varphi _{t}=\frac{1}{m_{t}}T(t){\text {id}}=\frac{1}{m_{t}}T(t)e_{1}\) for all \(t\ge 0\). Further, it is shown in [11, p. 176–177] that the assumption that \(\mathcal {H}(\overline{\mathbb {D}})\hookrightarrow (\mathcal {F}(\mathbb {D}),\Vert \cdot \Vert )\) embeds continuously is equivalent to \(\limsup _{n\rightarrow \infty }\Vert e_{n}\Vert ^{\frac{1}{n}}\le 1\).
6.2 Example
For the following spaces \((\mathcal {F}(\mathbb {D}),\Vert \cdot \Vert )\) the embedding \(\mathcal {H}(\overline{\mathbb {D}})\hookrightarrow (\mathcal {F}(\mathbb {D}),\Vert \cdot \Vert )\) is continuous:
-
(a)
The Hardy spaces \((H^{p},\Vert \cdot \Vert _{p})\) for \(1\le p\le \infty \) since \(\Vert e_{n}\Vert _{p}=1\) for all \(n\in \mathbb {N}\).
-
(b)
The Bergman spaces \((A_{\alpha }^{p},\Vert \cdot \Vert _{\alpha ,p})\) for \(\alpha >-1\) and \(1\le p<\infty \) since
$$\begin{aligned} \Vert e_{n}\Vert _{\alpha ,p}^{p}&=\frac{\alpha +1}{\pi }\int _{\mathbb {D}}|z|^{np}(1-|z|^{2})^{\alpha }\textrm{d}z =\frac{\alpha +1}{\pi }\int _{0}^{2\pi }\int _{0}^{1}r^{np+1}(1-r^{2})^{\alpha }\textrm{d}r \textrm{d}\theta \\&\le 2(\alpha +1)\int _{0}^{1}r^{p+1}(1-r^{2})^{\alpha }\textrm{d}r = (\alpha +1)B\left( \frac{p}{2}+1,\alpha +1\right) \end{aligned}$$for all \(n\in \mathbb {N}\) by [40, Eq. 3251-1, p. 327] with \(\mu :=p+2\), \(\lambda :=2\) and \(\nu :=\alpha +1\), where B denotes the Beta function, and thus \(\limsup _{n\rightarrow \infty }\Vert e_{n}\Vert _{\alpha ,p}^{\frac{1}{n}}\le 1\).
-
(c)
The Dirichlet space \((\mathcal {D},\Vert \cdot \Vert _{\mathcal {D}})\) since
$$\begin{aligned} \Vert e_{n}\Vert _{\mathcal {D}}^{2} =0+\frac{1}{\pi }\int _{\mathbb {D}}n^{2}|z|^{2n-2}\textrm{d}z =\frac{n^{2}}{\pi }\int _{0}^{2\pi }\int _{0}^{1}r^{2n-1}\textrm{d}r \textrm{d}\theta =\frac{2n^{2}}{2n} =n \end{aligned}$$for all \(n\in \mathbb {N}\) and thus \(\lim _{n\rightarrow \infty }\Vert e_{n}\Vert _{\mathcal {D}}^{\frac{1}{n}}=1\).
-
(d)
The v-Bloch spaces \((\mathcal {B}v(\mathbb {D}),\Vert \cdot \Vert _{\mathcal {B}v(\mathbb {D})})\) for bounded continuous \(v:\mathbb {D}\rightarrow (0,\infty )\) since
$$\begin{aligned} \Vert e_{n}\Vert _{\mathcal {B}v(\mathbb {D})}=0+\sup _{z\in \mathbb {D}}n|z|^{n-1}v(z)\le n\Vert v\Vert _{\infty } \end{aligned}$$for all \(n\in \mathbb {N}\) and thus \(\limsup _{n\rightarrow \infty }\Vert e_{n}\Vert _{\mathcal {B}v(\mathbb {D})}^{\frac{1}{n}}\le 1\).
-
(e)
The spaces \((\mathcal {H}v(\mathbb {D}),\Vert \cdot \Vert _{v})\) of weighted holomorphic functions on \(\mathbb {D}\) for bounded continuous \(v:\mathbb {D}\rightarrow (0,\infty )\) since
$$\begin{aligned} \Vert e_{n}\Vert _{v}=\sup _{z\in \mathbb {D}}|z|^{n}v(z)\le \Vert v\Vert _{\infty } \end{aligned}$$for all \(n\in \mathbb {N}\) and thus \(\limsup _{n\rightarrow \infty }\Vert e_{n}\Vert _{v}^{\frac{1}{n}}\le 1\).
In particular, the embedding \(\mathcal {H}(\overline{\mathbb {D}})\hookrightarrow (\mathcal {B}_{\alpha },\Vert \cdot \Vert _{\mathcal {B}_{\alpha }})\) for \(\alpha >0\) is continuous by Example 6.2 (d) because \(v_{\alpha }(z)=(1-|z|^2)^{\alpha }\le 1\) for all \(z\in \mathbb {D}\). Further, we note that Theorem 4.14, Theorem 4.15 and Theorem 4.17 in combination with Example 6.2 answer the question in [39, Remark 3.2, p. 72] for several spaces, namely, to give a sufficient condition such that \(C_{m,\varphi }(t)\in \mathcal {F}(\mathbb {D})\) for all \(t\ge 0\) where \((\mathcal {F}(\mathbb {D}),\Vert \cdot \Vert )\) is a space whose embedding \(\mathcal {H}(\overline{\mathbb {D}})\hookrightarrow (\mathcal {F}(\mathbb {D}),\Vert \cdot \Vert )\) is continuous.
We remark that Theorem 6.1 is not restricted to the case \(\Omega =\mathbb {D}\) (cf. [4, p. 177–178] (\(g=0\)) and [39, Remark 3.3, p. 72–73] in the case of \(\Vert \cdot \Vert \)-strongly continuous semigroups).
6.3 Remark
Let \(\Omega \subsetneq \mathbb {C}\) be open and simply connected, and \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) a sequentially complete Saks space such that \(\mathcal {F}(\Omega )\subset \mathcal {H}(\Omega )\). Suppose that \((S(t))_{t\ge 0}\) is a \(\gamma \)-strongly continuous semigroup on \(\mathcal {F}(\Omega )\) with generator (A, D(A)) of the form
for some \(G,g\in \mathcal {H}(\Omega )\). Choose a biholomorphic map \(h:\mathbb {D}\rightarrow \Omega \) by the Riemann mapping theorem and define the space \(\mathcal {F}_{h}(\mathbb {D}):=\{f\circ h\;|\; f\in \mathcal {F}(\Omega )\}\), which becomes a Banach space when equipped with the norm \(\Vert f\circ h\Vert _{\mathcal {F}_{h}(\mathbb {D})}:=\Vert f\Vert \) for \(f\in \mathcal {F}(\Omega )\). It is easy to check that the composition operator \(C_{h}:\mathcal {F}(\Omega )\rightarrow \mathcal {F}_{h}(\mathbb {D})\), \(C_{h}(f):=f\circ h\), is an isometric ismorphism w.r.t. the norms, an isomorphism \((\mathcal {F}(\Omega ),\tau _{{\text {co}}}) \rightarrow (\mathcal {F}_{h}(\mathbb {D}),\tau _{{\text {co}}})\), and \(C_{h}^{-1}=C_{h^{-1}}\). Then it follows as in the proof of Proposition 4.1 that \(C_{h}:(\mathcal {F}(\Omega ),\gamma (\Vert \cdot \Vert ,\tau _{{\text {co}}})) \rightarrow (\mathcal {F}_{h}(\mathbb {D}),\gamma (\Vert \cdot \Vert _{\mathcal {F}_{h}(\mathbb {D})},\tau _{{\text {co}}}))\) is an isomorphism as well. Therefore \((\mathcal {F}_{h}(\mathbb {D}),\Vert \cdot \Vert _{\mathcal {F}_{h}(\mathbb {D})},\tau _{{\text {co}}})\) is a sequentially complete Saks space such that \(\mathcal {F}_{h}(\mathbb {D})\subset \mathcal {H}(\mathbb {D})\) and the semigroup \((T(t))_{t\ge 0}\) on \(\mathcal {F}_{h}(\mathbb {D})\) given by
is \(\gamma (\Vert \cdot \Vert _{\mathcal {F}_{h}(\mathbb {D})},\tau _{{\text {co}}})\)-strongly continuous. Assume that \(\mathcal {H}(\overline{\mathbb {D}})\hookrightarrow (\mathcal {F}_{h}(\mathbb {D}),\Vert \cdot \Vert _{\mathcal {F}_{h}(\mathbb {D})})\) embeds continuously. Like in [39, Remark 3.3, p. 73] it follows that the generator (B, D(B)) of \((T(t))_{t\ge 0}\) fulfils
where \(G_{1}(z):=\frac{1}{h'(z)}G(h(z))\) and \(g_{1}(z):=g(h(z))\) for all \(z\in \mathbb {D}\). Hence we may apply Theorem 6.1 and obtain that there is a jointly continuous holomorphic co-semiflow \((m,\varphi )\) for \(\mathcal {F}_{h}(\mathbb {D})\) such that \(G_{1}\) is the generator of \(\varphi \), \(m_{t}(z)=\exp (\int _{0}^{t}g_{1}(\varphi _{s}(z))\textrm{d}s)\) for all \(t\ge 0\), \(z\in \mathbb {D}\), and \(T(t)=C_{m,\varphi }(t)\) for all \(t\ge 0\). Like in [39, Remark 3.3, p. 73] we get that \(S(t)=C_{\mu ,\psi }(t)\) for all \(t\ge 0\) with the jointly continuous holomorphic semiflow \(\psi \) on \(\Omega \) given by \(\psi _{t}:=h\circ \varphi _{t}\circ h^{-1}\) and its jointly continuous holomorphic semicocycle \(\mu \) given by \(\mu _{t}(z):=(m_{t}\circ h^{-1})(z)=\exp (\int _{0}^{t}g(\psi _{s}(z))\textrm{d}s)\) for all \(t\ge 0\) and \(z\in \Omega \).
7 Applications
In this short section we apply our results from the preceding sections. In the following proposition \(\mathcal {C}v(\mathbb {R})\) denotes the weighted space of continuous functions from Example 2.13 for \(\mathbb {K}=\mathbb {R}\).
7.1 Proposition
Let \(v:\mathbb {R}\rightarrow (0,\infty )\) be continuous, \(\varphi _{t}(x):=\left( x^{\frac{1}{3}}+\frac{t}{3}\right) ^3\), \(t,x\in \mathbb {R}\), and \(m:=(m_{t})_{t\in \mathbb {R}}\) be a cocycle for \(\varphi :=(\varphi _{t})_{t\in \mathbb {R}}\) such that \(\lim _{s\rightarrow 0}m_{s}(x)=1\) for all \(x\in \mathbb {R}\), \(m_{t}\in \mathcal {C}_{b}(\mathbb {R})\) for all \(t\in \mathbb {R}\), \(m_{(\cdot )}(x)\in \mathcal {C}^{1}(\mathbb {R})\), \(m_{t}(x)\ne 0\) for all \((t,x)\in \mathbb {R}^2\),
for all \(t\in \mathbb {R}\) and there exists \(t_{0}>0\) such that \(\sup _{t\in [0,t_{0}]}K(\varphi _{t})<\infty \). Then the following assertions hold.
-
(a)
The weighted composition semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) on \(\mathcal {C}v(\mathbb {R})\) w.r.t. the co-flow \((m,\varphi )\) is \(\gamma \)-strongly continuous, \(\tau _{{\text {co}}}\)-bi-continuous, locally \(\tau _{{\text {co}}}\)-equicontinuous and quasi-\(\gamma \)-equicontinuous.
-
(b)
The generator (A, D(A)) of \((C_{m,\varphi }(t))_{t\ge 0}\) fulfils

and
 , \(x\ne 0\), for all \(f\in D(A)\). If in addition
, \(x\ne 0\), for all \(f\in D(A)\). If in addition  , then \(D(A)=\{f\in \mathcal {C}^{1}(\mathbb {R}{{\setminus }}\{0\})\cap \mathcal {C}v(\mathbb {R})\;|\; [x\mapsto x^{\frac{2}{3}}f'(x)]\in \mathcal {C}v(\mathbb {R})\}\).
, then \(D(A)=\{f\in \mathcal {C}^{1}(\mathbb {R}{{\setminus }}\{0\})\cap \mathcal {C}v(\mathbb {R})\;|\; [x\mapsto x^{\frac{2}{3}}f'(x)]\in \mathcal {C}v(\mathbb {R})\}\).
Proof
(a) The flow \(\varphi \) is clearly \(C_{0}\). The assumption \(\lim _{s\rightarrow 0}m_{s}(x)=1\) for all \(x\in \mathbb {R}\) means that its cocycle m is also \(C_{0}\) and so the co-flow \((m,\varphi )\) is jointly continuous by Proposition 5.9. Further, \(C_{m,\varphi }(t)f=m_{t}\cdot (f\circ \varphi _{t})\) is continuous on \(\mathbb {R}\) and
for all \(t\in \mathbb {R}\) and \(f\in \mathcal {C}v(\mathbb {R})\) by (16). Hence \((m,\varphi )\) is a jointly continuous co-flow for \(\mathcal {C}v(\mathbb {R})\) and \((C_{m,\varphi }(t))_{t\ge 0}\) locally bounded by Proposition 2.3 since \(\sup _{t\in [0,t_{0}]}K(\varphi _{t})<\infty \) and \(\sup _{t\in [0,t_{1}]}\Vert m_{t}\Vert _{\infty }<\infty \) for some \(t_{1}> 0\) by Proposition 3.10. We conclude that statement (a) is valid by Example 2.13 and Theorem 4.10.
(b) Setting \(G:\mathbb {R}\rightarrow \mathbb {R}\), \(G(x):=x^\frac{2}{3}\), we note that

for all \((t,x)\in \mathbb {R}^2\). Thus \(N_{G}=\{0\}\) and \(t_{0}=\inf \varnothing =\infty \). We deduce that the first part of (b) follows from Theorem 5.10 (b). If additionally  , then we have
, then we have  and thus \(D(A)=\{f\in \mathcal {C}^{1}(\mathbb {R}{{\setminus }}\{0\})\cap \mathcal {C}v(\mathbb {R})\;|\;[x\mapsto x^{\frac{2}{3}}f'(x)] \in \mathcal {C}v(\mathbb {R})\}\). \(\square \)
and thus \(D(A)=\{f\in \mathcal {C}^{1}(\mathbb {R}{{\setminus }}\{0\})\cap \mathcal {C}v(\mathbb {R})\;|\;[x\mapsto x^{\frac{2}{3}}f'(x)] \in \mathcal {C}v(\mathbb {R})\}\). \(\square \)
Proposition 7.1 is interesting because it illustrates the phenomenon of non-differentiability of the elements in the domain of A at the zeros of G which cannot happen in the case of weighted composition semigroups on spaces of holomorphic functions (see Corollary 5.13). For \(m=v=\mathbb {1}\) the statement of Proposition 7.1 (a) is known due to e.g. [25, Theorems 2.1, 2.2, 2.3, p. 5]. Proposition 7.1 (b) generalises [26, Example 4.2, p. 124–125] where \(m=v=\mathbb {1}\).
7.2 Theorem
Let \(\Omega \subset \mathbb {C}\) be open and connected, \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) a sequentially complete Saks space such that \(\mathcal {F}(\Omega )\subset \mathcal {H}(\Omega )\) and \(\{\mathbb {1},{{\,\textrm{id}\,}}\}\subset \mathcal {F}(\Omega )\), and \((C_{m,\varphi }(t))_{t\ge 0}\) the weighted composition semigroup on \(\mathcal {F}(\Omega )\) w.r.t. a holomorphic co-semiflow \((m,\varphi )\). Then the following assertions hold.
-
(a)
\((C_{m,\varphi }(t))_{t\ge 0}\) is \(\gamma \)-strongly continuous and locally \(\gamma \)-equicontinuous if and only if \((m,\varphi )\) is a \(C_{0}\)-co-semiflow and \((C_{m,\varphi }(t))_{t\ge 0}\) locally bounded.
-
(b)
Suppose that \((\mathcal {F}(\Omega ),\Vert \cdot \Vert )\) is reflexive. Then \((C_{m,\varphi }(t))_{t\ge 0}\) is \(\Vert \cdot \Vert \)-strongly continuous if and only if \((m,\varphi )\) is a \(C_{0}\)-co-semiflow and \((C_{m,\varphi }(t))_{t\ge 0}\) locally bounded.
-
(c)
If \((C_{m,\varphi }(t))_{t\ge 0}\) is \(\Vert \cdot \Vert \)-strongly continuous with generator \((A_{\Vert \cdot \Vert },D(A_{\Vert \cdot \Vert }))\), then we have
 and
and 
and
 for all \(f\in D(A_{\Vert \cdot \Vert })\).
for all \(f\in D(A_{\Vert \cdot \Vert })\).
Proof
First, we note that the open set \(\Omega \subset \mathbb {C}\) is a locally compact, \(\sigma \)-compact space w.r.t. the relative topology induced by the metric space \(\mathbb {C}\). In particular, \(\Omega \) is a Hausdorff \(k_{\mathbb {R}}\)-space, and the co-semiflow \((m,\varphi )\) is jointly continuous if and only if it is \(C_{0}\) by Proposition 3.3 and Proposition 3.12. Second, if \(\varphi \) is \(C_{0}\), so jointly continuous, then \(\varphi _{(\cdot )}(z)\in \mathcal {C}^{1}[0,\infty )\) for all \(z\in \Omega \) and  by Theorem 3.7. Third, \(m_{(\cdot )}(z)\in \mathcal {C}^{1}[0,\infty )\),
by Theorem 3.7. Third, \(m_{(\cdot )}(z)\in \mathcal {C}^{1}[0,\infty )\),  and \(m_{t}(z)\ne 0\) for all \(t\ge 0\) and \(z\in \Omega \) by Proposition 3.14 (a) and Proposition 3.15 since \(\Omega \subset \mathbb {C}\) is connected.
and \(m_{t}(z)\ne 0\) for all \(t\ge 0\) and \(z\in \Omega \) by Proposition 3.14 (a) and Proposition 3.15 since \(\Omega \subset \mathbb {C}\) is connected.
(a) Due to [37, Proposition 3.6 (ii), p. 1137] and [22, I.1.10 Proposition, p. 10] a \(\gamma \)-strongly continuous, locally \(\gamma \)-equicontinuous semigroup of linear operators is locally bounded. Thus implication \(\Rightarrow \) follows from Remark 4.4 (b) and Proposition 4.5 (b). The converse implication \(\Leftarrow \) follows from Theorem 4.10 (a).
(b) Let \((C_{m,\varphi }(t))_{t\ge 0}\) be \(\Vert \cdot \Vert \)-strongly continuous. Then \((C_{m,\varphi }(t))_{t\ge 0}\) is locally bounded by [33, Chap. I, 5.5 Proposition, p. 39] and \(\gamma \)-strongly continuous by Proposition 4.1 with \(I:=\{t\}\) for all \(t\ge 0\) and since \(\gamma \) is coarser than the \(\Vert \cdot \Vert \)-topology. Due to the assumption \(\{\mathbb {1},{{\,\textrm{id}\,}}\}\subset \mathcal {F}(\Omega )\) the topology of \(\Omega \) is initial-like w.r.t. \((\varphi ,\mathcal {F}(\Omega ))\) by Remark 4.4 (b), and thus the co-semiflow \((m,\varphi )\) jointly continuous by Proposition 4.5 (b).
Let us turn to the converse. Suppose that \((m,\varphi )\) is a \(C_{0}\)-co-semiflow and \((C_{m,\varphi }(t))_{t\ge 0}\) locally bounded. Then \((m,\varphi )\) is jointly continuous and \((C_{m,\varphi }(t))_{t\ge 0}\) \(\gamma \)-strongly continuous by Proposition 4.5 (a). We deduce from Proposition 5.3 (b) that \((C_{m,\varphi }(t))_{t\ge 0}\) is \(\Vert \cdot \Vert \)-strongly continuous since \((\mathcal {F}(\Omega ),\Vert \cdot \Vert )\) is reflexive.
(c) By the the first part of the proof of (b) we get that \((C_{m,\varphi }(t))_{t\ge 0}\) is locally bounded and \((m,\varphi )\) a \(C_{0}\)-co-semiflow. Applying Proposition 5.3 (a) and Theorem 5.11, this finishes the proof of part (c). \(\square \)
Theorem 7.2 (b) implies [47, Lemma 3.1, p. 474] and [68, Theorem 1, p. 362] for the reflexive Hardy spaces \(H^{p}\), \(1<p<\infty \), by [47, Definition 1 (i), p. 469], Example 2.9 (a), Example 3.18 and Theorem 4.14 (a). It also answers the questions in [71, Example 7.4, p. 247–248] because it implies the \(\Vert \cdot \Vert \)-strong continuity of the weighted composition semigroup induced by the semicoboundary \((\varphi ',\varphi )\) for a jointly continuous holomorphic semiflow \(\varphi \) on \(\mathbb {D}\) (see Example 3.19) on reflexive spaces \((\mathcal {F}(\mathbb {D}),\Vert \cdot \Vert )\) such that \(\mathcal {F}(\mathbb {D})\subset \mathcal {H}(\mathbb {D})\) such as the Hardy spaces \(H^{p}\) for \(1<p<\infty \), the weighted Bergman spaces \(A_{\alpha }^{p}\) for \(\alpha >-1\) and \(1<p<\infty \), and the Dirichlet space \(\mathcal {D}\) due to Example 2.9 and Theorem 4.14 (and the computations thereafter). Further, Theorem 7.2 (b) in combination with Theorem 4.14 (a) and (b) gives back [63, Lemmas 2.13, 2.14, p. 828] and [77, Corollaries 3, 4, p. 8–9] for \(1<p<\infty \) by a different proof.Footnote 2 It also implies in combination with Theorem 4.14 (c) [70, Theorem 1, p. 167] where \(\mathcal {F}(\mathbb {D})=\mathcal {D}\) and \(m=\mathbb {1}\).
If \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) is a sequentially complete Saks such that \(\mathcal {F}(\Omega )\subset \mathcal {H}(\Omega )\) and \(\{\mathbb {1},{{\,\textrm{id}\,}}\}\subset \mathcal {F}(\Omega )\), then Theorem 7.2 (c) implies [12, Theorem 2, p. 72] where \(\Omega =\mathbb {D}\) and \(m=\mathbb {1}\) but it is only assumed that \((\mathcal {F}(\Omega ),\Vert \cdot \Vert )\) is complete and \(\tau _{{\text {co}}}\) coarser than the \(\Vert \cdot \Vert \)-topology (see [12, p. 67]). Moreover, Theorem 7.2 (c) generalises [68, Theorem 2, p. 364] (where \(m=m^{\omega }\) is a semicoboundary for \(\omega \in \mathcal {H}(\mathbb {D})\)) and the first part of [47, Theorem 2 (b), p. 471] by Example 2.9 (a) and Example 3.18 where \(\mathcal {F}(\mathbb {D})=H^{p}\) is the Hardy space for \(1\le p<\infty \). Theorem 7.2 (c) also yields [69, Theorem 1 (ii), p. 400–401] by Example 2.9 (b) where \(\mathcal {F}(\mathbb {D})=A_{\alpha }^{p}\) is the Bergman space for \(\alpha >-1\) and \(1\le p<\infty \) and \(m=\mathbb {1}\). Theorem 7.2 (b) and (c) combined with Theorem 4.14 (c) also imply the \(\Vert \cdot \Vert \)-strong continuity of the weighted composition semigroup on \(\mathcal {D}\) w.r.t. the holomorphic \(C_{0}\)-co-semiflow \((m,\varphi )\) in [70, Corollary 2, p. 170] and the form of its generator where \({\text {Fix}}(\varphi )=\{0\}\) and \(m=m^{\omega }\) with \(\omega (z):=z^{p}\) for all \(z\in \mathbb {D}\) for some \(p\in \mathbb {N}\). If \((\mathcal {F}(\Omega ),\Vert \cdot \Vert )\) is a Banach space such that \(\tau _{{\text {co}}}\) is coarser than the \(\Vert \cdot \Vert \)-topology and \(\mathcal {F}(\Omega )\subset \mathcal {H}(\Omega )\), then the assumptions in [39, Theorem 2.1 (ii), p. 68] that \(\Omega =\mathbb {D}\) and the continuity of \(\mathcal {H}(\overline{\mathbb {D}})\hookrightarrow (\mathcal {F}(\Omega ),\Vert \cdot \Vert )\) are stronger than in Theorem 7.2 (c) whereas vice versa the latter theorem has the stronger assumption that \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) is a sequentially complete Saks space.
We may also apply Theorem 7.2 (a) to weighted composition semigroups on the Hardy space \(H^{1}\) by Theorem 4.14 (a), the Bergman space \(A_{\alpha }^{1}\) for \(\alpha >-1\) by Theorem 4.14 (b), the Bloch type space \(\mathcal {B}_{\alpha }\) for \(\alpha >0\) by Theorem 4.15, the weighted spaces \(\mathcal {H}v(\Omega )\) and \(\mathcal {C}v(\Omega )\) of holomorphic resp. continuous functions on \(\Omega \) by Theorem 4.17 resp. Theorem 4.18 if \(\{\mathbb {1},{{\,\textrm{id}\,}}\}\subset \mathcal {H}v(\Omega )\) resp. \(\{\mathbb {1},{{\,\textrm{id}\,}}\}\subset \mathcal {C}v(\Omega )\). For instance, we have the following result for the Hardy space \(H^{\infty }\).
7.3 Corollary
Let \((m,\varphi )\) be a holomorphic co-semiflow on \(\mathbb {D}\). The weighted composition semigroup \((C_{m,\varphi }(t))_{t\ge 0}\) is \(\gamma \)-strongly continuous and locally \(\gamma \)-equicontinuous on \(H^{\infty }\) if and only if \((m,\varphi )\) is a \(C_{0}\)-co-semiflow and  .
.
Proof
This statement follows from Example 2.11, Theorem 4.17 with \(v:=\mathbb {1}\) and Theorem 7.2 (a). \(\square \)
7.4 Theorem
Let \(\Omega \subset \mathbb {C}\) be open, \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) a sequentially complete Saks space such that \(\mathcal {F}(\Omega )\subset \mathcal {H}(\Omega )\), and \((C_{m,\varphi }(t))_{t\ge 0}\) a locally bounded weighted composition semigroup on \(\mathcal {F}(\Omega )\) w.r.t. a holomorphic \(C_{0}\)-co-semiflow \((m,\varphi )\). Then the following assertions hold.
-
(a)
\((C_{m,\varphi }(t))_{t\ge 0}\) is \(\gamma \)-strongly continuous, \(\tau _{{\text {co}}}\)-bi-continuous, locally \(\tau _{{\text {co}}}\)-equicontinuous and locally \(\gamma \)-equicontinuous.
-
(b)
If \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\) is a C-sequential Saks space, then \((C_{m,\varphi }(t))_{t\ge 0}\) is quasi-\(\gamma \)-equicontinuous.
-
(c)
If \(m_{(\cdot )}(z)\in \mathcal {C}^{1}[0,\infty )\) for all \(z\in \Omega \), then
 and the generator (A, D(A)) of \((C_{m,\varphi }(t))_{t\ge 0}\) fulfils
and the generator (A, D(A)) of \((C_{m,\varphi }(t))_{t\ge 0}\) fulfils 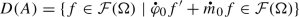
and
 for all \(f\in D(A)\).
for all \(f\in D(A)\). -
(d)
If \(m_{(\cdot )}(z)\in \mathcal {C}^{1}[0,\infty )\) for all \(z\in \Omega \), then
 and
and 
where \(\bigl [(m,\varphi ),\mathcal {F}(\Omega )\bigr ]\) is the space of \(\Vert \cdot \Vert \)-strong continuity of \((C_{m,\varphi }(t))_{t\ge 0}\).
Proof
By the first part of the proof of Theorem 7.2 we know that the \(C_{0}\)-co-semiflow \((m,\varphi )\) is jointly continuous, \(\varphi _{(\cdot )}(z)\in \mathcal {C}^{1}[0,\infty )\) for all \(z\in \Omega \) and  .
.
The parts (a), (b) and (c) follow directly from Theorem 4.10 and Theorem 5.11. Part (d) is a consequence of Proposition 5.3 (c) and Theorem 5.11. \(\square \)
Comparing Theorem 7.4 (d) with [5, Theorem 10, p. 9] resp. [12, Theorem 1, p. 71] where \(\Omega =\mathbb {D}\) and \(m_{t}=\varphi _{t}'\) for all \(t\ge 0\) resp. \(m=\mathbb {1}\) we see that the former theorem is more general w.r.t. the semicocycles and does not need the assumption \(\mathbb {1}\in \mathcal {F}(\Omega )\), and less general w.r.t. the tuples \((\mathcal {F}(\Omega ),\Vert \cdot \Vert ,\tau _{{\text {co}}})\). In the latter theorem it is only assumed that \((\mathcal {F}(\Omega ),\Vert \cdot \Vert )\) is complete and \(\tau _{{\text {co}}}\) coarser than the \(\Vert \cdot \Vert \)-topology (see [12, p. 67]). However, both theorems have the assumption on joint continuity of \(\varphi \) (see [12, (3’), p. 68]) and local boundedness of \((C_{m,\varphi }(t))_{t\ge 0}\) (see Proposition 2.3).
For \(H^{\infty }\subset \mathcal {F}(\mathbb {D})\subset \mathcal {B}_{1}\), \((\mathcal {F}(\mathbb {D}),\Vert \cdot \Vert )\) Banach, it holds \(\bigl [(\mathbb {1},\varphi ),\mathcal {F}(\mathbb {D})\bigr ]\subsetneq \mathcal {F}(\mathbb {D})\) by [3, Theorem 1.1, p. 844] for any non-trivial jointly continuous holomorphic semicocycle \((\mathbb {1},\varphi )\) for \(\mathcal {F}(\Omega )\) such that \(C_{\mathbb {1},\varphi }(t)\in \mathcal {L}(\mathcal {F}(\mathbb {D}))\) for all \(t\ge 0\). The weighted version is given in [39, Theorem 4.1, p. 74].
In the case \(\mathcal {F}(\mathbb {D})=H^{\infty }\) it holds \(\mathcal {A}\subset \bigl [(\mathbb {1},\varphi ),H^{\infty }\bigr ]\) by [3, Corollary 1.4, p. 844] for any jointly continuous holomorphic \(\varphi \), and \(\mathcal {A}\ne \bigl [(\mathbb {1},\varphi ),H^{\infty }\bigr ]\) for some \(\varphi \) by [3, Proposition 4.3, p. 852] where \(\mathcal {A}\) is the disc-algebra of holomorphic functions on \(\mathbb {D}\) that extend continuously to \(\overline{\mathbb {D}}\). If \(\varphi \) consists of rotations or dilations, then \(\mathcal {A}=\bigl [(\mathbb {1},\varphi ),H^{\infty }\bigr ]\) by [3, Proposition 4.1, p. 850].
Further, we have \(\bigl [(\mathbb {1},\varphi ),\mathcal {B}_{\alpha }\bigr ]\subsetneq \mathcal {B}_{\alpha }\) for \(\alpha >0\) and any non-trivial jointly continuous holomorphic semicocycle \((\mathbb {1},\varphi )\) for \(\mathcal {B}_{\alpha }\) such that \(C_{\mathbb {1},\varphi }(t)\in \mathcal {L}(\mathcal {B}_{\alpha })\) for all \(t\ge 0\) by [12, Theorem 3, p. 73]. In the case \(\alpha =1\) it holds \(\mathcal {B}_{0}\subset \bigl [(\mathbb {1},\varphi ),\mathcal {B}_{1}\bigr ]\) for any \(\varphi \) by [12, p. 73], and \(\mathcal {B}_{0}=\bigl [(\mathbb {1},\varphi ),\mathcal {B}_{1}\bigr ]\) if and only if the resolvent operator \(R(\lambda ,A)\in \mathcal {L}(\mathcal {B}_{1})\) is weakly compact on \(\mathcal {B}_{0}\) by [12, Corollary 1, p. 76] where \(\mathcal {B}_{0}\) is the little Bloch space of \(\mathcal {B}_{1}\), i.e. the space consisting of all \(f\in \mathcal {B}_{1}\) such that  . The assertion \(\mathcal {B}_{0}=\bigl [(\mathbb {1},\varphi ),\mathcal {B}_{1}\bigr ]\) is also equivalent to \(\varphi \) being elliptic and its generator G fulfilling the logarithmic vanishing Bloch condition by [19, Theorem 1.1, p. 4].
. The assertion \(\mathcal {B}_{0}=\bigl [(\mathbb {1},\varphi ),\mathcal {B}_{1}\bigr ]\) is also equivalent to \(\varphi \) being elliptic and its generator G fulfilling the logarithmic vanishing Bloch condition by [19, Theorem 1.1, p. 4].
Data Availability
No datasets were generated or analysed during the current study.
Notes
The multiplier space is defined as \(\mathcal {M}_{0}(\mathcal {F}(\Omega )):=\{g:\Omega \rightarrow \mathbb {K}\;|\;\forall \;f\in \mathcal {F}(\Omega ):\;gf\in \mathcal {F}(\Omega )\}\) in [14, p. 272] Thus we have \(\mathcal {M}(\mathcal {F}(\Omega ))\subset \mathcal {M}_{0}(\mathcal {F}(\Omega ))\). If \(\mathbb {1}\in \mathcal {F}(\Omega )\), then we even have \(\mathcal {M}(\mathcal {F}(\Omega ))=\mathcal {M}_{0}(\mathcal {F}(\Omega ))\) because \(\mathcal {F}(\Omega )\subset \mathcal {C}(\Omega )\). We incorporated continuity in the definition of our multiplier space since our semicocycles are by definition continuous.
References
Abate, M.: Iteration Theory of Holomorphic Maps on Taut Manifolds. Research and Lecture Notes in Mathematics. Mediterranean Press, Rende (1989)
Aliprantis, C.D., Border, K.C.: Infinite Dimensional Analysis: A Hitchhiker’s Guide, 3rd edn. Springer, Berlin (2006). https://doi.org/10.1007/3-540-29587-9
Anderson, A., Jovovic, M., Smith, W.: Composition semigroups on BMOA and \(H^{\infty }\). J. Math. Anal. Appl. 449(1), 843–852 (2017). https://doi.org/10.1016/j.jmaa.2016.12.032
Arendt, W., Chalendar, I.: Generators of semigroups on Banach spaces inducing holomorphic semiflows. Isr. J. Math. 229(1), 165–179 (2019). https://doi.org/10.1007/s11856-018-1793-y
Arévalo, I., Oliva, M.: Semigroups of weighted composition operators in spaces of analytic functions (2017). arXiv preprint arXiv:1706.09001v1
Batty, C.J.K.: Derivations on the line and flows along orbits. Pac. J. Math. 126(2), 209–225 (1987). https://doi.org/10.2140/pjm.1987.126.209
Bayart, F.: Hardy spaces of Dirichlet series and their composition operators. Monatsh. Math. 136(3), 203–236 (2002). https://doi.org/10.1007/s00605-002-0470-7
Bayart, F., Castillo-Medina, J., García, D., Maestre, M., Sevilla-Peris, P.: Composition operators on spaces of double Dirichlet series. Rev. Mat. Complut. 34(1), 215–237 (2021). https://doi.org/10.1007/s13163-019-00345-8
Berenstein, C.A., Gay, R.: Complex Analysis and Special Topics in Harmonic Analysis. Springer, New York (1995). https://doi.org/10.1007/978-1-4613-8445-8
Berkson, E., Porta, H.: Semigroups of analytic functions and composition operators. Mich. Math. J. 25(1), 101–115 (1978). https://doi.org/10.1307/mmj/1029002009
Bernard, E.: Weighted composition semigroups on Banach spaces of holomorphic functions. Arch. Math. (Basel) 119(2), 167–178 (2022). https://doi.org/10.1007/s00013-022-01738-w
Blasco, O., Contreras, M.D., Díaz-Madrigal, S., Martínez, J., Papadimitrakis, M., Siskakis, A.G.: Semigroups of composition operators and integral operators in spaces of analytic functions. Ann. Acad. Sci. Fenn. Math. 38, 67–89 (2013). https://doi.org/10.5186/aasfm.2013.3806
Bracci, F., Contreras, M.D., Díaz-Madrigal, S.: Continuous Semigroups of Holomorphic Self-Maps of the Unit Disc. Springer Monographs in Mathematics. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-36782-4
Brown, L., Shields, A.L.: Cyclic vectors in the Dirichlet space. Trans. Am. Math. Soc. 285(1), 269–303 (1984). https://doi.org/10.1090/S0002-9947-1984-0748841-0
Buchwalter, H.: Produit topologique, produit tensoriel et \(c\)-replétion. In: Colloque d’analyse fonctionnelle (Bordeaux, 1971), number 31–32 in Bull. Soc. Math. France, Mém., pp. 51–71. Soc. Math. France, Paris, (1972). https://doi.org/10.24033/msmf.65
Budde, C., Farkas, B.: Intermediate and extrapolated spaces for bi-continuous operator semigroups. J. Evol. Equ. 19(2), 321–359 (2019). https://doi.org/10.1007/s00028-018-0477-8
Chalendar, I., Partington, J.R.: Semigroups of weighted composition operators on spaces of holomorphic functions. In: Mashreghi, J. (ed.) Lectures on Analytic Function Spaces and their Applications, Volume 39 of Fields Institute Monographs, Chapter 7, pp. 255–281. Springer, Cham (2023). https://doi.org/10.1007/978-3-031-33572-3_7
Chalendar, I., Partington, J.R.: Weighted composition operators on the Fock space: iteration and semigroups. Acta Sci. Math. (Szeged) 89(1–2), 93–108 (2023). https://doi.org/10.1007/s44146-023-00056-z
Chalmoukis, N., Daskalogiannis, V.: Holomorphic semigroups and Sarason’s characterization of vanishing mean oscillation. Rev. Mat. Iberoam. (2022). https://doi.org/10.4171/RMI/1346
Chernoff, P.R.: Semi-groups of maps in a locally compact space. Proc. Am. Math. Soc. 53(2), 318–320 (1975). https://doi.org/10.1090/S0002-9939-1975-0448406-4
Contreras, M.D., Gómez-Cabello, C., Rodríguez-Piazza, L.: Semigroups of composition operators on Hardy spaces of Dirichlet series. J. Funct. Anal. 285, 1–36 (2023). https://doi.org/10.1016/j.jfa.2023.110089
Cooper, J.B.: Saks Spaces and Applications to Functional Analysis. North-Holland Mathematics Studies, vol. 28. North-Holland, Amsterdam (1978)
Daskalogiannis, V., Galanopoulos, P.: Semigroups of composition operators and integral operators in BMOA-type spaces. Complex Anal. Oper. Theory 15(8), 1–30 (2021). https://doi.org/10.1007/s11785-021-01168-6
Dorroh, J.R.: Semi-groups of maps in a locally compact space. Can. J. Math. 19, 688–696 (1967). https://doi.org/10.4153/CJM-1967-063-3
Dorroh, J.R., Neuberger, J.W.: Lie generators for semigroups of transformations in a Polish space. Electron. J. Differ. Equ. 1993(1), 1–7 (1993)
Dorroh, J.R., Neuberger, J.W.: A theory of strongly continuous semigroups in terms of Lie generators. J. Funct. Anal. 136(1), 114–126 (1996). https://doi.org/10.1006/jfan.1996.0023
Dunford, N., Schwartz, J.T.: Linear Operators, Part 1: General Theory. Pure and Applied Mathematics, vol. 7. Wiley, New York (1958)
Duren, P.L.: Theory of \(H^{p}\) Spaces. Pure and Applied Mathematics (Amsterdam), vol. 38. Academic Press, New York (1970)
Duren, P.L., Romberg, B.W., Shields, A.L.: Linear functionals on \(H^p\) spaces with \(0<p<1\). J. Reine Angew. Math. 238, 32–60 (1969). https://doi.org/10.1515/crll.1969.238.32
Eisner, T., Farkas, B., Haase, M., Nagel, R.: Operator Theoretic Aspects of Ergodic Theory. Graduate Texts in Mathematics, vol. 272. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-16898-2
Elin, M., Jacobzon, F., Katriel, G.: Continuous and holomorphic semicocycles in Banach spaces. J. Evol. Equ. 19(4), 1199–1221 (2019). https://doi.org/10.1007/s00028-019-00509-5
Elstrodt, J.: Maß- und Integrationstheorie. Grundwissen Mathematik, 7th edn. Springer, Berlin (2011). https://doi.org/10.1007/978-3-642-17905-1
Engel, K.-J., Nagel, R.: One-Parameter Semigroups for Linear Evolution Equations. Graduate Texts in Mathematics, vol. 194. Springer, New York (2000). https://doi.org/10.1007/b97696
Farkas, B.: Perturbations of Bi-continuous Semigroups. Ph.D. thesis, Eötvös Loránd University, Budapest (2003)
Farkas, B.: Adjoint bi-continuous semigroups and semigroups on the space of measures. Czech. Math. J. 61(2), 309–322 (2011). https://doi.org/10.1007/s10587-011-0076-0
Farkas, B., Kreidler, H.: Towards a Koopman theory for dynamical systems on completely regular spaces. Philos. Trans. R. Soc. A 378(2185), 1–15 (2020). https://doi.org/10.1098/rsta.2019.0617
Federico, S., Rosestolato, M.: \(C_0\)-sequentially equicontinuous semigroups. Kyoto J. Math. 60, 1131–1175 (2020). https://doi.org/10.1215/21562261-2019-0010
Gallardo-Gutiérrez, E.A., Yakubovich, D.V.: On generators of \(C_0\)-semigroups of composition operators. Isr. J. Math. 229(1), 487–500 (2019). https://doi.org/10.1007/s11856-018-1815-9
Gallardo-Gutiérrez, E.A., Siskakis, A.G., Yakubovich, D.: Generators of \(C_0\)-semigroups of weighted composition operators. Isr. J. Math. 255(1), 63–80 (2023). https://doi.org/10.1007/s11856-022-2389-0
Gradshteyn, I.S., Ryzhik, I.M.: Table of Integrals, Series, and Products, 8th edn. Academic Press, Amsterdam (2014). https://doi.org/10.1016/C2010-0-64839-5. Edited by D. Zwillinger and V. Moll
Hornor, W.E.: Semigroups of holomorphic self-maps of domains and one-parameter semigroups of isometries of Bergman spaces. Mich. Math. J. 51(2), 305–325 (2003). https://doi.org/10.1307/mmj/1060013198
Hurewicz, W.: Lectures on Ordinary Differential Equations, 2nd edn. MIT Press, Cambridge (1970)
Jafari, F., Tonev, T., Toneva, E., Yale, K.: Holomorphic flows, cocycles, and coboundaries. Mich. Math. J. 44(2), 239–253 (1997). https://doi.org/10.1307/mmj/1029005702
Jafari, F., Tonev, T., Toneva, E.: Automatic differentiability and characterization of cocycles of holomorphic flows. Proc. Am. Math. Soc. 133(11), 3389–3394 (2005). https://doi.org/10.1090/S0002-9939-05-07904-9
Komatsu, H.: Semi-groups of operators in locally convex spaces. J. Math. Soc. Jpn. 16(3), 230–262 (1964). https://doi.org/10.2969/jmsj/01630230
Kōmura, T.: Semigroups of operators in locally convex spaces. J. Funct. Anal. 2(3), 258–296 (1968). https://doi.org/10.1016/0022-1236(68)90008-6
König, W.: Semicocycles and weighted composition semigroups on \(H^p\). Mich. Math. J. 37(3), 469–476 (1990). https://doi.org/10.1307/mmj/1029004204
Kraaij, R.: Strongly continuous and locally equi-continuous semigroups on locally convex spaces. Semigroup Forum 92(1), 158–185 (2016). https://doi.org/10.1007/s00233-015-9689-1
Kruse, K.: Mixed topologies on Saks spaces of vector-valued functions. Topol. Appl. 345, 1–27 (2024). https://doi.org/10.1016/j.topol.2024.108843
Kruse, K., Schwenninger, F.L.: On equicontinuity and tightness of bi-continuous semigroups. J. Math. Anal. Appl. 509(2), 1–27 (2022). https://doi.org/10.1016/j.jmaa.2021.125985
Kruse, K., Seifert, C.: Final state observability and cost-uniform approximate null-controllability for bi-continuous semigroups. Semigroup Forum 106(2), 421–443 (2023). https://doi.org/10.1007/s00233-023-10346-1
Kruse, K., Seifert, C.: A note on the Lumer–Phillips theorem for bi-continuous semigroups. Z. Anal. Anwend. 41(3/4), 417–437 (2023). https://doi.org/10.4171/ZAA/1709
Kruse, K., Meichsner, J., Seifert, C.: Subordination for sequentially equicontinuous equibounded \(C_0\)-semigroups. J. Evol. Equ. 21(2), 2665–2690 (2021). https://doi.org/10.1007/s00028-021-00700-7
Kühnemund, F.: Bi-continuous semigroups on spaces with two topologies: Theory and applications. Ph.D. thesis, Eberhard-Karls-Universität Tübingen (2001)
Kühnemund, F.: A Hille–Yosida theorem for bi-continuous semigroups. Semigroup Forum 67(2), 205–225 (2003). https://doi.org/10.1007/s00233-002-5000-3
Kunze, M.: Continuity and equicontinuity of semigroups on norming dual pairs. Semigroup Forum 79(3), 540–560 (2009). https://doi.org/10.1007/s00233-009-9174-9
MacCluer, B.D., Shapiro, J.H.: Angular derivatives and compact composition operators on the Hardy and Bergman spaces. Can. J. Math. 38(4), 878–906 (1986). https://doi.org/10.4153/CJM-1986-043-4
Martín, M.J., Vukotić, D.: Norms and spectral radii of composition operators acting on the Dirichlet space. J. Math. Anal. Appl. 304(1), 22–32 (2005). https://doi.org/10.1016/j.jmaa.2004.09.005
Michael, E.A.: On \(k\)-spaces, \(k_{R}\)-spaces and \(k(X)\). Pac. J. Math. 47(2), 487–498 (1973). https://doi.org/10.2140/pjm.1973.47.487
Montes-Rodríguez, A.: Weighted composition operators on weighted Banach spaces of analytic functions. J. Lond. Math. Soc. (2) 61(2), 872–884 (2000). https://doi.org/10.1112/S0024610700008875
Parry, W.: Cocycles and velocity changes. J. Lond. Math. Soc. (2) 5(3), 511–516 (1972). https://doi.org/10.1112/jlms/s2-5.3.511
Pazy, A.: Semigroups of Linear Operators and Applications to Partial Differential Equations. Applied Mathematical Sciences, vol. 44. Springer, New York (1983). https://doi.org/10.1007/978-1-4612-5561-1
Perlich, L.: Dirichlet-to-Robin operators via composition semigroups. Complex Anal. Oper. Theory 13(3), 819–837 (2019). https://doi.org/10.1007/s11785-018-0806-5
Queffelec, H., Queffelec, M.: Diophantine Approximation and Dirichlet Series, 2nd edn. Texts Read. Math. 80. Springer, Singapore (2020). https://doi.org/10.1007/978-981-15-9351-2
Robinson, D.W.: Smooth cores of Lipschitz flows. Publ. Res. Inst. Math. Sci. 22(4), 659–669 (1986). https://doi.org/10.2977/PRIMS/1195177626
Sentilles, F.D.: Semigroups of operators in \(C(S)\). Can. J. Math. 22(1), 47–54 (1970). https://doi.org/10.4153/CJM-1970-006-8
Singh, R.K., Summers, W.H.: Composition operators on weighted spaces of continuous functions. J. Aust. Math. Soc. (Ser. A) 45(3), 303–319 (1988). https://doi.org/10.1017/S1446788700031013
Siskakis, A.G.: Weighted composition semigroups on Hardy spaces. Linear Algebra Appl. 84, 359–371 (1986). https://doi.org/10.1016/0024-3795(86)90327-7
Siskakis, A.G.: Semigroups of composition operators on Bergman spaces. Bull. Austral. Math. Soc. 35(3), 397–406 (1987). https://doi.org/10.1017/S0004972700013381
Siskakis, A.G.: Semigroups of composition operators on the Dirichlet space. Results Math. 30(1–2), 165–173 (1996). https://doi.org/10.1007/BF03322189
Siskakis, A.G.: Semigroups of composition operators on spaces of analytic functions, a review. In: F. Jafari, B.D. MacCluer, C.C. Cowen, A.D. Porter (eds) Studies on Composition Operators (Proc., Laramie, 1996), volume 213 of Contemp. Math., pp. 229–252. AMS, Providence (1998). https://doi.org/10.1090/conm/213
Snipes, R.F.: C-sequential and S-bornological topological vector spaces. Math. Ann. 202(4), 273–283 (1973). https://doi.org/10.1007/BF01433457
Stegenga, D.A.: Multipliers of the Dirichlet space. Ill. J. Math. 24(1), 113–139 (1980). https://doi.org/10.1215/ijm/1256047800
Vidal, T.F., Galicer, D., Sevilla-Peris, P.: Multipliers for Hardy spaces of Dirichlet series (2022). arXiv preprint arXiv:2205.07961v1
Wilansky, A.: Mazur spaces. Int. J. Math. Math. Sci. 4(1), 39–53 (1981). https://doi.org/10.1155/S0161171281000021
Wiweger, A.: Linear spaces with mixed topology. Stud. Math. 20(1), 47–68 (1961). https://doi.org/10.4064/sm-20-1-47-68
Wu, F.: Weighted composition semigroups on some Banach spaces. Complex Anal. Oper. Theory 15(8), 1–14 (2021). https://doi.org/10.1007/s11785-021-01158-8
Xiao, J.: Composition operators associated with Bloch-type spaces. Complex Var. Theory Appl. 46(2), 109–121 (2001). https://doi.org/10.1080/17476930108815401
Yosida, K.: Functional Analysis. Grundlehren Math. Wiss., vol. 123, 2nd edn. Springer, Berlin (1968). https://doi.org/10.1007/978-3-642-96439-8
Zhu, K.: Bloch type spaces of analytic functions. Rocky Mt. J. Math. 23(3), 1143–1177 (1993). https://doi.org/10.1216/rmjm/1181072549
Zhu, K.: Operator Theory in Function Spaces. Math. Surveys Monogr., vol. 138, 2nd edn. AMS, Providence (2007). https://doi.org/10.1090/surv/138
Author information
Authors and Affiliations
Contributions
K.K. wrote the manuscript and prepared the presented material fully by himself.
Corresponding author
Ethics declarations
Conflict of interest
The author has no relevant financial or non-financial interests to disclose.
Additional information
Communicated by Mamadou Mboup.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
K. Kruse acknowledges the support by the Deutsche Forschungsgemeinschaft (DFG) within the Research Training Group GRK 2583 “Modeling, Simulation and Optimization of Fluid Dynamic Applications”.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kruse, K. Weighted Composition Semigroups on Spaces of Continuous Functions and Their Subspaces. Complex Anal. Oper. Theory 18, 115 (2024). https://doi.org/10.1007/s11785-024-01559-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11785-024-01559-5



 for all
for all 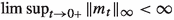 .
. ,
,  and
and  ,
, ,
, ,
, and
and 

 for all
for all  for all
for all 
 for all
for all  in the definition of
in the definition of  .
. , then
, then 
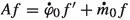 for all
for all 
 for all
for all 
 ,
,  , then
, then  and
and 
 for all
for all  and the generator (A, D(A)) of
and the generator (A, D(A)) of 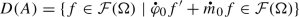
 for all
for all  and
and 