Abstract
We use methods from nonstandard analysis to unify and extend results from the theory of asymptotic fixed points on metric spaces. Among the topics we consider are Kirk’s asymptotic fixed point theorem with extensions, Boyd and Wong’s fixed point theorem, and Suzuki’s fixed point theorem for asymptotic contractions of the Meier–Keeler type. We also show how Suzuki’s asymptotic contractions of the final type can be modified to yield uniform convergence on compact and bounded sets.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
There is by now a large number of papers on asymptotic results in fixed point theory, many of them inspired by Kirk’s seminal paper [29]. The arguments in these papers are often long and complicated, and the purpose of the present paper is to demonstrate that nonstandard analysis provides a powerful method for unifying and simplifying many of the results.
The paper takes two parts. In the first part, we look at what might be called extrinsic fixed point theorems; results where the local contractive behavior of a function T is measured by external functions (\(\phi \), or a family \(\phi _n\)). We give a nonstandard proof of an extension of Kirk’s asymptotic fixed point theorem and then turn to some related questions, including Boyd and Wong’s [10] classic generalization of Banach’s fixed theorem and Suzuki’s [39] fixed point theorem for contractions of the Meier–Keeler type.
In the second part, we consider intrinsic conditions on the function T which lead to the existence of a fixed point. We begin with a closer look at Suzuki’s [40] asymptotic contractions of the final type (ACFs). We first give a simplified proof of his result that the ACF conditions are equivalent to the existence of an iterative fixed point, and then show how the conditions can be strengthened to guarantee stronger forms of convergence such as uniform convergence on bounded and compact sets.
The use of nonstandard analysis in fixed point theory is by no means new, see e.g. Baratella and Ng [9], Wiśnicki [41,42,43,44], and (in other contexts) Leth [34] and Živaljević [45]. It should also be pointed out that the ultraproduct approach to fixed point theorems initiated by Maurey [35] (see also Aksoy and Khamsi [1]) is very close to the nonstandard approach in spirit, although it technically may look quite different as it does not exploit the same machinery from mathematical logic. (In the fixed point literature, the term “nonstandard” often refers to ultraproduct methods and not to nonstandard analysis). In fact, Kirk’s original argument in [29] uses an essentially nonstandard argument, embedding a space into what in nonstandard analysis is called the nonstandard hull of a Banach space. The approach we take in this paper is more direct as we only need to work with the original metric space.
We shall only need a small fragment of nonstandard analysis, basically the nonstandard theory of real numbers and metric spaces. The elementary parts of introductions such as Goldblatt [23] and Arkeryd et al. [8] will do. Other suggested references are Albeverio et al. [2], Cutland [19, 20], Davis [21], and Hurd and Loeb [24]. For the convenience of the reader we have collected some of the more technical nonstandard results we need in the last section.
1 Extrinsic fixed point theorems
In 2003 Art Kirk [29] formulated and proved an asymptotic version of a metric space fixed point theorem of Boyd and Wong ([10]; see also Sect. 1.3 below). Kirk’s paper gave rise to a large number of variations and generalizations, see for example Arandelović [3], Arav et al. [4, 5], Chen [18], Hussain and Khamsi [25], Jachymski [26, 27], Kikkawa and Suzuki [28], Kirk and Xu [30], Leader [33], Reich and Zaslavski [36], and Suzuki [39, 40]. A particularly interesting development is the use of methods from “proof mining” (see [31]) to extract constructive proofs with explicit rates of (uniform) convergence from nonconstructive existence proofs, see, e.g., the papers by Gerhardy [22], Briseid [11,12,13,14,15,16], and Ariza-Ruiz et al [6].
We shall now describe some simple machinery by which asymptotic fixed points theorems can be proved. The advantages of our machinery are that the conditions are simple and intuitive, and the proofs short and straightforward. The disadvantage is that it requires nonstandard analysis.
1.1 Kirk’s theorem and extensions
We begin by specifying the kind of fixed points we are looking for:
Definition 1.1
Let T be a continuous function from a metric space X to itself. We say that \(x_{\infty }\in X\) is an iterative fixed point for T if
-
(i)
\(T(x_{\infty })=x_{\infty }\), and
-
(ii)
For every \(x\in X, \lim \nolimits _{n\rightarrow \infty }T^nx=x_\infty \).
Note that an iterative fixed point is necessarily a unique fixed point.
We next introduce the conditions we are going to work with for most of the first part of the paper.
Definition 1.2
Say that \(X, d, T, \phi _n\), and \(\phi \) satisfy the usual hypotheses provided
-
(i)
(X, d) is a complete metric space,
-
(ii)
\(T:X\rightarrow X\) is continuous,
-
(iii)
\(\phi , \phi _n:[0,\infty )\rightarrow [0,\infty )\),
-
(iv)
\(\phi _n\) converges to \(\phi \) on the range of d,
-
(v)
\(\phi \) is (upper) semicontinuous with \(\phi (0)=0\) and \(\phi (s)<s\) for \(s>0\), and
-
(vi)
\(d(T^nx,T^ny)\le \phi _n(d(x,y))\) for all \(x,y\in X\) and \(n\in {\mathbb {N}}\).
The seminal result on asymptotic fixed points is the following 2003 result of Kirk [29].
Theorem 1.3
Suppose that \(X, d, T, \phi _n\), and \(\phi \) satisfy the usual hypotheses, that the functions \(\phi _n\) and \(\phi \) are continuous, and that \(\phi _n\) converges to \(\phi \) uniformly on the range of d. Suppose moreover that T has a bounded orbit, that is, for some z the sequence \(\{T^n(z)\}_n\) is bounded. Then T has an iterative fixed point \(x_\infty \).
Remark
In Kirk’s original treatment, the condition that T is continuous was inadvertently left out. Since Kirk’s paper there have been numerous extensions and generalizations of the result above. Some of these are summarized in Corollary 1.10 below; mostly they involve dropping some of the continuity conditions, or weakening some of the boundedness conditions. More notably, Suzuki [39] showed that the condition of a bounded orbit is unnecessary and that the continuity conditions on \(\phi \) and \(\phi _n\) can be weakened. Suzuki’s approach is first to show that all asymptotic contractions are actually asymptotic contractions of the Meier–Keeler type (ACMKs), and then prove that all ACMKs have iterative fixed points. We shall instead give a direct proof of (an extension of) Kirk’s theorem in this section, and an independent proof of the fixed point theorem for ACMKs in Sect. 1.4. Let us also mention that using estimates from Gerhardy’s paper [22], Briseid [12] has given a constructive proof of Kirk’s theorem without the boundedness condition and with estimates for the rates of convergence.
In this section we will prove Kirk’s theorem without the boundedness condition and without the continuity conditions on \(\phi _n\) and \(\phi \):
Theorem 1.4
Suppose that \(X, d, T, \phi _n\), and \(\phi \) satisfy the usual hypotheses, and that \(\phi _n\) converges to \(\phi \) uniformly on the range of d. Then T has an iterative fixed point \(x_\infty \).
(We shall see later that even the condition on uniform convergence can be weakened somewhat.)
Unless otherwise indicated, X will always denote a complete metric space with metric d. If  , x is finite provided d(x, y) is finite for some standard \(y\in X\) (equivalently, for all standard y in X).Footnote 1
, x is finite provided d(x, y) is finite for some standard \(y\in X\) (equivalently, for all standard y in X).Footnote 1
We begin with a condition sufficient for any continuous function on X to have an iterative fixed point.
Proposition 1.5
Let T be a continuous function from a complete metric space X to itself. Suppose that for every x and y in X,

Then T has an iterative fixed point \(x_\infty \). Moreover, if (1.1) is true for all x in X and all finite y in  , then the convergence of \(T^nx\) is uniform on bounded subsets of X.
, then the convergence of \(T^nx\) is uniform on bounded subsets of X.
The converse to the first part of the proposition is easily seen to be true. There are some obvious/trivial generalizations, for example continuity of T can be replaced by continuity of \(T^m\) for some standard m, or even continuity of \(T^m\) at \(x_\infty \).
Call any points x and y eventually close if they satisfy condition (1.1) from this proposition.
Proof
Take \(x=y\in X\), this shows that \(\{T^nx\}_n\) is Cauchy, so by completeness converges to some \(x_\infty \). From continuity of T, \(T(x_\infty )=\lim \nolimits _{n\rightarrow \infty }T(T^nx)=\lim \nolimits _{n\rightarrow \infty }T^{n+1}x=x_\infty \), so \(x_\infty \) is a fixed point. Eventual closeness means that all such orbits converge to the same limit, so the fixed point is unique. Finally, let Y be a bounded subset of X, \(x\in X\),  , and i infinite. Then \(d(T^ix,T^iy)\approx 0\), so \(T^iy\approx T^ix\approx x_\infty \). By the nonstandard characterization of uniform convergence (see Proposition 3.1), this means that the convergence is uniform on Y. \(\square \)
, and i infinite. Then \(d(T^ix,T^iy)\approx 0\), so \(T^iy\approx T^ix\approx x_\infty \). By the nonstandard characterization of uniform convergence (see Proposition 3.1), this means that the convergence is uniform on Y. \(\square \)
We continue with two useful results.
Proposition 1.6
Suppose that \(T:X\rightarrow X\) and that for all infinite i and x, y in X, \(d(T^ix,T^iy)\approx 0\). Then:
-
1.
For all infinite \(i<j\) and x, y, z, w in X, \(d(T^ix,T^jy)\approx d(T^iz,T^jw)\).
-
2.
For all finite n, infinite i, and x in X, \(d(T^ix,T^{i+n}x)\approx 0\).
-
3.
For all finite m, n, infinite i, j, and x, y in X, \(d(T^{i+m}x,T^{j+n}y)\approx d(T^ix,T^jy)\).
Proof
For (1), \(d(T^ix, T^jy)\le d(T^iz, T^jw)+d(T^ix, T^iz)+d(T^jw, T^jy)\lessapprox d(T^iz, T^jw)\) by hypothesis. The opposite inequality follows by symmetry. (2) follows from the hypothesis by taking \(y=T^nx\). (3) follows from (1) by taking \(z=T^mx, w=T^ny\). \(\square \)
Here \(s\lessapprox t\) means that \(s<t\) or \(s\approx t\). Later we will use \(s\lnapprox t\) to mean that \(s<t\) and \(s\not \approx t\).
The next lemma extracts a basic argument from Boyd and Wong’s original proof of Theorem 1.12 (below).
Lemma 1.7
Suppose that the hypotheses of Proposition 1.6 hold. For all infinite \(i<j\), x, y in X, and hyperreal \(\gamma \), if \(0\lnapprox \gamma \lnapprox d(T^ix,T^jy)\) then there is an infinite k, \(i<k<j\), with \(\gamma \approx d(T^kx,T^jy)\).
Proof
Let k be the greatest hyperinteger in [i, j] with \(\gamma < d(T^kx,T^jy)\). Then \(d(T^{k+1}x,T^jy)\le \gamma <d(T^kx,T^jy)\le d(T^{k+1}x,T^jy)+d(T^kx,T^{k+1}x)\lessapprox d(T^{k+1}x,T^jy)\) by Proposition 1.6, since k is infinite. \(\square \)
Note that in the proof we also have that \(\gamma <d(T^kx,T^jy)\); this will be used in the proof of Theorem 1.12.
Proof of Theorem 1.4
By Proposition 1.5, it suffices to show that for any x, y in X and any infinite i and j, \(d(T^ix,T^jy)\approx 0\). We start with three claims:
Claim 1
For all \(x\ne y\) in X and infinite i, \(d(T^ix,T^iy)\le d(x,y)\). (In particular, \(d(T^ix,T^iy)\) is finite.) This follows since:
Claim 2
For all \(x\ne y\) in X and infinite i, \(d(T^ix,T^iy)\approx 0\).
To see this, let  , which exists by Claim 1. Suppose (for a contradiction) that \(\gamma >0\). Then there is an infinite i with \(d(T^ix,T^iy)\approx \gamma \) (Proposition 3.1). By Proposition 3.1 there exist infinite
, which exists by Claim 1. Suppose (for a contradiction) that \(\gamma >0\). Then there is an infinite i with \(d(T^ix,T^iy)\approx \gamma \) (Proposition 3.1). By Proposition 3.1 there exist infinite  with \(j+k=i\). Then:
with \(j+k=i\). Then:

a contradiction. (For the strict inequality in the last line we used the fact that  , which follows since otherwise \(\gamma =0\).) So \(\gamma =0\), proving Claim 2.
, which follows since otherwise \(\gamma =0\).) So \(\gamma =0\), proving Claim 2.
Claim 3
For all \(x\ne y\) in X and infinite i and j, there is an infinite n with \(d(T^ix, T^jy)\approx d(T^{i+n}x,T^{j+n}y)\).
Indeed, by Claim 2 and Proposition 1.6, for any finite n we have \(d(T^ix,T^jy)\approx d(T^{i+n}x,T^{j+n}y)\), so that
for every finite n. The claim now follows by overspill (Proposition 3.1).
Now, let x, y be elements of X, and i, j be infinite. Suppose for a contradiction that \(d(T^ix,T^jy)\not \approx 0\). Then \(x\ne y\), we may assume for definiteness that \(i<j\), and there is a standard \(\gamma \) with \(0\lnapprox \gamma \lnapprox d(T^ix,T^jy)\). By Claim 2 and Lemma 1.7 there is some k, \(i<k<j\), with \(\gamma \approx d(T^kx,T^jy)\). By Claim 3 there is an infinite n such that:
This is a contradiction, completing the proof. \(\square \)
1.2 Uniform convergence of the iterates
In this section we discuss conditions under which the iterates converge uniformly to the fixed point.
The following lemma is a straightforward nonstandard result about any function on any metric space.
Lemma 1.8
Let X be a metric space (not necessarily complete), and \(T:X\rightarrow X\) (not necessarily continuous). Suppose  are finite. Consider the statements:
are finite. Consider the statements:
-
(1)
For any infinite
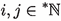 , \(d(T^ix,T^jy)\approx 0\).
, \(d(T^ix,T^jy)\approx 0\). -
(2)
The set \(\{d(T^ix,T^jy)~:~i,j \text { infinite}\}\) is bounded.
-
(3)
For any infinite
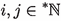 , \(d(T^ix,T^jy)\) is finite.
, \(d(T^ix,T^jy)\) is finite.
Then \(1\Rightarrow 2\Leftrightarrow 3\).
Suppose in addition that \(X, d, T, \phi _n\), and \(\phi \) satisfy the usual hypotheses, and that either
-
(a)
\(\phi _n\) converges to \(\phi \) uniformly on bounded subsets of the range of d; or
-
(b)
\(x, y\in X\), and \(\phi _n\) converges to \(\phi \) uniformly on the set
$$\begin{aligned} {\mathcal {O}}_T(x,y)=\{d(T^mx,T^ny)~:~m,n\in {\mathbb {N}}\} \end{aligned}$$
Then (1)–(3) are equivalent.
Proof
\((1\Rightarrow 2\Rightarrow 3)\) is trivial.
\((3\Rightarrow 2)\): Suppose \(\{d(T^ix,T^jy)~:~i,j \text { infinite}\}\) is not bounded. The set  is internal and contains all standard n, so by overspill (Proposition 3.1(8) it contains some infinite N, and (3) fails.
is internal and contains all standard n, so by overspill (Proposition 3.1(8) it contains some infinite N, and (3) fails.
\((2\Rightarrow 1)\): Put \(t=\sup \{{^\circ d}(T^ix,T^jy) : i,j\text { infinite }\}\). If \(t=0\) we’re done. Otherwise there are infinite i, j with \(t\approx d(T^ix,T^jy)\) (Proposition 3.1). Let \(k<i,j\) be infinite but sufficiently small that \(i-k\) and \(j-k\) are both infinite (Proposition 3.1). It follows:
Since \(0<\phi ({^\circ d}(T^{i-k}x,T^{j-k}y))\), \(\phi ({^\circ d}(T^{i-k}x,T^{j-k}y))\) (and therefore t) is strictly less than \({^\circ d}(T^{i-k}x,T^{j-k}y)\), contradicting maximality of t. \(\square \)
We can now strengthen Theorem 1.4.
Corollary 1.9
Suppose that \(X, d, T, \phi _n\), and \(\phi \) satisfy the usual hypotheses, and that either
-
(a)
\(\phi _n\) converges to \(\phi \) uniformly on bounded subsets of the range of d, or
-
(b)
\(\phi _n\) converges to \(\phi \) uniformly on sets of the form
$$\begin{aligned} {\mathcal {O}}_T(x,y)=\{d(T^mx,T^ny):m,n\in {\mathbb {N}}\} \end{aligned}$$for \(x,y\in X\).
Then T has an iterative fixed point \(x_\infty \). Moreover, if \(\phi _n\) converges to \(\phi \) uniformly on bounded subsets of the range of d, then the convergence of \(T^nx\) to \(x_\infty \) is uniform on bounded subsets of X.
Proof
For the proof of existence we examine some details in the proof of Theorem 1.4. Uniform convergence of \(\phi _n\) to \(\phi \) was only used twice (Eqs. 1.2 and 1.3), both times so that we could assume convergence on a possibly nonstandard element \(d(T^ix, T^jy)\). For standard x, y in X both d(x, y) and \(d(T^ix, T^jy)\) are in  , so both 1.2 and 1.3 still hold under hypothesis (b). If instead we assume hypothesis (a), 1.2 still holds because \(d(T^jx,T^jy)\) is in the star of the bounded set [0, d(x, y)). At 1.3, \(d(T^kx, T^jy)\) is in the star of the bounded set \([0, \gamma +1)\).
, so both 1.2 and 1.3 still hold under hypothesis (b). If instead we assume hypothesis (a), 1.2 still holds because \(d(T^jx,T^jy)\) is in the star of the bounded set [0, d(x, y)). At 1.3, \(d(T^kx, T^jy)\) is in the star of the bounded set \([0, \gamma +1)\).
It remains to prove the assertion about uniform convergence under hypothesis (a). Let x in X, y be a finite (but not necessarily standard) element of  , and let
, and let  be infinite. Then \(d(T^ix,T^jy)\le d(T^ix,T^jx)+d(T^jx,T^jy)\le d(T^ix,T^jx)+\phi _j(d(x,y))\approx d(T^ix,T^jx)+\phi (d(x,y))\) by uniform convergence of \(\phi _n\) on the bounded subset
be infinite. Then \(d(T^ix,T^jy)\le d(T^ix,T^jx)+d(T^jx,T^jy)\le d(T^ix,T^jx)+\phi _j(d(x,y))\approx d(T^ix,T^jx)+\phi (d(x,y))\) by uniform convergence of \(\phi _n\) on the bounded subset  of \({\text {range}}(d)\). Also, \(d(T^ix,T^jx)\approx 0\) by the first part of this proof (since x is standard), and
of \({\text {range}}(d)\). Also, \(d(T^ix,T^jx)\approx 0\) by the first part of this proof (since x is standard), and  by semicontinuity of \(\phi \), so \(d(T^ix,T^jy)<\infty \), and the conclusion follows from Lemma 1.8 and Proposition 1.5. \(\square \)
by semicontinuity of \(\phi \), so \(d(T^ix,T^jy)<\infty \), and the conclusion follows from Lemma 1.8 and Proposition 1.5. \(\square \)
Arandelović [3, Theorem 1] has collected some (standard) extensions of Kirk’s theorem into a result which we can now see as an easy consequence of this result.
Corollary 1.10
Suppose that \(X, d, T, \phi _n\), and \(\phi \) satisfy the usual hypotheses, and that for all \(x, y\in X\), \(\phi _n\) converges to \(\phi \) uniformly on bounded subsets of the range of d. Suppose that any of the following additional hypotheses hold:
-
(i)
T has a bounded orbit,
-
(ii)
\(\liminf \nolimits _{t\rightarrow \infty }(t-\phi (t))>0\), or
-
(iii)
\(\limsup \nolimits _{t\rightarrow \infty }\frac{\phi (t)}{t}<1\).
Then T has an iterative fixed point \(x_\infty \). Moreover, the convergence of \(T^nx\) to \(x_\infty \) is uniform on bounded subsets of X.
The proof is by ignoring conditions (i)–(iii).
To prove uniformity of the convergence Arandelović uses in his proof the following result of Arav, Santos, Reich and Zaslavski [4]:
Proposition 1.11
Suppose that \(X, d, T, \phi _n\), and \(\phi \) satisfy the usual hypotheses, and that \(\phi _n\) converges to \(\phi \) uniformly on bounded intervals [0, b). If there exists a fixed point \(x_\infty \in X\) then all sequences \(\{T^nx\}_n\) converge to \(x_\infty \), uniformly on bounded subsets of X.
This result also follows immediately from Corollary 1.9.
1.3 Theorem of Boyd and Wong
Kirk originally formulated his result as an asymptotic version of the following theorem of Boyd and Wong [10].
Theorem 1.12
Suppose (X, d) is a complete metric space, \(T:X\rightarrow X\) is continuous, \(\phi :[0,\infty )\rightarrow [0,\infty )\) is upper semicontinuous from the right with \(\phi (s)<s\) for \(s>0\), and \(d(Tx,Ty)\le \phi (d(x,y))\) for all \(x,y\in X\) Then T has an iterative fixed point \(x_\infty \).
Here upper semicontinuous from the right means that for all s,
In nonstandard terms, this is easily seen to be equivalent to: for all standard s, if \(t>s\) and \(t\approx s\) then \(\phi (t)\lessapprox \phi (s)\).
In this section we give a simple nonstandard proof of Theorem 1.12. We will abstract from this in the next section to simplify and improve other results from the literature.
Proof of Theorem 1.12
Let \(s>0\) and consider the sequence \(s, \phi (s), \phi (\phi (s))=\phi ^{(2)}(s), \phi ^{(3)}(s), \dots \). This monotonically decreases to some (standard) limit t, which is less than but infinitesimally close to \(\phi ^{(i)}(s)\) for all infinite i. If \(t>0\) and i infinite then \(t>\phi (t) > rapprox \phi (\phi ^{(i)}(s))\) (by upper semicontiuity of \(\phi \) from the right) \(=\phi ^{(i+1)}(s)\approx t\), a contradiction.
Thus, for all infinite i and standard \(s>0\), \(\phi ^{(i)}(s)\approx 0\). It follows that for all infinite i and \(x,y\in X\),
We need to show that any x and y in X are eventually close. Let \(i<j\) be infinite, and suppose \(d(T^ix,T^jy)\not \approx 0\). There is then a standard positive \(\gamma \) with \(d(T^ix,T^jy)>\gamma \). By Lemma 1.7 there is an infinite k with \(d(T^kx,T^jy)\approx \gamma <d(T^kx,T^jy)\). Then
a contradiction.\(\square \)
1.4 Suzuki and ACMK
In this section we give a simple proof of Suzuki’s results [39] that asymptotic contractions of Meier–Keeler (ACMK) type have iterative fixed points. We note that Suzuki’s proof of Theorem 1.14 required a careful approximation argument. Our arguments, by contrast, are simple and straightforward adaptations of the proof of Theorem 1.12.
Recall that \(T:X\rightarrow X\) is ACMK provided there is a sequence \(\phi _n:[0,\infty )\rightarrow [0,\infty )\) such that:
- \(\textrm{ACMK}_1\):
-
\(\limsup _n\phi _n(s)\le s\) for all \(s\ge 0\).
- \(\textrm{ACMK}_2\):
-
For every \(\alpha >0\) there is a \(\delta >0\) and \(\nu \in {\mathbb {N}}\) such that \(\phi _\nu (t)\le \alpha \) for all \(t\in [\alpha ,\alpha +\delta ]\).
- \(\textrm{ACMK}_3\):
-
\(d(T^nx,T^ny)<\phi _n(d(x,y))\) for \(x\ne y\) and \(n\in {\mathbb {N}}\).
Nonstandardly, \(ACMK_1\) says that \(\phi _i(s)\lessapprox s\) for infinite i, and \(ACMK_2\) says that \(\phi _\nu \) maps the right half of monads of \(\alpha \) to the left of or equal to \(\alpha \).
Given \(\alpha \) write \(\delta _\alpha , \nu _\alpha \) for the values given in the second condition.
As with all the earlier results, we begin with a proof that \(d(T^ix,T^iy)\approx 0\) for infinite i.
Lemma 1.13
Suppose that X is complete metric and \(T:X\rightarrow X\) is ACMK. Then for all infinite i and x, y in X, \(d(T^ix,T^iy)\approx 0\).
Proof
Fix \(x\ne y\) in X. Let i be infinite and m an arbitrary but standard natural number. Then \(d(T^ix,T^iy)<\phi _{i-m}(d(T^mx,T^my))\lessapprox d(T^mx,T^my)\) by \(ACMK_1\) and the fact that \(d(T^mx,T^my)\) is standard. It follows that \(\{{^\circ d}(T^ix,T^iy): i\text { infinite}\}\) is bounded above, so has a supremum t with \(t\le d(T^mx,T^my)\). This last inequality is standard and true for all m, so by transfer it holds as well for nonstandard m. For infinite i and \(m=i+\nu _t\) note \(t\le d(T^ix,T^iy)\lessapprox t\), so \(t\le d(T^mx,T^my)<\phi _{\nu _t}(d(T^ix,T^iy))\le t\) by \(ACMK_2\), a contradiction. \(\square \)
Theorem 1.14
Suppose that X is complete metric and \(T:X\rightarrow X\) is continuous and ACMK. Then T has an iterative fixed point \(x_\infty \).
Proof
Let \(x\ne y\) be standard, \(i<j\) be infinite. Suppose for a contradiction that \(d(T^ix,T^jy)\not \approx 0\). Let \(\alpha \) be standard with \(0<\alpha \lnapprox d(T^ix,T^jy)\). Let \(\gamma \) be standard with \(\alpha <\gamma \lnapprox \min \{\alpha +\delta _\alpha , d(T^ix,T^jy)\}\). By Lemma 1.7 and Proposition 1.6 there is a k with \(\alpha<\gamma \approx d(T^kx,T^jy)<\alpha +\delta _\alpha \). Then \(\gamma \approx d(T^{k+{\nu _\alpha }}x,T^{j+{\nu _\alpha }}y)<\phi _{\nu _\alpha }(d(T^kx,T^jy))\le \alpha \lnapprox \gamma \), a contradiction. The result now follows from Proposition 1.5. \(\square \)
Remark
In [39], Suzuki showed that all asymptotic contractions are actually ACMKs, and then used the result above to prove his version of Kirk’s theorem. We could have copied this approach here to give a second nonstandard proof of Kirk’s theorem.
2 Intrinsic fixed point theorems
In the second part of the paper we shall use nonstandard analysis to study mappings such as Suzuki’s asymptotic contractions of the final type (ACFs) introduced in [40]. In this setting there are no “asymptotic moduli of contraction” \(\phi _n\) as above, and instead the conditions are put directly on the iterates \(T^n\) of the original function T. Suzuki’s main result is that a continuous map \(T:X\rightarrow X\) on a complete metric space X has an iterative fixed point if and only if it is an ACF. We first provide a simple nonstandard version of Suzuki’s proof, and then show how we can strengthen the conditions of an ACF to get stronger forms of convergence such as uniform convergence on compact and bounded sets. These result are quite close in spirit to the uniformity results Briseid has studied in the extrinsic case using proof mining techniques (see [11, 12, 16]), and it would be interesting to see if proof mining can also be used to obtain rates of convergence in the present setting.
For another extension of Suzuki’s results, see [17].
2.1 ACFs and pointwise convergence
We assume throughout that \(T:X\rightarrow X\) is a continuous function on a complete metric space X. It is possible to use our techniques to obtain results even when these conditions are not satisfied, but we want to focus on the central ideas. Let us begin with the main definition:
Definition 2.1
\(T:X\rightarrow X\) is an ACF (an asymptotic contraction of the final type) if the following conditions hold:
- \(\textrm{ACF}_1\):
-
For all \(x\in X\) and
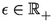 there exists a
there exists a 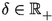 such that if \(d(T^kx,T^ky)<\delta \) for some \(y\in X\) and some \(k\in {\mathbb {N}}\), then \(\limsup _{n\rightarrow \infty } d(T^nx,T^ny)<\epsilon \).
such that if \(d(T^kx,T^ky)<\delta \) for some \(y\in X\) and some \(k\in {\mathbb {N}}\), then \(\limsup _{n\rightarrow \infty } d(T^nx,T^ny)<\epsilon \). - \(\textrm{ACF}_2\):
-
For all
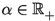 and all bounded sets \(B\subseteq X\), there exists a \(\delta >0\) such that for all \(x,y\in B\) with \(\alpha \le d(x,y)<\alpha +\delta \), there exists a \(\nu \in {\mathbb {N}}\) such that \(d(T^{\nu }x,T^{\nu }y)< \alpha \).
and all bounded sets \(B\subseteq X\), there exists a \(\delta >0\) such that for all \(x,y\in B\) with \(\alpha \le d(x,y)<\alpha +\delta \), there exists a \(\nu \in {\mathbb {N}}\) such that \(d(T^{\nu }x,T^{\nu }y)< \alpha \). - \(\textrm{ACF}_3\):
-
For all \(x\in X\) and all
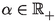 , there exist a \(\delta >0\) and a \(\nu \in {\mathbb {N}}\) such that if \(\alpha<d(T^nx,T^mx)<\alpha +\delta \) for some \(n,m\in {\mathbb {N}}\), then \(d(T^{\nu +n}x,T^{\nu +m}x)\le \alpha \).
, there exist a \(\delta >0\) and a \(\nu \in {\mathbb {N}}\) such that if \(\alpha<d(T^nx,T^mx)<\alpha +\delta \) for some \(n,m\in {\mathbb {N}}\), then \(d(T^{\nu +n}x,T^{\nu +m}x)\le \alpha \).
As we later want to strengthen these conditions to get stronger forms of convergence, we have changed Suzuki’s original definition somewhat to make the relationship between the different forms easier to see. To compare our conditions above to Suzuki’s original conditions C1–C4, note that his C4 is identical to our \(\textrm{ACF}_3\); the combination of his C2 and C3 implies our \(\textrm{ACF}_2\); and his C1 implies our \(\textrm{ACF}_1\). The reverse implications are less obvious, but the systems as a whole must still be equivalent as they are both equivalent to the existence of an iterative fixed point.
Remark
The strength of the ACF approach is that the conditions only compare the same iterates \(T^nx\) and \(T^ny\) of x and y. It’s easier to find sufficient and necessary conditions if we allow conditions on \(T^nx\) and \(T^my\) for different iterates, but such conditions are much harder to check; see Section 5 of [40] and the earlier papers [26, 33] for more information. Latif’s survey chapter [32] puts Suzuki’s contribution in the context of various kinds of generalizations of Banach’s fixed point theorem.
To prove Suzuki’s theorem, we first observe that as the existence of an iterative fixed point clearly implies \(\textrm{ACF}_1\)–\(\textrm{ACF}_3\), we may concentrate on the converse. We need four easy lemmas to prove the result.
Lemma 2.2
If \(T:X\rightarrow X\) satisfies \(\textrm{ACF}_2\), then for all \(x,y\in X\),
and hence there exists an infinite  such that \(d(T^ix,T^iy)\approx 0\).
such that \(d(T^ix,T^iy)\approx 0\).
Proof
Let
and assume for contradiction that \(\alpha \ne 0\). Choose a bounded set B containing x and y, and let  be the number guaranteed by \(\textrm{ACF}_2\). There obviously exists an \(i\in {\mathbb {N}}\) such that \(\alpha \le d(T^ix,T^iy)<\alpha +\delta \), and hence by (ii) a \(\nu \in {\mathbb {N}}\) such that \(d(T^{i+\nu }x,T^{i+\nu }y)<\alpha \), contradicting the definition of \(\alpha \).
be the number guaranteed by \(\textrm{ACF}_2\). There obviously exists an \(i\in {\mathbb {N}}\) such that \(\alpha \le d(T^ix,T^iy)<\alpha +\delta \), and hence by (ii) a \(\nu \in {\mathbb {N}}\) such that \(d(T^{i+\nu }x,T^{i+\nu }y)<\alpha \), contradicting the definition of \(\alpha \).
For the second part, note that if the infimum 0 is attained, then \(d(T^ix,T^iy)\) is zero for all infinite i, and if the infimum is not attained, the internal set

contains all positive elements of \({\mathbb {N}}\), and must by overspill (see Proposition 3.1) have infinite elements. \(\square \)
Remark
Note that the proof of Lemma 2.2 requires that \(\{T^nx\}\) and \(\{T^ny\}\) are standard sequences, and hence that x, y are standard elements. The proof doesn’t work for nonstandard elements  , not even if they are finite or nearstandard.
, not even if they are finite or nearstandard.
If we add \(\textrm{ACF}_1\), we can get the lemma above to hold for all infinite i:
Lemma 2.3
Assume that \(T:X\rightarrow X\) satisfies \(\textrm{ACF}_1\) and \(\textrm{ACF}_2\), and that \(x,y\in X\). Then \(d(T^ix,T^iy)\approx 0\) for all infinite  .
.
Proof
It clearly suffices to prove that given an  , we have \(d(T^nx,T^ny)<\epsilon \) for all infinite n. By \(\textrm{ACF}_1\) there is a
, we have \(d(T^nx,T^ny)<\epsilon \) for all infinite n. By \(\textrm{ACF}_1\) there is a  such that if there exists a k with \(d(T^kx,T^ky)<\delta \), then \(\limsup _{n\rightarrow \infty } d(T^nx,T^ny)<\epsilon \). By Lemma 2.2 there exists a finite k such that \(d(T^kx,T^ky)<\delta \), and hence \(d(T^{n}x,T^{n}y)<\epsilon \) for all infinite n. \(\square \)
such that if there exists a k with \(d(T^kx,T^ky)<\delta \), then \(\limsup _{n\rightarrow \infty } d(T^nx,T^ny)<\epsilon \). By Lemma 2.2 there exists a finite k such that \(d(T^kx,T^ky)<\delta \), and hence \(d(T^{n}x,T^{n}y)<\epsilon \) for all infinite n. \(\square \)
Lemma 2.4
Assume that \(T:X\rightarrow X\) satisfies \(\textrm{ACF}_1\) and \(\textrm{ACF}_2\). For \(x\in X\), we have \(d(T^ix,T^{i+\nu }x)\approx 0\) for all infinite i and all finite \(\nu \).
Proof
Use Lemma 2.3 with \(y=T^{\nu }x\). \(\square \)
Note that the proof above doesn’t work when \(\nu \) is infinite as Lemma 2.3 requires \(y=T^{\nu }x\) to be a standard element. If we add \(\textrm{ACF}_3\), we can extend the result to infinite \(\nu \) and hence prove:
Lemma 2.5
If \(T:X\rightarrow X\) is an ACF, then \(d(T^ix,T^jx)\approx 0\) for all \(x\in X\) and all infinite i, j.
Proof
It clearly suffices to show that if i is infinite, then \(d(T^ix,T^{i+n}x)\approx 0\) for all  . Choose
. Choose  and let
and let  be any number strictly less than the \(\delta \) produced by \(\textrm{ACF}_3\). As we can choose \(\alpha \) and \(\epsilon \) arbitrarily small, it obviously suffices to prove that \(d(T^ix,T^{i+n}x)\le \alpha +\epsilon \) for all
be any number strictly less than the \(\delta \) produced by \(\textrm{ACF}_3\). As we can choose \(\alpha \) and \(\epsilon \) arbitrarily small, it obviously suffices to prove that \(d(T^ix,T^{i+n}x)\le \alpha +\epsilon \) for all  . Assume not, and let n be the smallest number such that \(d(T^ix,T^{i+n}x)> \alpha +\epsilon \). Since \(d(T^{i+n-1}x,T^{i+n}x)\) is infinitesimal by Lemma 2.4, we must have \(\alpha<d(T^ix,T^{i+n}x)\approx \alpha +\epsilon <\alpha +\delta \). Applying (transfer of) Condition (iii), we get a standard \(\nu \in {\mathbb {N}}\) such that \(d(T^{i+\nu }x,T^{i+n+\nu }x)\le \alpha \), which is impossible since by Lemma 2.4, \(T^{i+\nu }x\) is only infinitesimally away from \(T^ix\) and \(T^{i+n+\nu }x\) is only infinitesimally away from \(T^{i+n}x\). In formulas,
. Assume not, and let n be the smallest number such that \(d(T^ix,T^{i+n}x)> \alpha +\epsilon \). Since \(d(T^{i+n-1}x,T^{i+n}x)\) is infinitesimal by Lemma 2.4, we must have \(\alpha<d(T^ix,T^{i+n}x)\approx \alpha +\epsilon <\alpha +\delta \). Applying (transfer of) Condition (iii), we get a standard \(\nu \in {\mathbb {N}}\) such that \(d(T^{i+\nu }x,T^{i+n+\nu }x)\le \alpha \), which is impossible since by Lemma 2.4, \(T^{i+\nu }x\) is only infinitesimally away from \(T^ix\) and \(T^{i+n+\nu }x\) is only infinitesimally away from \(T^{i+n}x\). In formulas,

and we have a contradiction. \(\square \)
We can now prove Suzuki’s theorem:
Theorem 2.6
The following are equivalent:
-
(i)
T is an ACF.
-
(ii)
T has an iterative fixed point.
Proof
According to Proposition 1.5, it suffices to show that \(d(T^ix,T^jy)\approx 0\) for all \(x,y\in X\) and all infinite  . But
. But
where the first term on the left is infinitesimal by Lemma 2.5 and the second term is infinitesimal by Lemma 2.3. \(\square \)
The arguments we have given in this section are basically Suzuki’s, but nonstandard techniques have made it possible to simplify some of the steps, especially the proof of Lemma 2.5 where Suzuki had to use a quite intricate induction argument.
2.2 Modes of convergence
Pointwise convergence to a fixed point is too weak for many applications, and in the rest of the paper we shall see how we can strengthen the ACF conditions to get stronger forms of (uniform) convergence. This section is devoted to the preliminary tasks of finding the nonstandard characterizations of these modes of convergence and of comparing their relative strength. Throughout the section, X and Y are metric spaces and f and \(f_n\), \(n\in {\mathbb {N}}\), are functions from X to Y.
For our purposes, a convenient notion of convergence is the following:
Definition 2.7
The sequence \(\{f_n\}\) converges continuously to f if for all convergent sequences \(x_n\rightarrow x\) in X, the images \(f_n(x_n)\) converge to f(x) in Y.
Remark
The notion of continuous convergence is an old one, and the reader may want to consult the classical paper by Arens and Dugundji [7] for a thorough study of it’s relationship to various topologies on the space of continuous functions (in the setting of net convergence on topological spaces). Note that if f is discontinuous, the constant sequence \(\{f\}\) does not converge continuously to f. In fact, it turns out that if a sequence \(\{f_n\}\) converges continuously to a function f, then f is necessarily continuous (see the final Sect. 3 for a proof), and hence we shall always assume that the limit function is continuous when we compare continuous convergence to other forms of convergence.
It is well-known that uniform convergence implies continuous convergence, but that pointwise convergence does not. We shall soon show that continuous convergence is, in fact, strictly between locally uniform convergence and uniform convergence on compacts, but before we prove this, it will be convenient to establish a nonstandard criterion for continuous convergence. Recall that a point y in  is nearstandard if it is infinitely close to some standard point \(x\in X\). This standard point x is called the standard part of y, and is denoted by
is nearstandard if it is infinitely close to some standard point \(x\in X\). This standard point x is called the standard part of y, and is denoted by  . We write
. We write  for the collection of all nearstandard points.
for the collection of all nearstandard points.
Proposition 2.8
A sequence \(\{f_n\}\) of functions converges continuously to f if and only if for all  ,
,  for all infinitely large
for all infinitely large  .
.
Proof
Assume first that for all nearstandard points  ,
,  for all infinitely large
for all infinitely large  . If \(\{x_n\}\) is a sequence in X converging to x,
. If \(\{x_n\}\) is a sequence in X converging to x,  for all infinite N, and hence \(f_N(x_N)\approx f(x)\). This proves that \(\{f_n(x_n)\}\) converges to f(x), and hence the convergence is continuous.
for all infinite N, and hence \(f_N(x_N)\approx f(x)\). This proves that \(\{f_n(x_n)\}\) converges to f(x), and hence the convergence is continuous.
Assume now that there is a point \(x\in X\) and a point  such that
such that  , but there is some infinite N such that \(f_N(y)\) is not infinitely close to f(x). Choose
, but there is some infinite N such that \(f_N(y)\) is not infinitely close to f(x). Choose  such that
such that  . For each nonzero \(n\in {\mathbb {N}}\), the sentence
. For each nonzero \(n\in {\mathbb {N}}\), the sentence

clearly holds in the nonstandard universe, and by transfer the sentence
holds in the standard universe. This means that for any \(n\in {\mathbb {N}}\), there is a point \(y_n\in X\) and a standard integer \(N_n>n\) such that \(d(x,y_n)<\frac{1}{n}\) and \(d(f(x),f_{N_n}(y_n))>\epsilon \). We now create a sequence \(\{x_n\}\) in X by letting \(x_{N_n}=y_n\) for an increasing sequence of \(N_n\)’s and letting \(x_n=x\) for the remaining terms. Clearly \(x_n\rightarrow x\), but \(d(f(x),f_n(x_n))>\epsilon \) for an infinite number of n’s, and hence the convergence is not continuous.\(\square \)
The proposition above should be compared to the following well-known, nonstandard description of uniform convergence (see, e.g., Proposition 13.1 in Hurd and Loeb [24] or Theorem 4.6.1 in Robinson’s book [38]).
Proposition 2.9
A sequence \(\{f_n\}\) of functions converges uniformly to f on a set \(B\subseteq X\) if and only if \(f_N(x)\approx f(x)\) for all \(x\in \,^{*}B\) and all infinite N.
Recall that a point in  is called compact if it is in the nonstandard version
is called compact if it is in the nonstandard version  of some compact set K. The collection of compact points is denoted by
of some compact set K. The collection of compact points is denoted by  . It is well-known (see, e.g., Theorem 2.2 in [24] or Proposition 2.1.6 in [2]) that
. It is well-known (see, e.g., Theorem 2.2 in [24] or Proposition 2.1.6 in [2]) that  with equality if and only if X is locally compact. We have:
with equality if and only if X is locally compact. We have:
Corollary 2.10
A sequence \(\{f_n\}\) of functions converges to f uniformly on compact sets if and only if for all  , \(f_N(y)\approx f(y)\) for all infinitely large
, \(f_N(y)\approx f(y)\) for all infinitely large  . If f is continuous, this is equivalent to
. If f is continuous, this is equivalent to  for all infinitely large
for all infinitely large  .
.
Proof
Assume first that \(\{f_n\}\) converges uniformly to f on compact sets, and that  . Then there is a compact set K such that
. Then there is a compact set K such that  , and since \(\{f_n\}\) converges uniformly on the compact K, we get \(f_N(y)\approx f(y)\) by Proposition 2.9.
, and since \(\{f_n\}\) converges uniformly on the compact K, we get \(f_N(y)\approx f(y)\) by Proposition 2.9.
For the contrary, assume that for all  , \(f_N(y)\approx f(y)\) for all infinitely large
, \(f_N(y)\approx f(y)\) for all infinitely large  . If K is a compact set,
. If K is a compact set,  , and hence for all
, and hence for all  , we have \(f_N(y)\approx f(y)\) for all infinitely large
, we have \(f_N(y)\approx f(y)\) for all infinitely large  . By Proposition 2.9, it follows that \(\{f_n\}\) converges uniformly to f on K.
. By Proposition 2.9, it follows that \(\{f_n\}\) converges uniformly to f on K.
The last statement follows by the nonstandard characterization of continuity (see Proposition 3.1), since  at all nearstandard (and hence all compact) points y. \(\square \)
at all nearstandard (and hence all compact) points y. \(\square \)
We now use the characterizations above to give an easy proof of:
Proposition 2.11
Assume that \(\{f_n\}\) is a sequence of functions converging pointwise to a continuous function f. If the convergence is locally uniform, then it is continuous. If the convergence is continuous, then it is uniform on compact sets.
Proof
Assume that the convergence is locally uniform, i.e. for every \(x\in X\) there is a ball B(x; r) where \(f_n\) converges uniformly to f. If \(\{x_n\}\) converges to x, then \(x_n\in B(x;r)\) for all sufficiently large \(n\in {\mathbb {N}}\), and hence for infinite N, we have \(f_N(x_N)\approx f(x_N)\approx f(x)\) where the last step uses the continuity of f. This shows that \(\{f_n\}\) converges continuously to f.
To prove that continuous convergence implies uniform convergence on compacts, assume that \(\{f_n\}\) converges continuously to f. By Proposition 2.8, this means that  for all nearstandard y and all infinite N. As the compact points are a subset of the nearstandard points, we get
for all nearstandard y and all infinite N. As the compact points are a subset of the nearstandard points, we get  for all compact points y, and by Corollary 2.10\(\{f_n\}\) converges uniformly to f on compact sets. \(\square \)
for all compact points y, and by Corollary 2.10\(\{f_n\}\) converges uniformly to f on compact sets. \(\square \)
Remark
The three notions of convergence in the proposition clearly coincide when the space is locally compact, but in general neither of the implications can be reversed. The arguments in Section 2 of Render’s paper [37] proves that continuous convergence and uniform convergence on compact sets only coincide in the locally compact case, and Example 1 below gives an example of continuous convergence that is not locally uniform.
Example 1
To produce a convergence that is continuous, but not locally uniform, let \(X=l_2\) with the usual norm, and let \(f_n:l_2\rightarrow l_2\) be defined by
To show that \(\{f_n\}\) converges continuously to \(\textbf{0}\), assume that \(\{{\textbf{x}}^{(n)}\}\) is a sequence in \(l_2\) converging to \({\textbf{x}}\). Since \(|\,|\!|f_n({\textbf{x}})|\!|-|\!|f_n({\textbf{x}}^{(n)})|\!|\,|\le |\!|f_n({\textbf{x}})-f_n({\textbf{x}}^{(n)})|\!|\le |\!|{\textbf{x}}-{\textbf{x}}^{(n)}|\!|\) and \(|\!|f_n({\textbf{x}})|\!|\rightarrow 0\), we see that \(|\!|f_n({\textbf{x}}^{(n)})|\!|\rightarrow 0\), and hence \(\{f_n\}\) converges continuously to \(\textbf{0}\).
To see that the convergence is not locally uniform, observe that in any ball \(B({\textbf{0}},r)\) around the origin, there will for all \(n\in {\mathbb {N}}\) be an element \({\textbf{v}}_n=\{0,0,\ldots ,0,\frac{r}{2},0,\ldots \}\in B({\textbf{0}},r)\) such that \(|\!|f_n({\textbf{v}}_n)|\!|=\frac{r}{2}\), and hence \(\{f_n\}\) does not converge uniformly to \({\textbf{0}}\) on \(B({\textbf{0}},r)\).
2.3 Continuous convergence and stable ACFs
We shall now show how to strengthen the conditions of an ACF to get a characterization of continuous convergence to the fixed point \(x_{\infty }\). The following simple example illustrates the main challenge.
Example 2
Let \(f:[0,2\pi ]\rightarrow [0,2\pi ]\) be a strictly increasing, continuous function such that \(f(0)=0\), \(f(2\pi )=2\pi \) and \(f(\theta )>\theta \) for all \(\theta \in (0,2\pi )\). Note that if we iterate f, \(f^{(n)}(\theta )\) increases strictly to \(2\pi \) for all \(\theta \in (0,2\pi )\), and 0 is a repelling and \(2\pi \) an attracting fixed point. We may move f to the unit circle \({\mathbb {T}}\) by defining \(T:{\mathbb {T}}\rightarrow {\mathbb {T}}\) by \(T(\cos \theta ,\sin \theta )=(\cos f(\theta ),\sin f(\theta ))\). Obviously, \(x_{\infty }=(1,0)\) is the unique fixed point for T, and \(T^n(x)\rightarrow x_{\infty }\) for all \(x\in {\mathbb {T}}\). It is easy to check directly that T is an ACF (this also follows immediately from Theorem 2.6), but the convergence is clearly not continuous as it not even uniform on the compact space \({\mathbb {T}}\) (we can make the convergence as slow as we want by making the initial \(\theta \) small).
The basic lesson of Example 2 is that to get stronger forms of convergence, we need to strengthen condition (i) in the definition of an ACF. This condition allows orbits that start close together to wander far apart as long as they wind up close together in the end, and this is clearly not good enough for continuous convergence. An obvious idea is to strengthen our first condition from
- \(\textrm{ACF}_1\):
-
For all \(x\in X\) and
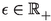 there exists a
there exists a 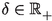 such that if \(d(T^kx,T^ky)<\delta \) for some \(y\in X\) and some \(k\in {\mathbb {N}}\), then $$\begin{aligned} \limsup _{n\rightarrow \infty } d(T^nx,T^ny)<\epsilon \end{aligned}$$
such that if \(d(T^kx,T^ky)<\delta \) for some \(y\in X\) and some \(k\in {\mathbb {N}}\), then $$\begin{aligned} \limsup _{n\rightarrow \infty } d(T^nx,T^ny)<\epsilon \end{aligned}$$
to
- \(\textrm{ACF}_1'\):
-
For all \(x\in X\) and
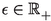 there exists a
there exists a 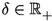 such that if \(d(T^kx,T^ky)<\delta \) for some \(y\in X\) and some \(k\in {\mathbb {N}}\), then $$\begin{aligned} \sup _{n\in {\mathbb {N}}} d(T^{k+n}x,T^{k+n}y)<\epsilon , \end{aligned}$$
such that if \(d(T^kx,T^ky)<\delta \) for some \(y\in X\) and some \(k\in {\mathbb {N}}\), then $$\begin{aligned} \sup _{n\in {\mathbb {N}}} d(T^{k+n}x,T^{k+n}y)<\epsilon , \end{aligned}$$
i.e., simply replace the \(\limsup \) by a \(\sup \).
Definition 2.12
A stable ACF is a map \(T:X\rightarrow X\) satisfying conditions \(\textrm{ACF}_1'\), \(\textrm{ACF}_2\) and \(\textrm{ACF}_3\).
We are ready for the main result of this section.
Theorem 2.13
Assume that X is complete and that \(T:X\rightarrow X\) is continuous. The following are equivalent:
-
(i)
T is a stable ACF.
-
(ii)
The sequence \(\{T^n\}\) converges continuously to an iterative fixed point \(x_{\infty }\) for T.
Proof
(i)\(\Rightarrow \)(ii): From Suzuki’s theorem we know that for every \(x\in X\), \(\{T^n(x)\}\) converges to an iterative fixed point \(x_{\infty }\). To prove that the convergence is continuous, we shall use the nonstandard characterization in Proposition 2.8; hence we need to show that if \(x\in X\) and  is infinitely close to x, then \(T^Ny\approx x_{\infty }\) for all infinite N. Given x and an
is infinitely close to x, then \(T^Ny\approx x_{\infty }\) for all infinite N. Given x and an  , \(\textrm{ACF}_1'\) produces a
, \(\textrm{ACF}_1'\) produces a  such that if for any k, \(d(T^kx,T^ky)<\delta \), then \(d(T^{k+n}x,T^{k+n}y)<\epsilon \) for all \(n\in {\mathbb {N}}\). Since \(d(T^0x,T^0y)=d(x,y)<\delta \), this implies (using transfer) that \(d(T^nx,T^ny)<\epsilon \) for all
such that if for any k, \(d(T^kx,T^ky)<\delta \), then \(d(T^{k+n}x,T^{k+n}y)<\epsilon \) for all \(n\in {\mathbb {N}}\). Since \(d(T^0x,T^0y)=d(x,y)<\delta \), this implies (using transfer) that \(d(T^nx,T^ny)<\epsilon \) for all  . Since
. Since  is arbitrary, we have \(T^n x\approx T^n y\) for all
is arbitrary, we have \(T^n x\approx T^n y\) for all  , and consequently \(T^Ny\approx T^Nx\approx x_{\infty }\) for all infinite N.
, and consequently \(T^Ny\approx T^Nx\approx x_{\infty }\) for all infinite N.
(ii)\(\Rightarrow \)(i): By Suzuki’s theorem we know that T is an ACF, and we only have to prove that \(\textrm{ACF}_1'\) is satisfied. This condition is equivalent to saying that for every \(x\in X\) and every  :
:

By the Transfer Principle, it suffices to prove the transferred formula

To do so, choose \(\delta \) to be any positive infinitesimal. It clearly suffices to show that if \(d(T^kx,T^ky)<\delta \) for some  , then \(T^{k+n}x\approx T^{k+n}y\) for all
, then \(T^{k+n}x\approx T^{k+n}y\) for all  . There are two cases to consider.
. There are two cases to consider.
k is finite: In this case \(T^kx\) is a standard point, and by continuous convergence we have \(T^n(T^kx)\approx T^n(T^ky)\) for all infinite n. For finite n, the same formula follows from the continuity of \(T^n\). Hence \(T^{k+n}x\approx T^{k+n}y\) for all  .
.
k is infinite: Since x is a standard point, we know that \(x_{\infty }\approx T^kx\approx T^ky\). By continuous convergence we see that for infinite n, \(x_{\infty }=T^nx_{\infty }\approx T^n(T^kx)\) and \(x_{\infty }=T^nx_{\infty }\approx T^n(T^ky)\). Thus \(T^{n}(T^kx)\approx T^{n}(T^ky)\) for all infinite  . For finite n, the same formula follows from continuity of \(T^n\) (using that \(T^kx\) and \(T^ky\) are both infinitely close to the standard point \(x_{\infty }\)), and hence we have also in this case proved that \(T^{k+n}x\approx T^{k+n}y\) for all
. For finite n, the same formula follows from continuity of \(T^n\) (using that \(T^kx\) and \(T^ky\) are both infinitely close to the standard point \(x_{\infty }\)), and hence we have also in this case proved that \(T^{k+n}x\approx T^{k+n}y\) for all  . \(\square \)
. \(\square \)
By Proposition 2.11, we now have:
Corollary 2.14
Stable ACFs converge uniformly on compact sets.
2.4 Uniform convergence on bounded sets
Recall that to show uniform convergence on bounded sets, we need to show that for all finite \(y\in \,^{*}X\), we have \(T^ny\approx x_{\infty }\) for all infinite n. To obtain this, we replace \(\textrm{ACF}_2\) and \(\textrm{ACF}_3\) by a single new condition
- \(\textrm{ACF}_2'\):
-
For all \(x\in X\), all bounded \(B\subseteq X\) and all
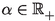 , there exist a
, there exist a 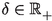 and a \(\nu \in {\mathbb {N}}\) such that for all \(y\in B\) and all \(n\in {\mathbb {N}}\): $$\begin{aligned} \alpha \le d(T^nx,T^ny)<\alpha +\delta \Longrightarrow d(T^{n+\nu }x,T^{n+\nu }y)<\alpha -\delta \end{aligned}$$
and a \(\nu \in {\mathbb {N}}\) such that for all \(y\in B\) and all \(n\in {\mathbb {N}}\): $$\begin{aligned} \alpha \le d(T^nx,T^ny)<\alpha +\delta \Longrightarrow d(T^{n+\nu }x,T^{n+\nu }y)<\alpha -\delta \end{aligned}$$
Definition 2.15
We call T a strictly stable ACF if it satisfies \(\textrm{ACF}_1'\) and \(\textrm{ACF}_2'\).
Note that although \(\textrm{ACF}_2'\) implies \(\textrm{ACF}_2\), it doesn’t in an obvious way imply \(\textrm{ACF}_3\). Hence we cannot automatically base our arguments on the pointwise convergence of \(\{T^nx\}\) for standard x as we could in the previous section.
It is easy to see that if \(\{T^n\}\) converges uniformly on bounded sets to a fixed point \(x_{\infty }\), then \(\textrm{ACF}_1'\) and \(\textrm{ACF}_2'\) hold. To prove the converse, we start with a version of Lemma 2.2 that also applies to nonstandard points y.
Lemma 2.16
Assume that T is continuous and satisfies \(\textrm{ACF}_2'\). If \(x\in X\) and  is finite, then
is finite, then

and hence there is an infinite  such that \(d(T^ix,T^iy)\approx 0\)
such that \(d(T^ix,T^iy)\approx 0\)
Proof
Let

and assume for contradiction that \(\alpha >0\). Choose a bounded set B such that  and use \(\textrm{ACF}_2'\) to pick \(\delta \) and \(\nu \). Since there must be \(n\in {\mathbb {N}}\) such that \(d(T^nx,T^ny)<\alpha +\delta \), we have \(d(T^{n+\nu }x,T^{n+\nu }y)<\alpha -\delta \), contradiction.
and use \(\textrm{ACF}_2'\) to pick \(\delta \) and \(\nu \). Since there must be \(n\in {\mathbb {N}}\) such that \(d(T^nx,T^ny)<\alpha +\delta \), we have \(d(T^{n+\nu }x,T^{n+\nu }y)<\alpha -\delta \), contradiction.
To show the second part, note first that if the infimum is attained, there is a finite n such that \(T^nx\approx T^ny\). By continuity of T, we see that \(T^{n+N}x\approx T^{n+N}y\) for all finite N. Since the set
is internal and contains all nonzero finite N, it also contains all sufficiently small infinite N, and hence there is an infinite \(i=n+N\) such that \(d(T^ix,T^iy)\) \(\approx 0\).
If, on the other hand, the infimum is not attained, the internal set

contains all nonzero finite N and hence an infinite N. Hence there is an infinite \(i\ge N\) such that \(d(T^ix,T^iy)\approx 0\). \(\square \)
We also have a parallel to Lemma 2.3:
Lemma 2.17
Assume that T is continuous and satisfies \(\textrm{ACF}_1'\) and \(\textrm{ACF}_2'\). If \(x\in X\) and  is finite, then \(d(T^ix,T^iy)\approx 0\) for all infinite
is finite, then \(d(T^ix,T^iy)\approx 0\) for all infinite  .
.
Proof
Given  , we use \(\textrm{ACF}_1'\) to find a \(\delta \) such that if \(d(T^kx,T^ky)<\delta \), then \(d(T^{k+n}x,T^{k+n}y)<\epsilon \) for all \(n\in {\mathbb {N}}\). By the previous lemma, we can find a finite k such that \(d(T^kx,T^ky)<\delta \), and by transfer, \(d(T^{k+n}x,T^{k+n}y)<\epsilon \) for all
, we use \(\textrm{ACF}_1'\) to find a \(\delta \) such that if \(d(T^kx,T^ky)<\delta \), then \(d(T^{k+n}x,T^{k+n}y)<\epsilon \) for all \(n\in {\mathbb {N}}\). By the previous lemma, we can find a finite k such that \(d(T^kx,T^ky)<\delta \), and by transfer, \(d(T^{k+n}x,T^{k+n}y)<\epsilon \) for all  . Since \(\epsilon \) is arbitrary, it follows that \(d(T^ix,T^iy)\approx 0\) for all infinite
. Since \(\epsilon \) is arbitrary, it follows that \(d(T^ix,T^iy)\approx 0\) for all infinite  . \(\square \)
. \(\square \)
Mimicking the proof of Lemma 2.5, replacing \(\textrm{ACF}_3\) by \(\textrm{ACF}_2'\) in an obvious way, it is now easy to see that if \(x\in X\), then \(\{T^nx\}\) is a Cauchy sequence.
Theorem 2.18
Assume X is complete and \(T:X\rightarrow X\) is continuous. The following are equivalent.
-
(i)
T is a strictly stable ACF.
-
(ii)
The sequence \(\{T^n\}\) converges uniformly on bounded sets to an iterative fixed point \(x_{\infty }\).
Proof
It is straightforward to check that (ii) implies (i). For the converse, Proposition 1.5 tells us that we only have to prove that if x is a point in X and y is a finite point in  , then \(d(T^ix,T^jy)\approx 0\) for all infinite
, then \(d(T^ix,T^jy)\approx 0\) for all infinite  . But
. But
where the first term on the right is infinitesimal since \(\{T^nx\}\) is a Cauchy sequence, and the second term is infinitesimal by Lemma 2.17. \(\square \)
3 Nonstandard analysis
Most of the following results appear in any introduction to nonstandard analysis (such as the references above); the rest are easy exercises.
Proposition 3.1
- 1:
-
A sequence \(\{x_n\}_n\subseteq X\) is bounded if and only if \(x_N\) is finite for all infinite N.
- 2:
-
A sequence \(\{x_n\}_n\subseteq X\) is Cauchy if and only if \(x_i\approx x_j\) for all infinite i, j.
- 3:
-
Functions \(\phi _n\) converge to a function \(\phi \) uniformly on D if and only if for all
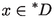 and infinite N, \(\phi _N(x)\approx \phi (x)\).
and infinite N, \(\phi _N(x)\approx \phi (x)\). - 4:
-
A real function f on an interval I is semicontinuous provided
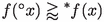 for all x nearstandard in
for all x nearstandard in 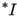 .
. - 5:
-
A real function f on an interval I is continuous at a point \(x\in I\) provided
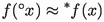 .
. - 6:
-
\(\limsup \nolimits _{t\rightarrow \infty }f(t)<L\) if and only if \(f(t)<\delta <L\) for some standard \(\delta \) and all positive infinite t.
- 7:
-
\(\liminf \nolimits _{t\rightarrow \infty }f(t)> L\) if and only if \(f(t)>\delta > L\) for some standard \(\delta \) and all positive infinite t.
- 8:
-
(Overspill) If an internal set
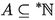 contains all but finitely many elements of \({\mathbb {N}}\) then A contains arbitrarily small infinite elements of
contains all but finitely many elements of \({\mathbb {N}}\) then A contains arbitrarily small infinite elements of 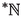 .
. - 9:
-
(Underspill) If an internal set
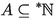 contains all sufficiently small infinite elements of
contains all sufficiently small infinite elements of 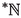 , then it also contains all sufficiently large elements of \({\mathbb {N}}\).
, then it also contains all sufficiently large elements of \({\mathbb {N}}\). - 10:
-
If \(f:{\mathbb {N}}\rightarrow {\mathbb {R}}\) and
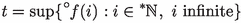 (respectively,
(respectively, 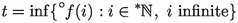 ) exists, then there is an infinite i with \(f(i)\approx t\). If \(f:{\mathbb {N}}^2\rightarrow {\mathbb {R}}\) and
) exists, then there is an infinite i with \(f(i)\approx t\). If \(f:{\mathbb {N}}^2\rightarrow {\mathbb {R}}\) and 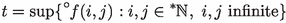 (respectively, \()\) exists, then there are infinite i, j with \(f(i,j)\approx t\).
(respectively, \()\) exists, then there are infinite i, j with \(f(i,j)\approx t\). - 11:
-
If
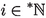 is infinite, then there is an infinite \(k<i\) such that \(j=k-i\) is also infinite.
is infinite, then there is an infinite \(k<i\) such that \(j=k-i\) is also infinite.
Let us also prove our claim from Sect. 2.2 that if a sequence \(\{f_n\}\) converges continuously to a function f, then f is continuous. The following lemma is well-known (a slightly different version is already in Robinson’s book [38] as Theorem 4.5.10), but for the convenience of the reader we include the proof here.
Lemma 3.2
Assume that X, Y are metric spaces and that  is an internal function satisfying:
is an internal function satisfying:
-
(i)
If
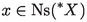 , then
, then 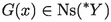 .
. -
(ii)
If
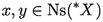 and \(x\approx y\), then \(G(x)\approx G(y)\).
and \(x\approx y\), then \(G(x)\approx G(y)\).
Then the function \(g:X\rightarrow Y\) defined by  is continuous.
is continuous.
Proof
Let a be a point in X and \(\{a_n\}\) a sequence converging to a. We must show that \(\{g(a_n)\}\) converges to g(a).
Let  be given. For all infinite N, \(a_N\approx a\) and hence \(G(a_N)\approx G(a)\) by (ii). This means that the internal set
be given. For all infinite N, \(a_N\approx a\) and hence \(G(a_N)\approx G(a)\) by (ii). This means that the internal set

contains all infinite  . By underspill (Proposition 3.1) it must also contain a finite N. Since by definition \(g(a_n)\approx G(a_n)\) and \(g(a)\approx G(a)\), this means that \(d(g(a_n),g(a))<\epsilon \) for all \(n\in {\mathbb {N}}\), \(n\ge N\). \(\square \)
. By underspill (Proposition 3.1) it must also contain a finite N. Since by definition \(g(a_n)\approx G(a_n)\) and \(g(a)\approx G(a)\), this means that \(d(g(a_n),g(a))<\epsilon \) for all \(n\in {\mathbb {N}}\), \(n\ge N\). \(\square \)
Proposition 3.3
Assume that \(\{f_n\}\) is a sequence of functions from a metric space X to a metric space Y. If \(\{f_n\}\) converges continuously to f, then f is continuous.
Proof
We apply the lemma to the function \(G=f_N\) for an (arbitrary) infinite N. By Proposition 2.8, the conditions of the lemma are satisfied, and hence the “standard part” g of G is continuous. But clearly \(f=g\), and the proposition follows. \(\square \)
Notes
Here and throughout, for the sake of readability we omit the star on functions when we are referring to the nonstandard extension: d instead of
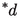 , \(\phi \) instead of
, \(\phi \) instead of 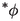 , and so on.
, and so on.
References
Aksoy, A.G., Khamsi, M.A.: Nonstandard Methods in Fixed Point Theory, Universitext. Springer, New York (1990)
Albeverio, S., Fenstad, J.E., Høegh-Krohn, R., Lindstrøm, T.: Nonstandard Methods in Stochastic Analysis and Mathematical Physics. Pure and Applied Mathematics, vol. 122. Academic Press Inc., Orlando (1986)
Arandelović, I.D.: Note on asymptotic contractions. Appl. Anal. Discrete Math. 1, 211–216 (2007)
Arav, M., Santos, F.E.C., Reich, S., Zaslavski, A.J.: A note on asymptotic contractions. Fixed Point Theory Appl. 39465, 6 (2007)
Arav, M., Reich, S., Zaslavski, A.J.: Uniform convergence of iterates for a class of asymptotic contractions. Fixed Point Theory 8, 3–9 (2007)
Ariza-Ruiz, D., Briseid, E., Jiménez-Melado, A., López-Acedo, G.: Rate of convergence under weak contractiveness conditions. Fixed Point Theory 14, 11–27 (2013)
Arens, R., Dugundji, J.: Topologies for function spaces. Pac. J. Math. 1, 5–31 (1951)
Arkeryd, L.O., Cutland, N.J., Henson, C.W. (eds.) Nonstandard Analysis, Volume 493 of NATO Advanced Science Institutes Series C: Mathematical and Physical Sciences. Kluwer Academic Publishers Group, Dordrecht (1997)
Baratella, S., Ng, S.-A.: Fixed points in the nonstandard hull of a Banach space. Nonlinear Anal. 34, 299–306 (1998)
Boyd, D.W., Wong, J.S.W.: On nonlinear contractions. Proc. Am. Math. Soc. 20, 458–464 (1969)
Briseid, E.M.: A rate of convergence for asymptotic contractions. J. Math. Anal. Appl. 330, 364–376 (2007)
Briseid, E.M.: Some results on Kirk’s asymptotic contractions. Fixed Point Theory 8, 17–27 (2007)
Briseid, E.M.: Addendum to the paper: Some results on Kirk’s asymptotic contractions. Fixed Point Theory 8, 321–322 (2007)
Briseid, E.M.: Fixed points of generalized contractive mappings. J. Nonlinear Convex Anal. 9, 181–204 (2008)
Briseid, E.M.: Logical aspects of rates of convergence in metric spaces. J. Symb. Logic 74, 1401–1428 (2009)
Briseid, E.M.: A new uniformity for asymptotic contractions in the sense of Kirk. Int. J. Math. Stat. 6(S10), 2–13 (2010)
Chancelier, J.-Ph.: Extensions and applications of ACF mappings. J. Math. Anal. Appl. 405, 466–474 (2013)
Chen, C.-M.: A note on asymptotic pointwise weaker Meir–Keeler-type contractions. Appl. Math. Lett. 25, 1267–1269 (2012)
Cutland, N.J. (ed.): Nonstandard Analysis and its Applications. London Mathematical Society Student Texts, vol. 10. Cambridge University Press, Cambridge (1988)
Cutland, N.J.: Loeb Measures in Practice: Recent Advances. Lecture Notes in Mathematics, vol. 1751. Springer, Berlin (2000)
Davis, M.: Applied Nonstandard Analysis, 2nd edn. Dover, New York (2005)
Gerhardy, P.: A quantitative version of Kirk’s fixed point theorem for asymptotic contractions. J. Math. Anal. Appl. 316, 339–345 (2006)
Goldblatt, R.: Lectures on the Hyperreals. Graduate Texts in Mathematics, vol. 188. Springer, New York (1998)
Hurd, A.E., Loeb, P.A.: An Introduction to Nonstandard Real Analysis. Academic Press, New York (1985)
Hussain, N., Khamsi, M.A.: On asymptotic pointwise contractions in metric spaces. Nonlinear Anal. 71, 4423–4429 (2009)
Jachymski, J.: An iff fixed point criterion for continuous self-mappings on a complete metric space. Aequationes Math. 48, 163–170 (1994)
Jachymski, J.: A note on a paper of I. D. Arandelović on asymptotic contractions. J. Math. Anal. Appl. 358, 491–492 (2009)
Kikkawa, M., Suzuki, T.: Three fixed point theorems for generalized contractions with constants in complete metric spaces. Nonlinear Anal. 69, 2942–2949 (2008)
Kirk, W.A.: Fixed points of asymptotic contractions. J. Math. Anal. Appl. 277, 645–650 (2003)
Kirk, W.A., Xu, H.-K.: Asymptotic pointwise contractions. Nonlinear Anal. 69, 4706–4712 (2008)
Kohlenbach, U.: Applied Proof Theory: Proof Interpretations and Their Use in Mathematics, Springer Monographs in Mathematics. Springer, Berlin (2008)
Latif, A.: Banach contraction principle and its generalizations. In: Almezel, S., Ansari, Q.H., Khamsi, M.A. (eds.) Topics in Fixed Point Theory, pp. 33–64. Springer, Berlin (2014)
Leader, S.: Equivalent Cauchy sequences and contractive fixed points in metric spaces. Stud. Math. 76, 63–67 (1983)
Leth, S.C.: Regions in the nonstandard plane that contain no standard point. J. Logic Anal. 4, 1–17 (2012)
Maurey, B.: Points fixes des contractions sur un convexe fermé de \(L_1\). Seminaire de Analyse Fonctionelle, École Polytechnique, Palaiseau (1980–1981)
Reich, S., Zaslavski, A.J.: A convergence theorem for asymptotic contractions. J. Fixed Point Theory Appl. 4, 27–33 (2008)
Render, H.: Nonstandard topology on function spaces with applications to hyperspaces. Trans. Am. Math. Soc. 336, 101–119 (1993)
Robinson, A.: Non-standard Analysis, 2nd edn. North-Holland, Amsterdam (1974)
Suzuki, T.: Fixed-point theorem for asymptotic contractions of Meir–Keeler type in complete metric spaces. Nonlinear Anal. 64, 971–978 (2006)
Suzuki, T.: A definitive result on asymptotic contractions. J. Math. Anal. Appl. 335, 707–715 (2007)
Wiśnicki, A.: Neo-compact sets and the fixed point property. J. Math. Anal. Appl. 267, 158–172 (2002)
Wiśnicki, A.: On a problem of common approximate fixed points. Nonlinear Anal. 52, 1637–1643 (2003)
Wiśnicki, A.: On fixed-point sets of nonexpansive mappings in nonstandard hulls and Banach space ultrapowers. Nonlinear Anal. 66, 2720–2730 (2007)
Wiśnicki, A.: Hyper-extensions in metric fixed point theory. J. Nonlinear Convex Anal. 16, 539–550 (2015)
Živaljević, R.: Infinitesimals, microsimplexes and elementary homology theory. Am. Math. Mon. 93, 540–544 (1986)
Acknowledgements
The authors are grateful to Eyvind Briseid for introducing them to some of these questions and to the referees for constructive comments.
Funding
Open access funding provided by University of Oslo (incl Oslo University Hospital)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lindstrøm, T., Ross, D.A. A nonstandard approach to asymptotic fixed point theorems. J. Fixed Point Theory Appl. 25, 35 (2023). https://doi.org/10.1007/s11784-022-01028-6
Accepted:
Published:
DOI: https://doi.org/10.1007/s11784-022-01028-6




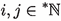 ,
, 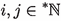 ,
, 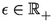 there exists a
there exists a 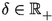 such that if
such that if 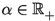 and all bounded sets
and all bounded sets 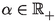 , there exist a
, there exist a 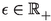 there exists a
there exists a 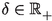 such that if
such that if 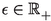 there exists a
there exists a 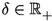 such that if
such that if 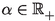 , there exist a
, there exist a 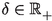 and a
and a 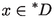 and infinite N,
and infinite N, 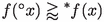 for all x nearstandard in
for all x nearstandard in 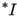 .
.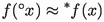 .
.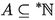 contains all but finitely many elements of
contains all but finitely many elements of 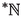 .
.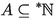 contains all sufficiently small infinite elements of
contains all sufficiently small infinite elements of 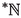 , then it also contains all sufficiently large elements of
, then it also contains all sufficiently large elements of 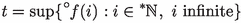 (respectively,
(respectively, 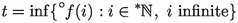 ) exists, then there is an infinite i with
) exists, then there is an infinite i with 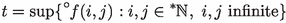 (respectively,
(respectively, 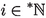 is infinite, then there is an infinite
is infinite, then there is an infinite 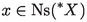 , then
, then 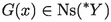 .
.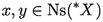 and
and 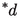 ,
, 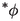 , and so on.
, and so on.