Lagrangian skeleta and plane curve singularities

Abstract

We construct closed arboreal Lagrangian skeleta associated to links of isolated plane curve singularities. This yields closed Lagrangian skeleta for Weinstein pairs $(\mathbb {C}^2,\Lambda )$ and Weinstein 4-manifolds $W(\Lambda )$ associated to max-tb Legendrian representatives of algebraic links $\Lambda \subseteq (\mathbb {S}^3,\xi _\text {st})$. We provide computations of Legendrian and Weinstein invariants, and discuss the contact topological nature of the Fomin–Pylyavskyy–Shustin–Thurston cluster algebra associated to a singularity. Finally, we present a conjectural ADE-classification for Lagrangian fillings of certain Legendrian links and list some related problems.

1 Introduction

The object of this note is to study a relation between the theory of isolated plane curve singularities,¹ as developed by Arnol’d and Gusein-Zade [8,9,10, 61] A’Campo [1,2,3,4] Milnor [76] and others, and arboreal Lagrangian skeleta of Weinstein 4-manifolds. In particular, we construct closed Lagrangian skeleta for the infinite class of Weinstein 4-manifolds obtained by attaching Weinstein 2-handles [28, 108] to the link of $f:\mathbb {C}^2\longrightarrow \mathbb {C}$, where f defines an isolated plane curve singularity at the origin. These closed Lagrangian skeleta allow for an explicit computation of the moduli of microlocal sheaves [60, 80, 98] and also explain the symplectic topology origin of the Fomin–Pylyavskyy–Shustin–Thurston cluster algebra [47] of an isolated singularity.

1.1 Main results

The advent of Lagrangian skeleta and sheaf invariants have underscored the relevance of Legendrian knots in the study of symplectic 4-manifolds [21, 28, 49, 97, 98]. The theory of arboreal singularities, as developed by Nadler [78, 79], provides a local-to-global method for the computation of categories of microlocal sheaves [80]. These invariants, in turn, yield results in terms of Fukaya categories [49, 50]. The existence of arboreal Lagrangian skeleta has been crystallized by L. Starkston [100] in the context of Weinstein 4-manifolds, where this article takes place.

Given a Weinstein 4-manifold $(W,\lambda _\text {st})$, it is presently a challenge to describe an associated arboreal Lagrangian skeleta $\mathbb {L}\subseteq W$. In particular, there is no general method for finding closed arboreal Lagrangian skeleta,² or deciding whether these exist. This manuscript explores this question by introducing a new type of closed arboreal Lagrangian skeleta for Legendrian links $\Lambda _f\subseteq (\mathbb {S}^3,\xi _\text {st})$ which are maximal-tb Legendrian representatives of the smooth link of an holomorphic germ f in $(\mathbb {C}^2,0)$. In practice, we restrict to studying polynomials $f:\mathbb {C}^2\longrightarrow \mathbb {C}$, $f\in \mathbb {C}[x,y]$, which define an isolated singularity at the origin, and also suppose that a real morsification ${\tilde{f}}_t\in \mathbb {R}[x,y]$ of f exists, $t\in (0,1]$. This is an assumption, and we will always take $f\in \mathbb {R}[x,y]$ as our germs. For simplicity of notation, we denote by ${\tilde{f}}$ a real morsification ${\tilde{f}}_t\in \mathbb {R}[x,y]$ for some generic but fixed choice of the deformation parameter $t\in (0,1]$. The discussion in this note unravels thanks to the following geometric fact.

Theorem 1.1

Let $f\in \mathbb {C}[x,y]$ define an isolated singularity at the origin, $\Lambda _f\subseteq (\mathbb {S}^3,\xi _\text {st})$ be its associated Legendrian link and $\tilde{f}\in \mathbb {R}[x,y]$ a real morsification. Then, the Weinstein pair $(\mathbb {C}^2,\Lambda _f)$ admits the closed arboreal Lagrangian skeleton

$$\begin{aligned} \mathbb {L}(\tilde{f})=L_{\tilde{f}}\cup \mathscr {T}(\vartheta _{{\tilde{f}}}), \end{aligned}$$

obtained by attaching the Lagrangian $\mathbb {D}^2$-thimbles $\mathscr {T}(\vartheta _{{\tilde{f}}})$ of $\tilde{f}$ to an embedded exact Lagrangian surface $L_{\tilde{f}}\subseteq \mathbb {C}^2$, where $L_{\tilde{f}}\subseteq \mathbb {C}^2$ is (compactly supported) smoothly isotopic to the Milnor fiber $M_f\subseteq \mathbb {C}^2$ of f.$\square$

The two objects $\Lambda _f$ and $\mathbb {L}(\tilde{f})$ in the statement of Theorem 1.1 require an explanation, which will be given. We rigorously define the notion of a Legendrian link $\Lambda _f\subseteq (\mathbb {S}^3,\xi _\text {st})$ associated to the germ $f\in \mathbb {C}[x,y]$ of an isolated curve singularity in Sect. 2. Note that the smooth link of the singularity $f\in \mathbb {C}[x,y]$, as defined by Milnor [76], and canonically associated to f, is naturally a transverse link $T_f\subseteq (\mathbb {S}^3,\xi _\text {st})$ [38, 53, 56]. The Legendrian link $\Lambda _f\subseteq (\mathbb {S}^3,\xi _\text {st})$ will be a maximal-tb Legendrian approximation of $T_f$. The notation $(\mathbb {C}^2,\Lambda _f)$ refers to the Weinstein pair $(\mathbb {C}^2,\mathscr {R}(\Lambda _f))$, where $\mathscr {R}(\Lambda _f)\subseteq (\mathbb {S}^3,\xi _\text {st})$ is a small (Weinstein) annular ribbon for the Legendrian link $\Lambda _f$.

The Lagrangian skeleton $\mathbb {L}(\tilde{f})$ is also defined in Sect. 2. Note that the Milnor fibration of $f\in \mathbb {C}[x,y]$ is a symplectic fibration on $(\mathbb {C}^2,\omega _\text {st})$, whose symplectic fibers bound the transverse link $T_f\subseteq (\mathbb {S}^3,\xi _\text {st})$. Nevertheless, the Lagrangian skeleton $\mathbb {L}(\tilde{f})$ is built from an exact Lagrangian surface $L_{\tilde{f}}$ and the vanishing cycles $\vartheta _{{\tilde{f}}}$ associated to a real morsification ${\tilde{f}}$. The Lagrangian surface $L_{\tilde{f}}$ is also introduced in Sect. 2. Intuitively, in the same manner that $\Lambda _f\subseteq (\mathbb {S}^3,\xi _\text {st})$ is a Legendrian approximation of $T_f\subseteq (\mathbb {S}^3,\xi _\text {st})$, the exact Lagrangian surfaces $L_{\tilde{f}}\subseteq (\mathbb {C}^2,d\lambda _\text {st})$ are Lagrangian analogues of the symplectic Milnor fiber $M_f\subseteq (\mathbb {C}^2,d\lambda _\text {st})$. Indeed, $L_{\tilde{f}}$ are smoothly indistinguishable from $M_f$, and they only become different geometric objects once we incorporate the symplectic structure $(\mathbb {C}^2,d\lambda _\text {st})$. Theorem 1.1 is a relative statement, being about a Weinstein pair $(\mathbb {C}^2,\Lambda _f)$ and not just about a Weinstein 4-manifold. Hence, it is useful in the absolute context, as follows.

Consider a Legendrian knot $\Lambda \subseteq (\mathbb {S}^3,\xi _\text {st})$ in the standard contact 3-sphere and the Weinstein 4-manifold $W(\Lambda )=\mathbb {D}^4\cup _\Lambda T^*\mathbb {D}^2$ obtained by performing a 2-handle attachment along $\Lambda$, i.e. its Weinstein trace. A front projection for $\Lambda$ (almost) provides an arboreal skeleton for the Weinstein 4-manifold $W(\Lambda )$, as explained in [100]. Nevertheless, the computation of microlocal sheaf invariants from this model is far from immediate, nor exhibits the cluster nature of the moduli space of Lagrangian fillings. The symplectic topology of a Weinstein manifold is much more visible, and invariants more readily computed, from a closed arboreal Lagrangian skeleton, i.e. an arboreal Lagrangian skeleton which is compact and without boundary. In particular, Theorem 1.1 provides such a closed Lagrangian skeleton associated to a real morsification:

Corollary 1.2

Let $f\in \mathbb {C}[x,y]$ define an isolated curve singularity at the origin, $\Lambda _f\subseteq (\mathbb {S}^3,\xi _\text {st})$ be its associated Legendrian link and $\tilde{f}\in \mathbb {R}[x,y]$ a real morsification. The four-dimensional Weinstein manifold

$$\begin{aligned} W(\Lambda _f)=\mathbb {D}^4\cup _{\Lambda _f} (T^*\mathbb {D}^2\cup {\mathop {\ldots }\limits ^{\pi _0(\Lambda _f)}}\cup T^*\mathbb {D}^2)) \end{aligned}$$

admits the closed arboreal Lagrangian skeleton

$$\begin{aligned} {\mathbb {L}}(\tilde{f})\cup _\partial (\mathbb {D}^2\cup {\mathop {\ldots }\limits ^{\pi _0(\Lambda _f)}}\cup \mathbb {D}^2), \end{aligned}$$

obtained by attaching the Lagrangian $\mathbb {D}^2$-thimbles of $\tilde{f}$ to the compactified surface ${\overline{L}}_{{\tilde{f}}}:=L_{{\tilde{f}}}\cup _\partial (\mathbb {D}^2\cup {\mathop {\ldots }\limits ^{\pi _0(\partial L_{{\tilde{f}}})}}\cup \mathbb {D}^2)$.$\square$

Let us see how Theorem 1.1 and Corollary 1.2 can be applied for two simple singularities, corresponding to the $D_5$ and the $E_6$ Dynkin diagrams. As we will see, part of the strength of these results is the explicit nature of the resulting Lagrangian skeleta and the direct bridge they establish between the theory of singularities and symplectic topology.

Fig. 1

The $D_5$-Legendrian link $\Lambda _f\subseteq (\mathbb {S}^3,\xi _\text {st})$ (Left) and a closed Lagrangian arboreal skeleton for the Weinstein 4-manifold $W(\Lambda _f)$ (Right), obtained by attaching 5 Lagrangian 2-disks to the cotangent bundle $(T^*\Sigma _2,\lambda _\text {st})$

Example 1.3

(i) First, consider the germ of the $D_5$-singularity $f(x,y)=xy^2+x^4$, the Legendrian link associated to this singularity is depicted in Fig. 1 (Left). The Weinstein 4-manifold $W(\Lambda _f)=\mathbb {D}^4\cup _{\Lambda _f} (T^*\mathbb {D}^2\cup T^*\mathbb {D}^2)$ admits the closed arboreal Lagrangian skeleton depicted in Fig. 1 (Right). This Lagrangian skeleton is associated to a real morsification $\tilde{f}(x,y)=(x+1)(4x^3-3x+2y^2-1)$ of f(x, y), whose divide $\{(x,y)\in \mathbb {R}^2:(x+1)(4x^3-3x+2y^2-1)=0\}$ is depicted in Fig. 4. The $D_5$-Dynkin diagram is readily seen in the unoriented intersection quiver of the boundaries of the Lagrangian 2-disks added to the (smooth compactification) of the genus 2 Milnor fiber; this unoriented intersection quiver for the vanishing cycles is also drawn in Fig. 4 (Left).

(ii) Second, consider the germ of the singularity $f(x,y)=x^3+y^4$, the link of the singularity is the maximal-tb positive torus knot $\Lambda _f\cong \Lambda (3,4)\subseteq (\mathbb {S}^3,\xi _\text {st})$. The Weinstein 4-manifold $W(\Lambda _f)=\mathbb {D}^4\cup _{\Lambda _f} T^*\mathbb {D}^2$ admits the closed arboreal Lagrangian skeleton depicted in Fig. 2. This Lagrangian skeleton is associated to a real morsification $\tilde{f}(x,y)=4x^3-3x+8y^4-8y^2+1$ of f(x, y); the Lagrangian skeleton is built by attaching six Lagrangian 2-disks to the Lagrangian zero section $\Sigma _3$ of the cotangent bundle $(T^*\Sigma _3,\lambda _\text {st})$ of a genus 3 surface. These 2-disks are attached along the six curves in Fig. 2, whose intersection quiver is (mutation equivalent to) the $E_6$ Dynkin diagram; this unoriented intersection quiver is also drawn in Fig. 4 (Right). See also Fig. 3 for an alternative closed Lagrangian arboreal skeleton, also associated to the simple $E_6$-singularity $f(x,y)=x^3+y^4$.$\square$

Fig. 2

Closed Lagrangian arboreal skeleton associated to the simple $E_6$-singularity $f(x,y)=x^3+y^4$, according to Corollary 1.2

Fig. 3

Another closed Lagrangian arboreal skeleton for the simple $E_6$-singularity $f(x,y)=x^3+y^4$. This is a more symmetric alternative to the closed Lagrangian skeleton in Fig. 2

Fig. 4

The two divides associated to the real morsifications that yield the Lagrangian skeleta in Figs. 1 and 2. The implicit equations for the divides are written in terms of the Chebyshev polynomials $T_n(w)$, determined by the relations $T_n(\cos (t))=\cos (nt)$. The (unoriented) quivers associated to these two divides are depicted with orange vertices and red edges. Note that the diagram obtained for $E_6$ is not the $E_6$ Dynkin diagram; once the quiver is properly oriented, it is mutation equivalent to an orientation of the $E_6$ Dynkin diagram

In the two cases of Example 1.3, the real morsifications can be explicitly obtained using Chebyshev polynomials $T_n(w)$, which are (uniquely) defined by the functional equations $T_n(\cos (t))=\cos (nt)$, $n\in \mathbb {N}\cup \{0\}$. It can be shown that $T_n(x)+T_m(y)$ is a real morsification of the singularity $f(x,y)=x^n+y^m$ and thus, for example, the expression $T_3(x)+T_4(y)=4x^3-3x+8y^4-8y^2+1$ is a real morsification of $E_6$, as used above and depicted in Fig. 4. In general, we will see that the vanishing cycles of a real morsification can be oriented, and then an oriented quiver can be associated to the skew-symmetric intersection form.

From now onward, we abbreviate “closed arboreal Lagrangian skeleton” to Cal-skeleton.³ Let $(W,\lambda )$ be a Weinstein 4-manifold, e.g. described by a Legendrian handlebody, a Lefschetz fibration or analytic equations in $\mathbb {C}^n$. There are two basic nested questions: Does it admit a Cal-skeleton? If so, how do you find one ? For instance, consider a max-tb Legendrian representative $\Lambda \subseteq (\partial \mathbb {D}^4,\lambda _\text {st})$ of any smooth knot, does $W(\Lambda )$ admit a Cal-skeleton ? It might be that not all these Weinstein 4-manifolds $W(\Lambda )$ admit such a skeleton: it is certainly not the case if the Legendrian knot $\Lambda$ were stabilized, hence the max-tb hypothesis is necessary. In general, the lack of exact Lagrangians in $W(\Lambda )$ would provide an obstruction.

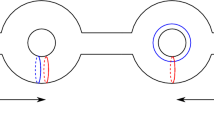
Remark 1.4

For simplicity, we focus on oriented exact Lagrangians. Non-orientable Cal-skeleta should also be of interest. For instance, consider the max-tb Legendrian left-handed trefoil knot $\Lambda ({\overline{3}}_1)\subseteq (\partial \mathbb {D}^4,\lambda _\text {st})$. Figure 5 (Right) depicts a planar front for it. Then the Weinstein 4-manifold $W(\Lambda ({\overline{3}}_1))$ admits a Cal-skeleton $\mathbb {R}\mathbb {P}^2\cup _{\mathbb {S}^1}\mathbb {D}^2$ given by attaching a Lagrangian 2-disk to a Lagrangian $\mathbb {R}\mathbb {P}^2$, as shown in Fig. 5. Indeed, the Weinstein 4-manifold given by Fig. 5 (Left), described by one Weinstein 1-handle and the (black) Weinstein 2-handle passing through it twice, is Weinstein equivalent to the standard cotangent bundle $(T^*\mathbb {R}\mathbb {P}^2,\lambda _\text {st},\varphi _\text {st})$, see e.g. [58]. The zero section $\mathbb {R}\mathbb {P}^2$ is chosen as its Lagrangian skeleton, and then a Lagrangian 2-disk—core of a Weinstein 2-handle—is attached along the blue circle depicted in the Weinstein handlebody diagram in Fig. 5 (Left). At this stage, we simplify the diagram by handle-sliding the black Legendrian knot along the blue Legendrian boundary of the Lagrangian 2-disk, and then cancel the Weinstein 1-handle with this latter (blue) Weinstein 2-handle; see [21]. This yields a front for the max-tb Legendrian left-handed trefoil knot $\Lambda ({\overline{3}}_1)\subseteq (\partial \mathbb {D}^4,\lambda _\text {st})$, as required. $\square$

Fig. 5

Cal-skeleton $\mathbb {R}\mathbb {P}^2\cup _{\mathbb {S}^1}\mathbb {D}^2$ associated to $\Lambda ({\overline{3}}_1)\subseteq (\partial \mathbb {D}^4,\lambda _\text {st})$

Symplectic invariants of Weinstein 4-manifolds W include (partially) wrapped Fukaya categories [12, 101] and categories of microlocal sheaves [80]. Microlocal sheaf invariants should be particularly computable if a Cal-skeleton $\mathbb {L}\subseteq W$ is given, yet worked out examples are scarce in the literature. In Sect. 4, we use⁴ Theorem 1.1 to compute the moduli space of simple microlocal sheaves on some of the Cal-skeleta $\mathbb {L}$ from Corollary 1.2.

Finally, Theorem 1.1 provides a context for the study of exact Lagrangian fillings of Legendrian links $\Lambda _f\subseteq (\mathbb {S}^3,\xi _\text {st})$ associated to isolated plane curve singularities. Indeed, let

$$\begin{aligned} \mathbb {L}({\tilde{f}})=L_{{\tilde{f}}}\cup \vartheta ({\tilde{f}}) \end{aligned}$$

be a Cal-skeleton for the Weinstein pair $(\mathbb {C}^2,\Lambda _f)$ for a real morsification ${\tilde{f}}$, as produced in Theorem 1.1. The exact Lagrangian filling $L_{{\tilde{f}}}$ may serve as a starting exact Lagrangian filling for the Legendrian link $\Lambda _f$, and then performing Lagrangian disk surgeries [96, 109] along the Lagrangian thimbles in $\vartheta$ is a method to construct additional⁵ exact Lagrangian fillings. In general, this strategy might be potentially obstructed, as the Lagrangian disks might acquire immersed boundaries when the Lagrangian surgeries are performed. That said, since Lagrangian disks surgeries yield combinatorial mutations of a quiver, Theorem 1.1 might hint towards a structural conjecture: we expect as many exact Lagrangian fillings $\Lambda _f$ as elements in the cluster mutation class of the intersection quiver for the vanishing thimbles $\vartheta$. It should be noted that C. Viterbo’s work is abundant in useful and remarkable results, but also bountiful in insightful questions and conjectures⁶: trying to follow his steps, Sect. 5 concludes with a discussion on such conjectural matters.

2 Lagrangian skeleta for isolated singularities

In this section we introduce the necessary ingredients for Theorem 1.1 and prove it. We refer the reader to [9, 54, 75] for the basics of plane curve singularities and [37, 38, 53, 85] for background on 3-dimensional contact topology.

2.1 The legendrian link of an isolated singularity

Let $f\in \mathbb {C}[x,y]$ be a bivariate complex polynomial which defines an isolated complex singularity at the origin $(x,y)=(0,0)\in \mathbb {C}^2$. The link of the singularity $T_f\subseteq (\mathbb {S}^3,\xi _\text {st})$ is the intersection

$$\begin{aligned} T_f=V(f)\cap \mathbb {S}^3_\varepsilon =\{(x,y)\in \mathbb {C}^2:f(x,y)=0\}\cap \{(x,y)\in \mathbb {C}^2:|x|^2+|y|^2=\varepsilon \}, \end{aligned}$$

where $\varepsilon \in \mathbb {R}^+$ is small enough. The intersection is transverse for $\varepsilon \in \mathbb {R}^+$ small enough [31, 76], and thus $T_f$ is a smooth link. The link $T_f$ is in fact a transverse link for the contact structure $\xi _\text {st}=T\mathbb {S}^3\cap i(T\mathbb {S}^3)$, as is the boundary of the (Milnor) fiber $M_f$ for the Milnor fibration [53, 56]. Equivalently, it is the transverse binding of the contact open book generated by

$$\begin{aligned} \frac{f}{\Vert f\Vert }:\mathbb {S}^3{\setminus } T_f\longrightarrow \mathbb {S}^1. \end{aligned}$$

The link of a singularity was first introduced by Wirtinger and Brauner [19] and masterfully studied by Milnor [76]. The book [31] comprehensively develops⁷ the smooth topology of link of singularities and their connection to 3-manifold topology. The contact topological nature of the associated open book was developed by Giroux [56].

Let us suppose that the germ of our singularity is irreducible.⁸ From a smooth perspective, the smooth isotopy class of $T_f$ is that of an iterated cable of the unknot [31]. Let $K_{l,m}$ be the oriented (l, m)-cable of a smooth link $K\subseteq \mathbb {S}^3$, i.e. an embedded curve in the boundary $\partial {{\mathcal {O}}}{} { p}(K)$ of the solid torus ${{\mathcal {O}}}{} { p}(K)$ in the homology class $l\cdot [\lambda ]+m\cdot [\mu ]$, with $\lambda$ the longitude and $\mu$ the meridian of ${{\mathcal {O}}}{} { p}(K)$. It is shown in [31, Chapter IV.7] that an iterated cable $K_{(l_1,\mu _1),(l_2,\mu _2),\ldots ,(l_r,\mu _r)}\subseteq \mathbb {S}^3$ is the link of an isolated singularity if and only if $\mu _{i+1}>(l_i\mu _i)l_{i+1}$, for $1\le i\le r-1$.

Remark 2.1

Given an isolated singularity f(x, y), there are algorithms for determining the smooth type of $T_f$, i.e., the sequence of pairs $\{(l_1,\mu _1),(l_2,\mu _2),\ldots ,(l_r,\mu _r)\}$. For instance, by applying the Newton–Puiseux algorithm to f(x, y) we may write

$$\begin{aligned} y=a_1x^{\frac{m_1}{n_1}}+a_2x^{\frac{m_2}{n_1n_2}}+a_3x^{\frac{m_3}{n_1n_2n_3}}+\ldots ,\quad a_i\in \mathbb {C}^* \end{aligned}$$

at each branch, where the exponents $m_1/n_1<m_2/(n_1n_2)<m_3/(n_1n_2n_3)<\cdots$ are increasing and $\text{ gcd }(m_i,n_i)=1$, for all $i\in \mathbb {N}$. The pairs $(n_i,m_i)\in \mathbb {N}^2$ are called the Puiseux pairs. For reference, the Newton pairs are then $(p_i,q_i)$ with $p_i=n_i$, $q_1=m_1$ and $q_i=m_i-m_{i-1}n_i$ for $i\ge 2$, and the cabling algebraic condition reads $p_i,q_i>0$. The topological pairs $(l_i,\mu _i)$ are given by $l_i=p_i=n_i$, $\mu _1=q_1$ and $\mu _{i+1}=q_{i+1}+p_ip_{i+1}\mu _i$ for $i\ge 1$, and the cabling algebraic condition translates into $l_i=p_i>0$ and $q_{i+1}=\mu _{i+1}-l_il_{i+1}\mu _i>0$, as above. The algorithm and these relations are explained in [31, Appendix to Chapter I].$\square$

In the finer context of contact topology, the transverse link $T_f\subseteq (\mathbb {S}^3,\xi _\text {st})$ is an iterated cable with maximal self-linking number $sl(T_f)={\overline{sl}}$, as it bounds the symplectic Milnor fiber $M_f\subseteq \mathbb {C}^2$ of $f\in \mathbb {C}[x,y]$, equiv. the symplectic page of the contact open book [39, 56]. By the transverse Bennequin bound [14], this self-linking must be equal to the Euler characteristc $-\chi (M_f)$. A fact about the smooth isotopy class of links of singularities is their Legendrian simplicity:

Proposition 2.2

Let $f\in \mathbb {C}[x,y]$ define an isolated singularity at the origin and $T_f\subseteq (\mathbb {S}^3,\xi _\text {st})$ be its associated transverse link. There exists a unique maximal Thurston–Bennequin Legendrian approximation $\Lambda _f\subseteq (\mathbb {S}^3,\xi _\text {st})$ of the transverse link $T_f$.

Proof

The classification of Legendrian representatives of iterated cables of positive torus knots is established in [71, Corollary 1.6], building on [40, 41]. The sufficent numerical condition for Legendrian simplicity is $\mu _{i+1}/l_{i+1}>{\overline{tb}}(K_i)$, where $K_i$ is the ith iterated cable in $K_{(l_1,\mu _1),(l_2,\mu _2),\ldots ,(l_r,\mu _r)}\subseteq \mathbb {S}^3$. The maximal Thurston-Bennequin equals ${\overline{tb}}(K_i)=A_i-B_i$, where $A_i,B_i\in \mathbb {N}$ are given by

$$\begin{aligned} A_i:=\sum _{\alpha =1}^i p_\alpha \prod _{\beta =\alpha +1}^i q_\beta \prod _{\beta =\alpha }^i q_\beta ,\qquad B_i:=\sum _{\alpha =1}^i \left( p_\alpha \prod _{\beta =\alpha +1}^i q_\beta \right) + \prod _{\alpha =1}^i q_\alpha ,\quad i\in \mathbb {N}, \end{aligned}$$

as defined in [71, Equation (2)], and satisfy $\mu _il_i>A_i-B_i$. In particular, an algebraic link satisfies $\mu _{i+1}/l_{i+1}>\mu _il_i>A_i-B_i={\overline{tb}}(K_i)$, for all $1\le i\le r-1$, and its max-tb representative is unique. $\square$

Proposition 2.2 implies that there exists a unique Legendrian link $\Lambda _f\subseteq (\mathbb {S}^3,\xi _\text {st})$, up to contact isotopy, whose positive transverse push-off $\tau (\Lambda _f)$, as defined in [53, Section 3.5.3], is transverse isotopic to the transverse link $T_f$. Note that two distinct Legendrian approximations of a transverse link [35, Theorem 2.1] differ by Legendrian stabilizations, which necessarily decrease the Thurston-Bennequin invariant.

Remark 2.3

Proposition 2.2 does not hold for $K\subseteq (\mathbb {S}^3,\xi _\text {st})$ an arbitrary smooth link. For instance, the smooth isotopy classes of the mirrors ${\overline{5}}_2,{\overline{6}}_1$ of the three-twist knot and the Stevedore knot admit two distinct maximal-tb Legendrian representatives each [27, Section 4]. That said, the knots ${\overline{5}}_2,{\overline{6}}_1$ are not links of singularities, as their Alexander polynomials are not monic, and thus they are not fibered knots [83].$\square$

Proposition 2.2 allows us to canonically define a Legendrian link associated to an isolated singularity:

Definition 2.4

Let f be the germ of an isolated singularity at the origin. A Legendrian link $\Lambda _f\subseteq (\mathbb {S}^3,\xi _\text {st})$ is associated to f if it is a maximal-tb Legendrian link $\Lambda _f\subseteq (\mathbb {S}^3,\xi _\text {st})$ whose positive transverse push-off $\tau (\Lambda _f)$ is transversely isotopic to the link of the singularity $T_f\subseteq (\mathbb {S}^3,\xi _\text {st})$.$\square$

Proposition 2.2 shows that the Legendrian isotopy class of a Legendrian link $\Lambda _f\subseteq (\mathbb {S}^3,\xi _\text {st})$ associated to f is unique. Thus, we refer to $\Lambda _f\subseteq (\mathbb {S}^3,\xi _\text {st})$ in Definition 2.4 as the Legendrian link associated to the germ f.

Example 2.5

(ADE Singularities) Let us consider the three ADE families of simple isolated singularities [11, Chapter 2.5]. Their germs are given by

$$\begin{aligned} (A_n)\quad f(x,y)= & {} x^{n+1}+y^2,\qquad (D_n)\quad f(x,y)=xy^2+x^{n-1},\qquad n\in \mathbb {N}, \\ (E_6)\quad f(x,y)= & {} x^3+y^4,\qquad (E_7)\quad f(x,y)=x^3+xy^3,\qquad (E_8)\quad f(x,y)=x^3+y^5. \end{aligned}$$

Fig. 6

The Legendrian link for the $A_n$-singularity is the max-tb $(2,n+1)$-torus link (Left). The Legendrian link for the $D_n$-singularity is the link given by the union of a max-tb $(2,n-2)$-torus link and a standard Legendrian unknot, in orange, linked as in the Legendrian front on the right (Right) (colour figure online)

The Legendrian link associated to the $A_n$-singularity is the positive $(2,n+1)$-torus link, with ${\overline{tb}}=n-1$. These links are associated to the braid $\sigma _1^{n+1}$, as depicted in Fig. 6 (Left). The Legendrian link associated to the $D_n$-singularity is the link consisting of the link associated to the $A_{n-3}$-singularity and the standard Legendrian unknot, linked as in Fig. 6 (Right). This is the topological consequence of the factorization $f(x,y)=x(y^2+x^{n-2})$. These $D_n$-links are associated to the (rainbow closure of the) positive braid $\sigma _1^{n-2}\sigma _2\sigma _1^2\sigma _2$, $n\ge 3$. Each of the three components $K_1,K_2,K_3$ of the $D_2$-link is a max-tb Legendrian unknot, with $K_1\cup K_2$ and $K_2\cup K_3$ forming each a (max-tb) Hopf link and $K_1\cup K_3$ forming the 2-unlink. The $D_3$-link is Legendrian isotopic to the $A_3$-link, i.e. a max-tb positive T(2, 4)-torus link.

The Legendrian links associated to the $E_6$ and $E_8$ singularities are the maximal-tb positive (3, 4)-torus Legendrian link and the Legendrian (3, 5)-torus link, as depicted in Fig. 7. The $E_7$ is a maximal-tb Legendrian link consisting of a trefoil knot and a standard Legendrian unknot, linked as in the center Legendrian front in Fig. 7. This is implied by the $f(x,y)=x(x^2+y^3)$ factorization of the $E_7$ singularity. The Legendrian links for $E_6,E_7$ and $E_8$ can also be obtained as the closure of the three braids $\sigma _1^{n-3}\sigma _2\sigma _1^3\sigma _2$, $n=6,7,8$. Figure 7 also depicts generators of the first homology group of the minimal genus Seifert surface; these generate the first homology of each Milnor fiber, and the $E_6,E_7$ and $E_8$ Dynkin diagrams are readily exhibited from their intersection pattern.$\square$

Fig. 7

The Legendrian links for the $E_6,E_7$ and $E_8$ simple singularities

The singularities $f(x,y)=x^a+y^b$, $a\ge 3,b\ge 6$, or $(a,b)=(4,4),(4,5)$, yield an infinite family of non-simple isolated singularities for which the associated Legendrian is readily computed to be the maximal-tb positive (a, b)-torus link, confer Remark 2.1. Two more instances are illustrated in the following:

Example 2.6

(Two Iterated Cables) Consider the isolated curve singularity

$$\begin{aligned} g(x,y)=x^7-x^6+4x^5y+2x^3y^2-y^4. \end{aligned}$$

The Puiseux expansion yields the Newton solution $y=x^{3/2}(1+x^{1/4})$ and thus $\Lambda _f\subseteq (\mathbb {S}^3,\xi _\text {st})$ is the maximal-tb Legendrian representative of the (2, 13)-cable of the trefoil knot. This Legendrian knot is depicted in Fig. 8 (Left). The reader is invited to show that the Legendrian knot $\Lambda _f\subseteq (\mathbb {S}^3,\xi _\text {st})$ of the singularity

$$\begin{aligned} h(x,y)=x^9-x^{10}+6x^8y-3x^6y^2+2x^5y^3+3x^3y^4-y^6, \end{aligned}$$

is the maximal-tb Legendrian representative of the (3, 19)-cable of the trefoil knot [54], as depicted in Fig. 8 (Right). (For that, start by writing the relation as $y(x)=x^{3/2}+x^{5/3}$.$)$ $\square$

Fig. 8

The Legendrian links $\Lambda _g$ and $\Lambda _h$ associated to the singularity $g(x,y)=x^7-x^6+4x^5y+2x^3y^2-y^4$, on the left, and the singularity $h(x,y)=x^9-x^{10}+6x^8y-3x^6y^2+2x^5y^3+3x^3y^4-y^6$, on the right

2.2 A’Campo’s divides and their conormal lifts

Let $f\in \mathbb {C}[x,y]$ define an isolated singularity at the origin, $\mathbb {D}^4_\varepsilon \subseteq \mathbb {C}^2$ be a Milnor ball for this singularity [75, Corollary 4.5], $\varepsilon \in \mathbb {R}^+$, $\mathbb {R}^2=\{(x,y)\in \mathbb {C}^2:\Im (x)=0,\Im (y)=0\}\subseteq \mathbb {C}^2$ the real 2-plane, and $\mathbb {D}^2_\varepsilon =\mathbb {D}^4_\varepsilon \cap \mathbb {R}^2$ a real Milnor 2-disk. First, we need the notion of a divide, called partage in [2], as follows:

Definition 2.7

[2] Let $\mathbb {D}^2_\varepsilon \subseteq \mathbb {R}^2$ be the 2-disk of radius $\varepsilon \in \mathbb {R}^+$. A divide is a proper generic immersion $\gamma :I\longrightarrow \mathbb {D}^2$ of a 1-manifold I into $\mathbb {D}^2$.$\square$

The image $\gamma (I)\subseteq \mathbb {D}^2_\varepsilon$ is also referred to as a divide, in a slight abuse of notation. Definition 2.7 belongs to the realm of real differential topology. A remarkable fact is that A’Campo explained how to associate a divide to certain real morsifications of a singularity. For that, consider a real morsification $\tilde{f}_t(x,y)$, $t\in [0,1]$, such that, for $t\in (0,1]$, $f_t(x,y)$ has only $A_1$-singularities, its critical values are real and the level set ${\tilde{f}}^{-1}_t(0)\cap \mathbb {D}^4_\varepsilon$, contains all the saddle points of the restriction $({\tilde{f}}_t)|_{\mathbb {D}^2_\varepsilon }$. Then, the intersection $D_{{\tilde{f}}}:={\tilde{f}}^{-1}(0)\cap \mathbb {D}^2_\varepsilon \subseteq \mathbb {R}^2$, where $\tilde{f}=f_1$, is a divide, and it is known as the divide of the real morsification $\tilde{f}_t$ [3, 9, 63].

Let us denote by $D_f$ a divide $D_{{\tilde{f}}}$ obtained from a real morsification $\tilde{f}_t$ of f. A divide $D_f$ is also referred to as an A’Campo divide for the singularity f. As in Definition 2.7, it is the image of a union of a smooth 1-manifold I under an immersion $i:I\longrightarrow \mathbb {R}^2$ [55, 62, 64], and it is a generic such immersion. In this manuscript, we assume that the germs of singularities that we consider admit such real morsifications. See [2, 61] for the existence and details of real morsifications, and see Fig. 4 for divides associated to real morsifications of the simple singularities $D_5$ and $E_6$.

Let us now move towards contact topology. By considering a divide $D_f\subseteq \mathbb {R}^2$ as a wavefront co-oriented in both conormal directions, its (biconormal) Legendrian lift is a Legendrian link $\Lambda _0(D_f)$ in the (ideal) contact boundary $(\partial (T^*\mathbb {R}^2),\lambda _\text {st}|_{\partial (T^*\mathbb {R}^2)})$. In this case, $(\partial (T^*\mathbb {R}^2),\lambda _\text {st}|_{\partial (T^*\mathbb {R}^2)})$ is considered with its Legendrian projection onto the zero section $\partial (T^*\mathbb {R}^2)\longrightarrow \mathbb {R}^2$, who fibers are Legendrian 1-spheres $\mathbb {S}^1\subseteq \partial (T^*\mathbb {R}^2)$. See [8, Section 3.1] for fronts and Legendrian fibrations and, e.g. [97, Section 2] and [53, Section 3.2].

The biconormal lift $\Lambda _0(D_f)\subseteq \partial (T^*\mathbb {R}^2)$ of the immersed curve $D_f$ to the (unit) boundary of the cotangent bundle $T^*\mathbb {R}^2$ can be constructed using the three local models:

• (i) The biconormal lift near a smooth interior point $P\in D_f$ is defined as

  $$\begin{aligned} \{u=(q,u_q)\in T^*{{\mathcal {O}}}{} { p}(P):\Vert u_q\Vert =1,T_qD_f\subseteq \ker (u_q) \text{ for } q\in D_f\cap {{\mathcal {O}}}{} { p}(P)\}, \end{aligned}$$

  for an arbitrary fixed choice of metric in $\mathbb {R}^2$, and neighborhood ${{\mathcal {O}}}{} { p}(P)\subseteq \mathbb {R}^2$. See the first row of Fig. 9.

• (ii) The biconormal lift near an immersed point $P\in D_f$ is defined as the (disjoint) union of the conormal lifts of each of its embedded branches through P. See the second row of Fig. 9.

• (iii) Finally, at the endpoint $P\in D_f$, the biconormal lift is defined as the closure in $T^*_P\mathbb {R}^2$ of one of the components of

  $$\begin{aligned} T^*_P\mathbb {R}^2\setminus \{u\in T^*_P\mathbb {R}^2:\Vert u_q\Vert =1,T_PD_f\subseteq \ker (u_q) \text{ for } q\in D_f\cap {{\mathcal {O}}}{} { p}(P)\}, \end{aligned}$$

  where the tangent line $T_PD_f$ is defined as the (ambient) smooth limit of the tangent lines $T_{q_i}D_f$ for a sequence $\{q_i\}_{i\in \mathbb {N}}$ of interior points $q_i\in D_f$ convering to $P\in D_f$. There are two such components, but our arguments are independent of such a choice. See the third row of Fig. 9.

Fig. 9

Local models for the divides $D_f$, on the left column, and their corresponding biconormal lifts, on the right column. Note that we have depicted the biconormal lift in its non-generic form (matching $D_f$ at the boundary), at the left of the right column, and also after a Legendrian front perturbation, at the right of the right column. The local model of the crossing is depicted in gray so that the conormal direction (in blue) is visible (colour figure online)

Remark 2.8

The restriction of the canonical projection $\pi :\partial (T^*\mathbb {R}^2)\longrightarrow \mathbb {R}^2$ is finite two-to-one onto the image of the interior points of I. The pre-image of $\pi$ at (the image of) endpoints contains an open interval of the Legendrian circle fiber. For instance, the full conormal lift of a point $p\in \mathbb {R}^2$ is Legendrian isotopic to the zero section $\mathbb {S}^1\subseteq (J^1\mathbb {S}^1,\xi _\text {st})$, as is the conormal lift of an embedded closed segment.$\square$

These local models define the Legendrian biconormal lift $\Lambda _0(D_f)\subseteq (\partial (T^*\mathbb {R}^2),\xi _\text {st})$ of the divide of the Morsification $\tilde{f}$. Let $\iota _0:\mathbb {S}^1\longrightarrow (\mathbb {S}^3,\xi _\text {st})$ be a Legendrian embedding in the isotopy class of the standard Legendrian unknot. A small neighborhood ${{\mathcal {O}}}{} { p}(\iota (\mathbb {S}^1))$ is contactomorphic to the 1-jet space $(J^1\mathbb {S}^1,\xi _\text {st})\cong (T^*\mathbb {S}^1\times \mathbb {R}_t,\ker \{\lambda _\text {st}-dt\})$, yielding a contact inclusion $\iota :(J^1\mathbb {S}^1,\xi _\text {st})\longrightarrow (\mathbb {S}^3,\xi _\text {st})$. Note that there exists a contactomorphism $\Psi :(\partial (T^*\mathbb {R}^2),\xi _\text {st})\longrightarrow (J^1\mathbb {S}^1,\xi _\text {st})$, where the zero section in the 1-jet space bijects to the Legendrian boundary of a Lagrangian cotangent fiber in $T^*\mathbb {R}^2$. This leads to the following:

Definition 2.9

Let $D_f\subseteq \mathbb {R}^2$ be the divide associated to a real morsification of a germ f defining an isolated singularity. The biconormal lift $\Lambda (D_f)\subseteq (\mathbb {S}^3,\xi _\text {st})$ is the image $\iota (\Psi (\Lambda _0(D_f)))$. That is, the biconormal lift $\Lambda (D_f)\subseteq (\mathbb {S}^3,\xi _\text {st})$ is the satellite of the biconormal lift $\Lambda _0(D_f)\subseteq (\partial (T^*\mathbb {R}^2),\xi _\text {st})$ with companion knot the standard Legendrian unknot in $(\mathbb {S}^3,\xi _\text {st})$.$\square$

The central result in N. A’Campo’s articles [3, 4] is that the Legendrian link $\Lambda (D_f)\subseteq S^3$ is smoothly isotopic to the transverse link $T_f$, see also [64]. The formulation above, in terms of the satellite to the Legendrian unknot, is not necessarily explicit in the literature on divides and their Legendrian lifts, but probably known to the experts, as it is effectively being used in Hirasawa’s visualization [62, Figure 2]. See also the work of Kawamura [70, Figure 2], Ishikawa and Gibson [55, 63] and others [26, 64]. The phrasing in Definition 2.9 might help crystallize the contact topological characteristics of each object.

Fig. 10

A co-oriented divide D for the $A_2$-singularity $f(x,y)=x^3+y^2$, as a front for its Legendrian link $\Lambda (D)\subseteq (\partial (T^*\mathbb {D}^2),\xi _\text {st})$. That is, the biconormal lift of D is $\Lambda (D)$. Its satellite along the standard unknot is the (unique) max-tb Legendrian trefoil $\Lambda (2,3)\subseteq (\mathbb {R}^3,\xi _\text {st})$

Example 2.10

• (i) The $A_1$-singularity admits two real morsifications $\tilde{f}_1(x,y)=x^2+y^2-1$ and $\tilde{f}_2(x,y)=x^2-y^2$, with corresponding divides

  $$\begin{aligned} D_1=\{(x,y)\in \mathbb {R}^2:x^2+y^2-1=0\},\quad D_2=\{(x,y)\in \mathbb {R}^2:x^2-y^2=0\}. \end{aligned}$$

  The biconormal lift $\Lambda _0(D_1)\subseteq (\partial (T^*\mathbb {R}^2),\xi _\text {st})$ consists of two copies of the Legendrian fibers of the fibration $\pi :\partial (T^*\mathbb {R}^2)\longrightarrow \mathbb {R}^2$. Each of these two copies is satellited to the standard Legendrian unknot, forming a maximal-tb Hopf link $\Lambda (D_1)\subseteq (\mathbb {S}^3,\xi _\text {st})$. Indeed, the second Legendrian fiber can be assumed to be the image of the first Legendrian fiber under the Reeb flow. Hence, the Legendrian link $\Lambda (D_1)\subseteq (\mathbb {S}^3,\xi _\text {st})$ must consist of the standard Legendrian unknot union a small Reeb push-off. Similarly, the biconormal lift $\Lambda _0(D_2)\subseteq (\partial (T^*\mathbb {R}^2),\xi _\text {st})$ equally consists of two copies of the Legendrian fibers of the fibration $\pi :\partial (T^*\mathbb {R}^2)\longrightarrow \mathbb {R}^2$, and thus both Legendrian links $\Lambda (D_1),\Lambda (D_2)$ are Legendrian isotopic in $(\mathbb {S}^3,\xi _\text {st})$.

• (ii) The $A_2$-singularity $f(x,y)=x^3+y^2$ admits the real morsification $\tilde{f}(x,y)=x^2(x-1)+y^2$, whose divide is $D=\{(x,y)\in \mathbb {R}^2:x^2(x-1)+y^2=0\}$. The divide $D\subseteq \mathbb {R}^2$ with its co-orientations is depicted in Fig. 10 (upper left). It depicts a wavefront homotopy, which yields a Legendrian isotopy in $(\partial (T^*\mathbb {R}^2),\xi _\text {st})$, and an additional move equivalence (as in [47, Definition 8.2]). In the first row, the first move separates the two conormals pictorially and the second move is a Reidemeister II, i.e. a safe (non-dangerous) self-tangency. The transition to the second row starts with a Reidemeister III move, which is a front homotopy. The first move in the second row is undoing the kink, also known as a U-turn—see [47, Figure 30]—and the second is a planar isotopy. Finally, the third row starts by depicting the change of front projections induced by the contactomorphism $\Psi$, and performs the satellite to the standard Legendrian unknot. The resulting Legendrian $\Lambda _f\subseteq (\mathbb {S}^3,\xi _\text {st})$ is the max-tb Legendrian trefoil knot $\Lambda (2,3)$ presented in one of its common fronts for $(\mathbb {R}^3,\xi _\text {st})$.$\square$

Remark 2.11

In general, divides for $A_n$-singularities are depicted in [47, Figure 4]. We invite the reader to study the $A_5$-singularity $f(x,y)=x^5+y^2$ with its divide

$$\begin{aligned} D=\{(x,y)\in \mathbb {R}^2:x^2(x^3+x^2-x-1)+y^2=0\} \end{aligned}$$

and discover the corresponding Legendrian isotopy, as in Fig. 10. The isotopy should end with the max-tb Legendrian link $\Lambda (2,5)\subseteq (\mathbb {S}^3,\xi _\text {st})$, e.g. expressed as the (rainbow) closure of the positive braid $\sigma _1^5$, equiv. the $(-1)$-framed closure of $\sigma _1^7$. The general case $n\in \mathbb {N}$ is similar.$\square$

Before we proceed with the proof of Theorem 1.1, we note the following contact topological property for the Legendrian links $\Lambda (D_{{\tilde{f}}})$ associated to divides of real morsifications $\tilde{f}$:

Proposition 2.12

Let $f\in \mathbb {C}[x,y]$ define an isolated singularity, $D_f\subseteq \mathbb {R}^2$ be the divide associated to a real morsification and $\Lambda (D_f)\subseteq (\mathbb {S}^3,\xi _\text {st})$ its biconormal lift. Then $\Lambda (D_f)$ admits an embedded exact Lagrangian filling in $(\mathbb {D}^4,\lambda _\text {st})$. In particular, the Thurston-Bennequin invariant of $\Lambda (D_f)$ is maximal.

Proof

Consider the plabic graph associated to the divide $D_f$ as in [47, Definition 6.11] and note that the alternating strand diagram associated to a plabic graph is Legendrian isotopic to $\Lambda (D_f)$. Indeed, they only differ by U-turns, at the boundary endpoints, and safe tangencies [47, Section 8] at the interior crossings. Now, from a smooth perspective, we can consider the Goncharov-Kenyon conjugate surface [59, Section 2.1] associated to this plabic graph, which bounds its alternating strand diagram. Thus, this is a smooth embedded surface in $\mathbb {S}^3$ bounding $\Lambda (D_f)\subseteq \mathbb {S}^3$ which can be pushed into an embedded surface $\mathbb {D}^4$, relative to the boundary. In short, the conjugate surface is a smooth surface filling for $\Lambda (D_f)$. This surface can be turned in an embedded exact Lagrangian, as done in [98, Proposition 4.9], which proves the first statement. The statement on the Thurston-Bennequin invariant follows from [24, Theorem 1.4]. $\square$

Figure 11 depicts a piece of such a Lagrangian filling near a crossing of the divide. See [98, Section 4] and [47, Section 6] for further details on the construction. Observe that the plabic graph associated to $D_f$ is not unique, e.g. it is possible to perform a square move at each crossing. The Hamiltonian isotopy of the Lagrangian filling, relative to the boundary, does typically depend on this choice and one should expect to build more than one Hamiltonian isotopy class of Lagrangian fillings with the method of Proposition 2.12.⁹

Fig. 11

A local depiction of the (Lagrangian) conjugate surface near a crossing of the divide (Right). The surface is depicted in darker blue, and it bounds a front, in blue, for the Legendrian link. The plabic graph associated to a crossing (Left) is shown the center. Note that there are two choices of (bi)coloring for the vertices, and the two surfaces differ by a square move, i.e., a Lagrangian mutation; both such choices yield embedded exact Lagrangian fillings (though not necessarily in the same Hamiltonian isotopy class)

2.3 Proof of Theorem 1.1

There is an interesting dissonance at this stage. The Legendrian link $\Lambda (D_f)\subseteq \mathbb {S}^3$ in Definition 2.9 and the transverse link $T_f\subseteq \mathbb {S}^3$ of the singularity are smoothly isotopic, yet certainly not contact isotopic. Their relationship is described by the following:

Proposition 2.13

Let $f\in \mathbb {C}[x,y]$ define an isolated singularity and $D_f\subseteq \mathbb {R}^2$ be the divide associated to a real morsification. The positive transverse push-off $\tau (\Lambda (D_f))\subseteq (\mathbb {S}^3,\xi _\text {st})$ of the Legendrian link $\Lambda (D_f)$ is contact isotopic to the transverse link $T_f\subseteq (\mathbb {S}^3,\xi _\text {st})$. In particular, $\Lambda (D_f)\subseteq (\mathbb {S}^3,\xi _\text {st})$ is Legendrian isotopic to the Legendrian link $\Lambda _f\subseteq (\mathbb {S}^3,\xi _\text {st})$ associated to the isolated singularity of $f\in \mathbb {C}[x,y]$.$\square$

Proof

First, we note that $\Lambda (D_f)$ is a maximal-tb Legendrian representative by Proposition 2.12. Thus the latter part of statement follows from the former and Proposition 2.2. Hence we now focus on the first part of the statement. In A’Campo’s isotopy [3, Section 3] from the link associated to the divide to the link of the singularity, the key step is the almost complexification of the Morsification $\tilde{f}:\mathbb {R}^2\longrightarrow \mathbb {R}$. This replaces the $\mathbb {R}$-valued function $\tilde{f}$ by an expression of the form

$$\begin{aligned} \tilde{f}_\mathbb {C}:T^*\mathbb {R}^2\longrightarrow \mathbb {C},\quad \tilde{f}_\mathbb {C}(x,u):=\tilde{f}(x)+i d\tilde{f}(x)(u)-\frac{1}{2}\chi (x)H(f(x))(u,u), \end{aligned}$$

which is a $\mathbb {C}$-valued function, where $u=(u_1,u_2)\in \mathbb {R}^2$ are Cartesian coordinates in the fiber. Here H(f(x)) is the Hessian of f, which is a quadratic form, and $\chi (x)$ is a bump function with $\chi (x)\equiv 1$ near double-points of the divide $D_f\subseteq \mathbb {R}^2$ and $\chi (x)\equiv 0$ away from them. The results in [3], see also [63, 64], imply that the transverse link of the singularity is isotopic to the intersection $\partial _\varepsilon (T^*\mathbb {R}^2)\cap {\widetilde{f}}^{-1}_\mathbb {C}(0)\subseteq (\partial _\varepsilon (T^*\mathbb {R}^2),\xi _\text {st})$ of the $\varepsilon$-unit cotangent bundle with the 0-fiber of $\widetilde{f}_\mathbb {C}$, $\varepsilon \in \mathbb {R}^+$ small enough.¹⁰ It thus suffices to compare this transverse link to the Legendrian lift $\Lambda (D_f)\subseteq (\partial _\varepsilon (T^*\mathbb {R}^2),\xi _\text {st})$, which we can check in each of the two local models: near a smooth interior point of the divide $D_f$ and near each of its double points. Note that the case of boundary points can be perturbed to that of smooth interior points, as in the second row of the local models depicted in Fig. 9 or the first perturbation in Fig. 10. We detail the computation in the first local model, the case of double points follows similarly.

The contact structure $(\partial _\varepsilon (T^*\mathbb {R}^2),\xi _\text {st})$ admits the contact form $\xi _\text {st}=\ker \{\cos (\theta )dx_1-\sin (\theta )dx_2\}$, $(x_1,x_2)\in \mathbb {R}^2$ and $\theta \in \mathbb {S}^1$ is a coordinate in the fiber – this is the angular coordinate in the $(u_1,u_2)$-coordinates above. The divide can be assumed to be cut locally by $D=\{(x_1,x_2)\in \mathbb {R}^2:x_2=0\}\subseteq \mathbb {R}^2$, as we can write $\tilde{f}(x_1,x_2)=x_2$, and thus its bi-conormal Legendrian lift is

$$\begin{aligned} \Lambda (D)=\{(x_1,x_2,\theta )\in \mathbb {R}^2\times \mathbb {S}^1:x_2=0,\theta =\pm \pi /2\}. \end{aligned}$$

Note that the tangent space $T_{(x_1,x_2)}\Lambda (D)$ of $\Lambda (D)$ is spanned by $\partial _{x_1}$, which satisfies

$$\begin{aligned} \langle \partial _{x_1}\rangle =\ker \{\cos (\theta )dx_1-\sin (\theta )dx_2\}, \text{ as } \cos (\theta )=0 \text{ at } \theta =\pm \pi /2. \end{aligned}$$

Since the model is away from a double point, $\tilde{f}_\mathbb {C}(x,u):=x_2+i(0,1)\cdot (u_1,u_2)^t=x_2+iu_2$ becomes the standard symplectic projection $\mathbb {R}^2\times \mathbb {R}^2\longrightarrow \mathbb {R}^2$ onto the second (symplectic) factor. The zero set is thus $x_2=0$ and $u_2=0$ and so the intersection with $T^\varepsilon \mathbb {R}^2$ is

$$\begin{aligned} \kappa =\{(x_1,x_2,\theta )\in \mathbb {R}^2\times \mathbb {S}^1:x_2=0,\theta =0,\pi \}, \end{aligned}$$

as the points with $|u_1|^2=\varepsilon$ are at $\theta$-coordinates $\theta =0,\pi$. The tangent space $T\kappa =\langle \partial _{x_1}\rangle$ is spanned by $\partial _{x_1}$, which is transverse to the contact structure along $\kappa$:

$$\begin{aligned} (\cos (\theta )dx_1-\sin (\theta )dx_2)(\partial _{x_1})=\pm 1,\quad \text{ at } \theta =0,\pi . \end{aligned}$$

It evaluates positive for $\theta =0$ and negative for $\theta =\pi$, which corresponds to each of the two branches in the biconormal lift. It is readily verified [53, Section 3.1] that $\kappa$ is the transverse push-off, positive and negative,¹¹ of $\Lambda (D)$, e.g. observe that the annulus $\{(x_1,x_2,\theta )\in \mathbb {R}^2\times \mathbb {S}^1:x_2=0,0\le \theta \le \pi \}$ is a (Weinstein) ribbon for the Legendrian segment $\{(x_1,x_2,\theta )\in \mathbb {R}^2\times \mathbb {S}^1:x_2=0,\theta =\pi /2\}$. $\square$

Proposition 2.13 implies that real morsifications $\tilde{f}$ yield models for the Legendrian link $\Lambda _f\subseteq (\mathbb {S}^3,\xi _\text {st})$ of a singularity $f\in \mathbb {C}[x,y]$, as introduced in Definition 2.4. That is, given an isolated plane curve singularity $f\in \mathbb {C}[x,y]$, the Legendrian link $\Lambda _f\subseteq (\mathbb {S}^3,\xi _\text {st})$ is Legendrian isotopic to the Legendrian lift $\Lambda (D_{\tilde{f}})\subseteq (\mathbb {S}^3,\xi _\text {st})$ of a divide $D_{\tilde{f}}\subseteq \mathbb {R}^2$ of a real morsification, and thus we now directly focus on studying the Legendrian links $\Lambda (D_{\tilde{f}})\subseteq (\mathbb {S}^3,\xi _\text {st})$.

Let us now prove Theorem 1.1. For that, we use N. A’Campo’s description [4] of the set of vanishing cycles associated to a divide of a real morsification. For each double point $p_i\in D$ in the divide $D:=D_{\tilde{f}}$, there is a vanishing cycle $\vartheta _{p_i}$. For each bounded region of $\mathbb {R}^2\setminus D$, which we label by $q_j$, there is a vanishing cycle $\vartheta _{q_j}$. These vanishing cycles are also naturally oriented by choosing the counter-clockwise orientation in the plane. First, we visualize those vanishing cycles by perturbing the divide $D\subseteq \mathbb {R}^2$ using the local models in Fig. 9, e.g., as depicted in Fig. 12.(i) and (ii). Let us denote this perturbed cooriented front by $D'\subseteq \mathbb {R}^2$, and note that $D'$ only uses one conormal direction at a given point. This perturbation is a front homotopy from $\Lambda (D_{{\tilde{f}}})$ and thus produces a Legendrian isotopy of the associated Legendrian links $\Lambda (D_{{\tilde{f}}})\cong \Lambda _f$ in $(\mathbb {S}^3,\xi _\text {st})$.

Fig. 12

(Left) Two front homotopies from the pieces of a divide to a (generic) Legendrian front, in line with the local models in Fig. 9. The vanishing cycle $\vartheta _p$ is drawn in the Lagrangian base $\mathbb {R}^2$. (Right) A perturbation of a divide for the $E_7$-singularity. The vanishing cycles $\vartheta _p$ coming from the double points of the divide are drawn in yellow, and the vanishing cycles $\vartheta _q$ coming from each of the three bounded interior regions are drawn in red (colour figure online)

Once the perturbation has been performed, we can draw the curves $\vartheta _{p_i},\vartheta _{q_j}$ as in Fig. 12. For instance, Fig. 12.(iii) depicts the case of the $E_7$-singularity with a particular choice of divide D and its perturbation $D'$, with $\vartheta _{p_i}$ in yellow and $\vartheta _{q_j}$ in red. That is:

• 1. For each double point $p_i\in D$, i.e. a crossing, the curve $\vartheta _{p_i}$ is a closed simple curve through the four new double points in $D'$,

• 2. For each closed region, $\vartheta _{q_j}$ is a simple closed curve which (exactly) passes through the double points at the perturbed boundary in $D'$ of the region $q_j$.

The algorithm in [4] constructs a model for the topological Milnor fiber of f by using the real morsification ${\tilde{f}}$, as follows. First, start with the conical Lagrangian conormal $L(D')\subseteq (T^*\mathbb {R}^2,\lambda _\text {st})$ of the perturbed divide $D'$. This Lagrangian conormal intersects the unit cotangent bundle of $T^*\mathbb {R}^2$ at $\Lambda (D')$ and thus, being conical, the information of $L(D')$ is equivalent to the information of the Legendrian link $\Lambda (D')\subseteq (\partial (T^*\mathbb {R}^2),\lambda _\text {st}|_{\partial (T^*\mathbb {R}^2)})$ with its front $D'\subseteq \mathbb {R}^2$. The intersection $L(D')\cap \mathbb {R}^2=D'$ with the zero section $\mathbb {R}^2\subseteq T^*\mathbb {R}^2$ is the divide $D'$. Second, consider the bounded regions in $\mathbb {R}^2\setminus D'$ which are not enclosed by either of the curves of type $\vartheta _{p_i},\vartheta _{q_j}$, described in (1) and (2) above. These are the bounded regions in $\mathbb {R}^2\setminus D'$ which do not come from a bounded square obtained by resolving a crossing (as in Fig. 9) nor from a bounded region in $\mathbb {R}^2\setminus D$. Each of these regions is represented by an embedded (exact) Lagrangian 2-disk, as they are contained in the Lagrangian zero section $(T^*\mathbb {R}^2,\lambda _\text {st})$. The topological surface obtained as the union of the Lagrangian conormal $L(D')$ with these Lagrangian 2-disks is a surface (with corners) which, upon smoothing, lies in the same smooth isotopy class of the Milnor fiber of f. This explains, following [4], that the union of the Lagrangian $L(D')$ with certain bounded Lagrangian regions in $\mathbb {R}^2\setminus D'$ is a model for the topological Milnor fiber.

Fig. 13

(Left) A Lagrangian model for the Milnor fiber of $E_7$ using the biconormal lift $L(D)'$ and some of the bounded regions in the zero section $\mathbb {R}^2\subseteq (T^*\mathbb {R}^2,\lambda _\text {st})$, filled in blue. (Right) The Lagrangian skeleton $L(D')\cup \mathbb {R}^2$ previous to trimming the unbounded region (also depicted in yellow) and the result of applying a holonomy homotopy, where the unbounded region is trimmed to $\mathbb {L}({\tilde{f}})$ (colour figure online)

Remark 2.14

For instance, in the example depicted in Fig. 12 (right), there are 10 such regions in $\mathbb {R}^2\setminus D'$ out of 17. We have depicted these regions in blue in Fig. 13 (left). Note that there are four crossings in D and three bounded regions in $\mathbb {R}^2\setminus D$. The union of these 10 regions with $L(D')$ yields a topological surface of genus 4 and 2 boundary components – those of the 2-component link $\Lambda (D_f)$. Its first Betti number indeed matches $\mu (E_7)=7$.$\square$

In addition to the above model for the Milnor fiber, the article [4] also guarantees that the curves $\vartheta _{p_i},\vartheta _{q_j}$ are vanishing cycles for the real morsification $\tilde{f}$. At this stage, the key fact that we use from A’Campo’s algorithm is that our choice of immersion of the divide $D'\subseteq \mathbb {R}^2$, given by the perturbation, exhibits Lagrangian 2-disks $\mathbb {D}^2_{p_i},\mathbb {D}^2_{q_j}\subseteq \mathbb {R}^2$ such that $\partial \mathbb {D}^2_{p_i}=\vartheta _{p_i}$ and $\partial \mathbb {D}^2_{q_j}=\vartheta _{q_j}$. The union of all these Lagrangian 2-disks $\mathbb {D}^2_{p_i}, \mathbb {D}^2_{q_j}$ constitutes the set $\mathscr {T}(\vartheta _{{\tilde{f}}})$ of Lagrangian $\mathbb {D}^2$-thimbles in the statement of Theorem 1.1.

For the curves $\vartheta _{p_i}$, this follows from Fig. 12.(i), or Fig. 9, where the 2-disk $\mathbb {D}^2_{p_i}$ is (a small extension of) the square given by the four double points in $D'$ appearing in the perturbation of $p_i\in D$. For $\vartheta _{q_j}$, the 2-disk $\mathbb {D}^2_{q_j}$ is chosen to be a small extension of the bounded region itself. These disks are (exact) Lagrangian because $\mathbb {R}^2\subseteq (T^*\mathbb {R}^2,\lambda _\text {st})$ is exact Lagrangian. The Liouville vector field in $(T^*\mathbb {R}^2,\lambda _\text {st})$ vanishes at $\mathbb {R}^2$ and is tangent to $L(D')$. Hence, the inverse flow of the Liouville field retracts the Weinstein pair $(\mathbb {R}^4,\Lambda (D'))$ to $L(D')$ union the zero section $\mathbb {R}^2$. This shows that $L(D')\cup \mathbb {R}^2$ is a Lagrangian skeleton of the Weinstein pair $(\mathbb {R}^4,\Lambda (D'))$. Figure 13 depicts this skeleton in its center, where the $\mathbb {R}^2$ is included in its entirety.

Now, the Lagrangian skeleton has an open piece at the unbounded part of $\mathbb {R}^2$. To complete our argument, it suffices to homotope the Lagrangian skeleton so that the unbounded part is trimmed to match the boundary $\mathscr {B}$ of the unbounded piece of $\mathbb {R}^2\setminus D'$. These skeletal modifications are explained in detail in [100, Section 3]. In a nutshell, one applies the holonomy modifications from [28, Section 12] to homotope the boundary at infinity of $\mathbb {R}^2$ until it coincides with $\mathscr {B}$, modifying the pseudo-gradient field accordingly and producing a Weinstein homotopy. In conclusion, the union of the conical Lagrangian $L(D')$, some bounded regions¹² of $\mathbb {R}^2\setminus D'$, and the Lagrangian 2-disks $\mathbb {D}^2_{p_i},\mathbb {D}^2_{q_j}\subseteq \mathbb {R}^2$ forms a Lagrangian skeleton of the Weinstein pair $(\mathbb {R}^4,\Lambda (D'))$, as required.$\square$

Remark 2.15

The referee also suggested the following (equivalent) viewpoint to smoothly construct the Milnor fiber, which can also be helpful. Consider the bipartite vertices of the $A\Gamma$-diagram [47, Definition 3.1] associated to the divide D: by definition, this is a black vertex at each crossing and a white vertex for each bounded region. In the perturbed front diagram $D'$, each black (resp. white) vertex yields a bounded region in the complement $\mathbb {R}^2\setminus {D'}$ whose boundary has all the conormals pointing outwards (resp. inwards). In the two types of curve in the proof above, the curves $\vartheta _{p_i}$ correspond to the black vertices and the curves $\vartheta _{q_j}$ correspond to the white vertices. A bounded region in the complement $\mathbb {R}^2\setminus {D'}$ whose boundary has all the conormals pointing outwards (resp. inwards) is called a source (resp. a sink); a region which is not a sink or a source is said to be mixed.

From this viewpoint, the smooth Milnor fiber for the morsification ${\tilde{f}}$ associated to $D=D_{{\tilde{f}}}$ can be constructed by consider a 2-disk for each bounded mixed region of $\mathbb {R}^2\setminus {D'}$ and attaching 1-handles connecting two such 2-disks for each intersection point of the pair of corresponding mixed regions.¹³ It should be possible to make this construction in the embedded and exact Lagrangian context: the 2-disks coming from the bounded mixed regions of $\mathbb {R}^2\setminus {D'}$ are (embedded exact) Lagrangians by virtue of being contained in the zero section of the cotangent bundle $(T^*\mathbb {R}^2,\lambda _\text {st})$, and one would just need to argue that the 1-handle attachment can be made an exact Lagrangian 1-handle attachment with boundaries as dictated by the fronts (i.e., that adding the conical Lagrangian piece $L(D')$ is tantamount to adding these Lagrangian 1-handles).$\square$

2.4 Lagrangian skeleta

Arboreal Lagrangian skeleta $\mathbb {L}\subseteq (W,\lambda )$ for Weinstein 4-manifolds are defined in [79, 100]. Given a Weinstein manifold $W=W(\Lambda )$, the arborealization procedure in [100] yields an arboreal Lagrangian skeleton $\mathbb {L}\subseteq (W,\lambda )$ with $\partial \mathbb {L}\ne \varnothing$. Intuitively, those Lagrangian skeleta are obtained by attaching 2-handles to $\mathbb {D}^2$ along a (modification of a) front for $\Lambda$, and thus roughly contain the same information as a front $\pi (\Lambda )\subseteq \mathbb {R}^2$ for $\Lambda$. Let $\Lambda \subseteq (\mathbb {S}^3,\xi _\text {st})$ be a Legendrian link and $(W,\lambda )$ a Weinstein manifold.

Definition 2.16

A compact arboreal Lagrangian skeleton $\mathbb {L}\subseteq \mathbb {C}^2$ for a Weinstein pair $(\mathbb {C}^2,\Lambda )$ is said to be closed if $\partial \mathbb {L}=\Lambda$. A compact arboreal Lagrangian skeleton $\mathbb {L}\subseteq W$ for a Weinstein manifold $(W,\lambda )$ is said to be closed if $\partial \mathbb {L}=\varnothing$.

The Lagrangian skeleta in Theorem 1.1 and Corollary 1.2 are arboreal and closed. For reference, we denote the two Cal-skeleta associated to a real morsification $\tilde{f}$ of an isolated plane curve singularity $f\in \mathbb {C}[x,y]$ by

$$\begin{aligned} \displaystyle \mathbb {L}({\tilde{f}}):=M_f\cup _{\vartheta ({\tilde{f}})}\displaystyle \bigcup _{i=1}^{|\vartheta ({\tilde{f}})|} \mathbb {D}^2,\qquad \displaystyle {\overline{\mathbb {L}}}( {\tilde{f}}):={\overline{M}}_f\cup _{\vartheta ({\tilde{f}})}\displaystyle \bigcup _{i=1}^{|\vartheta ({\tilde{f}})|} \mathbb {D}^2. \end{aligned}$$

The former $\mathbb {L}({\tilde{f}})$ is a Lagrangian skeleton for the Weinstein pair $(\mathbb {C}^2,\Lambda _f)$, and the latter for the Weinstein 4-manifold $W(\Lambda _f)$. The notation ${\overline{M}}_f$ stands for the surface obtained by capping each of the boundary components of the Milnor fiber $M_f$ with a 2-disk. The notation $\mathbb {L}(f)$ and ${\overline{\mathbb {L}}}(f)$ will stand for any Cal-skeleton obtained from a real morsification $\tilde{f}$ as in Theorem 1.1 and Corollary 1.2. Similarly, we will denote by $\vartheta (f)$ a collection of vanishing cycles $\vartheta ({\tilde{f}})$ obtained from a real morsification $\tilde{f}$, without necessarily specifying $\tilde{f}$.

Remark 2.17

In the context of low-dimensional topology, the 2-complexes underlying these Lagrangian skeleta are often referred to as Turaev’s shadows, following [103, Chapter 8]. In particular, it is known how to compute the signature of a (Weinstein) 4-manifold from any Cal-skeleton by using [103, Chapter 9]. Similarly, the SU(2)-Reshetikhin-Turaev-Witten invariant of the three-dimensional (contact) boundary can be computed with the state-sum formula in [103, Chapter 10]. It would be interesting to explore if such combinatorial invariants can be enhanced to detect information on the contact and symplectic structures.$\square$

3 Augmentation stack and the cluster algebra of Fomin–Pylyavskyy–Shustin–Thurston

In the article [47], the authors develop a connection between the topology of an isolated singularity f and the theory of cluster algebras. In concrete terms, they associate a cluster algebra A(f) to an isolated singularity. An initial cluster seed for A(f) is given by a quiver $Q(D_{\tilde{f}})$ coming from the A$\Gamma$-diagrams of a divide $D_{\tilde{f}}$ of a real morsification ${\tilde{f}}$ of f. Equivalently, by [4, 61], the quiver $Q(D_{\tilde{f}})$ is the intersection quiver for a set of vanishing cycles associated to a real morsification of f. The conjectural tenet in [47] is that different choices of Morsifications lead to mutation equivalent quivers and, conversely, two quivers associated to two real morsifications of the same complex topological singularity must be mutation equivalent.

There are two varieties associated to a cluster algebra, the $\mathcal {X}$-cluster variety and the $\mathcal {A}$-cluster variety [44, 59, 95]. In the case of the cluster algebra A(f) from [47], one can ask whether either of these varieties has a particularly geometric meaning. Our suggestion is that either of these cluster varieties is the moduli space of exact Lagrangian fillings for the Legendrian knot $\Lambda _f\subseteq (\mathbb {R}^3,\xi _\text {st})$, with the appropriate additional data (e.g. local systems). Equivalently, they are the moduli space of (certain) objects of a Fukaya category associated to the Weinstein pair $(\mathbb {C}^2,\Lambda _f)$; for instance, the partially wrapped Fukaya category of $\mathbb {C}^2$ stopped at $\Lambda _f$. In this sense, these cluster varieties are mirror to the Weinstein pair $(\mathbb {R}^4,\Lambda _f)$.¹⁴ Focusing on the Legendrian link $\Lambda _f\subseteq (\mathbb {R}^3,\xi _\text {st})$, let us then suggest an alternative route from a plane curve singularity $f\in \mathbb {C}[x,y]$ to a cluster algebra $\mathcal {A}(f)$, following Definition 2.4 and Proposition 2.2 and 2.13.

Starting with $f\in \mathbb {C}[x,y]$, consider the Legendrian,¹⁵$\Lambda _f\subseteq (\mathbb {R}^3,\xi _\text {st})$, where $(\mathbb {R}^3,\xi _\text {st})$ is identified as the complement of a point in $(\mathbb {S}^3,\xi _\text {st})$ and the Legendrian DGA $\mathscr {A}(\Lambda _f)$, as defined by Y. Chekanov in [25] and see [36]. Then we define $\mathcal {A}(f)$ to be the coordinate ring of functions on the augmentation variety $\mathcal {A}(\Lambda _f)$ of the DGA $\mathscr {A}(\Lambda _f)$. Technically, the DGA $\mathscr {A}(\Lambda _f)$ allows for a choice of base points, and the augmentation variety depends on that. Thus, it is more accurate to define:

Definition 3.1

Let $f\in \mathbb {C}[x,y]$ define an isolated singularity, the augmentation algebra $\mathcal {A}(f)$ associated to f is the ring of k-regular functions on the moduli stack of objects ${\text {ob}}({\text {Aug}}_+(\Lambda _f))$ of the augmentation category ${\text {Aug}}_+(\Lambda _f)$.$\square$

The ${\text {Aug}}_+(\Lambda )$ augmentation category of a Legendrian link $\Lambda \subseteq (\mathbb {R}^3,\xi _\text {st})$ is introduced in [84]. An exact Lagrangian filling¹⁶ defines an object in the category ${\text {Aug}}_+(\Lambda )$, and the morphisms between two such objects are given by (a linearized version of) Lagrangian Floer homology. In fact, there is a sense in which any object in ${\text {Aug}}_+(\Lambda )$ comes from a Lagrangian filling [88, 89], possibly immersed, and thus ${\text {ob}}({\text {Aug}}_+(\Lambda ))$ is a natural candidate for a moduli space of Lagrangian fillings. The algebra $\mathcal {A}(f)$ is known to be a cluster algebra [51] in characteristic two. The lift to characteristic zero can be obtained by combining [22] and [51].

By Proposition 2.2, $\mathcal {A}(f)$ is a well-defined invariant of the complex topological singularity. For these Legendrian links $\Lambda =\Lambda _f$, the Couture-Perron algorithm [30] implies that there exist a Legendrian front $\pi (\Lambda _f)\subseteq \mathbb {R}^2$ given by the $(-1)$-closure of a positive braid $\beta \Delta ^2$, where $\Delta$ is the half-twist; equivalently the front is the rainbow closure of the positive braid $\beta$ [20]. Hence, there is a set of non-negatively graded Reeb chords generating the DGA $\mathscr {A}(\Lambda _f)$ and ${\text {ob}}({\text {Aug}}_+(\Lambda _f))$ coincides with the set of k-valued augmentations of $\mathscr {A}(\Lambda _f)$ where exactly one base point per component has been chosen, k a field. The articles [22, 66] provide an explicit and computational model for ${\text {ob}}({\text {Aug}}_+(\Lambda _f))$, and thus $\mathcal {A}(f)$, as follows.

First, suppose that $\Lambda =\Lambda _f$ is a knot. Then, $\mathcal {A}(f)$ is the algebra of regular functions of the affine variety

$$\begin{aligned} X(\beta ):=\{\mathcal {B}(\beta \Delta ^2)+\text{ diag}_{i(\beta )}(t,1,\ldots ,1)=0\}\subseteq \mathbb {C}^{|\beta \Delta ^2|+1}, \end{aligned}$$

where $\mathcal {B}$ are the ($i(\beta )\times i(\beta )$)-matrices defined in [22, Section 3] and Computation 3.2 below, $i(\beta )$ is the number of strands of $\beta ,\Delta$, and $|\beta \Delta ^2|$ is the number of crossings of $\beta \Delta ^2$. In the case $\Lambda _f$ is a link with l components, the space ${\text {ob}}({\text {Aug}}_+(\Lambda _f))$ is a stack¹⁷, with isotropy groups of the form $(\mathbb {C}^*)^k$. If the tenet [47, Conjecture 5.5] holds, the affine algebraic type of the augmentation stack ${\text {ob}}({\text {Aug}}_+(\Lambda _f))$ of a Legendrian link should recover the Legendrian link $\Lambda _f$ and the complex topological type of the singularity f. Here is how to compute ${\text {ob}}({\text {Aug}}_+(\Lambda _f))$.

Computation 3.2

Let $\Lambda =\Lambda _f$ be an algebraic knot, we can find a set of equations for the affine variety ${\text {ob}}(Aug_+(\Lambda _f))$, essentially using [67], see also [22]. Consider a positive braid¹⁸$\beta ^\circ \in \text{ Br}^+_n$ such that the $(-1)$-closure of $\beta ^\circ$ is a front for $\Lambda =\Lambda (\beta ^\circ )$. For $k\in [1,n-1]$, define the following $n\times n$ matrix $P_k(z)$, with variable $z\in \mathbb {C}$:

$$\begin{aligned} (P_k(z))_{ij} = {\left\{ \begin{array}{ll} 1 &{} i=j \text { and } i\ne k,k+1 \\ 1 &{} (i,j) = (k,k+1) \text { or } (k+1,k) \\ z &{} i=j=k+1 \\ 0 &{} \text {otherwise;} \end{array}\right. } \end{aligned}$$

Namely, $P_k(z)$ is the identity matrix except for the $(2\times 2)$-submatrix given by rows and columns k and $k+1$, where it is $\left( {\begin{matrix} 0 &{} 1 \\ 1 &{} z \end{matrix}} \right)$. Suppose that the crossings of $\beta ^\circ$, left to right, are $\sigma _{k_1},\ldots ,\sigma _{k_s}$, $s=|\beta ^\circ |\in \mathbb {N}$, $\sigma _i\in \text{ Br}^+_{n}$ the Artin generators. Then the augmentation stack ${\text {ob}}({\text {Aug}}_+(\Lambda _f))$ is cut out in $\mathbb {C}^{s}\times \mathbb {C}^*={\text {Spec}}[z_1,z_2,\ldots ,z_s,t,t^{-1}]$ by the $n^2$ equations

$$\begin{aligned} \text{ diag}_n(t,1,1,\ldots ,1) + P_{k_1}(z_1)P_{k_2}(z_2)\cdots P_{k_s}(z_s)=0. \end{aligned}$$

(3.1)

The matrix $P_{k_1}(z_1)P_{k_2}(z_2)\cdots P_{k_s}(z_s)$ is denoted by $\mathcal {B}(\beta ^\circ )$. Equations 3.1 provide a computational mean to an explicit description of the affine varieties ${\text {ob}}({\text {Aug}}_+(\Lambda _f))$ that yield the cluster algebra $\mathcal {A}(f)$.$\square$

Example 3.3

Consider the plane curve singularity¹⁹ described by

$$\begin{aligned} f(x,y)= & {} -12 x^{10} y^2-4 x^9 y^2-2 x^7 y^4+6 x^6 y^4-4 x^3 y^6+x^{14}-2 x^{13}+x^{12}+y^8\\= & {} \left( 2 x^3 y^2-4 x^5 y+x^7-x^6-y^4\right) \left( 2 x^3 y^2+4 x^5 y+x^7-x^6-y^4\right) \end{aligned}$$

The Puiseux expansion yields $y(x)=x^{3/2}+x^{7/4}$ and using the Couture-Perron algorithm [30], or [47, Definition 11.3], a positive braid word associated to this singularity is

$$\begin{aligned} \beta =(\sigma _2\sigma _1\sigma _3\sigma _2\sigma _1\sigma _3\sigma _2\sigma _1)\sigma _3(\sigma _1\sigma _2\sigma _3\sigma _1\sigma _2\sigma _3\sigma _1\sigma _2)\sigma _1\sigma _3 \end{aligned}$$

The Legendrian $\Lambda _f\subseteq (\mathbb {R}^3,\xi )$ is the rainbow closure of $\beta$, and the $(-1)$-framed closure of $\beta ^\circ =\beta \Delta ^2$. Note that $\Lambda _f$ is a knot, and thus we will use one base point $t\in \mathbb {C}^*$ in the computation of $X(\beta )={\text {ob}}({\text {Aug}}_+(\Lambda _f))$. Following Computation 3.2 above, we can write equations for affine variety $X(\beta )$ as a subset $X(\beta )\subseteq \mathbb {C}^{31}\times \mathbb {C}^*$. We use coordinates $(z_1,z_2,\ldots ,z_{31};t)\in \mathbb {C}^{31}\times \mathbb {C}^*$, $(z_1,z_2,\ldots ,z_{19})$ corresponding to the 19 crossings of $\beta$ and $(z_{20},\ldots ,z_{31})$ account for the 12 crossings of $\Delta ^2\in {\text {Br}}^+_3$. There are a total of 16 equations, the first two of which read as follows:

$$\begin{aligned}&z_{11}+z_9 z_{12}+\left( z_9+\left( z_{11}+z_9 z_{12}\right) z_{18}\right) z_{20}+\left( z_{13}+z_9 z_{14}+\left( z_{11}+z_9 z_{12}\right) z_{15}\right) z_{21}\\&\quad +\left( z_9 z_{16}+\left( z_{11}+z_9 z_{12}\right) z_{17}+\left( z_{13}+z_9 z_{14}+\left( z_{11}+z_9 z_{12}\right) z_{15}\right) z_{19}+1\right) z_{23}=-t^{-1}\\&z_7+z_6 z_9+(z_8 z_{10}+z_6 z_{11}+(z_7+z_6 z_9) z_{12}+1) z_{18}+(z_8+z_6 z_{13}+(z_7+z_6 z_9) z_{14} \\&\quad +(z_8 z_{10}+z_6 z_{11}+(z_7+z_6 z_9) z_{12}+1) z_{15}) z_{22}+(z_6+(z_7+z_6 z_9) z_{16}\\&\quad +(z_8 z_{10}+z_6 z_{11}+(z_7+z_6 z_9) z_{12}+1) z_{17}\\&\quad +(z_8+z_6 z_{13}+(z_7+z_6 z_9) z_{14}+(z_8 z_{10}+z_6 z_{11}\\&\quad +(z_7+z_6 z_9) z_{12}+1) z_{15}) z_{19}) z_{24}+(z_8 z_{10}+z_6 z_{11}+(z_7+z_6 z_9) z_{12}\\&\quad +(z_7+z_6 z_9+(z_8 z_{10}+z_6 z_{11}+(z_7+z_6 z_9) z_{12}+1) z_{18}) z_{20}\\&\quad +(z_8+z_6 z_{13}+(z_7+z_6 z_9) z_{14}\\&\quad +(z_8 z_{10}+z_6 z_{11}+(z_7+z_6 z_9) z_{12}+1) z_{15}) z_{21}+(z_6+(z_7+z_6 z_9) z_{16}\\&\quad +(z_8 z_{10}+z_6 z_{11}+(z_7+z_6 z_9) z_{12}+1) z_{17}\\&\quad +(z_8+z_6 z_{13}+(z_7+z_6 z_9) z_{14}+(z_8 z_{10}+z_6 z_{11}\\&\quad +(z_7+z_6 z_9) z_{12}+1) z_{15}) z_{19}) z_{23}+1) z_{31}=0 \end{aligned}$$

The remaining 14 equations are longer, but can be readily obtained. This hopefully illustrates that the method is computationally immediate.²⁰$\square$

Remark 3.4

• (i) One may consider the moduli stack ${\text {ob}}({\text {Sh}}^1_{\Lambda _f}(\mathbb {R}^2))$ of sheaves with microlocal rank-1 along $\Lambda _f$, instead of ${\text {ob}}({\text {Aug}}_+(\Lambda _f))$. By [84], there is an equivalence of categories ${\text {Aug}}_+(\Lambda _f)\cong {\text {Sh}}^1_{\Lambda _f}(\mathbb {R}^2)$. The stack ${\text {ob}}({\text {Sh}}^1_{\Lambda _f}(\mathbb {R}^2))$ is a $\mathcal {X}$-cluster variety; the associated $\mathcal {A}$-cluster variety in the cluster ensemble is the moduli of framed sheaves [95].²¹ In short, the cluster algebra $\mathcal {A}(f)$ could have been defined in terms of the moduli space of constructible sheaves microlocally supported in $\Lambda$, instead of Floer theory.

• (ii) The ${\text {Aug}}_+$-category is Floer-theoretical in nature, e.g. its morphisms are certain Floer homology groups. It would have also been natural to consider the partially wrapped Fukaya category $W(\mathbb {C}^2,\Lambda _f)$, as defined [50, 101], or the infinitesimal Fukaya category $Fuk(\mathbb {C}^2,\Lambda )$ [77, 81]. These are Floer-theoretical Legendrian invariants associated to $\Lambda _f$, and thus the singularity $f\in \mathbb {C}[x,y]$, which might be of interest on their own.

4 A few computations and remarks

Consider the derived dg-category ${\text {Sh}}_\Lambda (M)$ of constructible sheaves in a closed smooth manifold M microlocally supported at a Legendrian link $\Lambda \subseteq (\partial (T^*M),\xi _\text {st})$, e.g. as introduced in [97, Section 1]. Equivalently, one may consider a conical Lagrangian $L\subseteq T^*M$ instead of $\Lambda \subseteq (\partial (T^*M),\xi _\text {st})$; in practice, the input data is a wavefront $\pi (\Lambda )\subseteq M$ [8]. Let ${\mu }\,{{\text {sh}}}$ denote the sheaf of microlocal sheaves defined²² in [80, Section 5]. There are two situations we consider, depending on whether the focus is on the Weinstein pair $(\mathbb {C}^2,\Lambda _f)$ or on the Weinstein 4-manifold $W(\Lambda _f)$:

• (i) Sheaf Invariants of the Weinstein pair $(\mathbb {C}^2,\Lambda _f)$.²³ The category of microlocal sheaves ${\mu }\,{{\text {sh}}}(\mathbb {L}(f))$ is an invariant of $(\mathbb {C}^2,\Lambda _f)$, as established in [60, 80, 97].²⁴ In this case, the global sections ${\mu }\,{{\text {sh}}}(\mathbb {L}(f))$ is a category equivalent to the more familiar ${\text {Sh}}_{\Lambda (f)}(\mathbb {R}^2)$. For simplicity, we focus on the moduli stack $\mathcal {S}(f)\subseteq {\text {ob}}({\text {Sh}}_{\Lambda (f)}(\mathbb {R}^2))$ of sheaves whose microlocal support is rank one, microlocally supported in the Legendrian link of an isolated plane curve singularity $f:\mathbb {C}^2\longrightarrow \mathbb {C}$. See [69, Section 7.5] or [60, Section 1.10] for a detailed discussion on these sheaves. In our case $\Lambda =\Lambda (f)$, $\mathcal {S}(f)$ is an Artin stack of finite type [97, Prop. 5.20], and typically is an algebraic variety or a G-quotient thereof, with $G=(\mathbb {C}^*)^k$ or ${\text {GL}}(k,\mathbb {C})$. Note that ${\mu }\,{{\text {sh}}}(\mathbb {L}(f))$ is equivalent to the wrapped Fukaya category of $\mathbb {C}^2$ stopped at $\Lambda _f$ [49].

• (ii) Sheaf Invariants of the Weinstein 4-manifold $W(\Lambda _f)$. The category ${\mu }\,{{\text {sh}}}({\overline{\mathbb {L}}}(f))$ of microlocal sheaves [80] on a Lagrangian skeleton ${\overline{\mathbb {L}}}(f)\subseteq W(\Lambda _f)$ is an invariant of $W(\Lambda _f)$, up to Weinstein homotopy [80] and up to symplectomorphism [49]. This category is²⁵${\text {Sh}}_{\vartheta (f)}({\overline{M}}_f)$, or $\mu loc({\overline{\mathbb {L}}}(f))$, in the notation of [96], i.e. the global sections of the Kashiwara-Schapira sheaf of dg-categories [96, Prop. 3.5] on the Lagrangian skeleton ${\overline{\mathbb {L}}}(f)$. For simplicity, we focus on the moduli stack $\theta (f)\subseteq {\mu }\,{{\text {sh}}}({\overline{\mathbb {L}}}(f))$ of microlocal rank-1 sheaves as well. Note that ${\mu }\,{{\text {sh}}}({\overline{\mathbb {L}}}(f))$ is equivalent to the wrapped Fukaya category of $W(\Lambda _f)$ by [49].

The moduli stack $\mathcal {S}(f)$ in (i) is isomorphic to the stack of microlocal rank-1 sheaves in ${\text {ob}}({\text {Sh}}_{\vartheta (f)}(M_f))$. This is because the union of $\mathbb {R}^2\subseteq T^*\mathbb {R}^2$ and the Lagrangian cone of $\Lambda \subseteq (T^+\mathbb {R}^2,\xi _\text {st})$ is a Lagrangian skeleton for the relative Weinstein pair $(\mathbb {C}^2,\Lambda )$, so is $\mathbb {L}(f)$ by Theorem 1.1, and ${\text {ob}}({\text {Sh}}_{\vartheta (f)}(M_f))$ is an invariant of the Weinstein pair $(\mathbb {C}^2,\Lambda )$, independent of the choice of Lagrangian skeleton. Thus, the difference between $\mathcal {S}(f)$ and $\theta (f)$ is at the boundary, which for $\mathcal {S}(f)$ might give monodromy contributions (and these become trivial on $\theta (f)$). In other words, since ${\overline{\mathbb {L}}}(f)$ is obtained from $\mathbb {L}(f)$ by attaching 2-disks (to close the boundary of the Milnor fiber $M_f$), the category ${\mu }\,{{\text {sh}}}({\overline{\mathbb {L}}}(f))$ is a homotopy pull-back of ${\mu }\,{{\text {sh}}}(\mathbb {L}(f))$.

Remark 4.1

There are currently two methods for computing $\mathcal {S}(f)$: either by direct means, as exemplified in [97], or by using the equivalence of categories $Aug_+(\Lambda (f))\cong {\text {Sh}}^{1}_{\Lambda _f}(\mathbb {R}^2)$ from [84, Theorem 1.3], the latter being denoted by $\mathcal {C}_1(\Lambda _f)$ in [84]. Thanks to the computational techniques available for augmentation varieties, the moduli of objects ${\text {ob}}(Aug_+(\Lambda (f)))$ is readily computable for $(-1)$-framed closures of positive braids as in Sect. 3 above, confer Computation 3.2. Similarly $\theta (f)$ could be computed directly, or by means of the isomorphism to the wrapped Fukaya category²⁶ of $W(\Lambda _f)$.$\square$

In this section, we take to opportunity to build on [80, 96] and perform an actual computation for a class of Cal-Skeleta coming from Theorem 1.1.

Fig. 14

A Cal-skeleta ${\overline{\mathbb {L}}}(f_{2n+1})$ for the Weinstein 4-manifolds $W(\Lambda (A_{2n+1}))$

4.1 Cal-skeleta for $A_n$-singularities

Consider the $A_n$-singularity $f_n(x,y)=x^{n+1}+y^2$. The Legendrian $\Lambda (A_n)\subseteq (\mathbb {R}^3,\xi _\text {st})$ associated to the singularity is the max-tb Legendrian $(2,n+1)$-torus link. By Theorem 1.1, a Lagrangian skeleton $\mathbb {L}(f_n)$ for the Weinstein pair $(\mathbb {C}^2,\Lambda _f)$ is obtained by attaching n 2-disks to a $(3/2-(-1)^{n}/2)$–punctured ${\lfloor }\frac{n-1}{2}{\rfloor }$–genus surface along an $A_n$-Dynkin chain of embedded curves. Similarly, Corollary 1.2 implies that a Lagrangian skeleton ${\overline{\mathbb {L}}}(f_n)$ for the Weinstein 4-manifold $W_n=W(\Lambda (A_n))$ is given by attaching n 2-disks to a ${\lfloor }\frac{n-1}{2}{\rfloor }$–genus surface along an $A_n$-Dynkin chain, as depicted in orange in Fig. 15, see also Fig. 14.

Fig. 15

The Cal-skeleta ${\overline{\mathbb {L}}}(f)$ for the Weinstein 4-manifolds $W(\Lambda (A_2))$ and $W(\Lambda (A_6))$. The relative Cal-skeleta ${\overline{\mathbb {L}}}(f)$ for the corresponding Weinstein pairs $(\mathbb {C}^2,\Lambda (A_2))$ and $(\mathbb {C}^2,\Lambda (A_6))$ are obtained by introducing one puncture to the surfaces

Let us compute $\theta (f_n)$ for $n\in \mathbb {N}$ even, so that $\Lambda (A_n)$ is a knot; the $n\in \mathbb {N}$ odd case is similar. The key technical tool is the Disk Lemma [68, Lemma 4.2.3]. The Disk Lemma explains, in precise terms, how to compute the category of microlocal sheaves on a two-dimensional Lagrangian skeleton $\mathbb {S}\cup _{\gamma }\mathbb {D}^2$ in terms of the category for the corresponding Lagrangian skeleton $\mathbb {S}$, where $\mathbb {D}^2$ is attached along an embedded smooth curve $\gamma \subseteq \mathbb {S}$. In brief, the Disk Lemma states that the microlocal sheaf category for $\mathbb {S}\cup _{\gamma }\mathbb {D}^2$ has as its objects pairs consisting of an object $\mathscr {F}_\mathbb {S}$ in the category for $\mathbb {S}$ and a (derived) trivialization of the microlocal monodromy of $\mathscr {F}_\mathbb {S}$ along $\gamma$, i.e. a homotopy from this microlocal monodromy to the identity.

The complement ${\overline{M}}_f\setminus \vartheta (f)$ of the vanishing cycles is a 2-disk, and the category of local systems is just $\mathbb {C}$-mod. Thus, the moduli of simple constructible sheaves on ${\overline{M}}_f$ microlocally supported on (the Legendrian lift of) the vanishing cycles $\vartheta (f)$ consists of a vector space $V=\mathbb {C}$ and maps $x_1,x_2,\ldots ,x_n\in End(V)$, one associated to each vanishing cycle. This is depicted in Fig. 15 for $n=2,6$, and note that $n=|\vartheta (f)|$. Denote by ${\overline{\mathbb {L}}}(f_n)_0\subseteq T^*{\overline{M}}_f$ the Lagrangian skeleton given by ${\overline{M}}_f$ union the conormal lifts of $\vartheta (f)$. These maps are not necessarily invertible in ${\mu }\,{{\text {sh}}}({\overline{\mathbb {L}}}(f_n)_0)$.

The skeleton ${\overline{\mathbb {L}}}(f_n)$ is obtained by attaching n Lagrangian 2-disks to ${\overline{\mathbb {L}}}(f_n)_0$, i.e. ${\overline{\mathbb {L}}}(f_n)$ is the homotopy push-out of ${\overline{\mathbb {L}}}(f_n)_0$ and the disjoint union of n 2-disks. In consequence, the category of microlocal sheaves on ${\overline{\mathbb {L}}}(f_n)$ is given by the homotopy pull-back of the category of microlocal sheaves on ${\overline{\mathbb {L}}}(f_n)_0$ and the category of microlocal sheaves on n disjoint 2-disks (which are just copies of $\mathbb {C}$-mod). Attaching a 2-disk along a vanishing $V_i$ cycle in $\vartheta (f)$, $i\in [1,n]$, has the effect of trivializing the “monodromy” corresponding map $x_i$, by the Disk Lemman [68, Lemma 4.2.3] cited above; see [96, Section 4] and [68, Section 4.2] for the details. Here, the monodromy²⁷ is given by restricting a microlocal sheaf to (an arbitrarily small neighborhood of) $V_i$. Note that in this restriction, we land into a 1-dimensional Lagrangian skeleton given by a circle $V_i\cong S^1$ union conical segments coming from the adjacent vanishing cycles. Let us call $\gamma _i$ the composition of maps from $cone(x_i)$ to itself obtained by going around $V_i$, each of the maps coming from traversing a segment. Then, the trivialization is a homotopy to the identity, and it translates into adding a map $\alpha _i$ such that $x_i\alpha _i-1=\gamma _i$.

Example 4.2

Consider the map $x_1$ in Fig. 15 (Left), which is depicted transversely to the vanishing cycle $V_1$. The restriction of a microlocal sheaf to a neighborhood of $V_1$ gives a microlocal sheaf for the skeleton $\mathbb {S}^1\cup T_p^{*,+}\mathbb {S}^1\subseteq T^*\mathbb {S}^1$, where $T_p^{*,+}\mathbb {S}^1$ is the positive half of the cotangent fiber at a point $p\in \mathbb {S}^1$. Such a microlocal sheaf is described by a (complex of) vector space(s) and an endomorphism. In this case the vector space is $V=\mathbb {C}$ and this endomorphism is identified with $\gamma _1=x_2$. Hence, trivializing along $V_1$ adds a map $\alpha _1\in End(\mathbb {C})$, which we can think of as a variable $\alpha _1\in \mathbb {C}$, such that $x_1\alpha _1+1=-x_2$. Similarly, trivializing along $V_2$, with $\gamma _2=-\alpha _1$, adds a variable $\alpha _2\in \mathbb {C}$ such that $1+x_2\alpha _2=-\alpha _1$. Hence $\theta (f)$ is the affine variety

$$\begin{aligned} \theta (f_3)=\{(x,y,z)\in \mathbb {C}^3:xyz+x-z-1=0\}. \end{aligned}$$

This affine variety appears in the study of isomonodromic deformations of the Painlevé I equation [105, Section 3.10], see also [18, Section 5]. $\square$

The vanishing cycles $V_1,V_n$ have simpler monodromies $\gamma _1,\gamma _n$, as they only intersect one other vanishing cycle. Adding the 2-disks to the skeleton ${\overline{\mathbb {L}}}(f_n)_0$ along $V_1,V_n$ yields a category of microlocal sheaves whose moduli space of simple objects is described by that of ${\overline{\mathbb {L}}}(f_n)_0$ and the two equations $x_1\alpha _1+1=-x_2$ and $x_n\alpha _n+1=-\alpha _{n-1}$. For each of the middle vanishing cycles $V_i$, $2\le i\le n-1$, we have the monodromy $\gamma _i=\alpha _{i-1}x_{i+1}$. In consequence, attaching the n 2-disks ${\overline{\mathbb {L}}}(f_n)_0$ along all the curves $V_i$, $i\in [1,n]$, leads to the moduli space

$$\begin{aligned} \theta (f)\cong & {} \{(x_i,\alpha _i)\in (\mathbb {C}^2)^n: x_1\alpha _1+1=-x_2, x_n\alpha _n+1\\= & {} -\alpha _{n-1}, 1+x_j\alpha _j=\alpha _{j-1}x_{j+1}, j\in [2,n-1]\}. \end{aligned}$$

Remark 4.3

Consider $(n+3)$-tuples of vectors $(v_1,\ldots ,v_{n+3})\in \mathbb {C}^2$, modulo ${\text {GL}}_2(\mathbb {C})$, the equations for $\theta (f)$ above can be read directly by writing the $(n+3)$-tuple as

$$\begin{aligned} \left( \begin{array}{c} 1\\ 0\end{array}\right) , \left( \begin{array}{c} 0\\ 1\end{array}\right) , \left( \begin{array}{c} -1\\ x_1\end{array}\right) , \left( \begin{array}{c} \alpha _1\\ x_2\end{array}\right) , \left( \begin{array}{c} \alpha _2\\ x_3\end{array}\right) , \left( \begin{array}{c} \alpha _3\\ x_4\end{array}\right) , \left( \begin{array}{c} \alpha _4\\ x_5\end{array}\right) , \ldots , \left( \begin{array}{c} \alpha _{n-1}\\ x_{n}\end{array}\right) , \left( \begin{array}{c} \alpha _n\\ -1\end{array}\right) , \end{aligned}$$

and imposing $v_i\wedge v_{i+1}=1$, where we have use the $GL_2(\mathbb {C})$ gauge group to trivialize the first two vectors, and one component of the third and last vectors. Boalch [18] names this moduli stack after Sibuya [99]. Note that [18, Section 5] points out that some of these equations were initially discovered by Euler [42]. In the context of open Bott–Samelson cells [95, 98], these spaces appear as the open positroid varieties $\{p\in \text{ Gr }(2,n+3): P_{i,i+1}(p)\ne 0\}$, where $P_{i,j}$ is the Plücker coordinate given by the minor at the i and j columns, and the index i is understood $\mathbb {Z}/(n+3)$-cyclically.$\square$

Finally, we notice that the cohomology $H^*(\theta (f),\mathbb {C})$, or that of $H^*(\mathcal {S}(f),\mathbb {C})$, can be an interesting invariant [97, Section 6]. For the case of $A_n$-singularities, we can use the fact that these are actually cluster varieties of $A_n$-type in order to compute their cohomology using [72, Section 6.2]. For $n=2m\in \mathbb {N}$ even, and removing any $\mathbb {C}^*$-factors coming from frozen variables, one obtains that the Abelian graded cohomology group is isomorphic to $\mathbb {Q}[t]/t^{m+1}$, $|t|=2$. In general, the mixed Hodge structure for these moduli spaces can be non-trivial, but for singularities of $A_n$-type, these cohomologies are of Hodge–Tate type, and entirely concentrated in $\bigoplus _{k\ge 0}H^{k,(k,k)}$.

Remark 4.4

It would be valuable to understand the relation between sheaf invariants of a singularity $f\in \mathbb {C}[x,y]$, such as ${\mu }\,{{\text {sh}}}(\mathbb {L}(f))$ and ${\mu }\,{{\text {sh}}}({\overline{\mathbb {L}}}(f))$, and classical invariants from singularity theory [3, 9, 10]. In particular, it could be valuable to develop more systematic methods to compute ${\mu }\,{{\text {sh}}}(\mathbb {L}(f))$ and ${\mu }\,{{\text {sh}}}({\overline{\mathbb {L}}}(f))$ both directly and from a divide.$\square$

5 Structural conjectures on Lagrangian fillings

Let $\Lambda \subseteq (\mathbb {S}^3,\xi _\text {st})$ be a max-tb Legendrian link. The classification of embedded exact Lagrangian fillings $L\subseteq (\mathbb {D}^4,\lambda _\text {st})$ with fixed boundary $\Lambda$, up to Hamiltonian isotopy, is a central question. The only Legendrian $\Lambda$ for which a complete classification exists is the standard unknot [33]. In this case, the standard Lagrangian flat disk is the unique filling: there is precisely one exact Lagrangian filling, up to Hamiltonian isotopy.

The recent developments [20, 22, 23] show that such finiteness is actually rare: e.g. the max-tb torus links (n, m) admit infinitely many exact Lagrangian filling, up to Hamiltonian isotopy, if $n,m\ge 4$. It is proven in [20] that Legendrian representatives of infinitely many types of either torus, satellite or hyperbolic knots admit infinitely many Hamiltonian isotopy classes of embedded exact Lagrangian fillings. This final section states and discusses Conjectures 5.1 and 5.4, which might help towards our understanding of the classification of exact Lagrangian fillings of Legendrian links.

Geometric strategy Given $\Lambda \subseteq (\mathbb {S}^3,\xi _\text {st})$, we would like to know whether it admits finitely many Lagrangian fillings or not, and in the finite case provide the exact count. Theorem 1.1 provides insight for the class of Legendrian links $\Lambda \subseteq (\mathbb {S}^3,\xi _\text {st})$ that are algebraic links and, more generally, arise from a divide. Indeed, Lagrangian fillings for $\Lambda$ can be constructed by using the Lagrangian skeleta for the Weinstein pair $(\mathbb {C}^2,\Lambda )$ built in the statement. For instance, the inclusion of the Lagrangian Milnor fiber $L_{\tilde{f}}\subseteq \mathbb {L}_{\tilde{f}}$ provides an exact Lagrangian filling, and performing Lagrangian disk surgeries along the Lagrangian 2-disks in $\mathbb {L}_{\tilde{f}}\setminus L_{\tilde{f}}$, which bound vanishing cycles, will potentially yield new Lagrangian fillings. This strategy can be implemented in certain cases but, in general, one must be able to find an embedded Lagrangian disk in the new Lagrangian skeleton (with an embedded boundary curve), to perform the next Lagrangian disk surgery. Curves being immersed rather than embedded²⁸, might a priori represent a challenge.²⁹ This geometric scheme has the following algebraic incarnation.

Algebraic strategy Consider the intersection quiver $Q_{\vartheta (\tilde{f})}$ of vanishing cycles for a real morsification $\tilde{f}$, Lagrangian disk surgeries induce mutations of the quiver [96] and the (microlocal) monodromies of a local system serve as cluster $\mathcal {X}$-variables [23, 98]. Thus, the cluster algebra $\mathcal {A}(Q(f))$ associated to the quiver, as it appears in [47], governs possible exact Lagrangian fillings for the Legendrian link $\Lambda$. That is, a Lagrangian filling $L\subseteq (\mathbb {D}^4,\lambda _\text {st})$ yields a cluster chart for this algebra [51, 98], and the Lagrangian skeleta from Theorem 1.1 provide a geometric realization for the quiver in the form of an exact Lagrangian filling with ambient Lagrangian disks ending on it.

The recent developments [20, 51, 96, 98] and the existence of the Lagrangian skeleta in Theorem 1.1 shyly hint towards the fact that, possibly, Lagrangian fillings are classified by the cluster algebra $\mathcal {A}(Q(f))$. That is, every cluster chart in $\mathcal {A}(Q(f))$ is induced by precisely one exact Lagrangian filling.³⁰ It should be emphasized that this is not known for any $\Lambda \subseteq (\mathbb {R}^3,\xi _\text {st})$ except the standard Legendrian unknot. It is possible that the case of the Hopf link $\Lambda (A_1)$ can be solved by building on the techniques in [92], which classifies exact Lagrangian tori near the Whitney sphere;³¹ this is currently work in progress.

Having presented the available evidence, we state the following conjectural guide:

Conjecture 5.1

(ADE Classification of Lagrangian Fillings) Let $\Lambda \subseteq (\mathbb {R}^3,\xi _\text {st})$ be the Legendrian rainbow closure of a positive braid such that the mutable part of its brick quiver is connected. Then one of the following possibilities occur:

• 1. $\Lambda$ is smoothly isotopic to the link of the $A_{n}$-singularity. Then $\Lambda$ has precisely $\frac{1}{n+2}{2n+2\atopwithdelims ()n+1}$ exact Lagrangian fillings.

• 2. $\Lambda$ is smoothly isotopic to the link of the $D_{n}$-singularity. Then $\Lambda$ has precisely $\frac{3n-2}{n}{2n-2\atopwithdelims ()n-1}$ exact Lagrangian fillings.

• 3. $\Lambda$ is smoothly isotopic to the link of the $E_6$, $E_7$ or the $E_8$-singularities. Then $\Lambda$ has precisely 833, 4160, and 25080 exact Lagrangian fillings, respectively.

• 4. $\Lambda$ has infinitely many exact Lagrangian fillings.

The following comments are in order:

• (i) In [45], Fomin and Zelevinsky classify cluster algebras of finite type. This is an ADE-classification, parallel to the classification of simple singularities [9], the Cartan–Killing classification of semisimple Lie algebras, finite crystallographic root systems (via Dynkin diagrams) and the like. Thus, Conjecture 5.1 first states that $\Lambda$ will have finitely many exact Lagrangian fillings, up to Hamiltonian isotopy, if and only if the associated quiver is ADE.

• (ii) The case of $\Lambda =\Lambda _f$ an algebraic link associated to a non-simple singularity $f\in \mathbb {C}[x,y]$ of a plane curve follows from [20], and the case of a Legendrian $\Lambda$ with a non-ADE underlying quiver has recently been proven in [52]. These approaches are based on the following fact: if there exists an embedded exact Lagrangian cobordism from $\Lambda _-$ to $\Lambda _+$ and $\Lambda _-$ admits infinitely many Lagrangian fillings, then so does $\Lambda _+$. See [22, 86] and [20, Section 6]. This itself initiates the quest for finding the smallest Legendrian link which admits infinitely many exact Lagrangian fillings. At present, if we measure the size of a link $\Lambda$ as $\pi _0(\Lambda )+2g(\Lambda )$, $g(\Lambda )$ the (minimal) genus of a (any) embedded Lagrangian filling, the smallest known Legendrian link has $g(\Lambda )=1$ and two components $\pi _0(\Lambda )=2$; it is built in [22]. Intuitively, it is the geometric link corresponding to the $\tilde{A}_{2}$ cluster algebra.

• (iii) According to (ii) above, the missing ingredient for Conjecture 5.1 is showing that (1), (2) and (3) hold. For the $A_n$-case (1), it is known that there are at least the stated Catalan number worth of exact Lagrangian fillings, distinct up to Hamiltonian isotopy. This was originally proven by Pan [87] and subsequently understood in [98, 102] from the perspective of microlocal sheaf theory. It remains to show that any exact Lagrangian filling of $\Lambda (A_n)$ is Hamiltonian isotopic to one of those; the first unsolved case is the Hopf link $\Lambda (A_1)$ having exactly two embedded exact Lagrangian fillings.³² For the $\Lambda (D_n),\Lambda (E_6),\Lambda (E_7)$ and $\Lambda (E_8)$ cases in Conjecture 5.1, one needs to first find the corresponding number of distinct Lagrangian fillings, and then show these are all. The construction part should be relatively accessible, in the spirit of either [23, 87, 98], and it is reasonable to suspect that these many fillings can be distinguished using either augmentations or microlocal monodromies.³³

• (iv) The numbers appearing in Conjecture 5.1. (i)–(iii) are the number of cluster seeds for the corresponding cluster algebra. Precisely, consider a root system of Cartan-Killing type $X_n$, $e_1,\ldots ,e_n$ its exponents and h the Coxeter number. Then the numbers in Conjecture 5.1 are $N(X_n)=\prod _{i=1}^n(e_i+h+1)(e_i+1)^{-1}$ for $X_n=A_n,D_n,E_6,E_7,E_8$. It is natural to strengthen Conjecture 5.1. (iv) to: 4. There exist a natural bijection between Hamiltonian isotopy classes of exact Lagrangian fillings of $\Lambda$ and cluster seeds of the (natural) cluster A-structure on the augmentation variety of $\Lambda$, decorated with one marked point per component. (The bijection assigns to a Lagrangian filling L the set $H^1(L,\mathbb {C}^*)$ of $\mathbb {C}^*$-local systems on L, which is naturally a subset of the augmentation variety and a cluster chart.)

Note that Conjecture 5.1 has a natural analogue for $W(\Lambda )$. Namely, the Hamiltonian isotopy classes of closed exact Lagrangians in $W(\Lambda )$ are precisely given by the numerics above. This aligns with the spirit of the nearby Lagrangian conjecture, now for surface skeleta: if we interpret $W(\Lambda )$ as “generalized cotangent bundle” $T^*\overline{\mathbb {L}}$, where $\mathbb {L}$ is a Cal-skeleton for $\Lambda$, then the conjecture would be that any closed exact Lagrangian is Hamiltonian isotopic to a Lagrangian which is either a subset of $\overline{\mathbb {L}}$ or can be obtained from it via (iterated) Lagrangian disk mutations.

The brick graph of a positive braid is defined in [13, 94], it can be enhanced to a quiver, which we call the brick quiver, following the algorithm in [95, Section 3.1] or [51, Section 4.2], which itself generalizes the wiring diagram construction in [16, 43].

Remark 5.2

The hypothesis of the mutable part of its brick quiver being connected is necessary. We could otherwise add a meridian to any positive braid, which would create a disconnected quiver; the resulting cluster algebra would be a product with $A_1$, which preserves being of finite type. It stands to reason that adding a meridian to a Legendrian link $\Lambda$ would yield a Legendrian link $\Lambda \cup \mu$ with exactly twice as many Lagrangian fillings. It is clear that there are at least twice as many Lagrangian fillings for $\Lambda \cup \mu$, as there are two distinct Lagrangian cobordisms from $\Lambda$ to $\Lambda \cup \mu$. The simplest case is $\Lambda =\Lambda _0$ the standard Legendrian unknot and $\Lambda \cup \mu \cong \Lambda (A_1)$ the Hopf link, which should have $2=2\cdot 1$ Lagrangian fillings, in accordance with Conjecture 5.1. The next case would be $\Lambda =\Lambda (A_1)$, so that $\Lambda (A_1)\cup \mu \cong \Lambda (D_2)$, in line with $\Lambda (D_2)$ conjecturally having $4=2\cdot 2$ Lagrangian fillings.$\square$

Note that the article [22] has provided the first examples of Legendrian links $\Lambda \subseteq (\mathbb {S}^3,\xi _\text {st})$ which are not rainbow closures of positive braids and yet they admit infinitely many Lagrangian fillings, up to Hamiltonian isotopy. These Legendrian links have components which are stabilized, not max-tb, and thus they cannot be rainbow closures of any positive braid. It would be interesting to extend Conjecture 5.1 to a larger class of links, possibly including $(-1)$-framed closures of certain positive braids, e.g., those with Demazure product equal to a half-twist, as studied in [22].

Remark 5.3

To the author’s knowledge, [33, 87], Theorem 1.1, and the recent [20, 22, 23, 51, 52], constitute the current evidence towards Conjecture 5.1. Hints towards Conjecture 5.1 might have appeared in the symplectic folklore in one form or another: e.g. the advent of Symplectic Field Theory led to the mantra of “pseudoholomorphic curves or nothing”³⁴, the subsequent arrival of microlocal sheaf theory to symplectic topology led to “sheaves or nothing”. In the current zeitgeist, cluster algebras provide a new algebraic invariant that one might hope to be complete.³⁵$\square$

In the line of Remark 5.3, a natural strengthening of Conjecture 5.1, under same the hypotheses, would be to speculate that there exists precisely one Hamiltonian isotopy class of Lagrangian fillings per each cluster seed in the augmentation variety associated to $\Lambda \subseteq (\mathbb {R}^3,\xi _\text {st})$. Given our current understanding, this might as well be the case. The statement is correct for the unknot and current work in progress indicates that it is correct for the Hopf link.

Finally, an ADE-classification is often part of a larger classification,³⁶ involving a few additional families. For instance, simple Lie algebras are classified by connected Dynkin diagrams, which are $A_n,D_n,E_6,E_7,E_8$, known as the simply laced Lie algebras, and $B_n,C_n,F_4$ and $G_2$. These latter cases, $B_n,C_n,F_4$ and $G_2$, are interesting on their own right. For instance, simple singularities are classified according to $A_n,D_n,E_6,E_7,E_8$, and $B_n,C_n,F_4$ then arise in the classification of simple boundary singularities [9, Chapter 17.4], as shown in [10, Chapter 5.2]. (See also D. Bennequin’s [15, Section 8] and [7].) In general, the tenet is that $B_n,C_n,F_4$ and $G_2$ arise when classifying the same objects as in the ADE-classification with the additional data of a symmetry.³⁷ This a perspective (and technique) called folding, ubiquitous in the study of $B_n,C_n,F_4,G_2$, which is developed in [46, Section 2.4] for the case of cluster algebras.

Let us consider a Legendrian $\Lambda \subseteq (\mathbb {R}^3,\xi _\text {st})$, a Lagrangian filling $L\subseteq (\mathbb {R}^4,\lambda _\text {st})$, $\partial L=\Lambda$, and a finite group G acting faithfully on $(\mathbb {R}^4,\lambda _\text {st})$ by exact symplectomorphisms, inducing an action on the boundary piece $(\mathbb {R}^3,\xi _\text {st})$ by contactomorphisms. For instance, $s:\mathbb {R}^4\longrightarrow \mathbb {R}^4$, $s(x,y,z,w)=(-x,-y,z,w)$ is an involutive symplectomorphism which restricts to the contactomorphism $(x,y,z)\mapsto (-x,-y,z)$ on its boundary piece $(\mathbb {R}^3,\ker \{dz-ydx\})$. Let us define an exact Lagrangian G-filling of $\Lambda$ to be an exact Lagrangian filling L of $\Lambda$ such that $G(L)=L$ and $G(\Lambda )=\Lambda$ setwise. Also, by definition, we say $\Lambda \subseteq (\mathbb {R}^3,\xi _\text {st})$ admits a G-symmetry if there exists a faithful action of G by contactomorphisms on $(\mathbb {R}^3,\xi _\text {st})$ such that $G(\Lambda )=\Lambda$ setwise. Examples of such symmetries can be readily drawn in the front projection, as shown in Fig. 16 for $\Lambda (A_9),\Lambda (D_8),\Lambda (E_6)$ and $\Lambda (D_4)$. Following the tenet above, the following classification might be plausible:

Conjecture 5.4

(BCFG Classification of Lagrangian Fillings) Let $\Lambda (\beta )\subseteq (\mathbb {S}^3,\xi _\text {st})$ the Legendrian rainbow closure of a positive braid $\beta$:

• 1. $(B_n)$ If $\Lambda (\beta )=\Lambda (A_{2n-1})$, the $\mathbb {Z}_2$-symmetry $(x,z)\longrightarrow (-x,z)$ for the front depicted in Fig. 16 lifts to a $\mathbb {Z}_2$-symmetry of $\Lambda (A_{2n-1})$. Then $\Lambda (A_{2n-1})$ has precisely ${2n\atopwithdelims ()n}$ exact Lagrangian $\mathbb {Z}_2$-fillings.

• 2. $(C_n)$ If $\Lambda (\beta )=\Lambda (D_{n+1})$, the $\mathbb {Z}_2$-symmetry $(x,z)\longrightarrow (-x,z)$ for the front depicted in Fig. 16 lifts to a $\mathbb {Z}_2$-symmetry of $\Lambda (D_{n+1})$. Then $\Lambda (D_{n+1})$ has precisely ${2n\atopwithdelims ()n}$ exact Lagrangian $\mathbb {Z}_2$-fillings.

• 3. $(F_4)$ If $\Lambda (\beta )=\Lambda (E_6)$, the $\mathbb {Z}_2$-symmetry $(x,z)\longrightarrow (-x,z)$ in the front depicted in Fig. 16 lifts to a $\mathbb {Z}_2$-symmetry of $\Lambda (E_6)$. Then $\Lambda (E_6)$ has precisely 105 exact Lagrangian $\mathbb {Z}_2$-fillings.

• 4. $(G_2)$ If $\Lambda (\beta )=\Lambda (D_4)$, the $\mathbb {Z}_3$-symmetry in the front depicted in Fig. 16 lifts to a $\mathbb {Z}_3$-symmetry of $\Lambda (D^4)$. Then $\Lambda (D_4)$ has precisely 8 exact Lagrangian $\mathbb {Z}_3$-fillings.

Fig. 16

Legendrian fronts for $\Lambda (A_{2n-1}),\Lambda (D_{n+1}),\Lambda (E_6),\Lambda (D_4)$ with G-symmetries, $G=\mathbb {Z}_2,\mathbb {Z}_3$. The upper row exhibits these symmetric fronts as divides of the associated singularities, and the lower row depicts them in the standard front projection $(x,y,z)\mapsto (x,z)$ for a Darboux chart $(\mathbb {R}^3,\xi _\text {st})$

For the $G_2$-case in Conjecture 5.4.(4), it might be helpful to notice that the $D_4$-singularity is topologically equivalent to $f(x,y)=x^3+y^3$. The $\mathbb {Z}_3$-symmetry cyclically interchanges the three linear branches of this singularity. In particular, we can draw a front for the Legendrian $\Lambda (D_4)$ as the (3, 3)-torus link, the rainbow closure of $\beta =(\sigma _1\sigma _2)^6$.³⁸

For the $B_n$-case in Conjecture 5.4.(1), the construction of ${2n \atopwithdelims ()n}$ distinct Lagrangian $\mathbb {Z}_2$-fillings likely follows from adapting [87]. Indeed, in the $\mathbb {Z}_2$-invariant front for $\Lambda (A_{2n-1})$, as depicted in Fig. 16, there are n crossing to the left, equivalently right, of the $\mathbb {Z}_2$-symmetry axis. We can construct a $\mathbb {Z}_2$-filling of $\Lambda (A_{2n-1})$ by opening those n crossings in any order, with the rule that we simultaneously open the corresponding $\mathbb {Z}_2$-symmetric crossing.³⁹ Should one distinguish these $\mathbb {Z}_2$-fillings via their augmentations, as in [87], an appropriate G-equivariant Floer theoretic invariant (e.g., G-equivariant DGA and its augmentations) needs to be defined. The perspective of microlocal sheaves [102] yields combinatorics closer to those of triangulations [45, Section 12.1], modeling $A_n$-cluster algebras, and thus might provide a simpler route to distinguish these fillings. In either case, Conjecture 5.4 calls for a G-equivariant theory of invariants for Legendrian submanifolds of contact manifolds.

5.1 Some questions

We finalize this section with a series of problems on Weinstein 4-manifolds and their Lagrangian skeleta. To my knowledge, there are several unanswered questions at this stage, including checkable characterizations of Weinstein 4-manifolds of the form $W(\Lambda _f)$, where $\Lambda _f$ is the Legendrian link of an isolated plane curve singularity. Here are some interesting, yet hopefully reasonable, problems:

Problem 1

Find a characterization of Legendrian links $\Lambda \subseteq (\mathbb {S}^3,\xi _\text {st})$ for which $(\mathbb {C}^2,\Lambda )$, or $W(\Lambda )$, admits a Cal-skeleton. (Ideally, a verifiable characterization.)

For instance, if $\Lambda \subseteq (\mathbb {S}^3,\xi _\text {st})$ is the rainbow closure of a positive braid, then $W(\Lambda )$ can be shown to admit a Cal-skeleton by methods similar to the ones presented in this manuscript. In contrast, if $\Lambda$ is a stabilized Legendrian knot, then $W(\Lambda )$ does not admit a Cal-skeleton.

Problem 2

Find necessary and sufficient conditions for a Lagrangian skeleton $\mathbb {L}\subseteq (W,\lambda )$ to guarantee that the Stein manifold $(W,\lambda )$ is an affine algebraic manifold. Similarly, characterize Legendrian links $\Lambda \subseteq (\mathbb {S}^3,\xi _\text {st})$ such that $W(\Lambda )$ is an affine algebraic variety.

Note that the standard Legendrian unknot $\Lambda _0\cong \Lambda (A_0)\subseteq (\mathbb {S}^3,\xi _\text {st})$ and the max-tb Hopf link $\Lambda (A_1)\subseteq (\mathbb {S}^3,\xi _\text {st})$ yield affine Weinstein manifolds, as we have

$$\begin{aligned} W(\Lambda _0)\cong & {} \{(x,y,z)\in \mathbb {C}^3:x^2+y^2+z^2=1\},\\ W(\Lambda (A_1))\cong & {} \{(x,y,z)\in \mathbb {C}^3:x^3+y^2+z^2=1\}. \end{aligned}$$

By [21, Section 4.1], the trefoil $\Lambda (A_2)$ is also an example of such a Legendrian link, as

$$\begin{aligned} W(\Lambda (A_2))\cong \{(x,y,z)\in \mathbb {C}^3:xyz+x+z+1=0\}. \end{aligned}$$

Heuristic computations indicate that $\Lambda (A_3)$ and $\Lambda (D_4)$ also have this property. See [73, 74] for a source of necessary conditions, and [93] for (topological) skeleta of affine hypersurfaces.

Problem 3

Find necessary and sufficient conditions for a Lagrangian skeleton⁴⁰$\mathbb {L}\subseteq (W,\lambda )$ to guarantee that the Stein manifold $(W,\lambda )$ is flexible.⁴¹ (Again, a verifiable characterization.) Similarly, characterize $\Lambda \subseteq (\mathbb {S}^3,\xi _\text {st})$ such that $W(\Lambda )$ is flexible.

Note that affine manifolds $W\subseteq \mathbb {C}^N$ might be flexible [21, Theorem 1.1]. In particular, it could be fruitful to compare Lagrangian skeleta of $X_m=\{(x,y,z)\in \mathbb {C}^3:x^my+z^2=1\}$ for $m=1$ and $m\ge 2$, e.g. the ones provided in [93].

Problem 4

Suppose that a Weinstein 4-manifold $W=W(\Lambda )$ is obtained as a Lagrangian 2-handle attachment to $(\mathbb {D}^4,\omega _\text {st})$. Given a Cal-skeleton $\mathbb {L}\subseteq (W,\lambda )$, devise an algorithm to find one such possible Legendrian $\Lambda \subseteq (\partial \mathbb {D}^4,\xi _\text {st})$.

(Note that such a Legendrian $\Lambda$ might not be unique, i.e. it could be possible that two non-isotopic Legendrian knots $\Lambda _1,\Lambda _2$ might have Weinstein isomorphic traces $W(\Lambda _1)\cong W(\Lambda _2)$.)

Problem 5

Let $L\subseteq (W,\lambda )$ be a closed exact Lagrangian surface. Study whether there exists a Cal-skeleton $\mathbb {L}\subseteq (W,\lambda )$ such that $L\subseteq \mathbb {L}$. In addition, study whether there exists a Legendrian handlebody $\Lambda \subseteq (\#^k\mathbb {S}^1\times \mathbb {S}^2,\xi _\text {st})$, so that $W=W(\Lambda )$, and L is obtained by capping a Lagrangian filling of a Legendrian sublink of $\Lambda$.

See [106] for an interesting construction in the case of Bohr-Sommerfeld Lagrangian submanifolds and see [34] for a general discussion on regular Lagrangians. The nearby Lagrangian conjecture holds for $W=T^*\mathbb {S}^2,T^*\mathbb {T}^2$, thus the answer is affirmative in these cases.

Problem 6

Characterize which cluster algebras A can arise as the ring of functions of the augmentation stack of a Legendrian link $\Lambda \subseteq (\mathbb {S}^3,\xi )$.

By using double-wiring diagrams [16], (generalized) double Bruhat cells satisfy this property [95]. It is proven in [22, 51] that the cluster algebras $A(\tilde{D}_n)$ of affine $D_n$-type have this property. Heuristic computations indicate that the affine types $\tilde{A}_{p,q}$ also verify this [22]. It might be reasonable to conjecture that cluster algebras of surface type all have this property.

Here is a variation on this problem. Suppose that a cluster algebra A arises, e.g., as an augmentation variety associated to a Legendrian link $\Lambda$. An interesting problem might be to characterize those elements of the cluster automorphism group of A which arise as Legendrian loops of $\Lambda$. In certain cases, this is known to be the case for Grassmannian braid symmetries [20, 48], the square of the Donaldson–Thomas transformation [52] and the Zamolodchikov operator [66].

In general, relating geometric properties of Lagrangian fillings to algebraic properties of cluster algebras should be fruitful. For instance, already in Type A, it would be interesting to geometrically characterize those Lagrangian fillings of the (2, n)-torus links that yield positive cluster seeds. More ambitiously, it would seem useful to be able to access geometrically, e.g. via holomorphic curve counts, the $\mathbb {Z}^t$-tropical structure, or the $\mathbb {R}^+$-positive structure, of the cluster varieties associated to some Legendrian links.

Problem 7

Let $a_3(\Lambda )$ be the number of $A_3$-arboreal singularities of a Cal-skeleton $\mathbb {L}\subseteq (W,\lambda )$. Find the number $a_3(W):=\min _{\mathbb {L}\subseteq W}a_3(\mathbb {L})$, where $\mathbb {L}\subseteq W$ runs amongst all possible Cal-skeleta. In particular, characterize Weinstein 4-manifolds $(W,\lambda )$ with $a_3(W)=0$.

Problem 8

Develop a combinatorial theory of symplectomorphisms in ${\text {Symp}}(W,d\lambda )$ in terms of Cal-skeleta $\mathbb {L}\subseteq (W,\lambda )$.

This is being developed in the case $\dim (W)=2$ by using A’Campo’s tête-à-tête twists [5, Section 3], see also [6, Section 5]. A (symplectic) mapping class in ${\text {Symp}}(W,d\lambda )$ is a composition of Dehn twists in this 2-dimensional case. This is no longer the case in $\dim (W)=4$, e.g., due to the existence of Biran-Giroux’s fibered Dehn twists, confer [104, Section 3] and [107, Section 2]. Note that $\pi _0({\text {Symp}}(W))$ might be infinite even if W contains no exact Lagrangian 2-spheres [20].

Problem 9

Compare Cal-skeleta $\mathbb {L}_1\subseteq (W_1,\lambda _1)$, $\mathbb {L}_2\subseteq (W_2,\lambda _2)$ for exotic Stein pairs $W_1,W_2$. That is, $W_1$ is homeomorphic to $W_2$, but not diffeomorphic. In particular, investigate skeletal corks: combinatorial modifications on a Cal-skeleton that can produce exotic Stein pairs.

In [82], Naoe uses Bing’s house [17] to study some such corks.

Problem 10

Find a contact analogue of Turaev’s Shadow formula⁴² [103, Chapter 10] for the contact 3-dimensional boundary in terms of the combinatorics of a Cal-skeleton $\mathbb {L}\subseteq (W,\lambda )$. That is, find a contact invariant⁴³ of $(\partial W,\lambda |_{\partial W})$ which can be computed in terms of the combinatorics of $\mathbb {L}\subseteq (W,\lambda )$.