1 Introduction

With recent advancements in hardware technologies, miniaturized robotic platforms become increasingly viable systems in dealing with complex real-world problems (Dorigo et al., 2021). To counter the inevitable limitations to their capabilities imposed by their small sizes, cooperative deployment of these robotic platforms in large groups can be an effective design paradigm in the future. However, it is a challenging task to coordinate and control the collective intelligent system effectively. One crucial building block of intelligent collective behavior is collective decision-making. It refers to the process where a group of agents come to a global decision without a centralized control mechanism. Such processes can be found in the behaviors of many naturally existing systems, such as that of molecules in physical and chemical reactions (Glansdorff et al., 1973), cells in biological organisms (Karsenti, 2008), as well as animal herd behavior (Couzin & Krause, 2003). In such systems, agents rely on local interactions among themselves as well as with the environment to achieve decision-making behaviors that alter the global state of the collective (Camazine et al., 2001). Researchers have been attempting to replicate such processes on self-organized artificial swarm intelligence systems, which can potentially exhibit high robustness, flexibility, and scalability (Şahin, 2005).

Among the collective decision-making behaviors, consensus forming is important in ensuring the coherent operation of any decentralized system, and thus has received much attention in the study of both natural and artificial swarm intelligence systems (Leadbeater & Chittka, 2007; Brambilla et al., 2013). Depending on the size of the decision space, consensus-forming approaches have been divided into discrete approaches and continuous approaches, each designed to tackle the corresponding scenarios. Among the two categories, discrete consensus-forming problems are also referred to as best-of-n problems (Parker & Zhang, 2009), where agents collectively select the best decision out of a discrete set according to the associated qualities. Such decision-making scenarios are prevalent in natural intelligent swarms, including house-hunting behaviors of honey bees (Reina et al., 2017) and path-finding behaviors of ants (Goss et al., 1989). On the other hand, examples of continuous consensus formation problems include velocity matching (Olfati-Saber, 2006) and altitude alignment (Bauso et al., 2003) when controlling decentralized dynamic systems.

Regarding decision-making scenarios of different levels of complexity, different collective decision-making strategies have been proposed. Among best-of-n decision-making scenarios with fewer potential options than involved agents, the dominant category of methodology is opinion-based approaches (Valentini et al., 2017). This category of decision-making strategies draws inspiration from the decision-making behaviors of various insect species and is characterized by individual agents having an explicitly chosen option, usually with an individually computed associated quality. The agents will then attempt to recruit their peers to their opinion during the decision-making process, while also verifying the quality of their options via individual interaction with the environment. The process continues until a consensus is achieved. Various opinion-based approaches differ in terms of the method with which the agents exchange information and change their opinions. Popular decision-making strategies here include voter model (Valentini et al., 2014), majority rule (Valentini et al., 2015), cross inhibition (Reina et al., 2015), and k-unanimity (Scheidler et al., 2015). Due to the limitation of individual agents to singular opinions, opinion-based strategies suffer from a lack of scalability when the number of options approaches that of the number of agents, and coverage of all options cannot be ensured by the available agents during the decision-making process, as observed in works on discrete collective estimation problem (Shan & Mostaghim, 2021; Shan et al., 2021). In such instances, randomness can be introduced to the decision-making processes of opinion-based strategies and ensure decision-making accuracy at the cost of speed. Attempts of adapting opinion-based strategies to scenarios with higher numbers of options usually still keep them below the number of available agents in the swarm (Reina et al., 2017; Talamali et al., 2019).

Another effective way to tackle more complex multi-option collective consensus-forming scenarios, where the number of options is on the same scale as the number of agents, is to consider and compare multiple options in parallel during the decision-making process. One such approach is to use ranked voting systems to enable the agents to exchange their relative preferences among the potential options (Shan et al., 2021). This approach also enables consensus-formation regarding the ranking of available options, also referred to as collective preference learning problem, where a much-extended decision space of size n! is tackled but with constraints on the construction of the consensus scenario (Crosscombe & Lawry, 2021; Shan & Mostaghim, 2023). Another parallel approach is for the agents to compute the qualities of the potential options directly, while utilizing opinion pooling (Lee et al., 2018a, b) or belief fusion (Shan & Mostaghim, 2020, 2021) to maximize the accuracy of the quality estimation. The performances of both aforementioned strategies when facing multi-option scenarios, with the number of options ranging from a few to on the same order of magnitude to the number of agents, have been well tested in previous literature (Shan & Mostaghim, 2021; Shan et al., 2021; Lee et al., 2018b). They are shown to be superior to opinion-based approaches in such scenarios when keeping a constant communication bandwidth constraint (Shan & Mostaghim, 2022).

On the other hand, continuous consensus-forming problems have been extensively studied from the perspective of decentralized multi-body vehicle control, in terms of unifying the speed, direction or location of the constituent vehicles(Ren & Beard, 2008). Similar methodologies can be applied to forming consensus regarding environmental features, such as in continuous collective estimation problems (Strobel et al., 2020). In continuous consensus scenarios, there is an ordinal ordering between different decisions, as well as a correlation in associated quality between decisions that are in proximity within the decision space. In addition, due to the continuous nature of the decision space, the decision qualities cannot be fully enumerated. Instead, agents assume a convexity of quality in the decision space and interpolate the desired result from those sampled by their peers.

The gap between the two categories encompasses many-option consensus-forming scenarios, where the decision space is still discrete, but its size exceeds that of the swarm, thus negatively affecting the performances of consensus approaches that rely on the enumeration of potential options. In this paper, we investigate the relative viabilities of approaching such a many-option consensus-forming scenario by extending both existing multi-option consensus-forming approaches and continuous consensus-forming approaches. The investigated scenario is a many-option discrete collective estimation scenario, which is extended compared to those used in previous related works (Shan & Mostaghim, 2021, 2022). This is a collective perception-based decision-making scenario (Valentini et al., 2016), and has proven to be capable of flexible configuration of decision-making problems of different levels of complexity and difficulty. As a benchmark continuous consensus strategy, we compare the performances of the considered discrete decision-making strategies with those of linear consensus protocol, a classic continuous consensus forming strategy for multi-agent systems (Olfati-Saber & Murray, 2004), and keep the implementation similar to previous literature on continuous collective estimation (Strobel et al., 2020). We also investigate the performances of the considered algorithms when facing both unordered and ordered options by constructing experimental scenarios whose number of options can be changed in two ways: changing the number of features and changing the level of decision space discretization, respectively.

2 Related works

Binary collective perception problem has been proposed by Valentini et al. (2016). The experimental setting consists of an arena filled with tiles of two colors. A series of opinion-based approaches are tested on a swarm of mobile robots with the aim of collectively determining the prevalent color out of the two. In the classical version of the problem, there are two available decisions and the respective fill ratios of the two colors are the associated qualities. This problem has since then been extended to multi-feature scenarios (Ebert et al., 2018; Bartashevich & Mostaghim, 2021), where the number of colors and thus potential options is extended to more than 2. It has been demonstrated that both opinion-based and belief fusion approaches can effectively handle multi-option scenarios.

Another extension to classical collective perception scenarios is collective estimation, where the robots aim to collectively determine the exact fill ratio of observed colors in the experimental arena (Strobel et al., 2018, 2020). Limiting the collective estimation problem into discrete fill ratio hypotheses has enabled the application of parallel discrete consensus-forming techniques such as belief fusion (Shan & Mostaghim, 2020, 2021) and ranked voting (Shan et al., 2021). In addition, parallel decision-making approaches have the benefit of enabling positive feedback within the decision-making process, which ensures fast and accurate convergences compared to the opinion-based approaches which are more constrained in terms of the speed versus accuracy trade-off.

Majority rule is a way to generate consensus in many naturally existing intelligent swarms and has been an important decision-making strategy for opinion-based approaches (Montes de Oca et al., 2011). It has been applied to various best-of-n problems, such as site selection (Valentini et al., 2015) and collective perception (Valentini et al., 2016). In best-of-n problems, majority rule decision-making strategies are usually implemented as follows. Individual agents have the capability to independently verify the quality of their current options during exploration. They will then seek to switch their current options to those of their peers if the majority of them possess a particular opinion. In order for the swarm to converge to the desired option, the frequency of opinion dissemination is modulated with respect to the computed option quality by the individual agent, such that agents with high-quality options spread their opinions further. The modulation can either be done by modifying the lengths of the control loops of the agents (Valentini et al., 2015) or by adding delays for opinion dissemination after the adoption of new opinion (Montes de Oca et al., 2011).

For multi-option scenarios, the majority rule decision-making mechanism can be extended using ranked voting to accommodate more potential options. Such approaches have been tested on discrete collective estimation scenarios (Shan et al., 2021). Different from single-vote implementations, the ranked voting strategy enables the agents to convey the relative qualities of the potential options via explicit message passing, thus reducing the necessity of dissemination frequency modulation. This leads to higher hardware requirements but also better performances compared to opinion-based approaches (Shan & Mostaghim, 2022).

Belief fusion decision-making strategies have their origins in consensus-forming techniques for artificial multi-agent systems, such as sensor networks (Hoballah & Varshney, 1989), that are capable of complex communication. They have also seen applications in site selection problems (Lee et al., 2018a, b) as well as discrete collective estimation problems (Shan & Mostaghim, 2020, 2021). In such strategies, the agents use both individual exploration and communication with their peers to obtain accurate estimates of the option qualities, which are then used by the agents to pick the desired option individually.

Comparison of opinion-based and parallel decision-making approaches while holding communication bandwidths constant has also been performed in order to provide a fair comparison of their performances (Shan & Mostaghim, 2022). It has been demonstrated that spending limited communication capacity on transmitting information regarding the relative qualities of multiple options is justified in terms of decision-making performances.

For any discrete consensus-forming strategy, non-linear positive feedback is crucial in ensuring fast and stable consensus (Leonard et al., 2024). It is defined as an increase in commitment by an individual agent to a particular decision as the number of already committed agents increases in a collective (Nicolis et al., 2011). Its benefit has also been supported by previous studies on discrete collective estimation. However, it has also been observed that strong positive feedback can cause the swarm to converge to a particular opinion without adequate environmental exploration, leading to erroneous results in consensus-forming tasks regarding global environmental features (Shan & Mostaghim, 2021).

Both ranked voting and belief fusion approaches face scaling communication and computation complexities as the number of options increases. Thus, when facing more complex decision-making scenarios, it becomes increasingly costly to track the qualities of all potential options exactly, especially transmitting the option qualities during the decision-making process. This limits the application of the aforementioned parallel collective decision-making approaches in more complex many-option to continuous collective decision-making scenarios.

For continuous consensus scenarios, the classical approach has been linear consensus strategies (Olfati-Saber et al., 2007). Such strategies iteratively update the decision variables by a value that linearly scales with the agent’s level of opinion divergence with its neighbors. Newer approaches build on top of linear consensus approaches by addressing their shortcoming when facing lower connectivity (Beal, 2016), non-linear system dynamics (Hui et al., 2008) or system delays (Xiao & Wang, 2008). When applied to a collective estimation problem with no constraints by the agents to change their decisions, we follow previous literature and apply a basic version of continuous consensus: the linear consensus protocol (Strobel et al., 2020). In the control of multi-body intelligent systems, a coherent collective behavior often requires that the agents’ velocities to be inexact consensus when responding to perturbations (Cavagna et al., 2022). However, in the investigated discrete collective perception problem, such effects are not modelled, therefore we simplify the problem of continuous consensus and only look at the accuracy, speed and uniformity of the consensus to gauge the performances of the investigated algorithms.

3 Problem statement

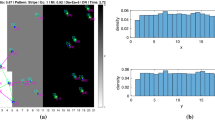
In this paper, we have extended the discrete collective estimation scenario investigated in previous related works (Shan & Mostaghim, 2020, 2021; Shan et al., 2021; Shan & Mostaghim, 2022) in terms of the problem complexity. The experimental arena is as shown in Fig. 1. The environment is filled with tiles composed of mixtures of different features represented using different colors, whose intensity s varies from 0 to 1 in every tile. The mean intensity of a particular color across all tiles is referred to as the fill ratio of that particular color.

Fig. 1
figure 1

Example of the experimental environment investigated in this paper; Red/yellow shows the pattern of the arena floor; Black shows the mobile robots roaming the arena (Color figure online)

Full size image

All tiles of the experimental arena can be expressed as follows:

$$\begin{aligned} ArenaTiles = \begin{bmatrix} \underline{T}_{0, 0} &{}&{} \underline{T}_{0, 1} &{}&{} \underline{T}_{0, 2} &{}&{}... \\ \underline{T}_{1, 0} &{}&{} \underline{T}_{1, 1} &{}&{} \underline{T}_{1, 2} &{}&{}... \\ \underline{T}_{2, 0} &{}&{} \underline{T}_{2, 1} &{}&{} \underline{T}_{2, 2} &{}&{}... \\ &{}&{}... \end{bmatrix}{.} \end{aligned}$$
(1)

For a tile on the ath row and bth column, the composition of colors is expressed using vector \(\underline{T}_{a,b}\). \(s_c\) represents the intensity of the color c for all C colors present. The intensities on a single tile sum up to 1:

$$\begin{aligned} \underline{T}_{{a,b}} = \begin{bmatrix} s_0&\,&s_1&\,&s_2&\,&...&\,&s_{C-1} \end{bmatrix}, \sum s = 1 {.} \end{aligned}$$
(2)

A group of mobile robots roam the arena, and their goal is to collectively determine the fill ratios for all observed colors. For the discrete collective decision-making strategies investigated, this is done to a predetermined decision space discretization precision P, which is varied together with the number of colors C to change the number of options the robots face. Different from the multi-feature decision-making scenario in Ebert et al. (2018), both the intensities of all colors in a single cell and the fill ratios of all colors sum to 1. Thus, in our experiments, there is a correlation among the observed color intensities, as encountering one color reduces the expected probability of encountering other colors. We therefore interpret a single decision by agent i regarding the fill ratios of the arena as an estimation of those of all present colors in the form of \(\underline{d}_i=\begin{bmatrix} d_{i,0}&\,&d_{i,1}&\,&...&\,&d_{i,C-1} \end{bmatrix}\). The decision space is a high-dimensional right-angle simplex, where the number of dimensions is \(C-1\) and the number of possible options per dimension is 1/P. The whole decision space has N distinct fill ratio options. N has the scale of \(O(\frac{1}{P}^C)\).

The number of potential options scales exponentially with the number of features C and inversely with the level of discretization precision P. We investigate both methods of changing the number of options. The key distinction between increasing the number of features and the level of discretization precision is that the former introduces unordered and weakly correlated decisions in terms of quality by expanding the decision space, while the latter introduces ordered and strongly correlated decisions in terms of quality by more finely dividing an existing decision space. Details of the generation of experimental environments are shown in Sect. 5.1

The robots are assumed to be simple reactive agents with limited communication, sensory and processing capabilities. They can only communicate with their peers within a limited distance, and also only detect the color of the arena ground directly beneath themselves.

4 Methodology

In this section, we present the details of the decision-making strategies investigated in this paper. We start with the introduction of the control mechanisms used for environmental exploration, which are shared by all considered strategies. We then present the three considered decision-making strategies applied to the aforementioned discrete collective estimation problem, namely iterative ranked voting (RV), discrete Bayesian belief sharing (DBBS) and linear consensus protocol (LCP). The former two are discrete consensus-forming strategies, while the latter is a continuous consensus-forming strategy.

4.1 Control mechanisms for environmental exploration

For all considered decision-making strategies, the robots use the same mechanism to explore the environment and obtain their own estimates of the fill ratio of the observed colors. Individual robots explore the experimental environment and form their own estimations, while communicating with their peers in order to converge to a consensus.

Table 1 Low-level control mechanism used to implement random walk
Full size table

The low-level mechanism that controls the movement of the robots during their environmental exploration is a finite-state machine with two possible motion states A and B, which alternate after each other, as shown in Table 1. They correspond to moving forward in a straight line and turning in place in a random direction respectively. The transitions are controlled by timers with randomly distributed lengths sampled from exponential distribution \(\text {exp}(40)s\) for \(A\xrightarrow {}B\) and uniform distribution \(\mathcal {U}(0,4.5)s\) for \(B\xrightarrow {}A\). Robot in motion state A will also switch to motion state B when an obstacle is detected in front of it, in order to avoid collisions.

For both discrete decision-making strategies, RV and DBBS, the decision space is discretized into a list of potential hypotheses with respect to the decision space discretization precision P. The robots use the following Bayesian statistics-based method to compute the likelihoods of the available hypotheses. The implementation here is similar to in previous literature on discrete collective estimation (Shan & Mostaghim, 2021; Shan et al., 2021; Shan & Mostaghim, 2022) but extended to accommodate more than 2 colors. Every robot stores a list of potential fill ratio hypotheses of all colors in a matrix H of size \(N\times C\) (we do not require \(N=C\)) as shown:

$$\begin{aligned} H=\begin{bmatrix}\underline{h}_0 \\ \underline{h}_1 \\ ... \\ \underline{h}_{N-1} \end{bmatrix} \text { where } \underline{h}_n = \begin{bmatrix}h_{n,0}&h_{n,1}&...&h_{n,C-1} \end{bmatrix}. \end{aligned}$$
(3)

Every row is a hypothesis consisting of the fill ratio combinations of all C considered colors, and is a potential option by the agents. They are computed using both the number of colors C and the discretization precision P by enumerating all possible fill ratios for individual colors from 0 to 1 and excluding the entries where the sum of fill ratios exceeds 1. It is assumed that the number of colors c and the discretization precision P are known beforehand, and thus this calculation is done before deployment.

During its environmental exploration, robot i stores the beliefs for every hypothesis computed from its environmental exploration in array \(\underline{\rho }_i\) of length N as follows:

$$\begin{aligned} \underline{\rho }_{i}= & {} \begin{bmatrix}l_0&l_1&l_2&...&l_{N-1} \end{bmatrix}^T \end{aligned}$$
(4)
$$\begin{aligned} \underline{\rho }_{i,0}= & {} \begin{bmatrix}1/N&1/N&1/N&...&1/N \end{bmatrix}^T {.} \end{aligned}$$
(5)

Every entry l represents the computed likelihood of a single hypothesis. All entries are initialized to value 1/N at the start of an experimental run when the robot does not have any information regarding the environment.

At every control loop, a robot makes an observation of the color of the ground beneath itself, if it is moving forward in motion state A. Observation collection is limited to during forward motion in order to prevent an agent from collecting multiple observations at the same location. The robot detects a random color present in the tile beneath it. The intensities of the colors on that tile are used as weights to determine which color is detected. The result is stored in an array of size C, with only the entry associated with the detected color being 1 while the others being 0. This can be represented as a weighted sampling operation from a set of vectors as follows:

$$\begin{aligned}{} & {} \text {{When the robot is on coordinate (a,b)}: }\underline{ob}\in _R\left\{ \begin{bmatrix} 1 \\ 0 \\ ... \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 1 \\ ... \\ 0 \end{bmatrix}... \begin{bmatrix} 0 \\ 0 \\ ... \\ 1 \end{bmatrix}\right\} \end{aligned}$$
(6)
$$\begin{aligned}{} & {} {\text {Sampling weights: } \underline{T}_{a,b}} = \begin{bmatrix} s_0&\,&s_1&\,&...&\,&s_{C-1} \end{bmatrix}{\text {respectively.}} \end{aligned}$$
(7)

The likelihood of making a color observation, given that a particular hypothesis is true, is the fill ratio of the color in the hypothesis, hence can be computed as \(H\cdot \underline{ob}\). Therefore, after each observation, the belief of robot i \(\underline{\rho }_i\) is modified by iteratively performing element-wise product (represented as \(\circ\)) of the observation likelihoods as follows:

$$\begin{aligned} \underline{\rho }_{i,t}=\text {normalize}(\underline{\rho }_{i,t-1} \circ (H \cdot \underline{ob})) {.} \end{aligned}$$
(8)

The iterative updates allow the belief of individual robots to gradually converge to the most likely fill ratio hypothesis.

For LCP, robot i only records the number of instances where each color is observed in array \(\underline{counter}_i\) of size C. It is updated after every observation as:

$$\begin{aligned} {\underline{counter}_{i,t}=\underline{counter}_{i,t-1} + \underline{ob}}{.} \end{aligned}$$
(9)

From here, the estimation proportion of colors can be easily calculated as:

$$\begin{aligned} \underline{r}_i=\underline{counter}_i/{||}\underline{counter}_i {||_1.} \end{aligned}$$
(10)

For all considered strategies, we assume a separate process of determining whether consensus has been achieved runs in parallel on all robots and terminates the decision-making process when consensus is reached for a certain period of time.

4.2 Decision-making strategies investigated

In this section, we present the details of the decision-making strategies investigated in this paper. We will cover the decision-making mechanisms of each strategy considered, how we are tuning the decision-making behavior of each strategy via parameters, and how we are controlling the communication bandwidth to achieve a fair comparison.

4.2.1 Iterative ranked voting

Algorithm 1 shows our implementation of a ranked voting-based (RV) decision-making strategy. We consider the best-performing voting system investigated in previous work on the subject (Shan et al., 2021), Borda count. We have modified the decision-making mechanism to suit a many-option scenario compared to previous implementations in discrete collective estimation works (Shan et al., 2021; Shan & Mostaghim, 2022), and is similar to the implementation in another previous work tackling the collective ranking problem (Shan & Mostaghim, 2023).

Algorithm 1
figure a

Iterative Ranked Voting (RV)

Full size image

Under RV decision-making strategy, robot i stores its current preference among the potential options in a ranked ballot \(\underline{ballot}_i\), which is initialized as an array of \(-1\)s representing that none of the options has been ranked. The robot starts a control loop by collecting an observation on the color of the arena floor beneath itself (line 3). Its environmental observations are stored in terms of the likelihoods of the potential options in \(\underline{\rho }_i\) (line 4). With the probability of the evidence rate \(r_e\), the robot updates its ballot \(\underline{ballot}_i\) with that computed from its observations \(\underline{\rho }_i\). \(\underline{\rho }_i\) is first converted to the ranking of the potential options with respect to the computed qualities via two consecutive argsort operations, which returns the indices that would sort the input elements in ascending order. The ranking is then combined with the robot’s current ballot via a Borda count ranked voting system. In implementation, the sorting operation has to give random rankings when facing tied options, such that no option is given a bias (line 5).

The robots then exchange their ballots with each other by broadcasting and receiving them through peer-to-peer communication (line 7 and 11). The ballots transmitted are limited in length to \(\eta N\), where the unranked options represent those with the least preference and are given the highest ranking of \(\eta N\) when the election is conducted. Robot i performs a pairwise election using its own ballot and the received ballot from robot j, if one is received (line 8–9). The combination of the two ballots is done in the same Borda count ranked voting system during environmental exploration (line 9). The robot spends the rest of the control loop broadcasting its ballot randomly at a probability \(\phi\), which is computed from \(\eta\) and works to keep the communication bandwidth between robots at the required level (line 11). The chosen decision of the robot \(\underline{d}_i\) is then obtained by choosing the hypothesis ranked first in the robot’s ballot (line 12).

The behavior of the RV decision-making strategy is controlled via the two parameters \(r_e\) and \(\eta\). \(r_2\) controls the relative frequency, and thus importance, between environmental exploration and communication with peers in the decision-making process. A higher \(r_e\) leads to a greater emphasis on individual exploration and vice versa. While \(\eta\) controls the strength of consensus enforcement within the robot swarm. As \(\eta\) increases, the number of considered options, thus weakening the consensus enforcement. At the same time, since the communication frequency \(\phi\) is inversely correlated with \(\eta\), a higher \(\eta\) value reduces the frequency of communication between robots and has the similar effect of weakening consensus enforcement.

4.2.2 Discrete bayesian belief sharing

Algorithm 2 shows our implementation of belief fusion decision-making strategy, discrete Bayesian belief sharing. It is similar to in previous related works (Shan & Mostaghim, 2021, 2022), with modifications made mainly to improve the stability of the algorithm.

Under this strategy, a robot computes the likelihoods for every considered hypothesis h given past observations ob. From Bayes’ theorem, we can obtain the following:

$$\begin{aligned} P(h|ob_0...ob_{t-1})=\frac{P(ob_0...ob_{t-1}|h)P(h)}{P(ob_0...ob_{t-1})}{.} \end{aligned}$$
(11)

Both the prior probability P(h) and the marginal likelihood \(P(ob_0...ob_{t-1})\) are assumed to be the same for all hypotheses. We can then apply the chain rule as follows:

$$\begin{aligned} P(ob_0...ob_{t-1}|h)= P(ob_0|h)P(ob_1|h, ob_0)...P(ob_{t-1}|h,ob_0...ob_{t-2}){.} \end{aligned}$$
(12)

Assume the observations \(ob_0\) to \(ob_{t-1}\) are all independent of each other, we have as follows:

$$\begin{aligned} P(ob_0...ob_{t-1}|h)= P(ob_0|h)P(ob_1|h)...P(ob_{t-1}|h){.} \end{aligned}$$
(13)

Here P(ob|h) is the probability of making an observation ob when hypothesis h is true, and is equal to the fill ratio of the associated color under that hypothesis.

The robot thus computes the quality array for decision making \(\underline{\rho }^*_i\) as the likelihoods of all considered hypotheses by taking an element-wise product of the probabilities of seeing the observed colors in the past observations by itself and its peers, as follows:

$$\begin{aligned} \underline{\rho }^*_i=\left( \prod _t H\cdot \underline{ob}_t\right) \left( \prod _{t'} H\cdot \underline{ob}'_{t'}\right) ^w{.} \end{aligned}$$
(14)

Here \(\underline{ob}\) are observations made by the robot itself, while \(\underline{ob}'\) are observations made by the robot’s peers. The latter is applied with a weight w that is adjustable via the algorithm’s parameters to control the strength of consensus enforcement in the swarm.

Algorithm 2
figure b

Discrete Bayesian Belief Sharing (DBBS)

Full size image

In our implementation, the robot starts its control loop with a similar environmental exploration compared to in RV strategy. The difference is that the computed quality estimates \(\underline{\rho }_i\) are bounded to a minimum value of 0.001/N to avoid underflow during the subsequent belief fusion process (line 5). During peer-to-peer communication, the robots exchange \(\underline{\xi }\) with each other (line 7 and 12). It is computed from a robot’s own quality estimates \(\underline{\rho }_i\) and its record of previously received quality estimates from its peers \(\underline{\rho }'_i\), with the latter subjected to a decay coefficient \(\mu\). Both \(\underline{\xi }\) and \(\underline{\rho }'\) are stored on a logarithmic scale to ensure numerical stability and prevent underflow (line 11). If received, \(\underline{\xi }_j\) will be used to update the quality estimates record of robot i \(\underline{\rho }'_i\), with the original value subjected to decay coefficient \(\lambda\). The normalization here is done by shifting all entries such that their mean is 0 (line 9). The decision is computed by taking the hypothesis with the highest quality when combining \(\underline{\rho }\) and \(\underline{\rho }'\) according to Equation 13 (line 13).

The decision-making behavior of the DBBS algorithm is controlled by the two decay coefficients \(\lambda\) and \(\mu\), which change the weight (w in Equation 13) of the neighbors’ opinions in the decision-making process of any robot. They have the same effects as in previous related works (Shan & Mostaghim, 2021, 2022). A higher value in either coefficient increases the strength of consensus enforcement, \(\lambda\) via increasing the weight of previous observations, while \(\mu\) via increasing the weight of neighbors’ opinions.

4.2.3 Linear consensus protocol

To gauge the validity of using the aforementioned discrete decision-making strategies in the investigated scenarios with high numbers of options, we employ the linear consensus protocol (LCP) as a baseline algorithm. We keep a similar implementation as in Strobel et al. (2020).

Algorithm 3
figure c

Linear Consensus Protocol (LCP)

Full size image

Different from the aforementioned discrete decision-making strategy, under LCP an individual robot stores its estimation of the fill ratios of every color in an array \(\underline{r}_i\) of size C, while the collected observations are stored in an array \(\underline{counter}_i\) of the same length. When an observation is collected during environmental exploration, \(\underline{counter}_i\) is updated by adding 1 to the occurrence of the observed color (line 4). The estimated fill ratios \(\underline{r}_i\) are obtained by computing the proportion of each color observed (line 5). Convergence to a consensus is encouraged within the swarm by the exchange of the robots’ decision arrays \(\underline{d}_i\) (line 10 and 18), which are collected to update a robot’s own decision \(\underline{d}_i\) via a numerical average of the robot’s previous decision, the fill ratio estimates from environmental exploration \(\underline{r}_i\) and all collected decisions from its peers stored in the set R. The size of R is the parameter l and is used to control the decision-making frequency of the swarm. A higher l means less frequent decision-making and each collected message has a lower impact on the computed final decision, leading to weaker consensus enforcement.

5 Experiments and results

In this section, we present our experiments in detail. We first introduce our experimental setup, focusing on the environmental settings and the parameter settings. Then, we show our experimental results, followed by analysis.

5.1 Experimental setup

Our experiments are done in a simulated physics-based environment constructed using Python.Footnote 1 The 20 simulated robots have the physical specification of e-pucks (Mondada et al., 2009) with a linear speed of 0.16 m/s, a rotational speed of 0.75 rad/s, a communication range of 0.5 m and a control loop length of 1 s. To maintain similar levels of data transmission between the compared strategies, we have utilized similar assumptions regarding the communication bandwidths as in previous related works (Shan & Mostaghim, 2022) shown in Table 2 and varies the communication probability \(\phi\) for the investigated strategies to control the communication bandwidth used. Our simulated communication paradigm seeks to model the operation of short-ranged peer-to-peer communication methods such as infrared (Kahn & Barry, 1997). The communication is strictly peer-to-peer, and is only in the form of one robot broadcasting a message and another robot receiving it. An individual robot has no uniquely identifying indices. If multiple robots within a neighborhood are broadcasting at the same time, a random message would be picked up by a receiving robot. The interference between a communicating pair and other robots is assumed to be minimal.

Table 2 Assumptions on the message format and sizes for all considered strategies
Full size table
Algorithm 4
figure d

Generation of experimental environment

Full size image

The experimental environment is extended to a higher number of environmental features and potential options compared to previous studies on the subject (Shan & Mostaghim, 2021; Shan et al., 2021). The environment is a 2-dimensional \(2{ }m\times 2{ }m\) arena covered by 400 tiles. Each tile has a mix of the considered colors of different proportions that sum up to 1, as shown in Fig. 2. We generate the experimental environments with an iterative approach to maintain the constraints of local color intensities while reaching the required fill ratio for the whole arena, as shown in Algorithm 4.

In line with previous related works, we have experimented on environments with different distributions of features, namely random distribution (Fig. 2a, b) and concentrated distribution (Fig. 2c). The generation of the two categories of environments is controlled by the parameter Pattern in Algorithm 4, while the level of concentration is controlled by parameter \(\alpha\). Environments with randomly distributed features are generated by randomly generating a color distribution for every color at every tile that has the mean equal to the desired fill ratio across the entire arena (line 4–7), and then normalizing all colors at every tile such that they sum up to 1 (line 10). On the other hand, a concentrated pattern of distribution is generated through an iterative process, where layers of radially distributed color blocks are placed at random locations and bring the fill ratios progressively closer to the required fill ratio (line 13–24). In this paper, the level of concentration \(\alpha\) is set to 0.5 for all experiments with concentrated feature distributions.

Fig. 2
figure 2

Examples of the experimental environments used a environment with 2 colors b environment with three colors c environment with concentrated distribution of features (Color figure online)

Full size image

Before the decision-making process, the decision space for every robot is computed. For LCP, it is the real number space of \(\underline{d}_i \in \Re , \sum \underline{d}_i=1\). For RV and DBBS, the decision space is discretized with respect to the required decision precision P into \(\begin{bmatrix} 0&1P&2P&...&1 \end{bmatrix}\) representing the fill ratio hypotheses for each individual color. The hypotheses are concatenated to form the fill ratio hypotheses of all considered colors, with those having a sum greater than 1 across all colors removed from the hypotheses list.

In order to compare the performances of both discrete and continuous collective decision-making strategies considered. We measure the performances using three metrics, scatter at convergence, error at convergence, and convergence time.

The scatter of all robots’ opinions at time t is defined as the sum of Euclidean distances between the centroid of all decisions regarding the fill ratios within the swarm and the individual decisions of the robots.

$$\begin{aligned} \text {Scatter}_t=\sum _{\forall i'}(\text {mean}_{\forall i}(\underline{d}_{i,t})-\underline{d}_{i',t})^2 \end{aligned}$$
(15)

Convergence is achieved when the scatter is at a minimum during an experimental run, limited to a time limit of 1200 s. The scatter at convergence can be represented as follows.

$$\begin{aligned} \text {ConvScatter}=\min (\text {Scatter}_t) \end{aligned}$$
(16)

The error at convergence is defined as the total absolute error between all robot’s fill ratio decisions and the true fill ratios \(\underline{fr}\) at the time of convergence.

$$\begin{aligned} t*= & {} \text {argmin}_{t}(\text {Scatter}_t) \end{aligned}$$
(17)
$$\begin{aligned} \text {ConvError}= & {} \sum _{\forall i}\text {abs}(\underline{fr} - \underline{d}_{i,t*}) \end{aligned}$$
(18)

Finally, convergence time is defined as the time taken to reach \(90\%\) of the minimum scatter value from the maximum scatter value during the experiment.

$$\begin{aligned} \text {ConvTime}=\min (t) \forall t {: \text {Scatter}_t} \le 0.9 \min (\text {Scatter}_t) + 0.1 \max (\text {Scatter}_t) \end{aligned}$$
(19)

The fill ratios tested for every considered number of features are shown in Table 3. For every number of features, two different fill ratio configurations are tested, with 40 experimental runs conducted for each fill ratio scenario at every parameter configuration of the considered strategies, as shown in Table 4. The aggregate across the two fill ratio configurations is used to determine the performances of the considered strategies at the corresponding parameter configurations. The performances of the considered strategies at different parameter settings are used to gauge the trade-offs between different performance metrics at different decision-making difficulty levels. To this end, we have employed a similar multi-objective analysis framework as in previous related works (Shan & Mostaghim, 2021; Shan et al., 2021; Shan & Mostaghim, 2022) and pay attention to the Pareto fronts of the performances in the error versus convergence time speed. To quantify the extent of the trade-off, we measure the spread of the Pareto fronts, which is computed as the volume bounded by the extreme points on the Pareto front. A higher spread means a more significant trade-off between speed and accuracy in the decision-making process, while a spread of 0 means the existence of a single best parameter configuration for the algorithm in that particular scenario.

Table 3 Fill ratios tested for every considered number of features and the resulting number of options at different discretization precision levels
Full size table
Table 4 Parameter values used in the experiments for all considered strategies
Full size table

5.2 Performances of the considered strategies with respect to different numbers of environmental features

In this subsection, we present the performances of the considered algorithms at different numbers of environmental features, i.e. different numbers of colors in the arena. The error versus convergence speed Pareto fronts of the considered strategies’ mean performances at different parameter configurations are shown in Fig.3a. The solid markers show the error versus convergence time performances at parameter configurations on the Pareto fronts, with the solid lines showing the Pareto fronts. The transparent markers show the position of the performances in the 3D space when considering scatter.

Comparing the performances of both discrete strategies RV and DBBS versus those of LCP in Fig.3a, it can be shown that discrete decision-making strategies have superior performances in terms of the error versus convergence time trade-off, as they outperform the Pareto fronts of LCP for all tested scenarios. RV and DBBS also produce lower scatter at convergence, showing a stronger ability to reliably reach consensus compared to LCP. In Fig.3a when the environmental features are randomly distributed, as the number of environmental features increases, the performances of both discrete strategies experience a significant drop in terms of convergence speed. On the other hand, LCP’s performances experience a drop in convergence speed on the top-left side of the Pareto fronts. As observed in Fig.3b, its performances also experience a slight drop in accuracy when facing more environmental features.

Fig. 3
figure 3

Performances of the considered strategies in all metrics when facing different numbers of randomly distributed environmental features a Error versus convergence time Pareto fronts, 3D space also includes scatter at convergence b Scatter plot for all tested parameter settings in terms of error versus convergence time; bandwidth=32 bits/s, decision space discretization precision=0.1

Full size image

In order to get a clearer view of the impact of the number of features on the performances of the individual strategies, Fig. 3b shows the scatter plot of error versus convergence time performances at different axis scales in terms of error. It can be seen more clearly that for both discrete strategies RV and DBBS, a higher number of environmental features diminishes the extent of the speed versus accuracy trade-off. For a higher number of features, there exists a singular best parameter configuration, as opposed to a Pareto front of equally good configurations observed at a lower number of features. On the other hand, LCP consistently displays speed versus accuracy trade-offs for all numbers of features. Between the two discrete strategies, RV sees more variations in its performances at different parameter settings when facing a higher number of features compared to DBBS, which produces performances that are clustered together for different parameter settings.

Table 5 Error vs convergence time spread and minimum mean error of the Pareto front of the considered strategies at different number of features; decision space discretization precision=0.1
Full size table

To quantify the impact of the number of environmental features on the extent of speed versus accuracy trade-off, Table 5 shows the spread of the Pareto fronts for the considered strategies at different number of features and at different bandwidth levels. In addition, the minimum mean error values indicate the positions of the Pareto front and show the limits of the performances of the considered strategies. For LCP, it can be observed that the main influence on the spread of Pareto front and the extent of speed versus accuracy trade-off comes from the bandwidth level. It also sees a slight increase in the spread of the Pareto front and a worsening of the accuracy at the extreme point of the Pareto front, as the number of features increases. This trend is, however, reversed for RV and DBBS, both of which show a drop in Pareto front spread when the number of features increases. Both discrete decision-making strategies can also maintain very low error at the extreme point of the Pareto fronts as the number of features increases.

Fig. 4
figure 4

Box plots showing the distribution of the convergence time of the considered algorithms at the best parameter configurations facing different number of features at different bandwidth levels; Red: LCP, Blue: RV, Black: DBBS; decision space discretization precision=0.1 (Color figure online)

Full size image

The box plots of the convergence times produced by the considered algorithms under the best parameter configurations in random environments are shown in Fig. 4. The parameter configurations chosen here are those corresponding to the center points on the Pareto frontiers of error versus convergence time performances. As a baseline, LCP generally experiences an increase in convergence speed when the communication bandwidth increases, and a decrease in convergence speed when the number of features increases. The latter holds for both multi-objective decision-making strategies, coupled with an increase in the variation of the convergence time. On the other hand, an increase in communication bandwidth does not have as strong a positive influence on the convergence speed of both discrete strategies, especially when facing a higher number of features. This causes the convergence speed of RV and DBBS to be close to that of LCP at high number of features and high bandwidths.

Fig. 5
figure 5

Performances of the considered strategies in all metrics when facing different numbers of concentrated environmental features a Error versus convergence time Pareto fronts, 3D space also includes scatter at convergence b Scatter plot for all tested parameter settings in terms of error versus convergence time; bandwidth=32 bits/s, decision space discretization precision=0.1

Full size image

Figure 5 shows the performances of the considered strategies when facing different numbers of concentrated features. A similar trend to that in random environments is observed. Concentrated feature distribution further reduces the convergence speed of the discrete decision-making strategies compared to LCP. For RV, further instability with respect to parameter settings is introduced, causing the bi-objective performances in error and convergence time when facing three features to exceed those when facing two features. Both discrete decision-making strategies also see a greater extent of error versus convergence time trade-off compared to random environments, while LCP does not see a significant reduction in performances.

The results above have shown that when considering error, convergence time and scatter, both tested discrete approaches, RV and DBBS, have superior performances compared to the LCP baseline decision space with a high number of features. This indicates that the parallel consideration of multiple potential options by RV and DBBS, when accounting for the increased bandwidth costs, is justified in terms of the decision-making performances.

At the same time, it is observed that an increase in the number of environmental features has a positive effect on the accuracy performances of the considered discrete decision-making strategies, especially DBBS. This is seen together with a significant decrease in the spread of the observed Pareto fronts, hence making the algorithms more sensitive in terms of parameter settings, but also presenting singular best configurations and reducing the trade-offs faced. This is in contrast to the behavior displayed by LCP, which sees a worsening in performance across all metrics when facing a higher number of features.

5.3 Performances of the considered strategies with respect to different decision space discretization precision

In this subsection, we present the performances of the considered strategies at different levels of decision space discretization. It is the second way where the number of potential options can be changed for the discrete decision-making strategies. For LCP, with its continuous decision space, the level of discretization has no effect on the decision-making performances.

Fig. 6
figure 6

Performances of the considered strategies in all metrics when randomly distributed environmental features at different levels of discretization precision a Error versus convergence time Pareto fronts, 3D space also includes scatter at convergence b Scatter plot for all tested parameter settings in terms of error versus convergence time; bandwidth=32 bits/s, number of features=2

Full size image

Figure 6 shows the performances of the considered strategies in randomly distributed environments when facing different levels of discretization precision. It can be observed that compared to the previous subsection for different numbers of features, the level of discretization precision has a smaller impact on the decision speed for the discrete decision-making strategies, but a bigger impact on the scatter and error. Notably, as shown in Fig. 6a, at finer discretization precision, both RV and DBBS show a significant increase in scatter at convergence, exceeding those produced by LCP. As shown in Fig. 6b, as the discretization precision becomes finer, both discrete strategies produce higher errors and shorter error versus convergence time Pareto fronts.

Table 6 Error vs convergence time spread and minimum mean error of the Pareto front of the considered strategies at different levels of discretization precision; number of features=2
Full size table

Table 6 shows the quantification of the changes in the Pareto fronts for RV and DBBS. It can be observed that for both RV and DBBS, there is a region with respect to precision and bandwidth settings where the error versus convergence time spread reaches a maximum, centered around precision of 0.05 and bandwidth of 32 bits/s. While for other scenarios, the spread of the Pareto fronts decreases. On the other hand, the minimum mean error increases steadily as precision decreases for both discrete strategies, while not being significantly affected by the bandwidth levels. These results show that a finer discretization precision has a negative impact on the decision-making accuracy of both discrete strategies. This is opposite to the impact of a higher number of features shown in the previous subsection. This negative impact is also not easily mitigated by allowing a higher frequency of communication or by parameter tuning of the decision-making strategy.

Fig. 7
figure 7

Box plots showing the distribution of the convergence time of the considered algorithms at the best parameter configurations facing random features at different bandwidth and discretization precision levels; Red: LCP, Blue: RV, Black: DBBS; number of features=2 (Color figure online)

Full size image

The distribution of the convergence time of the considered strategies is shown in Fig. 7. It can be confirmed that compared to different number of features shown in the previous subsection, decision precision has a smaller impact on both the median and the variation of the decision speed of the discrete strategies. As such, even at the smallest tested decision precision of 0.01, both discrete strategies are still significantly faster than the LCP baseline. For every decision precision tested, increasing the communication bandwidth also has a positive impact on the decision speed.

Fig. 8
figure 8

Performances of the considered strategies in all metrics when facing concentrated environmental features at different levels of discretization precision a Error versus convergence time Pareto fronts, 3D space also includes scatter at convergence b Scatter plot for all tested parameter settings in terms of error versus convergence time; bandwidth=32 bits/s, number of features=2

Full size image

Lastly, the performances of the considered algorithms when facing concentrated environmental features at different levels of discretization precision are shown in Fig. 8. For both discrete strategies, as discretization precision becomes finer, a similar trend of increasing error and convergence time is observed. The increase in convergence time at finer discretization precision is more significant than observed when facing random environmental features and makes the decision speed of the discrete strategies on par with that of LCP at the discretization precision of 0.01. On the other hand, LCP’s performances still do not significantly decrease compared to when facing random environmental features.

6 Discussion

Based on the experimental results presented in the previous section, we can make the following judgments. Firstly, in the decision-making scenarios investigated that go up to 101 options with two features and 1001 options with five features, parallel discrete consensus-forming strategies have an edge in terms of accuracy and speed compared to continuous consensus-forming strategies. This, coupled with the fact that continuous consensus-forming strategies have an inherent difficulty in forming an exact consensus in distributed systems (Elhage & Beal, 2010), means, that for continuous consensus forming, the discretization of the decision space and the adoption of discrete decision-making strategies can often be the best approach in reaching an accurate consensus, even if a moderate level of discretization precision is required.

The operation of parallel discrete decision-making strategies in a larger decision space, however, can be negatively impacted by the number of potential options. Based on the experimental results, both investigated discrete decision-making strategies, RV and DBBS, produce a smaller error and a higher convergence time when facing a larger decision space caused by a higher number of features, while showing a larger error and a less significant increase in the convergence time when facing a larger decision space caused by finer discretization precision. This distinction is caused by the differences in the correlations between the existing options and the new options introduced by the two different expansions to the decision space. When the number of features increases, the decision space expands in the number of dimensions, leading to unordered and weakly correlated options being added to the existing pool of potential options. It is thus less likely to mislead the swarm to erroneous options, but rather only increases the number of options the robots need to process. Thus, the impact of a higher number of features is similar to that of a smaller communication bandwidth, in that the decision-making process is slowed down but made more accurate due to the added time to explore the environment, as observed in Shan and Mostaghim (2021, 2022).

On the other hand, a finer discretization precision increases the number of options in the existing decision space, thus introducing many options that are correlated with the existing ones in terms of option qualities. These options can easily mislead the swarm and cause it to converge to an erroneous option, thus increasing the error, which is a similar effect to that caused by concentrated feature distribution (Shan & Mostaghim, 2021; Shan et al., 2021; Shan & Mostaghim, 2022). In addition, both sources of expansion of the decision space also reduce the extent of the speed versus accuracy trade-off, thus making the decision-making process more invariant with respect to parameter settings. This is a direct result of the expanded list of options, which makes it increasingly difficult to reach a fast consensus even when not considering the accuracy. This distinguishes scenarios with larger decision spaces from those with concentrated distribution of features. Its impact on the viability of discrete decision-making strategies in large decision spaces is two-fold: it reduces the need to make an additional judgment regarding parameter settings with respect to trade-offs between different decision-making metrics; however, it is also more important to select the best parameter settings to ensure good performances of the concerning strategies.

In previous literature on discrete collective estimation (Shan & Mostaghim, 2021, 2022), it has been observed that belief fusion approaches tend to have a stronger level of positive feedback than ranked voting approaches and can thus lead to faster but less accurate consensus. This trend is confirmed here, as DBBS tends to be faster and less accurate than RV in all experiments. However, it is more prevalent when facing more finely discretized options compared to a higher number of features. This highlights the importance of parameter tuning to restrict the strength of positive feedback in consensus-forming processes when facing ordered and correlated options.

Lastly, both discrete consensus strategies see more significant performance drops in terms of decision speed and accuracy when facing concentrated feature distributions compared to random feature distributions. As observed in previous literature (Bartashevich & Mostaghim, 2019; Shan & Mostaghim, 2021), the effect of a concentrated feature distribution is a dispersion of the individual robots’ opinions obtained from environmental exploration. In our experiments, LCP displays a more stable process in unifying the robots’ opinions, while both discrete strategies face increased difficulty as shown by an increased decision time and scatter at convergence. This is also caused by the stronger positive feedback effect in the discrete consensus strategies, which causes agents in physical proximity to reinforce the opinions of each other, thus preventing consensus with the rest of the swarm.

7 Conclusion

In this paper, we investigate the performances of discrete collective decision-making strategies in many-option consensus-forming scenarios with significantly more options than the number of agents. We have employed two discrete strategies: iterative ranked voting (RV) and distributed Bayesian belief sharing (DBBS). We have used linear consensus protocol (LCP) as a baseline. The considered strategies are experimented on an extended discrete collective estimation scenario, that accounts for expansion of the decision space due to two different factors: a higher number of environmental features and finer decision space discretization precision. The considered strategies are compared using three metrics: error, convergence time, and scatter at convergence, to measure the accuracy, speed and level of consensus of the strategies respectively. Trade-offs between the metrics are considered as we compare the Pareto fronts of the considered strategies’ performances.

Our results have shown that the investigated discrete decision-making scenarios can perform well in scenarios with a high number of options. Compared to the performances of LCP, adopting a discrete strategy has the benefit of producing, in general, lower error, convergence time and scatter at convergence. However, the performances of the discrete strategies are easily influenced by the environment. They respond differently to the different factors causing the expansion of the decision space. When facing a higher number of features, both RV and DBBS experience a decrease in error but an increase in convergence time. On the other hand, when facing a finer discretization precision, both discrete strategies experience an increase in error and a less significant increase in decision time, together with an increase in scatter. The distinction between the two effects is due to the differences in the correlation between potential options. Overall, discrete decision-making strategies are shown to be a viable alternative to continuous consensus-forming strategies if the nature of the decision-making problem allows discretization of the decision space. However, attention needs to be paid to the influence of environmental settings on their performances.

For future work, we plan to investigate ways to trim the number of potential options during many option decision-making scenarios, such that the limited communication bandwidths can be efficiently utilized, and the decision-making process can be more scalable and less negatively affected by the large decision space. At the same time, this paper touches only the straightforward interpretation of consensus regarding environmental perception in terms of accuracy speed and uniformity. This framework favors strong consensus enforcement via positive feedback. However, in the behaviors of natural intelligent swarms, effective collective behavior often does not mean exact uniformity. Therefore, ways to quantify collective cohesion without relying on level of uniformity need to be investigated for collective environmental perception scenarios.