Introduction

Understanding the causes and consequences of body size evolution has been at the core of ecological and evolutionary research since the beginning of those fields (Bonner, 2006). In part, this interest stems from the ease of measuring body size and its association with several allometrically-related traits (Peters, 1983). As a consequence, body size can be used as a proxy for other traits that are difficult to measure, such as metabolic rate, ingestion rate, and mass flow (Peters, 1983). Given this importance, several studies have sought to identify patterns of body size variation, which helped to elucidate many aspects related to the ecology and evolution of organisms (Brown, 1995; Peters, 1983). For instance, a prevalent observation in a variety of animal groups is that there are many more small-bodied species than large-bodied ones (Hutchinson & MacArthur, 1959). Indeed, previous studies found that a right-skewed distribution of body size is frequent across many groups of organisms (Brown, 1995). Another prominent debate has been on the positive relationship between latitude and body size, known as Bergmann's rule (Bergmann, 1847). Although no single mechanism has been proposed to explain this observation (e.g., heat-conservation hypothesis [Olalla-Tarraga et al., 2006]; starvation resistance hypothesis [Cushman et al., 1993]; phylogenetic constraints [Queiroz & Ashton, 2004]), Bergmann's rule has received mixed support in the literature (Ashton & Feldman, 2003; Henry et al., 2023; Meiri, 2011; Meiri & Dayan, 2003; Pincheira-Donoso et al., 2008; Riemer et al., 2018; Slavenko et al., 2019). Another recurring pattern in empirical data is the island rule (Benítez-López et al., 2021; Lomolino, 2005; Lomolino et al., 2013), which describes the tendency of small animals to evolve into larger sizes on small islands, while large animals tend to evolve into smaller sizes on the same islands, possibly due to reduced predation, competition, or due to resource limitation (Lomolino et al., 2013). Finally, Hutchinson (1959) proposed a link between body size and competition within communities, hypothesizing that two species at the same trophic level can coexist only if their size ratio was sufficiently large to avoid competitive exclusion (but see Horn & May, 1977; McA et al., 1987). Even though these patterns have been commonly explored, we still lack a comprehensive understanding of the evolution of body size, particularly with respect to the possibility of general principles that apply across different taxa.

The advent of phylogenetic comparative methods spurred new efforts into modeling changes in body size at a macroevolutionary scale. In particular, evolutionary studies, for the most part, have focused on assessing the relative fit of different models of evolution, with inconsistent results depending on the particular taxon. For instance, studies on mammals have found evidence that body size evolves according to an early burst model, in which much of the evolution in body size takes place at the beginning of the clade, and the evolutionary rate would decrease over time, consistent with the idea of radiation into empty niches (Cooper & Purvis, 2010). However, Harmon et al. (2010) found no evidence for this claim when they examined a variety of animal clades, concluding that models of random walk and selective peak were better supported. Likewise, Venditti et al. (2011) suggest a more complex model in which clades within mammals evolve according to separate rates of evolution, and not according to a single overall rate, whereas Landis and Schraiber (2017) incorporated pulses of evolutionary change through time in a novel approach and got more support from this model than from an early burst or Brownian motion. Therefore, the number of models proposed to explain body size evolution is large, yet there is still no consensus about which one best describes empirical data. A caveat commonly missed in these studies is that the model fit is usually evaluated among a limited set of models (Cooper & Purvis, 2010; Harmon et al., 2010; Landis & Schraiber, 2017). As a result, the best-fit model may still show a poor fit to the data but is still the best choice given the alternative models proposed (Pennell et al., 2015). However, to the best of our knowledge, no study to date tested the adequacy of models in body size evolution among terrestrial vertebrates, an essential approach to determine whether they are good descriptors of their evolution.

Despite the lack of a consensus regarding the best model for representing body size evolution in previous studies, there are overarching patterns concerning the variation of evolution across character states and lineages. For instance, Cooper and Purvis (2009) showed that large-bodied mammals have faster rates of evolution, although some but not all clades showed a high evolutionary rate for small sizes as well. Similarly, Baker et al., (2015) found evidence that large-bodied ancestors tend to generate changes in the size of their descendants with higher magnitude than when the ancestor is small. These differences in large-bodied species might be explained by the relaxation of size-linked constraints, such as genetic or developmental, or by the low population densities characteristic of larger species (Stanley, 1979), but none of these explanations were consistently supported in previous studies (Baker et al., 2015; Cooper & Purvis, 2009). Furthermore, given the physiological differences in ectotherms and endotherms, the rate of body size evolution could also be expected to vary among different taxa. Considering that endotherms have higher metabolic rates than ectotherms, the minimum body size in endotherms is constrained by the energetic demands of generating heat, as the relative metabolic rate increases with decreasing size (Peters, 1983). Additionally, ectotherms might have a constraint in the maximum body size by a minimum mass-specific metabolic rate, which decreases with increasing size but in ectotherms also increases with increasing temperature (Makarieva et al., 2005). Therefore, ectotherms in warmer areas could have larger body sizes than similar species in colder areas (Makarieva et al., 2005). These and other physiological differences might affect their respective body size distributions and consequently affect how these sizes evolve. Regardless, all of these studies usually focus on understanding the dynamics of a single class of animals, such as mammals (Baker et al., 2015; Cooper & Purvis, 2010; Venditti et al., 2011), birds (Cooney et al., 2017), or fishes (Albert & Johnson, 2012), but comparisons across taxa are scarce (e.g., Harmon et al., 2010; Landis & Schraiber, 2017). These comparisons might reveal general patterns of body size evolution that might not be linked to physiological or ecological differences across taxa.

In this study, we provide a comprehensive exploration of patterns of body size evolution across terrestrial vertebrates, focusing particularly on amphibians, squamates, birds, and mammals. We begin by using phylogenetic comparative methods to assess how body size evolved over time and across terrestrial vertebrate lineages. Then, we use posterior predictive modeling to test for different ways in which body size evolution departs from a constant-rate model of evolution. Finally, we contrast geographical patterns in rates of body size evolution. Hence, using this approach, we expected to find (1) heterogeneity across lineages and through time in the evolutionary rate of body size in terrestrial vertebrates; (2) that the rate of body size evolution increases as species become larger in all terrestrial vertebrates, given the relaxation of size-linked constraints; (3) a positive relationship between a region’s average body size and its average rate of body size evolution, given the previous prediction; and (4) that ectotherms and endotherms differ in their rates of body size evolution.

Materials and Methods

Data Sources

We obtained data on the phylogenetic relationships of amphibians, squamates, birds, and mammals from Jetz and Pyron (2018), Tonini et al. (2016), Jetz et al. (2012), and Upham et al. (2019), respectively. For each taxon, we compiled body mass data from several sources. Whenever there were differences among these sources, we calculated the mean, the median, and the maximum body size across them to account for this variability and repeated separate analyses with each alternative dataset to ensure the robustness of our results. For amphibians, we obtained body mass data from Oliveira et al. (2017; N = 552 species). We also obtained snout-vent length (SVL) data as a measure of body size from Oliveira et al. (2017) to convert them to body mass using reduced major axis regression (N = 5030). We estimated the slope between mass and length to construct an equation to predict species mass using only length data. To do this, we used the sma function in “smatr” 3.4–8 (Warton et al., 2012). For squamates, body mass data were obtained for a total of 9709 species from Feldman et al., (2016; N = 9699), Meiri (2019; N = 1991), and Myhrvold et al., (2015; N = 2255). We obtained body size data for birds from Wilman et al., (2014; N = 5265), Lislevand et al., (2007; N = 532), Ocampo et al., (2021; N = 1132), and Myhrvold et al., (2015; N = 7901), for a total of 9,093 avian species. Finally, we obtained body mass for mammals from Wilman et al., (2014; N = 4986), Ocampo et al., (2021; N = 227), Faurby et al., (2020; N = 5422), and Jones et al., (2009; N = 3019), for a total of 5548 mammal species with at least one measure of body size. Spatial data were retrieved from IUCN (2022) for amphibians, squamates, and mammals and from BirdLife International (2021) for birds.

Analyses

We began our analyses by exploring variations in body size over evolutionary time and across lineages. First, we visualized interspecific variation in body size for amphibians, squamates, birds, and mammals using histograms of log-transformed data, both for the entire group as well as for selected subclades. Given that results using mean, median, and maximum estimates for each species were nearly identical (Figs. 1 and S1–S2), we only considered analyses using species means in the main text. Considering that using the median is usually more robust statistically than the mean (given its sensitivity to extreme values), additional tests using medians instead of means were performed but provided nearly indistinguishable results (see Results). We mapped body size evolution onto each phylogeny (using the MCC topology) using the contMap function in “phytools” 0.7–70 (Revell, 2012), which uses maximum likelihood to estimate ancestral states. We also generated disparity-through-time (DTT) plots of body size using the dtt function in “geiger” 2.0.7 (Pennell et al., 2014a) to assess how the average disparity in each clade changed over time. Disparity between species was estimated using the average squared Euclidean distance between all observations. This metric allows us to evaluate if there were any bursts in the diversification of the groups (disparity closer to 1, indicating more variation within subclades than among them) or if species accumulation was steady over time (disparity closer to 0, indicating more variation among subclades rather than within them). To account for phylogenetic uncertainty, we repeated DTT calculations for 100 alternative topologies for each taxon. We compared the observed results with simulated data, computed as the average between 100 simulations for each of the alternative topologies indicated above, to assess if there were periods in which body size evolution was faster or slower than expected based on a constant-rates model. Additionally, we also performed a rank envelope test to calculate confidence intervals according to the Brownian Motion model, following Murrell (2018). According to this method, DTT curves are ranked by the most extreme disparity value relative to an ensemble of null models (Murrell, 2018). The rank_envelope function in GET 0.5 (Myllymäki & Mrkvička, 2019; Myllymäki et al., 2017) was used, specifying a two-sided alternative hypothesis. All body size measures were log10-transformed prior to the analyses.

We used posterior predictive simulations to explore ways in which body size evolution could depart from a constant-rate model. We began by fitting a Brownian Motion (BM) model to empirical body size data using fitContinuous in “geiger” 2.0.7 (Pennell et al., 2014a). Under this model, the covariance of species traits is directly proportional to their shared evolutionary history. Then, we assessed the adequacy of this model using the arbutus function (using nsim = 1) in “arbutus” 0.1 (Pennell et al., 2014b). This approach involves three main steps: (1) it calculates several test statistics of the data according to the chosen model of evolution, (2) it simulates datasets (N = 1 in this study for each alternative topology, see below) on the phylogeny using the parameters of the model estimated from the empirical data, and (3) the observed test statistics are compared to the simulations. These test statistics inform if and how the empirical data deviates from datasets simulated under the model in question. Here, we used four test statistics: Msig, the mean of the squared contrasts, which indicates if the overall rate of evolution might be under or overestimated; Cvar, the coefficient of variation of the absolute value of the contrasts, used to assess the extent of heterogeneity in the rate of evolution across the phylogeny; Sasr, the slope of a linear model fitted to the absolute value of the contrasts against the ancestral state inferred at the corresponding node, showing variation in the rate of evolution relative to the trait state; and Shgt, the slope of a linear model fitted to the absolute value of the contrasts against node depth, which can detect variation in the rate of evolution in time, identifying early bursts of evolution. More details about the test statistics can be obtained from Pennell et al. (2015). We repeated this process for 1000 alternative topologies available for each taxon to account for phylogenetic uncertainty but limited the analysis to one simulation per run per topology. All analyses were carried out in R 4.1.1 (R Core Team, 2021).

Finally, we assessed whether there is a spatial relationship between the average species mass of a region and its body size evolutionary rate. To achieve this, we mapped globally the median body size of the species present in each cell, as well as their median evolutionary rate. TreeAnnotator v2.6 (Bouckaert et al., 2019) was used to create maximum clade credibility trees, given that it is computationally challenging to calculate tip rates using a distribution of trees with thousands of tips. Then we calculated the rate of evolution of body size (mass and SVL) of each species using the RRphylo function in "RRphylo" 2.7–0, specifying the body size itself as a covariate (Castiglione et al., 2018). This method is based on phylogenetic ridge regression and assigns a different rate to each branch of the tree without applying an evolutionary model a priori (Castiglione et al., 2018). The maps were made using a projection of 10-arc minutes, using the packages “rgdal" 1.6–5 (Bivand et al., 2023), "sf" 1.0–12 (Pebesma, 2018), and "raster" 3.6.20 (Hijmans et al., 2023) in R 4.1.1 (R Core Team, 2021) and QGIS (QGIS Team, 2023) to process the geographical data.

Results

Body Size Frequency Distribution

There was considerable variation within and between taxa in their body mass distribution, both in terms of their means and degree of skewness (Fig. 1). The distribution of body mass in birds and mammals is particularly skewed, whereas amphibians show a notably lower level of skewness (Fig. 1e). Moreover, birds and mammals show larger body mass when compared to amphibians and squamates, with mammals having the largest mass and amphibians the smallest (Fig. 1e). When examining groups within classes, Gymnophiona is approximately symmetric in its distributions (skewness of 0.059), with caudate and anuran species showing a moderate (− 0.671) to high skewness (1.488), respectively (Fig. 1a). In squamates, Serpentes show the largest mean body mass with an almost symmetrical distribution (skewness = 0.133) as Gekkota (skewness = 0.140), whereas the other groups present a longer right tail and lower means (skewness > 0.5) (Fig. 1b). Within Aves, Apodiformes and Passeriformes have the smallest body masses in the class, with longer right tails than the other groups (skewness = 1.313 and 0.819, respectively) (Fig. 1c). Finally, in mammals, Chiroptera and Eulipotyphla exhibit the smallest body mass, followed by Rodentia, whereas Carnivora, Cetartiodactyla, and Primates have a larger mass, with the first two also having longer right tails (skewness > 1) (Fig. 1d). It is important to note that we did not include all the orders of birds and mammals in the figures, choosing only those with the highest species richness and grouping all other orders into the category “Other” (Fig. 1) to facilitate visualization and comparison.

Fig. 1
figure 1

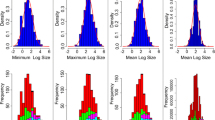
Density distribution of body mass (g) in terrestrial vertebrates. Distributions are shown for amphibians (a), squamates (b), birds (c), and mammals (d) separated by selected subclades, and for the entire taxa (e). Lines in (e) indicate the median body mass for each lineage. Body mass estimates for squamates, birds, and mammals were averaged across sources

Full size image
Fig. 2
figure 2

Character mapping and ancestral state estimation of body mass (g) for amphibians, squamates, birds, and mammals

Full size image
Fig. 3
figure 3

DTT (disparity-through-time) plots for body mass (g) for the studied taxa. Gray lines indicate the null expectation under the Brownian Motion model of evolution, and color lines correspond to the observed disparity variation in the empirical data. The polygons correspond to the rank envelope test. Estimates of body mass were log-transformed before the analyses. Each line represents alternative topologies

Full size image
Fig. 4
figure 4

Test statistics and evolutionary rates of body mass (g) generated using posterior predictive simulation. The first column corresponds to the rate of evolution under a Brownian Motion (BM) model for each taxon. Cvar (coefficient of variation of the absolute value of the contrasts), Sasr (slope of a linear model fitted to the absolute value of the contrasts against the ancestral state inferred at the corresponding node), and Shgt (slope of a linear model fitted to the absolute value of the contrasts against node depth) are indicated in the second, third, and fourth columns, respectively. Gray histograms are the null expectation under BM, and colored histograms are the statistics generated from the empirical data. Estimates of body mass were log-transformed before the analyses

Full size image
Fig. 5
figure 5

Geographical distribution of body mass (g) and the evolutionary rates of body mass (g) in each taxon studied. Both body mass and evolutionary rate were calculated as the median across all species within each cell

Full size image

Ancestral State Estimation

Mapping body size evolution onto the corresponding phylogenies indicated highly complex evolutionary patterns, with some intriguing similarities (Fig. 2). Small and intermediate body sizes in general tend to be widely distributed across the history of each group, whereas larger species seem to be concentrated in relatively small, terminal branches (Fig. 2). The largest body size in amphibians appears to be equally distributed between Anura, Caudata, and Gymnophiona (Fig. 2a), with a slightly larger number of species in Caudata and Gymnophiona. In squamates, the largest body sizes are concentrated mainly in the branches leading to Serpentes, whereas other lineages remained with smaller average sizes, with a few branches evolving increased body size, such as Anguimorpha and Iguania (Fig. 2b). Birds seem to have evolved from relatively larger body sizes, which became smaller mainly in Passeriformes and Apodiformes. On the other hand, Charadriiformes, Columbiformes, Piciformes, and Psittaciformes largely tended to retain their ancestral condition (Fig. 2c). Mammals showed a similar overall trend in relation to birds, but some lineages have attained even larger sizes in more recent times. Indeed, Cetartiodactyla, Carnivora, and Primates have lineages with the largest body sizes of all terrestrial vertebrates (Fig. 2d). Chiroptera and Eulipotyphla exhibited a decrease in average body size compared to the mammalian ancestor, which in turn is similar in mass to the average size of Rodentia. Analyses using the median estimates across sources showed almost identical results (Fig. S3).

Disparity-Through-Time

There was substantial heterogeneity in evolutionary rates over time in all taxa, although there wasn’t departions from the null expectation (Fig. 3). Amphibians and squamates (Fig. 3a, b) showed periods where the disparity accumulation increased, especially near the present (i.e., more variation in the trait within subclades than among them, indicating bursts in diversification). However, this was not the case for birds and mammals (Fig. 3c, d), except for a slight increase in disparity around 94 Mya (calculated using the mean of ages between topologies) for mammals. Yet, this increase was still within the expectation based on simulations. For birds, it is possible to note an abrupt decrease in disparification around 78–90 Mya (Fig. 3c) (i.e., more variation among subclades than within them, indicating steady species accumulation over time). One can see a similar trend in mammals but with an increase and a subsequent decline in disparity around 94 Mya (Fig. 3d). Analyses using the median estimates across sources yielded almost identical results (Fig. S4).

Adequacy of the Brownian Motion model

There was broad congruence across taxa in tests based on the model adequacy of a constant-rate model, with all but one statistic consistently departing from data generated with posterior predictive simulations in the same direction (Fig. 4). The Msig was the only statistic in which the observed values did not differ from the expectation, indicating that the BM model did not consistently over or underestimate the rates of evolution in these taxa. For this reason, we only show the estimated evolutionary rates (σ²) for each group (Fig. 4) and not the estimated mean of the squared contrasts. In general, amphibians and birds have similar distributions of σ² for body size, with amphibians having a median of 0.050 and birds 0.077, whereas squamates and mammals have higher median estimates of σ², with 0.284 for squamates and 0.167 for mammals. Therefore, ectotherms and endotherms do not show consistent differences in rates of evolution of body size. Interestingly, all taxa showed both Cvar and Sasr estimates that were higher than expected (Fig. 4), which confirms that rate heterogeneity exists across the phylogeny, as expected based on analyses shown in Figs. 2 and 3. In particular, these results regarding Sasr indicate that body size evolution is slower when the ancestor is small and accelerates as the ancestor increases in size. In addition, all clades have lower Shgt values than expected, which indicates that the higher the node depth, the less contrast in the trait, that is, the contrasts on the tips are higher than expected. The results were indiscernible when utilizing the median estimates (Fig. S5).

Geographical Distribution of Body Size and Its Evolutionary Rate

There was little overall correspondence between mean body mass and its evolutionary rate over geographical space within each clade, yet correspondence between clades was considerably less apparent (Fig. 5). For instance, amphibians in the northern part of North America, the southern part of South America, the southern part of Africa, Europe, and Western Asia showed larger median body sizes and higher evolutionary rates (Fig. 5). However, higher evolutionary rates were also found in Australia and the remainder of Asia. Similarly, squamates exhibit comparable patterns, with high values for body mass and evolutionary rates in Asia and Europe, Brazil, central Africa, and northern North America (Fig. 5), whereas Australia also presented high evolutionary rates with low average body size. However, for birds and mammals, there were differences between regions with large species and high rates of evolution. Large bird species are predominantly found at high latitudes, including Australia, northern North America, Europe, and Asia, as well as the southern part of South America. Meanwhile, high rates of evolution are found in the southern part of South America, the entire North America, and Europe, but with a tendency towards the south (Fig. 5). In contrast, large mammals and high evolutionary rates are found in northern North America, southern South America, and western Asia, while high evolutionary rates and larger species are found in North Africa and central and South Africa, respectively (Fig. 5).

Discussion

One would be hard-pressed to find a trait that is more consequential to so many aspects of the ecology, physiology, and evolution of an organism than its body size. Here, we provide a comprehensive exploration of body size evolution across terrestrial vertebrates. We found support for consistent departures from a constant-rate model across all clades (Figs. 4 and S5), suggesting that the evolution of body size may be characterized as a similar pattern across terrestrial vertebrates, but that it may be governed by different processes. In particular, they were characterized by rate heterogeneity between lineages, accelerating rate of evolution with increasing body size, and more contrasts than expected near the tips of the phylogenies (Figs. 4 and S5). Interestingly, although ectotherms tend to have smaller body sizes than endotherms (Fig. 1), their rates of evolution did not show substantial differences (Figs. 4 and S5), contrary to our initial expectations. Finally, although mean body size and rate of body size evolution showed a certain degree of geographical congruence within clades, there was limited correspondence between clades (Fig. 5), which might indicate that environmental drivers such as mean annual temperature might not be sufficient to generate convergent patterns at geographical scales. In aggregate, these results suggest that there might be common principles governing body size evolution in terrestrial vertebrates, although their underlying mechanisms are still poorly understood.

The results of our posterior predictive simulations showed evidence for a positive relationship between body size and its rate of evolution in all tested clades (Fig. 4). Hutchinson (1959) previously discussed the notion that small and large species may undergo distinct evolutionary processes due to the biased distribution of body sizes among species. Building upon this idea, Baker et al. (2015) arrived at a similar conclusion, demonstrating a positive relationship between evolutionary rate and body size when fitting branch-specific evolutionary rates to diverse mammal lineages. Potential mechanisms explaining this pattern, as proposed by Stanley (1979), include the relaxation of size-linked genetic or developmental constraints, as well as the low population densities characteristic of larger species. However, formal tests of these propositions are scarce (e.g., Baker et al., 2015; Cooper & Purvis, 2009). Still, another perspective to consider is that small species may exhibit decreased rates of evolution, instead of large mammals having increased rates. This alternative viewpoint could be explained by a possible lower physiological limit on size (Stanley, 1973), which makes evolution towards larger sizes more probable. Nevertheless, contrasting evidence from other studies cannot be ignored. Some studies speculate that small-sized species can also have higher evolutionary rates due to their faster life history (Bonner, 1965), while others find evidence that certain groups exhibit high rates of evolution in both small and large animals, with intermediate sizes showing lower rates (Cooper & Purvis, 2009). Nonetheless, our results suggest that smaller species generate descendants with less variation in body size, but further examination of lineages within terrestrial vertebrates may uncover different correlations and provide additional insights into this relationship.

Regarding variation in time, our results are not consistent with an adaptive radiation scenario in which body size evolution is faster early during the history of a clade and becomes increasingly slower as ecological space is occupied (Simpson, 1944). Other studies obtained similar results (Harmon et al., 2010; Venditti et al., 2011). Instead, we show that there is evidence for more contrast of body size near the present, and along with inspection of the DTT plots, the histories do not differ from the expected under a time-homogeneous, constant model of evolution. In particular, one can say that the results of DTT plots and Shgt statistics are contradictory, for the former points to no difference between the expectations of BM, while the latter indicates more contrast in the tips of the phylogenies than expected. However, as the Shgt indicates slopes close to 0 (i.e., little to no linear relationship between contrasts and node depth), we believe that the results are not conflicting.

The lack of a relationship between latitude and body size contradicts the expectations set by existing hypotheses. Bergmann's rule and the water conservation hypothesis posit that endotherms would tend to have larger body sizes at high latitudes to better conserve heat (Bergmann, 1847), and ectotherms to conserve water (Nevo, 1973), respectively. On the other hand, the heat balance hypothesis predicts that ectotherms would tend to have smaller sizes in high latitudes due to their inability to self-produce heat, benefiting from reductions in size in these locations (Olalla-Tarraga et al., 2006). Our results align with previous studies that also did not find evidence for Bergmann's rule (e.g., Johnson et al., 2023; Meiri, 2011; Meiri & Dayan, 2003; Pincheira-Donoso et al., 2008; Riemer et al., 2018; Slavenko et al., 2019; Womack & Bell, 2020), the water conservation hypothesis (e.g., Ashton & Feldman, 2003; Johnson et al., 2023; Servino et al., 2022), or the heat balance hypothesis (e.g., Johnson et al., 2023; Slavenko & Meiri, 2015; Slavenko et al., 2019). An alternative interpretation of these hypotheses could be that there is no latitudinal trend in body size, but rather in the rate of evolution of these sizes. However, even the rates of evolution in our study do not support this perspective. Overall, our findings contradict established hypotheses regarding the relationship between latitude and body size, but instead suggest that there may exist a spatial association between the average species mass of a region and its average evolutionary rate.

Although our results are consistent across a diversity of taxa, it is important to note some caveats in our analyses. First, the model adequacy approach may indicate problems in the data. For instance, as pointed out by Pennell et al. (2015), when both the Svar and the Shgt statistics show negative slopes in the observed data, it may be an indicator of problems in the estimated branch lengths of the phylogeny, considering that Svar (not used here) would indicate errors in branch lengths of shorter branches of the phylogeny and Shgt would point to more contrasts in the tips. However, we do not think this would be the case, given that all results were consistent across 1000 alternative topologies and every taxon tested. Furthermore, previous studies have demonstrated that ancestral state estimation using body size data might not be accurate, considering that most estimation methods assume a time-homogeneous process (Baker et al., 2015). Despite this limitation, given the absence of alternative methods for straightforwardly testing our hypotheses without making this assumption, we are compelled to utilize the available methods and adhere to the time-homogeneous assumption. Lastly, we recognize that a spatial regression would be essential for evaluating the valid statistical relationship between body size and its evolutionary rate globally, a step we did not undertake in this study. Nonetheless, our spatial analyses are primarily exploratory, and a more formal framework is required to make conclusive assertions.

In exploring differences in body size evolution in terrestrial vertebrates, we believe that future studies may explore how differences in lineages within these clades are structured, using data-driven approaches (e.g., Eastman et al., 2011; Thomas & Freckleton, 2012; Uyeda & Harmon, 2014), for example. Once this is achieved, it can be interesting to build a causal model to possibly explain how this heterogeneity is generated, using latitude or climate as explanatory variables, and assess if the same variables have equal power to predict body size evolution among terrestrial vertebrates. Thus, we hope that future studies would focus on describing how other aspects of body size evolution may also be general across terrestrial vertebrates and if the patterns uncovered here might be extended to other groups of organisms.