Introduction

Achieving target coating thickness is one of the main objectives in thermal spraying. When the coating thickness is out of the prescribed limits, the part needs to be reworked, which results in longer production times, waste of materials and overall additional costs. Therefore, it is crucial for process control to ensure repeatable coating thicknesses.

However, the control of the thermal spraying process is currently insufficient to reduce the variability of the thickness of the produced coatings, as observed in the studies by Wroblewski et al. (Ref 1) and Mauer et al. (Ref 2). In the two studies, no feedback about the coating thickness was used for controlling the process. A large variability in the coating thickness was also present in the study of Kuroda et al. (Ref 3), where an online, closed-loop control system was used to stop the process when the in situ measured coating thickness reached the target value. The observed variation was attributed to the influence of the coatings’ surface roughness on the thickness measurement. This example highlights one of the challenges faced when selecting an appropriate coating thickness measurement technique to be used as a feedback signal in an online, closed-loop control application. As discussed by Hudomalj et al. (Ref 4), the measurement technique must: (1) be capable of in situ measurement during spraying, (2) be nondestructive, and (3) produce results with a sufficiently small uncertainty. In the example of Kuroda et al. (Ref 3), the 3rd requirement seems to not have been fulfilled since the contribution to the uncertainty of the thickness measurement due to the imprecisely known coating properties, i.e., surface roughness, was too large.

A method that would sufficiently fulfill all the stated requirements is still missing despite the existence of a plethora of different options for measuring the thickness of thermally sprayed coatings. These range from commonly used, standardized methods as listed in (Ref 5) to more recent techniques based, for example, on eddy currents (Ref 6), evaluations of capacitance (Ref 7), laser-ultrasonics (Ref 8), thermography (Ref 9), terahertz investigations (Ref 10), and optical distance measurements of total coating thicknesses (Ref 3, 11) or of individual coating layers (Ref 12,13,14). One common challenge of the existing approaches is insufficient incorporation of the effect of the surface topography on the coating thickness measurement. The thermally sprayed coatings namely have a characteristically high surface roughness, especially relative to their thickness. In order to include the influence of the topography on the measurement of the coating thickness, it is necessary to record the thickness with a sufficient spatial resolution. This has already been done in offline settings for analysis of spray spots (Ref 15, 16) and spray beads (Ref 2, 15), where tactile scanners, confocal microscopes and triangulation laser-scanning microscopes were used. However, up to now, the same has not been achieved in situ. If in situ spatially resolved coating thickness measurements were available, they could be used to provide a robust feedback signal for an online, closed-loop control of the thermal spraying process.

This paper presents a novel approach for in situ spatially resolved coating thickness measurements. It is based on the same technique as presented by Hudomalj et al. in (Ref 4), where the coating thickness is measured based on a differential distance measurement of sample thickness before and after applying the coating. A high-resolution 3D camera is used to capture the surface topography and include it in the thickness measurement. The approach gives results independent of substrate and coating materials. Its capabilities are demonstrated on the example of atmospheric plasma spraying (APS) of yttria-stabilized zirconia (YSZ) on steel substrate. The technique provides not only measurements of coating thickness but also allows evaluation of surface roughness parameters as well as enables a nondestructive estimation of coating porosity. The measurement results are compared with standard reference methods.

Material and Methods

Experimental Setup

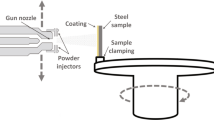
The developed in situ coating thickness measurement approach was tested during atmospheric plasma spraying of samples in a carousel arrangement. The coating setup is depicted in Fig. 1. Steel samples of dimensions 30 mm × 60 mm × 3 mm were mounted on a turntable with a diameter of 600 mm. An F4MB-XL gun (Oerlikon Metco, Wohlen, Switzerland) was used with two injectors placed on opposite sides along the vertical axis. The injectors were offset 7 mm from the spray axis and 2 mm from the nozzle exit. The nozzle had a diameter of 8 mm. The powder used in this study was 8 wt.% Y2O3-ZrO2 (8YSZ), 204NS-G (Oerlikon Metco, Wohlen, Switzerland).

Fig. 1
figure 1

Schematics of the coating setup. The coating setup was the same as used in (Ref 4). Reprinted from (Ref 4), available under CC BY 4.0 license at SpringerLink

Full size image

For the in situ measurement of the coating thickness, the setup schematically shown in Fig. 2 was added perpendicular to the spray direction. It consisted of a high-resolution 3D camera Gocator 3504 (LMI Technologies, Burnaby, Canada) which was used to measure the distance to the front side of the sample. With a measurement range of 7 mm and repeatability of 0.2 µm in the vertical direction over a field of view (FOV) larger than 12 mm × 16 mm at an XY resolution of about 7 µm, the camera is capable of capturing the sample’s surface topography. For further processing, the camera’s scans were resampled with a triangle-based cubic interpolation method onto a uniform grid with a resolution of 10 µm. The camera was positioned to have its center aligned with the middle of the sample.

Fig. 2
figure 2

Schematics of the in situ coating thickness measurement setup added to the coating setup. The measurement setup was based on the approach from (Ref 4). Reprinted from (Ref 4), available under CC BY 4.0 license at SpringerLink

Full size image

Besides the camera, the measurement setup included three pneumatically actuated length gauges ST 1287 (Heidenhain, Traunreut, Germany) with a measurement range of 12 mm and repeatability of 0.25 µm. They were used to measure distances to three points on the back side of the sample. The measurements were made at the same area where the camera observed the sample. The length gauges were used instead of another camera to reduce the costs of the measurement system.

The camera and the length gauge holders were installed on an invar plate to minimize the effect of thermal expansion on the relative positions of the sensors. For compensation of thermal expansion of the sample, a one-color pyrometer IN 5-L plus (LumaSense Technologies, Santa Clara, CA, USA) was used to measure the temperature in the vicinity of the thickness measurement position. Due to spatial limitations in the experimental setup, it measured the temperature of the coating. Therefore, it was assumed that the sample and the coating are at the same temperature.

The setup was used to measure the sample thickness before and after the coating. Before making the measurements after the end of the coating, it was waited (ca. 2 min) for the sample to cool down to room temperature (ca. 20 °C). Each measurement was repeated 5 times. The setup was also used to measure the thickness during the coating, but only after spraying every two layers. For these measurements, the turntable was briefly halted (ca. 3 s) and one measurement repetition performed before continuing with the spraying. During the measurement, the plasma gun was moved away from its spraying position to minimize the noise from plasma emissions on the optical system.

The performance of the measurement approach was evaluated at a wide range of coating thicknesses by producing samples with varying number of coating layers—i.e., 6, 10, 14, 18, and 22. Other process parameters were the same for all the runs as listed in Table 1. The average gun voltage during individual experiments ranged between 58.1 and 58.9 V. For the coating, no sample preheating or active cooling was used. Before the coating, the samples were grit-blasted with Al2O3 grit size #22, at a jet pressure of 3.5 bar, using a nozzle with a 10 mm diameter at a working distance of approximately 20 cm and under 60° angle. For each number of layers, two runs were conducted, resulting in a total of 10 runs.

Table 1 Process parameters used in experiments
Full size table

Comparison with Reference Evaluation of Coating Thickness

In order to assess the performance of the in situ measurement approach, the results were compared with reference measurements made by taking microscopic images of the coatings’ cross sections. Since this procedure is destructive, only the total coating thicknesses could be compared. Moreover, since the two methods measure the coating thickness differently, i.e., around an area versus along a line and with different resolutions, only the average coating thicknesses of the samples were compared. For the comparison, zeta scores were calculated (Ref 17):

$${\zeta }_{\overline{c} }=\frac{\overline{c }-{\overline{c} }_{r}}{\sqrt{{{u}_{\overline{c}} }^{2}+{{u}_{{\overline{c} }_{r}}}^{2}}}$$
(1)

where \(\overline{c }\) and \({\overline{c} }_{r}\) are the average coating thicknesses of the in situ and the reference methods, respectively, and \({u}_{\overline{c} }\) and \({u}_{{\overline{c} }_{r}}\) the respective measurement uncertainties.

For the reference microscopical method, an optical microscope was used with a 50 × magnification. For a valid comparison, the images had to be taken at the same position of the sample as the in situ measurements. Therefore, the coated samples were cut along their widths, 30 mm from the top, as depicted in Fig. 3. The preparation of the samples was done as per the ASTM E1920 standard (Ref 18).

Fig. 3
figure 3

Schematics of positions of reference microscopical measurements together with an example image with evaluated coating thicknesses

Full size image

In order not to rely on the thicknesses measured along just a single line of the coatings’ cross sections, the coating thicknesses were evaluated with the microscope on both sides of the sample cut. At each side of the cut, three images of the coatings’ cross sections were taken: one at the middle and two 5 mm away from the center, as shown in Fig. 3. Due to the width of the saw used for cutting of the sample, the two measurement lines were estimated to be a few millimeters apart, meaning all the images were taken inside of the same area as was observed with the in situ measurement.

At each taken image, the coating thickness was evaluated at 10 equidistantly spaced points (Fig. 3), in accordance with the ISO 1463 standard (Ref 19). The reference thickness value was calculated as the average of all evaluated thicknesses from both sides of the sample cut. The uncertainty in the reference thickness was estimated as the combined uncertainty of the experimental standard deviation of the mean, and the uncertainty due to the repeatability of thickness measurement at an individual point of an image. Other contributions to the uncertainty of the microscopic method were assumed to be negligible based on the performed calibration of the microscope.

Evaluation of In Situ Coating Thickness Measurements

The coating thickness measurement model used in this research is depicted in Fig. 4. It is based on a differential distance measurement of sample’s thickness before and after applying one or multiple layers of coating.

Fig. 4
figure 4

Model of coating thickness measurement—a differential distance measurement is performed before and after applying one or multiple layers of coating

Full size image

Distances to the front side of the sample are measured with the high-resolution camera located at origin \(O\). The surfaces captured with the camera before and after the coating are described by points \({P}_{Fb}\) and \({P}_{Fa}\), respectively. Distances to the back side of the sample are measured with the three pneumatically actuated length gauges. The length gauges \(i\in \left\{1, 2, 3\right\}\) are located at \({G}_{ib}\) and \({G}_{ia}\), before and after the coating, respectively, and have orientation \(s {\overrightarrow{d}}_{i}\). The distances measured by the length gauges \({l}_{ib}{, l}_{ia}\) are related to the points \({B}_{ib},{ B}_{ia}\) where the length gauges touch the back side of the sample:

$$\overrightarrow{{OB}_{ib}}={\overrightarrow{p}}_{i}+{l}_{ib}{\overrightarrow{d}}_{i}$$
(2)
$$\overrightarrow{{OB}_{ia}}={\overrightarrow{p}}_{i}+\overrightarrow{{G}_{ib}{G}_{ia}}+{l}_{ia}{\overrightarrow{d}}_{i}$$
(3)

where \({\overrightarrow{p}}_{i}=\overrightarrow{O{G}_{ib}}\) denotes the vectors to the positions of the length gauges before coating, and \(\overrightarrow{{G}_{ib}{G}_{ia}}\) the changes in their positions. In the model, it is considered that between the measurements before and after the coating, the temperature of the invar plate carrying the sensors can change by \({\Delta T}_{F}\). Assuming the thermal expansion of the fixture to be linear with coefficient \({\alpha }_{F}\), acting in Z direction, it follows:

$$\overrightarrow{{G}_{ib}{G}_{ia}}={p}_{iZ}\left({\alpha }_{F}{ \Delta T}_{F}+1\right)\overrightarrow{k}$$
(4)

where \({p}_{iZ}\) is the Z component of vector \({\overrightarrow{p}}_{i}\). Orientations \({\overrightarrow{d}}_{i}\) and positions \({\overrightarrow{p}}_{i}\) of the length gauges according to the camera’s coordinate system before the coating are determined during the calibration of the system.

To determine the sample thickness, the model assumes the back side of the sample is a perfect plane. The plane is determined by the points \({B}_{ib},{ B}_{ia}\), which give the sample’s unit normal vectors \({\overrightarrow{n}}_{sb}, {\overrightarrow{n}}_{sa}\) as well as the plane distances from the origin \({D}_{sb}, {D}_{sa}\) before and after the coating. Modeling the back side of the sample as a plane is considered valid because the back side of the sample remains smooth (i.e., not grit-blasted). Furthermore, sample bending due to residual stresses is considered to be negligible over the size of the observed area.

The sample thicknesses before and after coating are calculated as the minimum distances between the points of the sample’s front side \({P}_{Fb},{ P}_{Fa}\) and the back side planes as:

$${s}_{b}\left(x,y\right)={\overrightarrow{n}}_{sb}\cdot \overrightarrow{O{P}_{Fb}}+{D}_{sb}$$
(5)
$${s}_{a}\left(x,y\right)={\overrightarrow{n}}_{sa}\cdot \overrightarrow{O{P}_{Fa}}+{D}_{sa}$$
(6)

The model assumes that the substrate temperature can change by \({\Delta T}_{s}\) between the measurement before and after the coating, and that the resulting thermal expansion of the substrate is linear with coefficient \({\alpha }_{s}\), as described by:

$${s}_{b}^{\prime}(x,y)={s}_{b}(x,y)\left({\alpha }_{s}{ \Delta T}_{s}+1\right)$$
(7)

The coating thickness can be calculated as the difference in the sample thicknesses before and after coating as in:

$$c\left(x,y\right)={s}_{a}\left(x,y\right)-{s}_{b}^{\prime}(x,y)$$
(8)

Equation (8) gives an estimate of the coating thickness at a temperature that might be different from the room temperature at which the reference thickness measurements are done. However, since the total coating thicknesses are relatively small (i.e., below 400 µm), and since it was waited for the coating to cool down before measuring the total coating thickness after the spraying has finished, the effect of thermal expansion of the coating is negligible.

According to equation (8), it is required to know the sample thicknesses before \({s}_{b}\) and after \({s}_{a}\) the coating at the same positions \(\left(x,y\right)\). Therefore, it is necessary to know how the two sample measurements are aligned, i.e., to know the transformation between \({P}_{Bb}\) and \({P}_{Bb}{\prime}\). The used measurement approach leads to an underdetermined system to define this transformation. However, the maximal possible misalignment is limited by the positioning accuracy of the sample, i.e., by the accuracy of the turntable that is used to position the sample before and after the coating. Therefore, the possible misalignment between the two sample measurements can be included in the model as a random displacement in X and Y directions (\(\Delta x, \Delta y\)), contributing to the measurement uncertainty.

Based on the measurement model described by Eq (2)-(8), it is possible to estimate not only the expected value of coating thickness but also its measurement uncertainty following the GUM recommendations (Ref 20). The Monte Carlo method (MCM) (Ref 21) was used in this case instead of the commonly applied law of propagation. The latter would namely require determination of partial derivatives of the sample’s surface before and after the coating (described by points \({P}_{Fb}\) and \({P}_{Fa}\)), which would produce noisy results due to the high surface roughness and measurement noise.

With MCM, the total coating thickness of each run was evaluated based on all 5 × 5 combinations of repeated measurements before and after the coating. For the unmeasured model parameters, it was assumed that they were independent and uniformly distributed. Their estimated ranges are given in Table 2. Explanations for the assumed ranges are also provided. By randomly selecting 103 samples from each parameter distribution, 103 different parameter sets were formed. This resulted in 2.5 × 104 model evaluations \(N\) for each total coating thickness estimation.

Table 2 Estimations of coating thickness model parameters and their ranges
Full size table

ince each MCM evaluation produces an image \(I[n]\) of coating thickness, which has a size of more than 1 M pixels, this would require a large storage to determine the coating thickness distribution, and thus uncertainty at each position (i.e., pixel). Instead, each evaluated image was added to a running sum image \({I}_{S1}\) and its square to a running square sum image \({I}_{S2}\) as in:

$$\begin{array}{c}{I}_{Sj}\left[n\right]={I}_{Sj}\left[n-1\right]+{I[n]}^{j}\\ n=1,\dots ,N\\ j\in \left\{1, 2\right\}\end{array}$$
(9)

The expected image of the coating thickness \(C\) was evaluated as:

$$C={I}_{S1}/N$$
(10)

The image of the uncertainty of the coating thickness \(U\) was estimated based on the sample standard deviation according to (Ref 24):

$$U=k\sqrt{\frac{N {I}_{S2}-{{I}_{S1}}^{2}}{N(N-1)}}$$
(11)

where \(k=1.96\) to have a level of confidence of 95%.

For the comparison of the in situ measurement approach with the reference measurement, the samples’ average coating thicknesses are required. Each sample’s average coating thickness \(\overline{c }\) and its uncertainty \({u}_{\overline{c} }\) were determined based on the distribution of the averages \({\overline{c} }_{n}\) of the individual images \(I[n]\) of MCM evaluations:

$${\overline{c} }_{n}=\frac{1}{H W}\sum_{h=1}^{H}\sum_{w=1}^{W}I[n](h,w)$$
(12)
$$\overline{c }=E({\overline{c} }_{n})$$
(13)
$${u}_{\overline{c} }=\sqrt{\mathrm{Var}({\overline{c} }_{n})}$$
(14)

The measurement model described by eq. (2)-(8) can also be used for evaluation of the thickness of individual coating layers. However, there was only one measurement repetition made during the coating. In order to get an estimate also of the influence of the measurement repeatability in this case, the same distributions of the measured parameters were assumed in their MCM evaluations as they were observed for the measurements before and after the coating.

System Calibration

The measurement setup first needs to be calibrated before the coating thickness can be measured. The purpose of the calibration is to determine the orientations \({\overrightarrow{d}}_{i}\) and positions \({\overrightarrow{p}}_{i}\) of the length gauges \(i\in \left\{1, 2, 3\right\}\) according to the camera’s coordinate system (Fig. 4) with sufficient accuracy so that their contributions to the uncertainty of the coating thickness are sufficiently small.

The orientations \({\overrightarrow{d}}_{i}\) as well as the X and Y components of the positions \({\overrightarrow{p}}_{i}\) were determined based on the manufacturing tolerances of the sensors’ fixtures. A calibration procedure was conducted to determine also the Z component \({p}_{iZ}\) of the positions. This was required because on one hand, the measurement model is highly sensitive to variations of \({p}_{iZ}\), and thus requires determination of these parameters with a small uncertainty. On the other hand, \({p}_{iZ}\) are only imprecisely determined during the assembly of the setup.

The calibration procedure consisted of using the setup to measure the thickness of reference samples with uniform, known thicknesses. For this purpose, ceramic gauge blocks \(j\in \left\{1, \dots ,6\right\}\) of grade 1 (Ref 25 of different thicknesses \({r}_{j}\) between 2 and 5.5 mm were used. These were selected to calibrate the measurement system over a wide sample thickness range.

The model of the calibration measurement is depicted in Fig. 5. The camera records the sample’s front side, described by points \({P}_{Fij}\). A plane is fitted to the points \({P}_{Fij}\) using the ordinary least squares (OLS) method. The fitted plane is described by its unit normal vector \({\overrightarrow{n}}_{rij}\) and the distance to the origin \({D}_{rij}\). The following equations apply:

$$\overrightarrow{O{B}_{ij}}={\overrightarrow{p}}_{i}+{l}_{ij}{\overrightarrow{d}}_{i}$$
(15)
$${\overrightarrow{n}}_{rij}\cdot \overrightarrow{O{B}_{ij}}+{D}_{rij}=-{r}_{j}$$
(16)

where \({l}_{ij}\) is the measurement of the length gauge \(i\) when measuring the reference sample \(j\).

Fig. 5
figure 5

Model of calibration measurement—a differential distance measurement of a sample of a known, reference thickness

Full size image

Repeating the calibration measurement for 6 different reference samples \(j\) results in an overdetermined system, where an approximate solution for \({p}_{iZ}\) can be found using OLS. To assess also the influence of the repeatability of the calibration, each measurement was repeated 5 times and included in the OLS. To determine the expected values for parameters \({p}_{iZ}\) as well as their uncertainties, the MCM was used to incorporate also the influence of manufacturing tolerances as well as the uncertainties of the camera and the length gauges.

The calibration procedure needed to be conducted for each length gauge separately because the area of the gauge blocks is not large enough to enable their probing with multiple length gauges simultaneously. In order to verify the stability of the system calibration, the procedure was repeated at the end of the experimental session. No statistically significant difference in the calibrated parameters was observed.

Evaluation of Surface Roughness Parameters

Since the developed measurement approach is based on recording of the sample’s surface, it is possible to evaluate the surface roughness of the sample prior to coating as well as after depositing one or multiple coating layers. Both the profile and the areal roughness parameters can be calculated. For the scope of this paper, the parameters Ra, Sa, and Ssk were evaluated. For the evaluation, the cutoff was set to 2.5 mm.

The measurements of Ra of the coated samples were compared to reference measurements conducted with a profilometer (MarSurf XR 20, Goettingen, Germany). The measurements were conducted along three lines, spaced 5 mm apart. The average of the measurements was calculated for the comparison. The uncertainty of the parameters were estimated based on the experimental standard deviations of the means.

Estimation of Coating Porosity

Coating porosity \(\phi\) is the ratio of the volume of pores \({V}_{p}\) and of the total volume of the coating deposit \({V}_{t}\):

$$\phi =\frac{{V}_{p}}{{V}_{t}}$$
(17)

where the total volume of the coating deposit \({V}_{t}\) is the sum of the volume occupied by the pores \({V}_{p}\) and by the coating material \({V}_{c}\):

$${V}_{t}={V}_{p}+{V}_{c}$$
(18)

The volume of the coating material \({V}_{c}\) can be estimated based on the coating mass \({m}_{c}\) and the material density \(\rho\). It follows that the sample’s coating porosity can be estimated as:

$$\phi =1-\frac{{m}_{c}}{\rho \cdot w\cdot h\cdot \overline{t} }$$
(19)

where \(w\) and \(h\) are sample width and height, respectively, and \(\overline{t }\) the average sample’s coating thickness. Therefore, the coating porosity \(\phi\) can be estimated in a nondestructive way simply based on the sample’s dimensions and the in situ measured average coating thickness together with the deposited coating mass \({m}_{c}\), which can be calculated as the difference in the sample’s mass before \({m}_{sb}\) and after \({m}_{sa}\) coating:

$${m}_{c}={m}_{sa}-{m}_{sb}$$
(20)

The uncertainty in the porosity evaluated based on eq (19)-(20) was estimated according to the law of propagation. For the unmeasured model parameters, it was assumed that they were independent and uniformly distributed. Their estimated ranges are listed in Table 3. It is to be noted that model is very sensitive to the relative uncertainty of the average coating thickness, and thus requires its accurate estimation.

Table 3 Estimations of porosity model parameters and their ranges
Full size table

The samples’ porosities estimated based on the in situ measured thicknesses were compared with reference measurements. The reference values were determined based on microscopic images of the coating’s cross sections. An optical microscope with a 200 × magnification was used. Twelve images were acquired per sample. On each image, the area fraction of the pores was obtained using Olympus Stream Software (Olympus Corporation, Tokyo, Japan). For the evaluation of the area fraction, a rectangular region was manually selected to include only the coating. The selected portion of the image was threshold using automatic settings, giving the pores’ area fraction. According to Delesse’s principle (Ref 27), the pores’ area fractions should equal their volume fractions. The reference samples’ porosities were calculated as the average of the individual measurements and their uncertainties based on the experimental standard deviation of the mean.

Results and Discussion

Average Coating Thickness

Figure 6 shows the comparison between the average coating thicknesses measured with the reference and the in situ methods (on X- and Y-axis, respectively) for the 10 produced coatings. The error bars correspond to the intervals estimated to have a level of confidence of 95%. The colors denote the five different numbers of coating layers applied, and the markers the two different repetitions of each coating.

Fig. 6
figure 6

Comparison of the reference and the in situ coating thickness measurements (on X- and Y-axis, respectively) of the 10 produced coatings. The error bars correspond to the intervals estimated to have a level of confidence of 95%. The colors denote the five different numbers of coating layers applied, and the markers the two different repetitions of each coating

Full size image

From Fig. 6, it can be seen that the in situ measurements are close to the reference values. This was be confirmed by calculating the zeta scores according to (1), which indicate no statistically significant difference between the reference and the in situ results at a significance level of 5% for 9 out of 10 results. From Fig. 6, it can also be seen that the in situ method produces results with uncertainty independent of the total coating thickness. Nevertheless, from Fig. 6, it can be observed that 9 out of 10 in situ measurements are smaller than the reference, indicating an existence of a bias between them. This could be due to multiple reasons: imperfect calibration of the in situ measurement setup; assumptions made in the measurement model regarding compensation of thermal expansion and neglecting of possible sample deformation due to residual stresses; or a bias in the reference measurements. For a more precise evaluation of the developed in situ method, a more precise reference would be required since the evaluated uncertainty of the in situ method is lower than the uncertainty of the reference (i.e., approximately 6 µm versus 12 µm, respectively).

Spatially Resolved Coating Thickness

The presented measurement technique is not only capable of providing an in situ estimate of the average coating thickness of the sample; it also gives a 3D view of the deposited coating thickness around the observed area, i.e., around camera’s FOV. An example of this is shown in Fig. 7, where the origin is positioned at the center of camera’s FOV.

Fig. 7
figure 7

Spatially resolved coating thickness around the observed area of the sample from an example run

Full size image

The 3D view provides a better insight into the features of the deposited coating compared to the microscopical method—e.g., identification of coating thickness minima and maxima, and opens doors for future improved understanding of the deposition process as well as coating behavior in different applications. Furthermore, the method provides an estimate of the uncertainty of the coating thickness, as shown in Fig. 8 for a level of confidence of 95%.

Fig. 8
figure 8

Uncertainties of the spatially resolved coating thickness measurements from Fig. 7 (at a level of confidence of 95%)

Full size image

From Fig. 8, it can be seen that the uncertainty in the coating thickness at each point is large—much larger than the uncertainty of the average coating thickness. The reason for this lies in the high surface roughness of the sample and the deposited coating (described in the measurement model by points \({P}_{Fb}\) and \({P}_{Fa}\), respectively), together with the relatively large possible misalignment between the measurement of the sample thickness before and after the coating. As depicted in Fig. 9, a large misalignment (marked as \(\Delta x\) in Fig. 9) can cause a large measurement error in the coating thickness at each point (marked as \({c}_{e}(\Delta x)\) in Fig. 9), which is reflected in their measurement uncertainties. However, the possible imprecisely known misalignment does not influence the evaluation of the average sample’s coating thickness because its effect is averaged out. Moreover, the uncertainty of the spatially resolved coating thickness could be lowered by reducing the uncertainty of the misalignment. This could be achieved for example by having a more precise sample positioning system, or to use another high-resolution camera on the back side of the sample instead of the length gauges together with reference markers on the sample.

Fig. 9
figure 9

Schematic showing the influence of a possible misalignment \(\Delta x\) between the thickness measurement before and after the coating (i.e., points \({P}_{Fb}\) and \({P}_{Fa}\), respectively) on the coating thickness measurement \(c(x)\). The misalignment can cause a large measurement error \({c}_{e}(\Delta x)\), reflected as a large measurement uncertainty of the coating thickness at each point

Full size image

Layer Thickness

Based on the sample thickness measurements during the coating, it is possible to determine the thickness of the individual deposited layers. An example of how the average layer thickness was changing during one run is shown in Fig. 10. In this run, 18 layers of coating were sprayed. The thicknesses shown are for two deposited layers since the sample thickness was measured only after spraying every two layers. The error bars correspond to the intervals estimated to have a level of confidence of 95%.

Fig. 10
figure 10

Example of how the thickness of each two deposited layers changed during one run where a total of 18 layers were sprayed. The error bars correspond to the intervals estimated to have a level of confidence of 95%

Full size image

Based on Fig. 10, it seems that there was no statistically significant variation in the average layer thickness during the run. Similar observations were made for all 10 of the conducted runs. This can be seen in Fig. 11, which shows the histogram of the measured average thicknesses of each two deposited layers from all the experiments. It can be noticed that the width of the distribution is of similar size as the measurement uncertainty. Therefore, it seems the process remained stable during the experiments. To be able to detect possible process variations of the layer thickness during these runs, an even more accurate in situ measurement would be needed. This would require a more elaborate compensation of thermal expansion in the measurement model as well as an area distance measurement sensor with higher accuracy.

Fig. 11
figure 11

Histogram of thicknesses of each two subsequently deposited layers from all experiments

Full size image

From the sample thickness measurements during the coating, it is similarly possible to get a 3D view of the deposited coating thickness per individual pairs of layers. However, because of the small layer thicknesses and the current large measurement uncertainties due to the possible misalignments, the results are of limited usefulness.

Surface Roughness

Figure 12 shows the comparison of the profile roughness parameter Ra evaluated based on the in situ measurement versus the reference measurement (on Y- and X-axis, respectively). The error bars correspond to the intervals estimated to have a level of confidence of 95% (k = 4.3). The colors denote samples with the five different numbers of coating layers applied, and the markers the two different repetitions of each coating.

Fig. 12
figure 12

Comparison of the reference and the in situ profile roughness parameter Ra (on X- and Y-axis, respectively) of the 10 produced coatings. The error bars correspond to the intervals estimated to have a level of confidence of 95% (k = 4.3). The colors denote samples with the five different numbers of coating layers applied, and the markers the two different repetitions of each coating

Full size image

Calculating zeta scores shows no statistically significant difference in the results for 7 out of the 10 experiments (at a significance level of 5%). Nevertheless, the relatively large measurement uncertainty should be noted. The measurement is highly dependent on the positions of the measurements. Therefore, areal roughness parameters should provide a more representative description of the surface because the whole area is included. An example of how areal roughness parameter Sa of each two deposited layers changed during one run is shown in Fig. 13, marked with blue crosses. A total of 18 layers were sprayed in that run. The first data point is the measurement of the surface roughness of the substrate before the coating. The uncertainties of Sa are omitted for clarity. Based on the experimental standard deviation, the uncertainties were estimated to be smaller than 0.05 µm (at a level of confidence of 95%). In addition, Fig. 13 shows marked with orange dots the changes in the areal roughness parameter Ssk (i.e., skewness) during the same run.

Fig. 13
figure 13

Example of how surface areal roughness parameters Sa and Ssk of each two deposited layers changed during one run where a total of 18 layers were sprayed

Full size image

Figure 13 provides an insight into how the surface roughness of the sample was changing during the coating. Before the coating, i.e., after the grit blasting, the surface roughness was the largest. After applying the first pair of layers, it substantially decreased. With coating of additional layers, it slowly increased until reaching a plateau. This behavior can be explained by also considering the skewness, which changes from negative before the coating to positive after applying a pair of layers. The splats formed by impinging particles onto a negatively skewed surface do not flow much into the sharp valleys of the grit-blasted substrate, as noted by Patel et al. (Ref 28 Because the splats end up sitting mostly on top of the valleys, this creates a more uniform surface. With coating of subsequent layers, the influence of the substrate becomes less pronounced, and thus the surface converges to a topography defined only by the deposited splats.

Coating Porosity

Figure 14 shows the comparison of the porosities of all the 10 sprayed coatings evaluated based on the in situ and the reference methods (Y- and X-axis, respectively). The error bars correspond to the intervals estimated to have a level of confidence of 95%. The colors denote samples with the five different numbers of coating layers applied, and the markers the two different repetitions of each coating.

Fig. 14
figure 14

Comparison of porosity measurements based on the in situ and the reference methods (Y- and X-axis, respectively) for the 10 produced coatings. The error bars correspond to the intervals estimated to have a level of confidence of 95%. The colors denote samples with the five different numbers of coating layers applied, and the markers the two different repetitions of each coating

Full size image

From Fig. 14, it can be seen that the in situ method overestimates the porosity compared to the reference. The discrepancy stems from the difference in which pores are taken into account by each method. The reference method disregards the pores at the top and bottom coating interface as it only considers the rectangular area of the coating between them; while the in situ method incorporates them. Furthermore, the image analysis of the reference method has inherent difficulties with measuring small pores and microcracks in contrast to the large pores, as remarked by Portinha et al. (Ref 29). Moreover, the in situ method is influenced by the shadowing effect of the camera, which cast shadows are considered to be part of the porosity. At small coating thicknesses (i.e., the red data points in Fig. 14), the relative contribution of the pores that are taken into account differently by the two methods is larger compared to thick coatings, thus there is a larger difference between these results. Moreover, the relative uncertainty in the average coating thickness is also larger for thin coatings compared to the thicker coatings, resulting in less accurate results of the in situ-based method. Nevertheless, the results based on the in situ measured coating thickness can be used to provide a quick and nondestructive approximate estimation of coating porosity.

Conclusions and Outlook

In the paper, an approach for in situ spatially resolved coating thickness measurements was presented. The measurement technique is based on a high-resolution 3D camera to capture the surface topography and include it in the thickness measurement. The approach gives results independent of substrate and coating materials. The capabilities of the technique were demonstrated on the example of atmospheric plasma spraying of yttria-stabilized zirconia on steel substrate. It was shown that the measurement technique provides results of total coating thickness with excellent accuracy when compared to the reference microscopical method. Moreover, the measurement approach gives a 3D view of the coating thicknesses around the observed area, providing additional information about the deposited coating. Since it is applied in situ, it also gives information about thickness of individual coating layers, providing improved insight into the process. Furthermore, the measurement approach enables in situ evaluation of surface topography and its changes during the coating by calculating both the profile and areal roughness parameters. It was also demonstrated that due to the low measurement uncertainty of the coating thickness measurement, it is possible to estimate coating porosity in a quick and nondestructive way by simply weighting the part before and after the coating in addition to performing the thickness measurement.

Due to the excellent performance and the abundance of the information provided by the presented in situ measurement approach, it could be used in the future for automatic quality assurance, replacing the time- and cost-consuming manual laboratory analysis. The low measurement uncertainty of the coating thickness measurement and its applicability during spraying also make it a prime candidate to be used as a feedback signal for an online, closed-loop control of the thermal spraying process. Possibilities for shortening the measurement times during spraying shall be investigated to reduce possible influences of halting the process on the coating. In the future, the performance of the measurement approach on non-planar samples shall be investigated, where additional uncertainties arise with compensation of thermal expansion and lateral movement. The applicability of the measurement approach in other coating processes with similar requirements shall also be explored.