Introduction

In recent decades, reducing greenhouse gases in order to limit global warming has emerged as greatest ecological challenge for the modern transportation sector (Ref 1). Multi-material lightweight design of car bodies can substantially contribute to improve the efficiency of fossil fuels and thus to reduce CO2 emissions. In this context, a common approach is to substitute conventional mild steels with high-strength steels (HSS) and with aluminum alloys in the body-in-white (BIW), but without diminishing the crashworthiness of cars for maintaining the passenger safety (Ref 2). Integrating dissimilar materials in lightweight car bodies requires reliable and cost-efficient joining processes (Ref 3). Resistance spot welding (RSW) has predominantly been used as standard process for joining steels in the automotive industry (Ref 4). However, the thermally-induced formation of coarse-grained, layered intermetallic phases at the welding spot, which are susceptible to crack propagation, makes this process unsuitable for joining aluminum alloys with steels in series production (Ref 5, 6).

Formation of brittle intermetallic phases in aluminum-to-steel welding can be suppressed by means of other welding technologies (Ref 7,8,9). However, intermetallic phases are completely absent in mechanical joining based on plastic deformation of the components at room temperature, such as self-piercing riveting (SPR), mechanical clinching and hemming (Ref 10,11,12). In modern car body manufacturing, mechanical joining is usually combined with adhesive bonding to improve both static and dynamic properties of the joints. Comprehensive experimental studies revealed that these hybrid joints possess generally higher strength, stiffness and energy absorption than simple mechanical joints (Ref 3, 13). In particular, SPR combined with adhesive bonding, so-called riv-bonding, has been established as cost-efficient technology for joining aluminum alloy sheets with steel sheets in multi-material car bodies (Ref 14).

As reviewed by He et al. (Ref 15), numerical simulation of SPR for predicting the general joinability, the quality and the strength of joints is nowadays state of the art for similar (e.g., aluminum-aluminum (Ref 16,17,18,19,20,21)) as well as for dissimilar (e.g., aluminum-steel (Ref 21,22,23,24,25,26,27)) metal combinations. Few authors also investigated SPR combined with adhesive bonding of similar aluminum alloys by using the Simufact Forming finite element (FE) software: Potgorschek et al. investigated riv-bonding of 2.0/2.0-mm-thick 6xxx-T4 aluminum alloy sheets (Ref 28), whereas Liu et al. studied in detail riv-bonding of 1.2/2.0-, 1.8/2.0-, and 2.5/2.0-mm-thick 5754 aluminum alloy sheets (Ref 29). In both studies, the yield stress of the liquid adhesive was modeled as function of the strain rate. This simplified model is based on the rate-power-law of Ostwald and de Waele, which describes the shear stress as function of the shear rate (Ref 30). The feasibility of this approach was already demonstrated for clinch-bonding simulations (Ref 31, 32), and comparing the results of riv-bonding simulations with corresponding experiments shows also good agreement (Ref 28, 29). Some researchers studied riv-bonding of similar metal combinations (e.g., steel-steel (Ref 33,34,35), aluminum-aluminum (Ref 36)) using fluid-structure interaction (FSI), which combines computational fluid dynamics (CFD) and finite element method (FEM). However, they also reported that FSI simulations of riv-bonding are numerically unstable and require high computational effort. To the authors’ knowledge, riv-bonding of dissimilar aluminum-steel combinations so far has mainly been studied experimentally.

The most common approach for assessing the quality of SPR joints is metallographic sectioning and subsequent measurement of characteristic dimensions at the joint cross section, including in particular the height of the rivet head, the horizontal undercut (interlock) of the rivet, and the minimum bottom thickness of the lower sheet (Ref 14, 37). Haque et al. employed the characteristic force–displacement curve of the punch monitored during the riveting experiment for assessing the quality of SPR joints; however, they only did it for steel sheets (Ref 38). Based on a simple model, they proposed that this curve can be particularly used for estimating flaring of the rivet (Ref 39). Moreover, for quality assessment of riv-bonded joints the shape of the adhesive cavities should be additionally evaluated (Ref 40). In order to obtain reliable joints, it is well known that the types and dimensions of both the die and the rivet must match the actual material properties and the thicknesses of the sheets to be joined (Ref 41, 42). One also has to comply with requirements concerning stacking order and positioning of the sheets, which limits the existing design possibilities offered by multi-material design.

Abe et al. investigated SPR of 5052 aluminum alloy sheets with mild and high-strength steel sheets of different thicknesses using a conventional pip die and manganese-boron steel rivets. They reported better joinability when placing the steel sheets on the punch side (upper sheet) and the aluminum alloy sheet on the die side (lower sheet) (Ref 22). Large differences between the flow stresses of the sheets deteriorate the joinability. Increasing the tensile strength of the lower sheet tended to decrease flaring of the rivet which reduced the final interlock. Nevertheless, reliable joints were achieved for steel sheets with tensile strengths below 590 MPa (Ref 23). Sun and Khaleel came up with similar results. They stated that using lower sheets which are either strong (e.g., HSS) or comparatively thick (i.e., > 3 mm) may cause problems with creating the interlock (Ref 43, 44). In order to reduce the deformation resistance when riveting DP780 advanced high-strength steel with 6061-T6 aluminum alloy, Lou et al. applied direct current to the steel sheet during the SPR process. They were able to improve the mechanical properties of the joints by using this electro-plastic self-piercing riveting (EP-SPR) process (Ref 45).

Basic rules for configurations comprising two sheets state that the quality of joints tends to become better, if (i) the harder material is placed as upper sheet on the punch side, and if (ii) the thicker material is placed as lower sheet on the die side (Ref 37). One should note that recommendations concerning the favorable joining direction (“from high strength to low strength,” “from hard to soft” and “from thin to thick”) were determined for simple SPR joints which do not consider any adhesive layer between the sheets. However, industrial practice and numerical simulations have shown that both the amount of adhesive applied to the lower sheet and the initial distribution of the adhesive when clamping the sheet stack affect the subsequent SPR process. Therefore, this work investigates riv-bonding of 3.0-mm- and 1.0-mm-thick AW-6xxx aluminum alloy sheets with 1.5-mm-thick HC4xx HSS sheets using two rivet types combined with an epoxy-based single-component adhesive. In order to exploit the advantages offered by multi-material design, the joints were produced against the favorable joining direction, i.e., the HSS sheet was placed on the die side (lower sheet) and the aluminum alloy sheet was placed on the punch side (upper sheet). Based on the detailed analysis of the experiments, FE models introduced by Hönsch et al. (Ref 18, 19) and by Potgorschek et al. (Ref 28) were modified for simulating riv-bonding of dissimilar aluminum-steel joint configurations. These simulations can reduce the great experimental efforts required for finding the optimum combination of rivet type, die type and amount of adhesive.

Experimental Investigations

Materials

The nominal compositions of the sheet metals used in the present study, including two AW-6xxx aluminum alloys and two HC4xx steels (low alloyed steel HC420LA and dual phase steel HC450X), are given in Table 1, and their basic mechanical properties are summarized in Table 2. The four configurations of hybrid joints investigated in the present study are listed in Table 3.

Table 1 Nominal compositions of sheets (wt.%) according to supplier specifications
Full size table
Table 2 Mechanical properties of sheets according to supplier specifications
Full size table
Table 3 Configurations of hybrid riv-bonded joints
Full size table

Joining Procedure

A manual Tucker riveting system consisting of an ERC control unit and an electrically driven ERT80 spindle mounted on a massive C-frame was used for joining. Platelets of 30 mm × 30 mm for being utilized in the joining experiments were cut out of the sheets. SikaPower®-498/3 single-component epoxy-based adhesive was heated to the recommended processing temperature of 50-60 °C (Ref 46). A line of adhesive was deposited across the steel platelet by means of a manual cartridge gun before the steel platelet was stacked with the aluminum alloy platelet. The deposited mass of about 0.5 g was estimated based on the length (about 30 mm), the mean diameter (about 4 mm) and the density (1.3 g/cm3, (Ref 46)) of the adhesive line.

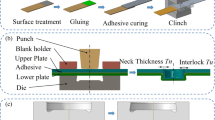
These steel/adhesive/aluminum stacks were placed on the Tucker T005 flat die (Ref 47), Figure 1(a), and clamped with constant force of 10 kN by the blankholder of the riveting system. Note that flat dies deform the lower sheet (i.e., in the present work the steel sheet) less than pip dies, which is particularly beneficial if materials of low ductility are riveted. Due to clamping, the adhesive between the platelets was distributed and portions of adhesive were even squeezed out of the joining gap. Thus, the thickness of the adhesive layer beneath the contact zone of the blankholder was significantly reduced. The comparatively high blankholder force was applied to make the adhesive layer as thin as possible. Especially the combination of U-type rivets with thick adhesive layers, i.e., with large volumes of adhesive, was identified as prone for crack formation. Direct measurement of the layer thickness was impossible, since the residual adhesive layer was not accessible after the blankholder had clamped the steel/adhesive/aluminum stack. Nevertheless, the actual layer thickness was likely about 0.1-0.2 mm, as the adhesive cavities in the experiments were quite similar to the cavities in the simulations obtained with the layer thickness of 0.1 mm.

Figure 1
figure 1

Cross sections of (a) T005 flat die, (b) C5.3×8.0-H4 rivet, and (c) U5.5×5.0-H6 rivet

Full size image

Right after clamping, the rivet was pushed with constant punch speed of 100 mm/s into the stack. Tucker C5.3×8.0-H4 and U5.5×5.0-H6 rivets made of manganese-boron steel (Ref 47), Figure 1(b) and (c), were used. During the SPR process, the force–displacement curve was monitored. As the punch stroke was displacement-controlled, several pretrials for determining the optimum stroke were performed for each of the joint configurations. The optimum punch stroke was 10.5 mm or 7 mm for joint configurations with the C-type or the U-type rivet, respectively. Finally, the riv-bonded joints were put for 20 min into a furnace to cure the adhesive at elevated temperature of 180-200 °C. This heat treatment simulated the paint baking process (also known as cathodic dip coating, CDC) which is typically applied to car bodies-in-white.

Assessment of Joint Quality

The quality of the joints was assessed on the basis of characteristic cross section features including height of the rivet head, horizontal undercut (interlock) of the rivet, minimum bottom thickness of the lower sheet, and shape of the adhesive cavities. For that purpose, the joints were sectioned and embedded into epoxy resin, before the cross sections were ground and polished. Adjustment of the material removal during grinding and polishing was important to ensure that each cross section was exactly located at the center axis of the rivet. The cross sections of the joints were finally captured using a Keyence VHX-6000 digital microscope. Moreover, hardness profiles for visualizing strain hardening of the sheets due to plastic deformation during the SPR process were measured at the cross sections using an automated EMCO-TEST DuraScan G5 hardness tester.

Numerical Simulations

Riv-bonding of two different joint configurations, C-1 (3.0-mm-thick upper aluminum alloy sheet and C5.3×8.0-H4 rivet) and U-1 (1.0-mm-thick upper aluminum alloy sheet and U5.5×5.0-H6 rivet), was modeled using the Simufact Forming 15 (Ref 48) finite element software.

Model Geometry and Mesh

Figure 2 shows the two-dimensional axisymmetric models of joint configurations (a) C-1 and (b) U-1. Each of these models includes rigid (punch, blankholder and flat die) as well as deformable (rivet, upper sheet, lower sheet and adhesive layer) components. As estimated in experimental and numerical studies on the distribution behavior of the adhesive, the initial thickness of the adhesive layer was 0.1 mm (Ref 28). The actual geometries of the flat die and of both rivets were captured using the GOM ATOS III Triple Scan optical measuring system. In addition, five cross sections of each rivet type were surveyed with a microscope for obtaining detailed information about the geometries of rivet tips and rivet shafts. Based on these measurements, the geometries of the rivets and of the flat die were created as input for the models. As proposed by Hönsch et al. (Ref 18, 19), elastic deformation of the riveting pliers during the SPR process must be considered. Therefore, a numerical spring acting parallel to the model axis was assigned to the bottom of the flat die.

Figure 2
figure 2

Axisymmetric models with details showing the initial meshes of joint configurations (a) C-1 and (b) U-1. Colored components of the models are elastoplastic deformable, whereas gray components are rigid (Color figure online)

Full size image

Deformable components were meshed with tetragonal “quad” elements: six layers of elements were used per millimeter of sheet thickness, and three layers of elements were used for the 0.1-mm-thick adhesive layer. The details of Figure 2 illustrate the initial mesh of each model. Note that these meshes had rather low influence on the quality of the final results, as severe deformation of the components required frequent automated remeshing during the simulations anyway. The specified minimum length of the element edges after each remeshing step was 0.12 mm for the metal sheets and 0.06 mm or 0.03 mm for the adhesive of joint configurations C-1 or U-1, respectively. However, inside of predefined “refinement boxes” these minimum lengths were still allowed to decrease. If the local thickness of the sheets or of the adhesive layer decreased below the predefined threshold thickness (“cut distance”) of 0.016 mm, mesh splitting was achieved by deletion of the corresponding elements. That finally enabled piercing of the sheets or separation of the adhesive layer, respectively.

Material Definitions

The material properties used in the models describe the elastoplastic deformation of the components at room temperature. Since riveting is usually accomplished very fast (i.e., within about 0.1 s which is much faster than conductive heat transfer), the influence of heating due to deformation and friction was assumed as negligible for the material properties.

Rivets

Flow curves of manganese-boron steel rivets were derived from results of uniaxial compression tests. Therefore, hollow-cylindrical samples were cut from shafts of C5.3×9.5-H4 rivets and compressed at different strain rates using a Gleeble 3800 testing machine. Strain rate-dependent flow curves for the H4 hardness class were iteratively determined by inverse modeling of the compression testing setup. Hönsch et al. provided detailed information about the elaborate testing and modeling procedures (Ref 49). They successfully used the obtained flow curves of the rivet for simulating SPR of aluminum alloy sheets (Ref 19). Flow curves of the U5.5×5.0-H6 rivet were extrapolated based on the hardness difference between the H4 and H6 hardness classes. Figure 3(a) shows the flow curves of the rivet steel for both classes.

Figure 3
figure 3

Flow curves of the (a) rivet steel, (b) sheet metals, and (c) adhesive used in the numerical models

Full size image

Sheets

Flow curves of the 1.5-mm-thick HC420LA steel sheet and of the 3.0-mm- and 1.0-mm-thick AW-6xxx aluminum alloy sheets were derived from results of quasi-static uniaxial tensile tests. For each of the sheet metals, bone-shaped tensile samples were tested using a Zwick/Roell Z100 testing machine. As proposed by Hönsch et al. (Ref 18, 19), flow curves were extrapolated based on the Hockett–Sherby law which was extended with a linear term to consider sufficient strain hardening for true strains beyond 0.2. Figure 3(b) illustrates the flow curves of the sheet metals.

Adhesive

Considering the liquid adhesive is the key challenge in FE modeling of riv-bonding processes. In order to address this issue, the viscoelastic properties of the liquid epoxy-based single-component adhesive were substituted with “equivalent” mechanical properties, as presented by Potgorschek et al. for riv-bonding of aluminum alloy sheets (Ref 28). The strain rate-dependent flow stress of the adhesive was calculated from the shear rate-dependent complex viscosity which was determined at different temperatures using a Paar Physica MCR300 rheometer. At each of these temperatures, the flow curve was finally obtained by power-law fitting of the calculated flow stresses. Figure 3(c) shows the flow curve at 40 °C used in this work for modeling the behavior of the adhesive during the SPR process. For comparison, the flow curve of the adhesive at the general process temperature of 20 °C is also included.

Process Definitions

According to the experiments, the predefined blankholder force was applied for clamping the sheet stack and for distributing the adhesive in the first process step. In the second process step, the rivet was pushed with predefined punch stroke and constant punch speed into the sheet stack. As both upper sheet and lower sheet had only 20 °C, the adhesive in between was assumed to cool down from its initial application temperature of 50-60 °C to 40 °C before the riveting process started. Since riveting is accomplished very fast, the temperature of the adhesive was assumed as constant during the process. Table 4 summarizes the main process parameters used in the FE simulations.

Table 4 Parameters of the riveting process
Full size table

Contact Conditions

The Coulomb–Tresca friction model available in Simufact Forming, which was already used in FE modeling of SPR (Ref 18, 19), riv-bonding (Ref 28, 29) as well as flat-clinch-bonding of aluminum alloy sheets (Ref 32), was also utilized in the present work. This hybrid friction model assumes that the friction shear stress at the contact interface, \(\tau_{F}\), increases proportional to the normal contact pressure, \(p\), until the shear stress limit, \(mk\), is reached (i.e., \(\tau_{F} = \mu p < mk\)). Beyond this limit, \(\tau_{F}\) stays constant (i.e., \(\tau_{F} = mk\)). \(k\) is the ultimate shear strength, \(m\) is the interface friction factor, and \(\mu\) is the Coulomb friction coefficient. Note that both, \(m\) and \(\mu\), are constant and smaller than unity. Table 5 provides an overview of the friction coefficients used for different contact pairs in the FE models.

Table 5 Friction coefficients used in the process models (Ref 19, 28)
Full size table

The comparatively low value of \(\mu =\) 0.10 for both sheet/rivet contact pairs was chosen for taking the beneficial effect of the rivet coating into account. Coatings may remarkably reduce friction during rivet setting, which improves the final quality and thus the mechanical behavior of SPR joints (Ref 50). However, using \(m =\) 0.30 (Ref 19) or \(m =\) 0.15 (Ref 28) for the sheet/rivet contact pairs was observed to have only negligible effect on the results. The comparatively high value of \(\mu =\) 0.30 for the lower sheet/flat die contact pair considers the rough and slightly contaminated surface of the die, which had previously been used for riveting aluminum alloys. Even local adhesion of aluminum on the surface of steel tools increases friction significantly (Ref 51). Sticking between the adhesive and the metal sheets was modeled using the “glued” contact type which prevented separation of mesh nodes of the sheet surface from adjacent mesh nodes of the adhesive. Separation was only allowed by deletion of elements during mesh splitting, if the thickness of the adhesive layer decreased below the predefined threshold thickness.

Results

Joint Cross Sections

Joints consisting of rivets without adhesive do not have any considerable practical relevance in the automotive industry. However, joint configuration C-1 was exemplarily produced without adhesive in order to illustrate the influence of the volume of adhesive on the joining gap between the upper aluminum alloy sheet and the lower steel sheet. Figure 4 reveals a significantly narrower or even missing gap for the joint without adhesive (a), whereas the gap is much larger for the joint with adhesive (b). Accordingly, excessive deformation of the sheets or even local cracking of the components may occur if the adhesive layer becomes too thick and if large volumes of adhesive must be displaced during the SPR process.

Figure 4
figure 4

Cross sections of joint configuration C-1 (a) without and (b) with adhesive. Color-hatched areas indicate the gaps between the sheets (Color figure online)

Full size image

Figure 5 shows cross sections of joint configurations (a) C-1, (b) C-2, (c) U-1 and (d) U-2. Despite asymmetric deformation of the rivet shaft sufficient interlock was obtained for each of the four joint configurations. The horizontal undercut was approx. 0.5 mm for the C-type rivets and approx. 0.2 mm for the U-type rivets. The height of the rivet head was negligible, but as shown in Figure 5(c) and (d) unfavorable gaps occurred between the heads of the U-type rivets and the upper aluminum alloy sheets. This issue could be solved by increasing slightly the punch stroke in order to push the rivet deeper into the stack.

Figure 5
figure 5

Cross sections of joint configurations (a) C-1, (b) C-2, (c) U-1 and (d) U-2. The red arrow indicates the position of the bottom crack at the lower steel sheet, and the green arrows indicate the positions of the aluminum chips (Color figure online)

Full size image

The minimum bottom thickness of the lower steel sheet was identified as critical with respect to the quality of the joints. Beneath the tip of the rivet severe local thinning and cracking of the steel sheet occurred particularly for joint configuration U-2, Figure 5(d). That was mainly due to the poor formability of the HC450X sheet, as indicated in Table 3 by the comparatively low total elongation and by the high \(R_{m} /R_{p}\) ratio (i.e., the high strain hardening tendency). Moreover, closer examination of Figure 5(c) and (d) reveals that thin aluminum chips had formed inside the side cavities between the sheets, as the cut-off piece of the upper AW-6014-PX sheet had been severely deformed within the narrow gap between the rivet tip and the lower steel sheet.

The hardness profiles of the sheets illustrated in Figure 6 were captured at the cross sections of the joints shown in Figure 5. Considerable hardening of the steel sheets occurred next to the rivets, as the profiles show two distinct peaks, particularly, when the U-type rivet was used. These peaks indicate local strain hardening due to plastic deformation of the steel sheet beneath the rivet tip, causing severe local thinning or even cracking at the bottom of the joint, as exemplarily shown in Figure 5(d).

Figure 6
figure 6

Hardness profiles of the sheets at the cross sections of the joints for the C-type rivet (continuous lines) and for the U-type rivet (dashed lines)

Full size image

Figure 7 compares cross sections of joint configurations (a) C-1 and (b) U-1 obtained from riv-bonding experiments (left hand side) and riv-bonding simulations (right hand side). The simulations were obviously able to predict the geometry of both joints, as height of the rivet head, interlock of the rivet and minimum bottom thickness of the lower HC420LA sheets agree well with the experiments. However, in the simulations shape and volume of the adhesive cavities were slightly different to the experiments. In particular, the volume of the side cavity of joint C-1 was overestimated, whereas the volume of the center cavity of joint U-1 was underestimated. Moreover, the cavity beneath the rivet head was smaller in the simulation than in the experiment. Closer examination of Figure 7(b) reveals a long crescent-shaped aluminum chip inside the side cavity between the upper and the lower sheet, as shown in detail in Figure 7(c).

Figure 7
figure 7

Cross sections of joint configurations (a) C-1 and (b) U-1 obtained from riv-bonding experiments (left) and from simulations (right); (c) detail showing the aluminum chip

Full size image

The simulation sequence of Figure 8 visualizes how the chip forms during the SPR process. (a) When the U-type rivet pierces the upper AW-6014-PX aluminum alloy sheet, the cut-off piece piles up in front of the rivet tip. (b) The edge of this cut-off piece is severely deformed and squeezed through the narrow gap between the flaring rivet tip and the deforming lower HC420LA steel sheet. (c) As the aluminum alloy is very ductile, a thin aluminum chip is extruded against the riveting direction into the cavity between the upper and the lower sheet. (d) At the end of the riveting process, the crescent-shaped chip has formed which is still connected with the cut-off aluminum piece located beneath the rivet tip. This secondary deformation of the upper aluminum alloy sheet is not mandatory for obtaining sufficient interlock between the rivet and the sheets. It can only occur, if the HSS sheet is placed as lower sheet at the die side, since the “soft” upper sheet is then deformed between the “hard” lower sheet and the “very hard” rivet.

Figure 8
figure 8

Simulation sequence illustrating the formation of the aluminum chip at punch displacements of (a) 4.5 mm, (b) 5.5 mm, (c) 6.5 mm, and (d) 7.5 mm

Full size image

Predicting the characteristic cross section features of the joints by means of FE simulations was finally successful. However, remeshing influenced considerably the numerical stability of the simulations and the quality of the results. Predefining proper remeshing parameters determined whether chip formation could be predicted. Moreover, the lower limit of the element size predefined for remeshing determined the resolvable minimum thickness of the adhesive layer. Nevertheless, severe deformation of the mesh caused numerical instabilities and required manual restarts of interrupted calculations, particularly for joint configuration U-1.

Force–Displacement Curves

Figure 9 illustrates typical force–displacement curves monitored in the experiments and calculated in the simulations for both joint configurations, C-1 and U-1. The die force includes (i) the constant blankholder force of 10 kN, and (ii) the punch force which increases with progressing displacement of the punch. The curves from both experiments and simulations show generally good agreement. In particular, the maximum force acting on the die, which is a key parameter for designing the riveting system, was predicted well in the simulations. It was about 70 kN and 60 kN for joint configurations C-1 and U-1, respectively. For joint configuration U-1, the slopes of the curves differ considerably at the end of the process. The reason for this difference was severe local thinning (initiated at the punch displacement of 5.0 mm) followed by partial cracking (occurred at the punch displacement of 6.7 mm) of the lower steel sheet beneath the rivet tip, as indicated by the dashed green curve of the experiment. However, the crack-free joint shown in Figure 5(c) indicates that cracking did not occur in each of the experiments.

Figure 9
figure 9

Force–displacement curves obtained from riv-bonding experiments and simulations for joint configurations C-1 and U-1

Full size image

Summary and Conclusions

Self-piercing riveting (SPR) combined with adhesive bonding—so-called riv-bonding—of 1.0-mm- and 3.0-mm-thick aluminum alloys AW-6014-PX and AW-6451-T4 with 1.5-mm-thick high-strength steels (HSS) HC420LA and HC450X was experimentally studied. Riv-bonding was performed against the favorable joining direction, i.e., in each of the four joint configurations investigated the “soft” aluminum alloy sheet was placed at the punch side, whereas the “hard” HSS sheet was placed at the die side. Moreover, numerical models of the riv-bonding process were built for two of the joint configurations using the Simufact Forming finite element (FE) software. The following conclusions can be drawn based on the results of the present study:

  1. 1.

    Hybrid joints of good dimensional quality possessing low height of the rivet heads and sufficient interlock were obtained, even when the HSS sheets were placed at the die side, i.e., when they were used as lower sheets. In general, the minimum bottom thickness of the lower steel sheets was also sufficient; however, when using the U-type rivet bottom cracking of the HC450X sheet occurred due to severe local deformation next to the rivet tip.

  2. 2.

    Using the “harder” metal (e.g., the high-strength steel) as lower sheet at the die side and the “softer” metal (e.g., the aluminum alloy) as upper sheet at the punch side may cause secondary deformation of the upper sheet metal. If this metal is very ductile, even large chips can be found inside the cavity between the sheets. This secondary deformation is not mandatory for creating the interlock between the rivet and the sheets.

  3. 3.

    Joint cross sections and force–displacement curves obtained from riv-bonding experiments and simulations show generally good agreement. Hence, the finite element (FE) simulation is obviously reliable for predicting the quality of hybrid joints. Considering the adhesive in the numerical model of the riv-boding process is, however, crucial for predicting accurately the cross section features of the joints, as the incompressible adhesive influences the flaring behavior of the rivet and the formation of cavities between the sheets.

  4. 4.

    Even for identical materials and process parameters, the characteristic dimensions of the cross sections of the hybrid joints may differ slightly from each other. These differences were not only observed in the results of the joining experiments, but also in the results of the joining simulations. However, differences in the simulation results are mainly triggered by predefined remeshing and mesh separation parameters.