Comparative Evaluation of Characterization Methods for Powders Used in Additive Manufacturing

Abstract

In recent years, the interest in additive manufacturing technologies has increased significantly, most of them using powders as feedstock material. It is therefore essential to check the quality of the powder before processing in order to ensure the same quality of the printed components at all times. This kind of quality assurance of a powder should be carried out independently of the additive manufacturing technology used. Since there is a lack of standards in this field, various powder analysis methods are available, with which, in principle, the same characteristics can often be measured, at least nominally. To verify the validity of these methods, three different nickel-based powders used for additive manufacturing were examined in the present study using standard methods (apparent density, tap density, Hall flow rate, optical microscopy, scanning electron microscopy) and advanced characterization methods (dynamic image analysis, x-ray microcomputed tomography, adsorption measurement by Brunauer–Emmett–Teller method). A special focus has been given on particle size distribution, particle shape, specific surface area, and internal porosity. The results of these measurements were statistically compared. This study therefore provides an insight into the advantages and disadvantages of various optical characterization techniques.

Introduction

With the growth of additive manufacturing (AM) technologies, the question about the right or a good powder for the corresponding processes is also being asked more and more frequently. Many researchers around the globe are currently trying to answer this question and are working on new characterization methods which, for example, deal with the spreading of powder layers (Ref 1,2,3). In addition to these methods for direct evaluation of the spreading behavior, there are also other new characterization methods which try to determine the suitability of a powder for those processes from an indirect measurement of different physical properties of the powder. These include various commercially available powder rheometers (GranuDrum from the company Granutools, REVOLUTION Powder Analyzer from the company Mercury Scientific Inc, MCR rheometers from the company Anton Paar, FT4 Powder Rheometer from the company Freeman Technology), which sometimes differ in their measuring principle. However, there are also traditional methods, having their origin in classical powder metallurgy, such as the measurement of flow rate and apparent density. Regardless of new or traditional methods, all data obtained depend on the size and shape of the particles contained in the powder. For instance, spherical powders flow faster and better than aspherical ones, and fine powders reach a limiting particle size at which a powder is finally too fine and the interparticular forces acting on the particles as e.g. friction, van der Waals or electrostatic forces, become too high to ensure good flow. For this reason, it is particularly important to look more closely at the methods used to examine size and shape. There are various investigation methods that lead to similar results, but some of them differ in their physical measurement principles or even in the calculation of certain parameters. Therefore, the scope of this study is placed on the comparison of these methods.

Particle size distributions were measured using x-ray microcomputed tomography (µCT), dynamic image analysis, optical microscope analysis, and laser diffraction. The characteristic diameters were also calculated for the distribution patterns. For measuring the particle shape, the mentioned methods were also used, with the exception of laser diffraction. In each case, the sphericity and the aspect ratio were measured. In addition, the specific surface area was also measured, which is influenced by both size and shape of the particles. The specific surface area was determined by x-ray microcomputed tomography, dynamic image analysis, optical microscope analysis and an adsorption measurement according to the Brunauer–Emmett–Teller (BET) model. Since the internal porosity could also be measured and evaluated using microcomputed tomography and optical microscope analysis, it was also included.

The data obtained are compared, discussed and evaluated in terms of their suitability. The use of a quite spherical powder was particularly helpful. In addition, however, two other powders were also investigated, which differ significantly in their size and shape.

Materials and Methods

Powders Used and Basic Characterizations

For this study, three different inert gas atomized IN718 superalloy powder grades were used, which differ in size and shape. They will be further referred to as powders A, B and C. In order to obtain representative results, correct sampling is crucial. Sampling is described in the ISO 3954:2007 (Ref 4) and ASTM B215-20 (Ref 5) standards. For this study, 1.5 kg of powder from each of the three powders was separated with a riffle divider into 15 samples of approximately 100 g each. These samples were then used for the following investigations. To define a certain initial state of the powders, some standardized basic powder characteristics were determined, such as the Hall flow rate (Ref 6), apparent density (Ref 7), tap density (Ref 8) and the Hausner ratio calculated from both densities.

The Hall flow rate test was performed by measuring the time it takes 50 g of powder to flow through the orifice of a calibrated funnel of defined dimensions. The results are given in s/50 g powder. The flow rate or, more correctly, “flow time”, as termed by H. H. Hausner (Ref 9) is a parameter to rate the flowability and the lower it is, the better a powder flows.

The apparent density was determined by filling a cup with powder using either the Hall funnel or, if the powder does not freely flow through it, using the Carney funnel, whose orifice is twice as wide. The mass of the powder in the cup was then weighed and as the used cup has a specified volume, the apparent density can be calculated. The results are given in g/cm³. The apparent density is a parameter for rating the filling behavior of a powder, and the higher it is, the more densely a powder is packed.

The tap density was measured by filling a graduated cylinder with a specific mass of powder. The cylinder was then tapped a certain number of times so that the powder inside was compacted. At the end, the compacted volume was read from the cylinder and the tap density was calculated taking the powder mass into account. The results are given in g/cm³. Like the apparent density, the tap density is a parameter for rating the filling behavior of a powder, and the higher it is, the more densely a loose powder bed can be compacted, with the maximum density of the loose powder bed being the tap density.

The Hausner ratio is defined as the ratio between tap (ρ_TD) and apparent density (ρ_AD) as shown in Eq 1.

Hausner ratio

$${\text{HR}} = \frac{{\rho_{{{\text{TD}}}} }}{{\rho_{{{\text{AD}}}} }}$$

(1)

Some state that the Hausner ratio can be used to describe both flowing and filling (Ref 10,11,12,13) as well as the cohesiveness of a powder (Ref 11). Others, however, conclude that the Hausner ratio does not correlate well with the flowability (Ref 14) and that the determination of the Hausner ratio differs too much from the process in AM techniques (Ref 15). In Ref 11, it is stated that with a higher Hausner ratio a powder is more cohesive and thus worse flowing or even non-flowing (considering the Hall flow rate test).

In addition, the powders were examined with an JEOL JSM 6490 HV scanning electron microscope (SEM); the density was measured using a Quantachrome Ultrapycnometer 1000 helium pycnometer. Furthermore, the interstitial content of carbon (LECO CS844), hydrogen (ELTRA H-500), nitrogen (LECO TCH600) and oxygen (LECO TCH600) was measured.

Particle Size Characteristics

Since the aim of this study is to compare and discuss the results from different powder analyzing techniques regarding their particle size measurements, the most important particle size characteristics will now be explained briefly. It should be noted that most of them are described in the ISO 9276-6:2008 (Ref 16) standard.

For the following characteristics, one should imagine having depicted the silhouette of a particle as shown in Fig. 1(a). Now measuring the area of the silhouette, the diameter of a circle with the same area as shown in Fig. 1(b) can be calculated according to Eq 2.

Fig. 1.

(a) Particle silhouette with marked area of 2D projection (A); (b) Circle with equal area (A)

Area equivalent diameter

$$x_{{{\text{area}}}} = \sqrt {\frac{4 \cdot A}{\pi }}$$

(2)

This is called “area equivalent diameter” (x_area). It is indicated that a measured particle size distribution by dynamic image analysis using the area equivalent diameter is comparable to one measured by laser diffraction (Ref 17).

Using the measured perimeter of the silhouette as shown in Fig. 2(a), the diameter of a circle with the same perimeter as shown in Fig. 2(b) can be calculated according to Eq 3.

Fig. 2.

(a) Particle silhouette with marked perimeter of 2D projection (P); (b) Circle with equal perimeter (P)

Perimeter equivalent diameter

$$x_{{\text{P}}} = \frac{P}{\pi }$$

(3)

This is called the “perimeter equivalent diameter” (x_P). Mathematically, the area equivalent diameter (x_area) must always be smaller or equal than the perimeter equivalent diameter (x_P).

To determine the Feret diameter (x_Fe), two parallel tangents are placed on the contour of the silhouette as shown in Fig. 3. For further evaluation with regard to particle shape characteristics, both the minimum and the maximum Feret diameter are required. To determine these, the silhouette is rotated for a defined number of rotation angles and a Feret diameter is measured. Finally, the smallest (x_{Fe min}) and the largest (x_{Fe max}) Feret diameter are determined from the list of these diameters.

Fig. 3.

Feret diameter (x_Fe)

Finally, the chord length will be explained, which is the only size characteristic not described in the ISO 9276-6:2008 standard. However, it is described in detail and especially uniformly by two different manufacturers of such analytical instruments as follows (Ref 18,19): The chord length is defined as the maximum distance between two horizontal boundary points of the silhouette contour. As with the Feret diameter there is a minimum and maximum chord length. To determine these, the silhouette is again rotated for a defined number of rotation angles and a chord length is measured. In the end, the smallest (x_{c min}) and the largest (x_{c max}) chord lengths are determined from the evaluated list. This procedure is shown for one rotation angle in Fig. 4, with the maximum chord length marked in red. It is indicated that a particle size distribution measured by dynamic image analysis using the minimum chord length (x_{c min}) is comparable to one measured by sieving analysis (Ref 17).

It is important to highlight that using only the silhouette of a particle means converting a three-dimensional object (particle) into a two-dimensional one (silhouette). Due to this simplification, there is a natural error in the exact evaluation of the particles, which should always be kept in mind when working with such methods.

Fig. 4.

Chord length (x_c)

Particle Shape Characteristics

The ISO 9276-6:2008 standard lists several parameters to describe the shape of a particle using its silhouette. For this study, two of them, the aspect ratio and the circularity, were considered and will therefore be explained briefly. Both are ratios of different particle size characteristics described in Sect. 2.2, and for both it applies that they would be 1 for a perfectly circular, two-dimensional silhouette. Any deviation from a circular shape results in a value below 1. As mentioned before, the two-dimensional silhouette is inferred to a three-dimensional particle, which is why a perfectly circular silhouette is equated with a perfectly spherical particle. This leads to a natural error in the evaluation for non-spherical particles whose silhouette is perfectly round at the correct angle. This can be the case, for example, with simple geometric shapes such as cones, cylinders, ellipsoids or similar. The aspect ratio—further referred to as B/L—is calculated using the minimum and maximum Feret diameters as shown in Eq 4, whereas the circularity—further referred to as C—is calculated based on the area as well as the perimeter of the silhouette, which can further be transformed so that the area equivalent diameter as well as the perimeter equivalent diameter can be used for the calculation, as shown in Eq 5.

Aspect ratio

$$B/L = \frac{{x_{{{\text{Fe}}\,\min }} }}{{x_{{{\text{Fe}}\,\max }} }}$$

(4)

Circularity

$$C = \sqrt {\frac{4 \cdot \pi \cdot A}{{P^{2} }}} = \sqrt {\frac{{4 \cdot A \cdot \pi^{2} }}{{\pi \cdot P^{2} }}} = \frac{{x_{{{\text{area}}}} }}{{x_{{\text{P}}} }}$$

(5)

Dynamic Image Analysis (DIA)

Dynamic image analysis was performed using a CAMSIZER X2 with an equipped X-Jet dispersion unit from the company Microtrac Retsch GmbH, the measuring principle of which will be explained briefly (Ref 20): For the measurement, the powder is dispersed dry with compressed air and is then passed in flight past the analysis unit. The passing particles are recorded by two different camera systems. The so-called “basic camera” has a lower magnification and captures coarser particles, while the “zoom camera” has a higher magnification and captures finer particles. Thus, the CAMSIZER X2 records the silhouette of the passing particles, which are then used for the evaluation of particle size and shape characteristics. The three-dimensional particles are therefore evaluated as two-dimensional objects, which, as already mentioned, leads to a certain natural error.

The CAMSIZER X2 can measure the particle size distribution, evaluate a multitude of various parameters for each particle and delivers fast and reproducible results in case of appropriate sampling. For this study, the volume-based particle size distribution (q₃, Q₃) and its characteristic diameters (d_10,3, d_50,3, d_90,3) using the minimum chord length as well as the area equivalent diameter were measured. For the determination of these diameters, the silhouettes of the particles were scanned in 64 different directions. In addition, the so-called volume-based sphericity (SPHT₃) and volume-based aspect ratio (B/L₃), each of which is a weighted arithmetic mean, and the volume-based specific surface area (S_V) were measured. The reason for measuring a volume-based and not number-based distribution and characteristics was that smaller particles often far exceed the number of larger ones and would therefore have had an out-of-proportion influence on the resulting size distribution. By this weighting, the focus was put on those particles which made up the largest proportion of the sample in terms of volume, but which were very low in number due to their larger size.

As the name already suggests, for the volume-based particle size distribution the volume of the particles (V) was needed. Regarding the measured particle diameter—either the minimum chord length or the area equivalent diameter—the calculation of the volume by the CAMSIZER X2 differed. When using the minimum chord length, the volume of a particle was calculated under the assumption that the particles were prolate spheroids, using the minimum chord length as width and the maximum Feret diameter as length, according to Eq 6.

Particle volume under the assumption of an ellipsoid

$$V = \frac{{\pi \cdot x_{{{\text{Fe}} \,\max }} \cdot x_{{{\text{c}}\,\min }}^{2} }}{6}$$

(6)

In contrary, when using the area equivalent diameter, the volume of a particle was calculated assuming that the particles were spheres, with the area equivalent diameter as their diameter. The characteristic diameters of the volume-based particle size distribution are defined as those diameters that correspond to the 10th (d_10,3), 50th (d_50,3) and 90th (d_90,3) percentile of the cumulative distribution by volume.

As can be seen in Eq 7, the sphericity (SPHT) is similar to the circularity from the ISO 9276-6:2008 standard and thus it also applies that the sphericity for a perfect sphere is 1.

Sphericity

$${\text{SPHT}} = \frac{4 \cdot \pi \cdot A}{{P^{2} }} = \left( {\frac{{x_{{{\text{area}}}} }}{{x_{{\text{P}}} }}} \right)^{2} = C^{2}$$

(7)

To obtain the volume-based sphericity of all measured particles (SPHT₃), again the volume of the particles was required, which, as already mentioned, was calculated differently by the CAMSIZER X2 depending on the use of the minimum chord length or the area equivalent diameter for the representation of the distribution. Finally, the volume-based sphericity was calculated according to Eq 8.

Volume-based sphericity for a total of n particles

$${\text{SPHT}}_{3} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} {\text{SPHT}}_{i} \cdot V_{i} }}{{\mathop \sum \nolimits_{i = 1}^{n} V_{i} }}$$

(8)

The aspect ratio of a single particle (B/L) was calculated as described in Sect. 2.2, and the volume-based aspect ratio of all measured particles (B/L₃) was calculated analogous to the volume-based sphericity in Eq 8.

A further characteristic, which was not described yet and therefore will be presented now, is the specific surface area. To obtain the volume-based surface area of all measured particles (S_V), not only the volume of the particles but also the surface area was required. Once more, the calculations by the CAMSIZER X2 differed depending on the used diameter. When using the minimum chord length, the particles were still considered as prolate spheroids and thus the surface area of a particle (S) was then calculated according to Eq 9.

Surface area

$$S = \pi \cdot x_{{{\text{c}}\,\min }} \cdot \left[ {\frac{{x_{{{\text{c}}\,\min }} }}{2} + \frac{{\left( {\frac{{x_{{{\text{Fe}}\,\max }} }}{2}} \right)^{2} }}{{\sqrt {\left( {\frac{{x_{{{\text{Fe}}\,\max }} }}{2}} \right)^{2} - \left( {\frac{{x_{{{\text{c}}\,\min }} }}{2}} \right)^{2} } }} \cdot \sin^{ - 1} \left( {\frac{{\sqrt {\left( {\frac{{x_{{{\text{Fe}}\,\max }} }}{2}} \right)^{2} - \left( {\frac{{x_{{{\text{c}}\,\min }} }}{2}} \right)^{2} } }}{{\frac{{x_{{{\text{Fe}}\,\max }} }}{2}}}} \right)} \right]$$

(9)

Here it should be said that the evaluation software can also consider the particles as oblate spheroids or even as triaxial ellipsoid. When using the area equivalent diameter, the surface area of a particle was calculated assuming that the particles were spheres. Finally, the volume-based specific surface area was calculated using the corresponding volume, as shown in Eq 10.

Volume-based surface area

$$S_{{\text{V}}} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} S_{i} }}{{\mathop \sum \nolimits_{i = 1}^{n} V_{i} }}$$

(10)

Furthermore, the mass-based specific surface area was calculated by dividing the volume-based specific surface area by the density of the powders as shown in Eq 11.

Mass-based surface area

$$S_{{\text{m}}} = \frac{{S_{{\text{V}}} }}{\rho }$$

(11)

Laser Diffraction (LD)

The determination of the particle size distribution using laser diffraction was performed by a Sympatec HELOS/BF with a RODOS/M dispersing unit and a VIBRI module for sample feeding and will be explained briefly (Ref 21): The principle behind the measurement is based on the fact that light is scattered when passing objects, in this case particles. The scattering pattern then depends on the particle size as described in the Mie-theory or Fraunhofer diffraction theory. As with the CAMSIZER X2, the powder is dispersed dry with compressed air. The particles then pass a beam of monochromatic light source, through which the light scatters. The scattering pattern is detected by several photo detectors and the detected signal is further converted into a particle size distribution.

Like the CAMSIZER X2, the Sympatec HELOS/BF instrument delivers fast and reproducible results in case of appropriate sampling as well.

With the used system only the volume-based particle size distribution and its characteristic diameters were calculated. Since this system is not using the silhouette of a particle but its light scattering pattern, the listed characteristics in Sects. 2.2 and 2.3 were not determined here.

Optical Microscope Analysis (OMA)

For analyzing particles using an optical microscope, metallographic samples of the powders were prepared. This means that not only a three-dimensional object is reduced to a two-dimensional one as in dynamic image analysis, but it also tends to be detected too small since the samples have to be ground. This effect is described in detail by Fischmeister (Ref 22). For the preparation of the samples, some powder was resin embedded and afterwards ground and polished. Next, stitched overview images of the size of ~ 5 × 5 mm² from the metallographic samples were taken using an Olympus BX-53M-RF optical microscope at 100× magnification and the Olympus Stream Desktop 2.2 software. These images were made in black and white with a fixed light source and level so that it was equal for each sample. To further evaluate the 8-bit grayscale image, a threshold was set to 180, and an object measurement was performed in which the software automatically identifies all objects in the image. Thereby, every identified object with a threshold below 180 was referred to as void and every identified object with a threshold above 180 was referred to as particle. This resulted in many small voids within the particles, which could be assigned to pores but also in one single giant void surrounding the particles, which was the embedding material. In order not to falsify the results, this object identified as void had to be removed for further evaluation. Therefore, not only particles could be investigated with this method but also internal pores.

In contrast to dynamic image analysis and laser diffraction measurements, the optical microscope analysis took significantly longer, which was mainly due to the time-consuming sample preparation.

The microscope evaluation software is able to determine a multitude of various parameters for each particle as well. The relevant particle size and shape characteristics from the software were the area and perimeter equivalent diameters, the minimum and maximum Feret diameters and the sphericity. However, the minimum chord length could not be determined by the software and thus, a similar parameter—the so-called minimum Extent—had to be evaluated. It is defined as the maximum length of a line connecting two boundary points. Unfortunately, it was not written within the manual if the particle was rotated for the evaluation or not. Another parameter that could not be evaluated by the software was the aspect ratio, which nevertheless could be calculated manually using the evaluated Feret diameters according to Eq 4.

For the calculation of the particle size distribution, a lower limit of the particle size had to be defined, as below this limit the detected particles were made up of too few pixels to guarantee a meaningful and, above all, correct evaluation. This could be noticed for example by the fact that the area equivalent diameter suddenly became bigger than the perimeter equivalent diameter. Thus, all particles the minimum extent of which was below 7.5 µm were not considered.

To calculate the percentage of internal pores contained by the powder particles, just the measured areas of the pixels below (pore) and above (particle) the threshold value of 180 were taken as shown in Eq 12.

Internal porosity

$${\text{Porosity}} = \frac{{A_{{{\text{pores}}}} }}{{A_{{{\text{particles}}}} + A_{{{\text{pores}}}} }} \cdot 100\%$$

(12)

Since this was simply a matter of determining the ratio between the corresponding pixels and not of evaluating meaningful pore shapes, the previously mentioned lower limit was not applied neither to particles nor to pores. Nevertheless, it should be mentioned that in principle it would also have been possible to calculate the shape of the pores and a pore size distribution. However, with the settings applied in this study, especially with respect to the magnification of the images, the obtained distribution would have been strongly distorted, because here again the lower limit would have had to be considered.

The optical microscope analysis was used to calculate the volume-based particle size distribution and its characteristic diameters, the volume-based sphericity and aspect ratio and the mass-based specific surface area using the minimum extent diameter as a substitute for the minimum chord length and the area equivalent diameter. Besides, the internal porosity of the particles was also determined.

X-Ray Microcomputed Tomography (µCT)

Using µCT, each sample consisting of a simple powder heap was additionally scanned with a voxel size of (1.00 μm)³ using an Easytom 160 (RX Solutions) microcomputed tomography system (µCT). The system was equipped with a 1920 * 1536 pixel flat panel detector. Voxel size was dictated by sample diameter (plastic tube with a diameter of 3 mm filled with powder) to cover the effective area of the detector so that the sample was completely within the field of view. Voltage was set to 100 kV with an exposure time of 2000 ms. Current was set to 200 μA, and a total of 1440 projections were acquired. Optimal scanning parameters were determined empirically in a scan series with varying voltage and integration time. Volume data was reconstructed using filtered back projection using xact64 (RX Solutions).

Image processing steps were performed in VGStudio Max 3.3.3 (Volume Graphics) to detect and quantify internal porosity in powder particles while the particle size distribution was extracted using the software Modular Algorithms for Volume Images (MAVI, Version 1.5.2). µCT volume data were smoothed in VGStudio Max using a median filter (filter mask size: 3 × 3 × 3) in order to reduce noise. Using MAVI, binarization (ISO50) and cell reconstruction were performed based on the implemented Preflooded Watershed method applying an empirically determined area threshold of 500. This image post-processing step provided the number, size, and shape of each extracted powder particle. Importantly, edge particles were omitted from the computation of average particles size to circumvent a bias in the computation of extracted features, e.g. mean diameter.

With the system used, the particles were analyzed three-dimensionally, unlike with dynamic image analysis. Even though the characteristics listed in Sect. 2.2 could also be evaluated of a three-dimensional object, the MAVI software did not provide this feature (Ref 23). In contrast, the software used the identified particles and measured the diameter in 13 different, always identical directions of each particle. These directions correspond to the discrete normal directions given by the unit cell of the cuboidal lattice. Out of these 13 diameters, an arithmetic mean was calculated. The software was also capable of measuring the surface area (S) as well as the volume (V) of the particles. The latter was determined simply by counting all voxels that belong to the particle.

By using the mean diameter and the volume of each particle, the volume-based particle size distribution and its characteristic diameters were calculated manually.

As the determination of the diameter differed compared to Sect. 2.2, the calculation of the shape characteristics also differed. The software thus calculated a so-called shape factor (f₁) using the volume and surface area as shown in Eq 13.

Shape factor

$$f_{1} = \frac{6 \cdot \sqrt \pi \cdot V}{{\sqrt {S^{3} } }} = \left( {\frac{{d_{{\text{V}}} }}{{d_{{\text{S}}} }}} \right)^{3}$$

(13)

By transforming this equation, again a simple relationship between two diameters is obtained: the diameter of a volume-equal (d_V) and of a surface-equal (d_S) ball. Compared to the sphericity determined by the CAMSIZER X2, the main difference was that the ratio of these diameters was counted to the power of three. To make the results as comparable as possible, the cube root was taken from this shape factor, and the result was then squared. Thus, the shape factor obtained by the MAVI software was approximated to the sphericity determined by the CAMSIZER. Finally, also a volume-based approximated sphericity value for all particles was calculated analogously to the one shown in Eq 8.

Furthermore, the MAVI software could not calculate the aspect ratio and as the determined diameters differed from the Feret diameters, once more an approximation was made. The minimum and maximum diameters from the 13 measured diameters were used, and a modified aspect ratio was calculated as shown in Eq 14.

Modified aspect ratio

$$B/L = \frac{{d_{\min } }}{{d_{\max } }}$$

(14)

This method was also used to determine the specific surface, since the total volume as well as the total surface area were measured three-dimensionally. Thus, the volume-based specific surface area was calculated according to Eq 10 and the mass-based specific surface area was calculated using the powder densities according to Eq 11.

Beside these size and shape characteristics the internal porosity of the particles was investigated. Here it should be said that the software used was also capable of calculating a size distribution concerning the identified pores and was also able to display them three-dimensionally in the investigated powder heap. What distinguishes the determination of internal porosity from optical microscope analysis is that not the cross-sectional area of a pore but its volume was used for calculation, since it was possible to evaluate the pores three-dimensionally.

However, since the size distribution could not be calculated meaningfully by any other method investigated, this would go beyond the scope of this study. Thus, only the internal porosity and an arithmetic mean pore diameter were determined and will be discussed.

BET and BJH Measurement

The tests were performed using a Quantachrome NOVA-2000e, which consists of a degassing and a measuring station. For the measurement, a certain amount of sample was weighed in a special sample vessel. Nitrogen was used as the measuring gas and helium as the purge gas after degassing. For the measurement with N₂ a Dewar vessel was used, which was filled with liquid nitrogen to reach the measuring temperature of 77 K. Prior to the measurement, the adhering moisture and the adsorbed gas molecules of the respective sample were removed in the degassing station by applying a vacuum and a temperature of 350 °C. The heating time was three hours. To prevent air ingress, the tube was refilled with helium at the end of the heating period. The subsequent measurement included 30 measuring points, which included the steps adsorption and desorption. The measuring cells were half immersed in liquid nitrogen, which was controlled by a float.

The measuring principle will be explained briefly (Ref 24,25,26,27): A defined quantity of gas is introduced into the measuring cells, whereby a quantity characteristic of the introduced gas is adsorbed on the surface. Thereby, the amount of gas adsorbed at a given constant temperature depends on the pressure or the relative pressure referred to the saturation vapor pressure. Increasing the pressure leads to multilayer adsorption and a pore filling process, whereby the pore diameter is directly dependent on the relative pressure. The amount of gas required for multilayer adsorption was described by Brunauer, Emmett and Teller, which also allows the volume of a monolayer to be calculated. For the determination of the specific surface area, only the monolayer volume has to be converted into the area required by the gas used. Furthermore, at pressures near the saturation vapor pressure of the gas used, all pores should be filled and thus, the total pore volume can be determined, which was described by Barrett, Joyner and Halenda (BJH). According to their method, also the pore size can be calculated, which correlates to the relative pressure once more. Yet, by using the BJH method only pores in the range of 0.35-500 nm (Ref 28) can be evaluated meaningfully and thus, the internal porosity was not measured.

With this method, the mass-based specific surface area was measured.

Results and Discussion

Basic Characterizations

In Fig. 5, 6, and 7, the SEM images of the powders used are shown. Looking first at the shape of the particles, it can be seen that powder A is much more spherical than the other two. Furthermore, powder A is free of any agglomerates. Only some isolated but very small satellites can be seen here. In contrast, powders B and C contain a non-negligible amount of agglomerates, consisting of fused smaller particles, adhering satellites and non-spherical particles. When looking at the scales in the images, it can be seen that the particles in powder A and B are approximately the same size, while the particles in powder C are significantly larger.

Fig. 5.

SEM image of powder A

Fig. 6.

SEM image of powder B

Fig. 7.

SEM image of powder C

In Table 1, the measured basic powder characteristics as well as the density and the interstitial contents are listed. Considering the flow rate (FR), it can be seen that it could not be measured with powder B. This is due to the fact that, compared to powder A, the shape differs significantly from that of a sphere, thus increasing the frictional forces between the particles to such an extent that the powder does not flow through the given orifice spontaneously. This can also be seen by looking at the measured apparent density (AD), where the superscripted letter indicates whether it was measured using the Hall (H) or the Carney (C) funnel. Comparing the apparent density as well as the tap density of powder A and B, the influence of the particle shape can be seen once more. The Hausner ratio exhibits the same trend as the flow rate. Powder A has the lowest Hausner ratio, and powder B, which does not flow spontaneously, has the highest. Thus, at least in this study, Hausner ratio and flow rate correlate.

Table 1 Basic powder characteristics (FR = flow rate; AD = apparent density; TD = tap density; HR = Hausner ratio), density (ρ) and interstitials content (C, H, N and O)

However, it should be stressed here that a non-measurable flow rate does not mean that the powder cannot be spread and processed in powder-bed AM technologies, as various studies have shown (Ref 29,30,31,32).

Considering the measured density as well as the interstitial content of all three powders, no significant differences can be observed. Only the measured density is always slightly below the nominal density of 8.20 g/cm³.

Particle Size Distribution

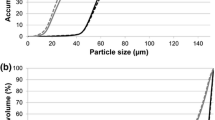
In Fig. 8, 9, and 10, the volume-based particle size distributions measured by microcomputed tomography (µCT), dynamic image analysis (DIA) and optical microscope analysis (OMA), using the minimum chord length for DIA and OMA, are shown. The class width was set to 1 µm. The smallest particles that could be measured were (1.00 µm)3 for the µCT measurement due to the resolution of the voxels, 0.8 µm in diameter for DIA due to the resolution of the cameras used according to the manufacturer and 7.5 µm in diameter for OMA due to the self-set lower limit for the particle size, although the resolution of the images made is 0.26 µm per pixel. When measuring particularly small particles, these methods are therefore difficult to compare, since their lower resolution limits differ considerably. However, since the powders investigated mainly contain particles with a diameter larger than approximately 10 µm, the results could still be compared.

Fig. 8.

Volume-based particle size distribution (x_{c min}) of powder A

Fig. 9.

Volume-based particle size distribution (x_{c min}) of powder B

Fig. 10.

Volume-based particle size distribution (x_{c min}) of powder C

For powder A (Fig. 8), the shapes of the distributions determined by DIA and OMA are quite similar, although the one determined by OMA is slightly shifted to the left. This was to be expected, since in comparison to DIA, only a cross section is measured instead of a silhouette of the entire particle. This cross section is always smaller than the silhouette of the particle, if the particle is not divided exactly in half (Ref 22). The same can be observed looking at the distributions of powder B (Fig. 9) and powder C (Fig. 10), with this effect being most pronounced for powder C. The reason for this is that the larger the examined particles are, the larger is the area in which the cross section of a particle is smaller than its silhouette. This increases the probability of finding “particles” that are too small and thus, the distribution shifts toward smaller particle sizes. This can be observed especially in the calculated characteristic diameters (d_10,3, d_50,3, d_90,3), which are listed in Table 2.

Table 2 Characteristic diameters (d_10,3, d_50,3, d_90,3) calculated from the volume-based particle size distribution using the minimum chord length (x_{c min}) and the area equivalent diameter (x_area)

When comparing the distribution measured by µCT of powder A to the one of the other two methods (DIA and OMA) in Fig. 8, it can be seen that the shape of the distributions differs significantly. The µCT distribution shows a distinct shoulder on the left side, which means that in the µCT measurement an increased number of smaller particles were found. It should be highlighted that the determination of the particle size differed between the methods mentioned. While for DIA and OMA the minimum chord length was measured in up to 64 directions (DIA), for µCT the actual diameter of the particle was measured only in 13 predefined directions. However, this difference was not to be expected, since powder A is the most spherical powder and therefore the influence of the method of measuring the particle size should be the smallest. The more interesting is that for powder B (Fig. 9) and C (Fig. 10) the shapes of the distributions are all very similar regardless of the measuring method. Comparing the characteristic diameters of the µCT and OMA distributions of powder B and C listed in Table 2, the values from OMA are again shifted toward smaller particle size.

In Fig. 11, 12, and 13, the volume-based particle size distributions measured by µCT, DIA, OMA and laser diffraction (LD), using the area equivalent diameter, are shown. The class width was again set to 1 µm, except for the LD measurement, where it was automatically increased by the measuring system as the particle size increased. Thus, the distribution measured by LD looks smoothened. The smallest particles that could be measured by the used LD system were 0.4 µm in diameter according to the manufacturer.

Fig. 11.

Volume-based particle size distribution (x_area) of powder A

Fig. 12.

Volume-based particle size distribution (x_area) of powder B

Fig. 13.

Volume-based particle size distribution (x_area) of powder C

Looking at powder A (Fig. 11), the shape of the distribution measured by µCT once more differs significantly from the others, whereas the shape of all other distributions is again quite similar. Once more, this cannot be observed for powder B (Fig. 12) and C (Fig. 13), where the shape of all differently measured distributions is quite similar and they are only sometimes shifted against each other. Due to this shift also the characteristic diameters listed in Table 2 are slightly shifted, whereby for the finer powders (A and B) the highest values were calculated from the distribution measured by DIA and the smallest ones from the one measured by LD. For the coarser powder C, the previously described impact on the shift for the values obtained by OMA is too pronounced and thus, once again these are the smallest values.

It is also particularly highlighting that the distributions measured by OMA are always the most irregular. This is mainly due to the fact that, compared to the other methods, the number of particles examined—listed in Table 3—is significantly lower as well as the fact that only the cross section of the particles is evaluated. To increase the number of particles detected, a larger area or more samples could have been examined, but this was not done due to the increased time required. Comparing the µCT results of powders A and B, which are in principle in a similar size range, the number of particles found in powder A is higher. This is due to the fact that the measurement is performed on a powder heap and since powder A has a higher apparent density but is more or less in the same size range, the number of particles found also exceeds that of powder B.

Table 3 Number of particles examined

Comparing the results from OMA of powder A and B, the number of particles found in powder B is twice as high as for powder A. This opposite trend is due to the fact that the shape of the particles in powder A was almost perfectly spherical, and spherical particles are more likely to detach from metallographic samples during grinding and polishing than non-spherical ones, which were further also covered with satellites and contain agglomerates and thus were more firmly locked within the embedding resin.

For the µCT measurement the examined sample volume and for OMA the examined sample area was always chosen to be constant. In contrast, the sample volume for DIA was based on the weighed sample quantity. However, since this was not always constant, it makes no sense to compare the number of investigated particles of the different powders. However, it is clear that the largest number of particles was measured by DIA, whereby it should be mentioned that a single measurement lasted only about 1-2 min.

Yet, it cannot be observed that the distributions and characteristic diameters obtained by DIA measuring the area equivalent diameter are similar to the one measured by LD. Even if the shape of the particle size distributions is generally very similar, no uniform trend according to the characteristic diameters can be determined comparing the methods investigated.

Since the powders used are not standardized and therefore the actual size and shape of the particles is unknown, an evaluation of the accuracy is not trivial. However, an attempt is made to use the most spherical powder as the spherical shape can be confirmed without any problems by means of the SEM images and the size measurement should therefore also be the most accurate.

Among the methods studied, that one which could probably provide the most accurate results is microcomputed tomography. However, the evaluation here was limited to only a few directions (13), although the particles could be analyzed much more precisely as three-dimensional objects. In addition, this method had the poorest resolution in the comparison. So, there is still room for improvement for this method. In addition, it should be noted that the MAVI software is normally used to evaluate foams and not to measure particle size distributions of a powder.

Optical microscopic analysis was probably the least accurate method. A silhouette of the particle is used like with dynamic image analysis, but due to the fact that it is obtained from a cross section of the particle, the distribution is always shifted to smaller particle sizes, which results in an additional error beside the simplification of a 3D object to a 2D one. There are a variety of solutions to this problem, which are also cited by Fischmeister (Ref 22), but were not applied for this study.

The results obtained by dynamic image analysis are therefore more accurate than the one from optical microscope analysis. In contrast to microcomputed tomography, a particle is examined in up to 64 different directions, although, as with optical microscope analysis, only a two-dimensional object (silhouette) is analyzed.

Even though the shape of the distributions is often very similar, all methods usually differ in their characteristic diameters. For the spherical powder A, the characteristic diameters determined by microcomputed tomography and optical microscope analysis are similar, but the measured distributions differ significantly. Thus, it is concluded that all results obtained from various methods are too different from each other and that it is not possible to generalize the results obtained from one of these methods, and therefore it is always necessary to specify the method used.

Particle Shape

In Table 4, the volume-based sphericity and aspect ratio obtained by µCT, DIA and OMA are listed. For these parameters, more or less the same applies for each powder. There is almost no difference in sphericity and aspect ratio when comparing values obtained by measuring different particle sizes (x_{c min} vs. x_area) using DIA and OMA. It is particularly noticeable that the values measured by OMA are significantly lower than those measured by DIA. The values of the µCT measurement are always between those of the other methods. This fact is especially surprising when considering the sphericity of powder A, since this is extremely spherical, as can be seen from the SEM image (Fig. 5). Here, the µCT measurement was expected to be able to determine the volume as well as the surface area very precisely. However, since the ratio between the diameters calculated from the particle volume and surface is significantly smaller than 1 for this very spherical powder, it indicates that the used setup for the µCT measurement is rather unsuitable and not comparable for determining the sphericity. This might be due to the resolution of the voxels of (1.00 µm)3 but also to the shape of the voxels (cubes), which results in an error when determining the volume and surface of very small and spherical particles, which are composed of only a few voxels. For better understanding, the sphericity value of 0.898 is discussed in more detail by means of an example: Imagine a powder containing only perfectly spherical particles with the d_{50, 3} value of powder A (35.0 µm). In this case, the sphericity would be equal to 1. In order to obtain a value of 0.898, each particle in the powder would have to attach, for example, five satellites in the form of hemispheres the diameter of which corresponds to 16.0% of the d_50,3 value (5.5 µm), as shown in Fig. 14. The ratio of the diameters is constant and so this example can be applied to the entire powder A, in which case each particle would have to have these five satellites attached to it. However, this is not the case, as clearly shown in the SEM image (Fig. 5). Another possibility is that powder A contains many larger, very aspherical particles, which would also significantly lower the sphericity value. However, these are not visible in the SEM image either and so it can be assumed that the value determined by µCT is simply too inaccurate. To investigate this in more detail, one could examine either a coarser and very spherical powder with the same resolution using the various methods or a standardized body with specified dimensions. Nevertheless, the µCT measurement is particularly interesting since the particles can be analyzed three-dimensionally. Furthermore, the modification of the aspect ratio of the µCT measurement can be concluded not to be a sufficient approximation to the standardized aspect ratio. Regardless of the µCT measurement, DIA certainly provides more trustworthy results than the OMA. However, the results obtained are again not comparable with each other. Comparing the sphericity of the different powders, powder A is always indicated as the most spherical one independently of the used method.

Table 4 Volume-based sphericity (SPHT₃) and aspect ratio (B/L₃) calculated once with the minimum chord length (x_{c min}) and once with the area equivalent diameter (x_area)

Fig. 14.

Five evenly spaced (trigonal bipyramidal), hemispherical satellites

Furthermore, a volume-based distribution for the sphericity was calculated using the diameter (µCT) and minimum chord length (DIA and OMA), as shown in Fig. 15, 16, and 17. Since the distribution calculated using the minimum chord length is not significantly differing from the one calculated using the area equivalent diameter, only the first one is shown and discussed. The class width was set to 0.05, whereby the maximum value is 1. Compared to the distributions determined by µCT and DIA, the distribution determined by OMA is not only clearly shifted to the left, but also differs noticeably in its shape, as a non-negligible percentage of aspherical particles was measured. Once more it should be highlighted that the values obtained by OMA were measured using only a cross section of the particles. These diagrams also show once again that the highest sphericity values were measured using DIA.

Fig. 15.

Cumulative volume-based sphericity distribution (x_{c min}) for powder A

Fig. 16.

Cumulative volume-based sphericity distribution (x_{c min}) for powder B

Fig. 17.

Cumulative volume-based sphericity distribution (x_{c min}) for powder C

To evaluate this data even further, for each class in the volume-based sphericity distribution (width = 0.05; total classes = 20) a volume-based particle size distribution and its characteristic median diameter (d_50,3) were calculated. This could only be done for the distributions determined by µCT and OMA. The achieved values for each class are plotted in Figs. 18, 19, and 20, whereby the size of the dots refers to the number of particles in the corresponding class. Once more it can be seen for each powder that the median diameters determined by OMA are always lower.

Fig. 18.

Median diameters of the volume-based particle size distributions (d_50,3) for each class of the volume-based sphericity distribution including the relations of the number of particles in the corresponding class for powder A

Fig. 19.

Median diameters of the volume-based particle size distributions (d_50,3) for each class of the volume-based sphericity distribution including the relations of the number of particles in the corresponding class for powder B

Fig. 20.

Median diameters of the volume-based particle size distributions (d_50,3) for each class of the volume-based sphericity distribution including the relations of the number of particles in the corresponding class for powder C

For powder A (Fig. 18), most of the particles are well spherical and the median diameter is quite constant independently of the sphericity and the used method. Only the most spherical particles (SPHT ≥ 0.90) measured by µCT are smaller. However, the trends of the different methods are equal.

For powder B (Fig. 19), the majority of the particles is not well spherical, which also agrees with the observations from the SEM image (Fig. 6). Regardless of the method used, a clear trend is evident here that the particles become smaller with increasing sphericity. This trend is much more pronounced in the µCT measurement than in the OMA. This could be mainly due to the fact that smaller particles solidify faster than larger ones during atomization and therefore satellites cannot attach to them. It is much more likely that these smaller particles, which solidify first, then finally adhere to larger ones as satellites.

For powder C (Fig. 20), the majority of the particles is not well spherical as well, but no such trend as for powder B could be observed. In contrast, the particle diameters remain more or less constant independently of the sphericity and the used method.

This showed that not only partly the determined final results for the sphericity of the various methods differ, but also partly the trends in the measured data, especially for aspherical powder. Due to these differences, it is once more not possible to generalize the results obtained from one of these methods, and therefore it is always necessary to specify the method used.

Specific Surface Area

In Fig. 21, the mass-based specific surface areas determined by adsorption measurement (BET), µCT measurement, DIA and OMA are shown. In addition, the relative values referred to the adsorption measurement were calculated and are listed together with the absolute values in Table 5. Comparing the results obtained by the measurements of different particle sizes (x_{c min} vs. x_area) for DIA and OMA, no significant difference can be observed. Regardless of the powder and the measured particle size, the mass-based specific surface area determined with OMA is slightly higher than that determined with DIA. The reason for this is that the particles measured by OMA tend to be recorded as too small. In general, the finer a powder is, the higher its specific surface area.

Table 5 Mass-based specific surface area (S_m)—absolute values and relative values referred to the adsorption measurement

Fig. 21.

Mass-based specific surface area (S_m)

The values obtained from the µCT measurements are already significantly higher than those from DIA and OMA, whereas those from the adsorption measurement exceed these values again and are about twice as high as those from DIA and OMA. According to the manufacturer, the accuracy of the adsorption measurement is approximately 0.1% and is therefore no explanation for the high difference.

The two most promising methods here are the µCT and adsorption measurement, since both take the particles into account in a certain way in three dimensions. Nevertheless, the measurement of sphericity by µCT already showed that the determination of the surface area was probably too inaccurate due to the measurement parameters used.

Further considering the most spherical powder A, the obtained values (Table 5) between the adsorption measurement and DIA as well as OMA diverge greatly. It would of course be expected that for aspherical powders such as powder B and C, the mass-based specific surface area determined by DIA or OMA would be significantly lower than the value determined by the adsorption measurement, but not for highly spherical powder. This effect of aspherical particles becomes clear when the ratio of the values obtained by DIA or OMA and the adsorption measurement for powder B or C is compared with those for powder A. One reason for this could be that particularly very small particles cannot be detected by either OMA or DIA (even with DIA, the camera systems used have a lower limit with respect to their resolution). Considering the SEM image of powder A (Fig. 5), very small particles can be seen between the larger particles, which would support this thesis. To test this hypothesis, it would be useful to investigate a fully dense coarse fraction of powder A. Another reason is probably that a high percentage of satellites and agglomerates, consisting of smaller particles, strongly increase the specific surface area. Yet, the influence of satellites and agglomerates on the specific surface area cannot be taken into account with the required precision by DIA and OMA. Another reason could be that when measuring by DIA and OMA, it is assumed for the calculation of the volume that the particles are prolate spheroids, which tends to give surfaces that are too small. However, since this should not apply to the spherical powder A, it cannot be due to this assumption. An additional reason, might be open micropores like the one shown in Figure 22. These can of course only be considered by means of adsorption measurement and if the number of these is very high, this will of course also increase the measured specific surface area. However, if there is a significant amount of open micropores, this should be noted in the adsorption measurement due to non-linear pairs of values. Since this was not the case, open micropores are not the decisive reason for this relatively high difference. In addition, no open micropores were observed in the OMA images. Since all these hypotheses could not be tested in this study or could even be disproved, it cannot be concluded which of the methods is the most accurate method to determine the mass-based specific surface area. Furthermore, only the results obtained by DIA and OMA might be comparable. But overall, it is again not possible to generalize the results obtained from one of these methods.

Fig. 22.

Open pores in powder C

Porosity

In Table 6, the internal porosity measured by µCT, OMA and helium pycnometry (HeP) is listed. The latter is obtained by calculating the ratio between the density measured by this method and the nominal (pore-free) density of the material (ρ_nom = 8.20 g/cm³). Just due to the fact that the nominal density is used for the calculation, there is already a non-negligible error, caused by deviations in the alloy composition, which can also cause the density of the alloy to vary. Nevertheless, the value was calculated once and listed. In comparison with the other methods, however, it is noticeable that the same trend does not even prevail here with regard to the largest and smallest internal porosity values.

Table 6 Internal porosity

Looking at the results achieved by µCT and OMA, it can be seen that powder A has the lowest internal porosity and powder C has the highest. The values obtained by µCT measurement are always lower. Even though it has already been shown that the determination of the volume by means of µCT is too inaccurate with the settings used—presumably especially for particularly small objects as pores—it is still to be preferred in comparison to OMA, since the pore is evaluated three-dimensionally. One reason for the internal porosity to be increased determined by OMA could be impurities on or scratches in the polished metallographic sample, which as dark appearing areas are incorrectly evaluated as pores.

Conclusions

In this study, different methods for measuring particle size, particle shape, specific surface area and internal porosity were investigated and compared using three superalloy powders grades with nominally identical composition, which differed, however, in size and shape. The results can be summarized as follows:

• 1. Examining the particle size and shape of the most spherical powder A showed that the resolution used for the x-ray microcomputed tomography measurements was probably too low. With a voxel size of (1.00 µm)3 particularly small particles could not be evaluated properly. In addition, the evaluation software used only allows the diameter to be measured in 13 predefined directions, which also results in a certain inaccuracy. This is mainly due to the fact that the software is commonly used to study foams. Nevertheless, microcomputed tomography is one of the most promising methods for the analysis of feedstock, material and AM components (Ref 33,34)—once the resolution is improved and the evaluation software upgraded so that smaller and finer particles can be examined much more comprehensively.

• 2. Both dynamic image analysis and optical microscope analysis simplify a three-dimensional object (particle) to a two-dimensional one (silhouette). In this case, the optical microscope analysis always delivers particle sizes that are too small due to the measurement of a cross section of the particles. Thereby it applies that the larger the particles in the powder, the more pronounced the shift. This affects not only the measured distribution, but also all other parameters (sphericity, aspect ratio, specific surface area). Since dynamic image analysis, however, always records the largest cross section of a particle, it thus also provides significantly more accurate results.

• 3. In the case of aspherical powder, the determined particle size distributions differ with respect to the measured particle size (minimum chord length vs. area equivalent diameter) regardless of the method used, which is mainly evident from the characteristic diameters. In terms of particle shape and specific surface area, this difference was hardly pronounced regardless of the powder.

• 4. For the determination of the specific surface area, none of the used method could be concluded to be the most accurate. Especially here it became clear that the measured values of the adsorption measurements are not comparable with those of the other methods.

• 5. Porosity measurement by helium pycnometry of alloys can be very inaccurate if the pore-free density of the material is not known exactly. In any case, microcomputed tomography or optical microscope analysis should be preferred. However, both methods have various inaccuracies. As already mentioned several times, the resolution of the microcomputed tomography measurement was too low and since many pores are relatively small, it can be assumed that the determined value also contains a certain error. Nevertheless, pores can be analyzed three-dimensionally in a larger powder volume. The optical microscope analysis offers only a two-dimensional recording of the pores and, in addition, dirt on or scratches in the metallographic sample can be erroneously evaluated as pores. Therefore, the microcomputed tomography measurement is preferable to the optical microscope analysis.

• 6. Regardless of the parameter measured (size, shape, specific surface area), it was shown that the measured data cannot be generalized, the results strongly depending on the method used, and therefore it is always important to specify the measurement method.