Introduction

Copper(II) oxide, also known as cupric oxide (CuO), has emerged as a promising material among the well-known transition metal oxides (Fe2O3 or Fe3O4, NiO, Co3O4, Cu2O, MnO2, and ZnO) due to its distinctive and notable features including eco-friendly nature, abundance, simplicity of fabrication, scalability, non-toxicity, and cost-effectiveness. As a result, it has been explored extensively to find emerging and advanced applications in solar cells, photovoltaics, photocatalysts,1,2 environmental remediation,3 electrodes in lithium-ion batteries, supercapacitors,4 high-temperature superconductors, magnetic storage media, varistors, and sensors.5 Additionally, due to the greater stability of Cu2+ compared to Cu1+, CuO, a monoxide, is more stable than its counterpart copper(I) oxide (Cu2O).

CuO is a p-type semiconductor with better optoelectronic properties in nano-sized domains (1–100 nm) than in bulk due to an increase in surface-to-volume ratio (aspect ratio), which promotes chemical reactivity and a large optical band gap value. Nano-CuO not only has a wide range of morphologies and shapes, but it also has remarkable properties such as high chemical and thermal stability, high solar absorbance, photovoltaic properties, remarkable thermal conductivity, super catalytic properties, good recyclability, rheological, and antioxidant properties, anti-fungal and anti-microbial properties, better electrical, mechanical, and electrical properties, and strong anti-ferromagnetic ordering even above the Néel temperature (TN ~ 231 K).6,7,8,9,10,11

Numerous chemical methods, including pulsed laser deposition, vapor–solid reaction, solid-state synthesis,12 vacuum evaporation,13 sol-gel,14 solvothermal/hydrothermal,15,16 microwave-assisted,16 and chemical spray pyrolysis methods,17 have been reported in the literature for the synthesis of nano-sized CuO with panoramic and versatile morphologies, such as zero-dimensional quantum dots, one-dimensional nanorods, nanowires, and nanoneedles,18,19 two-dimensional nano-flakes, nano-petals, nanosheets, and nano-leaves,20 and three-dimensional hierarchical superstructures (nanoflowers, nanospheres, and clusters).1,21 Most of these methods are costly, involve complex reaction steps, necessitate harsh reaction conditions (high pressure and high temperature) and organic solvents, and pose significant environmental and biological risk. As a result, researchers are seeking methods for the synthesis of nanostructures using reagents that are inexpensive, simple, eco-friendly, and safer, use less power, and are non-hazardous.22

The sonochemical method has become the preferred method for creating novel nanomaterials with attractive properties. Sonochemistry employs ultrasound (ν ~ 20 kHz-10 MHz) waves to produce the acoustic cavitation phenomenon, which consists of three major steps: the formation, growth, and sudden implosive collapse of bubbles in an aqueous medium. When solutions are exposed to highly energetic ultrasound irradiation, peculiar reaction conditions—very high pressure (> 20 × 106 Pa) and temperature (> 5000 K) followed by extremely high cooling rates (> 107 Ks−1)—develop, due to which extremely volatile local conditions are created, leading to breaking of bonds and subsequent formation of free radicals, and thus providing an alternative chemical method for inducing chemical reaction. This sonochemistry results in phase purity, smaller size, diverse morphologies, uniform particle-size distribution, high surface area, and improved thermal stability.23,24,25,26

The intrinsic strain in nanocrystals is caused by size confinement. This is an important elastic property that can be tuned by varying synthesis parameters such as reaction temperature, polymers, doping, pH, and concentration, which affect the optical, electrical, and magnetic properties of the nanomaterials. The XRD peak broadening comprises size-dependent and strain-induced broadening.24,27,28 As a result of XRD peak broadening, we are able to determine not only crystallite size and lattice strain, but also strain-dependent elastic properties such as stress and elastic energy density. Dislocation density, stacking faults, point defects, contact or sinter stress, and grain boundaries are the main contributors to intrinsic strain. By employing techniques such as the Debye–Scherrer method, Williamson–Hall plot (WHP), size–strain plot (SSP), Halder–Wagner HW method, Rietveld refinement, Warren–Averbach method, and Balzar method, quantitative analysis of the XRD profile can be carried out. The Debye–Scherrer method only helps to calculate the average crystallite size of the nanocrystals, whereas the other methods mentioned can also estimate the intrinsic strain in addition to the average crystallite size. The size and intrinsic strain in the WHP, SSP, and HW methods are attributed to the combination of the Lorentzian and Gaussian functions, whereas the Warren-Averbach and Balzar methods use Stokes–Fourier deconvolution.29

In this paper, we describe a simple, cost-effective, and environmentally friendly sonochemical method for producing CuO nanostructures (leaf-like, flower-like, and interconnected network-like structures) at room temperature and in an open-air environment without the use of a surfactant or template. The effect of varying the molar ratio of sodium hydroxide in the as-prepared samples, i.e. (CuCl2·2H2O:NaOH::1 of 2, 1 of 4, and 1 of 6) on the micro-structural, morphological, and optical properties of CuO nanostructures was studied. A comparative analysis was performed to interpret the XRD profiles of the samples using Scherrer's method, WHP, SSP, and HW method. The prepared samples were then characterized using field-emission scanning electron microscopy (FE-SEM), UV-Vis spectroscopy, and photoluminescence (PL) spectroscopy.

Materials and Methods

Materials

Analytical-grade (AR) chemicals, copper chloride (CuCl2, 99.9%) and sodium hydroxide (NaOH, 99%) were obtained from Merck and used as received without further purification for the synthesis of CuO nanostructures. Deionized water (DIW) was used in all chemical reactions.

Sonochemical Synthesis of CuO Nanostructures

The calculated quantities of 0.2 M CuCl2 and 0.4 M NaOH were dissolved in 30 mL of DIW in two separate glass beakers. At room temperature, both solutions were stirred separately to ensure complete precursor dissolution. The copper chloride solution in the beaker was sonicated, and sodium hydroxide solution was added dropwise. After 1 h of sonication, the dark gray precipitates were collected through filtration. To remove by-products and impurities, the precipitates were washed several times with deionized water and ethanol. The wet precipitates were then dried for 16 h in a vacuum oven at 60°C. The final yield was calculated by weighing dried precipitates. We synthesized three samples with varying concentrations of NaOH using the same method under similar conditions. The molar concentration of copper chloride was kept constant at 0.2 M in all of these reactions, while the concentration of NaOH was varied in steps from 0.4 M to 0.8 to 1.2 M. Three samples were prepared at different molar concentrations of sodium hydroxide, i.e. 0.4 M, 0.8 M and 1.2 M, and were designated as S1, S2, and S3, respectively, for further analysis.

Characterization

A high-resolution Rigaku SmartLab x-ray diffractometer (XRD) with Cu-Kα radiation (λ = 1.54059 Å) was used to determine the crystallite size and for structural analysis of the CuO nanostructures. The microscopic surface morphology of samples was investigated using FE-SEM (Nova NanoSEM 450). The optical characterizations were performed to explore electronic transitions using a UV-Vis spectrophotometer (Lambda 25, PerkinElmer) in the range of 190–1100 nm and a photoluminescence spectrophotometer (PL-55, PerkinElmer).

Results and Discussion

XRD Analysis

XRD is a powerful and widely used tool for determining the purity, structure, crystallinity, crystallite size, crystal imperfections such as intrinsic strain and stress, defects, elastic parameters, and elastic energy of materials.30 In 1933, the original structure of CuO was determined by Tunnel, which was subsequently refined by XRD.31 In contrast to other 3d transition metal oxides, traversing the periodic table from MnO to CuO, which generally crystallize into the cubic rock salt structure (sometimes with rhombohedral distortion), cupric oxide is an intriguing and exceptional member that is distorted both electronically and structurally.32 Cupric oxide, also known as tenorite, is composed of the d- and p-block elements copper and oxygen. It has a lower-symmetry monoclinic crystal structure (space group C62h) and is experimental of C2/c symmetry showing interesting anti-ferromagnetic ordering below 220 K.33 The monoclinic structures of a CuO unit cell with space-filling (Fig. 1a) and ball-and-stick (Fig. 1b) and polyhedral (Fig. 1c) arrangement are drawn in VESTA software using a crystallographic information file (CIF). In CuO, each atom is surrounded by the four nearest neighbors of other types of atoms. In other words, each copper atom is coordinated with four nearly coplanar oxygen atoms at the corner of an almost parallelogram, while each oxygen atom is linked to the four copper atoms in a distorted tetrahedron.34 The copper ions are at the center of inversion symmetry with a single fourfold site 4c (1/4, 1/4, 0) with atomic positions at (1/4, 1/4, 0), (3/4, 3/4, 0), (1/4, 3/4, 1/2), and (3/4, 1/4, 1/2) and the oxygen ions occupy site 4e (0, y, 1/4) with y = 0.416(2) with atomic positions at (0, y, 1/4), (0, 1/2 + y, 1/4), (0, \(\overline{y }\), 3/4), and (1/2, 1/2 − y, 3/4). The bond lengths of Cu–O, O–O, and Cu–Cu were reported to be 1.96 Å, 2.62 Å, and 2.90 Å, respectively.5

Fig. 1
figure 1

Structure of the monoclinic unit cells of CuO (a) with ball-and-stick, (b) with space-filling using CIF, and (c) polyhedra using CIF.

Full size image

Copper's oxidation state in cupric oxide is undisputedly +2. The square planar groups become more stable as a result of significant distortion in the local environment of Cu2+ surroundings caused by a strong Jahn-Teller effect. Cupric oxide bonding includes both ionic and covalent bonds.34 The bulk CuO is a narrow-band-gap p-type transition metal semiconductor material with earlier reported value of band gap energy, Eg ~ 1.20–1.90 eV.35

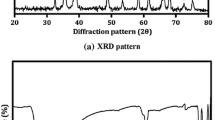
The XRD spectra of as-synthesized samples are shown in Fig. 2. The diffraction peaks at 2θ = 32.56°, 35.50°, 38.79°, 48.80°, 53.55°, 58.41°, 61.63°, 66.22°, 68.21°, and 72.44° correspond to crystal planes (110), (002), (111), (−202), (020), (202), (−113), (−311), (220), and (311), respectively, and can be indexed to monoclinic (tenorite) structure of CuO according to ICDD No: 96-901-4581.36 The absence of secondary phases indicates the purity of as-synthesized samples. The strongest peaks with 2θ values of 35.50° and 38.79° correspond to (−111)/(002) and (200)/(111) crystal planes of monoclinic CuO, respectively, indicating the preferred orientation of growth along these planes. On careful investigation, no impurity (Cu, Cu2O, Cu(OH)2)-related characteristic peak was observed in these diffraction patterns as shown in Fig. 2, which indicates that nanoparticles are highly pure and contain a single-phase of CuO monoclinic structures. Furthermore, an increase in the peak intensity indicates higher crystallinity while the decrease in the full width at half maximum (FWHM) suggests an increase in the crystallite size of the nanocrystals.

Fig. 2
figure 2

Comparison of XRD pattern for CuO nanoparticle samples S1, S2, and S3.

Full size image

The lattice parameters for the monoclinic structure of CuO nanoparticles (a ≠ b ≠ c, α = γ = 90° ≠ β) were calculated using the equation based on Bragg’s law37:

$$\frac{1}{{d}^{2}}= \frac{1}{{sin}^{2}\beta }\left(\frac{{h}^{2}}{{a}^{2}}+\frac{{k}^{2}{sin}^{2}\beta }{{b}^{2}}+\frac{{l}^{2}}{{c}^{2}}- \frac{2hklcos\beta }{ac}\right)$$
(1)

where a, b, and c are lattice constants, d is the interplanar spacing, β is the interfacial angle, and h, k, and l are the Miller indices. The calculated lattice parameter values were found to be in close agreement with the standard values (a = 4.6840 Å, b = 3.4230 Å, and c = 5.1290 Å, and β = 99.54°) of bulk monoclinic CuO crystals.

The macroscopic or bulk density (ρb) and x-ray density (ρx) are other structural parameters that are determined using the formula ρb = m/πr2h and ρx = 8 M/NaVcell, respectively, where m, r, and h represent the mass (in g), radius (in cm), and height (in cm) of the pallet, while the number 8 represents the number of molecules contained in the primitive cell of a monoclinic structure; M, Na, and Vcell represent the molecular weight, Avogadro’s number (6.02257 × 1023) and volume of the cell (in cm3), respectively.38,39 As can be seen from Table I, the values of ρb and ρx for all samples were in the range of 5.62–6.06 g cm−3 and 12.91–13.05 g cm−3, respectively. By comparing these densities, ρb was observed to be less dense (~2 times) than ρx, indicating the presence of minute cracks and pores in the as-synthesized macroscopic samples. Thus, a new structural parameter, known as the porosity (P), which has intra-granular or inter-granular sources, is obtained from the equation P = (1 − ρb/ρx) × 100%, and summarized in Table I. The porosity of sample S2 was observed to be the maximum (~ 56%) as compared to S1 and S3.

Table I Calculated values of lattice parameters (a, b, and c), cell volume (Vcell), bulk density (ρb), and x-ray density (ρx) and porosity (P) of CuO
Full size table

Scherrer Method

Bragg's XRD peak broadening is caused by a combination of instrumental and physical broadening. The XRD spectrum of the standard reference material, typically silicon, is collected for position calibration and instrumental broadening calculation to correct this aberration. The following equation can be used to correct instrumental broadening40:

$${\beta }^{2}={\beta }_{measured}^{2}-{\beta }_{instrumental}^{2}$$
(2)

The average crystallite size of the CuO nanoparticles for highly intense peaks (35.50° and 38.79°) was estimated using Scherrer’s formula23,39:

$$D=\frac{k\lambda }{\beta \mathrm{cos}\theta }$$
(3)

where k = 0.94 is the Scherrer constant, λ = 1.5406 Å is the radiation wavelength for CuKα radiation, β is the FWHM, and θ is Bragg’s angle or peak position. The average crystallite size values calculated for S1, S2, and S3 using Eq. 3 are given in Table II.

Table II Elastic parameters of S1, S2, and S3.
Full size table

Williamson–Hall Analysis

The physical properties of nanomaterials are significantly influenced by strain-dependent elastic properties such as stress and energy density. The XRD broadening caused by size confinement is mainly comprised of size-dependent and strain-induced broadening. Unlike the Scherrer method, the Williamson–Hall plot (WHP) considers not only the effect of size but also the intrinsic strain on XRD broadening.23 The WHP is a straightforward and preferred method for determining the average crystallite size and intrinsic strain of nanocrystals. The total broadening x-ray profile is the sum of the broadenings ascribed to the crystallite size and intrinsic microstrain, which can be written as29:

$${\beta }_{ }={\beta }_{\mathrm{size}}+{\beta }_{\mathrm{strain}}$$
(4)

The WHP obtained using the uniform deformation model (UDM), uniform stress deformation model (USDM), and uniform deformation energy density model (UDEDM) are useful in determining different elastic properties such as strain, stress, and energy density.

Uniform Deformation Model (UDM)

The intrinsic strain in nanocrystals is caused by crystal imperfections such as point defects, grain boundaries, triple junctions, and stacking. According to the UDM, the strain has an isotropic nature, which means that it is uniform in all crystallographic directions. The strain-induced profile broadening can be written as24,40:

$$\beta strain=4\epsilon .\mathit{tan}\theta $$
(5)

where ϵ is intrinsic strain.

Using Eqs. 3 and 5, the total broadening can be obtained as:

$$\beta =\frac{k \lambda }{D cos\theta }+4\epsilon .\mathit{tan}\theta $$
(6)

On rearranging,

$$\beta .\mathit{cos}\theta =\frac{k\lambda }{D}+4\epsilon .\mathit{sin}\theta $$
(7)

This is a straight-line equation and is known as the uniform deformation model (UDM). By plotting 4.sinθ (along the X-axis) and β.cosθ (along the Y-axis), the value of intrinsic strain (ϵ) and average crystallite size (D) can be extracted from the slope and intercept of the straight line, respectively (see Fig. 3), which are summarized in Table II.

Fig. 3
figure 3

Williamson–Hall plot for S1, S2, and S3 assuming the UDM.

Full size image

Uniform Stress Deformation Model (USDM)

The internal stresses existing within nanomaterials (natural or synthetic) can be attributed to many factors such as variations in temperature, phase transitions and elastic deformations. The stresses arising due to linear elastic deformation can be estimated by determining the value of Young’s modulus of the samples. In general, crystals are anisotropic rather than isotropic, as UDM assumes. As a result, an anisotropic factor, i.e. anisotropic strain, is introduced into the Williamson–Hall equation. This modified Williamson–Hall equation is known as the uniform stress deformation model (USDM). According to Hooke’s law, σ = Yϵ, where σ is the lattice deformation stress and Y is Young’s modulus. This equation is only an approximation, and stress is assumed to be uniform in all directions with extremely small microstrain. On applying Hooke’s law, Eq. 6 is modified as40:

$$\beta .\mathit{cos}\theta =\frac{k\lambda }{D}+\frac{4\sigma .sin\theta }{{Y}_{hkl}}$$
(8)

This equation also represents a straight line and is known as USDM.

Young’s modulus, Yhkl for monoclinic can be written as37,38:

$${S}_{33}^{\prime}=\frac{1}{{Y}_{hkl}}=\frac{{S}_{11}{h}^{4} + {S}_{22}{k}^{4} + {S}_{33}{l}^{4}+ \left(2{S}_{12}+ {S}_{66}\right){h}^{2}{k}^{2}+ \left(2{S}_{13}+ {S}_{55}\right){h}^{2}{l}^{2}+ \left(2{S}_{33} + {S}_{44}\right){k}^{2}{l}^{2}}{{\left({h}^{2}+ {k}^{2}+ {l}^{2}\right)}^{2}}$$
(9)

where Sij is the elastic compliance related to the stiffness constants, Cij, by following general equation: σij = Cijεij; εij = Sijσij. The elastic behavior of the monoclinic structure is described by 13 independent stiffness constants, C11, C22, C33, C44, C55, C66, C12, C13, C15, C23, C25, C35, and C46, whose values for monoclinic CuO crystal are 196.41 GPa, 125.01 GPa, 293.70 GPa, 20.28 GPa, 30.07 GPa, 56.44 GPa, 122.63 GPa, 114.64 GPa, −26.99 GPa, 96.89 GPa, −27.85 GPa, −48.95 GPa and −1.15 GPa, respectively. The Sij matrix for the monoclinic system is given as38:

$$\left(\begin{array}{c}\begin{array}{ccc}{S}_{11}& {S}_{12}& {S}_{13}\\ 0 & {S}_{22}& {S}_{23}\\ 0 & 0& { S}_{33}\end{array} \begin{array}{cc}0 & {S}_{15}\\ 0 & {S}_{25}\\ 0 & {S}_{35}\end{array} \begin{array}{c}0 \\ 0 \\ 0 \end{array}\\ \begin{array}{ccc}0 & 0& 0\\ 0 & 0& 0\\ 0 & 0& 0\end{array} \begin{array}{cc}{ S}_{44}& 0 \\ 0& {S}_{55}\\ 0& 0\end{array} \begin{array}{c}{ S}_{46}\\ 0\\ {S}_{66}\end{array}\end{array}\right)$$
(10)

In general, there are 81 compliances \({S}_{ijkl}^{\prime}\) constituting a fourth rank tensor, which can be transformed from the elastic compliances Smnop of the orthogonal system using the following equation41:

$${S}_{ijkl}^{\prime}=\mathrm{aim }.\mathrm{ ajn }.\mathrm{ ako }.\mathrm{ alp}.\mathrm{ Smnop}$$
(11)

By using Eqs. 10 and 11 along with the symmetry property of Sij, rules for transforming between two suffixes and four suffix notation and general elastic compliance transformation relation for monoclinic crystals from the orthogonal coordinate system,42 the corresponding values of S11, S22, S33, S44, S55, S66, S12, S13, S15, S23, S25, S35, and S46 are 13.520 × 10−12 m2N−1, 23.177 × 10−12 m2N−1, 54.950 × 10−12 m2N−1, 49.367 × 10−12 m2N−1, 49.174 × 10−12 m2N−1, 17.738 × 10−12 m2N−1, −12.550 × 10−12 m2N−1, −1.442 × 10−12 m2N−1, −1.840 × 10−12 m2N−1, −1.436 × 10−12 m2N−1, 7.862 × 10−12 m2N−1, 6.321 × 10−12 m2N−1, and 1.006 × 10−12 m2N−1, respectively.37 The average value of Young’s modulus (Yhkl) was obtained using Eq. 9 and estimated to be 69.45 GPa. Fig. 4 shows the plot of (4sinθ/Yhkl) along the X-axis vs. (βcosθ) along the Y-axis for each peak, whose slope and intercept give the values of stress and average crystallite size, respectively.

Fig. 4
figure 4

Williamson–Hall plot for S1, S2, and S3 assuming USDM.

Full size image

Uniform Deformation Energy Density Model (UDEDM)

The isotropic nature of the UDM and the linear proportionality between stress and strain predicted by Hooke's law cannot be justified because the majority of crystals contain various defects, dislocations, or agglomerates. Another model, known as the uniform deformation energy density model (UDEDM), is proposed in which strain energy density is considered to be the cause of strain that is uniform and anisotropic in all crystallographic directions. When the strain energy density (u) is considered, the proportionality constants between stress and strain become no longer independent. The following relationship can be used to calculate energy density43:

$$u=\frac{{\epsilon }^{2}{Y}_{hkl}}{2}$$
(12)

Using Eq. 12, Eq. 8 can be expressed as:

$$\beta .\mathit{cos}\theta =\frac{k\lambda }{D}+4\sqrt{\frac{2u}{{Y}_{hkl}}}.\mathit{sin}\theta $$
(13)

This is a straight-line equation known as the UDEDM equation. Using Eq. 13, a graph was plotted with the term (4sinθ.(2/Yhkl)1/2) along the X-axis and the term (βhkl.cosθ) along the Y-axis. The intercept and slope of the best-fitted line are used to calculate the average crystallite size and anisotropic energy density, respectively (see Fig. 5).

Fig. 5
figure 5

Williamson–Hall plot for S1, S2, and S3 assuming UDEDM.

Full size image

Size–Strain Plot Analysis

The WHP method takes into account the combined effect of size and intrinsic strain-induced broadening on XRD broadening as a function of Bragg's angle (θ). The SSP method, on the other hand, deals with XRD peak profiles, and more emphasis is placed on data from lower-angle reflections, where overlapping peaks are not observed, resulting in greater accuracy and precision. The XRD peak profile is a combination of Lorentzian (crystallite size dependent) and Gaussian functions (strain dependent), which can be represented as40:

$$\beta ={\beta }_{G}+{\beta }_{L}$$
(14)

where βG and βL are the XRD peak profile broadening due to Gaussian and Lorentzian functions, respectively.

Accordingly, the SSP calculations are carried out using the following equation28:

$${({d}_{hkl}\beta cos\theta )}^{2}= \frac{k\lambda }{D}{({d}_{hkl}}^{2}\beta cos\theta )+ \frac{{\varepsilon }^{2}}{4}$$
(15)

where dhkl is the lattice distance between hkl planes for the cubic crystal.

The graph using Eq. 15 is plotted with the term \({({d}_{hkl}}^{2}\beta cos\theta )\) along the X-axis and \({({d}_{hkl}\beta cos\theta )}^{2}\) along the Y-axis corresponding to each diffraction peak for nanoparticles and is shown in Fig. 6. The slope and intercept of best-fitted lines were used to calculate the values of crystallite size and intrinsic strain, which are summarized in Table II.

Fig. 6
figure 6

Size–strain plot for S1, S2, and S3.

Full size image

Halder–Wagner (HW) Method

The size and strain broadening in the x-ray profile are attributed to the Lorentzian and Gaussian functions in the SSP method, but the x-ray profile does not match well with either function. The Lorentzian function only fits the tail of the profile and does not fit well with the profile region; on the other hand, the Gaussian function fits the profile region but does not match the tail of the profile. To address this issue, Halder et al. proposed the HW method, which takes into account the peak broadening and line profile caused by the symmetric Voigt function.44 This function is a combination of the Lorentzian and Gaussian functions.45 This method gives more weight to more reliable reflections at low and intermediate angles with less overlapping peaks, rather than less significant reflections at higher angles with more overlapping peaks.

The Voigt function's full width at half maximum x-ray profile is29,37:

$${\beta }_{hkl}^{2}={\beta }_{G}^{2}+{\beta }_{hkl}.{\beta }_{L}$$
(16)

In this case, the crystallite size and lattice strain are estimated using the following relationships:

$${\left(\frac{{\beta }^{*}}{{d}^{*}}\right)}^{2}=\frac{K{\beta }^{*}}{D{\left({d}^{*}\right)}^{2}}+{\left(2\epsilon \right)}^{2}$$
(17)

where

$${\beta }^{*}=\frac{\beta cos\theta }{\lambda }and$$
(18)
$${d}^{*}=\frac{2 sin\theta }{\lambda }$$
(19)

represent the integral breadth of the reciprocal lattice point and the lattice spacing of the reciprocal cell, respectively, D and ε are crystallite size and intrinsic strain. On substituting Eqs. 18 and 19 into Eq. 17 and then rearranging, the equation becomes:

$${\left(\frac{\beta }{\mathrm{tan}\theta }\right)}^{2}=\frac{K\lambda \beta }{D\mathrm{tan}\theta \mathrm{sin}\theta }+16{\epsilon }^{2}$$
(20)

From the linear fitting of the plot between \(\frac{\beta }{\mathrm{tan}\theta \mathrm{sin}\theta }\) along the X-axis and \({\left(\frac{\beta }{\mathrm{tan}\theta }\right)}^{2}\) along the Y-axis for each peak (shown in Fig. 7), the slope and intercept along the Y-axis give the values of the crystallite size and strain, respectively, and are presented in Table II.

Fig. 7
figure 7

Halder-Wagner plots for S1, S2, and S3.

Full size image

The defects and vacancy concentration in nanocrystals are referred to as dislocation density (δ), which gives the direct measure of crystal defects in the crystalline nanocrystals. The dislocation density can be estimated from the crystallite size determined from the USDM model as follows24:

$$\delta =\frac{1}{{D}^{2}}$$
(21)

The dislocation density values for nanocrystalline samples S1, S2, and S3 are calculated using Eq. 21 and found to be 5.38 × 1014 lines/m2, 2.20 × 1014 lines/m2 and 3.12 × 1014 lines/m2, respectively (see Table II). The large values of dislocation density (~1014) indicate the presence of a higher degree of crystal defects such as interstitial sites and vacancies in all as-synthesized samples. The dislocation density of S1 is slightly larger than S2 and S3. With the decrease in the crystallite size, the percentage of atoms at the surface becomes more than the interior of the nano-sized crystals due to which the concentration of vacancies and interstitials is enhanced. The interstitially occupied atoms/ions do not deform the crystal structure, suggesting the stability of the crystal structure owing to the electrostatic attraction between the free electrons and the atomic nuclei.46

Table II shows that the average crystallite sizes of all samples (S1, S2, and S3) estimated by Scherrer's method, UDM model and SSP methods were reported to be in close agreement, ranging from about 8 to 16 nm. The average values of crystallite sizes estimated by HW were found to be little more than that of Scherrer's method, UDM model and SSP methods and were observed to be in the range of 20–23 nm. Furthermore, the USDM and UDEDM crystallite sizes were significantly larger than the other methods, which could be attributed the presence of agglomerates, defects and dislocations. Among the three models, Williamson–Hall’s USDM and UDEDM give importance to anisotropic strain owing to the density of deformation of energy. In reality, the crystals are non-homogeneous and anisotropic, exhibiting different properties in different directions. Moreover, the USDM model assumes the linear relation (Hooke’s law, σ = Yhklϵ) between stress and strain, which is not obeyed at large intrinsic strain values. At such values, the UDEDM model considers the uniform anisotropy strain that is given by the strain energy density. As for the case of intrinsic strain is concerned, the intrinsic strain measured by the UDEDM and HW methods give the same intrinsic strain (10−3) which was observed to be one order more than SSP method and two order more than USDM. Furthermore, intrinsic strain of the UDEDM and HW methods is ten times lesser than estimated by the UDM model (~2 × 10−2). In a comparative analysis, Figs. 3, 4, 5, 6, and 7 show that the experimental data in the UDM model as well as SSP method is the least scattered from linearity when compared to the USDM, UDEDM, and HW methods. As evident from values of R2 ~ 0.9 from Figs. 3 and 6, the UDM model and SSP method can be considered as better suited to calculating the intrinsic strain of the crystal.

Surface Morphology

The FE-SEM micrographs revealed 2D irregular flake-like morphology, without any stacking or appreciable agglomeration. A careful observation suggests that each flake is composed of an assemblage of a varied number of smaller, irregular, and rough strips. These 2D thin and rough surfaces are enriched with active sites (defects) and possess larger surface areas, which become the hot spots exhibiting remarkable electrochemical and sensing properties. Figure 8b and c indicates that irregular flakes or petals of an average thickness ~ 30–35 nm and diameter size ~ 250–300 nm aggregated into flower-like morphology.

Fig. 8
figure 8

FE-SEM of CuO nanoparticles showing randomly oriented leaf-like structures: (a) S1, (b) S2, (c) S2 at higher magnification and (d) S3.

Full size image

At a constant molar concentration of copper chloride, the morphology of as-synthesized samples changes from irregular leaf-like to flower-like and ultimately to 3D hierarchical structure as the molar concentration of sodium hydroxide varies from 0.4 M to 0.8 M and finally to 1.2 M, respectively (see Fig. 8). These flower-like or hierarchical nanostructures prepared by eco-friendly and facile sonochemical routes can provide a large surface area and better communication between the electrolyte ions and the modified electrode, suggesting the outstanding electrochemical properties of the as-synthesized materials.47

Reaction Mechanism

Since OH− is closely linked to the reaction which produces nanostructures, the concentration of NaOH is crucial in the growth of various CuO morphologies. The formation of such morphologies of nanostructures can be explained by homogeneous nucleation theory which enumerates the existence of two main stages, namely, nucleation and growth. In the nucleation stage, the Cu2+ react with OH− to make colloidal [Cu2+  − (OH)2−] complex in the solution, which ultimately results in the formation of CuO nuclei in a supersaturated solution. These nuclei make up an infinitesimally small assembly of atoms that undergoes structural fluctuations to reduce surface energy, which eventually leads to the evolution of CuO seeds or plate seeds. These seeds are larger and energetically more favored as compared to the nuclei. It is the crystallographic phase and surface energies of the seed that determine the final morphology. It should be mentioned that the formation of CuO nanostructures in aqueous solution is determined by the thermodynamic factor as well as the concentration of OH− as the kinetic factor. In the growth stage, the seeds adsorbed at each plane and grow at different planes with different rates, giving rise to secondary structures like flake-like morphology. The aggregation of nanoparticles in the same direction may be due to the presence of strong intermolecular forces such as van der Waals and π–π interaction. The nano-flakes grow preferentially along the lower surface energy. Because of the opposite electrical charges on the two sides of nano-flakes (i.e. the copper atom enriched side is positively charged and the other side enriched with oxygen atom is negatively charged), the nano-flakes possess high surface energy and become extremely unstable.48 Finally, as a result of Ostwald ripening, these flakes self-assemble to reduce the surface energy and evolve into stable three-dimensional hierarchical structures.24,49,50 Based on the above discussion, a schematic representation of the probable mechanism of formation for nanostructures is illustrated in Scheme 1.

Scheme 1
scheme 1

The growth mechanism for the formation of CuO nanostructures.

Full size image

In the present work, when CuCl2 reacts with NaOH in de-ionized water, Cu2+ combines readily with OH−, instead of H2O to produce Cu2+  − (OH)2− complexes, which decompose to form CuO nuclei and then grow into 3D hierarchical structures. The chemical reaction can be expressed as follows:

$$ {\text{Cu}}^{{{2} + }} + {\text{OH}}^{ - } \to [{\text{Cu}}^{{{2} + }} - \left( {{\text{OH}}} \right)_{{2}}^{ - } ] $$
(22)
$$ \begin{gathered} \left( {{\text{Complex}}} \right) \hfill \\ [{\text{Cu}}^{{{2} + }} - \left( {{\text{OH}}} \right)_{{2}}^{\begin{subarray}{l} \\ - \end{subarray} } ]\to {\text{CuO}} + {\text{ H}}_{{2}} {\text{O}} \hfill \\ \end{gathered} $$
(23)

UV-Vis Analysis

UV-Vis spectroscopy is one of the most convenient, fast, and non-destructive techniques to ascertain optical properties and energy structure. The determination of the optical band gap energy of the as-synthesized samples becomes imperative to find their potential optoelectronic applications. The room-temperature UV-Vis absorption spectra of as-synthesized samples are shown in Fig. 9. The optical band gap of CuO nanoparticles is estimated using the following classical Tauc’s formula23,51:

Fig. 9
figure 9

UV-Vis absorption spectrum and (inset) bandgap estimation using Tauc’s plot for CuO nanoparticle samples S1, S2, and S3.

Full size image
$${\left(\alpha h\upnu \right) }^{\frac{1}{\gamma }}=\left({h\upnu -\mathrm{ E}}_{g}\right)$$
(24)

where α is the absorption coefficient hν represents the energy of the incident photon, h is Planck’s constant, and Eg is the optical band gap energy that depends on the characteristics of the transition in a semiconductor. The values of γ = 3, 2, 1.5, and 0.5 correspond to indirect forbidden, indirect allowed, direct forbidden, and direct allowed transitions, respectively.52 The plot of (αhν)2 vs. hν gives a straight line for direct transition (γ = 0.5).

The extrapolation of this straight line to the X-axis gives the values of the optical band gap energy of as-prepared samples. As shown in the inset of Fig. 9, the values of Eg of S1, S2, and S3 nanostructures were found to be 3.80 eV, 3.70 eV, and 3.75 eV. The lower Eg value for S2 could be ascribed to the presence of defects and localized states within the band gap. The Eg of CuO nanostructures suggests that they do not respond to visible light, suggesting almost negligible photocatalytic properties in the presence of visible light. Generally, the value of Eg at room temperature for the bulk CuO lies in the range of 1.20–1.90 eV. The observed blue shift in the band gap energy might be ascribed to the quantum confinement effect due to nano-sized particles, which arises when the size of particle becomes comparable to the de Broglie wavelength of charge carriers, namely electrons and holes, generated by absorption of light.53

Photoluminescence (PL) Spectroscopy

The PL spectra reveal important information about trap states, point defects (vacancies, antisites, and interstitials), and the rate of recombination of e−–h+ pairs. Figure 10 shows the room-temperature PL spectra of the samples obtained at an excitation wavelength of 325 nm (xenon lamp) in the wavelength varying from 400 to 800 nm. In PL spectra, two prominent emission peaks were observed. The first sharp peak was observed at ~ 504 nm and the other at ~ 757 nm. Here, the green emission at wavelength 504 nm is considered to be attributable to defects in the crystalline structure. The defects in chemically synthesized CuO may be due to singly ionized oxygen vacancies and some non-stoichiometric structures. These defects can act as trap energy states in the band structure. The green emission peak at 504 nm (~2.46 eV) may be attributed to the radiative recombination of free excitons (e−−h+) and/or electronic transition of electrons from the conduction band maximum to energy trap states. The other weak emission peak observed at 757 nm (~1.63 eV) can be ascribed to the inter-band transitions related defect states which were produced owing to copper vacancies present in the CuO nanostructures. The samples S1, S2, and S3 have shown the emission peaks at 504 nm and 757 nm, without any appreciable shift in peak positions. The presence of copper vacancies in CuO makes it an intrinsically p-type semiconducting material.

Fig. 10
figure 10

Photoluminescence spectra for CuO nanoparticle samples S1, S2, and S3.

Full size image

However, the origin of deep-level emission in CuO is still a debatable topic. Recent theoretical calculations reveal that though copper vacancies are the most stable defect states in CuO in copper-rich as well as in oxygen-rich environments, they do not bring any noticeable variation in its electronic structure. In CuO, there exist three types of native point defects: (i) isolated copper or oxygen interstitials (Cui or Oi), vacancies (VCu or VO, where the subscript represents the missing host atom), and antisite defects (CuO or OCu, where XY suggests that the X atom is replaced by the Y atom).35 It is anticipated that point defects such as antisite defects (OCu) or oxygen vacancies (VO) may be responsible for deep-level emission. This appears to be true as the energy of the formation of these defects is not much different from the energy of the formation of copper vacancies.

Conclusions

In this study, CuO nanostructures were prepared using a simple, inexpensive, and environmentally friendly one-pot in situ sonochemical synthesis method that did not involve the use of any organic solvent, surfactant, or template. CuO nanostructures synthesized with varied molar concentrations of NaOH were found to have high purity and crystallinity, and a monoclinic structure. XRD profile broadening was used to carry out a comparative analysis of elastic properties including intrinsic strain, stress, elastic energy, and Young’s modulus using WHP (by assuming UDM, UDSM, and UDEDM), SSP, and HW methods. The crystallite size of all samples was measured by the Debye–Scherrer, WHP, SSP, and HW methods. The intrinsic strain estimated by the UDM model and SSP method were observed to be more appropriate than other methods. The FE-SEM micrographs revealed a variety of morphologies ranging from leaf-like to flower-like to network-like as the concentration of NaOH increased from 0.4 M to 0.8 M and finally to 1.2 M. UV-Vis and photoluminescence spectroscopy were utilized to determine the optical properties of CuO nanostructures. Tauc's plot was employed to estimate the optical band gap, which was found to be in the range of 3.70–3.80 eV. The PL spectroscopy revealed intense green emission at ~ 504 nm and weak emission at ~ 757 nm owing to the presence of different crystal defects. The observed optical band gap range and PL studies show that CuO nanostructures are suited for a wide range of prospective applications including energy storage devices, photovoltaics, spintronics, luminescent devices, catalysis, and biomedicine.