Introduction

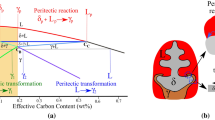
During the continuous casting process, the peritectic steel usually suffers from serious surface quality problems, such as deep oscillation mark, surface depression, crack, and even breakout, because of the significant volume shrinkage induced by the peritectic solidification.[1–4] Peritectic solidification involves two distinct stages[5]: the peritectic reaction (L + δ → γ) occurs at the three phase contact point (liquid + δ-ferrite + γ-austenite) just below the peritectic temperature, resulting in the separation of liquid and δ-ferrite by the lateral growth of γ-austenite around the δ/L interface. Subsequently, the peritectic transformation starts with the thickening of γ-austenite layer behind the advancing tip of γ-austenite towards both the liquid side and δ-ferrite side. This complicated peritectic phase transition during the steel solidification process closely depends on the steel composition and cooling rate and finally affects the steel quality. Therefore, lots of works have been performed to shed light on the fundamental knowledge of peritectic solidification of steel with the pursuit high quality of continuous casting of peritectic steel in the past few decades.[6,7,8,9]

The development of high-temperature laser-scanning confocal microscopy (HTLSCM) by Yin et al.[10] enables high-resolution in-situ observation at elevated temperature of phase transitions in peritectic steel. Shibata et al.[11] first conducted in-situ dynamic observation experiments on the peritectic solidification process of Fe-C alloys using HTLSCM, and concluded that the peritectic reaction is not controlled by carbon diffusion, but by either a massive transformation to γ-austenite or solidification of γ-austenite direct from the liquid. Griesser et al.[12,13] used a combination of HTLSCM and concentric solidification technology to study the peritectic transition mechanism during the solidification of Fe-C alloys and Fe-Ni alloys under conditions close to chemical and thermal equilibrium. The results revealed that the peritectic transition process is controlled by solute diffusion and it was found that the partial remelting of the δ phase is also affected by solute diffusion. Liu et al.[14] used the HTLSCM technology to study the peritectic phase transition process of Fe-C alloys under different cooling rates. The results showed that the γ phase nucleates and grows at the interface between the δ phase and the L phase, and the γ phase separates them rapidly. It was concluded that as the cooling rate increases, the carbon enrichment increases at interface inhibits the nucleation of γ phase. Moreover, X-ray imaging has a big advantage over HTLSCM to study the three-dimensional microstructure under the surface. The development of X-ray imaging by Yasuda et al.[15] enables high-resolution in-situ observation of dendritic solidification for pure Fe and peritectic steels in low contrast between solid and liquid phases at elevated temperature. The results revealed that there is the specific massive-like transformation during the solid phase transformation (δ → γ). Nishimura et al.[16] used the X-ray imaging technology to study the kinetic behavior of peritectic transformation of the Fe-C-Mn-Si alloy, and further showed that the interface movement rate is only affected by the interface elastic energy and solute distribution coefficient. Although the experimental methods including HTLSCM and X-ray imaging are powerful instruments for in-situ observation of the phase transition at elevated temperature, they are high cost and time-consuming experiments.

Due to the rapid rise of computer technology, numerical simulation method becomes an alternative method to study the phase transition during the peritectic steel solidification process. The progress of computational methods in mesoscopic modeling of microstructure evolution in steel is recently reviewed by Xiao et al.[17], and it seems that both cellular automata model (CA) and phase field model (PF) are prosperous stochastic methods to predict the microstructure evolution during the solidification process of steel. Spittle and Brown[18] first predicted the dendritic structure evolution during the solidification process of alloy by introducing the solute diffusion into the CA model. Yamazaki et al.[19] determined the position of the solid/liquid interface and δ/γ interface according to solid/liquid diffusion mass conservation and local equilibrium at the solid/liquid interface, and established a CA model of peritectic solidification. The simulation results showed that the number of initial γ grain is determined by the nucleation mechanism during the peritectic reaction. Su et al.[20] simulated the peritectic phase transformation behavior of C-Mn steel in a multi-component system, based on Scheil model. Ogawa et al.[21] proposed the 2D/3D CA model including δ/γ/L phases and simulated the γ grain coarsening and the evolution of microstructure. Fan et al.[22] proposed a CA model for simulating the peritectic transformation in the peritectic solidification process. They found that the simulation results are consistent with the experimental measurement data and showed that as the temperature decreases, the driving force for γ phase increases. However, the CA method has a weak physical foundation with respect to multiphase solidification, and it is greatly affected by the grid size. Compared with the CA model, PF model has a solid physical background and becomes more popular to predict the phase transition during the solidification process of peritectic alloy.

On basis of Ginzburg-Landau theory, the phase field method introduces changing order parameters to express the evolution of the diffusional solid/liquid interface and the solid/solid interface. Steinbach et al.[23] proposed the generalized multi-phase concept and established a phase field model of the multi-phase system based on the lowest free energy theory. This PF model was applied to predict the peritectic and eutectic solidification process of alloys, but a larger artificial interface width would reduce the accuracy of the phase field model. Later, Karma et al.[24,25] further introduced an anti-trapping current into the model. The results revealed that the multi-phase model can be used to simulate the solute distribution in the solid phase more reasonable. Ode et al.[26] established a multi-field coupled multi-phase field model with the assumption of local equilibrium at the phase interface based on the KKS model,[27,28,29] and studied the effect of interface energies on the advancing distance of the triple point during the peritectic solidification of Fe-C alloys. Ohno et al.[30] developed a quantitative multi-phase field model and investigated the effect of solute diffusion and interface energy on the peritectic solidification process of Fe-C alloys. Sadly, the arbitrary values of the solid diffusivities and interfacial energies were applied to this multi-phase field model. Pan et al.[31,32] proposed a quantitative multiphase field with the introduce of a modified step function to treat the multi-phase interface, and a good agreement between the predicted multiphase interface growth velocity and solute concentration field and experimental data are achieved. Moreover, the present authors[33] also used a combination of in-situ observation and phase field simulation to study the mechanism of the solidification process of peritectic steel. It was concluded that the peritectic transition is controlled by carbon diffusion, and the simulated results were in good agreement with experimental data. However, the above mentioned works mainly focused on the advancing triple point around the δ/L interface and thickening of γ-austenite platelet during the peritectic solidification process without taking into consideration dendritic growth. Luckily, many researchers realized that the multiphase interface does not simply advance around the flat interface for the most solidification process of steel, especially the continuous casting process, usually the dendritic solidification with multiphase transition is most observed phenomenon. Yang et al.[34,35,36,37] established a multi-field coupling model for the solidification of Fe-C alloys, and simulated the dendritic growth and peritectic transformation during the solidification of polycrystalline ferrite with two different thickness of primary austenite. The formation mechanism of microstructure and micro-segregation was analyzed, and the reason for the production of microscopic liquid channels and melting pools was explained by solute diffusion. Alves et al.[38,39,40] quantitatively investigated on the peritectic phase transformation during the isothermal solidification of Fe-Mn alloys using the phase field simulations. Feng et al.[41] investigated the relation between the rate of peritectic reaction and the curvature of the nucleation site of γ phase based on multi-phase field model. Although many studies on the mechanism of peritectic solidification have been carried out through phase field simulation methods, the fundamental knowledge of dendritic solidification with peritectic transition during the peritectic steel solidification process is lack and further works are still needed to be performed.

In this study, based on our previous work,[33] an improved multiphase field model is proposed to investigate the dendritic solidification with the peritectic transition of the low-carbon steel and the motions of the δ/L interface and the γ/L interface are synchronous. Solidification interface anisotropy is introduced into the present multiphase field model to consider the dendrite morphology, and a new random heterogeneous nucleation method is proposed to consider the γ phase nucleation at the δ/L interface. Later, the present multiphase field model is adopted to investigate the γ-phase growth around the solid/liquid (S/L) interface of dendrite and the single/multi dendritic growth with peritectic transition during the solidification of Fe-0.83 mol pct C binary alloy, and also the effect of undercooling on the dendritic growth with peritectic transformation are studied.

Multiphase Field Model

Model Description

Peritectic solidification of commercial steel is a typical multiphase reaction system, where the δ-ferrite, γ-austenite and liquid would coexist beneath the peritectic temperature, and can be described by the multiphase field model proposed by Steinbach et al.[23] In the peritectic system, three phase field variables with ϕi ∈[0, 1] are adopted to denote different phases (i = 1 for δ-ferrite, i = 2 for γ-austenite and i=3 for liquid) and should satisfy the following normalization condition

$$ \sum\limits_{i}^{3} {\phi_{i} = 1} $$
(1)

The time evolution of phase field variables during the peritectic solidification process is defined by the following time-dependent Ginzburg-Landau equation[42]

$$ \frac{{\partial \phi_{i} }}{\partial t} = - M\left( {\left\{ {\phi_{j} } \right\}} \right)\left. {\frac{\delta F}{{\delta \phi_{i} }}} \right|_{{\sum {\phi_{j} = 1} }}, $$
(2)

where M({ϕj}) is the mobility which depends on the phase field, t is the time and F is the free energy function of the peritectic system. Using a Lagrange multiplier, the functional derivative of F on the right-hand side of Eq. [2] with imposing the constraint of Eq. [1] is expressed as

$$ \left. {\frac{\delta F}{{\delta \phi_{i} }}} \right|_{{\sum {\phi_{j} = 1} }} = \frac{\delta F}{{\delta \phi_{i} }} - \frac{1}{N}\sum\limits_{j} {\frac{\delta F}{{\delta \phi_{j} }}}. $$
(3)

Thus, the time evolution of the phase field variables in the multiphase system given in Eq. [2] can be rewritten as the following form

$$ \frac{{\partial \phi_{i} }}{\partial t} = - \frac{{2}}{N}\sum\limits_{j \ne i} {s_{i} s_{j} M_{ij} } \left( {\frac{\delta F}{{\delta \phi_{i} }} - \frac{\delta F}{{\delta \phi_{j} }}} \right), $$
(4)

where Mij is the mobility of i/j interface, \(N = \sum\limits_{i} {s_{i} }\) and si is a step function, which represents the exist status of phase i (phase i exists, si = 1. Otherwise, si = 0), and can be determined by the modified interface field method proposed by Pan et al.[31] The difference \({{\delta F} \mathord{\left/ {\vphantom {{\delta F} {\delta \phi_{i} - }}} \right. \kern-\nulldelimiterspace} {\delta \phi_{i} - }}{{\delta F} \mathord{\left/ {\vphantom {{\delta F} {\delta \phi_{j} }}} \right. \kern-\nulldelimiterspace} {\delta \phi_{j} }}\) is the total driving force of phase transition between the phases i and j, and the functional derivative of F is composed of interface energy driving force \({{\delta F_{I} } \mathord{\left/ {\vphantom {{\delta F_{I} } {\delta \phi_{i} }}} \right. \kern-\nulldelimiterspace} {\delta \phi_{i} }}\) and chemical driving force \({{\delta F_{C} } \mathord{\left/ {\vphantom {{\delta F_{C} } {\delta \phi_{i} }}} \right. \kern-\nulldelimiterspace} {\delta \phi_{i} }}\), and given by

$$ \frac{\delta F}{{\delta \phi_{i} }} = \frac{{\delta F_{I} }}{{\delta \phi_{i} }} + \frac{{\delta F_{C} }}{{\delta \phi_{i} }} $$
(5)

and the first term \({{\delta F_{I} } \mathord{\left/ {\vphantom {{\delta F_{I} } {\delta \phi_{i} }}} \right. \kern-\nulldelimiterspace} {\delta \phi_{i} }}\) at the right-hand side of Eq. [5] can be described as[31]

$$ \frac{{\delta F_{I} }}{{\delta \phi_{i} }} = - \frac{1}{2}\varepsilon^{2} \nabla^{2} \phi_{i} + \omega_{ij} \phi_{i} (1 - \phi_{i} )(1 - 2\phi_{i} ), $$
(6)

where ε and ωij are, respectively, the gradient energy coefficient and potential height of i/j interface. In order to introduce the effect of interface anisotropy on the interface morphology, the gradient energy coefficient ε in Eq. [6] is replaced by ε(θ) and given by

$$ \varepsilon \left( \theta \right) = \varepsilon \left( {1 + \nu \cos \left( {k\theta } \right)} \right), $$
(7)

where ν is the magnitude of anisotropy and k is 4 for four-hold anisotropy. θ is the angle between normal direction of interface and x-axis, \(\theta {\text{ = arctan}}\left( {{{\phi_{iy} } \mathord{\left/ {\vphantom {{\phi_{iy} } {\phi_{ix} }}} \right. \kern-\nulldelimiterspace} {\phi_{ix} }}} \right)\). Therefore, the Laplacian term on the right-hand side of equation (6) evolves into three terms, when the interface anisotropy is considered

$$ \varepsilon^{2} \nabla^{2} \phi \Rightarrow \nabla \left( {\varepsilon^{2} \left( \theta \right)\nabla \phi } \right) - \frac{\partial }{\partial x}\left( {\varepsilon \left( \theta \right)\varepsilon{^{\prime}} \left( \theta \right)\frac{\partial \phi }{{\partial y}}} \right) + \frac{\partial }{\partial y}\left( {\varepsilon \left( \theta \right)\varepsilon{^{\prime}} \left( \theta \right)\frac{\partial \phi }{{\partial x}}} \right), $$
(8)

where \(\varepsilon{^{\prime}} \left( \theta \right)\) represents the derivative of gradient energy coefficient ε with respect to θ.

According to the equilibrium diffusion potential theory proposed by the KKS model,[27,28,29] the chemical driving force term with the dilute solution approximation can be expressed as

$$ \frac{{\delta F_{{\text{C}}} }}{{\delta \phi_{i} }} = f_{j} - \mu_{{\text{c}}} c_{j} \approx \frac{RT}{{V_{m} }}\left( { - c_{k,e}^{j} + c_{j,e}^{k} - c_{j} } \right), $$
(9)

where R is the universal gas constant, T is the temperature, Vm is the molar volume, cj is the solute concentration in phase j, ckj,e is the solute concentration in phase j in equilibrium with phase k, and phase k corresponds to a reference phase. In the present study, the liquid phase is chosen as a reference phase.

Peritectic solidification of commercial steel is a three phase system (δ-ferrite, γ-austenite and liquid), any two phase field variables are firstly calculated by Eq. [4] and the third phase field variable can be determined by Eq. [1]. Here, the time evolution of the phase field variables for both δ-ferrite and γ-austenite are given by

$$ \frac{{\partial \phi_{\delta } }}{\partial t} = - \frac{2}{N}\left\{ {s_{\delta } s_{L} M_{\delta L} \left[ {\frac{\delta F}{{\delta \phi_{\delta } }} - \frac{\delta F}{{\delta \phi_{L} }}} \right] + s_{\delta } s_{\gamma } M_{\gamma \delta } \left[ {\frac{\delta F}{{\delta \phi_{\delta } }} - \frac{\delta F}{{\delta \phi_{\gamma } }}} \right]} \right\}, $$
(10)
$$ \frac{{\partial \phi_{\gamma } }}{\partial t} = - \frac{2}{N}\left\{ {s_{\delta } s_{\gamma } M_{\gamma \delta } \left[ {\frac{\delta F}{{\delta \phi_{\gamma } }} - \frac{\delta F}{{\delta \phi_{\delta } }}} \right] + s_{\gamma } s_{L} M_{\gamma L} \left[ {\frac{\delta F}{{\delta \phi_{\gamma } }} - \frac{\delta F}{{\delta \phi_{L} }}} \right]} \right\}. $$
(11)

The solute diffusion in the multiphase system satisfies the Fick’s second law and is rewritten as

$$ \frac{\partial c}{{\partial t}} = \nabla \left( {\sum\limits_{i}^{N} {D_{i} \phi_{i} \nabla c_{i} } } \right), $$
(12)

where c is an average solute concentration, Di is the solute diffusivity in phase i, and ci is the solute concentration in phase i.

Moreover, interface perturbation has a great effect on the dendrite branch. Here, a noise term is introduced into the multiphase filed model to simply treat dendrite branch, and thus the phase field governing equation Eq. [2] is rewrote by

$$ \frac{{\partial \phi_{i} }}{\partial t} = \frac{{\partial \phi_{i} }}{\partial t} + 16\phi_{i}^{2} \left( {1 - \phi_{i} } \right)^{2} \chi \varpi, $$
(13)

where χ is a random number between − 1 and 1, ϖ is the time-dependent intensity factor.

Phase Interface Parameters

The phase grows with the interface evolution in the peritectic system, thus the phase interface parameter is very important for the multiphase simulation. Here, the gradient energy coefficient, ε, and the potential height, ωij, between phase i and phase j can be expressed as follows[31]

$$ \varepsilon = \sqrt {3\sqrt 2 \sigma_{ij} W_{ij} } , $$
(14)
$$ \omega_{ij} = 3\sqrt 2 \frac{{\sigma_{ij} }}{{W_{ij} }}, $$
(15)

where σij is the interface energy, and Wij is the thickness of the i/j interface.

According to the thin-interface limit analysis,[27,28,29] the mobility Mij is given as follows

$$ M_{ij} = \left( {\frac{15}{4}\frac{{a_{2} \varepsilon_{ij}^{2} }}{{\omega_{ij} D_{j} }}\frac{{RT_{m,ij} }}{{V_{m} }}\left( {1 - k_{ij} } \right)\left( {c_{j,e}^{i} - c_{i,e}^{j} } \right)} \right)\left[ {1 - \frac{1}{2}\left( {1 - k_{ij} \frac{{D_{i} }}{{D_{j} }}} \right)\chi_{ij} } \right], $$
(16)

where Tm,ij is the transition temperature between i and j phases of pure Fe, a2 is a constant and the recommend value is 0.6276.[30] χij is a parameter associated with the composition field at the i/j interface and it is given as 0 in the present study.

Heterogeneous Nucleation Model

When the temperature is lower than the peritectic temperature during the peritectic solidification process, γ-austenite would nucleate and grow. In fact, the nucleation process of γ-austenite is a complicate thermodynamic phenomenon in the nano-scale and difficultly treated by traditional phase field modeling. Therefore, a random heterogeneous nucleation model is proposed to simplify the nucleation process of γ-austenite in peritectic system. The flowchart of the nucleation process of γ-austenite is shown in Figure 1. When the temperature reaches the nucleation temperature of γ-austenite, a random number, \(Pv(x,y)\)∈[0, 1], generates and a threshold value for the nucleation λ is introduced to determine whether the pre-nucleation successes or not. If \(Pv(x,y) > \lambda\), pre-nucleation of γ-austenite successes, and artificial γ nucleus is set as circle with a radius of R. Otherwise, it is not. Moreover, in order to avoid the overlap of random γ nuclei, an additional step function \(Nu\left( {x,y} \right)\) is introduced in the present multiphase model

$$ Nu\left( {x,y} \right) = \left\{ {\begin{array}{*{20}l} 0 & {\left( {\phi _{\gamma } > 0} \right)or\left( {\phi _{\gamma } = 0\;{\text{and}}\;\phi _{\gamma } \left( {x + nx,y + ny} \right) > 0} \right)} \\ 1 & {{\text{otherwise}}} \\ \end{array} } \right. $$
(17)
Fig. 1
figure 1

The flowchart of the nucleation process of γ-austenite

Full size image

If \(Nu\left( {x,y} \right){ = }0\), γ-austenite nucleation is allowed. Otherwise, it is not allowed. The detailed determination of the step function \(Nu\left( {x,y} \right)\) is schematically shown in Figure 2. The red and yellow solid lines, respectively, represent the isolines of ϕδ = 0.01 and ϕδ = 0.99, the black dash line represents the isoline of ϕδ = 0.50, the green solid circle is the γ-austenite nucleus and the center is placed on the black dash line. Among them, the black open circle indicates the possible nucleation position. When \(Pv(x,y) > \lambda\), this point becomes the point of pre-nucleation (the pink solid circle). Whether the pre-nucleation point becomes active or not, it depends on whether there is γ phase in the scanned area with size of \(nx \times ny\). If there is no γ phase already in the scanned area, the pre-nucleation point becomes active (in other words, the γ-austenite nucleation successes). Otherwise, the pre-nucleation point becomes invalid.

Fig. 2
figure 2

The schematic diagram of γ-austenite nucleation

Full size image

Computational Details

The governing equations for present multiphase field model are discretized with explicit finite difference method and coding with C++. In order to assure the stability of numerical calculation, the simulation time step Δt is less than Δx2/(5.0DL). Here, time step Δt is 7.62 × 10−8 s and the interface thickness WδL is given as WδL = 3Δx, the thicknesses of the γ/L and γ/δ are calculated by WγL = WδLσδL/σγL and Wγδ = WδLσδL/σγδ. In addition, the calculation domain is meshed with NX × NY cells and the Neumann boundary condition is set at the calculation domain boundary, if not otherwise specified. In the present study, the commercial low-carbon steel is simplified into a Fe-0.83 mol pct C binary alloy, and the basic thermodynamic parameters can be directly determined by the equilibrium Fe-C binary phase diagram, as shown in Figure 3, such as: peritectic temperature, equilibrium concentration, liquidus slope, equilibrium partition coefficient, and so on. The specified thermodynamic parameters and other model parameters in the present study are listed in Table I.

Fig. 3
figure 3

The equilibrium Fe-C binary phase diagram

Full size image
Table I Physical and Thermodynamic Properties of Fe-C Alloy[30]
Full size table

Mesh Sensitivity

In order to ensure that the present multiphase field model has eliminated the mesh dependency, the results should achieve convergence while refining the mesh size. Then, the solidification of Fe-0.83 mol pct C binary alloy under constant temperature of 1776 K is simulated and the calculation domain is defined as 120 × 120 μm2. At the beginning of the simulation for the dendritic growth, a circular δ phase nucleus with a radius of 0.4 μm is placed in the certain of the square domain and the initial concentration of the nucleus is given as cδ0 = kδL·c0. Moreover, the Neumann boundary condition is adopted in this section and the time step Δt is given as 5.8 × 10−8 s, which is satisfied with the stability condition in Section II–D. Figure 4 shows the calculated δ phase dendrite tip velocity as a function of mesh size, Δx, during the isothermal solidification of Fe-C alloy. It is evident that tip velocity tends to stabilize at about 3.25 × 10−3 m s−1, if the mesh size is refined to be less than 0.08 μm. Therefore, the mesh size of 0.08 μm is adopted in the present study.

Fig. 4
figure 4

The effect of mesh size on the tip velocity

Full size image

Results and Discussion

γ Phase Growth Around the δ/L Interface

In order to predict the peritectic reaction of Fe-0.83 mol pct C binary alloy, a square domain with 400 × 400 cells is firstly employed to simulate the γ phase growth around the solid/liquid (S/L) interface of dendrite. It should be mentioned that a nucleus of δ phase is firstly placed at the left bottom of simulation domain, and grows freely until the temperature reaches the T0 = 1765.4 K, which is 3 K lower than the equilibrium peritectic temperature. In order to highlight the peritectic reaction process, the recording time starts at t0, which is slightly ahead of the occurring time of peritectic reaction. The evolution of the phase field and the concentration field during the peritectic reaction of isothermal solidification at 1765.4 K are, respectively, shown in Figures 5 and 6, where the recording evolution time is expressed by nΔt, and n is the iteration steps. It can be seen that when the temperature just reaches the peritectic reaction temperature, only two phases (δ phase and liquid phase) coexist in the calculation domain, and the δ phase is a quarter dendrite at the left bottom of the calculation domain as shown in Figure 5(a). Then, based on the nucleation assumption in Section II–C, many γ nuclei are suddenly nucleated at the δ/L interface of the quarter dendrite, as shown in Figure 5(b). After the γ nuclei nucleation succeeds on the δ/L interface, the γ phase begins to laterally grow with the movement of L/γ/δ triple point around the δ/L interface of δ dendrite. The advancing of L/γ/δ triple point is very fast and some adjacent γ nuclei begin to connect together at very short time, as shown in Figure 5(c). With the growth of all γ nuclei at the δ/L interface, a continuous γ phase forms between the δ dendrite and liquid and finally the δ phase and liquid are totally separated by the intervening γ phase, as shown in Figure 5(d). Here, it should be mentioned that all the γ nuclei form at the δ/L interface have the same crystallographic orientations as the δ dendrite. Therefore, after the δ dendrite totally wrapped by the continuous γ phase, the γ phase simultaneously grows into the liquid phase and δ phase and retains the original morphology of δ dendrite. Moreover, the growth rate of the γ phase at the δ dendrite root is slowest than any other positions at the dendrite interface, and thus the thickness of γ phase is thinnest around the dendrite shape, as shown in Figure 5(d), because the solute enrichment inhibited the γ phase growth at the dendrite root, as show in Figure 6. Before the peritectic reaction occurs, the δ dendrite grows into the liquid with solute rejection and enrichment at the δ/L interface, as shown in Figure 6(a). Later, γ nuclei with initial concentration of cγ0=cL·kγL randomly nucleate at the δ/L interface, as shown in Figure 6(b), and peritectic reaction starts with L + δ → γ. The solute enrichment induced by the advancing of L/γ/δ triple point around the δ/L interface leads to the partial remelting of δ phase close to the L/γ/δ triple point, as shown Figure 6(c), and it has been experimentally observed in peritectic solidification of Fe-C alloy using HTLSCM by Griesser et al.[12,13] When the δ dendrite is totally separated by the γ phase, only the peritectic transformation occurs with δ → γ and L → γ, and solute enriches at the L/γ interface, especially for the dendrite root.

Fig. 5
figure 5

The phase field evolution during the growth of γ-phase at T0 = 1765.4 K ((a) through (d) are at t = 0Δt, 1Δt, 10,000Δt, 19,000Δt, respectively)

Full size image
Fig. 6
figure 6

The solute concentration evolution during the growth of γ-phase at T0 = 1765.4 K ((a) through (d) are at t = 0Δt, 1Δt, 10,000Δt, 19,000Δt, respectively)

Full size image

Single Dendritic Growth with Peritectic Transition

During the solidification process of peritectic steel, the dendrite inevitably grows with peritectic transition, which is composed of peritectic reaction and peritectic transformation. Usually, peritectic reaction and peritectic transformation are unseparated phase transition process and simultaneously occur with γ phase growth. In order to emphasize the difference between the peritectic reaction and peritectic transformation and the dendritic solidification with peritectic transition of peritectic steel, the single dendritic growth with peritectic reaction and peritectic transformation are, respectively, numerically investigated in this section.

Single dendritic growth with peritectic reaction

The single dendritic growth with peritectic reaction and the γ phase growth around the single δ dendrite are simulated on a calculation domain with 1500 × 1500 cells. All the simulation conditions are same as those mentioned in Section III–A, except that the initial position of δ nucleus. In order to obtain a more developed dendrite morphology, a noise term is introduced into the multiphase field model in Eq. [2], and a preset δ nucleus grows freely at the center of simulation domain until the temperature reaches 1765.4 K at the time of t0. Figure 7 shows the evolution of the phase field during the dendritic solidification of isothermal condition at T0 = 1765.4 K, respectively. As shown in Figure 7(a), there is a δ dendrite at the center of the simulation domain, and with the influence of noise term, some secondary dendrite arms develop on the primary dendrite arms. Then, a large number of γ nuclei instantaneously nucleate at the δ/L interface of δ dendrite as shown in Figure 7(b). With the growth of the γ phase, the liquid and δ phase are gradually separated by the intervening γ phase, and thus some thin secondary dendrite arms of the δ phase are totally wrapped by the γ phase, and then the δ phase gradually transform into γ phase by peritectic transformation. However, due to the large circumference of δ dendrite and short evolution time, the intervening γ phase is still discontinuous at the δ/L interface of δ dendrite, as shown in Figure 7(c). With the further progress of solidification, the δ dendrite and liquid are totally separated by the continuous intervening γ phase, and the γ phase grows with γ/L interface and γ/δ interface, respectively, moving towards liquid and δ phase, resulting in the γ phase thickening, as shown in Figure 7(d). Due to larger solute diffusion coefficient in liquid than that in δ phase, the γ/L interface moves quickly than the γ/δ interface, and the γ phase grows faster into the liquid than the δ phase. Moreover, the dendritic growth with peritectic transition still maintains the δ dendrite morphology, and most of the secondary δ dendrite arms completely transform into γ phase. But most of the primary δ dendrite arms are still untransformed, because of the lower phase transformation velocity of δ → γ and high solute enrichment at the solidification front. Figure 8 shows the evolution of the solute concentration field during the dendritic solidification of isothermal condition at T0 = 1765.4K, respectively. It can be seen that due to the lower carbon solubility in δ phase, the solute would be rejected from dendrite trunk with the dendritic growth and enriched at the root of primary and secondary dendrite arms, as show in Figure 8(a). After the γ phase nucleation at the δ/L interface of δ dendrite, the γ phase grows with the consumption of δ phase and liquid. Although the carbon solubility in γ phase is higher than that in δ phase, it is lower than that in liquid. Therefore, with the growth of γ phase, the solute is also rejected from the solidified γ phase and enriched at the γ/L interface, and solute concentration in γ phase is higher than that in δ phase, as shown in Figures 8(b) through (d). Moreover, another important phenomenon should be pointed out the solute enrichment at the root of primary and secondary dendrite arms inhibits the γ phase growth, resulting in thinner γ phase at the dendrite root, as shown in Figure 7(d).

Fig. 7
figure 7

The phase field evolution during the growth of γ phase around the single δ dendrite at T0 = 1765.4K ((a) through (d) are at t = 0Δt, 1Δt, 10,000Δt, 19,000Δt, respectively)

Full size image
Fig. 8
figure 8

The solute concentration evolution during the growth of γ phase around the single δ dendrite at T0 = 1765.4K ((a) through (d) are at t = 0Δt, 1Δt, 10,000Δt, 19,000Δt, respectively)

Full size image

Single dendritic growth with peritectic transformation

As mentioned above, after the δ dendrite is totally wrapped by the γ phase, there are only two phase transformation processes during the γ phase growth in the three phase coexistence system, namely: the solid transformation (δ → γ) and the solidification of the liquid (L → γ). Here, the single dendritic growth with peritectic transformation is simulated in a square domain with 1500 × 1500 cells. A nucleus of δ phase is also firstly placed at the center of the simulation domain and grows freely until the temperature reaches T0, 1765.4 K. The evolution of the phase field during the single dendritic growth with peritectic transformation of isothermal solidification at T0 is shown in Figure 9. It should be mentioned here that the initial δ dendrite grows in an undercooled melt of Fe-0.83 mol pct C binary alloy and stops grow at t0 with sudden formation of γ phase film at the δ/L interface of δ dendrite, as shown in Figure 9(a). As the simulation process progresses, the thickness of the γ phase film continues to increase in two ways. One way is that the δ phase directly contact with the γ phase film transforms into the γ phase, and the γ/δ interface moves towards the δ phase. Another way is that the liquid phase directly transforms into the γ phase through solidification process, and the γ/L interface moves towards the L phase, as shown in Figures 9(b) and (c). It can be seen from Figure 9(d) that almost all the secondary δ dendrite arms transform into γ phase and the γ phase film becomes more and more thick. Because the crystallographic orientation of the γ phase film at the dendritic solidification front is artificially set as the δ dendrite, γ phase grows with the same dendrite morphology of δ phase. The concentration field during the single dendritic growth with peritectic transformation of isothermal solidification at T0 is shown in Figure 10. It should be mentioned that before the nucleation of γ phase at the δ/L interface, the δ phase grows into the undercooled melt with dendritic morphology and solute enriches at the dendritic solidification front, especially the highest solute enrichment at the dendrite root. At the beginning of peritectic transformation, γ phase film with the initial concentration of cγ0= cL·kγL forms at the δ dendrite boundary, as shown in Figure 10(a). With the γ phase growth, both the δ phase and liquid phase transform into γ phase, and the solute gradually enriches at the γ/L interface, as shown in Figures 10(b) through (d). Furthermore, the solute concentration in γ phase is among the δ phase and liquid phase, because the carbon solubility is different in δ phase, γ phase and liquid phase, and carbon solubility in γ phase is higher than that in δ phase, but lower than that in liquid. No matter what phase forms directly from liquid, the solute would be rejected from the dendrite trunk with dendritic growth and enriched at the dendrite boundary, especially at the dendrite root.

Fig. 9
figure 9

The phase field evolution during the single dendritic growth with peritectic transformation at T0 = 1765.4 K ((a) through (d) are at t = 1Δt, 2000Δt, 8000Δt, 20,000Δt, respectively)

Full size image
Fig. 10
figure 10

The concentration field evolution during the single dendritic growth with peritectic transformation at T0 = 1765.4 K ((a) through (d) are at t = 1Δt, 2000Δt, 8000Δt, 20,000Δt, respectively)

Full size image

In order to investigate the effect of undercooling on the peritectic transformation process (δ → γ), a numerical simulation is performed on a square domain with 1500×1500 cells. The initialization configuration for the dendritic growth with peritectic transformation at different undercooling is schematically shown in Figure 11. A δ dendrite locates in the calculation domain and thus calculation domain is divided into three zones, namely δ phase (ϕδ > 0.99), δ/L interface (0.01 < ϕδ < 0.99) and liquid phase (ϕδ < 0.01). Then, the γ phase nucleates at the δ/L interface, and the three phases begin to coexist in the calculation domain. The initial concentrations of three phases are cδ0 = 0.45mol pct, cγ0 = 0.85 mol pct and cL0 = 2.50 mol pct, respectively.

Fig. 11
figure 11

The schematic diagram of phase field initialization for peritectic transformation simulation

Full size image

Figure 12 shows the dendritic growth with peritectic transformation at different undercooling for same evolution time t = 10,000Δt. It can be seen that with the increase of undercooling, the intervening γ phase between the δ dendrite and liquid phase becomes more and more thick, but the δ dendrite arm becomes more and more thin, because the difference between the initial solute concentration and the equilibrium concentration becomes larger, and the driving force of the phase transition increases with the increase of undercooling. Therefore, the moving velocities of both γ/δ interface and γ/L interface are higher for the higher undercooling, and the more δ phase and liquid phase are consumed to form γ phase. It is found from Figure 12(e) that almost all the secondary δ dendrite arms transform into the γ phase under the high undercooling condition. Moreover, due to the of γ/L interface anisotropy, dendrite morphology is basically retained during the dendritic solidification process with peritectic transformation. On the contrary, the γ/δ interface has no anisotropy, and the shape of the γ/δ interface tends to be plane.

Fig. 12
figure 12

The phase field distribution during the peritectic transformation with different undercoolings below the equilibrium peritectic temperature at t = 10,000Δt: (a) 3 K, (b) 5K, (c) 8 K, (d) 12 K and (e) 15 K

Full size image

Multi Dendritic Growth with Peritectic Transition

In order to predict the γ phase growth of the polycrystalline ferrite system, a square domain with 1600 × 1600 cells is employed, and the periodic boundary condition is applied in the present simulation. It should be mentioned that eight nuclei of the δ phase with random crystallographic orientation are randomly placed in the simulation domain, and grow freely in the undercooled melt of T0 = 1765.4 K. The recording time starts at t0, where the γ phase nucleation and peritectic transition begin. Figure 13 shows the evolution of the phase field during the peritectic transition at T0, and some typical solidification phenomena are marked by boxes. It should be mentioned that the enlarged zones I, II and III are not same position in the simulation domain, but mainly emphasize some important solidification phenomena. It can be seen that the γ phase heterogeneous nucleation firstly occurs at the δ/L interface of δ dendrite and many γ nuclei can be easily found at the solidification front in the zone I enlarged from the square box as shown in Figure 13(a). Later, the γ phase grows around the δ/L interface of δ dendrite and thus δ phase and liquid are separated by the intervening γ phase at some positions of δ dendrite boundary. But the intervening γ phase is not long enough to wrap the whole δ dendrite boundary and there are some left δ/L interfaces, which can be clearly found in zone II. Moreover, the intervening γ phase between the δ phase and liquid phase gradually becomes thick with the consumption of both δ phase and liquid phase, as shown in Figures 13(b) and (c). After the γ phase completely wrapping the δ phase, only the dual interface movement (L → γ and δ → γ) occurs in the polycrystalline ferrite system as shown in Figure 13(d). The γ phases growing from different γ nuclei connect together and finally form continuous γ phase film, which can be clearly seen in zone III. In addition, the γ phase at the dendrite root grows slowly and the intervening γ phase is thinner than any other positions around the dendrite boundary, because of the inter-dendritic solute enrichment.

Fig. 13
figure 13

The phase field revolution during the peritectic solidification of polycrystalline ferrite at T0 = 1765.4 K ((a) through (d) are, respectively, at t = 1Δt, 5000Δt, 9000Δt, 25,000Δt)

Full size image

Conclusions

In this paper, an improved multiphase field model with a new random heterogeneous nucleation model for γ phase is proposed and adopted to study the dendritic peritectic solidification of low-carbon steel by introducing the anisotropy into the present model. The main results are concluded as follows:

  1. 1.

    When the temperature reaches nucleation temperature of γ phase, many γ nuclei suddenly nucleate at the δ/L interface of the δ dendrite, and begin to laterally grow with the movement of L/γ/δ triple point around the δ/L interface of δ dendrite. Finally, the δ dendrite are fully wrapped by the continuous intervening γ phase, and peritectic transformation starts with the γ/L interface and γ/δ interface, respectively, moving towards liquid phase and δ phase. The dendritic growth with peritectic transitions always maintains the δ dendrite morphology, but the γ/δ interface is plane during the dendritic solidification process, because anisotropy of solid phase interface (γ/δ interface) is not taken into consideration in the present study.

  2. 2.

    Due to carbon solubility in solid phase (δ phase and γ phase) lower than that in liquid phase, the solute would be rejected from the dendrite trunk with dendritic growth and enriched at the dendrite boundary, especially at the dendrite root. The solute enrichment at the dendrite root would inhibit the γ phase growth at the δ dendrite root and thus the thickness of γ phase is thinnest around the δ dendrite boundary. Moreover, the solute concentration in γ phase is among the δ phase and liquid phase, because the carbon solubility in γ phase is higher than that in δ phase, but lower than that in liquid.

  3. 3.

    Because the driving force of the phase transition increases with the increase of undercooling, more δ phase and liquid phase are consumed to form γ phase, and the intervening γ phase between the δ dendrite and liquid phase becomes more and more thick, but the δ dendrite arm becomes more and more thin.