1 Introduction

Despite being studied for many years, BiFeO3 (BFO) still attracts much attention from scientists worldwide. BFO belongs to the multiferroic class of materials. It is a rare example of a material that combines ferroelectric and magnetic orderings in a single phase at room temperature. The crystal structure of BFO can be viewed as a rhombohedral distortion of the ideal perovskite cell. There are two kinds of deformations with respect to the ideal perovskite structure: (1) relative polar displacement of Bi3+ and Fe3+ ions along the [111] pseudocubic direction and (2) opposite rotation of the oxygen octahedra around the [111] axis in the adjacent cells.[1] It was proved that the first one reduces crystal symmetry from cubic (Pm3m) to the rhombohedral (R3m) and leads to the appearance of spontaneous polarization along the diagonals of the pseudocubic unit cell.[2] The second one causes further lowering of the symmetry to the R3c space group and, it is believed to determine the spin canting and weak ferromagnetism in this system.[3]

In its bulk form, BFO is a ferroelectric material with polarization as large as 90 μC/cm2 and relatively high Curie temperature TC ~ 830 °C.[4] The ferroelectricity arises mainly due to stereochemically active lone 6s2 electronic pairs of Bi3+ ions. At the same time, BFO shows G-type antiferromagnetism in connection with superexchange interaction of neighboring Fe3+ ions up to the Néel temperature of about TN ~ 370 °C.[5] The iron magnetic moments belonging to antiferromagnetic sublattices are slightly canted due to the aforementioned opposite oxygen octahedra rotation. According to Dzyaloshinskii and Moriya's theory, the spin canting is a result of antisymmetric superexchange interaction.[6] Thus, a weak ferromagnetic moment perpendicular to the antiferromagnetic axis appears locally due to incomplete compensation of corresponding magnetic moments. However, as it was proved by neutron diffraction, there is a spin cycloid propagating in [10-1] pseudocubic direction with an exceptionally long period of about 62 nm.[7] All magnetic moments are confined to the plane defined by the electric polarization vector [111] and the cycloid propagation vector [10-1].[8] The spin cycloid cancels out macroscopic magnetization and inhibits magnetic hysteresis and linear magnetoelectric effect observation for bulk samples. Thus, many current scientific efforts tend to destroy the spin cycloid and release the inherent magnetization in order to improve the multiferroic properties of BiFeO3.

The cycloid can be destroyed in several ways, e.g., by the high magnetic field, strain, chemical doping, or formation of nanostructures or heterostructures. High-pulsed magnetic field investigations revealed a suppression of the cycloidal modulation at about 20 T accompanied by a jump of electric polarization and release of the weak ferromagnetic moment.[9] There are numerous reports in the literature describing spin cycloid destruction by chemical substitution of Bi3+ or/and Fe3+ ions by other ions.[10,11,12,13,14,15] Indeed, it enables to observe week ferromagnetism, but the magnetoelectric coupling coefficient measured in those samples is disappointingly small. In this context, the production of BFO in the form of nanoparticles or thin films with dimensions comparable or less than the spin cycloid wavelength seems to be the most promising approach. Wang et al. reported significant enhancement of electric polarization, growth of magnetization, and magnetoelectric coupling coefficient as large as 3 V/(cm × Oe) in the case of heteroepitaxially constrained thin films of BFO.[16]

The sol–gel method was proved to be a promising route for the preparation of substrate-free nanocrystalline BFO.[17,18,19,20,21,22] In this case, systematic enhancement of magnetic properties was observed along with the drop of grain size below the cycloid modulation period λ.[18] But whether the small grain size causes the destruction of spin cycloid or the magnetization enhancement is only a result of the increasing number of uncompensated surface spins seems to be a still open question.[18,19] Castillo et al. carried out interesting Mössbauer spectroscopy investigations of sol–gel prepared BFO powder with grain size d = 54 ± 14 nm and stated that the spin cycloid is preserved in this case.[19]

The main objectives of the present work were: (1) to study the influence of annealing temperature on the formation of BFO phase and its structure in the case of sol–gel synthesized samples, (2) to observe how the nanocrystalline character of the samples affects properties of spin cycloid and magnetic characteristics of BFO, and (3) to verify whether the grain size much less than λ causes destruction of the spin cycloid. The structure and morphology of samples were investigated using X-ray diffraction (XRD), scanning electron microscopy (SEM), and transmission electron microscopy (TEM). Magnetic properties were studied by means of standard measurements of magnetization and the Mössbauer spectroscopy (MS) method.

2 Materials and Methods

The sol–gel technique was employed for the preparation of BiFeO3. As chemical reagents, Bi(NO3)3·5H2O and Fe(NO3)3·9H2O with analytical grade were used. In the first step, bismuth nitrate pentahydrate (0.01 M), iron nitrate nonahydrate (0.01 M), and tartaric acid (0.02 M) were dissolved in ethylene glycol (10 mL) to make a sol. The solution was vigorously stirred for 3 hours and next dried at 70 °C for 5 hours. The prepared gel was washed with distilled water and ethylene alcohol repeatedly and dried overnight at 120 °C. The obtained xerogel was grounded in an agate mortar and annealed in the range of temperatures 350 °C to 800 °C for 4 hours. Samples annealed at 350 °C, 380 °C, 400 °C, 450 °C, 500 °C, 550 °C, 600 °C, 800 °C and subjected to investigations were marked as BFO350–BFO800.

Structural investigations were carried out using the X-ray diffraction method. XPert-Pro diffractometer worked in the standard Θ–2Θ mode was employed. The HighScore Plus program was used for phase and structural analyses.

For microstructure and morphology observations, the Quanta 250 FEG scanning electron microscope (SEM) was used. The microscope was working at 10 to 20 kV acceleration voltage in high-resolution mode. Chemical analysis was performed by an energy-dispersive X-ray spectrometer (EDX) integrated with the microscope. Prior to the SEM/EDX analysis, the samples were sputtered with graphite.

Magnetic measurements were performed with the Physical Properties Materials System (PPMS) provided by the Quantum Design using vibrating sample magnetometer (VSM) option. The measurements were carried out in the temperature range of 3 K to 400 K in the zero-field cooling (ZFC) and field cooling (FC) mode.

Room temperature Mössbauer spectra were registered in a transmission geometry and at constant-acceleration mode employing the POLON spectrometer. As a source of 14.4 keV gamma radiation, the 57Co source in a rhodium matrix was used. The calibration of the spectrometer was done using α-Fe foil. All the isomer shifts within this paper are related to α-Fe as a standard.

3 Results and Discussion

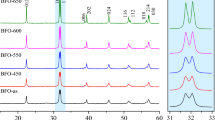
Figure 1 shows XRD patterns recorded for all of the studied BFO samples. The reference pattern for BiFeO3 marked with 01-082-1254 PDF number was depicted in the bottom panel of Figure 1 for comparison. The experimental diffractograms were fitted by means of the Rietveld refinement method, assuming the R3c space group of the rhombohedral crystal system. For BFO350 sample analysis showed that the majority phase is Bi24Fe2O39, and the BFO phase contribution is only 32.3 wt pct (Table I). Thus, this sample was not subjected to further investigations. For BFO380 the desired BFO phase dominates (94.2 wt pct), and only a small amount of parasitic Bi2(CO3)O2 was detected. In addition, the background elevation of the diffractogram in the vicinity of 2Θ = 30 deg may indicate the coexistence of a small number of amorphous regions with the crystalline BFO. In the case of the samples annealed at the Ta ≥ 400 °C, one can note sharp peaks on the diffractograms proving the formation of well-crystallized BFO phase. It is worth noting that the higher temperature (600 °C and 800 °C) promotes the formation of the Bi25FeO40 selenite phase, while for the lower temperatures (400 °C, 450 °C, and 550 °C) the only revealed parasitic phase is Bi2O3. The purest samples were obtained by annealing of xerogel at the temperature range of 400 °C to 550 °C. However, only the diffractogram of BFO500 turned out to be free of any peaks derived from side phases. The parasitic phases' contribution was significantly higher for the materials annealed at higher temperatures, i.e., 600 °C and 800 °C. The right panel of Figure 1 shows the magnification of XRD patterns in the vicinity of 2Θ = 32 deg. Thus the evolution of (104) and (110) peaks with changing annealing temperature can be observed. The obvious result is that the peaks become more broadened as the annealing temperature decreases. The average crystal grain size, <g>, and the mean level of lattice strains, <ε>, were estimated from the broadening of XRD peaks using the Williamson–Hall approach and assuming the spherical shape of crystallites. The angular position of XRD peaks belonging to the main BFO phase seems not to be affected by the annealing temperature. The detailed structural parameters, as well as the agreement indices derived from the Rietveld procedure, are listed in Table I. It can be noted that the lattice constants of all the samples are similar and close to that reported for bulk BFO: a = b = 0.5578 nm and c = 1.3868 nm.[1] It is also visible that the drop of Ta is accompanied by the significant grain size reduction and growth of the mean level of lattice strains.

Fig. 1
figure 1

XRD patterns registered for BFO samples and standard pattern for BiFeO3 (at the bottom). The right panel shows the magnification of the (104) and (110) doublet of most intensive lines. The following PDF reference patterns were used for phase analysis: BiFeO3 01-082-1254, Bi2O3 01-071-0467, Bi25FeO40 00-046-0416, Bi24Fe2O39 00-042-0201, Bi2(CO3)O2 01-084-1752

Full size image
Table I Structural Parameters of BFO Samples Derived From XRD Data Analysis
Full size table

In order to study the morphology and chemical composition of the prepared BFO powders, SEM and EDX measurements were carried out. The representative micrographs can be seen in Figure 2. The powders consist of highly agglomerated particles, and the decrease of their size with a drop of annealing temperature can be clearly observed. The middle panel of Figure 2 depicts particle size distributions, P(d), fitted by Gaussian function. In most cases, the distributions are symmetric and Gaussian-like. Only for the BFO800 sample, the P(d) reveals the coexistence of three fractions of particles with an average size of about 2.1, 4.9, and 8.1 μm, respectively. The samples BFO380, BFO400, BFO450, BFO500, and BFO550 can be classified as nanomaterials as their average particle size does not exceed 100 nm. On the other hand, the sample BFO800 can be regarded as the bulk-like one as it contains particles of the size of a few μm. Interestingly enough, the BFO500 and BFO550 samples show similar average particle sizes. The values of mean particle size, <d>, determined from SEM, and the mean grain size, <g>, from XRD studies are plotted together in Figure 3 as a function of annealing temperature. It is evident from the figure that the <g> values are compatible with <d> ones (within the error limit), suggesting that the nanoparticles are of single-crystalline nature. From the magnetic properties point of view, the samples BFO380, BFO400, and BFO450 seem to be the most interesting ones as their particle size is comparable with the spin cycloid wavelength (λ = 62 nm). The right panel of Figure 2 shows representative EDX spectra for the BFO samples. All the visible peaks were ascribed to Bi, Fe, O, and C (carbon appears due to sample preparation to SEM/EDX observations), and there is no trace of other elements. The EDX studies confirmed the chemical composition of the main BiFeO3 phase, i.e., the atomic ratio of Bi to Fe elements or molar ratio of Bi2O3 to Fe2O3 (chemical composition expressed in terms of simple oxides) was very close to 50:50. The values of average particle size <d> and the results of EDX chemical analysis are gathered in Table II.

Fig. 2
figure 2

SEM micrographs taken for (a) BFO380, (b) BFO400, (c) BFO450, (d) BFO500, (e) BFO550, (f) BFO600, (g) BFO800 samples. The middle panel shows the corresponding particle size distributions based on 300 particles measurement. The right panel depicts representative EDX spectra for each BFO sample

Full size image
Fig. 3
figure 3

The dependence of average crystal grain size derived from XRD analysis and average particle size from SEM on annealing temperature Ta. The BFO800 sample was not marked here as its particle is much bigger (1 to 2 orders of magnitude) than the other samples. The value of the cycloid period λ = 62 nm was marked by a red dashed line for comparison. The error bars denote standard deviation values

Full size image
Table II Results of SEM/EDX Studies; the Mean Value of Particle Size <d>, Theoretical and Experimental Content of Elements (Expressed in Terms of Simple Oxides)
Full size table

As the BFO500 sample was the purest one, it was subjected to TEM studies. Figure 4(a) shows the single-particle of about 90 nm size. Its magnification and Fourier transformed image are demonstrated in Figure 4(b). It can be noted that the nanoparticle has single-crystalline nature, which is in line with XRD and SEM results reported above. The single-crystalline nature of the nanoparticle is confirmed by sharp spots visible in the inset of Figure 4(b), illustrating reciprocal lattice points. Moreover, other authors reported earlier that in the case of sol–gel synthesis of BFO followed by the thermal treatment, it is possible to obtain single-crystalline nanoparticles.[17,23] One can note from Figure 4(b) the uniform interplanar spacings of dhkl = 0.3960 nm, which correspond to the (012) planes of a rhombohedral structure and the edge length of the pseudocubic unit cell. This result is in good agreement with our XRD results (dhkl = 0.3961 nm for (012) peak) as well as with the results of other authors (dhkl = 0.396 nm,[5] dhkl = 0.395 nm[24]).

Fig. 4
figure 4

TEM image of BiFeO3 nanoparticle (sample BFO500) (a), and its magnification (b). Interplanar distance for (012) family was marked, and corresponding Fourier transformation of the image was shown as an inset

Full size image

57Fe Mössbauer spectroscopy is known to be a powerful tool for studying the local magnetic properties of materials. It is well known that paramagnetic materials can show two types of Mössbauer spectra: single-line and double-line patterns. Single-line arises due to deexcitation of 57Fe nucleus from the excited state with the spin I = 3/2 to the ground state with I = 1/2. The double-line pattern appears when the electric field gradient (EFG) is present at the 57Fe site. In that case, I = 3/2 nuclear state splits into two sublevels due to electrostatic interaction between EFG and quadruple electric moment of the nucleus, and two nuclear transitions become possible. On the other hand, magnetically ordered materials show six-line Mössbauer spectra (sextets) corresponding to Zeeman splitting of 57Fe nuclear levels caused by the hyperfine magnetic field (HMF) present at the 57Fe site. Figure 5 shows Mössbauer spectra registered for our BFO samples. All of them are the superposition of a six-line pattern and doublets in the central part. Tiny doublets visible for BFO450, BFO500, BFO550, BFO600, and BFO800 are due to the occurrence of the small amounts of paramagnetic selenite phases like Bi25FeO40, which was revealed by XRD studies. For BFO600 and BFO800, two doublets (D1 and D2) were necessary to reproduce the paramagnetic-like part of the Mössbauer spectra. Most probably, it is due to the occurrence of tiny amounts of Bi2Fe4O9 (not visible for XRD) which very often forms as a parasitic phase during BiFeO3 synthesis. For the other samples annealed at lower temperatures, the doublet appears due to superparamagnetic (SPM) relaxations in small monodomain grains. SPM phenomena occur when thermally induced energy fluctuations can overcome the energy of magnetocrystalline anisotropy and change the direction of magnetization of grain from one easy axis to another.[25] If the SPM relaxation time (the average time between two flips of magnetization) is comparable with the time characteristic for Mössbauer spectroscopy measurement (about 10−8 to 10−9 seconds), then HMF averages to zero and paramagnetic-like doublet are expected in the Mössbauer spectrum. Obviously, the contribution of this component to the total spectrum increases with the drop of average particle size (lowering of annealing temperature). As it was proved by XRD studies, the sample BFO380 contains a significant amount of amorphous fraction. The amorphous BiFeO3 is manifested by a single doublet in the center of the Mössbauer spectrum having the quadrupole splitting (QS) range of 0.88 mm/s.[26] Therefore, two quadrupolar doublets were assumed during the fitting of the BFO380 spectrum: the first one for the SPM fraction and the second one for the amorphous BFO. It is worth noting that about one-third of Fe magnetic moments still remain in the blocked state, which is manifested by the coexisting sextet in the case of BFO380.

Fig. 5
figure 5

Mössbauer spectra registered for BFO samples and results of their fitting by the model assuming HMF and QS values distribution for cycloid. The right panel shows the magnification of line 6 (Color figure online)

Full size image

The characteristic feature of Zeeman sextets, both for bulk[27] and nanocrystalline[19,20] BFO samples, is their asymmetry with respect to the center of gravity. Moreover, the sextets exhibit inhomogeneous broadening of spectral lines, e.g., line 6 (from the left) is significantly broader than line 1, and line 2 is broader than line 5. According to Lebeugle et al.[28] these two effects are of different nature. The broadenings arise from cycloidal magnetic structure, i.e., from slight modulation of the hyperfine interactions energies as the magnetic moment rotates with respect to the principal axis of EFG, while the asymmetry comes from anisotropy of the magnetic hyperfine interaction at the Fe site with trigonal symmetry. In the case of our spectra, the inhomogeneous broadening and spectral asymmetry are also clearly visible in Figure 5. In order to express the spectral asymmetry quantitatively, the relative difference between line 1 and line 6 intensities (I1 and I6, respectively) of the raw Mössbauer data (assuming Lorentzian shape of lines) was calculated according to the formula:

$$ A = \frac{{I_{1} - I_{6} }}{{I_{6} }}. $$
(1)

In a similar way, the relative broadening of line 6 with respect to line 1 was calculated as follows:

$$ W = \frac{{\sigma_{6} - \sigma_{1} }}{{\sigma_{1} }}, $$
(2)

where σ1 and σ6 are the full widths at half minimum for lines 1 and 6 of the experimental sextets.

The results of the calculations are shown in Figure 6. It can be noted that the degree of inhomogeneous broadening is in the range of 40 to 50 pct for all of the samples except for BFO500, for which a significantly smaller value W = 24.5 pct was obtained. Similarly, the relative asymmetry A is about 25 to 40 pct with the unexpected minimum for BFO500; however, no clear dependence on annealing temperature (average particle size) was observed. The similar course of A and W characteristics allows one to roughly conclude that they are both due to the same reason—cycloidal magnetic structure. Interestingly enough, the asymmetry and inhomogeneous broadening of sextets persist to the lowest annealing temperature Ta = 380 °C. It can be explained by the existence of spin cycloid in the case of all the investigated samples, even the BFO400 and BFO380 for which the average particle size (38 and 21 nm) is well below the spin cycloid period λ = 62 nm. It is worth mentioning that the side phases detected for BFO380, BFO400, and BFO450 do not contain Fe. Thus, they do not contribute to the Mössbauer spectra. For the BFO550, BFO600, and BFO800, besides the Bi2O3 small amounts of Bi25FeO40 and/or Bi2Fe4O9 phases were detected. However, the later phases are paramagnetic at room temperature and exhibit quadrupolar doublet.[29] Thus, the detected parasitic phases do not affect the registered sextets, and they can not affect spectral asymmetry (A) and inhomogeneous broadening (W).

Fig. 6
figure 6

Inhomogeneous broadening (a) and the asymmetry of spectral lines (b) calculated from the raw Mössbauer data assuming the Lorentzian shape of lines

Full size image

As was mentioned above, the BFO shows the cycloidal arrangement of Fe3+ magnetic moments superimposed on G-type canted magnetic order. In the first approximation, Mössbauer spectrum measured for BFO can be fitted with two Zeeman sextets (two distinct values of HMF: B⊥ and B|| and two values of quadrupole shift QS) corresponding to two various orientations of Fe magnetic moments in the spin cycloid (i.e., parallel and perpendicular to the principal axis of EFG).[12] However, as it was proved by Palewicz[30] and Rusakov,[31] better agreement to the experimental results can be achieved by fitting the spectrum with the distribution of both HMF and QS values taking into account small modulation of the excited state energies arising when the HMF vector at the 57Fe nuclei is rotating with respect to the principal axis Vzz of the EFG tensor.

In this work, the magnetic part of the Mössbauer spectra was fitted assuming a model based on HMF and QS distributions described by Palewicz et al.[30] According to this model, HMF distribution is given by the formula:

$$ B(\theta ) = B_{||} - (B_{||} - B_{ \bot } )\,\,\sin^{2} \theta , $$
(3)

where θ is the angle between the HMF vector and principal axis Vzz of EFG tensor (hexagonal c-axis). B⊥ and B|| are the mentioned above values of HMF at the nuclei of Fe3+ ions corresponding to perpendicular and parallel orientations of HMF vector with respect to Vzz. Assuming that the quantization axis is parallel to the direction of the HMF vector and also to the Fe3+ magnetic moment direction the quadrupole shift parameter QS can be described as:

$$ QS(\theta ) = Q_{0} \cdot \frac{{3\cos^{2} \theta - 1}}{2} + Q_{c} $$
(4)

where: Q0 is the magnitude of QS, which is proportional both to EFG value and to the nuclear quadrupole moment. Qc is a constant term due to possible strong local magnetoelastic coupling.

In the first attempt, it was assumed that θ depends linearly on the distance x along the propagation direction:

$$ \theta (x) = \frac{2\pi }{\lambda }x, $$
(5)

where: λ denotes cycloid propagation period. In the second step, anharmonicity of the cycloid was included taking nonlinear θ(x) dependence:

$$ \sin \theta = sn\left( {\frac{4K(m)}{\lambda }x,m} \right), $$
(6)

where: sn(x,m) is the elliptic Jacobi function, K(m) is the complete elliptic integral of the first order and m is the anharmonicity parameter. One can note that for m = 0 the sn(x,m) function converges to sin(x) which corresponds to purely cycloidal case with θ(x) given by Eq. [5]. For m = 1, spin modulation becomes a square wave in which spins are ordered along one direction, and the system is similar to a typical antiferromagnet with domain structure.

The results of the Mössbauer spectra fitting by the model described above are shown in Figure 5 as a red curve. Fitting by the HMF and QS distributions led to satisfying compliance between the model and the experiment. It proves the presence of spin cycloid in all the samples. It is important to note that the model applied in this work allowed us to reproduce both the spectral asymmetry and the inhomogeneous broadening of lines of Mössbauer sextets. It seems that this is a consequence of combining HMF and QS angular distributions corresponding to cycloidal magnetic structure. Moreover, the asymmetrical character of line 6 of the spectra, which is a consequence of the coexistence of B⊥ and B|| is also nicely reproduced by the model (see the right panel of Figure 5).

The parameters derived from Mössbauer spectra fitting are gathered in Table III and Figure 7 as a function of annealing temperature Ta. The values of B⊥ and B|| (Figure 7(a)) slightly decrease with the decrease of annealing temperature (and thus a drop in mean particle size). Their values ~49.7 T and ~49.0 T are similar to those reported by Dzik et al.[12] It can be noted that the difference between B⊥ and B|| remains at the same level (0.5 to 0.7 T) for all the samples, except for the BFO400, for which a much bigger difference (about 2 T) was observed. This can indicate a slightly bigger tilting of oxygen octahedra and a higher canting angle in the case of BFO400. Moreover, the average HMF, <B>, monotonically decreases with the drop of mean particle size. It suggests the correlation between B⊥ and B||. In fact, it would be possible to replace both the fields by one effective <B> in the formula [3]; however, unlike <B>, B|| and B⊥ have clear physical meaning. The gradual decrease of HMF with the drop of particle size was reported earlier by Park et al.,[17] but they used a simplified two-sextet model for Mössbauer spectra fitting, claiming that there are two inequivalent iron sites.

Table III Results of Mössbauer Spectra Fitting Assuming HMF and QS Distribution for Spin Cycloid
Full size table
Fig. 7
figure 7

Annealing temperature dependence of the parameters derived from the fitting of Mössbauer spectra; (a) Bhf—hyperfine magnetic field, (b) QS—quadrupole shift, (c) P—contribution of a component to the total spectrum, and (d) m—anharmonicity parameter

Full size image

The magnitude of QS (Figure 7(b)) is almost constant for all the samples (Q0 ≈ − 0.5 mm/s) except for the value − 0.17 obtained for BFO400. These relatively high values of QS are due to strong EFG gradients induced by the asymmetric O2− surrounding of Fe ions. Figure 7(c) shows the contribution of sextet corresponding to the cycloidal spin ordering (main phase) to the total spectrum. It is clearly visible that below the annealing temperature Ta = 500 °C, the contribution of the main phase gradually decreases. This is due to the approaching of a superparamagnetic critical grain size dSPM. In particular, the contribution of SPM doublet to the total spectrum for BFO380 (<p> = 21 nm) is about 69 pct. Comparing this result with the particle size distribution for BFO380 (Figure 2(a)) allows us to estimate the critical grain size for SPM phenomena at room temperature being dSPM = 25.5 nm. However, one can note that the dSPM values derived by other experimental methods can differ as their characteristic measuring times are different. Figure 7(d) shows the variation of the anharmonicity parameter m with the change of annealing temperature. For the samples with the biggest particles BFO800, BFO600, and BFO550, the anharmonicity parameter (m = 0.4 to 0.5) is close to that reported for bulk samples.[30] Sudden reduction of m (to the value of 0.14) is visible for BFO500. It means that the spin cycloid in this sample is in a state very close to harmonic. It is important to recall that this is the only phase-pure sample that showed the lowest degree of asymmetry A and inhomogeneous broadening W (see Figure 6). The further drop of annealing temperature (a drop of particle size) causes the systematic increase of the anharmonicity parameter reaching the value m = 0.76 for BFO380. As was mentioned before, such an immense value of m corresponds to the significantly higher probability of B|| existence than for B⊥, which is connected with the gradual evolution of the spin order from cycloidal toward rectangular. It can indicate a tendency of the spin system to lose its cycloidal character in favor of purely antiferromagnetic order for grains with the size range of 20 to 30 nm. Thus MS investigations show that the cycloidal spin structure is preserved even for the samples with particle size below λ but the anharmonicity of modulation significantly increases for the specimens with the smallest particles.

The BFO samples were subjected to comprehensive magnetic measurements in the temperature range of 2 K to 400 K. Figures 8(a) and (b) present a comparison of magnetic hysteresis loops recorded for the investigated materials at 2 K and 300 K, respectively. As one can expect, the bulk-like BFO800 sample shows paramagnetic-like linear field dependence of magnetization with no trace of hysteresis, which is typical of antiferromagnetic samples. The drop of annealing temperature, accompanied by a reduction of particle size, leads to the appearance of hysteresis and significant growth of magnetization. It can be noted (Figure 8(c)) that the highest magnetization value was observed for BFO400 (d = 38 nm) and not for BFO380 (d = 21 nm). It can be explained by the worst crystallization of the BFO380 sample and significant amorphous fraction content as revealed by XRD studies. The origin of the enhancement of magnetization in nanocrystalline BFO is still a matter of debate.[18,19,23,32] Most of the researchers believe that it can be due to three factors: (1) incomplete compensation of antiferromagnetic sublattices at the surface of nanoparticles—surface-induced magnetization, (2) suppression of spiral spin structure, and (3) increase of spin canting angle introduced by a strain. Our results seem to confirm these findings. Magnetization increases significantly as the particle size approaches to spin cycloid period λ = 62 nm. However, as it was proved by MS results, the cycloidal spin structure is preserved even for the samples with average particle size well below λ suggesting surface-induced magnetization. On the other hand, the highest value of magnetization (Ms = 1.67 emu/g at 300 K) was observed for BFO400, which is the sample with the highest difference between B⊥ and B||. It can be indicative of a higher canting angle between antiferromagnetic sublattices. Thus, we claim that the magnetization enhancement is a combined effect of uncompensated surface spins and spin canting. In the latter case, however, the crucial fact is that the grain size is less than the cycloid period λ, and the spin cycloid does not average out completely the week ferromagnetic moment arising due to spin canting. Thus, the nanoparticles can exhibit a net magnetic moment which contributes to macroscopic magnetization enhancement to some extent. Figure 8(d) presents the dependence of coercivity Hc on the annealing temperature and the average particle size (in the inset) measured at different temperatures 2 K to 300 K. As one can see, the decrease of particle size causes an increase of coercivity. It can be explained by transformation from multidomain structure to single domain state of grains, and thus magnetization process evolves from domain wall motion to the mechanism of magnetization rotation. Moreover, as the particle size decreases (the increase of the number of surface ions), one can expect an enhancement of the role of surface anisotropy effects.[33] Much more tremendous growth of coercivity with lowering particle size can be observed in the temperature regime below 50 K. This tendency can be a manifestation of two phenomena (1) superparamagnetic relaxation blocking and (2) spin glass-like behavior of nanocrystalline BFO powder, as discussed in the next paragraph.

Fig. 8
figure 8

Magnetic hysteresis loops registered for BFO samples at 2 K (a) and 300 K (b). Values of magnetization (c), and coercive field Hc (d) for the samples annealed at different temperatures

Full size image

Figure 9 shows the temperature dependences of magnetization recorded in ZFC and FC modes and corresponding magnetic hysteresis loops. For the BFO800 bulk-like sample, almost flat M(T) characteristics and very small values of magnetization can be noted, which corresponds to the paramagnetic-like shape of the M(H) curve and once again confirms that cycloidal spin ordering cancels out weak ferromagnetic moment in a canted antiferromagnet. Furthermore, the sudden increase of magnetization below about 20 K is visible, but this is only a manifestation of the paramagnetic Bi25FeO40 parasitic phase. For the other samples, the noticeable irreversibility of magnetization is clearly visible, i.e., the ZFC and FC curves do not follow the same course. This type of magnetic response is typical of spin glasses or monodomain superparamagnetic particles. It is worth noting that the contribution of superparamagnetic fraction derived from MS studies was about 69 pct for BFO380 but only 20, 6.6, and 3 pct for BFO400, BF450, and BFO500, respectively. Thus, in the latter cases, the course of M(T) curves cannot only be explained by superparamagnetic phenomena, but it can be evidence of the strong interparticle interactions. One can suppose that if the nanoparticles of BFO are randomly distributed, they also have the random orientation of magnetic easy axes. Moreover, the individual particles possess net magnetic moment due to finite-size effects and spin canting, as discussed above. The drop of particle sizes results in the growth of their magnetic moment causing stronger interparticle interactions. Competition of dipolar magnetic interaction between neighboring particles with the randomness of magnetic axes orientation can lead to spin glass-like properties. In this case, however, unlike in the case of conventional spin glasses, we deal not with atomic spins but rather with the magnetic moments of individual nanoparticles.[18,19] Thus, the course of M(T) characteristics seems to be a result of the interplay between superparamagnetic relaxation effects and spin glass-like phenomenon.

Fig. 9
figure 9

Temperature dependences of magnetization registered in the magnetic field of 100 Oe in ZFC, FC modes (a), and corresponding magnetic hysteresis at 2 K and 300 K (b)

Full size image

4 Conclusions

BiFeO3 samples were successfully fabricated by sol–gel wet chemical method followed by annealing in the temperature range 350 °C to 800 °C. The influence of heat treatment temperature on the structure and magnetic properties has been discussed. It was shown that the desired phase forms above 380 °C. The purest samples were obtained by annealing of xerogel at the temperatures 400 °C to 550 °C. The sample annealed at 500 °C turned out to be free of any impurity phases. The higher temperature of heat treatment (600 °C and 800 °C) promotes the formation of the Bi25FeO40 selenite phase. As it was proved by SEM and XRD investigations lowering of temperature causes a systematic drop of the average particle size down to 21 nm for the sample annealed at 380 °C. Mössbauer spectra analysis revealed that cycloidal spin ordering does not disappear even for the samples with the average particle size well below the cycloid modulation period λ = 62 nm, but the cycloid becomes more anharmonic when the particle size drops below about 30 nm. Moreover, the gradual emergence of doublet related to superparamagnetic relaxations was observed with the drop of mean grain size, and the critical grain size for superparamagnetic relaxation at room temperature was found to be about 25.5 nm. Magnetic measurements proved that the decrease of particle size causes the appearance of the ferromagnetic hysteresis loop and significant magnetization enhancement. This effect was attributed to the increasing number of uncompensated surface spins and the net ferromagnetic moment appearing for nanoparticles with a size less than λ. Temperature characteristics of magnetization showed the coexistence of superparamagnetic relaxations phenomena with spin glass-like behavior introduced by strong interparticle interactions.