1 Introduction

In order to obtain the optimum process parameters in hot working, a precise prediction of flow stress within all stages of the process is necessary. Although empirical or semi-empirical models were developed for this purpose,[1,2,3,4,5] most of them have limitations. These models are basically appropriate for one or few special grades and usually, with any change in the process, their accuracy will decrease dramatically. To overcome this problem, physically based models have been developed and used for many cases to cover a wider range of operations and materials.[5,6,7,8,9,10,11]

One approved example of these physically based models which the current work is based on was originally developed by Siwecki and Engberg[9] and expanded further for different materials and processes. The model was successfully applied to various types of steels including micro-alloyed, CMn, and austenitic stainless steels.[12,13]

In this work, the behavior of a martensitic stainless steel during a series of hot compression tests was predicted by modifying the model and adjusting related variables. Using the model, grain growth, flow stress, recrystallization, and relaxation were simulated and the relevant variables for this alloy are found and will be used for future simulations of any hot working process. Except for the few material parameters that were adjusted for this new material and will be explained in the model chapter, rest of the parameters were kept unchanged from the previous works.[12,13] A major assumption in the modeling is that the precipitate structure does not change during the short time of deformation, i.e., the fraction and size of second phase particles will remain constant. The ratio of fraction and size is thus considered as an adjustable parameter and will be evaluated from the experiments. The experimental part of the work was carried out through a series of hot compression test in a Gleeble thermo-mechanical simulator machine and Thermo-Calc software[14] was used to generate the necessary thermodynamic data for modeling.

2 The Model

In order to develop a powerful tool for predicting and controlling microstructure evolution during a metal working process, it is necessary to have a good process model. For this purpose, a microstructure model was programed in the form of a MATLAB toolbox. This model and its calculation foundations have been described very well elsewhere.[12] Therefore, only the important aspects and adjustments that were implemented for this alloy will be summarized here.

The present model is a process simulation tool consisting of various sub-models focusing on microstructure evolution before, during, and after hot working.

In this work, material-related parameters were modified to get the best possible results. These parameters and their values will be discussed in the forthcoming sections with more details.

In the following, three key sub-models of the toolbox, i.e., flow stress, recrystallization, and grain growth will be explained together with the ratio of the volume fraction of the second phase particles over their mean radius and its important role in the model.

2.1 Flow Stress

The model can determine the flow stress based on a physical description of dislocation density evolution. A well-known dislocation density-dependent flow stress model which was proven to describe the flow stress for a wide range of crystalline materials and alloys[6,15,16] is used in this model and has the form of

$$ \sigma_{i} = \sigma_{0 } + m\alpha Gb\sqrt {\rho_{i} }. $$
(1)

In Eq. [1], σi denotes true stress and σ0 is all other strengthening contributions except the part which originates from dislocation density evolution, and it should not be mistaken with yield stress. G is the temperature-dependent shear modulus, m is the Taylor factor, α is a constant and has a value of 0.15,[17,18] b is the magnitude of Burgers vector, and ρ is dislocation density. Index (i) is for distinguishing between calculated flow stresses and respective dislocation density for deformed (σdef, ρdef) and recrystallized (σrec, ρrec) state of the material. Using the fraction of recrystallized material, Xrec, and a rule of mixture for these two states, the total flow stress can be obtained from

$$ \sigma = X_{\text{rec}} \sigma_{\text{rec}} + \left( {1 - X_{\text{rec}} } \right) \sigma_{\text{def}} . $$
(2)

It should be noted that although there are generally other contributors to σ0, they were neglected due to the high temperatures in this study and it is assumed to be mainly the strengthening effect from the second phase particles. The strengthening contribution of second phase particles depends on the alloying system, size and volume fraction of the particles, and the nature of the interaction between dislocation and particles.[19] If the precipitates are very strong, dislocations bypass them by bowing around them and leaving a dislocation loop behind which is known as Orowan bowing mechanism. When the precipitates are weak, dislocations will cut through them and pass by an unzipping method, the so-called Friedel mechanism.[20] Finally, they can also pass the precipitates by combining cross slip and climb.[21]

The strengthening effect related to Orowan bowing mechanism is given by

$$ \sigma_{0} = \frac{{0.8\,{\text{mGb}}}}{{L_{\text{prec}} }}, $$
(3)

where Lprec is particle spacing along a dislocation and is described as

$$ L_{\text{prec}} = \frac{{r_{\text{prec}} \sqrt {2\pi } }}{{\sqrt {3f_{\text{prec}} } }}. $$
(4)

In Eq. [4], fprec and rprec are volume fraction and mean size of precipitates, respectively.

Dislocation generation is described by the mean free distance of slip. Recovery of dislocations due to cross slip and climb is included into the model as well as the effect of second phase particles on the climb.

Dislocation evolution for calculating the flow stress can be derived by considering generation, recovery, and annihilation of the dislocations as given by Eq. [5].[12]

$$ \frac{{{\text{d}}\rho_{i} }}{{{\text{d}}t}} = \frac{m}{bL}\frac{{{\text{d}}\varepsilon }}{{{\text{d}}t}} - M_{\text{m}} \rho_{i}^{2} \left[ {1 - \frac{{3f_{\text{prec}} }}{{4r_{\text{prec}} \sqrt {\rho_{i} } }}} \right] - \varOmega \rho_{i} \frac{{{\text{d}}\varepsilon }}{{{\text{d}}t}}. $$
(5)

The first term on the right side of this equation describes the dislocation generation while the other two terms are attributed to recovery through climb and cross slip. ε is the plastic strain, t is time, and L is the dislocation mean free distance of slip. This distance is a function of dislocation density, geometrical slip distance due to second phase particles, and material grain size and can be expressed as

$$ \frac{1}{L} = 4 \frac{{f_{\text{prec}} }}{{r_{\text{prec}} }} + \frac{1}{{2R_{i} }} + \frac{{\sqrt {\rho_{i} } }}{{C_{\text{l}} }}, $$
(6)

where 2Ri is the grain size and Cl is a constant.

Furthermore, in Eq. [5], Mm denotes the rate parameter of recovery and can be obtained from

$$ M_{\text{m}} = \frac{{M_{0} Db^{3} G}}{T}, $$
(7)

where M0 is a material-dependent coefficient,[12] T is the temperature in Kelvin, and D is the self-diffusion coefficient which is equal to the product of vacancy concentration and vacancy migration.

In Eq. [5], Ω is a material parameter representing dynamic recovery and annihilation of dislocations. Although it is known that Ω is a temperature and strain rate-dependent parameter,[22] in this study for simplicity, it is assumed to have a constant value of 15. This value for Ω is found to give the best fit with experiment and it is in agreement with the values proposed by others at high temperatures.[22]

2.2 Grain Growth

Normal grain growth in the model is described as

$$ \frac{{{\text{d}}R_{\text{g}} }}{{{\text{d}}t}} = k_{\text{g}} M_{\text{g}} F_{\text{g}} , $$
(8)

where Rg is the grain size, t is time, kg is a constant for compensating solute drag effect on grain boundary mobility, Mg is the grain boundary mobility given as

$$ M_{\text{g}} = c_{\text{vi}} M_{\text{g0}} e^{{\frac{{Q_{{{\text{m}}0}} - Q_{\text{v}} }}{RT}}} , $$
(9)

where Mg0 is a material parameter that will be found after model calibration, cvi is vacancy concentration,[23] Qm0 is the activation energy for self-diffusion and set to be 280 kJ mol−1, and Qv is the activation energy for the creation of vacancies (vacancy generation by plastic deformation and annihilation by diffusion to vacancy sinks).[12]

Vacancy evolution in the model is described by

$$ \frac{{{\text{d}}c_{{{\text{v}},i}} }}{{{\text{d}}t}} = k_{\text{v1}} b\frac{{{\text{d}}\varepsilon }}{{{\text{d}}t}}\sqrt {\rho_{i} } - k_{\text{v2}} c_{{{\text{v}},i}} D_{\text{mv}} (c_{{{\text{v}},i}} - c_{\text{v0}} )\sqrt {\rho_{i} } , $$
(10)

where cv,i is the actual vacancy concentration while cv0 is the equilibrium concentration. kv1 and kv2 are constants, and Dmv is the vacancy migration.

Solute drag is modeled by adjusting the mobility for the climb and recrystallization/grain growth (quasi-stationary approximation for the evolution equations).[24]

In Eq. [8], Fg represents the driving force for the normal grain growth which is described by

$$ F_{\text{g}} = \frac{{\gamma_{\text{gb}} }}{{R_{\text{g}} }} - \left( {k\frac{{f_{\text{prec}} }}{{r_{\text{prec}} }}} \right), $$
(11)

where γgb denotes the grain boundary energy with a constant value of 0.8 [J m−2].[12] The second term in parentheses represents the retarding force due to Zener pinning, i.e., the mentioned fprec/rprec ratio multiplied by a constant (k) which is set to be 1.2 in this work.[25]

2.3 Recrystallization

In this toolbox, a recrystallization model by Engberg[12] which is a modified version of the Humphreys model[26,27] is used. The condition for recrystallization to start is fulfilled when the subgrain reaches a critical size, Rsub, and its misorientation reaches a critical value. The abnormal subgrain size, Rsub, is put equal to the mean free distance of slip, which is twice the size of the mean subgrain radius.

Recrystallization is assumed to start from a subgrain on a high-angle grain boundary when the driving force is larger than zero and when the subgrain misorientation is high enough to be considered as a new recrystallized grain. The misorientation is modeled through the dislocation density divided by the total number of generated dislocations (recovered dislocations are assumed to be responsible for the misorientation).

For recrystallization to happen, the driving force for it should be positive and in this model, the total driving force for recrystallization is calculated from

$$ F_{\text{recg}} = \frac{{\gamma_{\text{sub}} }}{{R_{\text{sub}} }} - \frac{{\gamma_{\text{gr}} }}{{R_{\text{rec}} }} + 0.5\,{\text{Gb}}^{2} \left( {\rho_{\text{def}} - \rho_{\text{rec}} } \right) - \left( {k\frac{{f_{\text{prec}} }}{{r_{\text{prec}} }}} \right), $$
(12)

where γsub is the boundary energy of subgrains, Rsub is the subgrain radius, γgr is boundary energy of recrystallized grains, Rrec is mean radius of the recrystallized grains, and 0.5 Gb2 is dislocation line tension.

The critical size that a subgrain has to reach to become a nucleus for recrystallization, i.e., when Frecg ≥ 0 and Rsub = Rcrit, is as follows:

$$ R_{\text{crit}} = \frac{{\gamma_{\text{gr}} - \gamma_{\text{sub}} }}{{0.5\,{\text{Gb}}^{2} \left( {\rho_{\text{def}} - \rho_{0} } \right) - \left( {k\frac{{f_{\text{prec}} }}{{r_{\text{prec}} }}} \right)}}, $$
(13)

where ρ0 is the initial dislocation density that is set to be 1012 [m−2] for the fully annealed material. The subgrain size is given by the mean free distance of slip, L.

The difference in kinetics with or without plastic deformation is taken care of by vacancy generation/annihilation that affects all diffusion-controlled mechanisms. Thus, the model for recrystallization works for the dynamic, meta-dynamic, and static cases.

In this model, dynamic recrystallization (DRX) starts when the critical conditions for recrystallization are fulfilled during the deformation.

The growth rate of the recrystallized grains in the model has a similar formulation to normal grain growth, and it is presented in Eq. [14].

$$ \frac{{{\text{d}}R_{\text{recg}} }}{{{\text{d}}t}} = k_{\text{r}} M_{\text{recg}} F_{\text{recg}}, $$
(14)

where Rrecg is the recrystallized grain size, kr is a constant, Mrecg is the recrystallized grain boundary mobility, and Frecg represents the driving force for the growth of recrystallized grains.[12]

2.4 f prec over r prec Ratio

This ratio, fprec/rprec, is an important quantity in the model and has a key role in calculating many other parameters, including the mean free path of dislocation slip, the recovery by dislocation climb, the driving force for grain and subgrain growth and recrystallization, and the critical size for the start of recrystallization. Recrystallization and normal grain growth are affected by Zener pinning due to second phase particles and the retarding force due to Zener pinning is a linear function of this ratio. The influence of second phase particles on the different microstructure development mechanisms is given by the ratio of the particle fraction and radius.

The correct ratio at each test temperature is defined by calibrating the model with the experimental data.

It should be mentioned that although this ratio generally changes with time, due to short deformation times in this study, it is assumed to remain constant. This ratio will be shown as f/r in the rest of the work.

3 Material and Experiments

The investigated material is a chromium steel produced by Sandvik Materials Technology with a nominal chemical composition of Fe-0.68C-0.7Mn-0.4Si-0.025(Max)P-0.01(Max)S-13Cr wt pct.

For uniaxial compression tests, cylindrical samples of diameter 10 mm and length of 15 mm were used in a Gleeble thermo-mechanical simulator. The samples were first heated up to near 1250 °C and soaked for 100 seconds at this temperature to reach a fully austenitic microstructure. Then they were cooled down, with the rate of 5 °C per second, to the deformation temperature and held there for 15 seconds in order to reach a uniform temperature distribution before deformation.

Since stress relaxation is proven to be a reliable technique to study both static recovery and static recrystallization,[28] the samples were held for almost 300 seconds after deformation to study the relaxation mechanisms in the material. Finally, all the samples were quenched to room temperature using compressed air. Figure 1 illustrates schematically the thermo-mechanical sequence of the tests.

Fig. 1
figure 1

Schematic diagram of the thermo-mechanical sequence in hot compression tests

Full size image

Compression tests were carried out at temperatures ranging from 900 to 1200 °C and strain rates of 0.01, 1, and 10 s−1. Test data, including instantaneous force, displacement, and temperature were used to determine the experimental true stress vs true strain, and stress relaxation curves.

All presented temperatures in this work were evaluated from the thermocouple wires attached to the middle outer surface of the samples.

To study the grain growth, samples were held in the furnace for six hours at two different temperatures, namely 1150 and 1250 °C. The latter temperature was chosen because it is the soaking temperature of the tests, and the former is added to get extra means of comparison with model results.

The microstructure of the samples was investigated by a light optical microscope (LOM) after polishing and etching them at ambient laboratory temperature using a modified Murakami solution of 10 grams K3Fe(CN)6, 10 grams potassium hydroxide, and 50 mL distilled water. The grain sizes were obtained by using linear intercept method on the LOM micrographs. In order to capture the grain growth behavior with more details, the grain size was measured in four stages during the test, i.e., beginning (time zero), after 15 minutes, after one hour, and finally after six hours. Here, time zero means when the samples heated up to the desired test temperature and after a holding time of 15 seconds to ensure an equal temperature all over the samples.

4 Results and Discussion

The LOM picture of the microstructure at the beginning of the grain growth test at 1150 °C is shown in Figure 2.

Fig. 2
figure 2

Light optical micrograph of the sample quenched from 1150 °C. Magnification is 50× and the scale bar is 200 μm

Full size image

During the grain growth tests, the mean grain sizes were determined using linear intercept method at four different stages. Table I summarizes the results of the measured grain size for all time steps and temperatures.

Table I Measured Average Grain Size at Two Test Temperatures and Four Different Time Steps
Full size table

From Table I, it is obvious that the grain growth has a higher rate at the early stages, which then drops to considerably lower values after a rather short time.

In order to obtain thermodynamic information, the Thermo-Calc software and TCFE7 database were used to calculate a phase diagram in the test temperature range according to the provided material composition. Figure 3 shows the resulting isopleth for varying carbon content and the dashed line indicates the alloy composition.

Fig. 3
figure 3

An isopleth of the investigated alloy calculated by Thermo-Calc. The dashed line shows the actual composition at desired temperature range. FCC_A1 is austenite, BCC_A2 is ferrite, and M7C3 and M23C6 are carbides while MNS is manganese sulfide

Full size image

For the different phases present within the test material, as illustrated in Figure 3, the equilibrium volume fraction at the desired temperatures is generated from the Thermo-Calc software. Table II shows the calculated volume fractions of each phase at various temperatures.

Table II Equilibrium Volume Fractions of the Particles in the Test Alloy at Different Temperatures Calculated by Thermo-Calc
Full size table

From both Figure 3 and Table II, it can be seen that the only stable particle, even at very high temperatures, is manganese sulfide (MnS) which was predominantly formed during the casting process.[29] M7C3 carbides are also present at test temperatures below 1180 °C.

4.1 Model Calibration

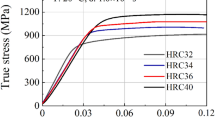
Necessary model parameters could be obtained from calibrating the model with the hot compression experiments. For this purpose, flow curves from the hot compression experiments at the strain rate of 10 s−1 were chosen and model parameters were adjusted in a way to minimize the deviation between model and experiments at all temperatures. Figure 4 shows the fitting result and Tables III and IV summarize the obtained model parameters.

Fig. 4
figure 4

Calibrating the model with experiment, calculated (dashed lines) and experimental (markers) stress–strain curves at strain rates 10 s−1 and temperatures, 900, 1000, 1100, and 1200 °C

Full size image
Table III σ0 and f/r Values in the Model for Different Temperatures
Full size table
Table IV Adjusted Model Parameters for the Current Alloy and Comparison with Other Alloys
Full size table

To calculate the flow stress, σ0 and its associated f/r ratio that gives the best fit with experiments were found from the fitting. Table III summarizes these values for each test temperature.

In Table III, σ0 increases generally with decreasing temperature, mainly because with decreasing the temperature more particles start to precipitate from the solid solution, which provides a stronger hardening effect in the material. Similarly, f/r values also increase with decreasing temperature that e.g., leads to decrease in driving forces for grain and subgrain growth and recrystallization. It should be mentioned that since just grain growth simulation was performed at 1150 and 1250 °C, only f/r ratios are shown and there are no σ0 values.

This alloy has higher contents of solute elements comparing to CMn steel, and this will lead to lower grain boundary mobility, slower subgrain, and recrystallized grain growth rate, mainly by solute drag effect. In order to imply these effects, model parameters were updated from their former values for CMn and austenitic stainless steel simulations,[12,13] and these values are compared in Table IV.

Here, Mg0 is a coefficient in calculating grain boundary mobility, which was reduced from its previous value to compensate for the lower mobility in this alloy. Cl, which is a coefficient in calculating the mean free distance of dislocation slip, was decreased to diminish L. Ω is related to the annihilation of dislocations that affects the dislocation recovery. Coefficient kr affects the growth rate of recrystallized grains, and lower kr decreases the growth rate of recrystallized grains. Increasing M0, which comes in the rate parameter calculations for recovery, i.e., Mm in Eq. [5], will reduce the dislocation evolution with time.

4.2 Modeling

Having the values in Tables III and IV, the stress–strain curves were simulated with the model and the outcome for different temperatures and strain rates of 0.01 and 1 s−1 are presented in Figure 5.

Fig. 5
figure 5

Calculated (dashed lines) stress–strain curves and experimental data (markers) at various strain rates and temperatures

Full size image

At most temperatures and strain rates, the model predicts stress values satisfactorily and the calculated curves follow the experimental points.

In Figure 5, there are fluctuations in the modeled stress–strain curves as a visual sign for prediction of DRX by model. Modeled curves, after initiating DRX, are oscillating around a constant value rather than the typical form of a single peak followed by steady-state stress that can be observed in the experimental curves. This oscillation in modeled curves originates from the calculations for the total flow stress. After initiation of DRX, model divides the material into two parts of deforming and recrystallized, which creates the oscillation in the stress–strain graphs.

In some experimental curves (markers) of Figures 4 and 5 with high strain rate or low temperatures, a drop in flow stress magnitude can be seen especially after strains larger than 0.4. This decrease in flow stress might resemble the DRX phenomenon but knowing that high temperatures and low strain rates are promoting DRX, it could be most probably explained as the effect of adiabatic heating in specimens or a reduction in the strain rate during the last steps of the experiment. In certain cases, they might happen simultaneously and intensify each other’s effect.

In other cases, the friction effect in the tests might balance adiabatic heating or reduced strain rate and consequently, no drop is visible in those curves.

In order to validate further the model, hold tests are performed and the result at two temperatures and strain rate of 1 s−1 is shown in Figure 6.

Fig. 6
figure 6

Computed (dashed lines) and measured (markers) flow stress at 1000 and 1100 °C from the hold tests

Full size image

The agreement between model and experiment is very good in holding tests despite the difference in holding time between deformations that was one second at 1000 °C and 15 seconds at 1100 °C.

Grain growth is another phenomenon that was modeled for two different soaking temperatures. Figure 7 demonstrates the grain growth simulation results for the material at 1150 and 1250 °C.

Fig. 7
figure 7

Modeled grain growth at two different soaking temperatures. Dashed lines show the simulation while asterisks and circles are measured values (Table I) at 1150 and 1250 °C, respectively

Full size image

It can be seen that the model can predict the grain growth behavior at both soak temperatures very well, and the average mismatch between the model and experiment (Table I) was less than 5 pct in both cases.

Figure 8 shows the stress relaxation results at different strain rates and temperatures.

Fig. 8
figure 8

Modeled relaxation at different temperatures after deformation with strain rates of 10 s−1 (a) and 1 s−1 (b). Dashed lines are modeled and markers are experimental measurements

Full size image

In Figure 8, there are some deviations between model and experiment at low temperatures. One explanation for this might be using a constant value for Ω in this work, while Bergström[22] found that Ω should change with temperature and strain rate.

In general, when the temperature difference in the experiments increases the fit between the model and experiment at all temperatures might not be equally good. The main reason for this is considering temperature-dependent parameters like Ω and Mg0 as constants in the model. Despite these approximations, the model works well. However, resolving this issue might enable the model to give equally good fits on more extended temperature ranges.

To investigate the recovery and recrystallization in more detail, two samples that might resemble the typical form of these phenomena are magnified in Figure 9 from the presented curves of above.

Fig. 9
figure 9

Simulated and experimental deformation and relaxation at 1200 °C and strain rate 10 s−1 during the deformation (a) and during relaxation (b) and 0.01 s−1 (c, d) showing dynamic and static recrystallized fraction (solid lines) and true stress, dashed lines (modeled), and markers (experimentally measured), values against true strain and time after deformation. Note the negligible amount of DRX in (a) and very low amount of recrystallized fraction in (d) calculated by the model (solid lines)

Full size image

In stress relaxation tests, the difference in slope of the curves can suggest whether static recovery or static recrystallization is the dominant softening mechanism, although judging only based on these graphs might be misleading. That being said, it seems that at higher strain rates no DRX happens, see Figure 9(a), and the stored energy in the material can be relaxed by meta-dynamic or static recrystallization as the noticeable change in the slope of the curves favor in Figure 9(b). On the other hand, at lowest strain rate, static recovery is more dominant as the invariable slope of the curves suggests in Figure 9(d). At this low strain rate, material already passed cycles of dynamic recrystallization as it can be clearly seen in Figure 9(c) and the driving force for a static recrystallization after deformation might be low. The calculated recrystallized fractions are also in agreement with the observed flow stress curves during relaxation.

5 Conclusions

A physically based model is employed to predict the microstructure evolution in a 13 pct chromium steel during and after hot compression tests at temperatures ranging from 900 up to 1200 °C and strain rates of 0.01, 1, and 10 s−1.

This model is based on the coupled set of equations for dislocation density evolution as a key variable that governs the stress state during deformation, recovery, and recrystallization.

The model considers and simulates work hardening, recovery, recrystallization, and grain growth during and after deformation. The advantage of this model is with only one or few experiments, the material-dependent parameters of the model can be calibrated and used for any new alloy and deformation condition.

The disadvantage of this model is considering some temperature-dependent material parameters such as Ω for dynamic recovery of dislocations and M0 for the dislocation climb as constants, which sometimes leads to not equally good fits at all temperatures.

The overall agreement between the results from the model and experiments was good, and the deviation between the model and experiment for simulating the grain growth for this alloy is less than 5 pct.

The deviation between the predicted stress by the model and measured values from the experiments might be due to some simplifications in the simulation, such as assuming a constant value for Ω at different temperatures and strain rates.

From relaxation tests, it is evident that static recovery is the dominant softening mechanism for samples deformed at low strain rates while static recrystallization is more dominant for samples deformed at high strain rates as the slope of the curves during the time after deformation suggests.