Morphological Stability of δ-Ferrite/γ Interphase Boundary in Carbon Steel

Abstract

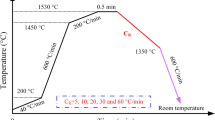
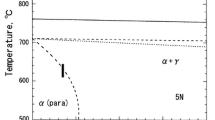
The morphological changes of the δ-ferrite/γ interphase boundary have been observed in situ with a high-temperature confocal scanning laser microscope (HTCSLM) during δ/γ transformations (δ → γ and γ → δ) of Fe-0.06 wt pct C-0.6 wt pct Mn alloy, and a kinetic equation of morphological stability of δ-ferrite/γ interphase boundary has been established. Thereafter, the criterion expression for morphological stability of δ-ferrite/γ interphase boundary was established and discussed, and the critical migration speeds of δ-ferrite/γ interphase boundaries are calculated in Fe-C, Fe-Ni, and Fe-Cr alloys. The results indicate that the δ-ferrite/γ interphase boundary is very stable and nearly remains absolute planar all the time during γ → δ transformation in Fe-C alloy. The δ-ferrite/γ interphase boundary remains basically planar during δ → γ transformation when the migration speed is lower than 0.88 μm/s, and the interphase boundary will be unstable and exhibit a finger-like morphology when the migration speed is higher than 0.88 μm/s. The morphological stability of δ-ferrite/γ interphase boundary is primarily controlled by the interface energy and the solute concentration gradient at the front of the boundary. During the constant temperature phase transformation, an opposite temperature gradient on both sides of δ-ferrite/γ interphase boundary weakens the steady effect of the temperature gradient on the boundary. The theoretical analysis of the morphological stability of the δ-ferrite/γ interphase boundary is coincident with the observed experimental results utilizing the HTCSLM. There is a good agreement between the theoretical calculation of the critical moving velocities of δ-ferrite/γ interphase boundaries and the experimental results.

Appendix

The distributions of the solute concentration and temperature on both sides of the δ/γ IB at a moment during δ → γ transformation of the Fe-C alloy are shown in Figure 4.

The diffusion process of the solute and temperature on both sides of the δ/γ IB can be governed by the Laplace equation as follows:

$$ \xi \left(\frac{{\partial^{2} }}{{\partial X^{2} }} + \frac{{\partial^{2} }}{{\partial Y^{2} }} + \frac{{\partial^{2} }}{{\partial Z^{2} }}\right)\nabla = \frac{\partial \nabla }{\partial t}, $$

(A1)

where $\xi$ is the thermal diffusion coefficient or the diffusion coefficient of the solute atom, t is the temperature.

When the perturbations with amplitude $\varepsilon$ emerge at the δ/γ IB, the shape of the interface is shown in Figure 5. The perturbations are simplified as a sine wave and the interfacial equation is: $x = \varepsilon \sin (\omega y)$,where $\omega$ is the frequency of perturbations.

Assuming the solute and heat transfer during the phase transformation is one-dimensional. Considering the existence of local equilibrium, after the phase transformation enters into a stable state, the distributions of the solute concentration and temperature on both sides of the interface satisfy the following four equations:

$$ \frac{{\partial^{2} T_{\gamma } }}{{\partial x^{2} }} - \frac{v}{{\alpha_{\gamma } }}\frac{{\partial T_{\gamma } }}{\partial x} = 0, $$

(A2)

$$ \frac{{\partial^{2} T_{\delta } }}{{\partial x^{2} }} + \frac{v}{{\alpha_{\delta } }}\frac{{\partial T_{\delta } }}{\partial x} = 0, $$

(A3)

$$ \frac{{\partial^{2} C_{\gamma } }}{{\partial x^{2} }} - \frac{v}{{D_{\gamma } }}\frac{{\partial C_{\gamma } }}{\partial x} = 0, $$

(A4)

$$ \frac{{\partial^{2} C_{\delta } }}{{\partial x^{2} }} + \frac{v}{{D_{\delta } }}\frac{{\partial C_{\delta } }}{\partial x} = 0, $$

(A5)

where $T_{\gamma }$ and $T_{\delta }$ are the temperatures within γ-phase and δ-phase, respectively; $\alpha_{\gamma }$, $\alpha_{\delta }$ are the thermal diffusion coefficients of γ-phase and δ-phase, respectively;$C_{\gamma }$ and $C_{\delta }$are the solute concentrations within γ-phase and δ-phase, respectively; $D_{\gamma }$ and $D_{\delta }$ are the solute diffusion coefficients of within γ-phase and δ-phase, respectively; $v$ is the migration speed of the interface.

The boundary conditions of Eq. [A2] are given as

$$ {\text{when}}\quad x = 0,\quad T_{\gamma } = T_{0} + L/C_{p}^{\gamma } , $$

$$ {\text{when}}\quad x = - \infty ,\quad T_{\gamma } = T_{0} , $$

where L is the latent heat of phase transformation, $C_{p}^{\gamma }$ is the specific heat of γ-phase, and T ₀ is the holding temperature.

The boundary conditions of Eq. [A3] are given as

$$ {\text{when}}\quad x = 0,\quad T_{\delta } = T_{0} + L/C_{p}^{\delta } , $$

$$ {\text{when}}\quad x = + \infty ,\quad T_{\gamma } = T_{0} , $$

where $C_{p}^{\delta }$ is the specific heat of δ-phase.

The boundary conditions of Eq. [A4] are given as

$$ {\text{when}}\quad x = 0,\quad C_{\gamma } = C_{0} , $$

$$ {\text{when}}\quad x = - \infty ,\quad C_{\gamma } = k_{S} C_{0} , $$

where C ₀ is the solute concentration of the alloy, $k_{S}$ is the partition coefficient of the solute, $k_{S} = C_{\gamma }^{0} /C_{\delta }^{0}$, $C_{\gamma }^{0}$ and $C_{\delta }^{0}$ are the solute concentrations within γ-phase and δ-phase when the δ/γ IB is planar,respectively.

The boundary conditions of Eq. [A5] are given as

$$ {\text{when}}\quad x = 0,\quad C_{\delta } = C_{0} /k_{S} , $$

$$ {\text{when}}\quad x = + \infty ,\quad C_{\delta } = C_{0} . $$

By solving Eqs. [A2], [A3], [A4], and [A5], the following equations can be obtained:

$$ T_{\gamma } = T_{0} + \frac{L}{{C_{p}^{\gamma } }}\exp \left( {\frac{v}{{\alpha_{\gamma } }}x} \right), $$

(A6)

$$ T_{\delta } = T_{0} + \frac{L}{{C_{p}^{\gamma } }}\exp \left( { - \frac{v}{{\alpha_{\delta } }}x} \right), $$

(A7)

$$ C_{\gamma } = C_{0} \left[ {k_{S} + (1 - k_{S} )\exp \left( {\frac{v}{{D_{\gamma } }}x} \right)} \right], $$

(A8)

$$ C_{\delta } = C_{0} \left[ {1 + \left( {\frac{1}{{k_{S} }} - 1} \right)\exp \left( { - \frac{v}{{D_{S} }}x} \right)} \right]. $$

(A9)

Because the solute enrichment in front of the interface and the interface curvature, the actual transformation temperature $T_{i}$ becomes

$$ T_{i} = T_{\gamma \to \delta } + m_{\gamma } C_{i} - K\varGamma , $$

(A10)

where $T_{\gamma \to \delta }$ is the γ → δ transformation temperature of pure solvent, $m_{\gamma }$ is the slope of the solubility curve of γ-phase in δ+γ phase region, $C_{i}$ is the solute concentration of γ-phase on the interface, $\varGamma$ is the constant of interface energy, $\varGamma = \sigma /\Delta S$, $\Delta S$ is the transformation entropy, $K$is the interface curvature, it can be obtained from Eq. [A11]:

$$ K = \left| {\frac{x\prime\prime }{{(1 + x^{\prime 2} )^{3/2} }}} \right| = \left| {\frac{{ - \varepsilon \omega^{2} \sin (\omega y)}}{{(1 + \varepsilon^{2} \omega^{2} \cos (\omega y))_{3/2} }}} \right| \approx \varepsilon \omega^{2} \sin (\omega y), $$

(A11)

where $x^{\prime}$and $x^{\prime\prime}$ are first derivative and second derivative$x$with respect to $y$.

According to the method presented by Mullins and Sekerka,[9] after the disturbance of the interface emerges, the interface temperature and solute concentration can be supposed as follows:

$$ T_{i} = T_{0}^{0} + a\varepsilon \sin (\omega y), $$

(A12)

$$ C_{i} = C_{0}^{0} + b\varepsilon \sin (\omega y), $$

(A13)

where $T_{0}^{0}$ and $C_{0}^{0}$ are the temperature and solute concentrations under the flat interface, respectively, a and b are the undetermined coefficients.

After the interface perturbations emerge, the temperature and the solute concentrations on both sides of the interface are changed as a function of x and y. Amending the temperature and solute concentration distribution equation of the flat interface, we have

$$ T_{\gamma } = T_{0} + \frac{L}{{C_{p}^{\gamma } }}\exp \left( {\frac{v}{{\alpha_{\gamma } }}x} \right) + T^{\prime}_{\gamma } \sin (\omega y), $$

(A14)

$$ T_{\delta } = T_{0} + \frac{L}{{C_{p}^{\delta } }}\exp \left( { - \frac{v}{{\alpha_{\delta } }}x} \right) + T^{\prime}_{\delta } \sin (\omega y), $$

(A15)

$$ C_{\gamma } = C_{0} \left[ {k_{S} + (1 - k_{S} )\exp \left( {\frac{v}{{D_{\gamma } }}x} \right)} \right] + C^{\prime}_{\gamma } \sin (\omega y), $$

(A16)

$$ C_{\delta } = C_{0} \left[ {1 + \left( {\frac{1}{{k_{S} }} - 1} \right)\exp \left( { - \frac{v}{{D_{S} }}x} \right)} \right] + C^{\prime}_{\delta } \sin (\omega y), $$

(A17)

where $T^{\prime}_{\gamma }$, $T^{\prime}_{\delta }$, $C^{\prime}_{\gamma }$, and $C^{\prime}_{\delta }$ are the change amplitudes of the temperature and solute concentration due to the disturbance, respectively.

For the two-dimensional transfer near the interface, when the transformation reaches stable state, the temperature and solute concentrations on both sides of the interface satisfy the following equations:

$$ \frac{{\partial^{2} T_{\gamma } }}{{\partial y^{2} }} + \frac{{\partial^{2} T_{\gamma } }}{{\partial x^{2} }} - \frac{v}{{\alpha_{\gamma } }}\frac{{\partial T_{\gamma } }}{\partial x} = 0, $$

(A18)

$$ \frac{{\partial^{2} T_{\delta } }}{{\partial y^{2} }} + \frac{{\partial^{2} T_{\delta } }}{{\partial x^{2} }} + \frac{v}{{\alpha_{\delta } }}\frac{{\partial T_{\delta } }}{\partial x} = 0, $$

(A19)

$$ \frac{{\partial^{2} C_{\gamma } }}{{\partial y^{2} }} + \frac{{\partial^{2} C_{\gamma } }}{{\partial x^{2} }} - \frac{v}{{D_{\gamma } }}\frac{{\partial C_{\gamma } }}{\partial x} = 0, $$

(A20)

$$ \frac{{\partial^{2} C_{\delta } }}{{\partial y^{2} }} + \frac{{\partial^{2} C_{\delta } }}{{\partial x^{2} }} + \frac{v}{{D_{\delta } }}\frac{{\partial C_{\delta } }}{\partial x} = 0. $$

(A21)

By introducing Eqs. [A14], [A15], [A16], and [A17] into Eqs. [A18], [A19], [A20], and [A21], respectively, we have

$$ \frac{{\partial^{2} T^{\prime}_{\gamma } }}{{\partial x^{2} }} - \frac{v}{{\alpha_{\gamma } }}\frac{{\partial T^{\prime}_{\gamma } }}{\partial x} - \omega^{2} T^{\prime}_{\gamma } = 0, $$

(A22)

$$ \frac{{\partial^{2} T^{\prime}_{\delta } }}{{\partial x^{2} }} + \frac{v}{{\alpha_{\delta } }}\frac{{\partial T^{\prime}_{\delta } }}{\partial x} - \omega^{2} T^{\prime}_{\delta } = 0, $$

(A23)

$$ \frac{{\partial^{2} C^{\prime}_{\gamma } }}{{\partial x^{2} }} - \frac{v}{{D_{\gamma } }}\frac{{\partial C^{\prime}_{\gamma } }}{\partial x} - \omega^{2} C^{\prime}_{\gamma } = 0, $$

(A24)

$$ \frac{{\partial^{2} C^{\prime}_{\delta } }}{{\partial x^{2} }} + \frac{v}{{D_{\delta } }}\frac{{\partial C^{\prime}_{\delta } }}{\partial x} - \omega^{2} C^{\prime}_{\delta } = 0. $$

(A25)

The general solution for Eq. [A23] can be obtained:

$$ T^{\prime}_{\delta } = J\exp (qx), $$

(A26)

where J and q are the constant and characteristic value, respectively.

The characteristic equation of the Eq. [A23] is $q^{2} + \frac{v}{{\alpha_{\delta } }}q - \omega^{2} = 0$, then $q = \frac{{ - v/\alpha_{\delta } \pm \sqrt {(v/\alpha_{\delta } )^{2} + 4\omega^{2} } }}{2}$. Taking into account the Eq. [A26] to meet the actual situation of the transformation process, $q = - [(v/(2\alpha_{\delta } ) + \sqrt {(v/(2\alpha_{\delta } ))^{2} + \omega^{2} } )] = - \omega_{\delta }^{ * }$, then Eq. [A26] becomes:

$$ T^{\prime}_{\delta } = J\exp ( - \omega_{\delta }^{ * } x). $$

(A27)

The boundary conditions of Eq. [A27] are given as

$$ {\text{when}}\quad x = \pm \infty ,\quad T^{\prime}_{\delta } = 0.\;{\text{But}}\,J\,{\text{cannot}}\;{\text{be}}\;{\text{determined,}} $$

$$ {\text{when}}\quad x = \varepsilon \sin (\omega y),\quad T_{\delta } = T_{i} . $$

The following form can be obtained from Eqs. [A12] and [A15]:

$$ T_{0}^{0} + a\varepsilon \sin (\omega y) = T_{0} + \frac{L}{{C_{p}^{\delta } }}\exp \left( { - \frac{v}{{\alpha_{\delta } }}\varepsilon \sin (\omega y)} \right) + T_{\delta }^{{\prime }} \sin (\omega y). $$

Because $v\varepsilon \sin (\omega y)/\alpha_{\delta }$ is very small, $\exp ( - v\varepsilon \sin (\omega y)/\alpha_{\delta } ) \approx 1 - v\varepsilon \sin (\omega y)/\alpha_{\delta }$, then

$$ \begin{aligned} T_{0}^{0} + a\varepsilon \sin (\omega y) \approx T_{0} + \frac{L}{{C_{p}^{\delta } }}\left[ {1 - \frac{v}{{\alpha_{\delta } }}\varepsilon \sin (\omega y)} \right] + T^{\prime}_{\delta } \sin (\omega y) \\ = T_{0} + \frac{L}{{C_{p}^{\delta } }} - \frac{L}{{C_{p}^{\delta } }}\frac{v}{{\alpha_{\delta } }}\varepsilon \sin (\omega y) + T^{\prime}_{\delta } \sin (\omega y), \\ \end{aligned} $$

$$ {\text{Namely}},{\text{ when}}\;x = \varepsilon \sin (\omega y),\quad T^{\prime}_{\delta } \approx \varepsilon (a - G_{\delta }^{0} ), $$

(A28)

where $G_{\delta }^{0}$ is the temperature gradient of δ-phase on the solid–liquid interface under the flat interface, $G_{\delta }^{0} = - \frac{L}{{C_{p}^{\delta } }}\frac{v}{{\alpha_{\delta } }}$.

Introducing Eq. [A28] into Eq. [A27], it can be obtained that $\varepsilon (a - G_{\delta }^{0} ) = J\exp ( - \omega_{\delta }^{ * } \varepsilon \sin (\omega y))$.

Eq. [A29] can be determined by introducing $J = \frac{{\varepsilon (a - G_{\delta }^{0} )}}{{\exp (\omega_{\delta }^{ * } \varepsilon \sin (\omega y))}} \approx \frac{{\varepsilon (a - G_{\delta }^{0} )}}{{1 - \omega_{\delta }^{ * } \varepsilon \sin (\omega y)}}$ into Eq. [A27]:

$$ T^{\prime}_{\delta } = \frac{{\varepsilon (a - G_{\delta }^{0} )}}{{1 - \omega_{\delta }^{ * } \varepsilon \sin (\omega y)}}\exp ( - \omega_{\delta }^{ * } x). $$

(A29)

Introducing Eq. [A29] into Eq. [A15], we have

$$ T_{\delta } = T_{0} + \frac{L}{{C_{p}^{\delta } }}\exp ( - \frac{v}{{\alpha_{\delta } }}x) + \frac{{\varepsilon (a - G_{\delta }^{0} )}}{{1 - \omega_{\delta }^{ * } \varepsilon \sin (\omega y)}}\sin (\omega y)\exp ( - \omega_{\delta }^{ * } x). $$

(A30)

By the same procedure, we have

$$ T_{\gamma } = T_{0} + \frac{L}{{C_{p}^{\gamma } }}\exp (\frac{v}{{\alpha_{\gamma } }}x) + \frac{{\varepsilon (a - G_{\gamma }^{0} )}}{{1 + \omega_{\gamma }^{ * } \varepsilon \sin (\omega y)}}\sin (\omega y)\exp (\omega_{\gamma }^{ * } x), $$

(A31)

where $G_{\gamma }^{0}$ is the temperature gradient of γ-phase on the solid–liquid interface under the flat interface, $G_{\gamma }^{0} = \frac{L}{{C_{p}^{\gamma } }}\frac{v}{{\alpha_{\gamma } }}$, $\omega_{\gamma }^{ * } = (v/(2\alpha_{\gamma } ) + \sqrt {(v/(2\alpha_{\gamma } ))^{2} + \omega^{2} } )$.

$$ C_{\gamma } = C_{0} \left[ {k_{S} + (1 - k_{S} )\exp \left( {\frac{v}{{D_{\gamma } }}x} \right)} \right] + \frac{{\varepsilon (b - G_{C\gamma }^{0} )}}{{1 + \omega_{c\gamma }^{ * } \varepsilon \sin (\omega y)}}\sin (\omega y)\exp (\omega_{C\gamma }^{ * } x), $$

(A32)

where $G_{C\gamma }^{0}$ is the concentration gradient of γ- phase on the solid–liquid interface under the flat interface, $G_{C\gamma }^{0} = C_{0} (1 - k_{S} )\frac{v}{{\alpha_{\gamma } }}$, $\omega_{C\gamma }^{ * } = (v/(2D_{\gamma } ) + \sqrt {(v/(2D_{\gamma } ))^{2} + \omega^{2} } )$.

$$ C_{\delta } = C_{0} \left[ {1 + \left( {\frac{1}{{k_{S} }} - 1} \right)\exp \left( { - \frac{v}{{D_{\delta } }}x} \right)} \right] + \frac{{\varepsilon (b - G_{C\delta }^{0} )}}{{1 - \omega_{c\delta }^{ * } \varepsilon \sin (\omega y)}}\sin (\omega y)\exp ( - \omega_{C\delta }^{ * } x), $$

(A33)

where $G_{C\delta }^{0}$ is the concentration gradient of δ-phase on the solid–liquid interface under the flat interface, $G_{C\delta }^{0} = - C_{0} (\frac{1}{{k_{S} }} - 1)\frac{v}{{D_{\delta } }}$, $\omega_{C\delta }^{ * } = (v/(2D_{\delta } ) + \sqrt {(v/(2D_{\delta } ))^{2} + \omega^{2} } )$.

By introducing Eqs. [A12] and [A13] into Eq. [A10], the equation is obtained as follows:

$$ a = m_{\gamma } b - \omega^{2} \varGamma . $$

(A34)

The migration speeds of the interface according to heat quantity transfer and mass transfer are equal, thus Eq. [A35] can be determined:

$$ \lambda_{\delta } (\frac{{\partial T_{\delta } }}{\partial x})_{i} - \lambda_{\gamma } \left( {\frac{{\partial T_{\gamma } }}{\partial x}} \right)_{i} = - \frac{L}{{C_{i} (1 - k_{S} )}}\left[ {D_{\gamma } \left( {\frac{{\partial C_{\gamma } }}{\partial x}} \right)_{i} - D_{\delta } \left( {\frac{{\partial C_{\delta } }}{\partial x}} \right)_{i} } \right]. $$

(A35)

By introducing Eqs. [A30], [A31], [A32], and [A33] into Eq. [A35], we have

$$ \lambda _{\delta } G_{\delta }^{0} \left[ {1 - \frac{v}{{\alpha _{\delta } }}\varepsilon \sin (\omega y)} \right] - \lambda _{\delta } \omega _{\delta }^{*} (a - G_{\delta }^{0} )\varepsilon \sin (\omega y) - \lambda _{\gamma } G_{\gamma }^{0} {\text{ }}\left( {1 + \frac{v}{{\alpha _{\gamma } }}\varepsilon \sin (\omega y)} \right) - \lambda _{\gamma } \omega _{\gamma }^{*} (a - G_{\gamma }^{0} )\varepsilon \sin (\omega y){\kern 1pt} = - {\text{ }}\frac{L}{{(C_{0}^{0} + b\varepsilon \sin (\omega y))(1 - k_{S} )}}\left\{ {D_{\gamma } G_{{C\gamma }}^{0} \left( {1 + \frac{v}{{D_{\gamma } }}\varepsilon \sin (\omega y)} \right) + D_{\gamma } \omega _{{C\gamma }}^{*} (b - G_{{C\gamma }}^{0} )\varepsilon \sin (\omega y){\kern 1pt} - D_{\delta } G_{{C\delta }}^{0} \left( {1 - \frac{v}{{D_{\delta } }}\varepsilon \sin (\omega y)} \right) + D_{\delta } \omega _{{C\delta }}^{*} (b - G_{{C\delta }}^{0} )\varepsilon \sin (\omega y)} \right\}.$$

After the arrangement,

$$ b = \frac{\begin{aligned} \frac{L}{{(1 - k_{S} )C_{0}^{0} }}[ - D_{\gamma } \omega_{C\gamma }^{ * } G_{C\gamma }^{0} - D_{\delta } \omega_{C\delta }^{ * } G_{C\delta }^{0} + v(G_{C\gamma }^{0} + G_{C\delta }^{0} )] \hfill \\ - \lambda_{\delta } G_{\delta }^{0} \frac{v}{{\alpha_{\delta } }} - \lambda_{\gamma } G_{\gamma }^{0} \frac{v}{{\alpha_{\gamma } }} + (\lambda_{\delta } \omega_{\delta }^{ * } + \lambda_{\gamma } \omega_{\gamma }^{ * } )\omega^{2} \varGamma + \lambda_{\gamma } \omega_{\gamma }^{ * } G_{\gamma }^{0} + C_{0}^{0} \lambda_{\delta } \omega_{\delta }^{ * } G_{\delta }^{0} \hfill \\ \end{aligned} }{{ - \frac{L}{{(1 - k_{S} )C_{0}^{0} }}(D_{\gamma } \omega_{C\gamma }^{ * } + D_{\delta } \omega_{C\delta }^{ * } ) - \lambda_{\delta } G_{\delta }^{0} /C_{0}^{0} + \lambda_{\gamma } G_{\gamma }^{0} /C_{0}^{0} + \lambda_{\delta } \omega_{\delta }^{ * } m_{\gamma } + \lambda_{\gamma } \omega_{\gamma }^{ * } m_{\gamma } }}. $$

The migration speed of the interface after the interface perturbation emerges can be expressed as follows:

$$ v_{0} + \frac{d\varepsilon }{dt}\sin (\omega y) = - \frac{1}{L}\left[ {\lambda_{\delta } \left( {\frac{{\partial T_{\delta } }}{\partial x}} \right)_{i} - \lambda_{\gamma } \left( {\frac{{\partial T_{\gamma } }}{\partial x}} \right)_{i} } \right]. $$

(A36)

Introducing $(\partial T_{\alpha } /\partial x)_{i}$ and $(\partial T_{\gamma } /\partial x)_{i}$ into Eq. [A36],

$$ - \frac{L}{\varepsilon }\frac{d\varepsilon }{dt}L = - \lambda_{\delta } G_{\delta }^{0} \frac{v}{{\alpha_{\delta } }} - \lambda_{\gamma } G_{\gamma }^{0} \frac{v}{{\alpha_{\gamma } }} + \lambda_{\delta } \omega_{\delta }^{ * } \omega^{2} \varGamma + \lambda_{\gamma } \omega_{\gamma }^{ * } \omega^{2} \varGamma + \lambda_{\delta } \omega_{\delta }^{ * } G_{\delta }^{0} + \lambda_{\gamma } \omega_{\gamma }^{ * } G_{\gamma }^{0} - (\lambda_{\gamma } \omega_{\gamma }^{ * } m_{\gamma } + \lambda_{\delta } \omega_{\delta }^{ * } m_{\gamma } )b. $$

By introducing b and arranging, the equation is obtained as follows:

$$ \frac{L}{\varepsilon }\frac{d\varepsilon }{dt} = \frac{{A\left\{ - \omega^{2} \varGamma - \frac{{\lambda_{\delta } G_{\delta }^{0} (\omega_{\delta }^{ * } - \frac{v}{{\alpha_{\delta } }}) + \lambda_{\gamma } G_{\gamma }^{0} (\omega_{\gamma }^{ * } - \frac{v}{{\alpha_{\gamma } }})}}{{(\lambda_{\delta } \omega_{\delta }^{ * } + \lambda_{\gamma } \omega_{\gamma }^{ * } )}} + \frac{{m_{\gamma } [D_{\gamma } G_{C\gamma }^{0} (\omega_{C\gamma }^{ * } - \frac{v}{{D_{\gamma } }}) + D_{\delta } G_{C\delta }^{0} (\omega_{C\delta }^{ * } - \frac{v}{{D_{\delta } }})]}}{{(D_{\gamma } \omega_{C\gamma }^{ * } + D_{\delta } \omega_{C\delta }^{ * } ) + v(1 - k_{S} )}}\right\} }}{{m_{\gamma } C_{0}^{0} (\lambda_{\delta } \omega_{\delta }^{ * } + \lambda_{\gamma } \omega_{\gamma }^{ * } ) + (\lambda_{\gamma } G_{\gamma }^{0} - \lambda_{\delta } G_{\delta }^{0} )\left[1 - \frac{{vC_{0} (D_{\gamma } \omega_{C\gamma }^{ * } + D_{\delta } \omega_{C\delta }^{ * } )}}{{(D_{\gamma } G_{C\gamma }^{0} - D_{\delta } G_{C\delta }^{0} )}}\right]}}, $$

(A37)

where $A = (\lambda_{\delta } \omega_{\delta }^{ * } + \lambda_{\gamma } \omega_{\gamma }^{ * } )[(\lambda_{\gamma } G_{\gamma }^{0} - \lambda_{\delta } G_{\delta }^{0} ) - L(D_{\gamma } \omega_{C\gamma }^{ * } + D_{\delta } \omega_{C\delta }^{ * } )/(1 - k_{S} )]$.