1 Introduction

In recent years, cyber-physical systems, which consist of physical and computational components, have drawn considerable attention[1]. The fact that computation, communication and control (3C) are now highly integrated in the concept of cyber-physical system (CPS). A typical CPS has the capabilities of sensing, controlling and communication, which can reflect the interaction and coordination between the physical and computational elements. Therefore, the design of control strategy in CPS is of crucial importance for stabilization and efficiency of system dynamics. CPS can be found in aerospace, automotive, transportation, infrastructure management and environmental monitoring [2, 3]. An important application of CPS is the flight control system[4]. And the efficacy of the control law will decide whether the CPS can bring its predominance into play or not[5].

Due to the unmodeled dynamics and external disturbances, the flight control system is a typical uncertain nonlinear system. Recently, adaptive backstepping design method has become an important method for the research of dealing with uncertainties[6–8]. A drawback of the conventional backstepping method may cause the problem of complexity resulting from the repeated differentiations[9]. Dynamic surface control (DSC) technique could solve the complexity problem in backstepping design method by introducing a first-order filter of the synthetic input at each step of the traditional backstepping design procedure[10]. Sliding mode control (SMC) has better robustness against the parameter uncertainties[11–13]. In [11, 12], SMC was proposed for the full envelop of the aircraft model with parameter uncertainties. The combination of SMC and adaptive backstepping control benefits from both approaches. The role of SMC is to achieve more robustness to disturbances and uncertainties[14]. However, unwanted chattering in the conventional sliding surface makes adaptive backstepping SMC unsuitable for high accuracy requirement. There are many methods which can be employed to reduce chattering such as integral sliding surface[15], high-order SMC[16] and dynamic SMC[17]. High-order sliding mode controllers can also be used to improve the system responses.

In this paper, the flight control CPS with aerodynamic coefficients and external disturbances is studied by adaptive backstepping SMC. The tracking differentiator is used to reduce the complexity of the computation. Nonlinear disturbance observer (NDO) is used to observe the uncertainties to compensate the control inputs[18, 19]. The highorder sliding mode control law is deigned to eliminate the chattering and improve the system response time. Simulation examples are given to illustrate the effectiveness of the proposed methods.

Nomenclature.

  • F: Aerodynamic forces about the body-fixed frame

  • L, M, N: Aerodynamic rolling, pitching, yawing moments

  • I: Moment of inertia

  • p, q, r: Roll, pitch, yaw rates about the body-fixed frame

  • \(\bar q\): Dynamic pressure

  • m: Aircraft mass

  • T: Thrust

  • S: Reference wing area

  • C*: Non-dimensional aerodynamic coefficient

  • V: Velocity

  • α, β: Angle of attack, sideslip angle

  • δ e , δ a , δ r : Elevator, aileron, rudder angles

  • ϕ, θ, ψ: Roll, pith, yaw angles

2 Problem statement

The body-fixed nonlinear equations of motion for an F-16 aircraft with external uncertainties and aerodynamic coefficients can be written as[20]

$$\left\{ {\begin{array}{*{20}c} {\dot x_1 = f_1 \left( {x_1 ,x_3 } \right) + g_1 \left( {x_1 ,x_3 } \right)x_2 + M_1 } \hfill \\ {\dot x_2 = f_2 \left( {x_1 ,x_2 } \right) + g_2 \left( {x_1 } \right)u + M_2 } \hfill \\ {\dot x_3 = f_3 \left( {x_1 ,x_2 } \right)} \hfill \\ {M_1 = \Delta f_1 (x_1 ) + \Delta g_1 (x_1 )x_2 + \left[ {h\left( {x_1 } \right) + \Delta h\left( {x_1 } \right)} \right]2} \hfill \\ {M_2 = \Delta f_2 (x_1 ,x_2 ) + \Delta g_2 (x_1 )u + d(t)} \hfill \\ \end{array} } \right.$$
(1)

x1 = [α, β, ϕ]T, x2 = [p, q, r]T, x3 = [θ, ψ]T,u = [δ e , δ a , δ r ]T. And the expressions of f1, g1, f2, g2, f3, h are the same as given in [20].

M i represents the compound uncertainties in the model. Δf, Δg and Δh represent the aerodynamic coefficients, d(t) is the external uncertainty. h represents the aerodynamic force component caused by the control surface deflection. It is seen as one part of the model uncertainties M1. The task of the controller to be designed is to track the commands of α, β and ϕ. Assumption 1 is used in the design and analysis process.

  • Assumption 1. The desired trajectory y c = [α c , β c , ϕ c ]T is bounded, namely

    $$\left\Vert {[{y_c},{{\dot y}_c},{{\ddot y}_c}]} \right\Vert \leq {c_0}$$

    where c0 ∈ R is a known positive constant and ∥·∥ denotes the 2-norm of a vector or a matrix.

    Lemmas 1 and 2 are used in the design and analysis process.

  • Lemma 1. There exist positive constants α m , β m and θ m ∈ R such that the magnitudes and derivatives of f1, f2, g1 and g2 are bounded for all α, β and θ ∈ R satisfying ∣α∣ ≤ α m and ∣β∣ ≤ β m . Furthermore, there exist g i 0 and g i 1 such that 0 < g i 0 ≤∥g i ∥ ≤ g i 1, i = 1, 2.

  • Lemma 2. There exist two arbitrary vectors x, y ∈ Rn satisfying

    $${x^{\rm{T}}}y \leq {{{\varepsilon ^p}} \over p}{\left\Vert x \right\Vert ^p} + {1 \over {q{\varepsilon ^q}}} + {\left\Vert y \right\Vert ^q}$$

    ε > 0, p > 1, q > 1 and (p − 1)(q − 1) = 1. When p = q = 2 and e2 =2, there exist x, y ∈ Rn such that xTy ≤∥x∥2 + ∥y∥2.

3 Controller design and stability analysis

3.1 Tracking differential filter

The derivative of the virtual control signal obtained through the filter can effectively reduce the amount of calculation in the backstepping control. The classical differential filter has amplification effect on noises. Nonlinear tracking differentiator (NTD) can overcome the drawback when it is used to simplify the calculation. Its expression is written as[21]

$$\left\{{\matrix{{{{\dot y}_1} = {y_2}} \hfill \cr{{{\dot y}_2} = \gamma sat({y_1} - {v_0}(t) + {\textstyle{{{y_2}\vert {y_2}\vert} \over {2\gamma}}},\delta)} \hfill \cr}} \right.$$
(2)

where v0(t) is the input signal, y1 is the tracking signal, y2 is the approximate differential signal of v0(t), sat(x, δ) is the saturation function, i.e.,

$$sat(x,\delta )\left\{ {\begin{array}{*{20}c} { - 1,x < - \delta } \\ {\frac{x} {\delta },\left| x \right| \leqslant \delta } \\ {1,x > \delta } \\ \end{array} } \right.$$
(3)

γ > 0, and the value of γ determines the tracking speed of NTD. From (2), the following equality is satisfied when v0(t) is bounded and γ is sufficiently large

$$\mathop {\lim}\limits_{\gamma \rightarrow \infty} \int_0^T {\vert {y_1}(t) - {v_0}\vert {\rm{d}}t = 0}$$
(4)

with T > 0. We can know that NTD does not affect the convergence of the tracking error of the control system[22]. And y2 is obtained by integrating the differential signal, which can effectively avoid the influence of noise.

3.2 Controller design

Define the tracking error of the states in the control system

$$\left\{{\matrix{{{e_1} = {x_1} - {x_{1c}}} \hfill \cr{{e_2} = {x_2} - {x_{2c}}} \hfill \cr}} \right.$$
(5)

where x1c = y c , x2c is the expected virtual input of the inner loop. The derivative of e1 is

$${\dot e_1} = {\dot x_1} - {\dot e_{1c}} = {f_1} + {g_1}{x_2} + {M_1} - {\dot y_c}.$$
(6)

NDO is adopted to estimate uncertainty M1, then

$$\left\{{\matrix{{{{\hat M}_1} = {z_1} + {p_1}} \hfill \cr{{{\dot z}_1} = - {L_1}{z_1} - {p_1}({L_1} + {f_1} + {g_1}{x_2})} \hfill \cr}} \right.$$
(7)

where L1 = diag {L11 L12 L13} is a positive constant, p1 is a nonlinear function to be designed, and L1 = ∂p1(x)/∂x. The virtual control \({{\bar x}_{2c}}\) to drive e1 → 0 based on NDO can be determined as

$${\bar x_{2c}} = - g_1^{- 1}({k_1}{e_1} + {f_1} + {\hat M_1} - {\dot y_c})$$
(8)

where k1 = diag{k11 k12 k13} is a positive constant. In order to obtain the filtering virtual control x2c, wepass \({{\bar x}_{2c}}\) through an NTD with γ > 0. The derivative of e2 is

$${\dot e_2} = {\dot x_2} - {\dot x_{2c}} = {f_2} + {g_2}u + {M_2} - {\dot x_{2c}}.$$
(9)

The NDO of the inner loop is given by

$$\left\{{\matrix{{{{\hat M}_2} = {z_2} + {p_2}} \hfill \cr{{{\dot z}_2} = - {L_2}{z_2} - {L_2}({p_2} + {f_2} + {g_2}u).} \hfill \cr}} \right.$$
(10)

Define a non-singular terminal sliding mode surface as follows:

$$S = {[{S_1},{S_2},{S_3}]^{\rm{T}}} = {e_2} + a\dot e_2^{{\textstyle{{{\rho _1}} \over {{\rho _2}}}}}$$
(11)

where a = diag {a1 a2 a3}, a i > 0, ρ1 and ρ2 are positive odd constants to be designed and \(1 < {{{\rho _1}} \over {{\rho _2}}} < 2,\dot e_2^{{{{\rho _1}} \over {{\rho _2}}}} = {[\dot e_{21}^{{{{\rho _1}} \over {{\rho _2}}}},\dot e_{22}^{{{{\rho _1}} \over {{\rho _2}}}},\dot e_{23}^{{{{\rho _1}} \over {{\rho _2}}}}]^T}\) Let S(t) = 0, t ≥ t r , then

$$\mathop {\lim}\limits_{t \rightarrow {t_s}} {e_2} = 0,\quad \mathop {\lim}\limits_{t \to {t_s}} {\dot e_2} = 0$$
(12)

where

$${t_s} = {t_r} + {{{\rho _1}} \over {{\rho _1} - {\rho _2}}}\mathop {\max}\limits_{1 \leq i \leq 3} \left({a_i^{{{{\rho _1}} \over {{\rho _2}}}}\Vert {e_{2i}}({t_r})\Vert ^{{{{{\rho _1} - {\rho _2}} \over {{\rho _2}}}}}} \right).$$
(13)

Therefore, the system will remain in the second-order sliding mode when t ≥ t s . The values of ρ1, ρ2, a determine the speed of convergence of the control system. In this paper, a high-order terminal sliding mode control law is proposed as

$$\left\{ {\begin{array}{*{20}c} {u = u_1 + u_2 } \\ {u_1 = - g_2^{ - 1} \left( {f_2 + \hat M_2 - \dot x_{2c} } \right)} \\ {u_{2i} = - \left( {g_2^{ - 1} } \right)_i \int_0^t {\left[ {\tfrac{{\rho _2 }} {{a_i \rho _1 }}\dot e_{2_i }^{2 - \tfrac{{\rho _1 }} {{\rho _2 }}} + k_{2i} S_i + k_{3i} \operatorname{sgn} (S_i )} \right]d\tau } } \\ {u_2 = [u_{21} ,u_{22} ,u_{23} ]^T } \\ \end{array} } \right.$$
(14)

where

$$\begin{array}{*{20}c} {k_2 = diag \{ k_{21} ,k_{22,} k_{23} \} ,} & {k_{2j} > 0, j = 1,2,3} \\ {k_3 = diag \{ k_{31} ,k_{32,} k_{33} \} ,} & {k_{3j} > 0,j = 1,2,3.} \\ \end{array} $$

3.3 Stability analysis

It can be assumed that the disturbances are slowly time-varying, so we can consider that Ṁ ≈ 0 and ėNDO = −L(x)eNDO[19].

Consider the following Lyapunov function candidate:

$${V_1} = {1 \over 2}e_1^{\rm{T}}{e_1} + {1 \over 2}e_{{\rm{NDO1}}e{\rm{NDO1}}.}^{\rm{T}}$$
(15)

The derivative of V1 is

$$\matrix{{\dot V = {\rm{e}}_1^{\rm{T}}{{\dot e}_1} + e_{{\rm{NDO1}}}^{\rm{T}}{{\dot e}_{{\rm{NDO1}}}} =} \cr{{\rm{e}}_1^{\rm{T}}(- {k_1}{e_1} + {g_1}{e_2} + {e_{{\rm{NDO1}}}}) - e_{_{{\rm{NDO1}}}}^{\rm{T}}{L_1}{e_{{\rm{NDO1}}{\rm{.}}}}} \cr}$$
(16)

From Lemma 2,

$$\matrix{{\dot V \leq - {\lambda _{\min}}({k_1} - 2I)\Vert{e_1}\Vert^{2} + e_1^{\rm{T}}{g_1}{e_2} -} \cr{{\lambda _{\min}}\left({{L_1} - {1 \over 4}I} \right)\Vert{e_{{\rm{NDO1}}}}\Vert{^2}.} \cr}$$
(17)

Let k1 > I and \({L_1} > {1 \over 4}I\). Then,

$${{\dot V}_1} \leq 0.$$
(18)

Therefore, we can know that e1 and eNDO1 are uniformly ultimately bounded if limt→∞ e2 (t) = 0. Consider the following Lyapunov function candidate

$${V_2} = {1 \over 2}{S^{\rm{T}}}S + {1 \over 2}e_{{\rm{NDO}}2}^{\rm{T}}{e_{{\rm{NDO}}2}}.$$
(19)

The derivative of V2 is

$${\dot V_2} = {S^{\rm{T}}}\dot S + e_{{\rm{NDO}}2}^{\rm{T}}{\dot e_{{\rm{NDO}}2}}$$
(20)

From (11),

$${\dot S_i} = {a_i}{{{\rho _1}} \over {{\rho _2}}}\dot e_{2i}^{{\textstyle{{{\rho _1}} \over {{\rho _2}}}} - 1}\left({{{\ddot e}_{2i}} + {{{\rho _2}} \over {{a_i}{\rho _1}}}\dot e_{2i}^{2 - {\textstyle{{{\rho _1}} \over {{\rho _2}}}}}} \right).$$
(21)

So,

$${\dot V_2} = \sum\limits_{i = 1}^3 {\left[ {{S_i}{a_i}{{{\rho _1}} \over {{\rho _2}}}\dot e_{2i}^{{\textstyle{{{\rho _1}} \over {{\rho _2}}}} - 1}\left({{{\ddot e}_{2i}} + {{{\rho _2}} \over {{a_i}{\rho _1}}}\dot e_{2i}^{2 - {\textstyle{{{\rho _1}} \over {{\rho _2}}}}}} \right) - {L_{2i}}e_{{\rm{NDO}}2}^2} \right].}$$
(22)

Substituting (14) into (9) yields

$${\dot e_2} = {g_2}{u_2}.$$
(23)

The derivative of ė2 is

$${\ddot e_{2i}} = - {{{\rho _2}} \over {{a_i}{\rho _1}}}{\dot e_2}^{2 - {{{\rho _1}} \over {{\rho _2}}}} - {k_{2i}}{S_i} - {k_{3i}}{\mathop{\rm sgn}} \left({{S_i}} \right).$$
(24)

Substituting (24) into (20) yields

$$\matrix{{{{\dot V}_2} =} \hfill \cr{\sum\limits_{i - 1}^3 {\left[ {{S_i}{a_i}{{{\rho _1}} \over {{\rho _2}}}{{\dot e}_{2i}}^{{{{\rho _1}} \over {{\rho _2}}} - 1}\left[ {- {k_{2i}}{S_i} - {k_{3i}}{\mathop{\rm sgn}} \left({{S_i}} \right)} \right]{L_{2i}}e_{{\rm{NDO}}2}^2} \right] =}} \hfill \cr{- \sum\limits_{i - 1}^3 {\left[ {{a_i}{k_{2i}}{{{\rho _1}} \over {{\rho _2}}}{{\dot e}_{2i}}^{{{{\rho _1}} \over {{\rho _2}}} - 1}S_i^2 + {a_i}{k_{3i}}{{{\rho _1}} \over {{\rho _2}}}{{\dot e}_{2i}}^{{{{\rho _1}} \over {{\rho _2}}} - 1}\left| {{S_i}} \right| + {L_{2i}}e_{{\rm{NDO}}2}^2} \right].}} \hfill \cr}$$
(25)

Let \(1 < {{{\rho _1}} \over {{\rho _2}}} < 2,{k_2} > 0,{k_3} > 0,{L_2} > 0\) and a > 0. Then,

$${\dot V_2} \le 0.$$
(26)

Accordingly, we can know that the tracking errors of the control system designed in this paper are locally uniformly ultimately bounded when \({k_1} > I,{k_2} > 0,{k_3} > 0,{L_1} > {1 \over 4}I,{L_2} > 0\) and \(1 < {{{\rho _1}} \over {{\rho _2}}} < 2\).

4 Simulation results

The proposed controller is tested by a numerical simulation on the attitude maneuver flight control system of an F-16 aircraft. The following command values of α d , β d , and ϕ d are applied to the aircraft in a steady-state level flight of V = 200 m/s, h = 4000 m, F T = 60 kN:

$$\matrix{{{\alpha _d} = 2.659,{\beta _d} = 0,{\phi _d} = 0,0 \le t < 1} \hfill \cr{{\alpha _d} = 10,{\beta _d} = 0,{\phi _d} = 50,1 \le t < 10} \hfill \cr{{\alpha _d} = - 2,{\beta _d} = 0,{\phi _d} = 0,10 \le t < 20.} \hfill \cr}$$

y c is obtained from y d by the following command filter to satisfy Assumption 1:

$${{{{\left[ {{y_c}} \right]}_i}} \over {{{\left[ {{y_d}} \right]}_i}}} = {{\omega _n^2} \over {{s^2} + 2s{\xi _n}{\omega _n} + \omega _n^2}},{\omega _n} = 4,{\xi _n} = 0.8,i = 1,2,3$$

where s is Laplace operator. The controller design parameters are chosen as k1 = 10I, k2 = 5I, γ = 10I, a = 5I, τ2 = 0.05, δ(0) = 10, where I represents the 3 × 3 identity matrix. NDO gains are chosen as

$$\matrix{{{L_1} = {\rm{diag}}\left\{{2\left({1 + {\alpha ^2}} \right),2\left({1 + {\beta ^2}} \right),2\left({1 + {\phi ^2}} \right)} \right\}} \hfill \cr{{L_2} = {\rm{diag}}\left\{{5\left({1 + {p^2}} \right),5\left({1 + {q^2}} \right),5\left({1 + {r^2}} \right)} \right\}.} \hfill \cr}$$

We assume that the uncertainties of the aerodynamic coefficients and external moment disturbance are time-varying. The time-varying uncertainties are given as

$${C_j} = \left[ {1 + 0.5\sin \left({0.5\pi t} \right)} \right]C_j^r,j = x,y,z,l,m,n$$
$$d\left(t \right) = \left[ {0.5\quad1.2\quad1.5} \right] \times {10^4}\sin \left(t \right)$$

where \(C_x^r,C_y^r,C_z^r,C_l^r,C_m^r\) and \(C_n^r\) are the standard aerodynamic coefficients.

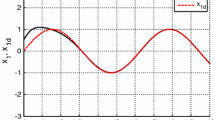
Figs. 1–3 present the simulation results when uncertainties do not exist. 0 represents the command signal. 1 represents the simulation result of the controller proposed in this paper. From Figs. 1–3, it is clear that the control law proposed in this paper can track the reference command signal effectively and make the tracking error converge.

Fig. 1
figure 1

Time response of α without uncertainties

Full size image
Fig. 2
figure 2

Time response of β without uncertainties

Full size image
Fig. 3
figure 3

Time response of ϕ without uncertainties

Full size image

To demonstrate the tracking performance of the proposed control law, the backstepping controller in [18] is applied contrastively. Figs. 4–9 present the simulation results when the uncertainties exist. 1 represents the simulation result of filtering backstepping terminal sliding mode controller proposed in this paper. 2 represents the simulation result of the backstepping controller proposed in [18]. The tracking error convergence curves of e1 = [e1α, e1β, e1ϕ] are used to reflect the tracking control performance of the two controllers. The simulation results reveal that, under the condition of aerodynamic parameter perturbation and external disturbance uncertainties, the proposed control scheme can track the reference command signal more quickly and more accurately. Figs. 7–9 show that the nonsingular high-order terminal sliding mode control method can effectively weaken the chattering.

Fig. 4
figure 4

Time response of e1α with uncertainties

Full size image
Fig. 5
figure 5

Time response of e1β with uncertainties

Full size image
Fig. 6
figure 6

Time response of e1ϕ with uncertainties

Full size image
Fig. 7
figure 7

Time response of δ e with uncertainties

Full size image
Fig. 8
figure 8

Time response of δ a with uncertainties

Full size image
Fig. 9
figure 9

Timeresponseof δ r with uncertainties

Full size image

5 Conclusions

A filtering backstepping terminal sliding mode controller is designed in this paper to compensate for the effect of system uncertainties in CPS with time-varying parameter perturbations and external disturbances. NTD is used to obtain the derivation of the virtual control signal, simplifying the design of the controller and reducing the amount of computation. Nonlinear disturbance observers can effectively observe the uncertainties of CPS. Nonsingular terminal sliding mode controller can increase system robustness and tracking accuracy, and can effectively weaken the control signal chattering. Simulation results show that the proposed control system can quickly and accurately track the reference command signal. The method proposed in this paper may be also used in the design in other CPS controllers with aerodynamic coefficients and external disturbance uncertainties.