Skip to main content
SpringerLink
Log in

Modeling and uncertainty estimation of gravity anomaly over 2D fault using very fast simulated annealing global optimization

  • Research Article - Applied Geophysics
  • Published:
Acta Geophysica Aims and scope Submit manuscript

Abstract

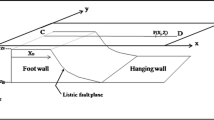
Difficult understanding of gravity effects on the 2D vertical and inclined faults for the delineation of subsurface structure for gravity exploration is slow and cumbersome. Hence, a fast and efficient algorithm is established for the interpretation of gravity anomaly over 2D inclined and vertical fault. The method can simultaneously determine all parameters such as the depth to the top (z) and base (h), dip angle (α), amplitude coefficient (k), and location of the fault plane on the surface (x0) of a hidden thin faulted slab from the observed gravity data. The developed algorithm can effectively interpret all parameters for dipping and vertical fault even though there is no subsurface drilling information. Interpretation of all the parameters suggests that there is no uncertainty for 2D inclined and vertical fault. However, if the detachment tip of the fault is at a larger depth, then the dip of the fault shows some uncertainty. The present code has been applied to non-noisy synthetic anomaly data and Gaussian noisy anomaly. Furthermore, the algorithm was also verified on three field examples from Egypt, and the USA for exploration. The appraised value of all the parameters is found to be in decent agreement with earlier published works and borehole information wherever available.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

References

  • Abdelrahman EM, Bayoumi AI (1989) Nomograms for delineating fault parameters from gravity data application to the Mersa Matruh Basin Egypt. J African Earth Sci 9:455–459

    Article  Google Scholar 

  • Abdelrahman EM, Tealeb AA, Ahmed HA (1991) Gravity map of Kalabsha area, northwest of Aswan Lake, and its structural significance. Geodynamics 14:125–135

    Article  Google Scholar 

  • Abdelrahman EM, El-Araby TM (1996) Shape and depth solutions from moving average residual gravity anomalies. J Appl Geophys 36:89–95

    Article  Google Scholar 

  • Abdelrahman EM, El-Araby TM, El-Araby HM, Abo-Ezz ER (2001) A new method for shape and depth determinations from gravity data. Geophysics 66:1774–1780

    Article  Google Scholar 

  • Abdelrahman EM, Bayoumi AI, El-Araby HM (1989) Dip angle determination of fault planes from gravity data Pure Appl. Geophys 130:735–742

    Google Scholar 

  • Abdelrahman EM, Abo-Ezz ER, Essa KS, El-Araby TM, Soliman KS (2006) A least- squares variance analysis method for shape and depth estimation from gravity data. J Geophys Eng 3:143–153

    Article  Google Scholar 

  • Abdelrahman EM, Essa KS (2013) A new approach to semi-infinite thin slab depth determination from second moving average residual gravity anomalies. Explor Geophys 44:185–191

    Article  Google Scholar 

  • Abdelrahman EM, El-Araby TM, Essa KS (2003) Shape and depth solutions from third moving average residual gravity anomalies using the window curves method. Kuwait J Sci Engrg 30:95–108

    Google Scholar 

  • Abdelrahman EM, Essa KS, Abo-Ezz ER (2013) A least-squares window curves method to interpret gravity data due to dipping faults. J Geophys Eng 10:025003

    Article  Google Scholar 

  • Abdelrahman EM, Essa KS (2015) Three least-squares minimization approaches to interpret gravity data due to dipping faults. Pure Appl Geophys 172:427–438

    Article  Google Scholar 

  • Abdelrahman EM, Gobashy M, Abo-Ezz E, El-Araby T (2019) A new method for complete quantitative interpretation of gravity data due to dipping faults. Contribution to Geophysics and Geodesy 49(2):133–151

    Article  Google Scholar 

  • Anderson NL, Essa KS, Elhussein M (2020) A comparison study using particle swarm optimization inversion algorithm for gravity anomaly interpretation due to a 2D vertical fault structure. J Appl Geophys 179:104120

    Article  Google Scholar 

  • Araffa SAS, Sabet HS, Gaweish WR (2015) Integrated geophysical interpretation for delineating the structural elements and groundwater aquifers at central part of Sinai Peninsula Egypt. J Afr Earth Sc 105:93–106

    Article  Google Scholar 

  • Balkaya C, Ekinci YL, Gokturkler G, Turan S (2017) 3D non-linear inversion of magnetic anomalies caused by prismatic bodies using differential evolution algorithm. J Appl Geophys 136:372–386

    Article  Google Scholar 

  • Barakat MG, Darwish M (1984) Contribution to the litho-stratigraphy of the lower cretaceous sequence in Mersa Matruh area, North Western Desert. Paper presented at Egyptian Petroluem Exploration Society, Cairo, Egypt

    Google Scholar 

  • Biswas A (2015) Interpretation of residual gravity anomaly caused by simple shaped bodies using very fast simulated annealing global optimization. Geosci Front 6:875–893

    Article  Google Scholar 

  • Biswas A, Parija MP, Kumar S (2017) Global nonlinear optimization for the interpretation of source parameters from total gradient of gravity and magnetic anomalies caused by thin dyke. Ann Geophys 60(2):G0218

    Article  Google Scholar 

  • Biswas A (2021). Interpretation and resolution of multiple structures from residual gravity anomaly data and application to mineral exploration, In: Samui P, Dieu BT, Dixon B (Eds), Basics of Computational Geophysics, Elsevier, 293–318. https://doi.org/10.1016/B978-0-12-820513-6.00005-9.

  • Chakravarthi V (2011) Automatic gravity optimization of 2.5D strike listric fault sources with analytically defined fault planes and depth-dependent density. Geophysics 76:121–131

    Article  Google Scholar 

  • Cordell L, Henderson RG (1968) Iterative three-dimensional solution of gravity anomaly data using a digital computer. Geophysics 33:596–601

    Article  Google Scholar 

  • Ekinci YL (2008) 2D focusing inversion of gravity data with the use of parameter variation as a stopping criterion. J Balkan Geophys Soc 11:1–9

    Google Scholar 

  • Ekinci YL (2016) MATLAB-based algorithm to estimate depths of isolated thin dike-like sources using higher-order horizontal derivatives of magnetic anomalies. Springerplus 5:1384

    Article  Google Scholar 

  • Ekinci YL, Balkaya Ç, Göktürkler G, Turan S (2016) Model parameter estimations from residual gravity anomalies due to simple-shaped sources using differential evolution algorithm. J Appl Geophys 129:133–147

    Article  Google Scholar 

  • Ekinci YL, Özyalın Ş, Sındırgı P, Balkaya G, Göktürkler G (2017) Amplitude inversion of 2D analytic signal of magnetic anomalies through differential evolution algorithm. J Geophys Eng 14:1492–1508

    Article  Google Scholar 

  • Ekinci YL, Balkaya Ç, Göktürkler G (2019) Parameter estimations from gravity and magnetic anomalies due to deep-seated faults: differential evolution versus particle swarm optimization. Turkish J Earth Sci 28:860–881

    Google Scholar 

  • Ekinci YL, Balkaya C, Göktürkler G, Özyalın S (2021) Gravity data inversion for the basement relief delineation through global optimization: a case study from the Aegean Graben System, western Anatolia. Turkey Geophys J Int 224(2):923–944. https://doi.org/10.1093/gji/ggaa492

    Article  Google Scholar 

  • Eliseyeva IS 1998 Methodical rules for the interpretation of gravimetrical and magnetometrical data by means of quasi-singular points method, in Russian, VNII Geofizika Moscow

  • Eppelbaum LV, Khesin BE (2012) Geophysical studies in the caucasus. Springer, Newyork

    Book  Google Scholar 

  • Essa KS (2007) A simple formula for shape and depth determination from residual gravity anomalies. Acta Geophys 55:182–190

    Article  Google Scholar 

  • Essa KS (2013) Gravity interpretation of dipping faults using the variance analysis method. J Geophys Eng 10:015003

    Article  Google Scholar 

  • Essa KS, Géraud Y, Diraison M (2021) Fault parameters assessment from the gravity data profiles applying the global particle swarm optimization. J Petrol Sci Eng. https://doi.org/10.1016/j.petrol.2021.109129

    Article  Google Scholar 

  • Evans K, Beavan J, Simpson D (1991) Estimating aquifer parameters from analysis of forced fluctuations in well level: an example from the Nubian formation near Aswan, Egypt: 1 Hydrogeological background and large-scale permeability estimates. J Geophys Res 12(127–12):137

    Google Scholar 

  • Fedi M, Hansen PC, Paoletti V (2005) Tutorial: analysis of depth resolution in potential-field inversion. Geophysics 70:A1–A11

    Article  Google Scholar 

  • Ferris C (1987) Gravity anomaly resolution at the Garber field. Geophysics 52:1570–1579

    Article  Google Scholar 

  • Geldart LP, Gill DE, Sharma B (1966) Gravity anomalies of two-dimensional faults. Geophysics 31:372–397

    Article  Google Scholar 

  • Grant FS, West GF, 1965. Interpretation theory in applied geophysics: New York, NY, USA: McGraw Hill Book Co, 584p.

  • Green R (1976) Accurate determination of the dip angle of a geological contact using the gravity method. Geophys Prospect 24:265–272

    Article  Google Scholar 

  • Gupta OP, Pokhriyal SK (1990) New formula for determining the dip angle of a fault from gravity data. SEG Technical Program Expanded Abstracts 9:646–649

    Google Scholar 

  • Hinze WJ, von Frese RRB, Saad AH (2013) Gravity and magnetic exploration – principles, practices, and applications. Cambridge University Press

    Book  Google Scholar 

  • Ingber L, Rosen B (1992) Genetic Algorithms and very fast simulated reannealing: a comparison. Mathematical and Computer Modeling 16(11):87–100

    Article  Google Scholar 

  • Japan National Gas Association and Japan Offshore Petroleum Development Association (1992) Petroleum and national gas resources of Japan. Japan National Gas Association and Japan Offshore Petroleum Development Association, Tokyo.

  • Lelièvre PG, Farquharson CG, Hurich CA (2012) Joint inversion of seismic travel times and gravity data on unstructured grids with application to mineral exploration. Geophysics 77:K1–K15

    Article  Google Scholar 

  • Lines LR, Treitel S (1984) A review of least-squares inversion and its application to geophysical problems. Geophys Prospect 32:159–186

    Article  Google Scholar 

  • Malleswara Rao MM, Ramana Murty TV, Murthy KSR, Vasudeva RY (2003) Application of natural generalised inverse technique in reconstruction of gravity anomalies due to a fault. Indian J Pure Appl Math 34:31–47

    Google Scholar 

  • McGregor DM, Wilson CDV (1967) Gravity and magnetics surveys of the younger gabbros of Aberdeenshire Q. J Geol Soc Lond 123:99–123

    Article  Google Scholar 

  • Mehanee SA (2014) Accurate and efficient regularized inversion approach for the interpretation of isolated gravity anomalies. Pure Appl Geophys 171:1897–1937

    Article  Google Scholar 

  • Mehanee SA, Essa KS (2015) 2.5D regularized inversion for the interpretation of residual gravity data by a dipping thin sheet: numerical examples and case studies with an insight on sensitivity and non-uniqueness. Earth, Planets and Space 67, 130.

  • Mosegaard K, Tarantola A (1995) Monte Carlo sampling of solutions to inverse problems. J Geophys Res 100(B7):12431–12447

    Article  Google Scholar 

  • Panisova J, Pasteka R (2009) The use of microgravity technique in archaeology: a case study from the St. Nicolas Church in Pukanec Slovakia. Contribut Geophys Geodesy 39:237–254

    Article  Google Scholar 

  • Paul MK, Datta S, Banerjee B (1966) Direct interpretation of two-dimensional structural fault from gravity data. Geophysics 31:940–948

    Article  Google Scholar 

  • Phillips JD, Hansen RO, Blakely RJ (2007) The use of curvature in potential-field interpretation. Explor Geophys 38:111–119

    Article  Google Scholar 

  • Rao K, Jain S, Biswas A (2021) Global optimization for delineation of self-potential anomaly of a 2-D inclined plate. Nat Resour Res 30:175–189

    Article  Google Scholar 

  • Radhakrishna Murthy IV, Krishnamacharyulu SKG (1990) Automatic inversion of gravity anomalies of faults. Comput Geosci 16:539–548

    Article  Google Scholar 

  • Reid AB, Allsop JM, Granser H, Millett AJ, Somerton IW (1990) Magnetic interpretation in the three dimensions using Euler deconvolution. Geophysics 55:80–91

    Article  Google Scholar 

  • Said R (1962) The geology of Egypt. Elsevier, Newyork

    Google Scholar 

  • Sawires R, Peláez JA, Fat-Helbary RE, Ibrahim, HA, García Hernández MT (2015). An updated seismic source model for Egypt, in: Moustafa A (Eds.) Earthquake engineering - from engineering seismology to optimal seismic design of engineering structures. IntechOpen, London, DOI: https://doi.org/10.5772/58971.

  • Sen MK, Stoffa PL (2013) Global optimization methods in geophysical inversion. Cambridge University Press, 302 pp.

  • Sharma SP (2012) VFSARES– A very fast simulated annealing FORTRAN program for interpretation of 1-D DC resistivity sounding data from various electrode array. Comput Geosci 42:177–188

    Article  Google Scholar 

  • Singh A, Biswas A (2016) Application of global particle swarm optimization for inversion of residual gravity anomalies over geological bodies with idealized geometries. Nat Resour Res 25:297–314

    Article  Google Scholar 

  • Singh KK, Singh UK (2017) Application of particle swarm optimization for gravity inversion of 2.5-D sedimentary basins using variable density contrast. Geosci Instrument Methods Data Syst 6:193–198

    Article  Google Scholar 

  • Tanner JG (1967) An automated method of gravity interpretation. Geophys J R Astron Soc 13:339–347

    Article  Google Scholar 

  • Telford WM, Geldart LP, Sheriff RE (1990) Applied Geophysics, 2nd Edition, Cambridge University Press, 770p.

  • Trivedi S, Kumar P, Parija MP, Biswas A (2020) Global Optimization of Model Parameters from the 2-D Analytic Signal of Gravity and Magnetic anomalies. In: Biswas A, Sharma SP (eds) Advances in Modeling and Interpretation in Near Surface Geophysics. Springer International Publishing, Switzerland AG, XV, pp 189–221

    Chapter  Google Scholar 

  • Utyupin YuV, Mishenin SG (2012) Locating the sources of potential fields in areal data using the singularity method. Russ Geol Geophys 53:1111–1116

    Article  Google Scholar 

  • Wada S, Sawada A, Hiramatsu Y, Matsumoto N, Okada S, Tanaka T, Honda R (2017) Continuity of subsurface fault structure revealed by gravity anomaly: the eastern boundary fault zone of the Niigata plain, central Japan. Earth, Planets and Space 69:15

    Article  Google Scholar 

  • Woodward-Clyde Consultants, 1985. Identification of earthquake sources and estimation of magnitudes and recurrence intervals. Internal Report 135, High and Aswan Dams Authority, Aswan, Egypt.

Download references

Acknowledgements

We thank the Associate Editor, Prof. Ivana Vasiljevic, and two anonymous reviewers for their insightful comments which helped us to improve the quality of the manuscript. This work forms a part of the Ph.D. thesis of KR, who thank the Council of Scientific and Industrial Research (CSIR), New Delhi, for the research fellowship. AB thank the Institute of Eminence (IoE) from Banaras Hindu University, Varanasi for seed grant to pursue this work.

Author information

Authors and Affiliations

  1. Department of Geology, Centre of Advanced Study, Institute of Science, Banaras Hindu University, Varanasi, 221005, India

    Khushwant Rao & Arkoprovo Biswas

Authors
  1. Khushwant Rao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Arkoprovo Biswas
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

The entire work has been carried out by both the author.

Corresponding author

Correspondence to Arkoprovo Biswas.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Communicated by Ivana Vasiljevic, Ph.D. (ASSOCIATE EDITOR)/Prof. Michal Malinowski (CO-EDITOR-IN-CHIEF).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rao, K., Biswas, A. Modeling and uncertainty estimation of gravity anomaly over 2D fault using very fast simulated annealing global optimization. Acta Geophys. 69, 1735–1751 (2021). https://doi.org/10.1007/s11600-021-00649-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11600-021-00649-8

Keywords

Search

Navigation