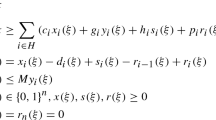1 Introduction

Inventory problems are amongst the most studied problems under uncertainty. Since the seminal works on inventory management (see [13]) demands are frequently considered as uncertain. From a practical point of view, uncertainty usually occurs when companies follow make-to-stock policies [2]. For the case of lot-sizing problems with uncertain demand see the survey [1].

One of the most important characteristics in lot-sizing problems is the need to define the set-up periods. Given their nature, the set-ups are frequently decisions taken a priori, that is, decisions taken during the planning phase which cannot be changed during the execution phase. In such cases, between two consecutive production periods there is no production and the decision maker (DM) can just observe the demands and hope not to incur into large amounts of stock (corresponding to positive inventory levels) or large amounts of backlogging (corresponding to negative inventory levels). Here we consider a variant of the lot-sizing problem with backlogging and set-ups, which is one of the most basic models in production planning (see [9]). In this variant the DM wishes to establish the production plan assuming that between consecutive production periods the worst-case between the two extreme scenarios (highest demand versus lowest demand) will occur, thus establishing a plan that prevents both excessive holding and backlog costs, where the holding costs correspond to the cost of keeping stocks.

The most common techniques in robust optimization have been employed in inventory models. Among other techniques, the well-known dualization approach introduced by Bertsimas and Sim [5] was employed for a simple inventory model in [6]; affine approximations were proposed in [4] for a retailer-supplier inventory model, and Bienstock and Özbay [7] introduced an exact decomposition approach to define robust basestock levels for an inventory model. However, all these seminal works on robust inventory models ignore set-ups. Later on, these approaches have been applied to more complex (and more practical) inventory problems where discrete decisions such as set-ups, that complicate the model considerably, are considered. The results presented by [6] are extended in [14] to a lot-sizing problem with remanufacturing, where uncertainty is considered on returns and demands. The same lot-sizing problem is solved using the exact decomposition algorithm in [3] where, in addition, a classical extended formulation for the lot-sizing problem is discussed for the robust case. In [11], a Lagrangian approach is proposed for robust problems with decomposable functions, which include the case of inventory problems, and a relation between the affine approximations and the dualization approaches is established using Lagrangian duality. Computational tests on lot-sizing problems show that the definition of set-ups decisions depend on the approach.

Approaches based on practical policies, such as FIFO policies, have been employed for lot-sizing models, see [12] for an inventory model with perishable products.

In relation to the common robust approximation approaches, our modeling approach follows a new direction. Instead of restricting the DM actions as in the dualization and in the affine approximation, we assume that the adversary follows a simple policy and the DM takes the optimal decisions considering that adversary’s policy. This approach has two main advantages. Firstly, it allows us to obtain a tractable model. Secondly, the adversary’s policy can be easily interpreted by the DM and corresponds to one of the evaluation rules that a DM may follow, by analysing the two extreme cases of the inventory level between two consecutive production periods. As a result, the introduced model is less conservative than the most common approaches in robust optimization.

In summary, our contributions are as follows: A new robust mixed-integer model is proposed for the basic lot-sizing problem with backlogging assuming the adversary follows a basic policy; a column-and-row generation algorithm is introduced to solve the robust model efficiently; and computational experiments are reported showing that our approach leads to solutions that have different structures from those using a deterministic model.

The rest of the paper is organized as follows: In Sect. 2 we introduce the robust model. In Sect. 3 we provide a column-and-row generation algorithm. Computational results are presented in Sect. 4 and Sect.  5 contains some concluding remarks and future research directions.

2 Problem formulation

2.1 Deterministic formulation

First, we consider the deterministic lot-sizing model. Consider a finite time horizon \(N=\{1,\ldots ,n\},\) where n is the number of time periods. Parameters \(h_t, b_t, p_t\) represent, for period t,  the unit holding, backlog, and production cost, respectively. The set-up cost is given by \(f_t\). The production capacity in period t is denoted by \(c_t.\) Variables \(x_t\) give the amount produced in period t,  and the inventory variables \(s_t\) and \(r_t\) give, respectively, the stock and backlog level at the end of period t. Binary variables \(y_t\) indicate whether a set-up occurs in period t. The deterministic capacitated lot-sizing problem with backlogging, denoted by DLS, is as follows:

$$\begin{aligned} min \quad&\sum_{t \in N} \Bigg(f_{t} y_{t}+h_{t} s_{t} + b_{t} r_{t}+p_{t} x_{t}\Bigg) \end{aligned}$$
(1)
$$\begin{aligned} s. t. \qquad&s_{t-1}+x_{t}+r_{t}=d_{t}+s_{t}+r_{t-1}, \qquad \forall t \in N \end{aligned}$$
(2)
$$\begin{aligned}&x_{t} \le c_t y_{t}, \qquad \forall t \in N \end{aligned}$$
(3)
$$\begin{aligned}&x_{t}, s_{t}, r_{t} \ge 0, \qquad \forall t \in N \end{aligned}$$
(4)
$$\begin{aligned}&y_{t} \in \{0,1\}, \qquad \forall t \in N \end{aligned}$$
(5)

The objective function (1) is to minimize the total cost, which includes the set-up, holding, backlogging and production costs. Constraints (2) are the inventory balance constraints. Constraints (3) ensure that if the production is positive in a given period t,  then there must occur a set-up at that period, and guarantees that the production doesn’t exceeds the production capacity. If no capacity is assumed, then we take \(c_t=\sum _{i \in N}d_i,\) for all \(t \in N.\) Constraints (4), (5) define the domain of the variables. We assume henceforward that \(s_0=r_0=0\) (which occurs in equations (2) for \(t=1).\) Notice that variables \(s_{n}\) and \(r_{n}\) may be positive to ensure feasibility.

2.1.1 The adversary policy

In the robust setting we assume that in each period t the demand \(d_t\) is not known with certainty and belongs to the (box) uncertainty set \([\overline{d}_{t}-\widehat{d}_{t}, \overline{d}_{t}+\widehat{d}_{t}],\) where \(\overline{d}_{t}\) is the nominal demand and \(\widehat{d}_{t}\) is the maximum allowed deviation.

Assume t and k,  \(k>t,\) are two consecutive production periods. The adversary has to decide whether to set the demands

$$\begin{aligned} d_{i}=\overline{d}_{i}-\widehat{d}_{i} \text{ for } \text{ each } i=t,\ldots ,k-1 \end{aligned}$$
(6)

or

$$\begin{aligned} d_{i}=\overline{d}_{i}+\widehat{d}_{i} \text{ for } \text{ each } i=t,\ldots , k-1. \end{aligned}$$
(7)

The decision depends on the inventory level at period t (before demand \(d_t\) is observed), which is given by \(s_{t-1}+x_{t}-r_{t-1}.\) If the inventory level is high, the adversary decides for the lowest values of demands (case (6)) leading to high holding costs. Otherwise, if the inventory level is low, setting the demands to its highest values (case (7)) leads to high backlogging costs.

From the point of view of robust theory, a decision-dependent uncertainty (see the seminal works [8, 10]) is considered. Given the set of production periods \(\{i_1,\ldots ,i_{p-1}\} \subseteq N\) defined by y variables, let \((I{(y)}_1,\ldots ,I{(y)}_p)\) be a partition of N defined by consecutive production intervals. That is, \(I{(y)}_1=\{1,\ldots ,i_1-1\}, I{(y)}_2=\{i_1,\ldots ,i_2-1\}, \ldots , I{(y)}_p=\{i_{p-1},\ldots ,n\}.\) Then the uncertainty set is given by

$$U(y) = \{ d_{i} = \bar{d}_{i} + \delta _{i} \hat{d}_{i} , - 1 \le \delta _{i} \le 1,\delta _{i} = \delta _{j} {\text{ if }}\exists \ell {\text{ such that }}i,j \in I(y)_{\ell } \}$$
(8)

It is important to notice that the adversary’s policy may not give the optimal solution to the following adversarial problem defined for the case of two consecutive production periods t and k (which corresponds to an interval \(I{(y)}_{\ell }\) in the partition):

$$\begin{aligned}&\displaystyle \max _{d \in \overline{U}[t,k-1]}C_{tk}(s_{t-1}+x_{t}-r_{t-1}) \end{aligned}$$
(9)

where \(C_{tk}(Q)\) represents the inventory cost between periods t and \(k-1\) when the inventory level at the beginning of period t is Q (which is given by \(\sum _{i=t}^{k-1} \max \{h_i (Q-\sum _{\ell =t}^{i}d_{\ell }), b_i (\sum _{\ell =t}^{i} d_{\ell }-Q)\}\)), and

$$\begin{aligned} \overline{U}[t,k-1]=\{d: {d}_{i} = \overline{d}_{i}+ \delta _i \widehat{d}_{i}, -1 \le \delta _{i} \le 1, i =t,\ldots ,k-1\}. \end{aligned}$$
(10)

Consider the following example with only one production period.

Example 1

Consider \(N=\{1,2,3\}\) with \(s_0=0,\) \(y=(1,0,0)\) (which corresponds to \(t=1\) and \(k=n+1=4),\) \(x=(7,0,0),\) \(\overline{d}_t=3, t \in N,\) \(\widehat{d}=(0.5,0.5,0.5),\) \(h_t=1, t \in N,\) \(b_t=1, t \in N.\) We can see that the adversarial problem (9) has optimal solution with \(d=(2.5, 2.5, 3.5),\) obtained with \(d_1=\overline{d}_1-\widehat{d}_1,\) \(d_2=\overline{d}_2-\widehat{d}_2,\) \(d_3=\overline{d}_3+\widehat{d}_3,\) giving an objective function value of 8, which does not correspond to any of the two extreme scenarios \(d^{L}=(2.5, 2.5, 2.5)\) and \(d^{U}=(3.5, 3.5, 3.5),\) both giving an objective function value of 7.

The adversary’s policy is optimal to the adversary problem (9) when the constraints \(\delta _i = \delta _j,\) for all \(i, j \in \{t,\ldots ,k-1\},\) are added to the definition of \(\overline{U}[t,k-1].\) Consequently, in addition to model a practical evaluation of the inventory levels, this policy has two advantages in relation to considering problem (9) for each interval \(I4{(y)}_{\ell }:\) (i) numerical tractability and (ii) reduction of conservatism.

The following proposition is fundamental to model the adversary’s decision.

Proposition 1

Let \(C_{tk}^{L}(Q) = \sum _{i=t}^{k-1} \max \{h_i (Q-\sum _{\ell =t}^{i}(\overline{d}_{\ell }-\widehat{d}_{\ell })), b_i (\sum _{\ell =t}^{i}(\overline{d}_{\ell }-\widehat{d}_{\ell })-Q)\}\) denote the inventory cost in case the demands are at their lowest value, and \(C_{tk}^{U}(Q) = \sum _{i=t}^{k-1} \max \{h_i (Q-\sum _{\ell =t}^{i}(\overline{d}_{\ell }+\widehat{d}_{\ell })), b_i (\sum _{\ell =t}^{i}(\overline{d}_{\ell }+\widehat{d}_{\ell })-Q)\}\) denote the inventory cost in case the demands are at their highest value, when t and k are consecutive production periods and the inventory level at the beginning of period t is Q. Assume \(h_i> 0, b_i > 0, i \in N.\) Then the function \(f_{tk}(Q)=C_{tk}^{L}(Q)-C_{tk}^{U}(Q)\) is strictly increasing in \([0, \sum _{i \in N}(\overline{d}_{i}+\widehat{d}_{i})]\).

The proof is left to the “Appendix”. As function \(f_{tk}(Q)\) is continuous (since both \(C_{tk}^{L}(Q)\) and \(C_{tk}^{U}(Q)\) are continuous), then using Proposition 1 we conclude that there exists a threshold point, denoted by \(Q_{tk},\) above which the adversary opts by (6) and below which opts by (7). That is, the adversary follows the policy (denoted by policy Adv):

$$\begin{aligned}&s_{t-1}+x_{t}-r_{t-1}- Q_{tk} > 0 \Rightarrow d_{i}=\overline{d}_{i}-\widehat{d}_{i}, i=t, \ldots , k-1 \end{aligned}$$
(11)
$$\begin{aligned}&s_{t-1}+x_{t}-r_{t-1}- Q_{tk} < 0 \Rightarrow d_{i}=\overline{d}_{i}+\widehat{d}_{i}, i=t, \ldots , k-1 \end{aligned}$$
(12)

For the case \(s_{t-1}+x_{t}-r_{t-1}- Q_{tk}=0\) the choice is arbitrary.

Let \(N'=N \cup \{n+1\}.\) Observe that for each pair of time periods \(t \in N, k \in N', k >t,\) the threshold point can be computed in advance. For instance, one can use the bisection method.

Example 2

Consider the data given in Example 1 except for the values of production variables x that are not specified. Let the inventory at period 1 be \(Q=s_0+x_1-r_0=x_1.\) Hence: \(C_{14}^{L}(Q)=\max \{1(Q-2.5),1(2.5-Q)\}+\max \{1(Q-5),1(5-Q)\}\) \(+\max \{1(Q-7.5),1(7.5-Q)\},\) and \(C_{14}^{U}(Q)=\max \{1(Q-3.5),1(3.5-Q)\}+\max \{1(Q-7),1(7-Q)\}\) \(+\max \{1(Q-10.5),1(10.5-Q)\}.\) The maximum possible value for demand is 10.5. For an inventory of \(Q=0\) we have \(C_{14}^{L}(Q)=2.5+5+7.5=15 < C_{14}^{U}(Q)=3.5+7+10.5=21.\) For \(Q=10.5\) we have \(C_{14}^{L}(Q)=8+5.5+3=16.5 > C_{14}^{U}(Q)=7+3.5+0=10.5.\) Since from Proposition 1 function \(f(Q) = C_{14}^{L}(Q)-C_{14}^{U}(Q)\) is increasing, we conclude that f(Q) has one zero in [0, 10.5]. Using the bisection method, we obtain as threshold point \(Q_{14}=7.5\) (which gives the zero of function f(Q)).

2.2 Formulation of the robust problem

Now we are at position to formulate the robust lot-sizing problem where the DM assumes (following a robust approach) that the worst-case between the two options will occur. The adversary’s policy can be modeled using auxiliary binary variables. For each \(t \in N \cup \{0\}, k \in N', k > t,\) binary variables \(\delta _{tk}\) indicates whether the demand should be at the highest allowed value, when t and k are consecutive production periods, and variables \(\gamma _{tk}\) indicate whether the demand should be at the lowest allowed value. Using these variables, the demand at period t is \(\overline{d}_{t}+\Delta _t\) where

$$\begin{aligned} \Delta _t=-\widehat{d}_{t} \sum _{i = 0}^{t} \sum _{k = t+1}^{n+1} \delta _{ik}+\widehat{d}_{t}\sum _{i = 0}^{t} \sum _{k = t+1}^{n+1}\gamma _{ik}. \end{aligned}$$

In addition, we use binary variables \(z_{tk}\) that indicate whether t and k are consecutive production periods. Variables \(z_{0k},\) \(\gamma _{0k},\) and \(\delta _{0k}\) (corresponding to \(t=0\)) model the case where k is the first production period. We assume \(z_{tk}=0,\) \(t \in N, k \le t\) and \(\delta _{0k}=0, k \in N,\) since in this case the highest cost occurs when the demand is higher.

The formulation to minimize the set-up and production costs, and the worst-case - in relation to policy Adv - inventory costs between production periods, is as follows:

$$\begin{aligned} min \qquad&\sum _{t \in N} (h_{t} s_{t} + b_{t} r_{t} + p_{t} x_{t}+ f_{t} y_{t}) \end{aligned}$$
(13)
$$\begin{aligned} s. t. \qquad&s_{t-1}+x_{t}+r_{t}=\overline{d}_{t}+\Delta _t +s_{t}+r_{t-1}, \; t \in N \end{aligned}$$
(14)
$$\begin{aligned}&(3)-(5) \nonumber \\&z_{tk} \le y_{t}, \; t \in N, k = t+1, \ldots , n \end{aligned}$$
(15)
$$\begin{aligned}&z_{tk} \le y_{k}, \; t \in N, k = t+1, \ldots , n \end{aligned}$$
(16)
$$\begin{aligned}&z_{tk} \ge y_{t}+y_{k}-1-\sum _{i = t+1}^{k-1}y_{i}, \; t \in N, k = t+1, \ldots , n \end{aligned}$$
(17)
$$\begin{aligned}&z_{t,n+1} \le y_{t}, \; t \in N \end{aligned}$$
(18)
$$\begin{aligned}&z_{t,n+1} \ge y_{t}-\sum _{i=t+1}^{n} y_{i}, \; t \in N \end{aligned}$$
(19)
$$\begin{aligned}&z_{0t} \le y_{t}, \; t \in N \end{aligned}$$
(20)
$$\begin{aligned}&z_{0t} \ge y_{t}-\sum _{i = 1}^{t-1}y_{i}, \; t \in N \end{aligned}$$
(21)
$$\begin{aligned}&\sum _{k = t}^{n+1} z_{tk} \le 1, \; t \in N \end{aligned}$$
(22)
$$\begin{aligned}&\gamma _{tk}+\delta _{tk}=z_{tk}, \; t \in N\cup \{0\}, k \in N' \end{aligned}$$
(23)
$$\begin{aligned}&s_{t-1}+x_{t}-r_{t-1}-Q_{tk}\le M (1-z_{tk}) +M \delta _{tk}, \; t \in N, k \in N' \end{aligned}$$
(24)
$$\begin{aligned}&Q_{tk}-s_{t-1}-x_{t}+r_{t-1} \le M (1-z_{tk})+M \gamma _{tk}, \; t \in N, k \in N' \end{aligned}$$
(25)
$$\begin{aligned}&z_{tk}, \gamma _{tk}, \delta _{tk} \in \{0,1\}, t \in N, k \in N' \end{aligned}$$
(26)

The objective function (13) is the same as the one for the deterministic model. The conservation constraints (14) are obtained from the deterministic constraints (2) by replacing the demand in period t, \(d_t,\) with \(\overline{d}_{t}+\Delta _t,\) which gives \(\overline{d}_{t}-\widehat{d}_{t}\) if one of the variables \(\delta _{ik},\) \(i \le t, k > t,\) is one, and \(\overline{d}_{t}+\widehat{d}_{t}\) if one of the variables \(\gamma _{ik},\) \(i \le t, k > t,\) is one. Constraints (15)-(17) model variables \(z_{tk}.\) Constraints (15), (16) ensure that variable \(z_{tk}\) is zero if there is no set-up in period t or period k. Constraints (17) force \(z_{tk}\) to be at least one if there is a set-up in periods t and k (\(y_t=y_k=1)\) and no set-up between these two periods (\(y_i=0, i =t+1,\ldots ,k-1\)). Constraints (18), (19) model variables \(z_{t,n+1}\) and constraints (20), (21) model variables \(z_{0t}.\) Constraints (22) ensure that if there is a set-up at time period t,  then there can be only one set-up following that period. Constraints (23) state that if t and k are consecutive production periods \((z_{tk}=1)\), than one of the variables \(\gamma _{tk},\) \(\delta _{tk}\) must be one, otherwise \((z_{tk}=0)\), both variables must be null. Constraints (24) and (25) model relations (11), (12). These constraints are active only when \(z_{tk}=1,\) that is, when t and k are consecutive production periods. In this case, if \(s_{t-1}+x_{t}-r_{t-1} > Q_{tk}\) then constraints (24) force \(\delta _{tk}\) to be one, otherwise, if \(s_{t-1}+x_{t}-r_{t-1} < Q_{tk}\) then constraints (25) force \(\gamma _{tk}\) to be one. In case \(s_{t-1}+x_{t}-r_{t-1}- Q_{tk} =0,\) either \(\delta _{tk}\) or \(\gamma _{tk}\) can be fixed to one. Constraints (26) define the domain of the variables.

We denote the robust model (3)–(5), (13)–(26) for the lot-sizing problem by RLS.

To compute the value of M,  one may bound the inventory at period t by the maximum possible accumulated demand during the entire horizon minus the initial inventory level, that is \(\sum _{i \in N}(\overline{d}_{t}+\widehat{d}_{t})-s_0.\) However, it is well-known that obtaining tighter bounds is very important to solve efficiently the model. Better bounds can be devised for each t and k,  and for each variable. In order to do that, the value of M must be adjusted to t and k and to the variable in each constraint. Thus, we replace M by \(M^{z1}_{tk}\) and \(M^{\delta }_{tk}\) in constraints (24) and by \(M^{z2}_{tk}\) and \(M^{\gamma }_{tk}\) in constraints (25).

First, consider the case of constraints (24). The role of variables \(z_{tk}\) and \(\delta _{tk}\) is different. The value \(M^{\delta }_{tk}\) becomes active when \(z_{tk}=\delta _{tk}=1,\) that is, when t and k are two consecutive production periods and the demand is at its highest value. In this case, \(s_{t-1}+x_{t}-r_{t-1}\) can be upper bounded by \(\sum _{i =t}^n(\overline{d}_i+\widehat{d}_i),\) thus, \(M^{\delta }_{tk}=\sum _{i =t}^n(\overline{d}_i+\widehat{d}_i)-Q_{tk}.\) However, looking at optimal solutions, a tighter bound that may cut feasible suboptimal solutions can be set to \(M^{\delta }_{tk}=\sum _{i =t}^{k-1}(\overline{d}_i+\widehat{d}_i)-Q_{tk}\) when non speculative costs are considered, that is, when it is less expensive to produce the demand of period k in period k,  than to produce it in period t and keep it in stock from t to k. For the coefficient of \(z_{tk},\) the bound occurs for the case \(z_{tk}=0.\) In this case we set \(M^{z1}_{tk}=\sum _{i =t}^{n}(\overline{d}_{t}+\widehat{d}_{t})-Q_{tk}.\) However, again, we can establish a tighter bound for \(s_{t-1}+x_{t}-r_{t-1}\) by determining the lowest time period \(u > t\) such that \((\overline{d}_u-\widehat{d}_u)(p_t+\sum _{i =t}^{u-1}h_i) \ge f_u+p_u(\overline{d}_u-\widehat{d}_u)\) (this means that it costs less to produce the demand in period u than to carry that demand from period t), and setting \(M^{z1}_{tk}=\sum _{i =t}^{u-1}(\overline{d}_{t}+\widehat{d}_{t})-Q_{tk}.\)

Similarly, in constraints (25), \(-s_{t-1}-x_{t}+r_{t-1}\) can be upper bounded by \(\sum _{i =1}^{t-1}(\overline{d}_i+\widehat{d}_i),\) giving \(M^{\gamma }_{tk} =\sum _{i =1}^{t-1}(\overline{d}_i+\widehat{d}_i)+Q_{tk}.\) Considering optimal solutions, a tighter bound can be devised by determining the largest u such that \((\overline{d}_u-\widehat{d}_u)(p_t+\sum _{i =u}^{t-1}b_i) \ge f_u+p_u(\overline{d}_u-\widehat{d}_u)\) (this means that it costs less to produce the demand in period u than to backlog that demand from period t), and setting \(M^{\gamma }_{tk} =\sum _{i =u+1}^{t-1}(\overline{d}_i+\widehat{d}_i)+Q_{tk}.\) For these constraints we can take \(M^{z2}_{tk}=M^{\gamma }_{tk}.\)

3 Column-and-row generation

Model RLS has some weaknesses, namely, it includes a large number of binary variables and a large number of big-M constraints (constraints (24), (25)). These constraints make the model large and weak in the sense that such constraints lead to a model providing poor linear relaxation bounds. Thus, applying an exact approach based on this mixed-integer model, such as the branch-and-cut, may lead to high running times. An approach to reduce the size of the model is to add constraints (24), (25) and the corresponding variables dynamically. Such inequalities become active when \(z_{tk} =1.\) The column-and-row generation algorithm proposed in Algorithm 1 generates dynamically these constraints as well as inequalities (23), which are not restrictive when constraints (24), (25) are omitted.

figure a

Observe if we aim to develop the most efficient implementation, instead of computing the threshold points \(Q_{tk}\) in a preprocessing phase, they can be computed in Step 6 when they are used.

4 Computational experiments

It is well-known that from a practical point of view only part of the decisions in the optimal solution may be implemented and the inventory costs may differ from those in the optimal solution since, most likely, the observed demands may not follow exactly the adversary policy. Here we assume that the set-up decisions are static and, therefore, will be implemented. Hence the examples and computational tests are oriented for these more rigid and important decisions in the production planning. First we present two examples that illustrate the usefulness of our approach.

Example 1

Consider an instance with \(n=4,\) \(f_t=60,\) \(p_t=0,\) \(h_t=1,\) \(b_t=2,\) for all \(t \in N,\) \(b_{n+1}=12,\) and \(\overline{d}=(20, 21, 21, 19),\) \(\widehat{d}_t=0.1\overline{d}_t,\) for all \(t \in N,\) and \(c=(33, 46, 48, 38).\)

The deterministic solution is \(y_1 = y_3 = 1,\) \(x_1 = 33,\) \(x_3 = 48,\) with cost 168. If the adversarial follows policy Adv, with the set-ups fixed, the objective function value is 172.26. The optimal robust solution has a single setup occurring in period 2 and a value of 168.7.

This example illustrates a case where the production capacity prevents the production plan to adjust to a variation in the demands, leading to large backlog costs. The drawback of this deterministic solution could be prevented using other robust approaches.

Example 2

Consider an instance with \(n=6,\) \(f_t=60,\) \(p_t=0,\) \(h_t=1,\) \(\overline{d}_t=20,\) \(\hat{d}_t=2,\) \(c_t=M,\) for all \(t \in N,\) and \(b_t=2,\) \(t \in N'.\) The deterministic model has optimal alternative solutions with \(y_2 = y_4 = 1,\) \(x_2 = 60,\) \(x_4 = 40,\) and \(y_1 = y_4 = 1,\) \(x_1= 60,\) \(x_4= 40,\) with cost 240. The robust solution is \(y_1 = y_4 = 1,\) with a worst-case cost (assuming the adversarial follows policy N) of 252. With the first deterministic solution the worst-case cost is 255.9375.

This example illustrates the main goal of our approach, that is, when the DM wishes to fix the set-up periods and alternative deterministic solutions exist with comparable costs, the robust solution chooses the one that prevents the occurrence of large inventory costs.

Next we present the computational experiments carried out to test the column-and-row generation algorithm and compare the deterministic and robust models. The formulations are written in Mosel and implemented in Xpress-IVE Version 5.8.1, with 64 bits. All the tests were run on a computer with a CPU Intel(R) Core i7-10510U, with 16GB RAM and using the Xpress Optimizer Version 39.01.02 with the default options.

4.1 Testing the column-and-row generation algorithm

In order to test the robust model RLS and the efficiency of Algorithm 1 we consider a set of instances with n varying in \(\{20, 30, 40, 50\}\) and with \(f_t=100,\) \(h_t=1,\) \(p_t\) randomly generated in [1, 2],  \(\overline{d}_t\) randomly generated in [18, 22],  \(\hat{d}_t=0.1 \overline{d}_t,\) \(c_t=M,\) for all \(t \in N,\) and \(b_t=2,\) \(t \in N'.\) Three instances are randomly generated for each set of parameters. The results are reported in Table 1 for both approaches with \(M=1000.\) Column n gives the corresponding value of n,  column ‘version’ gives the version of the instance generated. The number of iterations performed by Algorithm 1 is given in column ‘iter’. The running times in seconds are given in columns ‘time’. A running time limit of 2 h was imposed to each instance. The objective function value of the best feasible solution is given in columns ‘obj'. The values in boldface represent instances where the optimal solution was not obtained. Column ‘Sp' gives the number of set-up periods in the optimal solution.

Table 1 Computational results comparing Algorithm 1 with original robust model
Full size table

The results clearly indicate that solving the problem with Algorithm 1 is much faster than using the robust model RLS directly. All the instances are solved to optimality using Algorithm 1, although the running times increase considerable with the increase of n. Using directly the robust model, only instances up to \(n=30\) where solved to optimality. For the instances with \(n=40\) the optimal solution is obtained but the branch-and-cut failed to prove optimality within the time limit. We can also observe that the number of iterations required by Algorithm 1 is relatively small and it increases slightly with the increase of n.

In order to understand the behaviour of the two tested approaches, Table 2 gives the dimension of model RLS. As the values obtained are equal for the three versions, we give only the results for the number of periods n. The results are given both for the model without preprocessing and the model after the preprocessing phase.

Table 2 Dimension of model RLS
Full size table

4.2 Comparison with the deterministic solution

In Table 3 we give the results obtained using both the deterministic and the robust models. The data used is the same as the one given in Sect. 4.1 with the exception of the unit backlog cost which is given in column ‘\(b_t\)’. Column ‘Dobj’ gives the objective function of the deterministic model while columns ‘\(obj_D\)’ and ‘\(obj_R\)’ give the objective function value of the robust model for the corresponding model. For the deterministic case (under columns ‘Deterministic’) we first solve the deterministic model, then we fix the set-ups to their value in the optimal solution and optimize the resulting restricted robust model. The value in column ‘\(obj_D\)’ corresponds to the value of the solution obtained using this procedure. This means that the given cost corresponds to the case where the set-ups are fixed and the DM takes the optimal decisions regarding the production quantities while the adversary plays according to rule Adv. For the robust case (under columns RLS), the robust model RLS is solved and the objective function value and the number of set-ups of the optimal solution are given in columns \(obj_R\) and Sp,  respectively. Column ‘PiR’ gives, in percentage, the deviation between the cost obtained using the robust and the deterministic approaches, that is, \(100 \frac{obj_D-obj_R}{obj_R}.\) This percentage gives the gain of using the robust approach instead of the deterministic one when the solution is evaluated using the rule Adv, or, saying differently, is the price of ignoring uncertainty. The value in column ‘PoR’ gives, in percentage, the deviation between the nominal (deterministic) value and the value of the robust approach, that is, \(100 \frac{obj_R-Dobj}{obj_R},\) which is known as the price of robustness.

Table 3 Comparison of deterministic solution with the robust solutions for \(n=20\)
Full size table

From the results we observe that for all the tested instances, fixing the set-ups according to the deterministic model always leads to non-optimal decisions when facing uncertainty. For the third instance, the deviation (see column ‘PiR’) is larger than 5%. Additionally, we observe that for several instances the number of set-up periods differs according to the model used, which means that the structure of the solutions obtained are quite different. Additionally, we can also observe from column ‘PoR’ that the deviation between the deterministic and robust values is larger when the backlog costs are higher.

5 Conclusions

We propose a new robust model for a lot sizing problem that takes into account demand uncertainty where the adversary follows a simple policy, by setting the demand between consecutive production periods, either at its lower level or at its highest level. Such policy can be seen as a simple rule to evaluate the solution, and has the advantage that it can be easily understood by the decision makers. By design, the proposed model is less conservative than some of the most common robust models used in the literature because it restricts the actions of the adversary to the two possible options. Computational experiments show that the structure of the robust solutions are different from the deterministic ones, leading in some cases to different production (set-up) periods. The tests also show that the new model is large and a column-and-row generation algorithm improves the running times significantly. The proposed model is tractable but has a large number of binary variables and constraints. Despite the column-and-row generation algorithm proposed, further research is needed to solve large size instances. A possible direction of future research is to devise tighter formulations through extended formulations or families of valid inequalities. A second direction is to extend the idea of using heuristic policies for the adversary to obtain tractable robust models.