Equilibrium uniqueness in aggregative games: very practical conditions

Abstract

Various Nash equilibrium results for a broad class of aggregative games are presented. The main ones concern equilibrium uniqueness. The setting presupposes that each player has $\mathbb {R}_+$ as strategy set, makes smoothness assumptions but allows for a discontinuity of stand-alone payoff functions at 0; this possibility is especially important for various contest and oligopolistic games. Conditions are completely in terms of marginal reductions which may be considered as primitives of the game. For many games in the literature they can easily be checked. They automatically imply that conditional payoff functions are strictly quasi-concave. The results are proved by means of the Szidarovszky variant of the Selten–Szidarovszky technique. Their power is illustrated by reproducing quickly and improving upon various results for economic games.

1 Introduction

The present article deals with equilibrium uniqueness for games in strategic form with an aggregative structure. Equilibrium uniqueness comes down to equilibrium existence together with equilibrium semi-uniqueness, i.e. that there exists at most one equilibrium. Although equilibrium existence has been extensively studied in the literature, practical strong equilibrium (semi-)uniqueness results are lacking.

A milestone is (the following variant of) a result in [24] of Nikaido and Isoda (e.g. see Theorem 1 in [10]) for games in strategic form stating that for the existence of a Nash equilibrium, it is sufficient that strategy sets are convex compact subsets of an Euclidean vector space, payoff functions are continuous and conditional payoff functions are quasiconcave. We further refer to this result as the Nikaido–Isoda theorem.¹ The Nikaido–Isoda theorem applies to many classes of economic games, especially to games with an aggregative structure like oligopolistic, public good, cost-sharing, common resource and contest games (e.g. see [6, 17]). However, it does not address equilibrium semi-uniqueness and does not apply to games with a discontinuity at the origin, which especially occurs in contest games and oligopolistic games (see, e.g.  [16, 34, 41, 47]).² In addition, for various concrete games it may not be so clear whether its quasi-concavity assumption holds. So it would be useful to have a result that, for a setting similar to that for the Nikaido–Isoda theorem, also addresses equilibrium semi-uniqueness, allows for a discontinuity at the origin and is subject to conditions, in particular one concerning quasi-concavity, that for concrete games are easy to check in terms of the primitives of the game.³

The goal of the paper [6] of Cornes and Hartley was to present such a follow-up to the Nikaido–Isoda theorem for aggregative games. However, their paper was not able to be finished due to the death of Richard Cornes. The present study, finally, provides the intended follow-up; the games we deal with are referred to as ‘smooth aggregative games’. As primitives, we use what we call ‘marginal reductions’. These very useful objects were first introduced in [3] by Corchón. Our main results are summarized in four theorems, i.e. Theorems 1–4 in Sect. 3. These theorems are stated completely in terms of four assumptions; certainly the most interesting (and powerful) is Assumption A2 (see Sect. 3). The proofs of these theorems are by means of the Szidarovszky variant of the Selten–Szidarovszky technique using backward response and share functions. Theorem 1 presents results on whether equilibria are active or inactive, Theorem 2 deals with equilibrium semi-uniqueness, and Theorems 3 and 4 with equilibrium uniqueness.

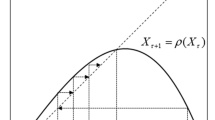
The origin of the Selten–Szidarovszky technique can be found in the article [31] of Selten dealing with aggregative games and in the articles [33, 35] of Szidarovszky dealing with homogeneous Cournot oligopolies. With it one can study the Nash equilibrium set for a broad class of games in strategic form with an aggregative structure; it also is very handy for performing comparative statics ( [1]). The power of the technique lies in the fact that it transforms the fixed point problem for the joint best response correspondence into a lower dimensional, usually 1-dimensional, fixed point problem for the aggregate backward response correspondence, which is much easier to handle and does not require deep theorems like Brouwer’s fixed point theorem. As a bonus, this approach provides an algorithm for the determination of the Nash equilibrium set. Section 4 also contains a short discussion of the Selten–Szidarovszky technique.⁴

Although the idea of how the Selten–Szidarovszky method works is simple and elegant, its implementation may be, as in the present article, subtle and technical. The technicalities are mainly due to the possible discontinuity at the origin, to the non-excluding of inactive players and to the proper handling of boundary issues. These technicalities are handled by further developing ideas in [6] (dealing with aggregative games and share functions), [46] (dealing with aggregative games and backward response functions) and [45] (dealing with Cournot oligopolies and share functions).

The further structure of the article is as follows. Section 2 presents the overall setting and defines the notion of ‘smooth aggregative game’. Proofs are in Sect. 4. The power of Theorems 1 – 4 is illustrated with two examples in Sect. 5 by reproducing quickly and improving upon various results for economic games. The first example deals with a homogeneous Cournot oligopoly with an industry revenue function that is possibly discontinuous at 0 and the second example with a class of games appearing in the managerial theory of the firm.

2 Setting

In this section we fix the setting for the games, referred to as almost smooth aggregative games, dealt with in the present article.

First of all we deal with a game in strategic form. We denote its player set by $N :=\{1,\ldots ,n\}$, the strategy set of player i by $X_i$ and his payoff function by $f_i$. We denote ${\mathbf {X}}:=X_1 \times \cdots \times X_n$, ${\mathbf {X}}_{\hat{\imath }} :=X_1 \times \cdots \times X_{i-1} \times X_{i+1} \times \cdots \times X_n$, identify ${\mathbf {X}}$ with $X_i \times {\mathbf {X}}_{\hat{\imath }}$, and accordingly write ${\mathbf {x}} \in {\mathbf {X}}$ as ${\mathbf {x}} =(x_i;{\mathbf {x}}_{\hat{\imath }} )$. For $i \in N$ and ${\mathbf {z}} \in {\mathbf {X}}_{\hat{\imath }}$, the conditional payoff function $f_i^{( {\mathbf {z}} )}$ is the function $X_i \rightarrow \mathbb {R}$ defined by $f_i^{( {\mathbf {z}} )}(x_i) = f_i(x_i;{\mathbf {z}})$. Let

$$\begin{aligned} \varDelta :=\{ (x,y) \in \mathbb {R}_+^2 \; | \; x \le y \} \text{ and } \varDelta ^+ :=\varDelta \setminus \{ (0,0) \}. \end{aligned}$$

(1)

Definition 1

An almost smooth aggregative game is a game in strategic form with $n \ge 2$ and $X_i = \mathbb {R}_+ \; (i \in N)$, and that satisfies the following assumptions.

• a. For every $i \in N$:

  • each function $f_i^{({\mathbf {z}})}$ with ${\mathbf {z}} \ne {\mathbf {0}}$ is twice differentiable; the function $f_i^{({\mathbf {0}})}$ is twice differentiable on $\mathbb {R}_{++}$ and its derivative at 0 exists in $\mathbb {R} \cup \{ + \infty \}$;

  • there exists a function $t_i: \varDelta \rightarrow \mathbb {R} \cup \{ + \infty \}$ such that for all ${\mathbf {z}} \in {\mathbf {X}}_{\hat{\imath }}$ and $x_i \in X_i$

    $$\begin{aligned} D f_i^{({\mathbf {z}})}(x_i) = t_i\left( x_i, x_i + \sum _l z_l\right) . \end{aligned}$$

    (2)

• b. For every $i \in N$

  • $t_i$ is on $\varDelta ^+$ continuous and

    $$\begin{aligned} \lim _{y \downarrow 0} t_i(0,y) = t_i(0,0); \end{aligned}$$

    (3)

  • $t_i$ is on $\varDelta ^+$ partially differentiable and $t_i$ is differentiable on the interior of its domain.

• c. For every $i \in N$ and for every $x_i \in X_i$ and ${\mathbf {z}} \in {\mathbf {X}}_{\hat{\imath }}$ with⁵$x_i+ \sum _l z_l \ne 0$

  $$\begin{aligned} D^2 f_i^{({\mathbf {z}})}(x_i) = (D_1+ D_2) t_i(x_i,x_i+ \sum _l z_l). \;\;\; \diamond \end{aligned}$$

  (4)

Assumption a features the aggregative structure.⁶ We refer to the conditional payoff function $f_i^{({\mathbf {0}})}$ as the stand-alone payoff function of player i. Note that at 0 discontinuous stand-alone payoff functions are allowed (which explains the ‘almost’ in ‘almost smooth’). Also note that we only suppose that $t_i$ is differentiable (instead of, as usual, twice continuous differentiability) on the interior of its domain. The function $t_i$ is uniquely determined and is referred to as marginal reduction for player i.⁷ The next assumption concerns additional smoothness.

As has become clear from articles like [28, 36, 39], smoothness assumptions play a very important role when one is looking for sufficient conditions for equilibrium semi-uniqueness. Assumptions b and c concern our further smoothness assumptions. The smoothness assumptions used are not independent. However, the way in which we state them is convenient for the presentation.⁸ Note that $t_i$ may take the value $+ \infty$ only at (0, 0) and that

$$\begin{aligned} t_i(0,0) \ne + \infty \; \Leftrightarrow \; f_i^{({\mathbf {0}})} \text{ is } \text{ differentiable } \; \Rightarrow \; f_i^{({\mathbf {0}})} \text{ is } \text{ continuous }. \end{aligned}$$

(5)

But if $f_i^{({\mathbf {0}})}$ is continuous at 0, then $t_i(0,0) = + \infty$ may hold. Also note that⁹

$$\begin{aligned} f_i^{({\mathbf {0}})} \text{ is } \text{ lower } \text{ semi-continuous }. \end{aligned}$$

(6)

Many economic games in strategic form that the literature deals with are almost smooth aggregative games.

3 Main results

Our main results, i.e. Theorems 1–4 below, can be stated completely in terms of some of the following additional assumptions A1, A2, A2’ and B for an almost smooth aggregative game. These assumptions are in terms of the marginal reductions $t_i: \{ (x_i,y) \in \mathbb {R}^2_+ \; | \; x_i \le y \} \rightarrow \mathbb {R} \cup \{ + \infty \}$ and use

$$\begin{aligned} {\tilde{N}} :=\{ i \in N \; | \; t_i(0,y)> 0 \text{ for } \text{ some } y > 0 \}. \end{aligned}$$

• A1. For all $i \in N$ and $y > 0$: $[0 \le x_i \le y \, \wedge \, t_i(x_i,y) = 0] \; \Rightarrow \; D_1 t_i(x_i,y) < 0$.

• A2. For all $i \in {\tilde{N}}$ and $y > 0$: $[0< x_i \le y \, \wedge \, t_i(x_i,y) = 0] \; \Rightarrow \; (x_i D_1 + y D_2) t_i(x_i,y) < 0$;

• A2’. For all $i \in {\tilde{N}}$ and $0 \le y < y'$: $t_i(0,y) \le 0 \; \Rightarrow \; t_i(0,y') \le 0$;

• B. For all $i \in {\tilde{N}}$, there exists ${\overline{x}}_i > 0$ such that $t_i(x_i,y) < 0$ for every $x_i,y$ with ${\overline{x}}_i < x_i \le y$.

The next section contains additional results, which also may be interesting in themselves, where the following additional assumption is also used:

• C. For all $i \in {\tilde{N}}$ and $x_i > 0$: $t_i(x_i,x_i) = 0 \; \Rightarrow \; (D_1 + D_2) t_i(x_i,x_i)$.

Below we also consider situations where such an assumption just holds for a specific player i; then we add [i] to the assumption; for example, A1[i], in Lemma 1. Of course, Assumption C[i] holds if Assumption A2[i] holds.

Assumptions A1 and A2 are sophisticated variants of what are called (generalised) Fisher-Hahn conditions in [27].¹⁰ Assumption A2, as it is a new one, certainly is the most interesting. Strategy sets are not compact; Assumption B deals with ‘essential compactness’ in the sense that it provides the appropriate compactness for our results dealing with equilibrium existence.

The simple Assumption A2’ in fact represents what we want to have in A2 by allowing there $x_i=0$. The reason for splitting up these assumptions is that it is from a theoretical point interesting to see what implies what.

In the theorems below also the set

$$\begin{aligned} N_> :=\{ i \in N \; | \; t_i(0,0) > 0 \} \end{aligned}$$

appears. Note that (3) implies

$$\begin{aligned} N_> \subseteq {\tilde{N}}. \end{aligned}$$

The sets ${\tilde{N}}$ and $N_>$ play an important role for a proper handling of boundary issues.

Remarks 1. Sufficient for Assumption A2’[i] to hold is that the function $t_i(0,\cdot )$ is decreasing.

2. If Assumption A2’[i] holds (so $i \in {\tilde{N}}$), then $i \in N_>$. So if Assumption A2’ holds, then $N_> = {\tilde{N}}$.

3. Proposition 1(3) below shows that Assumptions A1, A2 and A2’ guarantee that each conditional payoff function is strictly quasi-concave and therefore that each Nash equilibrium is then strict.

The following theorems present our main results for the Nash equilibrium set E. Proofs are in Sect. 4.¹¹

Our first theorem presents some results concerning active/inactive¹² and strict equilibria.

Theorem 1

Consider an almost smooth aggregative game.

• 1. If $N_> \ne \emptyset$, then each Nash equilibrium is active.

• 2.

  • (a) Suppose Assumption A1 holds. In any equilibrium, each player from $N \setminus {\tilde{N}}$ is inactive.

  • (b) Suppose Assumption A1 holds. If ${\tilde{N}} = \emptyset$, then $E = \{ {\mathbf {0}} \}$.

• 3. If Assumptions A1 and A2’ hold, then ${\mathbf {0}} \in E \; \Rightarrow \; E = \{ {\mathbf {0}} \}$. $\diamond$

Remark 4. Theorem 1 implies: if Assumptions A1 and A2’ hold, then $\# E \ge 2 \; \Rightarrow \; {\mathbf {0}} \not \in E$.

The next theorem deals with equilibrium semi-uniqueness.

Theorem 2

Consider an almost smooth aggregative game. If Assumptions A1, A2 and A2’ hold, then $\# E \le 1$. $\diamond$

Remark 3 implies that in Theorem 2 conditional payoff functions are strictly quasi-concave. As in this theorem stand-alone payoff functions may be discontinuous at 0, adding some effective compactness condition, like Assumption B, does not lead to equilibrium existence by means of a Nikaido–Isoda like theorem. However, by also adding some information about the type of discontinuity, as Theorem 3 shows, equilibrium existence follows.

Many types of discontinuities at 0 for stand-alone payoff functions $f_i^{({\mathbf {0}})}$ are possible. Concerning this, define for $i \in N$ the function ${\overline{t}}_i: \mathbb {R}_{++} \rightarrow \mathbb {R}$ by

$$\begin{aligned} {\overline{t}}_i(x_i) :=t_i(x_i,x_i) = D f_i^{({\mathbf {0}})}(x_i). \end{aligned}$$

(7)

and call¹³ player $i \in {\tilde{N}}$

• of class I if ${\overline{t}}_i(x_i) > 0$ for $x_i > 0$ small enough;

• of class II if ${\overline{t}}_i(x_i) < 0$ for $x_i > 0$ small enough.

Before continuing, it may be useful to illustrate these types of discontinuity by means of a homogeneous Cournot oligopoly. So consider such an oligopoly with at least two firms where each firm i has strategy set $\mathbb {R}_+$ and payoff function

$$\begin{aligned} f_i({\mathbf {x}}) = p\left( \sum _l x_l \right) x_i - c_i(x_i). \end{aligned}$$

(8)

Here $c_i$ is the cost function of firm i and p a price function with a positive proper price function¹⁴${\tilde{p}}(y)$. In order to guarantee that the game is a smooth aggregative game, we further suppose that ${\tilde{p}}$ is decreasing and twice differentiable and that every $c_i$ is twice differentiable. Let ${\overline{p}}(0) :=\lim _{y \downarrow 0} {\tilde{p}}(y) \in ] {0},{+\infty } ]$. We have $f_i^{({\mathbf {z}})}(x_i) = p( x_i + \sum _l z_l) x_i - c_i(x_i)$ and see that the marginal reductions $t_i: \varDelta \rightarrow \mathbb {R} \cup \{ + \infty \}$ are well-defined and given by

$$\begin{aligned} t_i(x_i,y) = \left\{ \begin{array}{c} D {\tilde{p}}(y) x_i + {\tilde{p}}(y) - D c_i(x_i) \text{ if } (x_i,y) \ne (0,0), \\ {\overline{p}}(0) - Dc_i(0) \text{ if } (x_i,y) =(0,0). \end{array} \right. \end{aligned}$$

(9)

Thus the game is a smooth aggregative game. Note that the stand-alone payoff function is discontinuous at 0 if and only if, denoting with $r_p :=p \cdot \mathrm {Id}$ the industry revenue function, $r_p$ is discontinuous at 0. As ${\tilde{p}}$ is decreasing, Assumption A2’ holds and therefore, by Remark 2, $N_> = {\tilde{N}}$. Also $N_> = \{ i \in N \; | \; {\overline{p}}(0)> Dc_i(0) \}$. With $\epsilon _{{\tilde{p}}}$ the price flexibility of ${\tilde{p}}$, i.e. with $\epsilon _{{\tilde{p}}}(x_i) :=x_i D {\tilde{p}}(x_i)/ {\tilde{p}}(x_i)$, we have ${\overline{t}}_i(x_i) = {\tilde{p}}(x_i) ( \epsilon _{{\tilde{p}}}(x_i) + 1) - Dc_i(x_i)$. For the case where ${\tilde{p}}(y) = y^{-\alpha }$, where $\alpha > 0$, this becomes ${\overline{t}}_i(x_i) = x_i^{-\alpha } (1 -\alpha ) - Dc_i(x_i)$. So if $\alpha > 1$, then i is of class II, if $0< \alpha < 1$, then i is of class I and if $\alpha =1$ and $Dc_i( x_i)> 0 \; ( x_i > 0)$, then i is of class II. Also $r_p$ is discontinuous at 0 if and only if $\alpha \ge 1$. (We continue with this example in Sect. 5.)

Theorem 3

Consider an almost smooth aggregative game. Suppose Assumptions A1, A2, A2’ and B hold. If ${\tilde{N}}$ contains at least one player of class I, then the game has a unique equilibrium. This equilibrium is active. $\diamond$

Note that both Theorem 2 and 3 deal with equilibrium semi-uniqueness while the Nikaido–Isoda theorem only addresses equilibrium existence. Proposition 11 in Sect. 4 provides a Nikaido–Isoda like result for smooth aggregative games which is derived by the Selten–Szidarovszky technique.

Theorem 4 deals with Theorem 3 in the case that ${\tilde{N}}$ does not contain a player of class I; Proposition 8(1) below shows that this is equivalent to that all players in ${\tilde{N}}$ being of class II. The equilibrium uniqueness result in part 3 of this theorem is less explicit than that in Theorem 3. But the fundamental result in its part 2 about the existence of $\lim _{y \downarrow 0} {\hat{b}}_i(y)/y$, makes that this limit in various cases (as illustrated in Examples 1 and 2 in the next section) can be calculated; its part 3 then gives a sufficient and necessary condition for equilibrium uniqueness.

Theorem 4

Consider an almost smooth aggregative game. Suppose Assumptions A1, A2, A2’ and B hold and all players in ${\tilde{N}}$ are of class II.

• 1. For all $i \in {\tilde{N}}$ and $y > 0$ small enough, there exists a unique ${\hat{b}}_i(y) \in ] {0},{y} \, [$ with $t_i({\hat{b}}_i(y),y) = 0$.

• 2. For every $i \in {\tilde{N}}$ the limit ${\overline{s}}_i :=\lim _{y \downarrow 0} \frac{{\hat{b}}_i(y)}{y}$ exists and ${\overline{s}}_i \in ] {0},{1} ]$.

• 3. $\sum _{i \in {\tilde{N}}} {\overline{s}}_i > 1 \; \Leftrightarrow \;[$ $\# E = 1$ and the unique equilibrium is active]. $\diamond$

Remark 5. ${\hat{b}}_i$ in Theorem 4 is the virtual backward response function of player i (see Definition 3 below).

Besides the above theorems, other interesting results can be observed. They can be found in the next section and are presented as propositions. Among other things, there is a result (i.e. Propositions 2 together with 4) that leads to the Selten–Szidarovszky technique in fact providing an algorithm for determining the equilibrium set.

The assumptions made in the above theorems may look technical at first sight. However, they can easily be checked for many games in the literature; we illustrate this in Sect. 5.

4 The Selten–Szidarovzsky technique

In this section we shall prove the statements of the four theorems in Sect. 3 by means of the Szidarovszky variant of the Selten–Szidarovzsky technique. Section 4.1 briefly discusses these variants. Sects. 4.2 and 4.3 deal with the transformation of the n-dimensional fixed point problem of the joint best response correspondence into a 1-dimensional fixed point problem for the aggregate virtual backward response function. In doing so, we have the opportunity to show, as this is theoretically interesting, how the Nash equilibrium problem relates to a specific nonlinear complementarity problem. Section 4.4 proves the four theorems by analysing the aggregate virtual backward response.

4.1 Two variants

As already mentioned in the introduction, the origin of the Selten–Szidarovszky technique can be found in the article [31] of Selten dealing with aggregative games and in the articles [33, 35] of Szidarovszky dealing with homogeneous Cournot oligopolies.¹⁵ Although there are various implementations of this technique, one can distinguish between two main variants: the ‘Selten variant’ and the ‘Szidarovszky variant’.

The ‘Selten variant’ is more general as it does neither require that strategy sets are real intervals nor a certain degree of smoothness of payoff functions. The Szidarovszky nicely exploits and handles the smoothness structure of the game. The main objects in both variants are backward response correspondences. In the Selten variant these correspondences are derived from the usual best response correspondences. In the Szidarovszky variant, best response correspondences are only implicitly present. In this variant, the (virtual) backward response correspondence for player i is derived from his marginal reduction $t_i$. In doing so, necessary (and perhaps sufficient) first order conditions are handled in a clever way.

Marginal reductions were first introduced in [3] by Corchón; in the present article a more sophisticated variant is used (also see footnote 7). In [9], left and right marginal reductions were introduced that can handle settings with weaker smoothness conditions (i.e. semi-differentiability).¹⁶ And [8] shows that marginal reductions also may make sense when one is dealing with higher dimensional strategy sets.

Both variants are very powerful and may be divided into a transformation part and an analysis part. The transformation part transforms the n-dimensional fixed point problem for the joint best response correspondence into a lower dimensional fixed point problem for the aggregate backward response correspondence. The analysis part analyses this fixed point problem. If the fixed point problem (as often is the case like in the present article) is 1-dimensional, equilibrium existence is guaranteed by a 1-dimensional fixed point theorem (may be the intermediate value theorem). As shown in [40] for the Selten variant, the transformation part allows for a purely algebraic setting, which is not necessarily a game theoretic one. Although there are various articles dealing with a systematic treatment of the Selten variant (e.g. [1, 21, 44]), such literature for the Szidarovszky variant is lacking; we are aware only of [46].

As we deal with smooth aggregative games, we shall use the Szidarovszky variant for proving these results. In fact, the present article concerns a major improvement of the implementation of this variant in [46].

4.2 The transformation part: nonlinear complementarity problem

In this subsection we always consider a smooth aggregative game.

Remember that each strategy set $X_i$ is equal to $\mathbb {R}_+$ and therefore that ${\mathbf {X}} =\mathbb {R}^n_+$. Denote for ${\mathbf {x}} \in {\mathbf {X}}$, $x_N :=\sum _l x_l$. Suppose ${\mathbf {e}} \in E$, i.e. ${\mathbf {e}}$ is a Nash equilibrium. Then Fermat’s theorem together with (2) imply for every $i \in N$

$$\begin{aligned} e_i > 0 \Rightarrow t_i(e_i,e_N) = 0 \text{ and } e_i = 0 \Rightarrow t_i(e_i,e_N) \le 0. \end{aligned}$$

This leads us to consider the following problem: find ${\mathbf {x}} \in {\mathbf {X}}$ such that for every $i \in N$

$$\begin{aligned} x_i\, t_i(x_i, x_N) = 0 \, \wedge \, t_i(x_i,x_N) \le 0. \end{aligned}$$

Denoting its set of solutions by $T_{\star }$, we thus have

$$\begin{aligned} E \subseteq T_{\star }. \end{aligned}$$

(10)

A fundamental observation is that ${\mathbf {x}} \in T_{\star }$ if and only if, writing $\varvec{\tau }({\mathbf {x}}) :=(t_1(x_1,x_N),\ldots ,t_n(x_n,x_N))$, ${\mathbf {x}}$ is a solution of the (well-defined¹⁷) nonlinear complementarity problem

$$\begin{aligned} {\mathbf {x}} \cdot \varvec{\tau }({\mathbf {x}}) = 0 \, \wedge \varvec{\tau }({\mathbf {x}}) \le {\mathbf {0}}. \end{aligned}$$

As far as we know, the literature on existence and uniqueness of solutions of nonlinear complementarity problems—and more generally on variational inequality problems (like the book [2] that, as a special case, considers equilibria of games in strategic form)—does not contain results that guarantee the equilibrium semi-uniqueness result of Theorem 2 and the equilibrium uniqueness results of Theorems 3 and 4.¹⁸ The reason is that this literature does not consider the effects of an aggregative structure. We shall approach the nonlinear complementarity problem through the Szidarovszky variant of the Selten–Szidarovszky technique, which takes this structure fully into account.

Proposition 2 shows a further relation between $T_{\star }$ and the equilibrium set E. In order to prove this proposition, we need some lemmas and introduce a general notion which also will be very useful for the remainder.

Definition 2

Let I be a subset of $\mathbb {R}$ and $g: I \rightarrow \mathbb {R}$ a function. We say that g has the AMSCFA-property (‘At Most Single Crossing From Above’) if the following holds: if m is a zero of g, then $g(x) > 0 \; (x < m)$ and $g(x) < 0 \; (x > m)$. $\diamond$

Remark 6. If either of the following conditions hold, then $g: I \rightarrow \mathbb {R}$ has the AMSCFA-property:

• (a) g is strictly decreasing;

• (b) I is a proper real interval, g is continuous and at every $x \in I$ with $g(x) =0$ differentiable with $Dg(x) < 0$;

• (c) I is a proper real interval and g is the derivative of a strictly pseudo-concave function.¹⁹

Lemma 1

Suppose Assumption A1[i] holds. Let $(x_i,y) \in \varDelta ^+$.

• 1. $t_i(x_i,y) =0 \; \Rightarrow \; [ t_i(x_i',y) > 0 \;\; (0 \le x_i'< x_i) \, \wedge \, t_i(x_i',y)< 0 \; (x_i < x'_i \le y) ]$.

• 2. $t_i(x_i,y) \le 0 \; \Rightarrow \; t_i(x_i',y)< 0 \; \; (x_i < x'_i \le y)$.

• 3. $t_i(x_i,y) \ge 0 \; \Rightarrow \; t_i(x_i',y) > 0 \; \; (0 \le x'_i < x_i)$. $\diamond$

Proof

• 1. As Ass. A1[i] holds, the function $t_i(\cdot ,y)$ has the above property b. Thus this function has the AMSCFA-property and the desired result follows.

• 2. By part 1 we may assume $t_i(x_i,y) < 0$. By contradiction, suppose $t_i(x_i',y) \ge 0$ for some $x'_i > x_i$. As $t_i(\cdot ,y)$ is continuous, there exists $x''_i \in ] {x_i},{x'_i} ]$ with $t_i(x''_i,y) =0$. By part 1, $t_i(x_i,y) >0$, a contradiction.

• 3. Analogous to part 2. $\square$ $\square$

Further on we shall use the following notation:

$$\begin{aligned} X_i^{\oplus } :=X_i \setminus \{ {\mathbf {0}} \} = \mathbb {R}_{++}. \end{aligned}$$

Lemma 2

Suppose $i \in N \setminus {\tilde{N}}$ and Assumption A1[i] holds.

• 1. $t_i(0,y) \le 0 \; (y \ge 0)$ and $t_i(x_i,y)< 0 \; (0 < x_i \le y)$.

• 2. If ${\mathbf {e}} \in T_{\star }$, then $e_i =0$.

• 3. Each conditional payoff function $f_i^{( {\mathbf {z}} )}$ is differentiable and strictly decreasing. $\diamond$

Proof

• 1. By definition of ${\tilde{N}}$, $t_i(0,y) \le 0 \; (y > 0)$. As $i \not \in N_>$, we also have $t_i(0,0) \le 0$. Lemma 1(2) implies $t_i(x_i,y)< 0 \; (0 < x_i \le y)$.

• 2. Suppose ${\mathbf {e}} \in T_{\star }$. This implies $e_i t_i(e_i,e_N) =0$ and $t_i(e_i,e_N) \le 0$. If $e_i \ne 0$, then $t_i(e_i,e_N) = 0$ and Ass. A1[i] implies $t_i(0,e_N) > 0$. As $e_N > 0$, this contradicts $i \not \in N {\setminus } {\tilde{N}}$. Thus $e_i=0$.

• 3. Fix ${\mathbf {z}} \in {\mathbf {X}}_{\hat{\imath }}$. By part 1, we have for every $x_i > 0$ that $D f_i^{({\mathbf {z}})}(x_i) = t_i(x_i,x_i + \sum _l z_l) < 0$ implying that $f_i^{({\mathbf {z}})}$ is strictly decreasing on $X_i^{\oplus }$. Next note that $f_i^{({\mathbf {z}})}$ is differentiable. Indeed: for ${\mathbf {z}} \ne {\mathbf {0}}$ this is clear and if ${\mathbf {z}} ={\mathbf {0}}$, then this follows from $i \not \in N_>$ and (5). Now, the continuity of $f_i^{({\mathbf {z}})}$ implies its strict decreasingness. $\square$

Lemma 3

Sufficient for $E \setminus \{ {\mathbf {0}} \} = T_{\star } \setminus \{ {\mathbf {0}} \}$ to hold is that the following conditions hold.

• i. For every $i \in N \setminus {\tilde{N}}$ Assumption A1[i] holds.

• ii. For every $i \in {\tilde{N}}$ Assumption A2’[i] holds.

• iii. For every $i \in {\tilde{N}}$ the conditional payoff functions $f_i^{({\mathbf {z}})} \; ({\mathbf {z}} \ne {\mathbf {0}})$ are pseudo-concave.

• iv. For every $i \in {\tilde{N}}$ the stand-alone payoff function $f_i^{({\mathbf {0}})}$ is pseudo-concave on $X_i^{\oplus }$. $\diamond$

Proof

By (10), it is sufficient to prove that $T_{\star } \setminus \{ {\mathbf {0}} \} \subseteq E$. Suppose ${\mathbf {e}} \in T_{\star } \setminus \{ {\mathbf {0}} \}$. In order to prove that ${\mathbf {e}} \in E$, we fix $i \in N$ and show that $e_i$ is a maximizer of $f_i^{({\mathbf {e}}_{\hat{\imath }})}$.

First suppose $i \in N \setminus {\tilde{N}}$. Then $e_i =0$ by Lemma 2(2). Now Lemma 2(3) guarantees that $e_i$ is a maximiser of $f_i^{({\mathbf {e}}_{\hat{\imath }})}$. Next suppose $i \in {\tilde{N}}$. We distinguish between four cases.

Case $e_i=0$ and $e_N - e_i \ne 0$: as ${\mathbf {e}}_{\hat{\imath }} \ne {\mathbf {0}}$, the function $f_i^{({\mathbf {e}}_{\hat{\imath }})}$ is pseudo-concave. As $D f_i^{({\mathbf {e}}_{\hat{\imath }})}(e_i)= t_i(e_i, e_N ) = t_i(0,e_N) \le 0$ and $e_i=0$, it follows that 0 is a maximiser of $f_i^{({\mathbf {e}}_{\hat{\imath }})}$.

Case $e_i=0$ and $e_N - e_i = 0$: this case cannot happen as ${\mathbf {e}} \ne {\mathbf {0}}$.

Case $e_i \ne 0$ and $e_N -e_i \ne 0$: as ${\mathbf {e}}_{\hat{\imath }} \ne {\mathbf {0}}$, the function $f_i^{({\mathbf {e}}_{\hat{\imath }})}$ is pseudo-concave. As $D f_i^{({\mathbf {e}}_{\hat{\imath }})}(e_i)= t_i(e_i, e_N ) = 0$, it follows that 0 is a maximiser of $f_i^{({\mathbf {e}}_{\hat{\imath }})}$.

Case $e_i \ne 0$ and $e_N -e_i = 0$: $D f_i^{({\mathbf {e}}_{\hat{\imath }})}(e_i)= t_i(e_i, e_N ) = 0$, i.e. $D f_i^{({\mathbf {0}})} (e_i) = t_i(e_i,e_i) = 0$. As $f_i^{( {\mathbf {0}} )}$ is pseudo-concave on $X_i^{\oplus }$, $e_i$ is a maximizer of the function $f_i^{( {\mathbf {0}} )}: X_i^{\oplus } \rightarrow \mathbb {R}$. By contradiction we now prove that $e_i$ also is a maximizer of $f_i^{( {\mathbf {0}} )}$. So suppose there exists $a_i \in X_i$ with $f_i^{( {\mathbf {0}} )}(a_i) > f_i^{( {\mathbf {0}} )}(e_i)$. It then follows that $a_i = 0$ and therefore that $f_i^{( {\mathbf {0}} )}(0) > f_i^{( {\mathbf {0}} )}(e_i)$. Now 0 is a maximizer of $f_i^{( {\mathbf {0}} )}$. This implies $t_i(0,0) = D f_i^{( {\mathbf {0}})}(0) \le 0$. Thus $i \not \in N_>$. By Remark 2, we have $i \in N_>$. A contradiction. $\square$

Lemma 3 clearly shows the importance of pseudo-concavity of the conditional payoff functions. Now we are going to study how this property relates to Assumptions A1, A2, A2’ and C.

For the proof of the next proposition it is crucial to realise that for all $(x_i,y) \in \varDelta ^+$

$$\begin{aligned} (D_1+D_2) t_i(x_i,y) = \Bigl ( \frac{ x_i D_1 + y D_2 }{y} + \frac{y-x_i}{y} D_1 \Bigr ) t_i(x_i,y). \end{aligned}$$

(11)

Proposition 1

• 1. Suppose $i \in {\tilde{N}}$. If Assumptions A1[i], A2[i] and A2’[i] hold, then the functions $f_i^{({\mathbf {z}})}$ with ${\mathbf {z}} \ne {\mathbf {0}}$ are strictly pseudo-concave.

• 2. Suppose $i \in {\tilde{N}}$. If Assumption C[i] holds, then $f_i^{({\mathbf {0}})}$ is on $X_i^{\oplus }$ strictly pseudo-concave.

• 3. If Assumptions A1, A2 and A2’ hold, then each function $f_i^{({\mathbf {z}})}$ is strictly quasi-concave. $\diamond$

Proof

• 1. Suppose Assumptions A1[i] and A2[i] hold and fix ${\mathbf {z}} \ne {\mathbf {0}}$. By the result in footnote 19, the proof is complete if for every $x_i \in X_i$ the implication $D f_i^{({\mathbf {z}})}(x_i) = 0 \; \Rightarrow \; D^2 f_i^{({\mathbf {z}})}(x_i) < 0$ holds. So suppose $D f_i^{({\mathbf {z}})}(x_i) =0$ and let $y = x_i + \sum _l z_l$. Now $y > 0$ and $t_i(x_i,y) =0$. By (4), we have to prove that $(D_1+D_2) t_i(x_i,y) < 0$. Well, if $x_i > 0$, then this follows from (11) and Ass. A1[i] and A2[i]. Now suppose $x_i =0$. Assumption A2’[i] implies: $t_i(0,y) = 0 \; \Rightarrow \; D_2 t_i(0,y) \le 0$. With Ass. A1[i] the desired result follows.

• 2. Suppose Assumption C[i] holds. The proof is complete if for every $x_i \in X_i^{\oplus }$ the implication $D f_i^{({\mathbf {0}})}(x_i) = 0 \; \Rightarrow \; D^2 f_i^{({\mathbf {0}})}(x_i) < 0$ holds. So suppose $D f_i^{({\mathbf {0}})}(x_i) =0$. Now $t_i(x_i,x_i) =0$. By (4), we have to prove that $(D_1 + D_2)t_i(x_i,x_i) < 0$. Well, this is guaranteed by Ass. C[i].

• 3. Suppose Assumptions A1, A2 and A2’ hold. Fix i and ${\mathbf {z}}$. If $i \not \in {\tilde{N}}$, then Lemma 2(3) implies that $f_i^{({\mathbf {z}})}$ is strictly quasi-concave. Now suppose $i \in {\tilde{N}}$. By Part 1, we still have to prove that $f_i^{({\mathbf {0}})}$ is strictly quasi-concave. Well $f_i^{({\mathbf {0}})}$ is on $X_i^{\oplus }$ differentiable, and by part 2 there also strictly pseudo-concave. This implies that $f_i^{({\mathbf {0}})}$ is on $X_i^{\oplus }$ strictly quasi-concave. As, by (6), $f_i^{({\mathbf {0}})}$ is lower semi-continuous at 0, it follows that $f_i^{({\mathbf {0}})}$ is strictly quasi-concave. $\square$

Lemma 3 and Proposition 1(1,2) imply:

Proposition 2

If Assumptions A1, A2 and A2’ hold, then $E \setminus \{ {\mathbf {0}} \} = T_{\star } \setminus \{ {\mathbf {0}} \}$. $\diamond$

4.3 The transformation part: 1-dimensional fixed point problem

Also in this subsection we always consider a smooth aggregative game.

If Assumptions A1, A2 and A2’ hold, then Proposition 2 guarantees that $E \setminus \{ {\mathbf {0}} \} = T_{\star } \setminus \{ {\mathbf {0}} \}$. The aim of this subsection is to show with Proposition 4 that $T_{\star }$ equals the set of fixed points of a specific 1-dimensional fixed point problem.

Definition 3

Consider a smooth aggregative game.

• 1. For $i \in N$, define the correspondences $b_i: Y \multimap \mathbb {R}$ and $s_i: Y^{\oplus } \multimap \mathbb {R}$ by

  $$\begin{aligned} b_i(y) :=\{ x_i \in X_i \; | \; x_i \in [0,y] \, \wedge \, x_i t_i(x_i,y) = 0 \, \wedge \, t_i(x_i,y)\le 0 \}, \;\;\; s_i(y) :=b_i(y) / y. \end{aligned}$$

  The correspondence $b_i$ is called the virtual backward response correspondence of player i and the correspondence ${{s}}_i$ the virtual share correspondence of player i.

• 2. Define the correspondences $b: Y \multimap \mathbb {R}$ and $s: Y^{\oplus } \multimap \mathbb {R}$ by²⁰

  $$\begin{aligned} b(y) :=\sum _{i \in N} b_i(y), \;\;\; s(y) :=\sum _{i \in N} s_i(y) = b(y)/y. \end{aligned}$$

  The correspondence b is called the aggregate virtual backward response correspondence and the correspondence s the aggregate virtual share correspondence. $\diamond$

Virtual backward response correspondences provide global information on the marginal reductions $t_i$. In the definition we added ‘virtual’. Roughly stated, the reason for adding ‘virtual’ is that $b_i(y)$ coincides with the notion of backward response as defined in the Selten variant of the Selten–Szidarovszky technique in situations where conditional payoff functions are pseudo-concave.

Further denote for $i\in N$, by $V_i$ the essential domain of the correspondence $b_i$, i.e. the set $\{ y \in Y \; | \; b_i(y) \ne \emptyset \}$. Now, the essential domain of $s_i$ is $V_i^{\star } :=V_i \setminus \{ 0 \}$, that of b is $V :=\cap _{i \in N} V_i$, that of s is $V^{\star } :=V \setminus \{0 \}$. Let ${\hat{b}}_i :=b_i \upharpoonright \,V_i$, i.e. the restriction of the correspondence $b_i$ to $V_i$; so ${\hat{b}}_i: V_i \multimap \mathbb {R}$. Finally, let ${\hat{s}}_i :={{s}}_i \upharpoonright \,V_i^{\star }$, ${\hat{b}} :=b \upharpoonright \,V$ and ${\hat{s}} :=s \upharpoonright \,V^{\star }$.

Here is a further important consequence of Assumption A1:

Proposition 3

If Assumption A1[i] holds, then for every $y \in Y$ the set $b_i(y)$ contains at most one element. $\diamond$

Proof

By contradiction, suppose $x_i, x'_i \in X_i$ with $0 \le x_i < x'_i$ belong to this set. Note that it follows that $y \ne 0$. Also $t_i(x'_i,y) = 0$. If $x_i=0$, then $t_i(0,y) \le 0$ and Lemma 1(2) gives the contradiction $t_i(x'_i,y) < 0$. If $x_i > 0$, then $t_i(x_i,y) = 0$ and Lemma 1(1) gives the contradiction $t_i(x'_i,y) < 0$. $\square$

In the following we shall always assume that Assumption A1[i] holds when we deal with $b_i$ or $s_i$ and that Assumption A1 holds when we deal with b or s. Therefore, Proposition 3 implies that the correspondences ${\hat{b}}_i, {\hat{s}}_i, {\hat{b}}$ and ${\hat{s}}$ are singleton-valued. We shall interpret (and refer to) these correspondences as functions. So ${\hat{b}}_i: V_i \rightarrow \mathbb {R}$, ${\hat{s}}_i: V_i^{\star } \rightarrow \mathbb {R}$, ${\hat{b}}: V \rightarrow \mathbb {R}$ and ${\hat{s}}: V^{\star } \rightarrow \mathbb {R}$. (Of course, we cannot exclude that $V_i =\emptyset$.) Denote by $\mathrm {fix}({\hat{b}})$ the set of fixed points of ${\hat{b}}$.

Proposition 4

Suppose Assumption A1 holds.

• 1. $T_{\star } = \{ ({\hat{b}}_1(y),\ldots ,{\hat{b}}_n(y)) \; | \; y \in \mathrm {fix}({\hat{b}}) \}$.

• 2. $T_{\star } \setminus \{ {\mathbf {0}} \} = \{ y ({\hat{s}}_1(y),\ldots ,{\hat{s}}_n(y)) \; | \; y \in V^{\star } \text{ with } {\hat{s}}(y) = 1 \}$. $\diamond$

Proof

• 1. ‘$\subseteq$’: Suppose ${\mathbf {x}} \in T_{\star }$. With $y = x_N$, we have for every $i \in N$ that $x_i t_i(x_i,y) = 0$ and $t_i(x_i,y) \le 0$. For every $i \in N$ it follows that $y \in V_i$ and ${\hat{b}}_i(y) = x_i$; thus $y \in V$. As $y= \sum _{i \in N} x_i = \sum _{i \in N} {\hat{b}}_i(y) = {\hat{b}}(y)$, $y \in \mathrm {fix}({\hat{b}})$ holds. ‘$\supseteq$’: suppose $y \in \mathrm {fix}({\hat{b}})$. Then $y \in V$, ${\hat{b}}(y) =y$ and for every i we have ${\hat{b}}_i(y) t_i({\hat{b}}_i(y),y) = 0$ and $t_i({\hat{b}}_i(y),y) \le 0$. It follows that $({\hat{b}}_1(y),\ldots ,{\hat{b}}_n(y)) \in T_{\star }$.

• 2. By part 1. $\square$

Remember that the Nash equilibrium set is the same as the set of fixed points of the joint best response correspondence. Proposition 4 together with Proposition 2 show how the n-dimensional fixed point problem for this correspondence is related to a 1-dimensional fixed point problem for the aggregate virtual best response correspondence ${\hat{b}}$. In particular: if Assumption A1 holds, then (10) and Proposition 4(1) imply:

$$\begin{aligned} {\mathbf {e}} \in E \; \Rightarrow \; [e_N \in \mathrm {fix}({\hat{b}}) \text{ and } {\hat{b}}_i(e_N) = e_i \; (i \in N) ]. \end{aligned}$$

(12)

This result may shortly be paraphrased as ‘Nash sums are fixed points of the aggregate virtual backward response function’. Note that this result does not presuppose that conditional payoff functions are pseudo-concave.

4.4 The analysis part

Also in this subsection we always consider a smooth aggregative game.

Lemma 4

Suppose $i \in N \setminus {\tilde{N}}$ and Assumption A1[i] holds. Then $V_i = Y$ and ${\hat{b}}_i(y) = 0 \; (y \in Y)$. $\diamond$

Proof

By Lemma 2(1), $t_i(0,y) \le 0 \; (y \in Y)$. This implies the desired results. $\square$

Proof of Theorem 1

(2a, 2b, 3) 2a. Suppose $i \not \in {\tilde{N}}$ and ${\mathbf {e}} \in E$. By contradiction we prove that $e_i = 0$. So suppose $e_i > 0$. By Lemma 2(1), $t_i(e_i, \sum _l e_i) < 0$. Therefore (10) implies $e_i=0$, a contradiction.

2b. Suppose ${\tilde{N}} = \emptyset$. Theorem 1(2a) implies that we still have to prove that ${\mathbf {0}} \in E$. Fix $i \in N$. We have to prove that 0 is a maximiser of $f_i^{({\mathbf {0}})}$. Well, apply Lemma 2(3).

3. Suppose Assumptions A1 and A2’ hold and ${\mathbf {0}} \in E$. By Theorem 1(1), $N_> = \emptyset$. By Remark 2, ${\tilde{N}} = \emptyset$. By Theorem 1(2b), $E= \{ {\mathbf {0}} \}$. $\square$

Lemma 5

• 1. Sufficient for player $i \in {\tilde{N}}$ to be of class I or class II is that ${\overline{t}}_i$ has the AMSCFA-property.

• 2. Suppose $i \in {\tilde{N}}$ is of class II and ${\overline{t}}_i$ has the AMSCFA-property. Then ${\overline{t}}_i < 0$. $\diamond$

Proof

• 1. Suppose ${\overline{t}}_i$ has the AMSCFA-property. In the case where ${\overline{t}}_i$ has a zero, say m, we have, ${\overline{t}}_i(x_i) >0$ for $x_i \in ] {0},{m} \, [$ and thus that i is of class I. Now suppose that ${\overline{t}}_i$ does not have a zero. As ${\overline{t}}_i$ is continuous, we have ${\overline{t}}_i > 0$ and then i is of class I or ${\overline{t}}_i < 0$ and then i is of class II.

• 2. We prove this by contradiction. So suppose ${\overline{t}}_i(a_i) \ge 0$ for some $a_i > 0$. As i is of class II, ${\overline{t}}_i(x_i) < 0$ for $x_i > 0$ small enough. The continuity of ${\overline{t}}_i$ implies that there exists $l_i \in ] {0},{a_i} ]$ with ${\overline{t}}_i(l_i) = 0$. As ${\overline{t}}_i$ has the AMSCFA-property, we have ${\overline{t}}_i(x_i) > 0$ for $0< x_i < l_i$, a contradiction with player i being of class II. $\square$

Define the function $\sigma : T_{\star } \rightarrow \mathbb {R}$ by

$$\begin{aligned} \sigma ({\mathbf {x}}) \; := \; \sum _{i \in N} x_i. \end{aligned}$$

Because, by (10), $E \subseteq T_{\star }$ holds, one may refer to $\sigma \upharpoonright \,E$ as the equilibrium aggregator.

The following result deals with the aggregate virtual share function ${\hat{s}}: V^{\star } \rightarrow \mathbb {R}$.

Proposition 5

Suppose Assumption A1 holds.

• 1. The equilibrium aggregator is injective.

• 2. Suppose Assumption A2’ holds. Then each of the following conditions is sufficient for $\# T_{\star } \le 1$ to hold.

  • (a) the function ${\hat{s}} -1$ has the AMSCFA property on the subset where ${\hat{s}}$ is positive.

  • (b) ${\hat{s}}$ is strictly monotone on the subset where it is positive. $\diamond$

Proof

• 1. By contradiction. So suppose ${\mathbf {x}}, {\mathbf {x}}' \in T_{\star }$ with ${\mathbf {x}} \ne {\mathbf {x}}'$ and $x_N = x'_N \; =: \; y$. Note that $y \ne 0$. Fix $i \in N$ with $x'_i > x_i$. We have $t_i(x'_i,y) = 0 \ge t_i(x_i,y)$. But now Lemma 1(1) implies $t_i(x_i,y) > 0$.

• 2a. If ${\tilde{N}} = \emptyset$, then, by Lemma 2(2), $T_{\star } \subseteq \{ {\mathbf {0}} \}$ and we are done. Now suppose ${\tilde{N}} \ne \emptyset$. We prove the desired result by contradiction. So suppose ${\mathbf {x}}, {\mathbf {x}}' \in T_{\star }$ with ${\mathbf {x}} \ne {\mathbf {x}}'$. As ${\tilde{N}} \ne \emptyset$ and Ass. A2’ holds, Remark 2 guarantees $N_> \ne \emptyset$. Fix $i \in N_>$. As $t_i(0,0) > 0$, it follows that ${\mathbf {x}} \ne {\mathbf {0}}$ and ${\mathbf {x}}' \ne {\mathbf {0}}$. We may suppose that $x'_N \ge x_N$. By part 1, $x_N \ne x'_N$. So $x'_N > x_N$. Proposition 4(2) implies ${\hat{s}}(x_N) = {\hat{s}}(x'_N) =1$. So ${\hat{s}}(x_N) -1 = {\hat{s}}(x'_N) -1 = 0$. But this contradicts the assumption that ${\hat{s}}-1$ has the AMSCFA property on the subset where ${\hat{s}}$ is positive.

• 2b. Note that this condition implies the condition in 2a. $\square$ $\square$

Of course, in Proposition 5(2b) it is also sufficient that ${\hat{b}}$ is strictly decreasing on the subset where it is positive. Note also that Proposition 5 does not presuppose that ${\hat{s}}$ is continuous or that conditional payoff functions are strictly quasi-concave.

Proposition 5(1) immediately implies the following variant of Proposition 2 (part i) in [15].

Proposition 6

Consider a symmetric almost smooth aggregative game. If Assumption A1 holds, then each equilibrium is symmetric. $\diamond$

Proof

Indeed. Suppose ${\mathbf {e}}$ would be an asymmetric equilibrium. Then a suitable permutation of the actions in ${\mathbf {e}}$ gives another asymmetric equilibrium ${\mathbf {e}}'$. As $\sigma ({\mathbf {e}}) = \sigma ({\mathbf {e}}')$ we have a contradiction with the injectivity of $\sigma$. $\square$

Lemma 6

• 1. If $f_i^{({\mathbf {0}})}$ is strictly pseudo-concave on $X_i^{\oplus }$, then ${\overline{t}}_i$ has the AMSCFA-property.

• 2. If $i \in {\tilde{N}}$ and Assumption C[i] holds, then ${\overline{t}}_i$ has the AMSCFA-property. $\diamond$

Proof

• 1. As ${\overline{t}}_i(x_i) = D f_i^{({\mathbf {0}})}(x_i)$, ${\overline{t}}_i$ is the derivative of a strictly pseudo-concave function and therefore (see Remark 6) has the AMSCFA-property.

• 2. By part 1 and Proposition 1(2). $\square$

Proposition 7

Suppose, Assumptions A1 and C hold. If every player in ${\tilde{N}}$ is of class II, then at each active equilibrium at least two players are active. $\diamond$

Proof

By contradiction. So suppose ${\mathbf {e}} \in E$ with ${\mathbf {e}} \ne {\mathbf {0}}$ and $\# \{ j \in N \; | \; e_j \ne 0 \} \le 1$. So $\# \{ j \in N \; | \; e_j \ne 0 \} = 1$. Let $e_i \ne 0$ and $e_j = 0 \; (j \ne i)$. By (10), ${\mathbf {e}} \in T_{\star }$; therefore $t_i(e_i,e_i) = 0$. Lemma 2(2) implies that $i \in {\tilde{N}}$. By Lemma 6(2), ${\overline{t}}_i$ has the AMSCFA-property. By Lemma 5(2), $t_i(x_i,x_i) = {\overline{t}}_i(x_i) < 0$, a contradiction. $\square$ $\square$

For $i \in N$ let

$$\begin{aligned} V_i^+ :=\{ y \in Y \; | \; \text{ there } \text{ exists } x_i \in ] {0},{y} ] \text{ with } t_i(x_i,y) = 0 \}, \\ V_i^{++} :=\{ y \in Y \; | \; \text{ there } \text{ exists } x_i \in ] {0},{y} \, [ \text{ with } t_i(x_i,y) = 0 \}. \end{aligned}$$

Thus we have

$$\begin{aligned} V_i^{++} \subseteq V_i^+ \subseteq V_i^{\star } \subseteq V_i \subseteq Y. \end{aligned}$$

If Assumption A1[i] holds and ${\mathbf {e}} \in E$, then with (10) we obtain

$$\begin{aligned} e_i >0 \; \Rightarrow [t_i(e_i, e_N)=0 \, \wedge \, e_N \in V_i^+ \, \wedge \, {\hat{b}}_i(e_N) = e_i], \\ e_i= 0 \; \Rightarrow \; [t_i(e_i,e_N) \le 0 \, \wedge \, e_N \in V_i \, \wedge \, {\hat{b}}_i(e_N) = e_i]. \end{aligned}$$

Lemma 7

Suppose Assumption A1[i] holds.

• 1. $V_i^{++}$ is open in $\mathbb {R}$.

• 2. If $V_i^{++} \ne \emptyset$, then ${\hat{b}}_i$ is differentiable on $V_i^{++}$ with $D{\hat{b}}_i = - \frac{D_2 t_i}{D_1 t_i}$ on $V_i^{++}$. $\diamond$

Proof

The first statement is clear if $V_i^{++} = \emptyset$. Further suppose $V_i^{++} \ne \emptyset$. For every $y \in V_i^{++}$ we have $({\hat{b}}_i(y),y) \in \mathrm {Int}(\varDelta )$ and $t_i({\hat{b}}_i(y),y) = 0$. As $t_i: \mathrm {Int}(\varDelta ) \rightarrow \mathbb {R}$ is differentiable and Ass. A1[i] holds, a variant of the classical implicit function theorem in [14] applies and implies that $V_i^{++}$ is open and ${\hat{b}}_i$ is differentiable on $V_i^{++}$. Differentiating the identity $t_i({\hat{b}}_i(y),y) = 0 \; (y \in V_i^{++})$, the second statement follows. $\square$ $\square$

Lemma 8

Suppose $i \in {\tilde{N}}$ and Assumptions A1[i], A2’[i] and C[i] hold.

• 1. Suppose $y \in V_i$ and $y' > y$. Then ${\hat{b}}_i(y) = 0 \; \Rightarrow \; [y' \in V_i \, \wedge \, {\hat{b}}_i(y') = 0]$.

• 2. $V_i^+$ is a real interval.

• 3. $V_i^+ < V_i \setminus V_i^+$.²¹$\diamond$

Proof

• 1. Suppose ${\hat{b}}_i(y) = 0$. We have $t_i(0,y) = t_i({\hat{b}}_i(y),y) \le 0$. As $y' > y$, Ass. A2’[i] gives $t_i(0,y') \le 0$. Thus $y' \in V_i$ and ${\hat{b}}_i(y') = 0$.

• 2. Suppose $y< y'' < y'$ with $y, y' \in V_i^+$. As ${\hat{b}}_i(y) > 0$ and $t_i({\hat{b}}_i(y),y) =0$, Lemma 1(1) gives $t_i(0,y) > 0$ and $t_i(y,y) \le 0$. In the same way, $t_i(0,y') > 0$ and $t_i(y',y') \le 0$. Ass. A2’[i] implies $t_i(0,y'') > 0$. And as ${\overline{t}}_i$ is continuous and has, by Lemma 6(2), the AMSCFA-property, it follows that $t_i(y'',y'') \le 0$. As $t_i(\cdot ,y'')$ is continuous, there exists $x_i \in ] {0},{y''} ]$ with $t_i(x_i,y'')= 0$. Thus, as desired, $y'' \in V_i^+$.

• 3. Suppose $y \in V_i^+$ and $y' \in V_i \setminus V_i^+$. As $y \ne y'$, ${\hat{b}}_i(y) > 0$ and ${\hat{b}}_i(y') = 0$, part 1 implies $y <y'$. $\square$ $\square$

Proposition 8

• 1. If Assumption C[i] holds, then i is of class I or class II.

• 2. If $i \in N_>$, $t_i(0,0) \ne + \infty$ and $t_i: \varDelta \rightarrow \mathbb {R}$ is continuous, then i is of class I.

• 3. If $i \in N_>$ and $f_i^{({\mathbf {0}})}$ is continuously differentiable, then i is of class I. $\diamond$

Proof

• 1. By Lemmas 5(1) and  6(2).

• 2. As $t_i(0,0) > 0$ and $t_i: \varDelta \rightarrow \mathbb {R}$ is continuous, it follows that i is of class I.

• 3. Now $\lim _{x_i \downarrow 0} {\overline{t}}_i(x_i) = \lim _{x_i \downarrow 0} D f_i^{({\mathbf {0}})} (x_i) = D f_i^{({\mathbf {0}})} (0) = t_i(0,0) > 0$. This implies that i is of class I. $\square$

Now we address the zeros of ${\overline{t}}_i$. Of course, each such zero belongs to $V_i^+ \setminus V_i^{++}$ and is a stationary point of $f_i^{({\mathbf {0}})}$. Sufficient for ${\overline{t}}_i$ to have a unique zero is that ${\overline{t}}_i$ has a zero and ${\overline{t}}_i$ has the AMSCFA-property. If ${\overline{t}}_i$ has a zero and has the AMSCFA-property, then we denote this zero by

$$\begin{aligned} \underline{x}_i; \end{aligned}$$

(13)

if also Assumption A1[i] holds, then ${\hat{b}}_i ( \underline{x}_i ) = \underline{x}_i$. In addition to Lemma 8(2,3) we have:

Lemma 9

Suppose $i \in {\tilde{N}}$ and Assumptions A1[i], A2’[i] and C[i] hold.

• 1. $V_i^{++}$ is an open real interval. If $\underline{x}_i$ is well-defined, then $V_i^{++}$ is a proper interval.

• 2. $V_i$ is a real interval. Even: if $y \in V_i$, then also $y' \in V_i$ for every $y' > y$.

• 3. If $V_i^+ \setminus V_i^{++} \ne \emptyset$, then

  • (a) $\underline{x}_i$ is well-defined and $V_i^{+} \setminus V_i^{++} = \{ \underline{x}_i \}$.

  • (b) $V_i^+$ is a proper interval and $\underline{x}_i \in V_i^+$ is a left boundary point of $V_i^+$.

• 4. $V_i^{++} = \emptyset \; \Rightarrow \; V_i^+ = \emptyset$. $\diamond$

Proof

By Lemma 6(2), ${\overline{t}}_i$ has the AMSCFA-property.

• 1. First statement: by Lemma 7(1), $V_i^{++}$ is open. In order to show that $V_i^{++}$ is an interval, we suppose $y, y' \in V_i^{++}$ and fix $y'' \in ] {y},{y'} \, [$. By Lemma 8(2), $y'' \in V_i^+$. The proof is complete if we show that ${\hat{b}}_i(y'') \ne y''$. This we do by contradiction, so suppose ${\hat{b}}_i(y'') = y''$. Then ${\overline{t}}_i(y'') = t_i(y'',y'') = t_i({\hat{b}}_i(y''),y'') = 0$. As ${\overline{t}}_i$ has the AMSCFA-property, ${\overline{t}}_i(y) > 0$ follows. By Lemma 1(1), as ${\hat{b}}_i(y) < y$, $0 = t_i({\hat{b}}_i(y), y)> t_i(y,y) > 0$, a contradiction. Second statement: suppose that $\underline{x}_i$ is well-defined. So $t_i(\underline{x}_i, \underline{x}_i ) = 0$ holds. By Lemma 1(1), $t_i(0,\underline{x}_i) > 0$. Fix ${\tilde{x}}_i > \underline{x}_i$. We have $t_i({\tilde{x}}_i,{\tilde{x}}_i) < 0$. Consider the open interval $] { (0, \underline{x}_i ) },{ ({\tilde{x}}_i, {\tilde{x}}_i) } \, [$ in $\varDelta ^+$. As $t_i: \varDelta ^+ \rightarrow \mathbb {R}$ is continuous, there exists $(x_i,y) \in \varDelta ^+$ with $0< x_i < y$ and $t_i(x_i,y) = 0$. Thus $y \in V_i^{++}$. As, by the above $V_i^{++}$ is an open interval, it follows that $V_i^{++}$ is a proper interval.

• 2. By contradiction. So suppose $y \in V_i$, $y' > y$ and $y' \not \in V_i$. As $y' \not \in V_i$, we have $t_i(0,y') > 0$. Lemma 8(1) implies ${\hat{b}}_i(y) > 0$ and therefore $t_i({\hat{b}}_i(y),y) =0$. With Lemma 1(1) if follows that $t_i(y,y) \le 0$. As ${\overline{t}}_i$ is continuous and has the AMSCFA-property, it follows that $t_i(y',y') \le 0$. As $t_i(0,y') > 0$, the continuity of $t_i(\cdot ,y')$ implies the existence of $x_i \in ] {0},{y'} ]$ with $t_i(x_i,y') =0$. Thus $y' \in V_i^+$, a contradiction.

• 3a. Suppose $V_i^+ \setminus V_i^{++} \ne \emptyset$. Let $y \in V_i^+ \setminus V_i^{++}$. Then $t_i({\hat{b}}_i(y),y) = 0$ and ${\hat{b}}_i(y) = y$. Thus ${\overline{t}}_i(y) = t_i(y,y) = t_i({\hat{b}}_i(y),y) = 0$. As ${\overline{t}}_i$ has a zero y and the AMSCFA-property, $y = \underline{x}_i$ follows. So $V_i^{+} \setminus V_i^{++} = \{ \underline{x}_i \}$.

• 3b. Suppose $V_i^+ \setminus V_i^{++} \ne \emptyset$. By Lemma 8(2), $V_i^+$ is an interval. Parts 3a and 1 imply that $V_i^{++}$ is proper. So $V_i^+$ also is proper. Further suppose $y' \in V_i^{++}$. Then $t_i({\hat{b}}_i(y'),y') = 0$ and ${\hat{b}}_i(y') < y'$. Lemma 1(1) implies $t_i(y',y') < 0$. The AMSCFA-property implies $\underline{x}_i < y'$. As $V_i^{++}$ and $V_i^+$ are intervals, $\underline{x}_i \in V_i^+$ is a left boundary point of $V_i^+$.

• 4. By contradiction. So suppose $V_i^{++} = \emptyset$ and $V_i^+ \ne \emptyset$. By part 3a, $V_i^+ = \{ \underline{x}_i \}$. By part 1, $V_i^{++}$ is a proper interval, a contradiction. $\square$ $\square$

If $i \in N \setminus {\tilde{N}}$ and Assumption A1[i] holds, then by Lemma 4 we have $V_i = Y$ and ${\hat{b}}_i(y) =0 \; (y \in Y)$. In the case Assumption A1 holds, this implies for the domain $V^{\star } = \cap _{i \in N } V_i^{\star }$ of ${\hat{s}} = \sum _{i \in N} {\hat{s}}_i$ that $V^{\star } = \cap _{i \in {\tilde{N}}} V_i^{\star }$ and²²

$$\begin{aligned} {\hat{s}} = \sum _{i \in {\tilde{N}}} {\hat{s}}_i. \end{aligned}$$

(14)

Proposition 9

• 1. Suppose $i \in {\tilde{N}}$ and Assumptions A1[i], A2[i] and A2’[i] hold. Then ${\hat{s}}_i$ is decreasing and strictly decreasing on $V_i^{+}$.

• 2. Suppose that Assumptions A1, A2 and A2’ hold.

  • (a) ${\hat{s}}$ is decreasing.

  • (b) The subset on which ${\hat{s}}$ is positive is an interval.

  • (c) ${\hat{s}}$ is strictly decreasing on the subset where it is positive. $\diamond$

Proof

• 1. Consider ${\hat{s}}_i: V_i^{\star } \rightarrow \mathbb {R}$. By Lemma 6(2), ${\overline{t}}_i$ has the AMSCFA-property. First suppose $V_i^{++} = \emptyset$. By Lemma 9(4), $V_i^{+} = \emptyset$ and thus ${\hat{s}}_i$ is strictly decreasing on $V_i^+$. On $V_i \setminus V_i^+ = V_i$, ${\hat{b}}_i =0$ and therefore ${\hat{s}}_i=0$. So ${\hat{s}}_i=0$ on $V_i^{\star }$ and thus there decreasing. Next suppose $V_i^{++} \ne \emptyset$. By Lemma 9(1), $V_i^{++}$ is a proper open interval. With Lemma 7(2), we obtain for every $y \in V_i^{++}$

  $$\begin{aligned} D {\hat{s}}_i(y) = - \frac{ {\hat{b}}_i(y) D_1 t_i( {\hat{b}}_i(y), y) + y D_2 t_i ({\hat{b}}_i(y),y) }{ y^2 \cdot D_1 t_i( {\hat{b}}_i(y), y) }. \end{aligned}$$

  Ass. A1[i] and A2[i] imply that $D {\hat{s}}_i(y) < 0 \; (y \in V_i^{++})$. It follows that ${\hat{s}}_i$ is strictly decreasing on $V_i^{++}$. If $V_i^{++} = V_i^+$, then ${\hat{s}}_i$ is strictly decreasing on $V_i^{+}$. Now suppose $V_i^{++} \ne V_i^+$. Then, by Lemma 9(3), $V_i^{+} \setminus V_i^{++} = \{ \underline{x}_i \}$ and $\underline{x}_i$ is a left boundary point of the proper interval $V_i^+$. As ${\hat{b}}_i(\underline{x}_i) = \underline{x}_i$, we have ${\hat{s}}_i(\underline{x}_i) = 1$. As ${\hat{s}}_i \le 1$, it follows that ${\hat{s}}_i$ is strictly decreasing on $V_i^{+}$. Also ${\hat{s}}_i$ is decreasing: indeed, ${\hat{s}}_i> 0$ on $V_i^{+}$, ${\hat{s}}_i=0$ on $V_i \setminus V_i^{+}$ and, by Lemma 8(3), $V_i^+ < V_i \setminus V_i^+$.

• 2. By Lemma 6(2), ${\overline{t}}_i \;(i \in {\tilde{N}})$ has the AMSCFA-property. Lemma 9(2) implies that $V^{\star }$ is an interval.

• 2a. By (14) and part 1.

• 2b. By part 2a.

• 2c. We may suppose that the subset where ${\hat{s}}$ is positive contains at least two elements. Let $y_a, y_b$ with $y_a < y_b$ such elements. So $s(y_a) > 0$ and $s(y_b) > 0$. Part 1 implies ${\hat{s}}_i(y_a) - {\hat{s}}_i(y_b) \ge 0 \;(i \in {\tilde{N}})$. Fix $j \in {\tilde{N}}$ with ${\hat{s}}_j(y_a) > 0$. If also ${\hat{s}}_j(y_b) > 0$, then by part 1, ${\hat{s}}_j(y_a) - {\hat{s}}_j(y_b) > 0$. If ${\hat{s}}_j(y_b) = 0$, then, ${\hat{s}}_j(y_a) - {\hat{s}}_j(y_b) = {\hat{s}}_j(y_a)> 0$. Thus, as desired, $s(y_a) - s(y_b) = \sum _{i \in {\tilde{N}}} ({\hat{s}}_i(y_a) - {\hat{s}}_i(y_b) ) > 0$. $\square$ $\square$

Proof of Theorem 2

By (10) and Propositions 5(2b) and 9(2c). $\square$

According to Lemma 7(2), supposing Assumption A1[i] holds, the function ${\hat{b}}_i$ is continuous on $V_i^{++}$. The following proposition considers this issue further.

Proposition 10

Suppose $i \in {\tilde{N}}$ and Assumptions A1[i], A2’[i] and C[i] hold. Then $V_i$ is a real interval and the function ${\hat{b}}_i: V_i \rightarrow \mathbb {R}$ is continuous. $\diamond$

Proof

By Lemma 6(2), ${\overline{t}}_i$ has the AMSCFA-property. Lemma 9(2) guarantees that $V_i$ is a real interval. It is sufficient to prove that ${\hat{b}}_i$ is continuous on each bounded proper subinterval I of $V_i$ which is closed in $\mathbb {R}$. Fix such an interval. Further we consider ${\hat{b}}_i: I \rightarrow \mathbb {R}$. As $0 \le {\hat{b}}_i(y) \le y \; (y \in I)$, ${\hat{b}}_i$ is bounded. As I is compact and ${\hat{b}}_i$ is bounded, continuity of ${\hat{b}}_i$ is equivalent to the closedness of its graph, i.e. with the subset $\{ (y, {\hat{b}}_i(y) ) \; | \; y \in I \}$ of $\mathbb {R}^2$. In order to prove that this set is closed take a convergent sequence $( ( y_m, {\hat{b}}_i(y_m) ) )$ in this set with limit $(y_{\star }, {\hat{b}}_{\star } )$. Noting that (as I is closed) $y_{\star } \in I$ (so $y \ne 0$), we have to prove that ${\hat{b}}_{\star } = {\hat{b}}_i(y_{\star })$. We distinguish between two cases.

Case where $y_{\star } > 0$: we have $0 \le {\hat{b}}_i(y_m) \le y_m$, ${\hat{b}}_i(y_m) t_i({\hat{b}}_i(y_m), y_m ) = 0$ and $t_i({\hat{b}}_i(y_m), y_m ) \le 0$. Taking limits and noting that $t_i: \varDelta ^+ \rightarrow \mathbb {R}$ is continuous, we obtain $0 \le {\hat{b}}_{\star } \le y_{\star }$, ${\hat{b}}_{\star } t_i({\hat{b}}_{\star }, y_{\star }) =0$ and $t_i({\hat{b}}_{\star }, y_{\star } ) \le 0$. Thus, as desired, ${\hat{b}}_{\star } = {\hat{b}}_i(y_{\star })$.

Case where $y_{\star } = 0$: as ${\hat{b}}_i(0)=0$, we have to prove that ${\hat{b}}_{\star } =0$. Well, as $0 \le {\hat{b}}_i(y_m) \le y_m$ and $\lim y_m = y_{\star } = 0$, the desired result follows. $\square$ $\square$

Lemma 10

Suppose $i \in {\tilde{N}}$ and Assumption C[i] holds.

• 1. Suppose i is of class I and Assumption B[i] holds.

  • (a) $\underline{x}_i$ (in (7)) is well-defined and $\underline{x}_i \le {\overline{x}}_i$.

  • (b) if Assumption A1[i] holds, then $V_i^{\star } = [ {\underline{x}_i},{+\infty } \,[$ and ${\hat{b}}_i(y) \le {\overline{x}}_i \; (y \ge \underline{x}_i)$.

• 2. Suppose i is of class II.

  • (a) $\{ y \in Y^{\oplus } \; | \; t_i(0,y) > 0 \} \subseteq V_i^{++}$.

  • (b) $V_i^{\star } = ] {0},{+\infty } ]$.

  • (b) if Assumptions A1[i] and B[i] hold, then ${\hat{b}}_i(y) \le {\overline{x}}_i \; (y > 0)$. $\diamond$

Proof

By Lemma 6(2), ${\overline{t}}_i$ has the AMSCFA-property.

• 1a. As ${\overline{t}}_i$ is of class I, ${\overline{t}}_i(x_i) > 0$ for $x_i > 0$ small enough. By Ass. B[i], also ${\overline{t}}_i < 0$ for $x_i > {\overline{x}}_i$. As ${\overline{t}}_i$ is continuous, it follows that ${\overline{t}}_i$ has a zero. As ${\overline{t}}_i$ has the AMSCFA-property, this zero equals $\underline{x}_i$. Of course, $\underline{x}_i \le {\overline{x}}_i$ follows.

• 1b. Suppose Assumption A1[i] holds. First statement ‘$\subseteq$’: by contradiction. So suppose $y \in V_i^{\star }$ and $y < \underline{x}_i$. The AMSCFA-property gives $t_i(y,y) = {\overline{t}}_i(y) > 0$. By Lemma 1(3), $t_i(x_i,y) > 0$ for all $x_i \in X_i$ with $0 \le x_i \le y$. Thus $y \not \in V_i$, a contradiction. First statement ‘$\supseteq$’: suppose $y \ge \underline{x}_i$. If $t_i(0,y) \le 0$, then $y \in V_i$. Now suppose $t_i(0,y) > 0$. By the AMSCFA-property, $t_i(y,y) \le 0$. As ${t}_i(\cdot ,y)$ is continuous, there exists $x_i \in [0,y]$ with $t_i(x_i,y) = 0$. Thus $y \in V_i$. Second statement: this is clear if ${\hat{b}}_i(y) = 0$. Now suppose ${\hat{b}}_i(y) > 0$. We have $0 =t_i({\hat{b}}_i(y),y)$. So Ass. B[i] implies that ${\hat{b}}_i(y) \le {\overline{x}}_i$.

• 2a. Suppose $y \in Y^{\oplus }$ with $t_i(0,y) > 0$. By Lemma 5(2), $t_i(y,y) < 0$. As $t_i(\cdot ,y)$ is continuous, there exists $x_i \in ] {0},{y} \, [$ with $t_i(x_i,y) = 0$. So $y \in V_i^{++}$.

• 2b. ‘$\subseteq$’: trivial. ‘$\supseteq$’: suppose $y > 0$. If $t_i(0,y) \le 0$, then $y \in V_i^{\star }$. Now suppose $t_i(0,y) > 0$. By part 2a, $y \in V_i^{++} \subseteq V_i^{\star }$.

• 2c. Suppose Assumption A1[i] and B[i] hold. Fix $y > 0$. The statement is clear if ${\hat{b}}_i(y) = 0$. Now suppose ${\hat{b}}_i(y) > 0$. We have $0 =t_i({\hat{b}}_i(y),y)$. So Ass. B[i] implies that ${\hat{b}}_i(y) \le {\overline{x}}_i$. $\square$ $\square$

Proposition 11

Suppose Assumptions A1, A2’, B and C hold and that for every $i \in {\tilde{N}}$ the conditional payoff functions $f_i^{({\mathbf {z}})} \; ({\mathbf {z}} \ne {\mathbf {0}})$ are pseudo-concave. If ${\tilde{N}}$ contains at least one player of class I, then $\# E \ge 1$ and even an active equilibrium exists. $\diamond$

Proof

For $i \not \in {\tilde{N}}$, by Lemma 4, $V_i = \mathbb {R}_{+}$ and ${\hat{b}}_i(y) =0 \; (y \ge 0)$. Let $N' :=\{ k \in {\tilde{N}} \mid k \text{ is } \text{ of } \text{ class } \text{ I } \}$; by assumption, $N' \ne \emptyset$. By Lemma 6(2), every ${\overline{t}}_i$ has the AMSCFA-property. So by Lemma 5(1), each player in ${\tilde{N}}$ is of class I or II. Lemma 10(1b,2b) implies for $V^{\star } = \cap _{i \in N} V_i^{\star } = \cap _{ i \in {\tilde{N}} } V_i^{\star }$ that $V^{\star } = [ {\underline{x}},{+\infty } \,[$ where $\underline{x} = \max \{ \underline{x}_k \; | \; k \in N' \}$.

Consider ${\hat{s}}: [ {\underline{x} },{+\infty } \,[ \rightarrow \mathbb {R}$. By (14), ${\hat{s}} = \sum _{i \in {\tilde{N}}} {\hat{s}}_i$. Fix $k_{\star } \in N'$ such that $\underline{x} = \underline{x}_{k_{\star }}$. Now

$$\begin{aligned} {\hat{s}}(\underline{x}) = \sum _{k \in {\tilde{N}}} {\hat{s}}_k(\underline{x}) = \sum _{k \in {\tilde{N}}} {\hat{s}}_k(\underline{x}_{k_{\star }}) \ge {\hat{s}}_{k_{\star }}(\underline{x}_{k_{\star }}) = 1. \end{aligned}$$

As Ass. B holds and $Y = \mathbb {R}_+$, we can fix ${\overline{y}} > 0$ with ${\overline{y}} \ge \sum _{k \in {\tilde{N}}} {\overline{x}}_k$. By Lemma 10(1a), ${\overline{y}} \ge \sum _{k \in N'} {\overline{x}}_k \ge \sum _{k \in N'} \underline{x}_k \ge \underline{x}$. Thus ${\overline{y}} \in V^{\star }$ and ${\overline{y}} \ge \underline{x}_k \; (k \in N')$. So with Lemma 10(1b,2c) we obtain,

$$\begin{aligned} {\hat{s}}( {\overline{y}} )= \sum _{k \in {\tilde{N}} } \frac{ {\hat{b}}_k({\overline{y}}) }{{\overline{y}}} \le \sum _{ k \in {\tilde{N}} } \frac{ {\overline{x}}_k }{{\overline{y}}} \le 1. \end{aligned}$$

Proposition 10 implies that ${\hat{s}}$ is continuous. By the intermediate value theorem, there exists $y_{\star }\in V^{\star }$ with ${\hat{s}}(y_{\star }) = 1$. Thus $y_{\star } \in \mathrm {fix}({\hat{b}})$. Proposition 4(1) implies $({\hat{b}}_1(y_{\star }), \ldots , {\hat{b}}_n(y_{\star }) ) \in T_{\star } \setminus \{ {\mathbf {0}} \}$. Lemma 3 and Proposition 1(2) now guarantee that $({\hat{b}}_1(y_{\star }), \ldots , {\hat{b}}_n(y_{\star }) ) \in E \setminus \{ {\mathbf {0}} \}$. $\square$ $\square$

Proof of Theorem 3

Suppose ${\tilde{N}}$ contains at least one player of class I. Note that, using Proposition 1(1,2), Proposition 11 applies and guarantees that there exists an active equilibrium. By Theorem 2 this a unique equilibrium. $\square$

Proof of Theorem 4

• 1. Suppose $i \in {\tilde{N}}$. So there exists ${\tilde{y}}_i > 0$ with $t_i(0,{\tilde{y}}_i ) > 0$. As i is of class II, Ass. A2’ and Lemma 10(2a) imply $y \in V_i^{++} \; (0< y < {\tilde{y}}_i)$ and thus ${\hat{b}}_i(y) \in ] {0},{y} \, [ \; (0< y < {\tilde{y}}_i)$. Now $t_i({\hat{b}}_i(y),y) =0$ follows.

• 2. By part 1, ${\hat{s}}_i(y) > 0 \;(0< y < {\tilde{y}}_i)$. By Proposition 9(1), the function ${\hat{s}}_i$ is strictly decreasing on $] {0},{ {\tilde{y}}_i} \, [$. As ${\hat{s}}_i \le 1$, the desired result follows.

• 3. By Lemma 10(2b), we have $V_i^{\star } = \mathbb {R}_{++} \; (i \in {\tilde{N}})$. So $V^{\star } = \mathbb {R}_{++}$.

‘$\Rightarrow$’: suppose $\sum _{i \in {\tilde{N}} }{\overline{s}}_i > 1$. So ${\tilde{N}} \ne \emptyset$; by Remark 2 now also $N_> \ne \emptyset$. By Theorem 2 and 1(1) we still have to prove that $\# E \ge 1$. Consider ${\hat{s}}: ] {0},{+\infty } ] \rightarrow \mathbb {R}$. By part 2, we obtain $\lim _{y \downarrow 0} {\hat{s}}(y) = \lim _{y \downarrow 0} \sum _{i \in {\tilde{N}} } {\hat{s}}_i(y)= \sum _{i \in {\tilde{N}} } {\overline{s}}_i > 1$. As $Y = \mathbb {R}_+$, we can fix ${\overline{y}} > 0$ with ${\overline{y}} \ge \sum _{k \in {\tilde{N}}} {\overline{x}}_k$. By Lemma 10(2c), we have ${\hat{b}}_i({\overline{y}}) \le {\overline{x}}_i \; (i \in {\tilde{N}})$. It follows that ${\hat{b}}({\overline{y}}) = \sum _{ \in {\tilde{N}}} {\hat{b}}_k({\overline{y}}) \le {\overline{y}}$ and therefore ${\hat{s}}({\overline{y}}) \le 1$. Proposition 4(1) implies $({\hat{b}}_1(y_{\star }), \ldots , {\hat{b}}_n(y_{\star }) ) \in T_{\star } \setminus \{ {\mathbf {0}} \}$. Lemma 3 and Proposition 1(2) now guarantee that $({\hat{b}}_1(y_{\star }), \ldots , {\hat{b}}_n(y_{\star }) ) \in E \setminus \{ {\mathbf {0}} \}$.

‘$\Leftarrow$’: suppose the game has a unique equilibrium, say ${\mathbf {e}}$, and ${\mathbf {e}} \ne {\mathbf {0}}$. By (12), $e_i = {\hat{b}}_i(e_N) \; (i \in N)$. As $e_N \ne 0$, this implies ${\hat{s}}(e_N) = 1$. For $i \in {\tilde{N}}$, by the proof of part 2, ${\hat{s}}_i$ is strictly decreasing on $] {0},{ {\tilde{y}}_i} \, [$. This implies ${\hat{s}}_i(e_N) < {\overline{s}}_i$ and thus $1 = {\hat{s}}(e_N) = \sum _{i \in {\tilde{N}} } {\hat{s}}_i(e_N) < \sum _{i \in {\tilde{N}} } {\overline{s}}_i$. $\square$

5 Applications

In this section we illustrate with two examples the power of our main theorems. The power of these theorems lies in the facts that with them one quickly can reproduce, improve upon and unify many results for economic games (like oligopolistic, public good, cost-sharing, common resource, contest games and games appearing in the managerial theory of the firm) in the literature.

The first example deals with a homogeneous Cournot oligopoly with an industry revenue function that is possibly discontinuous at 0. The second example illustrates how the results can be applied to various games appearing in the managerial theory of the firm.

5.1 Cournot oligopoly

So again consider the Cournot oligopoly given by (8) in Sect. 3.

Theorem 5

Suppose the proper price function ${\tilde{p}}$ is positive, twice differentiable, $D {\tilde{p}} < 0$, has decreasing price flexibility $\epsilon _{{\tilde{p}}}$ and each cost function $c_i$ is twice differentiable, convex and strictly increasing. Further, let²³

${\overline{p}}(0) :=\lim _{y \downarrow 0} {\tilde{p}}(y) \in ] {0},{+\infty } ]$, ${\overline{p}}(\infty ) :=\lim _{y \rightarrow \infty } {\tilde{p}}(y) \in [ {0},{+\infty } \,[$, $\overline{\epsilon _{{\tilde{p}}}} :=\lim _{y \downarrow 0} \epsilon _{{\tilde{p}}}(y) \in ] {-\infty },{0} ]$, ${\overline{Dc}}_i :=\lim _{x_i \rightarrow \infty } Dc_i(x_i) \in ] {0},{+\infty } ]$. Suppose there exists at least one firm i with ${\overline{p}}(0)> Dc_i(0)$.

• 1. Each equilibrium is active and strict.

• 2. If $\overline{\epsilon _{{\tilde{p}}}} < -1$ or $\epsilon _{{\tilde{p}}} = -1$, then at each equilibrium at least two firms are active.

• 3. The game has at most one equilibrium.

Further suppose that ${\overline{p}}(\infty ) - {\overline{Dc}}_i < 0 \; (i \in N)$. Then

• 4. If $\overline{\epsilon _{{\tilde{p}}}} > -1$, then the game has a unique equilibrium.

• 5. Suppose $\overline{\epsilon _{{\tilde{p}}}} \le -1$ or $\epsilon _{{\tilde{p}}} = -1$.

  • (a) $n > -\overline{\epsilon _{{\tilde{p}}}} \; \Leftrightarrow \;$ the game has a unique equilibrium.

  • (b) $n \le - \overline{\epsilon _{{\tilde{p}}}} \; \Leftrightarrow \;$ the game does not have an equilibrium. $\diamond$

Proof

We already have seen that Assumption A2’ holds and that therefore ${\tilde{N}} = N_>$. Also, by assumption, $N_> \ne \emptyset$. So Theorem 1(1) implies the first statement in part 1. As $c_i$ is convex, it follows that $Dc_i( x_i)> 0 \; ( x_i > 0)$. As ${\overline{t}}_i(x_i) = {\tilde{p}}(x_i) ( \epsilon _{{\tilde{p}}}(x_i) + 1) - Dc_i(x_i)$, it follows that if $\overline{\epsilon _{{\tilde{p}}}} < -1$ or $\epsilon _{{\tilde{p}}} = -1$, then every $i \in {\tilde{N}}$ is of class II, and if $-1 < \overline{\epsilon _{{\tilde{p}}}} \le 0$, then every $i \in {\tilde{N}}$ is of class I. As $D\epsilon _{{\tilde{p}}} = D ( D {\tilde{p}} \cdot \frac{ \mathrm {Id} }{ {\tilde{p}} } ) \le 0$, it follows that $D^2 {\tilde{p}} \cdot \mathrm {Id} + D {\tilde{p}} \le \mathrm {Id} \cdot \frac{ {( D {\tilde{p}} )}^2 }{ {\tilde{p}} }$. For $y > 0$ and $x_i \in ] {0},{y} ]$ with $t_i(x_i,y) =0$, we obtain

$$\begin{aligned} (x_i D_1 + y D_2) t_i(x_i,y)= & {} x_i ( D {\tilde{p}} (y) - D^2 c_i(x_i) ) + y ( D^2 {\tilde{p}} (y) x_i + D {\tilde{p}}(y) ) \\= & {} x_i ( y D^2 {\tilde{p}} (y) + D {\tilde{p}} (y) ) + y D {\tilde{p}}(y) - x_i D^2 c_i(x_i) \\\le & {} x_i y \frac{ {( D {\tilde{p}}(y) )}^2 }{ {\tilde{p}}(y) } + y D {\tilde{p}}(y) - x_i D^2 c_i(x_i) \\= & {} \frac{ y D {\tilde{p}}(y) }{ {\tilde{p}}(y) } ( t_i(x_i,y) + Dc_i(x_i) ) - x_i D^2 c_i(x_i) \\= & {} \epsilon _{{\tilde{p}}}(y) D c_i(x_i) - x_i D^2 c_i(x_i). \end{aligned}$$

As $c_i$ is strictly increasing and convex we here have (noting that $x_i \ne 0$) $D c_i(x_i) >0$. Therefore as $\epsilon _{\tilde{p }}(y) < 0$ and $D^2 c_i(x_i) \ge 0$, it follows that Assumption A2 holds. Of course, also Ass. A1 holds. Now Remark 3 implies that the second statement in part 1 holds. Part 1 and Proposition 7 now imply part 2. And Theorem 2 guarantees that the game has at most one equilibrium; so part 3 holds.

Further suppose that ${\overline{p}}(\infty ) - {\overline{Dc}}_i < 0 \; (i \in N)$. Now we prove that Assumption B holds. Fix $i \in {\tilde{N}}$. As ${\overline{p}}(\infty ) - {\overline{Dc}}_i < 0$, there exists ${\overline{x}}_i > 0$ with ${\tilde{p}}({\overline{x}}_i) - D c_i({\overline{x}}_i) < 0$. As $c_i$ is convex it follows for every $y \ge x_i > {\overline{x}}_i$ that $t_i(x_i,y) \le {\tilde{p}}(y) - D c_i(x_i) \le {\tilde{p}}( {\overline{x}}_i ) - D c_i({\overline{x}}_i) < 0$. Now Theorem 3 implies part 4.

Further suppose $\overline{\epsilon _{{\tilde{p}}}} \le -1$. Each player is of class II. So Theorem 4(3) applies and guarantees that the proof of part 5a is complete if we show that $\sum _{i \in {\tilde{N}} }{\overline{s}}_i = \frac{n}{-\overline{\epsilon _{{\tilde{p}}}}}$. Well, first note that ${\overline{p}}(0) = +\infty$; this follows from the identity ${\tilde{p}}(y) = {\tilde{p}}(1) e^{ \int _y^1 - \frac{ \epsilon _{{\tilde{p}}}(\xi ) }{\xi } \, d \xi }$. Next, by Theorem 4(1), for all $i \in {\tilde{N}}$ and $y > 0$ small enough there exists a unique $b_i(y) \in ] {0},{y} ]$ with $t_i(b_i(y),y) = 0$. As $0 = D {\tilde{p}}(y) b_i(y) + {\tilde{p}}(y) - Dc_i(b_i(y)) = {\tilde{p}}(y) ( - \epsilon _{{\tilde{p}}}(y) s_i(y) + 1 ) - Dc_i(b_i(y))$, we have

$$\begin{aligned} s_i(y) = \frac{1}{-\epsilon _{{\tilde{p}}}(y) } \left( 1- \frac{ Dc_i(b_i(y)) }{{\tilde{p}}(y)} \right) . \end{aligned}$$

(15)

As $Dc_i$ is continuous at 0 and $0 \le b_i(y) \le y$, we obtain ${\overline{s}}_i = \lim _{y \downarrow 0} s_i(y) = \frac{1}{ - \overline{\epsilon _{{\tilde{p}}}} }$. Thus, as desired, $\sum _{i \in {\tilde{N}} }{\overline{s}}_i = \frac{n}{-\overline{\epsilon _{{\tilde{p}}}}}$.

As the game has at most one equilibrium, part 5b follows from part 5a. $\square$

Theorem 5, dealing with decreasing price flexibility, in particular applies to the proper price function ${\tilde{p}}(y) = y^{-\alpha }$ where $\alpha > 0$; here the price flexibility $\epsilon _{{\tilde{p}}}$ is constant, i.e. $-\alpha$. For this case the first results appeared in [34] for $\alpha =1$, wherein also a structural equivalence between this case and rent-seeking games was shown.²⁴ The case for $\alpha > 0$ is dealt with in [7]. Results for Cournot oligopolies with decreasing price flexibility can be found in [38, 42, 43, 45]; Theorem 5 also essentially follows from results in this literature. However, in Theorem 5, the smoothness assumptions for the proper price function and cost functions are weaker, our proof is very short and follows from our general results for smooth aggregative games

Finally, we use the opportunity to illustrate how the Selten–Szidarovszky technique is at the base of an algorithm for determining the equilibrium set. Again consider the above oligopoly with ${\tilde{p}}(y) = y^{-\alpha }$ and suppose there $n=3, \alpha =1$ and $c_i(x_i) = i x_i^2$. By Theorem 4(1), for all $i \in {\tilde{N}}$ and $y > 0$ small enough, there exists a unique ${\hat{b}}_i(y) \in ] {0},{y} ]$ with $t_i({\hat{b}}_i(y),y) = 0$, that is with $y^{-\alpha } ( 1 - \alpha \frac{{\hat{b}}_i(y)}{y} ) = Dc_i({\hat{b}}_i(y))$. From (15) we obtain ${\hat{b}}_i(y) = \frac{y}{1+2iy} \; (y > 0)$. This leads to (maybe by using a program like Maple) ${\hat{b}}(y) = \sum _{i=1}^3 {\hat{b}}_i(y) = \frac{44 y^3+ 24y^2 +3y}{48 y^3 + 44y^2 +12y +1}$ and that ${\hat{b}}$ has $y_{\star }=0.797..$ as a unique fixed point. By Theorem 1(1), ${\mathbf {0}}$ is not an equilibrium. Therefore, using Propositions 1 and  4(2), we obtain that the game has (0.307.., 0.1903.., 0.137..) as unique equilibrium.

5.2 Oligopoly model with alternative objectives

We pick up here an idea in [18] and quickly and roughly show how the results in the present article can be used to further elaborate on it.

[18] deals with a Cournot oligopoly model in which each firm’s objective is to maximize the weighted average of profit and another factor such as revenue, market share, output, negative of cost or profit per worker. This can be realised by modifying the payoff function of the general Cournot oligopoly game (8) as follows:

$$\begin{aligned} f_{i}({\mathbf {x}})= (1-\theta _i)\Bigl ( p\left( \underset{l}{\sum }x_{l}\right) x_{i}-c_{i}(x_{i}) \Bigr ) +\theta _{i}h_{i}\left( x_{i},\underset{l}{\sum }x_{l}\right) . \end{aligned}$$

(16)

Here $\theta _{i}\in [ {0},{1} \,[$ is a weight assigned on the objective represented by the alternative objective function $h_i: \varDelta \rightarrow \mathbb {R}$.²⁵

Various results for games dealing with a single alternative objective can be found in the literature. For the revenue objective take $h_i(x_i,y) = p(y)x_i$ (e.g. [29]), for market share $h_i(x_i,y) = x_i/y$ (e.g. [30]), for output $h_i(x_i,y) = x_i$ (e.g. [32]), for negative of cost $h_i(x_i,y) = -c_i(x_i)$ (e.g. [20]) and for profit per worker $h_i(x_i,y) = \frac{p(y) x_i -c_i(x_i)}{N(x_i)}$ where $N(x_i)$ represents the employment level of workers associated with the output level $x_i$ (e.g. [32]).

The marginal reduction $t_i$ becomes

$$\begin{aligned} t_i(x_i,y) = (1 - \theta _i) (Dp(y) x_i + p(y) - Dc_i(x_i) ) + \theta _i (D_1 h_i(x_i,y) + D_2 h_i(x_i,y) ). \end{aligned}$$

And note that concerning Assumption A2 we have (using short notations)

$$\begin{aligned} x_i D_1 t_i + y D_2 t_i= & {} (1 - \theta _i) (t_i - D c_i - x_i D^2c_i +y D^2 p - p) \\&\quad +\, \theta _i (x_i D_{11} h_i + x_i D_{12} h_i + y D_{21} h_i + y D_{22} h_i). \end{aligned}$$

The analysis in [18] is by assuming the generalised Fisher–Hahn conditions $D_1 t_i < 0$ and $D_2 t_i \le 0$ assuming that each firm has the same cost function and the same alternative object function. It is clear (especially by having already results like Theorem 5) that by using our Assumptions A1 and A2 much more general results can be obtained.