1 Introduction

Earthquake early warning (EEW) aims to provide sufficient time for preventing disaster before the strong ground motion arrives. Ground motion prediction is an important component of EEW system. Traditional methods of ground motion prediction for EEW predict the peak ground motion and trigger an alarm when the ground motion is predicted to be above a specific threshold. They can be classified as front detection, on-site, and network methods (Allen et al. 2009).

The front detection methods use one or more front stations between the source and the target cities and trigger a warning if the ground shaking is above a certain level. The Seismic Alert System (SAS) for Mexico City at the Pacific coast uses the front detection method to provide approximate 60 s for earthquakes. The EEW system in Istanbul uses seismometers along the Northern shore of the Marmara Sea based on the front detection method (Alcik et al. 2009). The front detection methods can provide warning if the epicenter is far from the city, but it cannot determine the magnitude or the severity of the earthquake.

On-site methods and network methods determine source location and magnitude in the first few seconds after P wave detected. The strength of ground motion at a specific location is then calculated by applying a ground motion prediction equation (GMPE) based on hypocenter distance and earthquake magnitude, such as the amplitude of P wave (Wu and Kanamori 2005; Kanda et al. 2009), the dominant ground motion period, and average ground motion period (Nakamura 1988; Allen and Kanamori 2003; Wu et al. 2007). The prediction accuracy of these methods is affected by the precision of the hypocenter location and magnitude determination, which is a challenging task for EEW systems. Since 2007, Japan Meteorological Agency (JMA) provided an EEW system based on determining the hypocenter and magnitude (Hoshiba et al. 2008) and reported the performance of the 2011 M W9.0 Tohoku earthquake (Hoshiba et al. 2011). The performance obtained by M W9.0 earthquake using network methods revealed two issues: under-prediction of ground motions for the large fault rupture and overprediction for the multiple simultaneous aftershocks (Hoshiba and Aoki 2015).

The traditional methods above cannot predict the ground motion in real time and most of the methods suffer from the low precision of hypocenter and magnitude determination. In recent years, some approaches have been proposed for real-time estimation of ground motion without estimating the source parameters (Hoshiba 2013; Hoshiba and Aoki 2015).

Hoshiba (2013) applied boundary integral equation based on Kirchhoff–Fresnel integral theorem to predict real-time ground motion. The incoming seismic wave directions of front stations are required, instead of the source parameters. The estimation of wave field direction is more reliable than the estimation of source parameters. The performance of the method is limited because the amplitude and the phase information are hard to estimate, and the assumption of amplitude and phase has to be made in the method. In addition, the computation time cannot fit to real-time application.

Hoshiba and Aoki (2015) investigated numerical shake prediction method to predict real-time ground motion for EEW system. Data assimilation technique (Kalnay 2003) is used to estimate the current distribution of seismic ground motion. Radiative transfer theory (RTT) (Sato et al. 2012) is used for simulating seismic wave propagation. The computation time of the method is fast enough for real-time estimation of ground motion.

The numerical shake prediction method is promising for real-time ground motion prediction, but 2-D space simulation is used in the system for simplicity. Because wave propagation on 2-D space is not in accordance with real situation (seismic waves propagate in 3-D space), the predicted strong ground motion is observed to arrive earlier than real ground motion under the 2-D space. Overprediction also occurs through 2-D space simulation. Since the wave propagates in 3-D spaces, handling the difference between the 2-D and 3-D spaces is important for real-time ground motion prediction method.

In this article, for accurate real-time ground motion prediction, we propose 3-D space numerical shake prediction, which aims to simulate the wave propagation precisely. For the simulation of seismic wave propagation, radiative transfer theory in 3-D space is adopted in this paper. For efficient computation, Direct Simulation Monte Carlo (DSMC) simulation is used to model the wave energy propagation as particles carrying specific energies with 3-D moving directions. Data assimilation technique is incorporated to predict the motion of earth sphere by using the real-time record of seismic stations. Because of 3-D space model is more close to the real scenario, overprediction problem occurred in 2-D space is expected to alleviate in 3-D space model. For real-time computation, the computation time of our method is mainly determined by the number of partition grids. Although 3-D space model needs more grids number to model, the computation results show that it can be calculated in real time. We apply our method using the actual data from KiK-net stations in JMA scale of the 2011 M W9.0 Tohoku earthquake as an example. Both 2-D and 3-D space models are studied and compared in the paper, and the performance of ground motion prediction in 3-D space model shows that our model can predict the real-time ground motion precisely.

2 Method

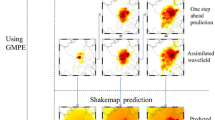
In order to predict the real-time ground motion of a specific region, the propagation of wave over time should be modeled, and the estimation of ground motion should be calculated given the observations of seismic stations. We propose our method as 3-D space numerical shake prediction. The framework of our method is shown in Fig. 1. The key of our method is wave propagation modeling and data assimilation. In Sect. 2.1, we introduce the 3-D space model and the grid partition method used in this article. The propagation of seismic wave is modeled using radiative transfer theory in 3-D space, which is introduced in Sect. 2.2. For modeling, the propagation energy is used instead of amplitude, and the energy propagation is solved by DSMC method which uses a large number of particles with directions and speeds. By using data assimilation technique, the energy distribution of any region is corrected by the real-time seismometer record, which is described in Sect. 2.3. Data assimilation corrects the energy distribution by comparing the difference of the real state and the wave propagation predicted by RTT. The prediction process is the application of wave propagation, and it is described in Sect. 2.4.

Fig. 1
figure 1

Schematic illustration of our method from data assimilation to prediction

Full size image

2.1 3-D space model

In this section, we introduce the 3-D space model of our method. Before we introduce the method, the notation is defined first. For a specific region of interest, the objective of the method is to calculate the ground motion for a given time t. For the region of interest, space model is introduced first by dividing the region into grids in identical size. Let x be the space model with horizontal parameter I 1, vertical parameter I 2, and depth parameter I 3, and with its corresponding increments △x, △y, and △z, respectively, as shown in Fig. 2. The ith grid is calculated as i = I 1 × I 2 × (i 3 − 1) + I 1 × (i 2 − 1) + i 1, where i 1 = 1,2,…,I 1, i 2 = 1,2,…,I 2, i 3 = 1,2,…,I 3. The total number of grids is I = I 1 × I 2 × I 3. We use the center of each grid to represent the location of the grid, therefore, the location at the ith component of U n is x i  = ((i 1 − 0.5) △x, (i 2 − 0.5) △y, (i 3 − 0.5) △z). In the region, y n is denoted as the observation of the stations at time n, where y is composed of Y stations: y n  = [y 1 n , y 2 n ,…,y Y n ]. For the time n, the seismic record y n is obtained. Our task is to estimate the U n given y 0, y 1, … y n , and use the U n to predict U n+1.

Fig. 2
figure 2

3-D space model. The space is partitioned by I 1, I 2, I 3 grids in x (east–west), y (north–south), z (depth) axes, respectively. The grid contains I 1 × I 2 × I 3 grids, and the stars represent the seismic stations. The triangle in the figure represents the center of the grid, and the index is i = I 1 × I 2 × (i 3 − 1) + I 1 × (i 2 − 1) + i 1

Full size image

2.2 Wave propagation modeling based on RTT and DSMC

In this section, we introduce the simulation method of wave propagation. The simulation of wave propagation solves the problem of how to calculate U n (the energy distribution of regions at time n) given U n-1 (the energy distribution of regions at time n − 1).

The analytical solution of the wave propagation modeled in 3-D space is hard to derive. For modeling the wave propagation in 3-D space, we use RTT as the simulation method. RTT method is based on the Boltzmann equation and is used to interpret seismogram envelopes of high-frequency seismic waves (Sato et al. 2012). Energy propagation is considered instead of wave propagation in the RTT method, because the interference of incoherent fluctuation waves destroys the phase information. The mean energy density is derived by using the local Born approximation and the multi-scale analysis. Compared with the finite-difference method and boundary integral equation, it costs less computational time, which is important for EEW application.

RTT represents scattering and attenuation processes while neglecting interference effect (Sato et al. 2012), and the radiated transfer equation in the 3-D space model is formed as:

$$\begin{aligned} & \partial {}_{t}f({\varvec{x}},t;{\varvec{q}}) + v_{0} ({\varvec{x}}){\varvec{q}}\partial_{x} f({\varvec{x}},t;{\varvec{q}}) = \\ & -\,v_{0} ({\varvec{x}})g_{0} ({\varvec{x}})f({\varvec{x}},t;{\varvec{q}}) - v_{0} ({\varvec{x}})h_{0} f({\varvec{x}},t;{\varvec{q}}) + v_{0} ({\varvec{x}})\frac{1}{4\uppi }\oint {{\text{d}}\varOmega_{{{\varvec{q}}^{{\prime }} }} } g({\varvec{x}},{\varvec{q}} - {\varvec{q}}^{{\prime }} )f({\varvec{x}},t;{\varvec{q}}^{{\prime }} ), \\ \end{aligned}$$
(1)

where q is a unit vector which represents the direction of wave energy propagation, the real function f(x,t;q) represents the directional distribution of mean energy density in direction q, dΩ q′ is a solid angle element in direction q′, and v 0(x) is the velocity of S wave (v S) at x. The velocity of S wave is assumed to be independent of the location x, and we could set v 0(x) as a constant denoted as v 0. g(x) is the scattering coefficient at x with the solid angle. In this article, we assume that the velocity structure and the attenuation structure are homogeneous, and scattering does not cause wave conversion. The isotropic scattering strength and intrinsic absorption are assumed to be independent of location x, which means g 0(x) and h 0(x) can be set as constants: g 0(x) = g 0, h 0(x) = h 0. By setting v 0(x) = v 0, g 0(x) = g 0 and h 0(x) = h 0, Eq. (1) can be rewritten as follows:

$$\begin{aligned} & \partial {}_{t}f({\varvec{x}},t;{\varvec{q}}) + v_{0} {\varvec{q}}\partial_{x} f({\varvec{x}},t;{\varvec{q}}) \\ & = - v_{0} g_{0} f({\varvec{x}},t;{\varvec{q}}) -\,v_{0} h_{0} f({\varvec{x}},t;{\varvec{q}}) + v_{0} \frac{1}{4\uppi }\oint {{\text{d}}\varOmega_{{q^{\prime}}} } g({\varvec{x}},{\varvec{q}} - {\varvec{q}}^{{\prime }} )f({\varvec{x}},t;{\varvec{q}}^{{\prime }} ). \\ \end{aligned}$$
(2)

The radiative transfer equation models the range of descriptions for wave energy propagation across the 3-D space heterogeneous medium with respect to time. The radiative transfer Eq. (2) cannot be solved by analytical solutions, so approximation algorithms should be used for solving the problem. In this paper, we use DSMC method (e.g., Gusev and Abubakirov 1987; Hoshiba 1991, 1995, 1997; Yoshimoto 2000) to solve the radiative transfer Eq. (2) for modeling scattering and attenuation (absorption) process. The DSMC method represents energy as particles and simulates the wave energy propagation by the movement of a large amount of particles. The integral of energy in specific region denoted by Eq. (2) is calculated as the sum of the particle energies in that region.

For representing the particle movement direction in 3-D space, we use two angles to represent the unique direction. Figure 3 shows the propagation process of a particle with scattering and absorption, and the implementation details are described below. The particles are represented as M and the mth particle at time n locates at X n,m . During the time interval △ t, if scattering does not occur, the particle is expected to move by v 0(x)△ t q Ω1, and it travels in direction Ω 1. Direction Ω 1 which is a unit vector can be represented as the angles θ and φ. θ is the angle between the projection of particle direction on xy plane with the x axis, and φ is the angle between the projection of particle direction on xy plane and the direction of particle. If scattering occurs, the particle changes direction.

Fig. 3
figure 3

Propagation of an particle in 3-D space of DSMC for RTT

Full size image

For modeling the scattering process, the DSMC method models the probability that energy does not scatter during the time interval △ t is exp[− g 0 v 0(x)△ t]. Therefore, the probability that scattering occurs for the time interval △ t is exp[− g 0 v 0(x)△ t], and the probability density from Ω q′ to Ω q is 1/4π. Because the scattering is assumed to be isotropic, the scattering probability of each particle is the same.

The scattering process is implemented in the following procedures. Three independent uniform random variables between 0 and 1 are λ 1, λ 2, and λ 3. When λ 1 ≥ g 0 v 0(x)△ t, which means that the particle does not scatter, the location is X n,m  = X n−1,m  + v 0 △ t q Ω1. When λ 1 < g 0 v 0(x)△ t, the location of the particle with scattering is X n,m  = X n−1,m  + v 0 △ t q Ω2. The new traveling direction is Ω 2, which can be represented as (2πλ 2, 2πλ 3) at the next time step, and Ω 1 = Ω 2 is used for the new traveling direction. Thus, the direction is [cosφcosθ, cosφsinθ, sinφ]. If the mth particle is located at X n,m at elapse time n, it will be at X n+1,m in the no-scattering case. In the scattering case, the new propagation direction is given by (2πλ 2, 2πλ 3), in which λ 2, λ 3 are random variables between 0 and 1.

For modeling the absorption process, let the mth particle has energy q n,m at time n which attenuates due to absorption as follows:

$${\varvec{q}}_{n,m} = {\varvec{q}}_{n - 1,m} \exp [ - h_{0} v_{0} ({\varvec{x}})\Delta t] \approx {\varvec{q}}_{n - 1,m} [1 - h_{0} v_{0} ({\varvec{x}})\Delta t],$$
(3)

h 0 v 0(x)△ t ≪ 1 is assumed, and for each step the energy decreases slowly. In this article, the amount of attenuation for each particle is the same, because h 0 is assumed to be homogeneous. Whether scattering occurs or not, the energy of the particle is attenuated when elapse time increases.

We can estimate the future situation from the present situation with location X n,m , direction Ω 1 and energy q n,m . The procedure repeats for m = 1,2,3…,M. As one-step-ahead prediction conducted by particle method, the distribution of f(x,t; q) is determined by the spatial, temporal, and directional distribution of particles. The particles should be reconstructed at different time step t n to minimize the fluctuations during data assimilation.

2.3 Data assimilation

Using the wave propagation process described in Sect. 2.2, the energy propagation of wave can be modeled. The real-time seismic wave record could be observed by seismic stations, and the difference of the prediction and the real observation can be used to improve the modeling process. In this article, we use data assimilation to improve the computation accuracy of wave energies by comparing the prediction of seismic stations and the real observation of them. Data assimilation is a numerical method widely used in predicting weather, oceanology, and atmospheric forecast based on the estimation of present condition (Kalnay 2003; Hoshiba and Aoki 2015).

We can calculate the distribution of wave field at t = t n from one time step before t n−1 in which the elapse time interval △ t follows t n−1 = t n  − △ t. In this section, we propose a data assimilation method for calculating the present ground motions based on the observation of seismic stations.

At time t n , the 3-D field of the initial conditions for the model variables: \({\varvec{U}}^{n} = \left( {U_{1}^{n} ,\;U_{2}^{n} ,\; \ldots U_{j}^{n} \ldots U_{p}^{n} } \right)\) is ordered by grid elements and time points, and j indicates the jth element in the model space, and the total number of elements is p.

In the data assimilation process, one-step-ahead prediction U nb is combined with the actual observation y n to estimate the present situation U na . In the prediction process, one-step-ahead prediction is repeatedly applied to predict the future situation.

Let \({\varvec{U}}_{\rm a}^{n}\) be an optimum wave field for \({\varvec{U}}^{n}\),\({\varvec{U}}_{\rm b}^{n}\) be a background field available at grid points in three dimensions, and \({\varvec{y}}_{0}\) be a vector of length q which is the number of stations for the observational field, respectively. It means the distributions before and after the combination with the actual observation are denoted by \({\varvec{U}}_{\rm b}^{n}\) and \({\varvec{U}}_{\rm a}^{n}\). A is applied to the wave field distribution after the combination at time t n-1. Thus, Eq. (2) is expressed as:

$${\varvec{U}}_{\rm b}^{n} = A({\varvec{U}}_{\rm a}^{n - 1} ),$$
(4)

where A is the wave propagation process described in Eq. (2). \({\varvec{U}}_{\rm a}^{n - 1}\) is the optimum wave field at time n − 1, and \({\varvec{U}}_{\rm b}^{n}\) is calculated by the one-step wave propagation simulation for the previous time n − 1 using Eq. (2). Using the difference of the seismic wave energy computed by Eq. (4) and the real-time wave energy, data assimilation in this section is expressed as:

$${\varvec{U}}_{\rm a}^{n} = {\varvec{U}}_{\rm b}^{n} + {\varvec{W}}\left[ {{\varvec{y}}_{0}^{n} - {\varvec{H}}\left( {{\varvec{U}}_{\rm b}^{n} } \right)} \right],$$
(5)

In which \({\varvec{y}}_{0}^{n} - {\varvec{H}}({\varvec{U}}_{\rm b}^{n} )\) is observational increments, W is \(p \times q\) matrix which represents weight matrix. \({\varvec{W}}\left[ {{\varvec{y}}_{0}^{n} - {\varvec{H}}\left( {{\varvec{U}}_{\rm b}^{n} } \right)} \right]\) indicates one-step-ahead predicting correction in the wave propagation simulation from \({\varvec{U}}_{\rm a}^{n}\) and \({\varvec{U}}_{\rm b}^{n}\) which are obtained from Eq. (2). Figure 3 indicates the application of repeated one-step-ahead prediction of wave propagating simulation. Observed data are used at each time step for the data assimilation technique.

W represents the relation between background errors and observational errors in one-step-ahead prediction:

$${\varvec{W}} = {\varvec{BH}}^{\rm T} \left( {{\varvec{R}} + {\varvec{HBH}}^{\text{T}} } \right)^{ - 1},$$
(6)

B and R represent background error covariance and observational error covariance, respectively. H is a \(q \times p\) matrix, and it represents the perturbation of the observational space, which means the interpolation of grid point’s location onto the observational point’s location. The size of fluctuation is smaller than the grid interval included in the observational error as well as the instrumental error. \({\varvec{HBH}}^{\text{T}}\) is a \(q \times q\) matrix and indicates an approximation by the interpolation of background error covariance between observational points.

$${\varvec{HBH}}^{\text{T}} = \left[ {\begin{array}{*{20}c} {b_{11} } & {b_{12} } & \cdots & {b_{1q} } \\ {b_{21} } & {b_{22} } & \cdots & {b_{2q} } \\ \vdots & \vdots & \vdots & \vdots \\ {b_{q1} } & {b_{q2} } & \cdots & {b_{qq} } \\ \end{array} } \right],$$
(7)

\(b_{jk}\) is the background error covariance between the kth and jth elements in the space model. Background error is assumed to fit a Gaussian-type correlation: \(b_{kj} = \sigma \mu_{kj}\) in which \(\mu_{kj} = \exp \left( {\frac{{ - r^{2} }}{{l^{2} }}} \right)\) represents the correlation of background error between the kth and jth elements, \(\sigma_{{}}\) denotes the standard deviation of the element background error and r is the distance between the kth grid’s center and the jth station, l is the correlation distance.

The observational error matrix R can be defined as follows:

$${\varvec{R}} = \sigma^{{\prime }} \left[ {\begin{array}{*{20}c} {\mu^{'}_{11} } & {\mu^{'}_{12} } & \cdots & {\mu^{'}_{1q} } \\ {\mu^{'}_{21} } & {\mu^{'}_{22} } & \cdots & {\mu^{'}_{2q} } \\ \vdots & \vdots & \vdots & \vdots \\ {\mu^{'}_{q1} } & {\mu^{'}_{q2} } & \cdots & {\mu^{'}_{qq} } \\ \end{array} } \right],$$
(8)

where σ′ denotes the standard deviation of observational error for each element, and \(\mu^{{\prime }}_{jk}\) denotes the correlations assumed for observational error between the kth and jth elements. No correlations are assumed for observational error at different locations. If \(k \ne j\), \(\mu^{{\prime }}_{kj} = 0\); if \(k = j\), \(\mu^{{\prime }}_{kj} = 1\). Therefore, the matrix R can be expressed as σ′E, where E is the identity matrix.

\({\varvec{BH}}^{\text{T}}\) is a \(p \times q\) matrix, which is approximated by the interpolation of the background error covariance between grids and observation points.

$${\varvec{BH}}^{\text{T}} = \left[ {\begin{array}{*{20}c} {b^{o}_{11} } & {b^{o}_{12} } & \cdots & {b^{o}_{1q} } \\ {b^{o}_{21} } & {b^{o}_{22} } & \cdots & {b^{o}_{2q} } \\ \vdots & \vdots & \vdots & \vdots \\ {b^{o}_{p1} } & {b^{o}_{p2} } & \cdots & {b^{o}_{pq} } \\ \end{array} } \right],$$
(9)

where \(b_{ij}^{o} = \mu_{ij}^{o} \sigma\). \(\mu_{ij}^{o}\) is the correlation between M i and O i , and it is assumed to be a Gaussian-type correlation: \(\mu_{ij}^{o} = \exp \left( {\frac{{ - a^{2} }}{{l^{2} }}} \right)\), in which a is distance between the ith grid and the jth station and l is correlation distance.

The weight matrix W is calculated by background error, observational error, and their correlation covariances. The error ratio σ′/σ can be used in determining the distribution of W ij instead of the individual values σ′ and σ. With larger correlation distance l, the correction \({\varvec{W}}\left[ {{\varvec{y}}_{0}^{n} - {\varvec{H}}\left( {{\varvec{U}}_{\rm b}^{n} } \right)} \right]\) is applied in a wider area around the jth station.

When observational errors are assumed to be much larger than background error (σ′ ≫ σ),\({\varvec{W}} \approx 0\), \({\varvec{U}}_{\rm a}^{n} \approx {\varvec{U}}_{\rm b}^{n}\). As iterative application of Eqs. (4) and (5), observations have no effect, and the results are just the simulation of wave propagation. In contrast, in the σ ≫ σ′ case, the one-step-ahead prediction has little effect on Eq. (5), and the actual observations are independent at each time step.

All past observations \({\varvec{y}}_{0}^{n - 1} ,{\varvec{y}}_{0}^{n - 2} ,{\varvec{y}}_{0}^{n - 3} \cdots\) to the present observation \({\varvec{y}}_{0}^{n}\) are used to estimate the present distribution \({\varvec{U}}_{\rm a}^{n}\). Real-time data assimilation technique enables estimating \({\varvec{U}}_{\rm a}^{n}\) in real time; the real-time shake map can be obtained from observations and the real-time wave propagation simulation.

In DSMC method, the integral of wave energy with respect to direction is used, and \({\varvec{U}}_{\rm b}^{n}\) is described as:

$$U_{\rm b}^{ni} = F\left( {{\varvec{x}}_{i} ,t_{n} } \right) = \int\limits_{0}^{4\uppi } {f_{\rm b} \left( {{\varvec{x}}_{i} ,t_{n} ;{\varvec{q}}} \right)} {\text{d}}{\varvec{q}},$$
(10)

in which \(U_{\rm b}^{ni}\) is the ith element of \({\varvec{U}}_{\rm b}^{n}\) vector, F is the energy density distribution in the 3-D space, \({\varvec{x}}_{i}\) is the location of the ith grid. f b means energy density before the combination of data assimilation with actual observational data.\({\varvec{U}}_{\rm b}^{n}\) can be obtained from one-step-ahead prediction as shown in Eq. (4), and \({\varvec{U}}_{\rm a}^{n}\) is combined from the present observation \({\varvec{y}}_{0}^{n}\) using data assimilation as shown in Eq. (5).

When \(U_{\rm a}^{ni} < U_{\rm b}^{ni}\), which means overprediction occurs at the ith grid, it is necessary to reduce the energy, which can be represented as follows:

$$f_{\rm a} \left( {{\varvec{x}}_{i} ,t_{n} ;{\varvec{q}}} \right) = \frac{{U_{\rm a}^{ni} }}{{U_{\rm b}^{ni} }}f_{\rm b} \left( {{\varvec{x}}_{i} ,t_{n} ;{\varvec{q}}} \right).$$
(11)

In the other case, when \(U_{\rm a}^{ni} > U_{\rm b}^{ni}\), which means under-prediction occurs, we add the extra amount of energy \(\left( {U_{\rm a}^{ni} - U_{\rm b}^{ni} } \right)\) radiated from the location of the ith grid. We assumed the radiation is assumed to be isotropic, and \(f_{\rm a}\) is expressed as:

$$f_{\rm a} \left( {{\varvec{x}}_{i} ,t_{n} ;{\varvec{q}}} \right) = f_{\rm b} \left( {{\varvec{x}}_{i} ,t_{n} ;{\varvec{q}}} \right) + \frac{{\left( {U_{\rm a}^{ni} - U_{\rm b}^{ni} } \right)}}{4\uppi },$$
(12)

\(f_{\rm a} \left( {{\varvec{x}}_{i} ,t_{n - 1} ;{\varvec{q}}} \right)\) conducts one-step-ahead prediction, and \(f_{\rm b} \left( {{\varvec{x}}_{i} ,t_{n} ;{\varvec{q}}} \right)\) can be calculated from the RTT simulation of propagation using Monte Carlo particle method. Based on Eq. (4),\({\varvec{U}}_{\rm b}^{n}\) is estimated, and \({\varvec{U}}_{\rm a}^{n}\) can be obtained by combining \({\varvec{U}}_{\rm b}^{n}\) with the actual observation \({\varvec{y}}_{0}^{n}\) in the data assimilation technique as shown in Eq. (10). Then, \(f_{\rm a} \left( {{\varvec{x}}_{i} ,t_{n} ;{\varvec{q}}} \right)\) can be estimated from Eq. (11) or (12). As these steps repeat, strength distribution of ground motion can be estimated precisely.

F(x,t) represents the distribution of energy intensity and is assumed to be proportional to the envelop of \(A_{\text{NS}}^{2} \left( {{\varvec{x}},t} \right) + A_{\text{EW}}^{2} \left( {{\varvec{x}},t} \right) + A_{\text{UD}}^{2} \left( {{\mathbf{x}},t} \right)\), which is the band-passed squared seismic wave acceleration records at location x (Hoshiba et al. 2001, Hoshiba and Aoki 2015).

2.4 Prediction

As data assimilation used in predicting the present \({\varvec{U}}_{\rm a}^{n}\), the future situation can also be estimated. Although future observation is not yet available, the wave propagation physics is calculated without data assimilation. The same procedures of RTT simulation section are adopted to simulate wave propagation for prediction. That is, \({\varvec{U}}_{p}^{n + 1} = P\left( {{\varvec{U}}_{\rm a}^{n} } \right)\), in which \({\varvec{U}}_{p}^{n + 1}\) means the prediction at time step n + 1. This repeating process enables us to predict the situation after k time step:

$${\varvec{U}}_{p}^{n + k} = P\left( {{\varvec{U}}_{p}^{n + k - 1} } \right) = P^{2} \left( {{\varvec{U}}_{p}^{n + k - 2} } \right) = \cdots = P^{k - 1} \left( {{\varvec{U}}_{p}^{n + 1} } \right) = P^{k} \left( {{\varvec{U}}_{\rm a}^{n} } \right).$$
(13)

P means the seismic wave propagation in a iteration at every time step. The process is described in Eq. (4).

3 Data

We apply the method described above to actually observed data in this section and use the 2011 M W9.0 Tohoku earthquake which occurred on the plate boundary east off Honshu island as an example in this article. We use the record of KiK-net seismic stations in the borehole as the observation data. Because the seismic stations in the borehole are nearly the rock soil profile, we do not consider the site amplification factor for simplicity.

JMA intensity is defined as logarithm (log10) of the mean square root of the three-component accelerogram’s amplitude by band-pass from 0.5 to 10 Hz and weight (1/freq)1/2 (Campbell and Bozorgnia 2011; Hoshiba and Aoki 2015). Because the energy density F is also proportional to the band-passed accelerogram’s amplitude, the relationship between the JMA intensity and the energy density F in RTT can be expressed as \(F = C10^{{I_{j} ({\varvec{x}},t)}}\)(Hoshiba and Aoki 2015), in which C is constant independent of location x and time t, and \(I_{j} \left( {{\varvec{x}},t} \right)\) represents the time trace of JMA intensity measured at x in real-time manner.

4 The 2011 M W9.0 Tohoku earthquake

The 2011 M W9.0 Tohoku Earthquake occurred off the pacific coast and caused strong ground motion around northeastern Japan on March 11, 2011. It generated a huge tsunami which killed more than 18,000 people and left more than 12,000 people missing (Fire Disaster Management Agency, Japan, report of April 11, 2011). In this earthquake, even the data of acceleration > 1000 cm/s2 were recorded at some stations in the Kanto district where the hypocentral distance exceeds 300 km (Hoshiba and Aoki 2015). Some authors proposed source models based on multiple strong-motion generation areas (SMGAs) to explain the area of strong ground motions, i.e., a source model with 4 SMGAs (Asano and Iwata 2012), models with 5 SMGAs proposed by Kurahashi and Irikura (2013). All studies identified that they needed at least 2 major SMGAs off Miyagi prefecture in the Tohoku district and several SMGAs off Fukushima prefecture southwest of the hypocenter.

The parameters for RTT to data assimilation are listed in Table 1, in which scattering strength g 0 and absorption strength h 0 have been determined by Hoshiba (1993). Here the data assimilation is processed at 1 s intervals (△ t = 1 s). Figures 4 and 5 show the results of applying the proposed method above using 3-D and 2-D space, respectively.

Table 1 Parameters of RTT simulation and data assimilation in the 2011 M W9.0 Tohoku earthquake
Full size table
Fig. 4
figure 4

Example of prediction in 3-D space model using the data from 2011 Tohoku M W9.0 earthquake. a Seismic intensity on JMA scale; b real-time shake map (assimilated distributions); (c, d) the predictions of 10 and 20 s, respectively. The blue point represents the location of Tokyo

Full size image
Fig. 5
figure 5

Example of prediction in 2-D space model using the data from the 2011 Tohoku M W9.0 earthquake. a Seismic intensity on JMA scale; b Real-time shake map after data assimilation; (c, d) the prediction of 10 s and the prediction of 20 s. The blue point represents the location of Tokyo

Full size image

The results of the simulation for 2011 M W9.0 Tohoku Earthquake in 3-D space model are shown in Fig. 4. Figure 4a shows the observation of Peak Ground Velocity (PGV) corresponding to y n0 at various time step n in real time. Figure 4b shows the shake map which is the seismic intensity distribution after data assimilation in 3-D space model at various elapse times. Figure 4c, d shows the prediction results of the seismic intensity distribution of 10 and 20 s, respectively. As shown in Fig. 4, strong ground motion propagating in northern Kanto can be observed at 160 s of elapse time and is predicted to reach the north of Tokyo in 20 s later. The strong shaking around the north of Tokyo is actually observed at 180 s of elapsed time. After the main shock, at around 170 s of elapsed time, the second SMGA is predicted to occur on the southeast of Tohoku after 10 s and to arrive Tokyo. The strong shaking is actually observed to reach the southeast of Tohoku and arrived Tokyo at 180 s of elapsed time. The shaking is continuous around this area caused by multiple events of the aftershocks.

Figure 5 shows the result of data assimilation and prediction of 2011 M W9.0 Tohoku earthquake in the 2-D space model. Figure 5b shows the shake map after data assimilation in 2-D space model at various elapse times. Figure 5c, d shows the predictions of the seismic intensity of 10 and 20 s, respectively. Strong ground motion propagating in northern Kanto can be observed at 160 s of elapse time as shown in Fig. 5 and is predicted to reach Tokyo in less 20 s later. At 180 s of elapsed time, the actual strong shaking is observed around Tokyo.

Comparing Figs. 4 with 5, we can observe that the prediction of the seismic intensity of the shake map under 3-D space is more closed to the real observation than that under 2-D space. Under 2-D space, the energy propagates faster than the real observation, because the S velocity propagates on 2-D plane, which makes it overpredicting the real ground motion. The energy prorogating in 3-D space is more concentrated than that in 2-D space, making the magnitude of ground motion is kept in several seconds. This phenomenon is observed in the record of seismic stations. Because of the inaccurate modeling of the velocity of S wave in 2-D space, the energy in the specific region vanishes too fast than the real observation.

Figure 6 shows the predicted seismic intensity of 5, 10, and 20 s in advance; 3-D space and 2-D space models are compared by JMA scale. We compare the residual between the prediction value and the actual observation of the station whose code is AKTH02. Comparing the 2-D and 3-D space model, the residual of the prediction using 3-D space model get relative lower than that using 2-D space model. The 5 s prediction obtains the least residual, which is in accordance with the real observation: the fewer time to predict in advance, the more accurate prediction of seismic wave energy. Overprediction can be alleviated by shortening the lead time. Comparing the 2-D and 3-D space model, the overprediction problem is alleviated using 3-D space model because of the more accurate modeling of wave direction and velocity.

Fig. 6
figure 6

Comparison of the 5, 10, 20 s prediction of the 2-D and 3-D space model with the real observation of AKTH02 station. a the comparison of 3-D space model; b the comparison of 2-D space model; c the residual of the predictions with real observations of the AKTH02 station

Full size image

We compare the average residual between the predictions of 5, 10, and 20 s with the real observation for all the 163 stations, and the average residual is shown in Fig. 7. As Fig. 7 shows, the residual of the 3-D space model is smaller than that of the 2-D space model, and the residual 5 s prediction in advance is smaller than that of 10 and 20 s prediction, which means that we get more accurate prediction when using less time in advance to predict.

Fig. 7
figure 7

Comparison of the average residual of the predictions with real observations of all 163 KiK-net stations

Full size image

Computation time efficiency is very important to real-time EEW application. In operation, computation time should be less than actual elapsed time. Grid number p, sites number q, and particles number M affect the computation time of the proposed method. We use p = 200 × 100 × 3 = 60,000 grids, q = 163 stations, and M = 106 particles in this example. In our implementation, it takes 0.6 s CPU time for data assimilation at each time step (△t = 1) and it takes 0.34 s for prediction of the 20 s future ground motion by using a desktop PC. The total time in this method is 0.94 s at each time step, and the computation time is reasonably short for actual application to real-time EEW. The process can also be accelerated using more powerful computers.

The assimilation of real-time shake maps in Fig. 4 enables us to predict the future situation. The seismic wave propagation is imaged by following Huygen’s principle, by which multiple simultaneous secondary sources produce a propagating wave front at different regions. Strong ground motions reach the Tohoku region repeatedly, but the first two SMGAs of Miyagi prefecture do not cause very strong shaking in the Kanto region. The strong shaking occurred in the Kanto region due to later ruptures. As observed in Fig. 4, the propagation of seismic wave can be predicted accurately using numerical shake prediction in 3-D space model.

5 Discussion

The proposed method in this article is different from the conventional methods of many EEW systems. The proposed method aims to predict the real-time ground motion of the next several to tens of seconds using dense seismic network. It is difficult to completely reconstruct the spatial distribution of ground motion by a limited number of source parameters, which usually are these five parameters: latitude, longitude, depth, origin time, and magnitude. Even if the estimation of source parameters is precise, the prediction of ground motion is not necessarily similarly precise. The period of time to estimate the source parameters should be regarded as blind time to the EEW system.

In contrast, discrepancies between the estimated situation and the observation are minimized by data assimilation. The actual observation is reflected as much as possible to estimate the space–time distribution of ground motion before step time forward to prediction. All the data information up to the present can be used to estimate the present situation of wave propagation in the proposed method.

However, the conventional EEW methods have their own merits. For the determination of the peak ground motion for a specific region, the conventional methods can predict the peak ground motion after P wave detection of one or several seismic stations. For predicting peak ground motion, the lead time of conventional EEW methods is shorter than that of the proposed method. The prediction time and accuracy are a trade-off for EEW systems, and the combination of the conventional EEW systems and the proposed method could be considered to lead to the solution with the best possible trade-off.

The appropriate assumption of the error ratio σ′/σ is an important factor for improving the precision of estimation in data assimilation. The error ratio from the reliabilities of observation and simulation σ′/σ is assumed in this article. When observation is more precise than simulation, σ′/σ < 1 is applied. When simulation is more precise than observation, σ′/σ > 1 is used. The new observation of ground shaking corresponds to the wave field estimation more rapidly with decreasing σ′/σ. Therefore, at early stage too large error ratio may lead to under-prediction. On the other hand, when the error ratio is too small, observations may easily include small fluctuations which lead to jerky propagation.

Finally, we discuss the difference between the method of particles calculation in the 3-D space model and the 2-D space model. The 2-D space model corresponds to the assumption of \(f\left( {x,y,z,t;\theta } \right) = f\left( {x,y,0,t;\theta } \right)\), in which x and y are the two horizontal axes and z is the depth. When energy is assumed to propagate in the 2-D image, the lead time to strong ground motion arrived may be overpredicted. Thus, the strength of ground motion tends to be slightly overpredicted. In 3-D spaces, because the direction of particle is three-dimensional, the velocity reflected on 2-D space is smaller than that of 2-D space. Therefore, the speed of wave prorogation is more close to the real velocity, and the overprediction problem is alleviated as shown in the Tohoku earthquake.

6 Conclusions

In this paper, we propose a 3-D space numerical shake prediction method for real-time ground motion prediction. Wave propagation modeling in 3-D space is more precise than that in 2-D space. Our method models the wave energy propagation using radiative transfer theory in 3-D space, mainly by radiative transfer equation. Direct Simulation Monte Carlo method is adopted to solve the radiative transfer equation, and this method can be executed by computer conveniently. Data assimilation technique is integrated to model the present wave energy using the real-time record of seismic stations, without using the information of earthquake parameters such as hypocenter and magnitudes. In 3-D space model, the computation time in 3-D space could be fit for real-time EEW estimations. The 2011 M W9.0 Tohoku earthquake is studied as an example. The prediction results is compared between model in 3-D space and 2-D space and shows that our numerical shake prediction method based on 3-D space model can simulate the wave propagation precisely. Overprediction problem occurred in 2-D space is alleviated when 3-D space model is used, suggesting that our method can model the wave propagation in earthquake, even the earthquake that has large fault rupture situation and contains multiple events occurred simultaneously.

7 Data and resources

We obtained the strong-motion acceleration data on KiK-net from the National Research Institute for Earth Science and Disaster Prevention Web site (http://www.kyshin.bosai.go.jp).