1 Introduction

Surface wave tomography from earthquake data or ambient noise cross-correlations has been widely used to investigate crust and upper mantle shear wave velocity structures globally or regionally. A majority of surface wave studies have focused on the inversion of isotropic shear wavespeeds (e.g., Simons et al. 1999; Huang et al. 2003; Yao et al. 2008; An et al. 2009; Li et al. 2009; Zheng et al. 2010; Sun et al. 2010; Yang et al. 2012; Li et al. 2013), while some other studies focus on the inversion of radially or azimuthally anisotropic shear velocity structures. These studies are important for understanding shape or lattice preferred orientations of minerals and deformation styles in the crust and upper mantle (Savage 1999; Mainprice 2007; Montagner 2007). For instance, Shapiro and Ritzwoller (2002) and Zhou et al. (2006) used earthquake Rayleigh and Love waves to obtain global models of shear wavespeed radial anisotropy in the upper mantle, that is, the difference between the vertically polarized shear wavespeed (V SV) and the horizontally polarized shear wavespeed (V SH). Ambient noise tomography using both Rayleigh and Love waves can produce high-resolution shear wavespeed radial anisotropy in the crust (e.g., Huang et al. 2010; Moschetti et al. 2010; Guo et al. 2012; Luo et al. 2013).

In regions with good azimuthal path coverage, period-dependent 2-D phase/group velocity maps with azimuthal anisotropy can be obtained either from direct inversion of phase/group velocity dispersion measurements (e.g., Montagner 1986; Su et al. 2008; Fry et al. 2010; Yao et al. 2010; Yi et al. 2010; Endrun et al. 2011; Lu et al. 2014) or from localized estimation of phase velocity and its azimuthal anisotropy by solving the Eikonal equation (Lin et al. 2009) or the Helmholtz equation (Lin and Ritzwoller 2011). Montagner and Nataf (1986) proposed a linearized inversion method for inverting azimuthal anisotropy of surface wave dispersion for shear wavespeeds with azimuthal and radial anisotropy at depths. This method has been used to obtain upper mantle azimuthal anisotropy regionally (e.g., Montagner and Jobert 1988; Silveira and Stutzmann 2002; Yao et al. 2010) and globally (e.g., Montagner and Tanimoto 1990). Another approach to obtain the depth-dependent V SV and azimuthal anisotropy is following a two-step procedure based on waveform inversions: (1) nonlinear surface waveform inversion to obtain 1-D path-averaged V SV models and (2) tomographic inversion to invert all 1-D path-averaged V SV models for 3-D V SV structures and azimuthal anisotropy (e.g., Simons et al. 2002; Debayle et al. 2005).

The inversion of (isotropic) shear wavespeed structure from surface wave dispersion is nonlinear and inversion results may depend on the initial reference model. A number of global optimization algorithms can be applied to invert dispersion data for shear wavespeed models, including the Monte-Carlo approach (Shapiro and Ritzwoller 2002), the Neighborhood Algorithm (Sambridge 1999a, b; Yao et al. 2008), the Genetic Algorithms (Shi and Jin 1995; Wu et al. 2001), etc. Instead of just giving one best-fit model in the linearized inversion approach, these global searching methods typically perform (quasi-) random walks in the model space, retain a subset of models that satisfy certain misfit criteria, and finally give an ensemble of acceptable models. From Bayesian statistical analysis of the generated model ensemble, we can access uncertainties of model parameters and correlations between different model parameters (e.g., Sambridge 1999b; Yao et al. 2008).

From Montagner and Nataf (1986), the inversion of azimuthally anisotropic parameters of shear wavespeeds depends on the isotropic part shear wavespeed structure. Therefore, a reliable isotropic shear wavespeed model is important for robust estimation of azimuthally anisotropic model parameters. In this study, we propose a two-step inversion method using the Neighborhood Algorithm and Bayesian analysis (Sambridge 1999a, b) to invert azimuthally anisotropic Rayleigh wave dispersion data for the 1-D model of depth-dependent shear wavespeed and azimuthal anisotropy. We will first describe the details of the proposed methodology and then apply this method in SE Tibet. Finally, we will discuss the proposed methodology and the inversion results.

2 Methodology

2.1 Rayleigh wave azimuthal anisotropy

From Smith and Dahlen (1973) Rayleigh-wave phase velocity c(ω, M, ψ) at location M for an angular frequency ω and propagation azimuth ψ (with respect to north) can be expressed as

$$ \begin{aligned} c(\omega ,M,\psi ) & = c_{0} (\omega ) + a_{0} (\omega ,M) + a_{1} (\omega ,M)\cos 2\psi + a_{2} (\omega ,M)\sin 2\psi \\ & \quad + a_{3} (\omega ,M)\cos 4\psi + a_{4} (\omega ,M)\sin 4\psi , \\ \end{aligned} $$
(1)

where c 0(ω) is the reference phase velocity from a reference model, and a 0 is the isotropic phase velocity perturbation with respect to the reference phase velocity, a 1,2 and a 3,4 are the azimuthally anisotropic coefficients for the 2ψ (180° periodicity) and 4ψ (360° periodicity) terms, respectively. As noted by Montagner and Nataf (1986), the 4ψ terms are negligibly small for Rayleigh waves. Therefore, by ignoring the 4ψ terms in Eq. (1), the perturbation of phase velocity with respect to the reference c 0(ω) can be written as

$$ \delta c_{\text{R}} (\omega ,M,\psi ) \approx a_{0} (\omega ,M) + a_{\text{c}} (\omega ,M)\cos 2\psi + a_{\text{s}} (\omega ,M)\sin 2\psi , $$
(2)

where a c, a s are used here to replace a 1, a 2, respectively in Eq. (1) in order to denote the cosine and sine terms.

Following Montagner and Nataf (1986), we express the Rayleigh-wave phase velocity perturbation δc R(M, ω, ψ) at location M as

$$ \begin{aligned} \delta c_{\text{R}} (M,\omega ,\psi ) \approx & \int_{0}^{H} {\Bigg[ {\frac{{\partial c_{\text{R}} }}{\partial A}\left( {\delta A + B_{\text{c}} \cos 2\psi + B_{\text{s}} \sin 2\psi } \right)} \Bigg.} {\mkern 1mu} + \\ \frac{{\partial c_{\text{R}} }}{\partial C}\delta C + \frac{{\partial c_{\text{R}} }}{\partial F}\left( {\delta F + H_{\text{c}} \cos 2\psi + H_{\text{s}} \sin 2\psi } \right){\mkern 1mu} + \\ \frac{{\partial c_{\text{R}} }}{\partial L}\Bigg. {\left( {\delta L + G_{\text{c}} \cos 2\psi + G_{\text{s}} \sin 2\psi } \right)} \Bigg]{\text{d}}z \\ \end{aligned} $$
(3)

The four parameters (A, C, F, L) in (3) together with the other one N describe the equivalent transversely isotropic medium with a vertical symmetry axis with \( A = \rho V_{\text{PH}}^{2}, \) \( C = \rho V_{\text{PV}}^{2}, \) \( L = \rho V_{\text{SV}}^{2}, \) \( N = \rho V_{\text{SH}}^{2}, \) in which ρ is density, V PH and V PV are the horizontally and vertically “propagating” P-wave velocities, V SH and V SV are the horizontally and vertically “polarized” S-wave velocities, respectively. The other six parameters B s,c, G s,c, and H s,c give the 2ψ azimuthal variations (180° periodicity) of A, L, and F, respectively. The kernels ∂c R/∂p i (p i  = A, L, or F) can be calculated from a 1-D reference model. A generalized least squares inversion approach can be implemented to solve the Eq. (3) to obtain these elastic parameters (Montagner and Nataf 1986).

Montagner and Nataf (1986) found that the ∂c R/∂L term has the largest contribution in Eq. (3), ∂c R/∂A is comparably large in the crust and negligibly small in the upper mantle, but ∂c R/∂F is somewhat smaller. Therefore, we can approximate (3) by ignoring the ∂c R/∂F term as

$$ \begin{aligned} \delta c_{\text{R}} (M,\omega ,\psi ) \approx & \int_{0}^{H} {\left[ {\frac{{\partial c_{\text{R}} (\omega )}}{\partial A}\left( {\delta A + B_{\text{c}} \cos 2\psi + B_{\text{s}} \sin 2\psi } \right) + } \right.} \\ \frac{{\partial c_{\text{R}} (\omega )}}{\partial L}\left. {\left( {\delta L + G_{\text{c}} \cos 2\psi + G_{\text{s}} \sin 2\psi } \right) + \frac{{\partial c_{\text{R}} }}{\partial C}\delta C} \right]{\text{d}}z \\ \end{aligned} $$
(4)

Since for every azimuth ψ, (4) holds, thus we have

$$ a_{0} (\omega ,M) \approx \int_{0}^{H} {\left[ {\frac{{\partial c_{\text{R}} (\omega )}}{\partial A}\delta A + \frac{{\partial c_{\text{R}} (\omega )}}{\partial L}\left. {\delta L + \frac{{\partial c_{\text{R}} }}{\partial C}\delta C} \right]{\text{d}}z} \right.} , $$
(5)
$$ a_{\text{c,s}} \left( {\omega ,\,M} \right) \approx \int_{0}^{H} {\left[ {\frac{{\partial c_{\text{R}} \left( \omega \right)}}{\partial A}B_{\text{c,s}} + \frac{{\partial c_{\text{R}} \left( \omega \right)}}{\partial L}G_{\text{c,s}} } \right]} {\text{d}}z $$
(6)

The use of the subscript c,s in (6) means there are two equations, one taking the subscript c and the other one taking s in all corresponding variables in (6). This notation will be similarly used hereinafter. Equation (5) can be used to solve for δA, δL, and δC from the isotropic part of Rayleigh-wave phase velocity perturbations using the (iterative) linearized inversion method. However, usually only δL can be well resolved due to large sensitivity of ∂c R/∂L in (5) (Montagner and Nataf 1986).

2.2 Inversion for shear wavespeeds and azimuthal anisotropy

We can invert for the isotropic part V SV of a layered model from dispersion data using global searching algorithms, for instance, Metropolis Monte-Carlo Algorithm (Shapiro and Ritzwoller 2002), Neighborhood Algorithm (Sambridge 1999a, b; Yao et al. 2008), etc. Typically we perform forward calculations of the isotropic part dispersion data c pred(ω) from an ensemble of the generated models (a function of V P, V S and ρ), which are compared with the observed isotropic part dispersion measurements c obs(ω) = c 0(ω) + a 0(ω,M) in order to obtain best fitting models.

In this study, we use the global searching Neighborhood Algorithm (NA) and Bayesian analysis (Sambridge 1999a, b) to estimate L and G c,s as well as their uncertainties. The NA involves two stages: (1) the NAS stage (Sambridge 1999a), which consists of a model space search based on Voronoi cells to identify the “good” fitting model regions; and (2) the NAB stage (Sambridge 1999b), which employs the Bayesian statistical analysis of the generated model ensemble in the NAS stage to compute the posterior mean model parameters and their uncertainties from the 1-D marginal posterior probability density functions (1-D PPDFs or 1-D marginals) and trade-offs between different two model parameters from the 2-D PPDFs (or 2-D marginals).

From (6), we note that the reliable estimation of azimuthal anisotropy (G s,c and B s,c) relies on accuracy of the sensitivity kernels ∂c R/∂L and ∂c R/∂A, therefore it is important to first obtain a good isotropic reference model to compute these kernels. Therefore, we propose a two-step inversion strategy:

  1. (1)

    Step 1: Perform the NA to estimate the layered V SV (or L) as well as their uncertainties from the isotropic part Rayleigh wave dispersion data (c obs(ω), at all available frequencies). We use the method due to Herrmann and Ammon (2004) to compute the dispersion for an isotropic model. V PH (or A) and ρ are linked to V SV (or L) using some empirical relationships in the crust (Brocher 2005) and upper mantle (Masters et al. 2000). We refer to Yao et al. (2008, 2010) for the details of this step.

  2. (2)

    Step 2: Perform the NA to estimate to G c and B c (or G s and B s) from the azimuthally anisotropic part of Rayleigh wave dispersion data, a c(ω, M) (or a c(ω, M)), using the perturbation Eq. (6) with the elastic parameters (e.g., L & A) obtained from Step 1. (Note: there is no direct forward calculation method available to compute a c,s(ω, M) from an azimuthally anisotropic model).

The objective of Step 1, which gives an optimal 1-D isotropic model, allows for more accurate calculation of sensitivity kernels in (6) for the subsequent estimation of the azimuthally anisotropic parameters (G s,c and B s,c) in Step 2.

For a layered model (K layers) and N d data measurements (i.e., phase velocity measurements at N d different frequencies), Eq. (6) can be rewritten as

$$ \hat{a}_{{{\text{c}},{\text{s}}}} (\omega_{j} ) \approx \sum\limits_{i = 1}^{K} {\left\{ {\frac{{\delta c_{\text{R}} (\omega_{j} )}}{{\delta A^{(i)} }}B_{\text{c,s}}^{(i)} + \frac{{\delta c_{\text{R}} (\omega_{j} )}}{{\delta L^{(i)} }}G_{\text{c,s}}^{(i)} } \right\}} $$
(7)

or

$$ \hat{a}_{\text{c,s}} (\omega_{j} ) \approx \sum\limits_{i = 1}^{K} {\left\{ {\left( {A^{(i)} \frac{{\delta c_{\text{R}} (\omega_{j} )}}{{\delta A^{(i)} }}} \right)\frac{{B_{\text{c,s}}^{(i)} }}{{A^{(i)} }} + \left( {L^{(i)} \frac{{\delta c_{\text{R}} (\omega_{j} )}}{{\delta L^{(i)} }}} \right)\frac{{G_{\text{c,s}}^{(i)} }}{{L^{(i)} }}} \right\}}, $$
(8)

where ω j is the jth frequency (j = 1, 2, …, N d), \( \hat{a}_{\text{c,s}} (\omega_{j} ) \) are the predicted data at frequency ω j , δc R(ω j ) is the perturbation of the phase velocity at frequency ω j , δL (i) (or δA (i)) is the perturbation of L (or A) of the ith layer, and \( G_{\text{c,s}}^{(i)} \) and \( B_{\text{c,s}}^{(i)} \) are the azimuthally anisotropic parameters of the ith layer. If there exists some simple relationship between the perturbation (in percent) of \( B_{\text{c}}^{(i)} \) (or \( B_{\text{s}}^{(i)} \)) and the perturbation of \( G_{\text{c}}^{(i)} \) (or \( G_{\text{s}}^{(i)}) \) as

$$ \frac{{B_{\text{c,s}}^{(i)} }}{{A^{(i)} }} = \gamma^{(i)} \frac{{G_{\text{c,s}}^{(i)} }}{{L^{(i)} }} = \gamma^{(i)} \hat{G}_{\text{c,s}}^{(i)}, $$
(9)

where \( \gamma^{(i)} = {{\left[ {{{B_{\text{c,s}}^{(i)} } \mathord{\left/ {\vphantom {{B_{\text{c,s}}^{(i)} } {A^{(i)} }}} \right. \kern-0pt} {A^{(i)} }}} \right]} \mathord{\left/ {\vphantom {{\left[ {{{B_{\text{c,s}}^{(i)} } \mathord{\left/ {\vphantom {{B_{\text{c,s}}^{(i)} } {A^{(i)} }}} \right. \kern-0pt} {A^{(i)} }}} \right]} {\left[ {{{G_{\text{c,s}}^{(i)} } \mathord{\left/ {\vphantom {{G_{\text{c,s}}^{(i)} } {L^{(i)} }}} \right. \kern-0pt} {L^{(i)} }}} \right]}}} \right. \kern-0pt} {\left[ {{{G_{\text{c,s}}^{(i)} } \mathord{\left/ {\vphantom {{G_{\text{c,s}}^{(i)} } {L^{(i)} }}} \right. \kern-0pt} {L^{(i)} }}} \right]}} \) is a constant and \( \hat{G}_{\text{c,s}}^{(i)} = {{G_{\text{c,s}}^{(i)} } \mathord{\left/ {\vphantom {{G_{\text{c,s}}^{(i)} } {L^{(i)} }}} \right. \kern-0pt} {L^{(i)} }} \), Eq. (8) becomes

$$ \hat{a}_{\text{c,s}} (\omega_{j} ) \approx \sum\limits_{i = 1}^{K} {\left( {\gamma^{(i)} A^{(i)} \frac{{\delta c_{\text{R}} (\omega_{j} )}}{{\delta A^{(i)} }} + L^{(i)} \frac{{\delta c_{\text{R}} (\omega_{j} )}}{{\delta L^{(i)} }}} \right)\hat{G}_{\text{c,s}}^{(i)} }. $$
(10)

The sensitivity kernels \( \frac{{\delta c_{\text{R}} (\omega_{j} )}}{{\delta A^{(i)} }} \) and \( \frac{{\delta c_{\text{R}} (\omega_{j} )}}{{\delta L^{(i)} }} \) can be computed using the normal mode theory (Anderson and Dziewonski 1982). Here we compute these kernels using a difference method. In Eq. (10), if the density variation is ignored for each layer, the perturbation of A and L can be obtained as

$$ \left\{ \begin{gathered} \delta A^{(i)} \approx 2\rho V_{\text{PH}}^{(i)} \delta V_{\text{PH}}^{(i)} \hfill \\ \delta L^{(i)} \approx 2\rho V_{\text{SV}}^{(i)} \delta V_{\text{SV}}^{(i)} \hfill \\ \end{gathered} \right.. $$
(11)

So for a given velocity model, we perturb V PH (or V SV) of the ith layer to obtain δA (i) (or δL (i)), and then calculate the phase velocity perturbations δc R(ω j ) by performing forward dispersion calculations. Thus, the sensitivity matrix \( \frac{{\delta c_{\text{R}} (\omega_{j} )}}{{\delta A^{(i)} }} \) or \( \frac{{\delta c_{\text{R}} (\omega_{j} )}}{{\delta L^{(i)} }} \) is constructed using a simple difference method.

Figure 1 shows an example of a 1-D spherical Earth velocity model and the corresponding Rayleigh wave fundamental mode phase velocity sensitivity kernels (∂c R/∂L and ∂c R/∂A) at 20, 60, and 100 s. Figure 2 shows the sensitivity kernel image in the period range of 10–125 s with a period interval of 5 s. It is evident that c R is mostly sensitive to L (or V SV) at depths around 1/3 wavelength. Although c R has little sensitivity to A (or V PH) of the upper mantle, it still has considerably large sensitivity to A (or V PH) of the upper and middle crust.

Fig. 1
figure 1

1-D velocity model (left) and its corresponding sensitivity kernels for ∂c R/∂L and ∂c R/∂A at different periods (right)

Full size image
Fig. 2
figure 2

Sensitivity kernel images of ∂c R/∂L and ∂c R/∂A in the period range of 10–125 s. The color bar shows the value of sensitivity. The white line in the left plot gives depths of 1/3 wavelength of the Rayleigh wave fundamental mode

Full size image

The misfit between the predicted and observed data for azimuthal anisotropy in the NA is defined as

$$ \varPhi_{\text{c,s}} = \sqrt {\frac{1}{{N}_{\text{d}}}\sum\limits_{j = 1}^{{N}_{\text{d}}} {\left( {\frac{{\hat{a}_{\text{c,s}} (\omega_{j} ) - a_{\text{c,s}} (\omega_{j} )}}{{\sigma_{\text{c,s}} (\omega_{j} )}}} \right)^{2} } }, $$
(12)

where σ c,s(ω j ) are the standard error of the observed data a c,s(ω j ), respectively, which are obtained from surface wave tomographic inversion (Montagner 1986; Yao et al. 2010).

The azimuthally anisotropic wavespeed of vertically polarized shear wave can be expressed as

$$ \hat{\beta }_{\text{SV}} \approx \sqrt {\frac{{L + G_{\text{c}} \cos 2\psi + G_{\text{s}} \sin 2\psi }}{\rho }}. $$
(13)

Since G c,s is typically much smaller than L, that is, G c,s/L ≪ 1, (13) can be approximated as

$$ \begin{aligned} \hat{\beta }_{\text{SV}} \approx & V_{\text{SV}} \left( {1 + \frac{{G_{\text{c}} }}{2L}\cos 2\psi + \frac{{G_{\text{s}} }}{2L}\sin 2\psi } \right) \\ = V_{\text{SV}} \left[ {1 + \varLambda_{\text{SV}} \cos 2(\psi - \phi_{\text{F}} )} \right] \\ \end{aligned}$$
(14)

where Λ SV and ϕ F are the magnitude of azimuthal anisotropy (in percent) of V SV and the azimuth angle of the fast polarization axis, respectively, which are given by

$$ \varLambda_{\text{SV}} = 0.5\sqrt {\hat{G}_{\text{c}}^{2} + \hat{G}_{\text{s}}^{2} }, $$
(15)
$$ \varPhi_{\text{F}} = 0.5\tan^{ - 1} (\hat{G}_{\text{s}} /\hat{G}_{\text{c}} ). $$
(16)

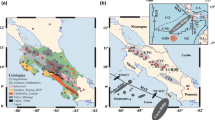
3 Application to SE Tibet

Yao et al. (2010) investigated the depth-dependent shear wavespeed and azimuthal anisotropy in the lithosphere of SE Tibet. They used the NA to invert for the isotropic shear wavespeed model in the crust and upper mantle from the isotropic Rayleigh-wave phase velocity dispersion data in the period band 10–150 s at each grid point, which is the same as Step 1 of this study. Then they used the linearized inversion method by Montagner and Nataf (1986) (see Eq. (4)) to invert the dispersion data with azimuthal anisotropy simultaneously for isotropic and azimuthally anisotropic shear wavespeeds at depths. Similar approaches have been taken by Lin et al. (2010) to invert for layered anisotropic model in the western US.

For the proposed two-step approach to invert for depth-dependent shear wavespeed azimuthal anisotropy, we have first validated our method using the synthetic data. We construct a 1-D layered velocity model with varying magnitudes and fast axes of shear wavespeed azimuthal anisotropy in the crust and upper mantle. Since dominant anisotropic minerals, e.g., olivine in the upper mantle as well as mica and amphibole-rich minerals in the crust, will tend to result in similar fast polarization axes of P- and S-waves as well as similar ratios of \( {{\hat{B}_{c,s}^{(i)} = B_{c,s}^{(i)} } \mathord{\left/ {\vphantom {{\hat{B}_{c,s}^{(i)} = B_{c,s}^{(i)} } {A^{(i)} }}} \right. \kern-0pt} {A^{(i)} }} \) and \( {{\hat{G}_{\text{c,s}}^{(i)} = G_{\text{c,s}}^{(i)} } \mathord{\left/ {\vphantom {{\hat{G}_{\text{c,s}}^{(i)} = G_{\text{c,s}}^{(i)} } {L^{(i)} }}} \right. \kern-0pt} {L^{(i)} }} \)(Barruol and Kern 1996; Montagner and Nataf 1986), we set \( \gamma^{(i)} = \hat{B}_{\text{c,s}}^{(i)} /\hat{G}_{\text{c,s}}^{(i)} = 1 \) for each layer for simplicity, similarly as Lin and Ritzwoller (2011). Then we compute the isotropic part Rayleigh-wave phase velocity dispersion (Herrmann and Ammon 2004) and azimuthally anisotropic terms a c,s(ω) using Eq. (6) or (7). We follow Step 1 in our proposed procedure to obtain the optimal isotropic velocity model from the NA and then follow Step 2 to obtain the \( \hat{G}_{\text{c,s}}^{(i)} \) and \( \hat{B}_{\text{c,s}}^{(i)}. \) Our tests show that the inversion results of \( \hat{G}_{\text{c,s}}^{(i)} \) are quite accurate if we only invert for \( \hat{G}_{\text{c,s}}^{(i)} \) with γ (i) set to be 1. If we simultaneously estimate \( \hat{G}_{\text{c,s}}^{(i)} \) and \( \hat{B}_{\text{c,s}}^{(i)} \) without any constraints on their ratios, the inversion results of some model parameters will deviate from the true values and also have larger uncertainties due to trade-offs between different model parameters. This is quite similar to surface wave dispersion inversion for velocity structures. Since it is difficult to constrain vp structures only from dispersion data, we usually only invert for vs structures from dispersion data but relating vp (also density) to vs using some empirical relationships in the inversion (e.g., Yao et al. 2008).

Then we choose the azimuthally anisotropic phase velocity dispersion data of Rayleigh waves at the grid point (101.5°, 28.5°) from Yao et al. (2010) to illustrate the details of the proposed two-step procedure. In the first step, the isotropic part dispersion in the period band 10–150 s (Fig. 3a) is used to invert for the isotropic shear wavespeed model (with vp and density related to vs) using the NA following the procedure by Yao et al. (2008). Here the Moho depth is fixed in the inversion with its value (54 km) approximately inferred from the receiver function analysis by Xu et al. (2007). We have eight parameters to be estimated, that is, shear wavespeed perturbations of the three crustal layers and five upper mantle layers with respect to a reference model. The final obtained isotropic shear wavespeed model is the posterior mean model (black line in Fig. 3b) from the Bayesian analysis of the model ensemble generated by the neighborhood search.

Fig. 3
figure 3

a The observed isotropic part of the Rayleigh-wave phase velocity dispersion curve in SE Tibet with standard errors (red x with bars) (Yao et al. 2010) and the predicted dispersion curve (dashed blue line) of (b) the obtained posterior mean shear wavepseed model (black line) from the NA. The gray area in (b) gives the range of model standard errors

Full size image

In the second step, we use the observed data of phase velocity azimuthal anisotropy a c,s(ω j ) as well as their standard error σ c,s(ω j ) at the same grid point (Yao et al. 2010) to estimate depth-dependent azimuthally anisotropic parameters G s,c (and B s,c). Due to worse azimuthal ray path coverage at periods above 100 s, we only use data in the period band 10–100 s in this step. First, we need to compute the sensitivity kernels ∂c R/∂L and ∂c R/∂A from the obtained isotropic model (Fig. 3b). Here we choose \( \gamma^{(i)} = \hat{B}_{\text{c,s}}^{(i)} /\hat{G}_{\text{c,s}}^{(i)} = 1 \) for all layers. Depth-dependent G c and G s are separately estimated from the observed period-dependent a c (blue dashed line in Fig. 4) and a s (red dashed line in Fig. 4) using the NA, respectively, with the misfit function defined as Eq. (12). Here, we estimate G c,s in the six depth ranges: upper crust (0–17 km), middle crust (17–35 km), lower crust (35–54 km), and three upper mantle layers (54–90 km, 90–140 km, 140–210 km). Figure 5 shows the posterior mean value (black line) and the corresponding standard error (shaded area) of each G c,s/L parameter from the 1-D PPDFs (Fig. 6). It appears that most 1-D PPDFs for \( \hat{G}_{\text{c,s}}^{(i)} = {{G_{\text{c,s}}^{(i)} } \mathord{\left/ {\vphantom {{G_{\text{c,s}}^{(i)} } {L^{(i)} }}} \right. \kern-0pt} {L^{(i)} }} \) (Fig. 6) show a Gaussian distribution, and the 1-D PPDFs for G c/L are systematically narrower than those for G s/L, indicating a smaller standard error of G c/L than that of G s/L (see also Fig. 5). This is probably due to the oscillating feature of a s (Fig. 4) that are used for estimating G s/L. Figure 7 shows some examples of 2-D PPDFs that are usually used to quantify the trade-offs between different model parameters. For this particular example, the correlation between G c/L (or G s/L) of two nearby depth ranges seems small as indicated by the relatively circular shape of the 2-D confidence levels.

Fig. 4
figure 4

The observed phase velocity azimuthal anisotropy terms a c (dashed blue) and a s (dashed red) and the predicted a c (solid blue) and a s (solid red) from the posterior mean model in Fig. 5. The error bar in red and blue shows the standard errors of the observed a c and a s, respectively, which are obtained from the phase velocity tomography (Yao et al. 2010)

Full size image
Fig. 5
figure 5

The posterior mean model (black line) and its standard error (shaded area) of \( \hat{G}_{\text{c}} = G_{\text{c}} /L \) (left) and \( \hat{G}_{\text{s}} = G_{\text{s}} /L \) (right) from the 1D PPDFs in Fig. 6 using the NA

Full size image
Fig. 6
figure 6

The 1-D PPDFs (shaded area) for each \( \hat{G}_{\text{c}} = G_{\text{c}} /L \) or \( \hat{G}_{\text{s}} = G_{\text{s}} /L \) parameter in a certain depth range from the NA. The black line in each plot indicates the posterior mean value of each parameter

Full size image
Fig. 7
figure 7

The 2-D PPDFs (shaded area) from the NA for two different \( \hat{G}_{\text{c}} = G_{\text{c}} /L \) (or \( \hat{G}_{\text{s}} = G_{\text{s}} /L \)) parameters. The black, blue, and red lines give the 99 %, 90 %, and 60 % confidence levels, respectively. The white triangle in each plot gives the posterior mean model in Fig. 6

Full size image

Using the predicted a c,s (Fig. 4) from the posterior mean model (Fig. 5), we can compute the magnitude of the Rayleigh wave azimuthal anisotropy and azimuth of the fast polarization axis at each period, similar as the Eqs. (15, 16), and compare with the observed ones as shown in Fig. 8a. The fitting is quite good in the period range of 10–70 s with dominant sensitivity to shear wavespeed structures up to about 150 km. The G c,s/L in the depth range of 140–210 km estimated from the NA may have large uncertainties due to worse fitting of the data in the period band of 75–100 s. Finally, Fig. 8b shows the depth-dependent magnitude and fast polarization azimuth of shear wavespeed azimuthal anisotropy using the Eqs. (15, 16). In our example, the magnitude of shear wavespeed azimuthal anisotropy in the crust is smaller (2 %–3 %) with nearly N–S fast polarization axes, probably due to the deformation caused by the southward expansion of the Tibetan crustal material in SW China (Zhang et al. 2004; Royden et al. 2008). However, the uppermost mantle layer (54–90 km) exhibits a large magnitude of azimuthal anisotropy (~6 %) with the fast polarization axis in the ENE–WSW direction, which is quite different from the pattern of crust azimuthal anisotropy. In the depth range of 90–140 km in the upper mantle, the shear wavespeed is very low (~0.4 km/s lower than the global average) and the magnitude of azimuthal anisotropy is also large (~5 %). However, there exists significant azimuth difference of the fast polarization axes in the uppermost mantle layer (54–90 km) and the underlying layer (90–140 km) that has much lower shear rigidity. Our results indicate that there could exist large differences of shear wavespeed azimuthal anisotropy in the crust and upper mantle in SE Tibet, reflecting complicated deformation patterns in this region (e.g., Yao et al. 2010; Yao 2012; Shi et al. 2012; Sun et al. 2012; Chen et al. 2013).

Fig. 8
figure 8

a The observed (black bar) and the predicted (red bar) period-dependent phase velocity azimuthal anisotropy. The open circle gives the isotropic phase velocity. Bars in a vertical (or horizontal) direction indicate a N–S (or E–W) fast polarization axis for Rayleigh wave propagation. b Depth-dependent shear wavespeed azimuthal anisotropy obtain from the NA: the black line for the magnitude of azimuthal anisotropy (Λ SV) and the red bars for the direction of fast axes (Φ F) in each layer (vertical for a N–S direction and horizontal for a E–W direction). The number beside the red bar gives the azimuth angle (with respect to north) of the fast axis (Φ F). For comparison, the blue line and the green bars show the linearized inversion results of Λ SV and Φ F, respectively, from Yao et al. (2010)

Full size image

4 Discussion and conclusions

In this study, we propose a two-step approach using the NA for the point-wise inversion of depth-dependent shear wavespeeds and azimuthal anisotropy from Rayleigh wave azimuthally anisotropic dispersion data. Based on the well-constrained isotropic velocity model obtained from the isotropic dispersion data, we take a difference scheme to compute approximate Rayleigh-wave phase velocity sensitivity kernels to azimuthally anisotropic parameters G c,s and B c,s. The use of the global search NA and Bayesian analysis (Sambridge 1999a, b) allows for more reliable estimates of depth-dependent shear wavespeeds and azimuthal anisotropy as well as their uncertainties.

We compare the results from this two-step global optimization approach with those from the traditional linearized inversion approach (Yao et al. 2010) in Fig. 8. Both methods show very similar directions of fast axes between 0 and 150 km at depths; however, the magnitude of azimuthal anisotropy shows some differences, in particular in the upper mantle. In the linearized inversion approach, Yao et al. (2010) imposed vertical smoothing and damping to stabilize the inversion results (Montagner and Nataf 1986). The vertical smoothing (or correlation) length is 20 km at the surface and gradually increases to about 35 km at 200 km depth (Yao et al. 2010). However, in the NA approach, we only fit the observed data and do not impose any model regularization terms in the misfit function (Eq. 12). This may explain the fact that the recovered magnitude of azimuthal anisotropy from our approach is larger than that from the linearized inversion approach in the upper mantle. However, both methods show that the upper mantle azimuthal anisotropy is stronger than that in the crust. Since we ignore the ∂c R/∂F terms in the forward problem, this may also introduce some differences of the inversion results.

In the proposed approach, we invert for G c and G s separately using the misfit function defined in Eq. (12). We can also invert for G c and G s simultaneously by defining a new misfit function Φ = Φ c + Φ s. With this new misfit function, we have investigated the inversion results and the model standard errors from the NA using synthetic data. Our results show that some of the model parameters are not well estimated from the NA and have larger uncertainties compared to the separated inversion scheme. This is probably because the number of model parameters has been doubled in the simultaneous inversion approach, therefore introducing more trade-offs between different parameters. So it is more reliable to invert for G c and G s separately.

Surface waves can provide better depth-dependent azimuthal anisotropy (Yao et al. 2010; Lin and Ritzwoller 2011) than shear wave splitting measurements in the crust and upper mantle (Savage 1999; Wang et al. 2008). Therefore, it may provide more reliable constraints on crust and upper mantle deformation patterns by examining radial variations of azimuthal anisotropy. Modeling of receiver functions can give constraints on layered anisotropy in the crust (e.g., Ozacar and Zandt 2004; Levin et al. 2008) although this approach is still very challenging in real practice. The Moho converted Pms phase splitting analysis from receiver functions can also provide constraints on average crustal azimuthal anisotropy, for instance, in SE Tibet (Xu et al. 2006; Sun et al. 2012; Chen et al. 2013; Sun et al. 2013). However, there still exists considerable inconsistency among these results. For example, Chen et al. (2013) and Sun et al. (2013) found that the splitting time of the Pms wave is smaller than 0.3 s at most stations in SE Tibet. However, Sun et al. (2012) used a more comprehensive analysis method and found 0.5–0.9 s splitting time of the Pms wave at a few stations in regions with thick crust in SE Tibet. Therefore, results of crustal azimuthal anisotropy from receiver function analysis may still have some uncertainties due to the use of different methods and data selection criteria.

Montagner et al. (2000) derives formulas to compute the shear wave splitting time and fast axes from depth-dependent G c,s and L, which provides a direct link between shear wave splitting measurements and shear wavespeed azimuthal anisotropy from surface wave data. For instance, Yao et al. (2010) computed the contribution of shear wave splitting from crustal azimuthal anisotropy obtained from surface wave data and found that the thick crust in SE Tibet may contribute almost 1 s splitting time, which is close to the observed shear wave splitting time in that region. Their results suggest that the contribution of crustal anisotropy to shear wave splitting may be significant in SE Tibet, similarly as inferred from the receiver function anisotropy analysis (Sun et al. 2012). However, shear wave splitting analysis from crustal earthquakes in this region (Shi et al. 2012; Chang et al. 2014) indicates much smaller crustal azimuthal anisotropy (splitting time about 0.01–0.03 s per 10 km). Although different methods have their uncertainties in estimation of crustal azimuthal anisotropy, it is still very puzzling that there exist large differences on the estimated splitting time from crustal anisotropy in different studies. Therefore, in the future it is very important to integrate different datasets together, for instance, anisotropic dispersion data, receiver functions, and shear wave splitting measurements, to better constrain the depth-dependent azimuthal anisotropy and deformation patterns in the crust and upper mantle in SE Tibet and other tectonically active regions in the world.