Introduction

Many safety and environmental issues, related to the supply of quite rare raw materials and to the production and widespread use of lithium-ion batteries, have forced researchers to find new electrochemical energy conversion devices, possibly based on more abundant and eco-sustainable materials. Among these, metal-air batteries represent a solution with great potential [1]. In these devices, the redox reaction that provides faradaic current occurs between a metal anode and atmospheric oxygen. Specifically, the anode is oxidized in the discharge, releasing electrons to an external circuit, while the oxygen of the air, diffusing through the porous carbon-based cathode, accepts the electrons and combines with metal ions to form discharge products. During the charging, the reactions reverse. Therefore, the air cathode plays a crucial role in metal-air batteries because acts non only as a medium to assure a suitable gas diffusion, but also as a site for accumulating discharge products. In particular, carbon-based air cathodes with a wide hierarchical pore size distribution show improved electrochemical performances [2], due to the more efficient transport of oxygen to the electrolyte interface and also to their electrocatalytic activity for the two foremost reactions occurring in metal-air batteries, namely the oxygen reduction reaction (ORR) and the oxygen evolution reaction (OER) [3]. Electrochemical reactions involving oxygen are at the basis of the operating principle not only of metal-air batteries, but also of other energy conversion devices, such as electrolysers and fuel cells, which have strategic technological importance. Therefore, all the researches on new materials to be used as electrocatalyst for oxygen reactions are of great relevance and in continuous development [4,5,6,7,8]. For what concerns the carbon based materials, their ORR electrocatalytic activity is associated with the presence of defects in the graphitic layers, as edges or point defects caused by vacancy or impurity, that serve as active sites to dissociate O2 into atomic oxygen which reacts with H2O to forms hydroxide ions in the redox reactions [9]. Therefore, the introduction of defects into carbonaceous materials used as cathodes results in more active sites for electrochemical reactions where nucleation of reaction products occurs, possibly resulting also in the decreasing of particle size [10]. As a result, increased discharge capacity and low cycle overpotentials are observed in many metal-air batteries prepared with defective carbon-based cathode [11,12,13,14].

Aluminum is a very interesting metal to be used as anode in metal-air cells, due to its high specific capacity (2980 mAh g−1), its abundance on the Earth’s crust and its recyclability.

Quasi-solid and solid polymer electrolytes represent the materials of choice for the realization of safer aluminum-air batteries [15], as well as for other multivalent metal-air batteries [16]. Recently, with the aim to realize aluminum-air batteries based on environmentally friendly materials [17, 18], we have developed new quasi-solid and solid gel electrolytes based on aqueous solutions and synthetic biodegradable or natural polymers, such as polyvinyl alcohol and xanthan gum [19,20,21,22,23,24]. These gel polymer electrolytes are characterized by good ionic conductivity, almost comparable with those of aqueous solutions [21], showing also interesting self-corrosion inhibition properties of the metal anode [23]. In all our previous studies, mainly focused on new electrolytes, we always used benchmark cathodes, prepared with commercial powders made of platinum dispersed on carbon (Pt/C,10 wt. % Pt, Merck), to allow easier comparison with literature data.

Herein, cathodes made of three different commercial carbons were tested in primary aluminum-air cells assembled with Xanthan-based alkaline gel electrolytes, and compared to the Pt/C benchmark cathodes used in the same cells. In particular, we tested two low-cost activated carbons and a commercial multiwalled carbon nanotubes. The aim was to continue further with the study of batteries made of environmentally friendly materials and therefore using, possibly, also noble metal-free cathodes. The study was effected by discharge tests in three-electrode configuration and electrochemical impedance spectroscopy of cells, while scanning electron microscopy/energy dispersive X-ray analysis, laser Raman spectroscopy, adsorption/desorption, and polarization measurements were used for the characterization of materials.

Materials and methods

The xanthan-based electrolyte was prepared by mixing and kneading powders of xanthan gum (powders from Xanthomonas campestris, Merck) in 11 M KOH solution at a ratio of 700 mg mL−1 at room temperature. The resulting gels were yellowish and gummy materials (Fig. 1a), quite resistant to compression (Fig. 1b and c). The fully characterization of this electrolyte is reported in ref. [21, 22].

Fig. 1
figure 1

Left: the alkaline xanthan based gel electrolyte. a) before compression, b) during compression with five brass weights of 110 g each, c) after compression. Right: alkaline cell components. The spacer was used to fix the electrolyte thickness in all the assembled cells

Full size image

Air cathodes were prepared using carbon cloth (H2-Planet, 0.35 mm thick, 116 g m−2) as support. Discs of 13 mm diameter were cut from the carbon cloth foils and pasted with different carbon based suspensions. The suspensions were prepared by mixing polyvinylidene fluoride (Merck, powder form) to the carbon powders in a weight ratio of 1:10, and by adding 1 cm3 of solvent (1-methyl-2- pyrrolidinone, Merck) per 220 mg of solid mixture. The carbon-based materials used for the suspensions were platinum-dispersed actived carbon (Pt/C, 10 wt. % Pt, provided by Merck in powder form), multiwalled carbon nanotubes (MWCNTs, from Nanostructured and Amorphous Materials Inc., 20–40 nm diameter, 1–2 µm length, 95% purity, 40–600 m2/g) and two different powdered activated charcoal, one produced from wood (product number 05105, Merck, hereafter named AC1) and the other from generic natural-organic material (product number161551, Merck, hereafter named AC2). After drying at 80 °C for 4 h, the final Pt concentration in the Pt/C cathodes was 2.5% wt of the cathode total weight. The amount of the carbon pasted on each cathode was about 12 mg, while the total weight of the cathodes was about 45 mg. The cathodes prepared with different carbons and the cells assembled with different cathodes were named X-cathodes and X-cells respectively, where X = AC1, MWCNTs, AC2, and Pt/C.

Ultrapure aluminium (Puratronic, 0.5 mm thick, 99.998%, Alfa Aesar) was used as the anode in the form of a 13-mm diameter disc in an aluminum-air cells. The weight of anodes varied between 150 and 170 mg.

The aluminum-air cells were assembled by pressing, in an open support, 2.6 mm thick electrolyte between anode and cathode using 10 mm diameter Teflon spacers (Fig. 1).

The carbonaceous materials were characterized by laser Raman spectroscopy by using the radiation emitted by a He–Ne laser (633 nm) as excitation radiation. The laser radiation was filtered with a band pass filter (Thorlabs-FL632.8–3—Ø1" Laser Line Filter, CWL = 632.8 ± 0.6 nm, FWHM = 3 ± 0.6 nm) and focused on the samples with 150-mm quartz lens. A bandpass filter (Chroma RET270lp, OD ≥ 6 at λ < 269 nm) was used to remove the scattered laser light and to pass the Stokes-shifted Raman signals from 675 to 724 nm (1000–2000 cm−1). The filtered radiation was then collected by a 200-mm-F/4 quartz objective lens and focused on the input slit of the spectrograph (Acton SpectraPro® SP-2300 spectrometer, 1200 grooves/mm, 300 mm, triple grating). The resolution of the acquired spectra was 0.5 nm (10 cm−1). The spectra were acquired by using a 700 nm blazed grating, a back-illuminated CCD (Princeton Instruments, PIXIS 100B) and WinSpec/32© software. The optimized parameters giving the best S/N ratio of the spectra were 20 s CCD exposure time and 10 accumulations. The Raman spectra were fitted using the Origin© software.

N2 adsoprtion/desorption experiments were carried out at − 196 °C with a Quantachrome autosorb-iQ, after degassing for 6 h at 150 °C. Specific surface area of the samples was calculated by the Brunauer–Emmett–Teller (BET) method. Pore size distribution (PSD) of each sample was obtained by quenched solid density functional theory (QSDFT), which provides pore size information over the complete range of micro- and mesopores and accounts for the heterogeneity and surface roughness in carbon materials [25]. The calculation model assumed slit-like pore and were applied on the desorption branch.

A scanning electron microscope (SEM, Phenom ProX) equipped with energy-dispersive X-ray spectrometer (EDX) detector was used for morphological and elementary analysis of cathode and anode surfaces.

The electrochemical performances of aluminum-air cells and cathodes were studied by using an Autolab PGSTAT302N electrochemical workstations. The ORR performances of different cathodes contacted with solid alkaline electrolytes were evaluated by using a three-electrode cell setup where the cathode was the working electrode, 1cm2 platinum plate was the counter electrode and Ag/AgCl (saturated KCl) was the reference electrode. The I-V curves were acquired by starting from OCV and varying the potential towards more negative values at scan rate of 1 mV s−1. The discharge tests were effected in a three electrode cell configurations by using the reference electrode (Ag/AgCl, saturated KCl). The electrochemical impedance spectroscopy (EIS) tests were performed in a two electrode cell configuration by setting the workstations in potentiostatic mode, with the applied frequency ranging from 1 MHz to 50 mHz and a potential amplitude perturbation of 10 mV. The impedance spectra were taken at open-circuit voltage (OCV). The spectra were simulated by using the NOVA software.

Results and discussion

Raman spectroscopy, BET analysis, and surface morphology of cathodes

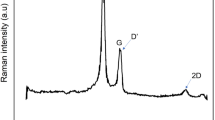
In the range 1000–2000 cm−1 from the laser excitation energy, Raman spectra of carbonaceous materials show two main bands centered at about 1580 and 1350 cm−1 [26,27,28,29]. The band at 1580 cm−1, referred as G band, identify the carbon atom vibrations against each other in ordered layers and is characteristic of graphene and graphitic materials. When disorder due to defects is introduced into the graphitic structures, this band broaden and additional bands arise at about 1200, 1357, and 1620 cm−1. The defects include point defects, due to vacancies or impurities, and boundary or edge. These bands are referred to as D1, D2, and D’ band (D denote disorder-induced). An additional broad band between 1500 and 1550 cm.−1 (hereafter referred to as D3 band) is assigned to amorphous graphitic phase, characteristic of interstitial disorder. It is generally accepted that the area ratio of the D2 and G bands give a good estimation of the order in carbonaceous materials. In particular, the D2 and G bands in Raman spectra are usually used to quantify the crystallite size (La) of 3D graphite through the relation [27]

$${L}_{a}=\frac{560}{{E}_{L}^{4}}{\left(\frac{{I}_{D}}{{I}_{G}}\right)}^{-1}$$
(1)

where La is given in nm, EL is the laser excitation energy, given in eV, the constant 560 is given in units of eV4/nm and ID and IG are the D and G peak areas respectively.

However, it should be considered that the D2 band intensity depends on defect type and density, as these affect the scattering cross-section. In addition, controlled experiments on graphene demonstrate that the D2 position is correlated with specific doping [28]. Therefore, in not controlled experiments and without knowing the preparation procedure of the carbonaceous materials, the evaluation of La from 1) have to be considered qualitative. In Fig. 2 (black lines), the Raman spectra of the sampled carbonaceous powders are reported.

Fig. 2
figure 2

Raman spectra of the sampled carbonaceous powders. The black lines are experimental data. The lines used in the fits are reported with red, green, blue, blue cyan and dark yellow lines for D1, D2, D3, G, and D’ bands respectively. The magenta lines are the fits of the spectra

Full size image

The D2 and G band are clearly observed in all samples. The band at 1550 cm−1, is not observed in MWCNTs spectrum that, instead, shows two not-overlapped bands at 1330 and 1580 cm−1 with a shoulder at 1620 cm−1.

For a better identification of band parameters (center, linewidth and area), a fit was performed by considering a combination of Lorentzian-shaped bands for D1, D2, G, and D’ and a Gaussian-shaped band for D3 [26]. The D’ line was considered in the fit only for the MWCNTs spectrum. In the other spectra the insertion of D’ line in the fit caused not-convergence. In Table 1, the fit parameters are reported with the La values as retrieved from 1).

Table 1 Fit parameters of D2 and G bands. Xc is center, W is linewidth, and A is the peak area. La was evaluated from 1)
Full size table

Apart the MWCNTs which show the characteristic nanotube’s Raman spectrum with well separated D2 and G bands, clearly different from other carbonaceous materials, the linewidths of the Raman bands of the other samples, fitted with four D bands and the G band, well correlate with the size of crystallites, namely they increase by decreasing crystallite size. Notably, the AC2 spectrum is very similar to that of the Pt/C, while AC1 spectrum is quite different, with narrower D1 and G band, down-shifted D band and higher ratio of the peak area IG/ID. These spectral features indicate that AC1 exhibits a higher structural order and degree of graphitization than the AC2 and Pt/C samples. Therefore, AC1 powders could be electrically more conductive than the other samples [30]. In addition, the shift of D-band may be correlated with specific defects or doping [31].

Figure 3a displays the adsorption/desorption isotherm of the four carbons. Figure 3b shows the relative PSDs.

Fig. 3
figure 3

N2 adsorption/desorption isotherm of four carbon materials (a) and relative pore size distribution (b)

Full size image

All carbonaceous materials, with the exception of MWCNTs, show a type IV isotherm with an H4 hysteresis loop, which is typical of slit-like pores in complex materials containing micro- and mesoporosity, such as hierarchical carbons [32]. Concerning MWCNTs, the isotherm is peculiar of this kind of material and totally different from that of other carbon materials. It is due to a multi-stage adsorption process in different types of pores: inner micropores (< 2 nm), small inner mesopores (3–4 nm) and aggregated pores (20–40 nm). Aggregated pores are those formed by the confined space among the isolate nanotubes in a relatively stable aggregate structure. Aggregated pores normally contribute to more than 78% of the total adsorption amount [33].

From the PSDs of Fig. 3b, it appears that all the carbonaceous materials show a similar micro/mesoporous network, with sharp maxima at 0.43–0.47 and 1.50–1.55 nm. AC2 shows a further mesoporosity in the range 2–5 nm. This kind of hierarchical micro-mesoporous structure can favor ionic diffusion [34]. Concerning MWCNTs, the fitting model for PDS distribution was applied only for slit-like micropore (0.56 nm) and small mesopore (1.6–2.9 nm). The pore volume of both inner micro and mesopores is one order of magnitude smaller. Furthermore, the structure is not hierarchical. The BET surface area of the samples is reported in Table 2.

Table 2 Specific surface area from BET analysis
Full size table

From Table 2, it results that the surface area of AC2 is higher than the other activated carbons, also in accordance with the higher mesoporosity, while the surface area of AC1 is similar to that of Pt/C samples.

To evaluate the homogeneity of the cathodes prepared with the different carbons, all the samples were visualized under the scanning electron microscope. In Fig. 4, the SEM images of the cathodes prepared with the sampled carbonaceous materials are reported.

Fig. 4
figure 4

SEM images of cathodes prepared with AC1 (upper-left), MWCNT(upper-right), AC2 (bottom- left) and Pt/C (bottom right)

Full size image

The cathode prepared with the Pt/C powders has a microscopic structure consisting of three-dimensional pieces of carbon on which platinum nanoparticles appear well dispersed. The typical dimensions of the pieces of carbon are of the order of tens of microns. Incorporated into the cathode structure, these carbon pieces form very wide channels for air entry.

AC1-cathode has a structure with smaller and more numerous channels and it is characterized by the presence of micrometric splinters of different sizes, typical of the woody origin of these carbons [35].

MWCNTs-cathode has a very closed structure as the nanotubes tend to aggregate when mixed in the solvent used for the preparation of the cathodes.

AC2-cathode has a mixed structure of splinters or flakes and three-dimensional pieces. Overall it appears denser than that prepared with AC1.

The EDX analysis, effected for the search for impurities, showed that only the cathodes prepared with AC2 have impurities, in particular phosphorus and sodium, in atomic concentrations lower than 1%.

Electrochemical characterization

The electrochemical equations governing an alkaline aluminum-air cell and the standard electrode potentials are

$$\begin{array}{*{20}c} {{\text{Al}} + {\text{4 OH}}^{ - } - {\text{3e}}^{ - } \to {{\text{Al}}\left( {{\text{OH}}} \right)_{{{4}}}}^{ - } } & {\left( {{\text{E}}^\circ = - {2}.{\text{35 V}}} \right)} \\ \end{array}$$
(2)
$$\begin{array}{*{20}c} {{\text{O}}_{{2}} + {\text{2 H}}_{{2}} {\text{O}} + {\text{4e}}^{ - } \to {4}\left( {{\text{OH}}} \right)^{ - } } & {\left( {{\text{E}}^\circ = 0.{\text{4 V}}} \right)} \\ \end{array}$$
(3)

and the total reaction is:

$$\begin{array}{*{20}c} {{\text{Al}} + {3}/{\text{4 O}}_{{2}} + {3}/{\text{2 H}}_{{2}} {\text{O}} \to {\text{Al}}\left( {{\text{OH}}} \right)_{{3}} } & {\left( {{\text{E}}^\circ = {2}.{\text{75V}}} \right)} \\ \end{array}$$
(4)

In addition, a competing reaction occurs on aluminum anode causing self-corrosion

$${\text{Al}} + {\text{3 H}}_{{2}} {\text{O}} \to {\text{Al}}\left( {{\text{OH}}} \right)_{{3}} + {3}/{\text{2 H}}_{{2}}$$
(5)

In saturated condition, Al(OH)4− precipitates and forms aluminum hydroxide on electrode surfaces and in the electrolyte. The parasitic reaction 5) determines, in addition to the production of H2, also that of Al(OH)3, as in reaction 4). Namely, both the electrochemical and parasitic reactions contribute to the failure of the cell caused by the oxide/hydroxide coating on anode or by the electrolyte clogging due to formed solid products. The more efficient the electrochemical reaction 4) is, the more reduced the parasitic reaction 5) is, and therefore, it is reduced the production of oxides released by the parasitic reaction, that alter the cell functioning and contribute to the decrease of its capacity. For this reason, it becomes essential to couple efficient air cathodes to aluminum anodes. An air cathode is efficient when it has the right physical structure, to effectively diffuse the air oxygen and to accumulate the reaction products without or at least with little obstruction, an appreciable electrical conductivity and a good catalytic activity.

The catalytic activity may be evaluated through polarization studies effected by linear sweep voltammetry (LSV). The LSV is a polarization technique that gives indications on the activity of a cathode for oxygen reactions as a whole, but it does not decouple the two main processes, namely intrinsic activity and mass transfer capability, that must be equally considered as determining factors affecting the electrocatalytic performance of ORR catalysts [36]. To decouple the processes and obtain kinetic information from LSV curves, rotating disk electrode setup apparatus and kinetic models based on the Koutecky–Levich (K–L) equation should be used [37, 38]. On the other hand, a three-electrode setup of polarization measurements let to compare the ORR performance of different cathodes, contacted with solid electrolytes, in more practical conditions [39]. Anyway, LSV is generally acknowledged as simple and effective method for qualitatively assessing the activity of a cathode for oxygen reactions. The typical LSV curve is S-shaped and different slopes of the “S” show how the reaction is controlled on an electrode by applying a given potential. In the case of the ORR for example, at potential very close to the OCV, the rate of the reaction is quite slow and the current density increases slightly as the potential decreases. When an onset in the potential (Eonset) is reached, the reaction accelerates as the potential decrease at lower values, resulting in a remarkable increase of the current density. The curves show an inflection at certain potential values (half waves potential or E1/2). By further decreasing the voltage, the current tends to plateau values. The two parameters, Eonset and E1/2, are usually used to qualitatively verify the activities of catalysts for ORR. The more positive these potential values are, the more active the material is for ORR. The LSV curves of different cathodes contacted with solid alkaline hydrogel are reported in Fig. 5. All the curves in Fig. 5 clearly show the typical ORR polarization curve trend [40] from which the Eonset and E1/2 can be deduced.

Fig. 5
figure 5

LSV curves of different cathodes contacted with solid alkaline hydrogel. The red stars indicate the E1/2 as retrieved from the first derivative maximum of the curves

Full size image

From Fig. 5, the Eonset values of the curves of AC1 and MWCNTs -cathodes show similar values and are clearly shifted at more positive values with respect to the other curves. In particular, the LSV curve of AC1-cathode show also more positive values of E1/2, suggesting its better activity for ORR among all cathodes.

To evaluate the cathode performance in Al-air cells, we performed discharge test on each X-cell. The OCV of fresh assembled cells are 1.66 V, 1.6 V, 1.72 V, and 1.76 V for AC1, MWCNTs, AC2 and Pt/C cell respectively. The measured voltages of aluminum-air cells are always lower than the theoretical 2.75 V value. As for other galvanic cells, this is due to both Faradaic and non-Faradaic process. The concentrations of oxidized and reduced species affect the potential of the electrodes that, under non-standard condition, are described by the Nernst equation [41, 42]. The polarization, due to a charge carrier depletion or accumulation on electrodes, is a non-Faradaic process that lowers the voltage of the cell. The extent of the polarization is described by the overpotential that, in a galvanic cell, determine a less negative potential on anode and a less positive on cathode [43]. Therefore, in the discharge tests, decoupling the anodic and cathodic potentials, through a three electrode measurements, allows a better understanding of the electrode overpotentials and their effects on the overall cell electrochemical performances. In addition, the three electrode discharge tests allow to univocally attribute the ultimate cell failure to a specific electrodic interface.

In Fig. 6, the three-electrode discharge tests effected at 6 mA cm−2 on cells prepared with different cathodes are reported. Cathodic and anodic potentials are reported vs standard hydrogen electrode (SHE). The test was interrupted when the cell voltage was lower than 0.5 V.

Fig. 6
figure 6

Three electrode discharge tests effected at 6 mA cm−2 on cells assembled with AC1 (green line), MWCNTs (orange line), AC2 (blue line), and Pt/C (black line) -cathodes. The cell potential cutoffs were set at 0.5 V

Full size image

As clearly results from the Fig. 6, the cathode prepared with AC1 gives superior discharge capacity. The cathodic potential of AC1-cell is higher than all the other cathodic potentials, notably including also that of Pt/C-cell. This means that the electrons arriving on cathode from the anodic reaction are more efficiently neutralized in the ORR reaction (Eq. 2). This is due to some catalytic activity of these defective carbons, as their Raman spectrum features seems to suggest and LSV measurements confirm. Overall, the AC1-cell potential during functioning is always at least 0.2 V higher than those of other cells. As results from the Fig. 6, the ultimate failure of all aluminum-air cells is mainly due to anodic potential increasing to more positive values. This means that the anodic reaction (reaction 2) is hindered by oxide or hydroxide formation on anode surface or by the electrolyte drying or clogging at the anodic interface, while the cathodes are still well functioning for the ORR (reaction 3).

To further check the performances of the carbonaceous materials, in Fig. 7, the three electrode discharge tests performed at higher currents (left) and the polarization/power curves (right) are reported.

Fig. 7
figure 7

Left: three electrode discharge test at 12, 15 and 18 mA cm−2. The middle and the lower curves report the anodic and cathodic potentials respectively. Right: polarization (dashed lines) and power curves (solid lines) of the cells assembled with different cathodes. The curves referring to measurements effected with the different cathodes are in different colors

Full size image

From these figures, in all cases AC1-cell results, on average, more performant, namely its power is higher than that of the other cells as well as the values of its potentials as a function of the applied current (figure right). From Fig. 7, left, in the range of current density 12–18 mA cm−2, the AC1-cell capacity results comparable or slightly higher than that of the other cells. The cell potential at 15 mA cm−2 is higher than that at 12 mA cm−2. This may be due to a better contacts of the solid electrolyte–electrode interfaces that can result in slightly increased cell capacity or cell potentials. In addition, the solid electrolyte is more instable at higher currents. In fact, at the end of the short measurement (1 h or less), the electrolytes were found hardened and brittle only on the anode side while they were still gummy as fresh electrolyte on the cathode side. Therefore, the anodic interface may be critically altered during the measurements. For this reason, the anodic potentials suffer from greater uncertainty during the measurement and they collapse first, as clearly shown by the figures, while the cathode potentials are more and more constant. Anyway, regardless of all the indeterminations in the anodic potentials/capacity evaluations, from all the repeated electrochemical tests it results the AC1-cell cathodic potentials are always higher (namely have lower overpotentials) with respect that of the other cells, even at higher currents. These data show that cathodes prepared with AC1, among all those tested, are certainly the most efficient for quasi solid state aluminum-air cells.

The anode surface of all cells was investigated by SEM after the discharge tests (Fig. 8). The anodes were gently cleaned with distillated water before analysis. The surface in contact with the electrolyte appeared brighter with respect that of non-discharged anodes. Some hard, thin white films were unevenly formed on the back of the anodes, with the exception of anode of AC1-cell, which results cleaner. These films did not allow, for all cells, an accurate evaluation of anodic efficiency based on anode mass loss measurement. At higher magnification, the surfaces exposed to electrolyte were found uniformly hollowed. The corrosion of ultrapure aluminum in alkaline solutions causes large circular pits [44]. The change of the anode surface after discharge, appearing with numerous large pits merging into each other, is due to aluminum oxidation by both to electrochemical reaction and self-corrosion. EDX analysis on discharged anode surface contacted with the electrolyte shows an oxygen content lower than that of non-discharged aluminum, namely on average 2% versus 5% in atomic concentration, proving that the aluminum electrodes were not covered with oxide at the end of the discharge. Instead, after the discharge, the electrolytes were found hardened on the anode side, while on the cathode side they were still wet and gummy.

Fig. 8
figure 8

SEM image of anode of the cell assembled with AC1 (upper-left), MWCNTs (upper-right), AC2 (bottom left) and Pt/C (bottom right). The inset in the upper-right figure is the image of not discharged anode

Full size image

To gain further insights on the different cathode performances, EIS measurements were performed on cells in two-electrode configuration, before and after the discharge tests. In Fig. 9, EIS analysis in the range 1–50 mHz, is reported in the form of Nyquist plot. The cells are described by the equivalent circuit reported in the inset of Fig. 9b.

Fig. 9
figure 9

Nyquist plot of different cells before (a) and after (b) the discharge tests. The scattered point are experimental results, the continuous lines are the results of the fitting. The inset of figure b depicts the equivalent circuit used for fitting the experimental data

Full size image

In the equivalent circuit, represented in the inset of Fig. 9b, Re, R1, and R2 describe electrolyte resistance and charge transfer resistance at anode and cathode respectively. The CPEs are the constant phase elements and describe the double layer capacity of the electrode interfaces [45]. In particular, the impedance of the CPE is given by.

$${\text{Z}}_{{{\text{CPE}}}} \, = \,{\text{Q }}({\text{i}}\omega )^{{ - {\text{N}}}}$$

For N = 1, 0, and − 1 the CPE represents respectively capacitance, resistance and inductance respectively, while for N = 0.5 it represents the Warburg resistance. Other values of N are associated with the altered behavior of the ideal elements due to particular conditions of the real systems, such as surface roughness, thickness or composition of electrode coatings or reaction rate on the electrodes.

In Table 3, the fit parameters of the Nyquist plots of Fig. 9 are reported. Although characterized by a quite large error, the fit parameters show that the cathodic resistance (R2) of the AC1 cell is significantly lower than that of the other cells before the discharge. This is related to the best functioning of the AC1-cathode with respect the others. After the discharge, all the cathodic resistances are lower with respect their initial values, indicating activation of catalytic surfaces and still well-functioning cathodes at the end of measurements. In particular, R2 values of AC1 and MWCNTs cells are much lower with respect to AC2 and Pt/C cells. In addition, from the impedance spectra acquired after the discharges, similarities emerge between the spectrum of AC1 and MWCNTs, as it clearly results in Fig. 9b. In particular, the values of their cathodic charge transfer resistance are very close. The charge transfer resistance represents a measure of the difficulty encountered when an electron is moved from one atom or compound to another atom or compound. Therefore, also the EIS analysis shows that both AC1 and MWCNTs are inherently efficient for ORR, as also LSV curves show. The reduced discharge performances of the cells realized with MWCNTs-cathodes are more likely due to an inefficient mass transfer of the reaction products on the cathode, because of its more compact structure, rather than to an inefficient catalytic activity.

Table 3 The fit parameters of Nyquist plots recorded before (lines 1–4) and after (lines 5–8) the discharge tests of cells assembled with different cathodes
Full size table

Conclusions

Different carbon-based cathodes have been tested in primary aluminum-air cells prepared with alkaline gel electrolytes and compared with a benchmark platinum-based cathode. Among them, cells assembled with cathodes made of an inexpensive commercial activated carbon (AC1, activated charcoal produced from wood) have shown superior electrochemical performances with improved cell discharge capacities and higher potentials with respect to all other cells. From the BET analysis, the porosity of all the samples resulted to be hierarchical and their surface areas are almost the comparable, with the exception of MWCNTs. Therefore, the O2 absorption capability or the hierarchical structure that favors the ionic diffusion of AC1 are unlikely the main cause of the improved electrochemical performances of AC1-cells. Instead, these can be mainly due to the higher AC1 electrocatalytic activity for ORR, as resulted from LSV analysis, because of defects or some doping in the graphite planes, as evidenced by the Raman spectra features. The EIS analysis carried out on non-discharged and discharged cells confirms the latter findings, showing for the AC1-cell reduced cathodic charge-transfer resistances.

Finally, we highlight that the final failure of the AC1-cell is due to an increase in the anodic potential towards more positive potentials, while the cathodic potential remains almost constant. This means that the electrochemical performance of these cells could be further improved by considering mitigation strategies of parasitic reactions to reduce unwanted solid products on the anode surface and at the anode-electrolyte interface and/or by considering other electrolyte design.