Abstract
Capital tax competition is known to result in inefficiently low tax rates and an undersupply of public goods. The provision of public goods and with it the welfare of all countries can be enhanced via tax coordination. Based on the standard Zodrow-Mieszkowski-Wilson tax-competition model this paper analyzes the conditions under which tax coordination by a group of countries is self-enforcing. In our analytical framework, there always exists a rather small stable tax coalition. For some subset of the parameter space the grand coalition is stable, even if the total number of countries is large. If the stable coalition is small, it is not very effective in mitigating the inefficiency of the non-cooperative Nash equilibrium. The ineffectiveness is increasing in the total number of countries.







Similar content being viewed by others
Notes
Apart from competition in capital taxes, a major concern of closer international integration is competition in consumption taxes via cross border shopping. See e.g. Aiura and Ogawa (2013) and Kanbur and Keen (1993). Since the analytical frameworks needed for studying consumption tax competition/coordination differ significantly from those needed for capital tax competition/coordination, we refrain from putting our approach to capital tax coordination in the context of the literature on consumption tax competition/coordination.
There is a tax rate higher than the average tax rate in the non-cooperative Nash equilibrium such that the maximum aggregate welfare (= social optimum) would be attained, if all countries would adopt that rate. However, to make all countries better off in the transition from non-coordination to the social optimum one may need suitable transfers, if countries are heterogeneous. See Bucovetsky and Smart (2006) and Hindriks et al. (2008).
Finus (2003) made this observation with regard to the literature on international environmental agreements whose formation and stability face similar barriers as the tax coordination, in terms of the formal analysis. Interestingly, formal analogies also exist regarding the industrial organization literature on cartels.
To the best of our knowledge, this is true in such disconnected areas of research as cartel theory, as the theory of international environmental agreements and as tax coordination theory.
In a model with capital that causes global pollution (Eichner and Pethig 2014) the socially optimal environmental agreement may also be self-enforcing.
We follow textbook arguments and assume that the production function is positive and increasing, which implies that \(k_i\) has to be restricted to the interval \(\left[ 0, \frac{a}{b} \right] \).
We choose the restrictive functional forms (1) and (2) for reasons of tractability. Production functions of type (1) are employed by Bucovetsky (1991), Grazzini et al. (2003) and by Devereux et al. (2008). A linear utility function of type (2) is assumed by Keen and Lahiri (1998). In fact, various contributions to the capital tax literature use the functional forms (1) and (2), e.g. Peralta and Ypersele (2005), Bucovetsky (2009), Kempf and Rota-Graziosi (2010), Ogawa 2013 and Itaya et al. (2014).
To ensure full employment of capital in the social optimum, we impose the condition
$$\begin{aligned} \frac{a}{b \bar{k}} > 1 - \frac{\varepsilon }{1+2 \varepsilon }. \end{aligned}$$(11)That condition is an analogue to Assumption 1 in Bucovetsky 2009, and it is implied by the condition \((a/b\bar{k}) > 1 + n \varepsilon / (n-1)(1+\varepsilon )\) which is a natural constraint for keeping \(r_o\) (defined in (10)) positive.
For more details and for the definition of (54) we refer to Appendix D.
The equilibrium tax rates (12) and their ranking are due to Itaya et al. (2014). However, Itaya et al. immediately proceed from these results to the analysis of the compliance issue in the context of a repeated game, while our focus is on coalition stability. To prepare the ground for our stability analysis, we find it useful to characterize in more detail the coalition-fringe equilibria and their dependence on the coalition size m.
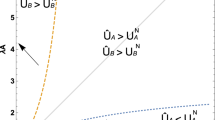
In their Proposition 1 (p. 162) Konrad and Schjelderup (1999) find in an exercise with marginal changes of tax rates that compared to the non-cooperative equilibrium all countries may be better off in the presence of a tax coalition. However, they do not establish our result of Proposition 1(i) that fringe countries benefit more than coalition countries.
The asymmetric taxes and capital flows generate production inefficiencies.
The ranking \(r^* + t^*_c> r_o + t_o > r^* + t^*_f\) follows from \(k^*_f> k_o > k^*_c\) and \(X_k > 0\).
Observe that \(\mathcal{T}^c (1) =\mathcal{T}^f (1) =t_o\) and \(\mathcal{W}^c (1) =\mathcal{W}^f (1) =w_o\).
The observation that the welfare gap \(\mathcal{W}^f(m) - \mathcal{W}^c(m)\) increases in m holds not only in Example 1 but also for any values of the parameters. This can be seen by differentiation of (32) in the “Appendix A” with respect to m.
This notion of self-enforcement or stability was originally introduced by D’Aspremont et al. (1983) in the context of cartel formation. It was then applied in various different areas, in particular in the study of stability of international environmental agreements.
Burbidge et al. (1997) and Bucovetsky (2009) also analyze the stability of the grand coalition in their models of heterogeneous countries. Burbidge et al. (1997) show that the grand coalition is realized as a unique equilibrium if there are only two countries, but this is not the case if there are more than three countries. Bucovetsky (2009) points out that the grand coalition is stable if the population share of the smallest country exceeds some threshold.
The function \(\bar{F}(n)\) in (23) is further specified in “Appendix E”.
Straightforward but tedious calculations yield \(\mathcal{W}^f (n-1) - \mathcal{W}^c (n-1) = \frac{(n-2)b n \varepsilon ^2 \bar{k} [(1+2 \varepsilon ) n^2 - 2 \varepsilon n + 2 \varepsilon ]}{2 (n-1)^2 (2 + 3 \varepsilon )^2}\).
In addition, the function H is discontinuous between \(m=99\) and \(m=100\). But we need not care about that discontinuity because it is only the integers that count.
This invariance is due to the special parametric functional forms employed. It is the outcome of our computations with the the software ‘Mathematica’.
The non-cooperative equilibrium is the coalition fringe equilibrium with \(m=1\).
References
Aiura H, Ogawa H (2013) Unit tax versus ad valorem: a tax competition model with cross-border shopping. J Public Econ 105:30–38
Bucovetsky S (1991) Asymmetric tax competition. J Urban Econ 30:167–181
Bucovetsky S (2009) An index of capital tax competition. Int Tax Public Finan 16:727–752
Bucovetsky S, Smart M (2006) The efficiency consequences of local revenue equalization: tax competition and tax distortions. J Public Econ Theory 8:119–144
Burbidge JB, DePater JA, Myers GM, Sengupta A (1997) A coalition-formation approach to equilibrium federations and trading blocs. Am Econ Rev 87:940–956
Conconi P, Peroni C, Rieszman R (2008) Is partial tax harmonization desirable? J Public Econ 92:254–267
D’Aspremont C, Jacquemin A, Gabszewicz JJ, Weymark JA (1983) On the stability of collusive price leadership. Can J Econ 16:17–25
de Zeeuw AJ (2008) Dynamic effects on the stability of international environmental agreements. J Environ Econ Manag 55:163–174
Devereux M, Lockwood B, Redoano M (2008) Do countries compete over corporate tax rates? J Public Econ 92:1210–1235
Eichner T, Pethig R (2014) Self-enforcing environmental agreements and capital mobility. Reg Sci Urban Econ 48:120–132
Finus M (2003) Stability and design of international environmental agreements: The case of transboundary pollution. In: Folmer H, Tietenberg T (eds) The international yearbook of environmental and resource economics 2003/2004. Edward Elgar, Cheltenham
Grazzini L, van Ypersele T (2003) Fiscal coordination and political competition. J Public Econ Theory 5:305–325
Hindriks J, Peralta S, Weber S (2008) Competing in taxes and investment under fiscal equalization. J Public Econ 92:2392–2402
Itaya J-I, Okamura M, Yamaguchi C (2014) Partial tax coordination in a repeated game setting. Eur J Polit Econ 34:263–278
Kanbur R, Keen M (1993) Jeux sans frontieres: tax competition and tax coordination when countries differ in size. Am Econ Rev 83:877–892
Keen M, Konrad KA (2013) The theory of international tax competition and tax coordination. In: Auerbach AJ, Chetty R, Feldstein M, Saez E (eds) Handbook of public economics, vol 5, Elsevier, North Holland, pp 257–328
Keen M, Lahiri S (1998) The comparison between destination and origin principles under imperfect competition. J Int Econ 45:323–350
Kempf H, Rota-Graziosi G (2010) Endogenizing leadership in tax competition. J Public Econ 94:768–776
Konrad KA, Schjelderup G (1999) Fortress building in global tax competition. J Urban Econ 46:156–167
Marchand M, Pestieau P, Sato M (2003) Can partial fiscal coordination be welfare worsening? A model of tax competition. J Urban Econ 54:451–458
Ogawa H (2013) Further analysis on leadership in tax competition: the role of capital ownership. Int Tax Public Finan 20:474–484
Peralta S, van Ypersele T (2005) Factor endowments and welfare levels in an asymmetric tax competition game. J Urban Econ 57:258–274
Vrijburg H, de Mooij RA (2016) Tax rates as strategic substitutes. Int Tax Public Finan 23:2–24
Wilson JD (1986) A theory of inter-regional tax competition. J Urban Econ 19:296–315
Zodrow RG, Mieszkowski P (1986) Pigou, Tibout, property taxation, and the underprovision of local public goods. J Urban Econ 19:356–370
Author information
Authors and Affiliations
Corresponding author
Additional information
Helpful comments from two anonymous referees are gratefully acknowledged. Remaining errors are the authors’ sole responsibility.
Appendices
Appendix
1.1 Appendix A: Proof of (13) and (14)
The coalition’s first-order condition is given by
where \(r_c := a - b \bar{k} - \Theta _c\), \(k_c := \bar{k} - \frac{t_c}{b} + \frac{\Theta _c}{b}\) and \(\Theta _c := \frac{m t_c + \sum _{j \in F} t_j}{n}\) or equivalently
The first-order condition of the fringe country (8) can be written as
where \(r_f := a - b \bar{k} - \Theta _f\), \(k_f := \bar{k} - \frac{t_f}{b} + \frac{\Theta _f}{b}\) and \(\Theta _f := \frac{t_f + \sum _{j \ne f} t_j}{n}\). Accounting for \(r_f\), \(k_f\) and \(\Theta _f\) turns (26) into
Since all fringe countries are alike, a necessary condition for a symmetric equilibrium is \(t_i=t_f\) for all \(i \in F\) and thus
Solving (25) and (27) with respect to \(t_c\) and \(t_f\) yields
Substracting \(W^c(t_c, t_f, m)\) from \(W^f(t_c, t_f, m)\) yields
Next, we insert \(t_c^*\) and \(t_f^*\) from (29) and (30) in (31) to obtain after some rearrangement of terms
Substracting \(W^c(t_o, t_o, m) = \left( a - \frac{b \bar{k}}{2} + t_o \varepsilon \right) \bar{k}\) from \(W^c(t_c, t_f, m)\) yields
Next, we insert \(t_c^*\) and \(t_f^*\) from (29) and (30) and \(t_o = \frac{n \varepsilon \bar{k} b}{(n-1) (1+ \varepsilon )}\) in (33) to obtain after some rearrangement of terms
(32) and (34) establishes \(W^f(t_c^*, t_f^*, m)> W^c(t_c^*, t_f^*, m) > W^c(t_o, t_o, m) \equiv w_o\). \(\square \)
1.2 Appendix B: Proof of (17)
Making use of (29), (30), (1), (4) and \(k_o= \bar{k}\) in \(X(k) +(\bar{k}-k) r\) we get after rearrangement of terms
1.3 Appendix C: Proof of Proposition 1
Differentiation of \(t_c^* = \mathcal{T}^c(m)\) and \(t_f^* = \mathcal{T}^f(m)\) from (29) and (30) with respect to m yields
Define the welfare functions
Total differentiation of \(\mathcal{W}^c(m) := W^c(\mathcal{T}^c(m), \mathcal{T}^f(m), m) \) and \(\mathcal{W}^f(m) := W^f(\mathcal{T}^c(m), \mathcal{T}^f(m), m) \) yields
where
Finally, we insert \(t_c^* =\mathcal{T}^c(m) \) and \(t_f^*=\mathcal{T}^f(m)\) from (29) and (30) in (46) to obtain after rearrangement of terms
Observe that \(t_c^*> t_f^*>0\) implies \(W^c_{t_f}>0\) in (43), \(W^c_m>0\) in (44), \(W^f_{t_c}>0\) in (45) and \(W^f_m>0\) in (47). Using this information together with \( \mathcal{T}_m^c>0\), \(\mathcal{T}_m^f>0\) from (37), (38) and \(W^f_{t_f}>0\) from (48) in (41) and (42) establishes \(\frac{{\mathrm {d}}\mathcal{W}^c(m)}{{\mathrm {d}}m}>0\) and \(\frac{{\mathrm {d}}\mathcal{W}^f(m)}{{\mathrm {d}}m}>0\). \(\square \)
1.4 Appendix D: Feasibility constraint on the parameter space
Throughout the paper we restrict our attention to feasible economies, i.e. to those economies that exhibit non-negative rates of return on capital. As mentioned in footnote 9, in the social optimum the rate of return on capital is positive, if and only if
Next, consider coalition-fringe equilibria.Footnote 26 Inserting \(\mathcal{T}^c (m)\) and \(\mathcal{T}^f (m)\) from (13) into (5) and solving for \(r=0\) establishes that in the coalition-fringe equilibrium the rate of return on capital is positive, if and only if
Differentiation of Q(m) with respect to m yields after rearrangement of terms
Observe that \(Q_m>0\) for all \(m \in [1, n-1]\). Hence, Q(m) attains its largest value at \(n-1\), formally
Finally, verify that
In view of (49)–(53) an economy is feasible if the parameters \((a, b , \bar{k},n, \varepsilon )\) satisfy
The non-negativity of the rate of return on capital for Example 1 is shown in Figs 8.
1.5 Appendix E: Proof of (20)–(23)
Making use of \(\hat{w} = (1+\varepsilon ) a \bar{k} - b \bar{k}^2 \left( \frac{1}{2} +\varepsilon \right) \) and inserting \(t_c^*\) and \(t_f^*\) from (29) and (30) in \(W^f(t_c, t_f, m)\) yields after rearrangement of terms
Setting \(\mathcal{W}^f(n-1) - \hat{w}\) equal to zero and solving for \(\frac{a}{b \bar{k}}\) yields after rearrangement of terms
It is then straightforward to show that
Differentiation of \(F(\varepsilon ,n )\) with respect to \(\varepsilon \) and n yields
In addition, the function F has the properties
and it holds \(\bar{F}_n (n) = \frac{2 n^3 -n^2 - 1-4n}{9(n-1)^2} >0\) for \(n \ge 2\).
Appendix F: Proof of Proposition 3
The proof of Proposition 3 follows from Table 1 and is supplemented by Fig. 9 which illustrates the function \(\tilde{M}(\varepsilon , n)\) for \(n \in [10, 200]\) and \(\varepsilon \in [0,2]\). Analogous figures can be generated for \(\varepsilon >2\).
Rights and permissions
About this article
Cite this article
Eichner, T., Pethig, R. Self-enforcing capital tax coordination. J Bus Econ 88, 915–940 (2018). https://doi.org/10.1007/s11573-018-0895-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11573-018-0895-7