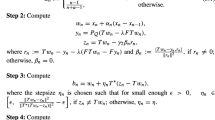Skip to main content
SpringerLink
Log in

Solving a system of split variational inequality problems

  • Published:
ANNALI DELL'UNIVERSITA' DI FERRARA Aims and scope Submit manuscript

Abstract

In this paper, we introduce a system of split variational inequality problems in real Hilbert spaces. Using a projection method, we propose an iterative algorithm for solving this system of split variational inequality problems. Further, we prove that the sequence generated by the iterative algorithm converges strongly to a solution of the system of split variational inequality problems. Furthermore, we discuss some consequences of the main result. The iterative algorithms and results presented in this paper generalize, unify and improve the previously known results of this area.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Baiocchi, C., Capelo, A.: Variational and Quasi-variational Inequalities. Wiley, New York (1984)

    MATH  Google Scholar 

  2. Bensoussan, A., Lions, J.L.: Applications of Variational Inequalities to Stochastic Control. North-Holland, Amsterdam (1982)

    MATH  Google Scholar 

  3. Byrne, C., Censor, Y., Gibali, A., Reich, S.: Weak and strong convergence of algorithms for the split common null point problem. J. Nonlinear Convex Anal. 13, 759–775 (2012)

    MathSciNet  MATH  Google Scholar 

  4. Censor, Y., Bortfeld, T., Martin, B., Trofimov, A.: A unified approach for inversion problems in intensity modulated radiation therapy. Phys. Med. Biol. 51, 2353–2365 (2006)

    Article  Google Scholar 

  5. Censor, Y., Elfving, T.: A multiprojection algorithm using Bregman projections in product space. Numer. Algorithm 8, 221–239 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  6. Censor, Y., Gibali, A., Reich, S.: Algorithms for the split variational inequality problem. Numer. Algorithm 59, 301–323 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  7. Cohen, C., Chaplais, F.: Nested monotony for variational inequalities over product of spaces and convergence of iterative algorithms. J. Optim. Theory Appl. 59, 185–195 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  8. Ferris, M., Pang, J.S.: Engineering and economics applications of complementarity problems. SIAM Rev. 39, 669–713 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  9. Fichera, G.: Problemi elastostatici con vincoli unilaterali: Il problema di Signorini ambigue condizione al contorno. Atti Accad. Naz. Lincei. Mem. Cl. Sci. Nat. Sez. Ia 7(8), 91–140 (1963/64)

  10. Giannessi, F., Maugeri, A.: Variational Inequalities and Network Equilibrium Problems. Plenum Press, New York (1995)

    Book  MATH  Google Scholar 

  11. Glowinski, R.: Numerical Methods for Nonlinear Variational Problems. Springer, Berlin (1984)

    Book  MATH  Google Scholar 

  12. Goebel, K., Reich, S.: Uniform Convexity, Hyperbolic Geometry, and Nonexpansive Mappings. Marcel Dekker, New York, Basel (1984)

    MATH  Google Scholar 

  13. Kassey, G., Kolumban, J.: System of multi-valued variational inequalities. Publ. Math. Debr. 56, 185–195 (2000)

    MathSciNet  MATH  Google Scholar 

  14. Kassay, G., Reich, S., Sabach, S.: Iterative methods for solving systems of variational inequalities in reflexive Banach spaces. SIAM J. Optim. 21, 1319–1344 (2011)

  15. Kazmi, K.R.: Split nonconvex variational inequality problem. Math. Sci. 7, 36 (2013). doi:10.1186/2251-7456-7-36

  16. Kazmi, K.R., Khan, F.A., Shahzad, M.: Existence and iterative approximation of a unique solution of a system of general quasi-variational inequality problems. Thai J. Math. 8(2), 405–417 (2010)

    MathSciNet  MATH  Google Scholar 

  17. Kazmi, K.R., Khan, F.A., Shahzad, M.: A system of generalized variational inclusions involving generalized \(H(.,)\)-accretive mapping in real \(q\)-uniformly smooth Banach spaces. Appl. Math. Comput. 217(23), 9679–9688 (2011)

    MathSciNet  MATH  Google Scholar 

  18. Kazmi, K.R., Rizvi, S.H.: A hybrid extragradient method for approximating the common solutions of a variational inequality, a system of variational inequalities, a mixed equilibrium problem and a fixed point problem. Appl. Math. Comput. 218(9), 5439–5452 (2012)

    MathSciNet  MATH  Google Scholar 

  19. Kazmi, K.R., Rizvi, S.H.: Iterative approximation of a common solution of a split equilibrium problem, a variational inequality problem and a fixed point problem. J. Egypt. Math. Soc. 21, 44–51 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  20. Kazmi, K.R., Rizvi, S.H.: An iterative method for split variational inclusion problem and fixed point problem for a nonexpansive mapping. Optim. Lett. 8, 1113–1124 (2014). doi:10.1007/s11590-013-0629-2

    Article  MathSciNet  MATH  Google Scholar 

  21. Konnov, I.V.: Relatively monotone variational inequalities over product sets. Oper. Res. Lett. 28, 21–26 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  22. Masad, E., Reich, S.: A note on the multiple-set split convex feasibility problem in Hilbert space. J. Nonlinear Convex Anal. 8, 367–371 (2007)

    MathSciNet  MATH  Google Scholar 

  23. Moudafi, A.: Split monotone variational inclusions. J. Optim. Theory Appl. 150, 275–283 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  24. Nagurney, A.: Network Economics: A Variational Inequality Approach. Kluwer Academic Publishers, Dordrecht (1993)

    Book  MATH  Google Scholar 

  25. Pang, J.S.: Asymmetric variational inequalities over product of sets: applications and iterative methods. Math. Program. 31, 206–219 (1985)

    Article  MATH  Google Scholar 

  26. Stampacchia, G.: Formes bilinearires coercitives sur les ensembles convexes. C. R. Acad. Sci. Paris 258, 4413–4416 (1964)

    MathSciNet  MATH  Google Scholar 

  27. Verma, R.U.: Generalized system of relaxed cocoercive variational inequalities and projection methods. J. Optim. Theory Appl. 121(1), 203–210 (2004)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The author is grateful to the anonymous referee for his valuable comments and suggestions.

Author information

Authors and Affiliations

  1. Department of Mathematics, Aligarh Muslim University, Aligarh, 202002, India

    Kaleem Raza Kazmi

Authors
  1. Kaleem Raza Kazmi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kaleem Raza Kazmi.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kazmi, K.R. Solving a system of split variational inequality problems. Ann Univ Ferrara 62, 71–82 (2016). https://doi.org/10.1007/s11565-015-0237-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11565-015-0237-4

Keywords

Mathematics Subject Classification

Search

Navigation