Effects of Stage Structure on Coexistence: Mixed Benefits

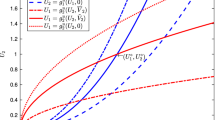
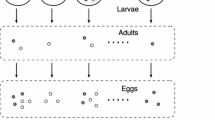
Abstract

The properties of competition models where all individuals are identical are relatively well-understood; however, juveniles and adults can experience or generate competition differently. We study here less well-known structured competition models in discrete time that allow multiple life history parameters to depend on adult or juvenile population densities. A numerical study with Ricker density-dependence suggested that when competition coefficients acting on juvenile survival and fertility reflect opposite competitive hierarchies, stage structure could foster coexistence. We revisit and expand those results. First, through a Beverton–Holt two-species juvenile-adult model, we confirm that these findings do not depend on the specifics of density-dependence or life cycles, and obtain analytical expressions explaining how this coexistence emerging from stage structure can occur. Second, we show using a community-level sensitivity analysis that such emergent coexistence is robust to perturbations of parameter values. Finally, we ask whether these results extend from two to many species, using simulations. We show that they do not, as coexistence emerging from stage structure is only seen for very similar life-history parameters. Such emergent coexistence is therefore not likely to be a key mechanism of coexistence in very diverse ecosystems, although it may contribute to explaining coexistence of certain pairs of intensely competing species.

Appendices

Appendix 1: Invasion Analysis

We develop here the method to obtain invasion criteria in two-species two-life stages models including competition on two vital rates, such as model 1 combining competition on fertility and juvenile survival.

We first place ourselves at the exclusion equilibrium where species 1 lives without species 2:

$$\begin{aligned} \tilde{n}= \begin{pmatrix} n_{1j}^*\\ n_{1a}^*\\ 0\\ 0\\ \end{pmatrix}. \end{aligned}$$

(22)

To compute the equilibrium densities $n_{1j}^*$ and $n_{1a}^*$, we have to solve the following system corresponding to the model with a single species (we dropped here species-specific indices for simplicity):

$$\begin{aligned} \left\{ \begin{array}{r c l} n_j &{}=&{} (1-\gamma )s_j(n)n_j + f(n)n_a\\ n_a &{}=&{} \gamma s_j(n)n_j + s_an_a \end{array} \right. \end{aligned}$$

(23)

with fertility f(n) and juvenile survival $s_j(n)$ affected by intra-specific competition only, according to the relations

$$\begin{aligned} f(n)=\frac{\pi }{1+\alpha n_a} \quad \text {and} \quad s_j(n) = \frac{\phi }{1+\beta n_a}. \end{aligned}$$

(24)

We now express $n_j$ according to $n_a$:

$$\begin{aligned} n_j&= (1-s_a)n_a\frac{1}{\gamma s_j(n)} \end{aligned}$$

(25)

$$\begin{aligned}&= (1-s_a)\left( \frac{1+\beta n_a}{\gamma \phi }\right) n_a \end{aligned}$$

(26)

and then, as we have by assumption $n_a \ne 0$ and $n_j \ne 0$, we obtain

$$\begin{aligned} n_j&= (1-\gamma )s_j(n)n_j + f(n)n_a\\ \Leftrightarrow 1&= (1-\gamma )\frac{\phi }{1+\beta n_a} + \frac{\pi }{1+\alpha n_a}\frac{n_a}{n_j} \\ \Leftrightarrow 1&= (1-\gamma )\frac{\phi }{1+\beta n_a} + \frac{\pi \phi \gamma }{(1-s_a)(1+\beta n_a)(1+\alpha n_a)}\\ \Leftrightarrow (1+\beta n_a)(1+\alpha n_a)&= (1-\gamma )\phi (1+\alpha n_a) + \frac{\pi \gamma \phi }{1-s_a} \end{aligned}$$

that leads to the polynomial of degree 2:

$$\begin{aligned} \alpha \beta n_a^2 + (\alpha + \beta - \alpha (1-\gamma )\phi )n_a+1-(1-\gamma )\phi -\frac{\pi \gamma \phi }{1-s_a} = 0. \end{aligned}$$

(27)

We denote $C= (1-\gamma )\phi$ and $D= \frac{\pi \gamma \phi }{1-s_a}$ and we find the solutions of the polynomial equation:

$$\begin{aligned} n_a^* = \frac{(\alpha C-\alpha -\beta ) \pm \sqrt{(-\alpha C + \alpha + \beta )^2 - 4\alpha \beta (-C-D+1)}}{2\alpha \beta }. \end{aligned}$$

(28)

We search for a positive solution and we have $C=(1-\gamma )\phi < 1$ which implies $\alpha C - \alpha - \beta < 0$ assuming positive interaction coefficients ($\alpha >0$ and $\beta >0$). Positivity is then equivalent to:

$$\begin{aligned}&(\alpha C-\alpha -\beta ) + \sqrt{(-\alpha C + \alpha + \beta )^2 - 4\alpha \beta (-C-D+1)} > 0 \end{aligned}$$

(29)

$$\begin{aligned}&\iff - 4\alpha \beta (-C-D+1) > 0 \end{aligned}$$

(30)

$$\begin{aligned}&\iff C+D > 1. \end{aligned}$$

(31)

The equivalence is provided by the fact that the left term has its square inside the square root. We define the inherent net reproductive number as $C+D = (1-\gamma )\phi +\frac{\pi \gamma \phi }{1-s_a}$ that must exceed 1 to have a viable species. We finally obtain the densities at a stable positive equilibrium for the model with a single species:

$$\begin{aligned} \left\{ \begin{array}{r c l} n_j^* &{}=&{} (1-s_a)(\frac{1+\beta n_a^*}{\gamma \phi })n_a^*\\ n_a^* &{}=&{} \frac{(\alpha (1-\gamma )\phi -\alpha -\beta ) + \sqrt{(-\alpha (1-\gamma )\phi + \alpha + \beta )^2 - 4\alpha \beta (-(1-\gamma )\phi -\frac{\pi \gamma \phi }{1-s_a}+1)}}{2\alpha \beta } \end{array} \right. \end{aligned}$$

(32)

provided that

$$\begin{aligned} C+D = (1-\gamma )\phi +\frac{\pi \gamma \phi }{1-s_a} > 1. \end{aligned}$$

(33)

We have then obtained the densities at the exclusion equilibrium. We have now to evaluate the stability of the equilibrium $(n_j^*,n_a^*,0,0)$: if it is locally asymptotically stable, the excluded species cannot invade the community starting from very small density. Conversely, if it is unstable, this means that the excluded species can invade provided that equilibria of the single-species model are restricted to stable fixed points. This last restriction is important. Indeed, if the single-species model has a stable two-cycle or an even more complex fluctuating attractor, the fixed point will already be unstable, and a proper invasion analysis should instead be done on this more complex attractor. Two-cycles tend to occur for $s_a=0$ (Cushing et al. 2007), as shown in Supplement C. So long as $s_a>0$ this model does not show 2-cycles—so far as we have seen numerically and following the argumentation of Cushing et al. (2007) for model 2. The combination $s_a = 0$ and $\gamma = 1$ renders the projection matrix primitive, which in turns creates possibilities for bifurcations towards two-cycles directly from the trivial single-species (0,0) equilibrium (Cushing and Li 1989; Cushing 2006). We therefore restrict ourselve to the case $s_a>0$, although the equations derived above in this Appendix for the single-species fixed point are also valid whenever $s_a=0$.

To evaluate the (un)stability of the exclusion equilibria in the two-species system, we have to compute the eigenvalues of the Jacobian of the 2 species system evaluated at the exclusion equilibrium. The full system iterated over a time step reads:

$$\begin{aligned} \left\{ \begin{array}{r c l} n_{1j}(t+1) &{}=&{} (1-\gamma _1)\frac{\phi _1}{1+\beta _{11}n_{1a}(t)+\beta _{12}n_{2a}(t)}n_{1j}(t) + \frac{\pi _1}{1+\alpha _{11}n_{1a}(t)+\alpha _{12}n_{2a}(t)}n_{1a}(t)\\ n_{1a}(t+1) &{}=&{} \gamma _1 \frac{\phi _1}{1+\beta _{11}n_{1a}(t)+\beta _{12}n_{2a}(t)}n_{1j}(t) + s_{1a}n_{1a}(t)\\ n_{2j}(t+1) &{}=&{} (1-\gamma _2)\frac{\phi _2}{1+\beta _{22}n_{2a}(t)+\beta _{21}n_{1a}(t)}n_{2j}(t) + \frac{\pi _2}{1+\alpha _{22}n_{2a}(t)+\alpha _{21}n_{1a}(t)}n_{2a}(t)\\ n_{2a}(t+1) &{}=&{} \gamma _2 \frac{\phi _2}{1+\beta _{22}n_{2a}(t)+\beta _{21}n_{1a}(t)}n_{2j}(t) + s_{2a}n_{2a}(t). \end{array} \right. \end{aligned}$$

(34)

We place ourselves at the abovementioned exclusion equilibrium where species 1 dominates the community and species 2 is absent. The Jacobian evaluated at this point is a $4 \times 4$ matrix and it has the following triangular block form (see also Cushing 2008):

$$\begin{aligned} \begin{pmatrix} B_1 &{} B_2 \\ 0 &{} B_3 \\ \end{pmatrix}. \end{aligned}$$

(35)

Therefore, we only need to know the eigenvalues of the $2 \times 2$ matrices $B_1$ and $B_3$. The $B_1$ matrix corresponds to the Jacobian of the system in the absence of species 2, so provided that the single-species equilibrium is stable, we can infer that it has a spectral radius lower than 1. Unfortunately, although all simulations that we have done, even for very large fertilities or low competition coefficients, provide a stable equilibrium for $C+D>1$, it is not straightforward to show local stability analytically. Indeed matrix $B_1$ writes:

$$\begin{aligned} \begin{pmatrix} (1-\gamma ) \frac{\phi }{1+\beta n_a} &{} \frac{1-\gamma }{\gamma } \left( \frac{-\beta n_a}{1+\beta n_a}\right) (1-s_a) + \frac{\pi }{1+\alpha n_a} \left( 1-\frac{\alpha n_a}{1+\alpha n_a}\right) \\ \gamma \frac{\phi }{1+\beta n_a} &{} \frac{-\beta n_a}{1+\beta n_a}+s_a \end{pmatrix} \end{aligned}$$

(36)

with $n_a$ given by Eq. 32, making the use of Jury conditions (used below on the simpler $B_3$ block) difficult here, although the determinant simplifies somewhat. We therefore conjecture the stability of the single-species equilibrium, with a spectral radius of $B_1$ below 1, which we deem reasonable in this context. The $B_3$ matrix is given by:

$$\begin{aligned} B_3 = \begin{pmatrix} (1-\gamma _2)\frac{\phi _2}{1+\beta _{21}n_{1a}^*} &{} \frac{\pi _2}{1+\alpha _{21}n_{1a}^*} \\ \gamma _2\frac{\phi _2}{1+\beta _{21}n_{1a}^*} &{} s_{2a} \\ \end{pmatrix}. \end{aligned}$$

(37)

The $B_3$ matrix block, which is part of the Jacobian, also corresponds to the projection matrix of species 2 when invading species 1, which implies that the exclusion equilibrium is not stable when species 2 has a growth rate larger than 1 (i.e., the modulus of $B_3$’s leading eigenvalue is larger than 1). The stability of this two-dimensional system can be investigated thanks to the Jury conditions, given by the Eqs. (38, 39, 40):

$$\begin{aligned} 1- {{\,\textrm{tr}\,}}J(\textbf{n})+\det J(\textbf{n})&>0 \end{aligned}$$

(38)

$$\begin{aligned} 1+ {{\,\textrm{tr}\,}}J(\textbf{n}) + \det J(\textbf{n})&> 0 \end{aligned}$$

(39)

$$\begin{aligned} 1- \det J(\textbf{n})&> 0 \end{aligned}$$

(40)

with $J(\textbf{n})$ the Jacobian matrix of the two-compartment system whose stability is being evaluated. If these three conditions hold, the system is stable. If the first condition (Eq. 38) is violated, one of the eigenvalues of $J(\textbf{n})$ is larger than 1, which means in our context that the excluded species can invade the community. The violations of the conditions (39) and (40) correspond to the creation of limit cycles or invariant loops (Neubert and Caswell 2000). We then check these conditions on the $B_3$ matrix. We have:

$$\begin{aligned} {{\,\textrm{tr}\,}}B_3&= (1-\gamma _2)\frac{\phi _2}{1+\beta _{21}n_{1a}^*} + s_{2a} \\ \det B_3&= (1-\gamma _2)\frac{\phi _2}{1+\beta _{21}n_{1a}^*}s_{2a} - \gamma _2\frac{\phi _2}{1+\beta _{21}n_{1a}^*}\frac{\pi _2}{1+\alpha _{21}n_{1a}^*}. \end{aligned}$$

We start with the third condition (40):

$$\begin{aligned} 1- (1-\gamma _2)\frac{\phi _2}{1+\beta _{21}n_{1a}^*}s_{2a} + \gamma _2\frac{\phi _2}{1+\beta _{21}n_{1a}^*}\frac{\pi _2}{1+\alpha _{21}n_{1a}^*} > 0. \end{aligned}$$

(41)

This equation will always be satisfied with biologically meaningful parameters and strictly competitive interaction between species:

• The third term of (41) is positive because each parameter is positive,

• $(1-\gamma _2)\frac{\phi _2}{1+\beta _{21}n_{1a}^*}s_{2a} < 1$ because $0 \le \gamma \le 1$, $0 \le \phi \le 1$ and all $\beta$’s are positive.

Since ${{\,\textrm{tr}\,}}B_3 > 0$, the first Jury’s condition implies the second ((38) $\Rightarrow$ (39)). Then, we only have to check the first Jury condition to describe the stability of the system:

Fig. 4

Parameter values and coexistence regions of the three parameter sets of Table 2 (A - set 1, B - set 2, C - set 3) chosen to promote different scenarios of coexistence

$$\begin{aligned}&1-(1-\gamma _2)\frac{\phi _2}{1+\beta _{21}n_{1a}^*} + s_{2a}+(1-\gamma _2)\frac{\phi _2}{1+\beta _{21}n_{1a}^*}s_{2a} - \gamma _2\frac{\phi _2}{1+\beta _{21}n_{1a}^*}\frac{\pi _2}{1+\alpha _{21}n_{1a}^*} > 0 \\&\quad (1-\gamma _2)\frac{\phi _2}{1+\beta _{21}n_{1a}^*} - (1-\gamma _2)\frac{\phi _2}{1+\beta _{21}n_{1a}^*}s_{2a} + \gamma _2\frac{\phi _2}{1+\beta _{21}n_{1a}^*}\frac{\pi _2}{1+\alpha _{21}n_{1a}^*}< 1-s_{2a}\\&\quad (1-\gamma _2)\phi _2(1-s_{2a})< (1-s_{2a})(1+\beta _{21}n_{1a}^*)- \frac{\gamma _2\phi _2\pi _2}{1+\alpha _{21}n_{1a}^*}\\&\quad (1-\gamma _2)\phi _2\frac{1}{1+\beta _{21}n_{1a}^*} + \frac{\gamma _2\phi _2\pi _2}{1-s_{2a}}\frac{1}{(1+\beta _{21}n_{1a}^*)(1+\alpha _{21}n_{1a}^*)} < 1. \end{aligned}$$

We finally have the following condition for the stability of the exclusion equilibrium:

$$\begin{aligned} \frac{C_2}{1+\beta _{21}n_{1a}^*}+\frac{D_2}{(1+\beta _{21}n_{1a}^*)(1+\alpha _{21}n_{1a}^*)} < 1 \end{aligned}$$

(42)

with $C_2= (1-\gamma _2)\phi _2$ and $D_2= \frac{\pi _2\gamma _2\phi _2}{1-s_{2a}}$.

This last expression (Eq. 15) gives us an invasion criteria that is larger than 1 if, conversely, species 2 is able to invade the community when rare.

Note that if we remove the competition on one vital rate by setting all the competition coefficients associated to this vital rate to 0, we re-obtain the invasion criteria given by Fujiwara et al. (2011) for their model where a single vital rate was affected by competition. This ensures some internal coherence to the analytical results.

Appendix 2: Coexistence Regions Obtained Through Sensitivity Analysis for the Three Scenarios of Coexistence

To have another, complementary representation of the sensitivities, we estimated coexistence regions for the three parameter sets using the definition given by Barabás et al. (2014b). Note that we arbitrarily use the term region in place of domain to separate the regions found with this sensitivity analysis from the domains of coexistence found through invasion analysis. The method consists in using the sensitivities at the equilibrium for each parameter in order to determine the region of parameter space where species both persists despite changes in parameter values. It is calculated by finding the smallest (positive and negative) perturbation that would lead to the extinction of one of the species from the value of sensitivities and densities at equilibrium, and makes the (crude) approximation that sensitivities are not only valid close to the fixed point but also far away from it. The coexistence regions for the three parameter sets are presented in Fig. 4.

We see here smaller coexistence regions in the third scenario, consistent with this equilibrium being more sensitive (less robust) to perturbations.

Appendix 3: Additional Simulations with S Species, $S>2$

The meta-parameter sets, used in the parameter distributions from which the vital rate parameters for each species have been drawn, are provided in Table 3.

Table 3 (Meta)-Parameter sets used to draw parameter values to simulate community dynamics with (a, b) parameters of the Beta distribution for $\phi$, $s_{a}$ and $\gamma$ ($a = a_{\phi _i} = a_{s_{a,i}} = a_{\gamma _i}$ and $b= b_{\phi _i} = b_{s_{a,i}} = b_{\gamma _i}$)

Fig. 5

Population dynamics of a community with initially 40 species and opposite competitive hierarchies on fertility and juvenile survival. All species have very similar vital rates due to a low variance in the distribution used to draw the parameter. Each line corresponds to one species

Fig. 6

Rank of $\beta _{ij}$ versus rank of $\alpha _{ij}$ under a negative correlation of $\beta _{ij}$ and $\alpha _{ij}$ of $-0.9$

Fig. 7

Frequencies of outcomes predicted by pairwise invasion criteria for a parameter set with 40 species with very close parameters and a negative correlation between $\alpha _{ij}$ and $\beta _{ij}$ with $\phi = 0.9\sigma$

Fig. 8

Frequencies of outcomes predicted by pairwise invasion criteria—for single-vital-rate-competition models—for a parameter set with 40 species with very close parameters and bimodal distribution of interspecific coefficients drawn to promote situations of opposite exclusion within each pair of species

Fig. 9

Frequencies of outcomes predicted by pairwise invasion criteria for a parameter set with 40 species, with very close parameters and permuted competition coefficient that promoted before permutation situations of reciprocal exclusion within each pair of species

Fig. 10

Histograms of the number of species persisting at equilibrium, with initially 40 species, and for 200 permutations of inter-specific competition coefficients. The bar in gray indicates the number of species persisting at equilibrium for the original $\alpha _{ij}$ and $\beta _{ij}$ with $\text {Corr}(\alpha _{ij}, \beta _{ij})<0$ and reciprocal exclusion for each pair of species

For initially 40 species, a small variance of parameters across species, and opposite competitive hierarchies, we obtained the dynamics illustrated in Fig. 5.

The population dynamics highlighted in Fig. 5 demonstrates that 3000 time steps are enough to reach a stable number of coexisting species.

We verified our hypothesis that a negative correlation between $\alpha _{ij}$ and $\beta _{ij}$ leads to opposite hierarchies in sets of coefficients associated to fertility and juvenile survival by plotting the rank of $\alpha _{ij}$ against the rank of $\beta _{ij}$. For 40 species, these ranks are plotted in Fig. 6.

The negative correlation between ranks in Fig. 6 confirmed that the negative correlation between $\alpha _{ij}$ and $\beta _{ij}$ was creating the expected opposite competitive hierarchies.

However, opposite competitive hierarchies may not be sufficient to promote reciprocal exclusion (e.g., exclusion of 1 by 2 in the fertility competition model and of 2 by 1 in the juvenile survival competition model) of species within each or most pairs of species. To make the comparison between 2 and S-species model, we have to check that we consider situations that are fully comparable, i.e., where species would exclude each other out in a two-species contest on either $\alpha$ or $\beta$ competition. We therefore checked if the trade-off between being competitive on $\alpha$ and $\beta$ could promote such reciprocal exclusion or priority effects (in models with a single parameter that is density dependent) within pairs of species. We computed the invasion criteria of such simple models (where only one vital rate is affected by competition) for each pair of species composing the communities. For a community of initially 40 species and a small variance in parameters across species, we found the coexistence outcomes in simpler models highlighted in Fig. 7.

We found that for a community of 40 species, the proportions of pairs of species where a priority effect or a reciprocal exclusion are indicated (by the simpler models with density-dependence a single vital rate) are low when we assume only a negative correlation between $\alpha _{ij}$ and $\beta _{ij}$.

In fact, when we simply use a negative correlation to create opposite competitive hierarchies, we draw our couple of values ($\alpha _{ij}$, $\beta _{ij}$) in a Gaussian distribution, and then most of the values are close to their means, which does not allow to obtain pairs of species where each species is strongly competitive on a different vital rate, and exclude the other if the competition was on this vital rate only. Therefore, even if there are opposite competitive hierarchies within pairs of species modelled, this setup is unlikely to generate situations where species exclude each other when considering single-vital-rate-competition.

To consider S-species scenarios where species can exclude each other out if competition was solely on $\alpha$ or solely on $\beta$ (hereafter referred to as ‘reciprocal exclusion’), we changed our structure of correlation to generate situations where within most pairs of species, each species is strongly competitive on a different vital rate (e.g. species 1 excludes species 2 in the model with only fertility competition and vice-versa in the model with only juvenile survival competition).

Our method to achieve reciprocal exclusion of pairs (for single-vital-rate-competition) consisted in drawing pairs $(a_{ij},b_{ij})$ from a bivariate normal distribution with $\mu _{a_{ij}}<\mu _{b_{ij}}$ and $\text {Corr}(a_{ij},b_{ij}) < 0$. We then always assign $(a_{ij},b_{ij})$ to $(\alpha _{ij}, \beta _{ij})$ and $(b_{ji},a_{ji})$ to $(\alpha _{ji}, \beta _{ji})$. In this way, for each pair of species (i, j), species i is competitive on $\alpha$ and species j is competitive on $\beta$. We acknowledge that this may be hard to grasp, and suggest to the reader to use the code to create an example.

We computed the invasion criteria for each pair of species and counted how often each invasion scenario in single-vital-rate-competition models, which we represented in the histogram of Fig. 8.

We succeeded to generate reciprocal exclusion within most pairs of species. Moreover, we showed that a permutation of competition coefficients was sufficient to remove the structure of reciprocal exclusion (Fig. 9).

However, as for our simple negative correlation between competitive ranks for $\alpha$ and $\beta$, this new parameter set where reciprocal exclusion occurs within most pairs of species does not allow to significantly increase the number of extant species at $t=3000$ time steps (Fig. 10).

Therefore, even if competition is highly structured in a way that makes species exclude each other out when a single vital rate is density-dependent, which should greatly promote situations of emergent coexistence, we did not observe a positive effect of this structure on species richness in a community larger than $S=2$. We therefore conclude that emergent coexistence is highly unlikely in many-species contexts.