On Nonlinear Pest/Vector Control via the Sterile Insect Technique: Impact of Residual Fertility

Abstract

We consider a minimalist model for the Sterile Insect Technique (SIT), assuming that residual fertility can occur in the sterile male population. Taking into account that we are able to get regular measurements from the biological system along the control duration, such as the size of the wild insect population, we study different control strategies that involve either continuous or periodic impulsive releases. We show that a combination of open-loop control with constant large releases and closed-loop nonlinear control, i.e., when releases are adjusted according to the wild population size estimates, leads to the best strategy in terms of both number of releases and total quantity of sterile males to be released. Last but not least, we show that SIT can be successful only if the residual fertility is less than a threshold value that depends on the wild population biological parameters. However, even for small values, the residual fertility induces the use of such large releases that SIT alone is not always reasonable from a practical point of view and thus requires to be combined with other control tools. We provide applications against a mosquito species, Aedes albopictus, and a fruit fly, Bactrocera dorsalis, and discuss the possibility of using SIT when residual fertility among the sterile males, can occur.

Appendices

Appendix A: Proof of Theorem 2, p. 13

We consider that we release sterile insects with a period of $\tau .$ From (22) and (23) we get, for $t\in [n\tau ,(n+1)\tau ),$

$$\begin{aligned} \begin{aligned} F(t)&\le F(n\tau ) e^{-(1-r)\rho \theta (t-n\tau )},\\ M(t)&\le M(n\tau ) e^{-\mu _M (t-n\tau )} \\&\quad + F(n\tau ) \frac{r\rho ({\mathcal {N}}_F^{-1}-\theta ) }{\mu _M-(1-r)\rho \theta } \left( e^{-(1-r)\rho \theta (t-n\tau )}-e^{-\mu _M (t-n\tau )}\right) . \end{aligned} \end{aligned}$$

We impose the condition

$$\begin{aligned} M_S(t) \ge {\varvec{\kappa }}(t) M(t),\quad t\in [n\tau ,(n+1)\tau ). \end{aligned}$$

(28)

This is verified if, for $t\in [n\tau ,(n+1)\tau ),$

$$\begin{aligned} M_S(t)\ge & {} {\varvec{\kappa }}(t) \left( M(n\tau ) e^{-\mu _M (t-n\tau )} \right. \\&\left. + F(n\tau )\frac{r\rho ({\mathcal {N}}_F^{-1}-\theta ) }{\mu _M-(1-r)\rho \theta } \left( e^{-(1-r)\rho \theta (t-n\tau )}-e^{-\mu _M (t-n\tau )}\right) \right) . \end{aligned}$$

Since $\kappa$, introduced in (25), decreases as a function of $M+F,$ and M and F remain larger than $M(n\tau )e^{\mu _M (t-n\tau )}$ and $F(n\tau )e^{\mu _F (t-n\tau )},$ respectively, we get that

$$\begin{aligned} {\varvec{\kappa }}(t) =\kappa (M(t)+F(t)) \le \kappa \left( M(n\tau )e^{\mu _M (t-n\tau )}+F(n\tau )e^{\mu _F (t-n\tau )} \right) =: \kappa _{\max }^n. \end{aligned}$$

Thus, if for $s\in [0,\tau ),$ it holds

$$\begin{aligned} M_S(n\tau +s)= & {} \big (M_S(n\tau )+\tau \varLambda _n\big ) e^{-\mu _Ss} \nonumber \\\ge & {} \kappa _{\max }^n \Big ( M(n\tau ) e^{-\mu _M s} + F(n\tau )\frac{r\rho ({\mathcal {N}}_F^{-1}-\theta ) }{\mu _M-(1-r)\rho \theta }\nonumber \\&\times \, \left( e^{-(1-r)\rho \theta s}-e^{-\mu _M s}\right) \Big ). \end{aligned}$$

(29)

then (M, F) converges asymptotically to 0. This last equation is equivalent to

$$\begin{aligned} \tau \varLambda _n\ge & {} -M_S(n\tau ) + \kappa _{\max }^n \Big (M(n\tau ) e^{(\mu _S-\mu _M)s} \\&+ F(n\tau ) \frac{r\rho ({\mathcal {N}}_F^{-1}-\theta ) }{\mu _M-(1-r)\rho \theta } \left( e^{(\mu _S-(1-r)\rho \theta ) s}-e^{(\mu _S-\mu _M) s}\right) \Big ), \end{aligned}$$

Since $\mu _S \ge \mu _M$ and $\theta \le {{\mathcal {N}}}_F^{-1}$, assuming the additional condition $\theta \le \dfrac{\mu _S}{\mu _F} {{\mathcal {N}}}_F^{-1}$, one has that all the coefficients and exponents in the r.h.s. of latter expression are positive, so a stronger inequality is obtained if we take $s=\tau$ for the exponential expressions with positive coefficient and $s=0$ for the one with negative coefficient. Thus, we impose

$$\begin{aligned} \tau \varLambda _n\ge & {} -M_S(n\tau ) + \kappa _{\max }^n e^{(\mu _S-\mu _M)\tau } \Big (M(n\tau ) \\&+ F(n\tau ) \frac{r\rho ({\mathcal {N}}_F^{-1}-\theta ) }{\mu _M-(1-r)\rho \theta } \left( e^{({\mu _M}-(1-r)\rho \theta ) \tau }-1\right) \Big ). \end{aligned}$$

This ends the proof.

Appendix B: Proof of Theorem 3, page 12

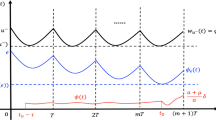
Like in Bliman et al. (2019), we need to adapt the proof of previous Theorem 2, given in Appendix 7. We have, for $m=0,\dots ,p-1,$ and $s\in [0,\tau ),$

$$\begin{aligned} \begin{aligned} M_S(s+(np+m)\tau )&= \big (\varLambda _{np+m}\tau + M_S((np+m)\tau ) \big ) e^{-\mu _S s} \\&= \Big (\varLambda _{np+m} \tau + \varLambda _{np+m-1} \tau e^{-\mu _S \tau } + \dots + \varLambda _{np} \tau e^{-m\mu _S\tau } \\&\quad + M_S(np\tau )e^{-m\mu _S\tau } \Big )e^{-\mu _S s}. \end{aligned} \end{aligned}$$

We have,

$$\begin{aligned} \kappa \big ( (np+m)\tau + s \big ) \le \kappa \big ( M_{\min }^{np+m}+F_{\min }^{np+m}\big )=: \kappa _{\max }^{np+m}, \end{aligned}$$

where $M_{\min }^{np+m}$ and $F_{\min }^{np+m}$ were introduced in (4). As done above in (29), we impose

$$\begin{aligned}\begin{aligned}&\Big (\varLambda _{np+m} \tau + \varLambda _{np+m-1} \tau e^{-\mu _S \tau } + \dots + \varLambda _{np} \tau e^{-m\mu _S\tau } + M_S(np\tau )e^{-m\mu _S\tau } \Big )e^{-\mu _S s} \\&\quad \ge \kappa _{\max }^{np+m}\Big ( M(np\tau ) e^{-\mu _M(m\tau +s)} \\&\qquad + F(np\tau ) \frac{r\rho ({\mathcal {N}}_F^{-1}-\theta )}{\mu _M-(1-r)\rho \theta } \left( e^{-(1-r)\rho \theta (m\tau +s)}-e^{-\mu _M(m\tau +s)}\right) \Big ). \end{aligned} \end{aligned}$$

By multiplying by $e^{\mu _S(m\tau +s)}$ both sides of latter inequality, we get

$$\begin{aligned} \begin{aligned}&\varLambda _{np+m} \tau e^{\mu _S m\tau } + \varLambda _{np+m-1} \tau e^{\mu _S (m-1)\tau } + \dots + \varLambda _{np} \tau + M_S(np\tau ) \\&\quad \ge \kappa _{\max }^{np+m}\Big ( M(np\tau ) e^{(\mu _S-\mu _M)(m\tau +s)} \\&\qquad + F(np\tau ) \frac{r\rho ({\mathcal {N}}_F^{-1}-\theta )}{\mu _M-(1-r)\rho \theta } \left( e^{(\mu _S-(1-r)\rho \theta ) (m\tau +s)}-e^{(\mu _S-\mu _M)(m\tau +s)}\right) \Big ). \end{aligned} \end{aligned}$$

This inequality gives the strongest condition when $s=\tau$. Thus, we enforce,

$$\begin{aligned} \begin{aligned}&\varLambda _{np+m} \tau e^{\mu _S m\tau } + \varLambda _{np+m-1} \tau e^{\mu _S (m-1)\tau } + \dots + \varLambda _{np} \tau + M_S(np\tau ) \\&\quad \ge \kappa _{\max }^{np+m}\Big ( M(np\tau ) e^{(\mu _S-\mu _M)(m+1)\tau } \\&\qquad + F(np\tau ) \frac{r\rho ({\mathcal {N}}_F^{-1}-\theta )}{\mu _M-(1-r)\rho \theta } \left( e^{(\mu _S-(1-r)\rho \theta ) (m+1)\tau }-e^{(\mu _S-\mu _M)m\tau }\right) \Big ). \end{aligned} \end{aligned}$$

We get, for $m=0,\dots ,p-1$,

$$\begin{aligned} \begin{aligned}&\varLambda _{np+m} \tau \ge e^{-\mu _S m\tau }\Big [ - \varLambda _{np+m-1} \tau e^{\mu _S (m-1)\tau } - \dots - \varLambda _{np} \tau - M_S(np\tau ) \\&\quad + \kappa _{\max }^{np+m}\Big ( M(np\tau ) e^{(\mu _S-\mu _M)(m+1)\tau } \\&\quad + F(np\tau ) \frac{r\rho ({\mathcal {N}}_F^{-1}-\theta )}{\mu _M-(1-r)\rho \theta } \left( e^{(\mu _S-(1-r)\rho \theta ) (m+1)\tau )}-e^{(\mu _S-\mu _M)m\tau }\right) \Big ) \Big ]. \end{aligned} \end{aligned}$$

The result follows.