Introduction

The field of medical diagnostics has experienced a vital transition due to the combination of advanced technology and a more profound comprehension of human physiology. The early detection and observation of cancer have become critical problems in this dynamic environment. The world of terahertz (THz) technology is a new field, which is distinguished by its special capacity to analyze biological materials at the molecular level. The current work seeks a comprehensive investigation into the design and development of a small, triple-band sensor, utilizing the terahertz spectrum’s potential of metamaterials (MTMs). This sensor has the potential to completely transform the way that human blood cancer is diagnosed. Through the combination of THz technology, metamaterial engineering, and cancer detection, this work aims to bring in a new era of fast, highly accurate, non-invasive diagnostics that may completely change the way blood cancer is treated [1]. Since water is one of the primary components of tissue, terahertz radiation (100 GHz to 10 THz) has a shallow penetration depth. For tissues with a high water content, this penetration range typically reaches a few hundred microns, while for tissues with a high fat content, it would be in centimeter range [2, 3].

The terahertz radiation of electromagnetic spectrum is located between microwaves and infrared light, creating an interesting gap. This spectral region, often known as the “THz gap,” spans from 0.1 to 10 THz. Historically, technological constraints have made it difficult to utilize THz gap. However, new developments in THz sources, detectors, and imaging methods have brought this technology into the front of biomedical research and opened up a wide range of possible uses. THz technology’s non-ionizing characteristic, which makes THz radiation safe for biological samples and human tissues, is one of its main advantages. There is no intrinsic risk of DNA damage or ionization from THz waves, unlike ionizing radiation modes of X-rays. This crucial feature establishes THz technology as a feasible path for non-invasive medical diagnostics, with a multitude of applications ranging from tracking wound healing processes to cancer detection [4].

Terahertz (THz) waves have many uses in wireless communications [5, 6], THz imaging [7, 8], and energy harvesting [9,10,11,12]. In 2021, Muhammad et al. developed a polarization-insensitive dual-wideband fractal meta-absorber for terahertz applications, achieving 90% absorption in two bands [13].

In 2023, Muhammad et al. presented a wideband, polarization-insensitive tunable graphene-supported terahertz metamaterial absorber. It exhibits over 90% absorption from 2.3 to 6.4 THz, offering potential for high-speed optical switches and THz detectors [14].

Metamaterials are artificial structures with micrometer-scale sub-wavelength designs that are either non-periodic or periodic. They enable the control and manipulation of electromagnetic waves, including THz waves. Metamaterials are particularly useful in a variety of applications because they can absorb THz radiation. Modern THz metamaterial absorbers exhibit several resonance responses, a large and narrow bandwidth [15, 16]. Combining sub-unit cells [17, 18], piling metal-dielectric-metal layers [19], or employing composite materials like graphene or doped silicon [20, 21] can all result in an enhancement in the bandwidth. With various metal-dielectric-metal combinations, fractal geometry is normally employed to achieve a broadband absorption [22]. In 2020, Rana et al. introduced a wideband terahertz metamaterial absorber based on Pythagorean-tree fractal geometry, demonstrating absorptivity from 7.5 to 10 THz. It holds promise for bolometers, THz detection, and communication [23].

The achievement of a wideband terahertz absorption between 7.5 and 10 THz was demonstrated by Bilal et al. [24]. In 2022, Subhan et al. introduced a broadband, tunable terahertz absorber using slotted-square graphene meta-rings, aiming to efficiently absorb THz radiation (2.2 to 4.6 THz). The absorber, a graphene meta-square ring with various slots, induces multiple plasmonic resonances for potential applications like switching and cloaking [25].

Recently, high-sensitivity THz sensors based on metamaterial absorbers have received considerable attention [26]. A highly sensitive THz sensor can be made using the resonance peak frequency, which is sensitive to the test analyte’s refractive index. By increasing the overlap of THz biosensor, Zhou et al. dramatically increased its sensitivity [27]. A metamaterial THz sensor with a flexible substrate was proposed by Yao et al. [28]. Their simulation demonstrated refractive index sensitivity at two distinct resonance peaks of 60 and 100 GHz/RIU, respectively. Wang et al. produced a dual-band terahertz metamaterial absorber made of two identical square metallic patches. With a high sensing sensitivity of 1.9 THz/RIU, resonance peaks of nearly unity absorption were also obtained. However, there are yet some issues to be solved such as complex design and limited bandwidth, despite the fact that several structures have been proposed to accomplish multiband or wideband absorption for sensor applications [27].

In general, by scaling the structure size of the metallic patterns, the resonance frequency of the metamaterial absorber can be effectively tuned or altered from optical to microwave regimes [29, 30]. For instance, Qian et al. demonstrated a total visible band meta-surface perfect absorber based on coupled Mie resonance. Using an electric split-ring resonator with a side length of 39 mm, nearly complete absorption at 0.70 THz was demonstrated [31]. A microwave metamaterial absorber operating at 8.96 GHz was created by enlarging an array pattern of 1.8-mm dielectric cube material [32]. These light absorbers have yielded a very narrow absorption bandwidth (usually less than 20% of the resonance frequency), making them particularly interesting in domains connected to sensing, such as the detection of environmental changes and the assessment of analyses’ refractive indices.

The high application prospects for multiple-band metamaterial absorbers in material detection and analysis, thermal imaging, and sensing have led to a recent shift in the focus of metamaterial absorber research to multiple-band light absorption. In general, the superposition effect of various single-band resonance absorption peaks can be used to generate the multiple-band metamaterial absorbers. For multiple-band metamaterial absorbers, stacking and super-unit coplanar structures are the two most common fabrication methods. For instance, a triple-band metamaterial absorber can be made by cascading three metallic layers [1, 33]. Three different sizes of metallic patterns were integrated in a super-unit coplanar structure to provide a triple-band of nearly perfect absorption response [34]. The tendency toward minimalism, compactness, and simplicity are particularly predominant in modern technology design. However, it is obvious that none of the methods mentioned above fit with the predominant styles. Although several different approaches have been reported to create a multiple-band absorption response, the absorption strength and sensing capabilities of the multiple-band absorbers are far from satisfactory. Here, the two main aspects of the originality of this work are highlighted. First, what matters is how easy and efficient the multiple-band metamaterial absorbers’ structural design is. Second, by enhancing the multiple-band metamaterial absorbers’ sensing capabilities, the design’s application scope was expanded.

Layout of the Unit Cell Model

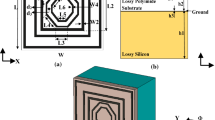
Different structural models were designed to serve as a perfect absorber, as shown in Fig. 1. The models were made of polyethylene terephthalate (PET) dielectric intermediate layer sandwiched between two aluminum (Al) layers. The Al metallic layers have a conductivity of 3.56 × 107 S/m and thickness of 0.2 μm, while the PET substrate thickness was set to be 0.2 μm.

Fig. 1
figure 1

Various structural designs for a perfect absorber: a model 1, b model 2, and c model 3 (the proposed one)

Full size image

The intricate design of our sensor was pivotal in achieving three unique resonance points, significantly enhancing sensitivity for precise blood cancer detection. By leveraging terahertz (THz) technology and metamaterials (MTMs), our aim was to develop a sensor with unparalleled accuracy. Our investigations demonstrated excellent responses in two bands concerning incident and polarization angles, crucial for reducing signal-to-noise ratio issues and improving image reconstruction. These high-resolution images are trusted by medical professionals, aiding in accurate diagnosis and treatment planning. The complexity of our design is justified by its ability to achieve multiple resonance points, enhancing sensitivity and ensuring robust performance across various angles and polarizations, thus advancing blood cancer diagnostics and improving patient outcomes.

The proposed MTM absorber-based sensor was designed using full-wave finite integration technique (FIT)-based commercial electromagnetic solver. Due to the high efficiency of CST microwave studio, MTM characteristics can be extracted, considering different boundary conditions such as PEC/PEC, PEC/PMC, and unit cell. To obtain the best design parameters, PEC/PEC was applied in the x/y directions with an open space boundary in the z-direction. Furthermore, it could be useful to find out the effect of square patches shown in Fig. 2a, b. The proposed operation’s boundary conditions are shown in Fig. 2c. Due to limitations in fabrication resources and time constraints, we were unable to conduct physical measurements of the proposed sensor. The high fabrication costs and lengthy manufacturing process posed significant challenges for our research team.

Fig. 2
figure 2

The proposed structural design of a perfect absorber: a model 4, b model 5 (proposed design), and c proposed design with ports

Full size image

This work demonstrates the realization of an MTM absorber-based sensor by presenting five distinct configurations (referred to as model 1 to 5) for the diagnosis of human cancer. The dielectric constant (ϵr) and the loss tangent (tan (δ)) of the PET substrate are 2.9 and 0.019, respectively. The optimized dimensions were obtained by evaluating the five aforementioned models, while the value of the parameters presented in Fig. 2a is tabulated in Table 1.

Table 1 The complete list of the optimized parameters of the proposed sensor
Full size table

Results and Discussion

The absorption coefficient (A) was calculated using the following equation:

$$A=1-{\left[{S}_{11}\right]}^{2}- {\left[{S}_{12}\right]}^{2}$$
(1)

Here, S12 is the transmission coefficient (T), and S11 is the reflection coefficient (R). A strong absorption mechanism can be obtained through capturing the travelling waves, which leads to a high electrical and/or magnetic loss. These losses are related to the imaginary parts of the relative permittivity (ε = ε′ − jε″) and/or permeability (µ = µ′ − jµ″). These are two important parameters used to determine the wave absorption performance of the EM wave absorbers and transmitters. A material’s ability to store electrostatic energy and to be polarized by an electric field, as well as its ability to aid in signal propagation, are measured by its relative dielectric constant (εr). As the frequency changes, so does the relative dielectric constant. The measurement of signal loss during transmission line propagation is called the loss tangent, or tan (δ)). Since the metallic layer at the bottom prevents the transmission of the waves, transmission coefficient can be neglected. In order to investigate the effects of split ring resonators and complementary star-shaped resonator, five different simulations were performed and the results are presented without sensor layer. In order to reveal the absorption characteristics between 100 MHz and 1 THz, the backside of PET substrate was covered with aluminum.

Figures 3 and 4 show the evaluated proposed design with a single square split ring resonator (model 1), and its effect on absorption is given in Fig. 3a. It can be seen from the figure that a single resonance with 90% absorption has occurred around 0.9 THz. Another simulation was performed on a wider split ring resonator (model 2), where a small shift in frequency was seen at nearly 0.02 THz, which led to lowering the absorption about 12% in comparison to that of model 1.

Fig. 3
figure 3

The absorption characteristics of the two designs: models 1 and 2

Full size image
Fig. 4
figure 4

The three designs of absorption traits: a models 3 and 4 and b model 5

Full size image

Figure 4 shows the absorption spectra of three additional models, namely, 3, 4, and 5. The models were designed based on a combination of an asterisk shape with square split resonators. It is noticeable that the asterisk plays a vital role in producing a perfect absorption resonance peak at about 0.55 THz, as shown in Fig. 4a. Therefore, the addition of square split resonators around the asterisk is to broaden and increase the number of perfect absorption peaks, as shown in Fig. 4b.

Complementary star resonators (model 3) as well as the square split ring resonator, which is placed at the edges of substrate (model 4), were analyzed and the absorption variation with frequency is shown in Fig. 4a. The complementary star creates a resonance peak around 0.55 THz with absorption of 100%, while the square split ring (model 4) did not create any resonance peak within the studied frequency band.

Model 5 was created by assembling all the mentioned models in order to achieve the proposed work design. Results showed three absorption peaks at around 0.55, 0.8, and 0.9 THz (see Fig. 4b). The resonance peaks are mainly attributed to the effect of metallic elements. Hence, the tuning process gives us the flexibility of creating resonances and hence increasing the absorption by manipulating a proper design and placement of resonators.

The triple-band biosensor excels over single-band biosensors in the terahertz band due to its expanded spectral coverage, enabling simultaneous detection of multiple biomolecular resonances and providing redundancy for enhanced reliability. Conversely, single-band biosensors may be limited in detecting multiple biomarkers simultaneously, leading to increased false positives or negatives. Yet, they may lack specificity and be more susceptible to noise and errors, posing a single point of failure if the resonant frequency shifts. The triple-band terahertz metamaterial biosensor offers increased specificity and multiplexing capability, allowing for simultaneous detection of various analytes with minimized measurement errors. While it may present challenges like fabrication complexity, single-band biosensors offer simplicity and cost-effectiveness. However, they may lack sensitivity and specificity compared to triple-band counterparts. The choice between the two depends on factors such as biomarker range and desired precision. Triple-band biosensors hold promise for increased sensitivity, leveraging multiple resonant frequencies for improved cancer detection, while single-band biosensors offer simplicity but may sacrifice sensitivity for targeted detection. Ultimately, the selection should align with the specific application’s requirements and constraints. Figures 1, 2, 3, and 4 remained unchanged for a clear and step-by-step presentation of our research findings.

With the aim of obtaining the best resonance characteristics, it would be useful to show the effect of substrate and metal type by simulating five different materials and five different metals. The PET dielectric layer was used as a substrate due to its ease of implementation in the terahertz frequency regions. The selection of PET for THz application can be made possible due to its relatively small dielectric constant compared to the common substrates. This is because the low dielectric constant of the PET guarantees minimizing the parasitic capacitances that are developed between traces and conductive structures at terahertz frequency. Noteworthy, for the PET to be plugged into the CST, a custom substrate resembling the PET properties was created within the CST software.

As can be seen from Fig. 5a, Arlon 410, Arlon 430, FR4, and Roger 5870 materials were utilized as a substrate. The resonance frequency is inversely proportional to the capacitance (C), which means the value of C decreases with the increase in resonance frequency. Since capacitance value increases as the dielectric constant increases, the resonance frequency is therefore decreased according to the formula of \(1/\sqrt{LC}\), as shown in Fig. 5a. Resonance peaks are also related to the loss tangent of the materials. Hence, one can see that the absorption level decreased when materials with more loss tangent than PET were used. Furthermore, gold, iron, silver, and copper were compared with aluminum as a selected resonator material, as shown in Fig. 5b. The conductivity of these materials are 4.56 × 107, 1.04 × 107, 6.30 × 107, 5.8 × 107, and 3.56 × 107 S/m, respectively according to the material library in the CST software. Therefore, different resonance characteristics would be expected in accordance with the conductivity variation. Figure 5b shows the impacts of resonance materials on the absorption. It is easily noticeable that resonance materials do not have an effect on resonance shift compared to that of the dielectric substrates. However, it is affecting the absorption intensity value due to the effect of plasmonic resonance response.

Fig. 5
figure 5

The recommended design’s absorption spectra under varied a substrate material and b resonator material circumstances

Full size image

Figure 6 shows the effect of incident angle on the absorption response of the proposed metamaterial absorber. It was observed that with the change of incident angle along the y-axis, the same positions for the resonance peaks were retained on the x-axis, implying that the proposed absorber is independent on the incident angle of the electromagnetic waves. Noteworthy, each vertically aligned strip of the resonance peaks presented the same color, which indicates the consistency of the absorption value throughout the incident angle variation. Furthermore, when we look at the polarization angle plot (Fig. 6b), similar result is observed which is due to the symmetric design of the proposed work. Hence, it is concluded that the proposed design is important for specific sensing applications.

Fig. 6
figure 6

The effect of angle change on absorption rate is investigated: a angle of incident and b polarization angle

Full size image

Figures 7 and 8 show the electric (E) and magnetic (H) fields’ distribution along the proposed MTM absorber at the main three resonance frequencies. We observed that the E-field is densely distributed across the upper and lower diagonal of the resonator, while the H-field is mainly distributed at the edges of the split resonators.

Fig. 7
figure 7

Distributions of the metamaterial structure field are shown on a color map: a E-field at 0.548 THz, b E-field at 0.804 THz, and c E-field at 0.9 THz

Full size image
Fig. 8
figure 8

The field distributions of the proposed metamaterial structure are depicted on a color map: a H-field at 0.548 THz, b H-field at 0.804 THz, and c H-field at 0.9 THz

Full size image

Figures 9 and 10 show the surface current and power loss distribution within the proposed MTM absorber at three different resonance frequencies. One can see that the surface current is distributed in the clockwise direction at the two low resonance frequencies, which leads to produce magnetic fields that are of the same direction as the incident magnetic fields. This has led to reinforce the H-field on the asterisk resonator, as shown in Fig. 8. However, the high resonance frequency contributes to weakening the H-field distribution around the asterisk due to the anticlockwise circulation of the surface current.

Fig. 9
figure 9

The surface current distribution of the recommended metamaterial design: a at 0.548 THz, b at 0.804 THz, and c at 0.9 THz

Full size image
Fig. 10
figure 10

Investigation of power loss at a 0.548 THz, b 0.804 THz, and c 0.9 THz

Full size image

Noticeably, the power loss is more prominent around the square resonators in the low frequency range. This can be related to the electric field intensity, shown in Fig. 7, which is responsible to originate the electric power loss. At high-frequency resonance, the electric field became denser above and below the diagonal of the MTM absorber, and hence, the power loss was more pronounced accordingly.

Diagnosis of Blood Cancer

Because of its special characteristics that aid in the diagnosis of blood malignancies, terahertz radiation is sensitive to the bonding mechanisms found in the whole blood. Cancer cells exhibit distinct refractive indices, absorption coefficients, and dielectric properties, which enable THz metamaterial-based absorption spectrum and THz metamaterial-based imaging to reveal subtle cell changes. THz metamaterial absorber-based sensors leverage resonance peaks in the THz absorption spectrum to distinguish abnormal cells/tissues from healthy ones. When blood cells are placed on top of the absorber, the absorption spectrum varies depending on the presence of cancer. The setup for diagnosis of cancer using the proposed absorber is shown in Fig. 11. The components of blood cells, which normally consist of 45% red blood cells, 55% plasma, and a very little quantity of white blood cells, have an increase in absorption coefficient and a drop in refractive index. Plasma is mostly made up of water (92%), dissolved proteins, and salts (8%).

Fig. 11
figure 11

Diagnosing blood cancer with the proposed sensor

Full size image

The THz MTM absorber is covered by a cover slip of thickness T2, on top of which the blood sample is placed having thickness T3. The absorption spectrum varies both in terms of resonance frequencies and in terms of absorption coefficient for normal and for cancer blood cells, as shown in Figs. 12, 13, and 14. The absorption coefficients and the resonance frequencies for both normal and cancer blood cells are shown in Table 2.

Fig. 12
figure 12

The suggested sensor measures the blood’s normal and malignant absorption coefficients; the frequency range is between a 0–1 THz and b 0.40–0.55 THz

Full size image
Fig. 13
figure 13

The suggested sensor measures the blood’s normal and malignant absorption coefficients; the frequency range is between a 0–1 THz and b 0.66–0.75 THz

Full size image
Fig. 14
figure 14

The suggested sensor measures the blood’s normal and malignant absorption coefficients; the frequency range is between a 0–1 THz and b 0.75–0.85 THz

Full size image
Table 2 Resonance frequencies of normal versus cancerous blood cells by employing the proposed structure
Full size table

Thus, based on the variations in the resonance frequency and the absorption coefficient, the diagnosis of cancer in the blood can be achieved accurately. Another important observation is that the presence of cancer cells increases the absorption coefficient, which can be clearly seen at the second and third resonance peaks. The cancer cells absorb more incident THz radiation compared to the normal cells. This may be due to difference in dielectric properties and refractive index of the cancer cells, refractive indices of 1.376 for normal blood and 1.390 for blood cancer [35,36,37,38,39]. Thus, THz imaging can be utilized as another method to diagnose the blood cancer, as shown in Fig. 15.

Fig. 15
figure 15

The use of THz imaging technique in the diagnosis of blood cancer

Full size image

In this setup, the Jurkat cells from the blood are placed on the THz MTM absorber. When THz radiation is incident on it, depending on the presence of cancer, the electric field, and magnetic field distribution will vary as shown in Figs. 16, 17, 18, and 19, for different resonance frequencies.

Fig. 16
figure 16

The E-field THz imaging technique results at 0.548 THz: a normal blood and b blood cancer

Full size image
Fig. 17
figure 17

The H-field using THz imaging technique results at 0.548 THz: a normal blood and b blood cancer

Full size image
Fig. 18
figure 18

The H-field THz imaging technique results at 0.9 THz: a normal blood and b blood cancer

Full size image
Fig. 19
figure 19

The electric energy density THz imaging technique results at 0.804 THz: a normal blood and b blood cancer

Full size image

The electric field and magnetic field intensity is measured by the color, with blue being low and red being high. The figure shows that the electric field intensity is higher in the presence of cancer cells, as indicated by the red color in the right image (Fig. 17b). This suggests that cancer cells absorb radiation more than normal cells. This difference in absorption is due to the unique properties of cancer cells, such as their higher water content and increased blood supply, which affects their refractive index, absorption coefficient, and dielectric properties. These properties result in a higher absorption of terahertz radiation by cancerous tissue compared to that of normal tissue. Thus, the resonance mode at 0.548 THz is sensitive to the presence of cancerous cells in blood, which can be detected by magnetic field imaging.

Thus, it can be seen clearly from the imaging techniques that the electric and magnetic field densities vary depending on the presence of cancer cells. For normal blood cells, the electric and magnetic fields were less concentrated compared to the Jurkat cells with cancer. Thus, when the cells are affected with cancer, they tend to absorb the THz radiation, and hence based on the intensity of these fields, the presence of cancer can be diagnosed effectively, where the proposed design structure shows 3 resonance peaks between 100 MHz and 1 THz, as summarized in Table 3 and compared with the previous works. The minimum sensitivity was found to be 930 GHz/RIU between 0.45 and 0.5 THz, while the maximum sensitivity was obtained for other peaks between 0.75 and 0.85 THz with a value of 2540 GHz/RIU. Noteworthy, in spite of the simplicity of the designed structure, it has a high sensitivity, which makes it a promising candidate for future medical applications and advances in cancer diagnosis.

Table 3 Bio-sensing performance comparisons of various sensor applications based on THz metamaterial
Full size table

The figure of merit (FOM), quality factor (Q-factor), and sensitivity (S) are critical attributes defining a sensor’s performance. The FOM quantifies selectivity, expressed as the ratio of sensitivity to the full-width at half-maximum (FWHM) of the resonant dip:

$${\text{FOM}}=\frac{S}{{\text{FWHM}}}$$
(2)

The quality factor (Q-factor) measures resonance sharpness, determined by the ratio of the resonant wavelength (λ) to the FWHM:

$${Q}_{{\text{factor}}}=\frac{\lambda }{{\text{FWHM}}}$$
(3)

Terahertz (THz) sensing benefits from metamaterial-based biosensors, enhancing sensitivity. Two sensitivity definitions prevail: frequency sensitivity:

$$S=\frac{\Delta f}{\Delta n}$$
(4)

where Δf signifies the resonance peak’s frequency shift and Δn denotes refractive index (RI) change, typically in refractive index units (RIU) and intensity frequency:

$$S=\frac{\Delta I}{\Delta n}$$
(5)

where ΔI represents variation in resonant intensity [40, 41].

Conclusions

In conclusion, this work represents a significant advancement in the field of medical diagnostics, specifically in the context of diagnosing blood cancers. Leveraging the unique capabilities of THz technology and metamaterial engineering, the proposed sensor offers a promising avenue for the fast, highly accurate, and non-invasive diagnosis of blood cancer. The proposed sensor’s effectiveness is further underscored by its ability to visualize the differences between normal and cancerous blood cells using THz imaging techniques. The electric and magnetic field intensity distributions clearly indicate that cancer cells absorb THz radiation more than the normal cells. This difference in absorption, as depicted in the mentioned images, provides a powerful diagnostic tool for the presence of cancer in the blood. As summarized in Table 4, the proposed study compared with the current state of the art showed a large Q value, sensitivity, and FOM factor. The proposed work outperformed the previous published one in terms of Q factor, S value, FOM, and application. Although the proposed work suffers from difficulties during applications of metamaterial sensors, it is promising with this S value, unique design. and application sides.

Table 4 A comparison between the study on perfect metamaterials in the terahertz band and the suggested biosensor
Full size table