The high-cyclic model for sand tested beyond the usual ranges of application

Abstract

The high-cycle accumulation (HCA) model proposed by Niemunis et al. (Comput Geotech 32(4):245–263, 2005) predicts permanent deformations due cyclic loading with many small cycles (i.e. $N \ge 10^4$ cycles of strain amplitudes ${\varepsilon }^{{\rm ampl}}\le 10^{-3}$). In the presented tests, the pressure range $p^{{\rm av}}$ is extended from 3 to 9 bar; the influence of the void ratio $e \in (0.72, 0.95)$ and amplitudes of strains $\varepsilon ^{{\rm ampl}} \in (0.1{\%}, 1{\%})$ is tested in the extended range. Some empirical HCA functions could be confirmed and some require modifications. An interesting qualitative controversy pertains to the direction of circulation in the P–Q-plane for a validation of the polarization function $f_\pi$, which does influence the rate of accumulation contrarily to the HCA assumption. The previous assumption that $\dot{\varepsilon }^{{{\rm acc}}}$ remains constant above a certain pressure level, i.e. is independent of $p^{{{\rm av}}}$, was experimentally refuted. Investigations on the cyclic preloading ($\dot{f}_N$) using 21 cyclic triaxial tests with varried monotonic strain paths between the cycle packages found a relationship of the direction of the monotonic strain path and the capacity to reduce cyclic preloading. This study’s findings deepen the understanding of how cyclic preloading is reduced, but the tests also highlight the need for future research in the area.

1 Introduction

A reliable finite element (FE) prediction of settlements and deformations demands a realistic constitutive description of the soil. For the complex condition of a high-cycle loading, the constitutive model must be covering among others the amplitude of the loads, mean pressure, average stress ratio, void ratio and the preloading history. The explicit high-cycle accumulation model (HCA model) of Niemunis et al. [26] has been proposed for this applications and used in many practical cases.

In Europe, numerous offshore wind farms will be built in the North and Baltic Seas. During their serviceability period, which is generally 25 years, offshore wind turbines (OWT) will be subjected to primarily to high cyclic wind and wave loads. For a variety of construction situations, the HCA model [12, 27, 30] was used to simulate several complicated loadings in FE calculations. A dense North Sea sand with a permeability of $k = 5\cdot 10^{-6}$ m/s was investigated by Jostad et al. [12]. Herein, the HCA model demonstrated a reliable prognosis of the long-term deformations, also in contrast to other implicit and explicit material models.

Machaček et al. [19] used the HCA model in FE calculations to evaluate the settling behaviour of the ship lock Uelzen I, which is a well-documented geotechnical structure with long-term monitoring. The comparison of the numerical predictions with the HCA model and the field measurements can be judged as quite satisfying.

For the preliminary design of a gas turbine foundation subjected to dynamic loading, Galindo et al. [5] showed satisfactory results with the usage of the HCA model. The settlement behaviour was studied herein with a reduced calibration program of the key parameters of the model. Pasten et al. [28] evaluated different accumulation functions to examine the soil response to repetitive loading. The key benefit highlighted here is the HCA model’s ability to forecast accumulation as a function of cycle count, stress level, and initial density, among a selection few other constitutive models.

The HCA model is based on extensive laboratory studies on various cyclic triaxial tests under drained conditions. In this article, the HCA model is investigated beyond its usual limits of application. The rate of strain accumulation will be thoroughly investigated in an extended range its main influencing parameters. These extensions are carried out in order to be able to apply this explicit material model in an extended range of practical applications with complicated boundary conditions.

2 Symbols and notation

Herein, the stress conditions in a test are described by the average mean effective pressure $p^{{\rm av}}$ (with $p = (\sigma _1' + 2 \sigma _3')/3$), the average deviatoric stress $q^{{\rm av}}$ (with $q = \sigma _1' - \sigma _3'$), average stress ratio $\eta ^{{\rm av}}= q^{{\rm av}}/p^{{\rm av}}$ and deviatoric stress amplitude $q^{{\rm ampl}}$. The isometric variables $P = \sqrt{3} p$ and $Q = \sqrt{3/2} q$ [24] are in many cases advantageous over the conventional Roscoe invariants p, q because the lengths of the stress paths and the angles between stress increments (or polarizations of amplitudes in our case) are preserved, i.e. they are the same as in the principal stress coordinate system. The axial strain $\varepsilon _1$ and the volumetric strain $\varepsilon _v = \varepsilon _1 + 2 \varepsilon _3$ are used to calculate the lateral strain $\varepsilon _3 = (\varepsilon _v - \varepsilon _1)/2$, the deviatoric strain $\varepsilon _q = 2/3 (\varepsilon _1 - \varepsilon _3)$ and the isometric strain variables $\varepsilon _P = \varepsilon _v/\sqrt{3}$ and $\varepsilon _Q = \sqrt{3/2} \varepsilon _q$. The total strain magnitude is defined as $\varepsilon = \Vert {\varvec{\varepsilon }}\Vert = \sqrt{(\varepsilon _1)^2 + 2 (\varepsilon _3)^2}$, i.e. as the Frobenius norm of the strain tensor. The above quantities can be split into a resilient = elastic = amplitude portion $\sqcup ^{{\rm ampl}}$ and a residual = plastic = trend = accumulated portion $\sqcup ^{{\rm acc}}$. The plastic strain can be measured as the irreversible deformation after a closed stress cycle. In the HCA model the plastic strain due to a single cycle is termed “the accumulation rate” (per cycle). Given the elastic stiffness, one may calculate the accumulation rate from mixed- or strain-controlled cycles too, as illustrated in [26]. In the context of the HCA model, a rate is understood as the derivative with respect to the number of cyles, $\dot{\sqcup } = \partial \sqcup / \partial N$. Normalisation is denoted by $\mathbf{A}^\rightarrow = \mathbf{A}$/$||A||$.

The rate of strain accumulation is described by the product

$$\begin{aligned} \dot{{\varvec{\varepsilon }}}^{{\rm acc}}= \dot{\varepsilon }^{{\rm acc}}{{\textbf {m}}} \end{aligned}$$

(1)

of the scalar intensity $\dot{\varepsilon }^{{\rm acc}}= \Vert \dot{{\varvec{\varepsilon }}}^{{\rm acc}}\Vert$ and the direction (a unit tensor) ${{\textbf {m}}}$. Both, the intensity $\dot{\varepsilon }^{{\rm acc}}$ and the flow rule ${{\textbf {m}}}$ are empirical functions and will be presented in the next section. In the triaxial case, the flow rule can be related to the ratio $\dot{\varepsilon }_v^{{\rm acc}}/\dot{\varepsilon }_q^{{\rm acc}}$. The values of $\dot{\varepsilon }^{{\rm acc}}$ and $\dot{\varepsilon }_v^{{\rm acc}}/\dot{\varepsilon }_q^{{\rm acc}}$ are measured indirectly using their time integrals.

3 Equations of the HCA model

The basic equation of the HCA model proposed by Niemunis et al. [26] reads

$$\begin{aligned} \dot{\varvec{\sigma }} = {{\textsf {E}}}: (\dot{{\varvec{\varepsilon }}} - \dot{{\varvec{\varepsilon }}}^{{\rm acc}}- \dot{{\varvec{\varepsilon }}}^{{\rm pl}}) \end{aligned}$$

(2)

with the rate $\dot{\varvec{\sigma }}$ of the effective Cauchy stress $\varvec{\sigma }$ (compression positive), the strain rate $\dot{{\varvec{\varepsilon }}}$ (compression positive), the accumulation rate $\dot{{\varvec{\varepsilon }}}^{{\rm acc}}$, a plastic strain rate $\dot{{\varvec{\varepsilon }}}^{{\rm pl}}$ (necessary only for stress paths trying to surpass the yield surface). These rates are interrelated by the barotropic elastic stiffness ${\textsf {E}}$. Depending on the boundary conditions, Eq. (2) predicts either a change of average stress ($\dot{\varvec{\sigma }} \ne {{\textbf {0}}}$) or an accumulation of residual strain ($\dot{{\varvec{\varepsilon }}} \ne {{\textbf {0}}}$) or both.

For $\dot{{\varvec{\varepsilon }}}^{{\rm acc}}$ the multiplicative form Eq. (1) is used with the flow rule ${{\textbf {m}}}= \dot{{\varvec{\varepsilon }}}^{{\rm acc}}/\Vert \dot{{\varvec{\varepsilon }}}^{{\rm acc}}\Vert = (\dot{{\varvec{\varepsilon }}}^{{\rm acc}})^\rightarrow$ (a unit tensor) and the intensity $\dot{\varepsilon }^{{\rm acc}}= \Vert \dot{{\varvec{\varepsilon }}}^{{\rm acc}}\Vert$. Based on the test results [39, 45] which are corroborated by the literature [4, 18] the flow rule of the modified Cam clay (MCC) model is adopted for ${{\textbf {m}}}$:

$$\begin{aligned} {{\textbf {m}}}= \left[ \displaystyle \frac{1}{3} \left( p^{{\rm av}}- \displaystyle \frac{(q^{{\rm av}})^2}{M^2 p^{{\rm av}}}\right) \textbf{1} + \displaystyle \frac{3}{M^2} (\varvec{\sigma }^{{\rm av}})^*\right] ^\rightarrow \end{aligned}$$

(3)

For the triaxial compression or extension the critical stress ratio M is

$$\begin{aligned} M_{cc} = \displaystyle \frac{6 \sin \varphi _{cc}}{3-\sin \varphi _{cc}} \quad \text{or}\quad M_{ec} = - \displaystyle \frac{6 \sin \varphi _{cc}}{3+\sin \varphi _{cc}}, \end{aligned}$$

(4)

respectively. The critical friction angle $\varphi _{cc}$ is slightly different from the one from monotonic triaxial tests (denoted as $\varphi _{c}$).

Table 1 Summary of the functions and material constants of the HCA model

The intensity of strain accumulation $\dot{\varepsilon }^{{\rm acc}}$ in Eq. (1) is calculated as a product of six functions:

$$\begin{aligned} \dot{\varepsilon }^{{\rm acc}}= f_{{\rm ampl}}\,\dot{f}_N\,f_e\,f_p\,f_Y\,f_{\pi } \end{aligned}$$

(5)

each considering a single influencing parameter (see Table 1), i.e. the strain amplitude $\varepsilon ^{{\rm ampl}}$ (function $f_{{\rm ampl}})$, the cyclic preloading $g^A$ ($\dot{f}_N$), void ratio e ($f_e$), average mean pressure $p^{{\rm av}}$ ($f_p$), average stress ratio $\eta ^{{\rm av}}$ or $\bar{Y}^{{\rm av}}$ ($f_Y$) and the effect of polarization changes ($f_\pi = 1$ for a constant polarization [40]).

The normalized stress ratio $\bar{Y}^{{\rm av}}$ used in $f_Y$ is zero for isotropic stresses ($\eta ^{{\rm av}}= 0$) and one on the critical state line ($\eta ^{{\rm av}}= M_{cc}$). The function Y of Matsuoka and Nakai [20] is used for that purpose:

$$\begin{aligned} \bar{Y}^{{\rm av}}= \displaystyle \frac{Y^{{\rm av}}- 9}{Y_c - 9} \quad \text{ with }\quad Y_c = \displaystyle \frac{9 - \sin ^2{\varphi _{cc}}}{1 - \sin ^2{\varphi _{cc}}} \end{aligned}$$

(6)

$$\begin{aligned} Y^{{\rm av}}= \frac{27 (3 + \eta ^{{\rm av}})}{(3 + 2 \eta ^{{\rm av}}) (3-\eta ^{{\rm av}})} \end{aligned}$$

(7)

For a constant strain amplitude, the function $f_N$ simplifies to:

$$\begin{aligned} f_N = C_{N1} \left[ \ln (1 + C_{N2} N) + C_{N3} N \right] \end{aligned}$$

(8)

Detailed investigations on the elastic stiffness ${\textsf {E}}$ in Eq. (2) may be found in [42, 44]. A more general formulation for the flow rule ${{\textbf {m}}}$ enabling to consider anisotropy has been published in [47]. The required material model parameters $C_{{\rm ampl}}$, $C_{N1}$, $C_{N2}$, $C_{N3}$, $C_{e}$, $C_{p}$ and $C_{Y}$ of the remaining functions from Table 1 are determined from drained cyclic triaxial tests or correlations with grain size distribution parameters or from index tests. The large experimental effort for the calibration of the material constants of the HCA model lead to the development of a simplified calibration procedure based on correlations with the grain size distribution curve and index test results [41, 46].

4 Material and testing procedures

The drained cyclic tests have been performed in three different types of test devices, using three different sample geometries and two different saturation conditions. Full cylinder samples (diameter $d = 100$ mm, height $h = 200$ mm) with fully saturation (Fig. 1a) have been used in the tests of Sects. 5.1, 5.2 and 5.3. The tests of Sect. 5.4 have been performed in a cyclic triaxial device shown in Fig. 1b, with local measurements of deformation on cuboid-shaped samples ($a \times b = 90$ mm, $h = 180$ mm) analogous to [1, 2, 7, 9,10,11, 15, 16]). The cyclic variation of cell pressure, which can lead to membrane penetration effects [23, 25, 33] and other sources of errors of global deformation measurements (e.g. system compliance, bedding error), can be avoided by applying local strain measurements [15]. LDTs, i.e. strips of stainless steel equipped with strain gauges (Fig. 1b), were applied for that purpose. The cuboid-shaped samples were tested in the dry condition and without water in the pressure cell, in order to guarantee the long-term stability of the LDT measurements. The cell air pressure was kept constant to maintain a constant temperature in the cell, which is necessary for reliable LDT measurements. The cyclic variation of lateral effective stress was realized by an oscillation of pore air pressure.

Fig. 1

Three types of devices used in the present study: (a) cyclic triaxial device with water-saturated full cylinder samples, (b) cyclic triaxial device with local strain measurements using LDTs on dry cuboid-shaped samples, (c) hollow cylinder device, (d) external loads and stresses acting on an element of soil in the hollow cylinder test [14]

In a hollow cylinder triaxial device (Fig. 1c), the tests of Sect. 5.5 were performed. The samples had an outer diameter $d_a = 100$ mm, an inner diameter $d_i = 60$ mm and a height $h = 200$ mm analogous to [3, 6, 29, 32, 49, 50]. The volume changes of both the full and the hollow cylinder samples were measured via the pore water. Thus, the samples were tested fully water-saturated. In the hollow cylinder device, an independent cyclic variation of vertical force F, torsional moment $M_T$, outer cell pressure $p_a$ and inner cell pressure $p_i$ (Fig. 1d) allows independent oscillations of three normal stresses ($\sigma _z$ in vertical, $\sigma _r$ in radial and $\sigma _{\theta }$ in circumferential direction) and one shear stress component $\tau _{\theta z}$. These four stresses can be converted to three principal stresses $\sigma _1$, $\sigma _2$ and $\sigma _3$ by means of a rotation of the coordinate system by the angle $\alpha$. In the tests of Sect. 5.5, only the rotation $0.1^\circ \le {\theta} \le 4.0^\circ$ by a torsional moment $M_T$ was applied, keeping $p_a = p_i$ constant. The problem of inhomogenes stresses $\sigma _{\theta }$ and $\sigma _r$ for $p_a = p_i$ and sample slenderness for twist angles $\theta \ge 4^\circ$ is absent in terms of element tests.

Air-pluviated samples of Karlsruhe fine sand (KFS) have been used in all tests of this series exepted of the tests in Sect. 5.5. The uniform KFS (mean grain size $d_{50} = 0.14$ mm, uniformity coefficient $C_u =d_{60}/d_{10} = 1.5$, minimum void ratio $e_{\min } = 0.677$, maximum void ratio $e_{\max } = 1.054$, grain density $\varrho _{s} = 2.65$ g/cm$^3$, subangular grain shape) has been prepared in the experiments. In Sect. 5.5 the coarser “Karlsruhe sand” (KS, mean grain size $d_{50} = 0.56$ mm, uniformity coefficient $C_u = d_{60}/d_{10} = 1.46$, minimum void ratio $e_{\min } = 0.544$, maximum void ratio $e_{\max } = 0.846$, grain density $\varrho _{s} = 2.64$ g/cm$^3$, subangular grain shape) was used. All tests on fully saturated samples were carried out on samples with parameters of Skempton $B = \Delta u/\Delta \sigma _3 \ge 0.98$, although for sand samples values greater than 0.97 are generally considered to be sufficiently well saturated.

5 Discussion of HCA functions

5.1 Function of cyclic preloading $f_N$

Tests in [17] demonstrate that the sand “remembers” its previous cyclic loading when packages of cycles are applied one after another. Similar test series could be found in the literature [8, 13, 31, 43]. Packages of cycles with different amplitudes have been applied on a compacted granite ballast in [31]. These tests proved that the final accumulated strains were independent of the order of the applied packages, analogously to the Miners’s rule for fatigue [21]. The experiments confirmed the effect already observed in [48] that the monotonic loading due to the change of the average stress state erases part of the memory of the sand with respect to its cyclic preloading history, described in the HCA model by the preloading variable $g^A$. The reduction of $g^A$ by a monotonic change of the mean pressure was described by a factor r, which was determined on basis of recalculations of the tests with the HCA model.

Laboratory tests in [38] presented packages of loading cycles applied on a sample of Cuxhaven sand one after another. Tests with packages of cycles with increasing loading amplitudes and constant average stress ratio $\eta ^{{\rm av}}$ and mean pressure $p^{{\rm av}}$ were performed. The HCA model handles this load case well and reproduces the accumulation curves satisfactorily. Another test in this series with cycle packages interrupted by monotonic loading, i.e. the average stress ratio $\eta ^{{\rm av}}$ was changed monotonically, exposed the reduction of the cyclic preloading by monotonic strains resulting from the loading path. The average mean pressure $p^{{\rm av}}$ was constant throughout the test. The packages of cycles that follow a monotonic change of the average stress ratio $\eta ^{{\rm av}}$ show an increased rate of strain accumulation $\dot{\varepsilon }^{{\rm acc}}$. The HCA model cannot consider this effect as yet. Based on these results, the cyclic preloading $g^A$ can be reduced or completely erased by sufficiently large monotonic straining. To study this reduction in detail, numerous laboratory investigations were carried out in the scope of this work. Their results will be described here and introduced to the HCA model.

In this section, the tests consisted of axial stress cycles. For studying the reduction of cyclic preloading, packages of cycles on different average stress states with different monotonic stress paths in the p–q-stress space were applied on the specimens. In 21 tests, 3 to 9 packages of cycles with $N = 25{,}000$ cycles and a loading frequency of $f = 0.2$ Hz were applied. All tests were evaluated regarding the accumulated strain $\varepsilon ^{{\rm acc}}$ after the number of cycles N. After the evaluation, the tests were recalculated by the HCA model, wherein many tests showed the need of a reduction factor r for the cyclic preloading variable $g^A$ by $g^A\cdot r$. This reduction factor was first introduced in [37] and has a value range of $0 \le r \le 1$. In this context $r = 0$ represents a complete erasing of the cyclic preloading in between the packages, whereby $r = 1$ leaves the evolution of the cyclic preloading unaffected. For a more general investigation on the reduction of cyclic preloading by monotonic deformations, the idea of applying multiple packages of cycles on different average stress states was extensively continued. Table 2 shows the variation of the tests by the different monotonic changes of the stress state between the packages. Different stress path lengths, as well contrasting path directions were tested. Figure 2 visualizes the three tests types.

Table 2 Stress paths $\Delta p^{{{\rm av}}}$, $\Delta \eta ^{{\rm av}}$, resulting average strain spans $\Delta \bar{\varepsilon }$ and the affiliated average reduction factor $\bar{r}$

Fig. 2

Schematic stress paths: (a) Variation of the mean pressure interrupting cycle packages, (b) variation of the stress ratio interrupting the cycle packages and (c) simultaneous change of mean pressure and stress ratio

Changes of the effective mean pressure $p^{{\rm av}}$ are exemplarly in Fig. 2a. Table 2 matches the measured monotonic strains to the applied monotonic loading change in the p–q-space for the shown three types of tests. The overall results of the experiments carried out in this work are shown in Fig. 3, which helps to better estimate a correlation between the strain increment $\Delta \varepsilon$ arising from the monotonic stress path and the reduction factor r. The curve fitting cannot provide any firm conclusions because of the large scatter. The monotonic deviatoric loading along the critical state line (CSL) degradates the cyclic preloading faster than a simple increase of the average mean pressure, no matter if it is an increase by $\Delta p^{{{\rm av}}} = 100$ kPa or $\Delta p^{{{\rm av}}} = 300$ kPa which is consistent with the results presented in Table 2.

Fig. 3

(a) Accumulation of strain $\varepsilon ^{{\rm acc}}$ in a test with experimentally change of the average stress ratio $\eta ^{{\rm av}}$ between the cycle packages; determination of the reduction factor r from recalculation and (b) correlation between the monotonic strain and the reduction factor r used to find the best possible accordance of the HCA model to the test results. Extended from [35]

In the context of Table 2, positive $\Delta \eta$ means a change of the stress ratio leading to a stress state closer to the CSL than the stress state before (Table 2 represents compression, as well as extension tests). The mean values $\Delta \bar{\varepsilon }$ and $\bar{r}$ result from all determined values for the respective change of the stress state. All test results in this section contribute to the understanding of the reduction of the cyclic preloading. They also show the necessity of further investigations to enable implementation of the reduction of the cyclic preloading into the HCA model.

5.2 Function of the mean pressure $f_p$

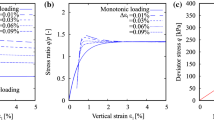
Investigations by Wichtmann [37] for eight different sands indicated that the barotropic function $f_p$ could overestimate the accumulation intensity $\dot{\varepsilon }^{{{\rm acc}}}$ for pressures $p^{{\rm av}}\ge 300$ kPa. The pressure range investigated so far for the HCA model was 50 kPa $\le p^{{\rm av}}\le 300$ kPa. Individual experiments suggested that $\dot{\varepsilon }^{{{\rm acc}}}$ remains constant above a certain pressure level. In the triaxial devices used so far, the mean pressure $p^{{\rm av}}\le 300$ kPa could be tested at the pore (back) pressure $u = 500$ kPa, for safety reasons. For some practical applications pressures $p^{{\rm av}}\ge 300$ kPa may be of interest. Therefore it should be experimentally clarified if $f_p$ should be assumed to be constant above a certain limiting pressure.

Therefore, the testing device from Fig. 1a was equipped with an additional plexiglas cylinder, with burst protection and pressure transducers for up to 900 kPa [22]. This corresponds to an enhancement of the previous pressure range by a factor of 3. The pore (back) pressure was chosen to be $u = 500$ kPa in all tests in order to achieve a sufficient saturation. For a constant stress ratio $\eta ^{{\rm av}}= 0.75$ and amplitude-pressure-ratio $\varsigma = q^{{\rm ampl}}/p^{{\rm av}}= 0.3$ the mean pressures 200 kPa $\le p^{{\rm av}}\le 900$ kPa were investigated. Data for smaller pressures $p^{{\rm av}}\le 150$ kPa were available from [37].

Fig. 4

Tests on samples with $38\% \le D_{r0} \le 42\%$ (a) accumulated strain $\varepsilon^{acc}$ and (b) strain amplitude $\varepsilon^{ampl}$ over number of cycles $N$ for mean pressures $200 \le p^{{\rm av}}\le 900$ kPa, a constant stress ratio $\eta ^{{\rm av}}= 0.75$ and amplitude-pressure-ratio $\varsigma = q^{{\rm ampl}}/p^{{\rm av}}= 0.3$

Figure 4 shows the results of the new tests for both, the accumulated strain $\varepsilon ^{{{\rm acc}}}$ and the strain amplitude $\varepsilon ^{{\rm ampl}}$ versus the number of cycles N with the exception of the experiment with $p^{{\rm av}}= 500$ kPa, where the maximum density $D_{r0} = 42$% was present. It can be seen that the values of the strain amplitude $\varepsilon ^{{\rm ampl}}$ (which is expected due to the constant amplitude-pressure relationship) as well as the accumulated strain $\varepsilon ^{{{\rm acc}}}$ increase with increasing mean pressure $p^{{\rm av}}$. Even for large pressures, an increase of the permanent deformation rate with increasing mean pressure can thus be recognized at constant $\varepsilon ^{{\rm ampl}}$. The previous assumption that $\dot{\varepsilon }^{{{\rm acc}}}$ remains constant above a certain pressure level, i.e. is independent of $p^{{{\rm av}}}$, could not be confirmed. For large pressures, a further decrease of the accumulated strain rate $\dot{\varepsilon }^{{{\rm acc}}}$ with mean pressure can be confirmed. Thus, no changes to the pressure function $f_p$ were necessary. The coefficient $C_p$ corresponding to the pressure range of the respective problem may be slightly different. The parameter $C_p$ can be determined for different numbers of cycles from the tests with different mean pressures. For this purpose, the accumulated strain after defined number of cycles N is divided by the void ratio function $f_e$ and the amplitude function $f_{{\rm ampl}}$ of the HCA model in order to purify the test results from the influences of the different void ratios and strain amplitudes (Fig. 5). The resulting mean value of the parameter $C_p = 0.09$ determined for the pressure range $p^{{{\rm av}}}\le 900$ kPa is clearly smaller as the value for the pressure range 50 kPa $\le p^{{{\rm av}}} \le 300$ kPa determined by Wichtmann [37] on the same sand $C_p = 0.24$ (Table 3). Here $C_p$ represents a factor averaged according to the number of cycles analogous to [37].

Fig. 5

Accumulated strain $\varepsilon ^{{{\rm acc}}}/(\bar{f}_e \bar{f}_{{\rm ampl}}$) as a function of the mean pressure $p^{{{\rm av}}}$. Investigated mean pressures 200 kPa $\le p^{{\rm av}}\le 900$ kPa and data of former tested pressures $p^{{\rm av}}\le 150$ kPa [37]

Table 3 Parameter $C_p$ of the pressure function of the HCA model for different numbers of cycles N

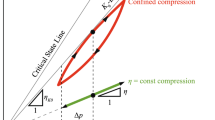
5.3 Circulation changes in P–Q-plane

The circulation of cycles was claimed in [26] to be of no importance in the HCA model. This was based on multiaxial direct simple shear tests in which shearing was applied at the $K_0$ initial stress state. As it turned out in the present study, the circulation may significantly affect the accumulation rate. Seven different cyclic triaxial tests with relative density $D_{r0} \approx 40$%, $N = 10^4$ cycles and circular stress paths in the P–Q-plane with a radius $r_{PQ} = 40$ kPa arround the stress state $\eta _{PQ} = Q/P = 0.24$, $P = 346$ kPa were examined. Three experiments were carried out with a counterclockwise (CCW) circulation (Fig. 6a) and three tests with clockwise (CW) circulation (Fig. 6b). The accumulated strains $\varepsilon ^{{{\rm acc}}}$ and strain amplitudes $\varepsilon ^{{\rm ampl}}$ of tests are shown in Fig. 6c, d. The difference between the direction of circulation results in 33% lower accumulated strain $\varepsilon ^{{{\rm acc}}}$ of the CW tests than the CCW tests (Fig. 6c). For the CCW as well as CW test approximately the same strain amplitude $\varepsilon ^{{\rm ampl}}$ was obtained (Fig. 6d). Some tests were repeated and turned out to be reproducible.

Fig. 6

Dimensional drawing of the stress path in the P–Q-plane for (a) counterclockwise circulation (CCW, orange) and (b) clockwise (CW, red) with indication of the critical state line CSL. (c) accumulated strains $\varepsilon ^{{{\rm acc}}}$ and (d) strain amplitudes $\varepsilon ^{{\rm ampl}}$ from cyclic triaxial tests on specimens with $D_{r0}\approx 40$% in the average stress state $\eta _{PQ} = 0.24$, $P = 346$ kPa. The seventh test (black) was first run for $N = 100$ cycles in CW and then 9900 cycles in CCW direction (color figure online)

A seventh test (black) with similar relative density was first run for $N = 100$ cycles in CW direction (Fig. 6c, d). Then 9900 cycles followed in the CCW direction. Up to $N = 100$ cycles, the CW test are reproduced. After changing the direction of circulation, no effect on the accumulation rate can be seen. Consequently, a change in the direction of circulation leads to no change in $\dot{\varepsilon }^{{{\rm acc}}}$.

Figure 6a, b shows graphically the explanation for the different accumulation rates of the different circulations. The stress path in the P–Q-plane was idealized as a square. The sides of the square where the path moves towards the CSL, i.e. in the direction of the flow surface, could have a decisive influence on the permanent strains. In the case of the CCW stress path, path $1 \rightarrow 2$ represents this portion (Fig. 6a), in the case of the CW stress path, path $2 \rightarrow 3$ (Fig. 6b). Presumably, path $1\rightarrow 2$ ultimately leads to a larger accumulated strain $\varepsilon ^{{{\rm acc}}}$ due to the larger deviatoric stress Q for $P = 346$ kPa, $\eta _{PQ} = 0.24$.

Tests with lower inclinations of the average stress state P = 346 kPa and $\eta _{PQ} = 0.11, -0.11$ and $-0.24$ are shown in Fig. 7. For $\eta _{PQ} = 0.11$ and $-0.11$ the accumulated strains $\varepsilon ^{{{\rm acc}}}$ of the CW and CCW tests are almost equal (Fig. 7b, c). When applying the same stress path at $\eta _{PQ} = -0.24$ larger accumulated strains $\varepsilon ^{{{\rm acc}}}$ were reached. Furthermore, a larger deformation is obtained for the CW test than for the CCW test due to the direction to the CSL.

However, the HCA model has not yet included a dependence of the accumulation rate $\dot{\varepsilon }^{{{\rm acc}}}$ on the circulation. One could try to define the circulations from Fig. 6a, b as an objective function of stress. In the space of principal (average) stresses the circulation would correspond to the rotation (a fourth-order tensor given by the Euler-Rodriguez formula) that transforms the isotropic unit compression tensor $-{\vec {\delta }}_{ij}$ to the direction of the average deviatoric stress ${\vec {\sigma }}_{ij}^*$ According to such definition, the circulations denoted as CCW (orange) are different below and above the hydrostatic axis. Analogously, the circulations denoted as CW (red) correspond to different rotations too. Judging by the results in Fig. 6b, the sense of rotation does not affect the accumulation rate. Neither the Lode angle seems to be of importance. Hence, the difference between CW (red) and CCW (orange) cycles is not a stress function. Probably, it results from an anisotropy induced by the preparation of samples. The modeling would require an additional tensorial state variable.

Fig. 7

Accumulated strains $\varepsilon ^{{{\rm acc}}}$ and strain amplitudes $\varepsilon ^{{\rm ampl}}$ from cyclic triaxial tests on specimens with relative density $D_r \approx 0.4$ in the average stress state (a) $\eta _{PQ} = 0.24$, (b) $\eta _{PQ} = 0.11$, (c) $\eta _{PQ} = -0.11$ and (d) $\eta _{PQ} = -0.24$ with $P = 346$ kPa

5.4 Function $f_e$ of the void ratio

It has been experimentally demonstrated [37] that the reduction in the accumulation rate $\dot{\varepsilon }^{{{\rm acc}}}$ with increasing initial relative density $D_{r0}$ is less significant at high relative densities $D_{r0} > 80$%. Due to the scarcity of data in this range, the function $f_e$ was regarded for $D_{r0} > 80$% as uncertain. Moreover, the preparation technique could have caused a loose zone at the top of the sample with much faster accumulation. This conjecture [37] had to be verified. A series of tests were carried out, Fig. 8 to clarify this issue [15, 34]. Five very dense samples ($D_{r0} \approx 90$%) were tested. Global and local (LDTs) displacement measurements enabled an in-depth analysis of the deformation.

Fig. 8

Test results from specimens with relative densities $D_{r0}>$ 0.8. (a) accumulated strain $\varepsilon^{acc}$ and (b) strain amplitude $\varepsilon^{ampl}$ over number of cycles $N$ for an average mean pressure $p^{{\rm av}}= 200$ kPa, stress ratio $\eta ^{{\rm av}}= 0.75$ and an applied deviatoric stress amplitude $q^{{\rm ampl}} = 60$ kPa

In order to reveal a possible concentration of accumulated deformations in a loosened layer at the specimens head, the deformations of the whole specimen measured outside the compression cell at the load stamp (global deformation measurement) are compared with local deformation measurements directly at the specimen. The specimens were prepared using the air pluviation method and were examined in totally dry condition. The results of all five performed experiments with a variation of the initial density $D_{r0} \approx 90$% is shown in Fig. 8. The curves of the accumulated strain $\varepsilon ^{{{\rm acc}}}$ and strain amplitude $\varepsilon ^{{\rm ampl}}$ over the 10,000 cycles applied are shown. The local values from the middle third of the sample confirmed the function $f_e$ for the accumulation rate. Moreover, as expected, a slight decrease in strain amplitudes $\varepsilon ^{{\rm ampl}}$ with density was observed.

The data could be well approximated by the void ratio function $f_e$ of the HCA model. The experimental data could be fairly well fitted despite the significant curvature for $e \ge 0.85$. The parameter $C_e$ of the void ratio function was determined to be $C_e = 0.62$ for $D_{r0} \ge 90{\%}$ ($e < 0.752$) with LDTs (Table 4). It differs only slightly from the model parameter $C_e = 0.60$ determined in [37] with global deformation measurement. According to [37], $C_e$ should be averaged over the number of cycles (Fig. 9).

Table 4 Parameter $C_e$ of the void ratio function of the HCA model for different numbers of cycles N

Fig. 9

Accumulated strain (and amplitude-purified) $\varepsilon ^{{{\rm acc}}}$/$\bar{f}_{{\rm ampl}}$ as a function of e and values of the parameter $C_e$ of the function of void ratio from the HCA model for different numbers of cycles N

5.5 Function of the strain amplitude $f_{{\rm ampl}}$

Only the tests in this section were carried out with the coarser Karlsruhe sand. Figure 10 shows the results of the hollow cylinder triaxial tests with increasing twist angle $\theta$ on samples with relative densities 44% $\le D_{r0} \le 84$%. A smaller increase of the accumulated strains $\varepsilon ^{{{\rm acc}}}$ is shown for tests with higher relative densities and lower twist angles $\theta$. The progress of the strain amplitude $\varepsilon ^{{\rm ampl}}$ is almost constant after a slight decrease. In Fig. 11 the residual strain is plotted as a function of the strain amplitude $\varepsilon ^{{\rm ampl}}$. The values of $\varepsilon ^{{{\rm acc}}}$ were normalized with $f_e$ in order to consider the influences of the void ratio. It is obvious that the relationship $\varepsilon ^{{{\rm acc}}} \sim (\varepsilon ^{{\rm ampl}})^2$ loses its validity for large strain amplitudes (starting from approx. $\varepsilon ^{{\rm ampl}} = 10^{-3}$) as already mentioned in [36]. Thus, these experiments in the hollow cylinder device confirm the previous observations for an extended strain range up to $\varepsilon ^{{\rm ampl}} \le 10^{-2}$.

Fig. 10

Comparison of accumulated strain $\varepsilon ^{{{\rm acc}}}$/$f_e$ and total strain amplitude $\varepsilon ^{{\rm ampl}}$ for different torsion angles 0.1 $\le \theta \le 4^\circ$ and relative densities after the first irregular cycle. (a, b) $D_{r0} \approx 50$% and (c, d) $D_{r0} \approx 80$% on hollow cylinder samples of coarse grained Karlsruhe sand

Fig. 11

Accumulated strain $\varepsilon ^{{{\rm acc}}}$/$f_e$ as a function of $\varepsilon ^{{\rm ampl}}$ from Fig. 10 for numbers of cycles $N = 20$, 100 and 1000

6 Summary and conclusions

This study discusses five of the six HCA model functions. A factor of three was added to the prior pressure range, increasing it to $p^{{\rm av}}\le 900$ kPa. The experiments revealed that even under high pressures, the permanent deformations increased as mean pressure increased. Therefore, if the calculated pressure parameter $C_{\rm p}$ is used at high pressure (300 kPa $\le p^{{{\rm av}}} \le 900$ kPa), no improvement to the current pressure function $f_{\rm p}$ is required. As a result, the HCA model’s applicability might be further increased to high pressure levels for a wider variety of applications. The validation of relative densities $D_{r0} \approx 90{\%}$, revealed a decline in the accumulation intensity, $\dot{\varepsilon }^{{{\rm acc}}}$. Additionally, these studies demonstrate that strain amplitudes $\varepsilon ^{{\rm ampl}}$ do indeed somewhat decrease even for high initial densities. In studies on the cyclic preloading ($\dot{f}_N$), a further analysis employing 21 cyclic triaxial tests with various monotonic strain paths between the cycle packages discovered a link between the direction of the monotonic strain path and the ability to reduce cyclic preloading. The results of this study add to the understanding of how cyclic preloading is decreased, but the tests also demonstrate the need for more investigation in this area.

Circulation changes in the P–Q-plane for a validation of the polarization function $f_\pi$ showed a dependence of the direction of rotation on the stress state in both the compression and extension area. This dependence is currently not considered in the HCA model. Investigations with large strain amplitudes $10^{-4} \le \varepsilon ^{{\rm ampl}} \le$ 10$^{-2}$ in the hollow cylinder triaxial device confirmed the limitation of the strain amplitude of $\varepsilon ^{{\rm ampl}} = 10^{-3}$ in the HCA model.