BCV bentonite hydromechanical behaviour and modelling

Abstract

It is assumed that clay materials such as bentonites will be used as the buffer and backfill of high-level radioactive waste disposal. Due to the very long timescale, the design can be based only on mathematical models that have been thoroughly validated via the use of high-quality laboratory data. The presentation of an extensive laboratory dataset, accompanied by the validation of a bentonite constitutive model, comprises the main topic of this paper. The objectives of the laboratory research were to determine the basic hydromechanical properties of BCV bentonite and to study the stress path behaviour of this bentonite. The laboratory results revealed that the hydromechanical behaviour is highly dependent on the stress path assumed, as well as the method of water introduction into the sample. The results further indicate that the micro- and macrostructures are constantly evolving, which exerts a significant impact on the determination of the material properties and the development of mathematical models. Moreover, it was demonstrated that swelling pressure tests, although they are typically considered to be element tests (with constant fields of state variables), when adopted by researchers for the calibration of constitutive models, do not in fact constitute element tests. A hypoplastic model of the behaviour of bentonite was implemented and validated using the experimental data obtained. It was demonstrated that the hypoplastic model accurately predicted the main behavioural features of bentonite that are important in terms of the prediction of the behaviour of the buffer in nuclear waste repositories.

1 Introduction

It is planned that high-level radioactive waste (especially spent nuclear fuel) will be disposed of in a deep geological repository (DGR), the safety of which is based on a multibarrier system (see Fig. 1). The waste will be placed in waste disposal packages (WDP) which will be sealed with a buffer in disposal boreholes; the other underground workings will subsequently be backfilled. It is assumed that clay materials such as bentonites and montmorillonitic clays will be used as the buffer and backfill materials due to their highly favourable sealing behaviour, which is based on their low levels of permeability and high swelling ability.

Fig. 1

Scheme of the deep geological repository planned in the Czech Republic ©SÚRAO

Since the radioactive waste emplaced in the DGR must be isolated from the biosphere for up to 1 million years, it must be proved that the multibarrier system is able to function over such a long period of time. This is possible only via the creation of mathematical models that are validated using high-quality experimental data (Wigger [23] Laloui [13]). This paper presents both the extensive experimental database compiled on the behaviour of BCV bentonite and the validation of a constitutive model.

The objectives of the laboratory research were to determine the basic hydromechanical properties of BCV bentonite in both its powder and compacted powder forms and to study the stress path behaviour of this bentonite, as well as to compile a complex dataset for this material with respect to its use as the reference research material in the ongoing development of the Czech DGR concept. The aim of the research team, which is composed of several institutions and coordinated by the Czech nuclear waste agency SURAO, was to obtain similarly comprehensive data to that contained in datasets available on other widely used bentonites such as MX-80 bentonite (Cui et al. [5] and FEBEX bentonite [21]). All the tests were performed by the various laboratories involved on the same batch of bentonite in order to ensure the consistency of the tested material, which is rather unusual for other bentonite datasets available in the literature. In order to obtain similar datasets for the development and calibration of models, experimental results are usually obtained from various sources that consider differing batches of material over several years ([6], Thatcher [20]). Since bentonites are natural materials, their composition and properties vary between both sources and batches (Dixon [6]), which may lead to biased results. A single batch-based complex dataset provides high-quality data for the development and validation of constitutive models.

The investigation of the stress path behaviour is particularly important since it is known that bentonite materials evince complex (micro)structures and that the state of the material leads to changes in its various properties and behaviour. This may have important consequences in terms of the design of the engineered barrier system (EBS) since, for example, the swelling pressure may differ significantly depending on whether, and to what extent, the deformation of the material is allowed. It is important to note that the experimental dataset presented in this paper does not include the consideration of experiments conducted at elevated temperatures. The effect of temperature is also being studied extensively and will be described in forthcoming publications.

The data obtained from the laboratory research was used as a tool for the development, calibration and validation of a hypoplastic bentonite material model for FEM analysis purposes [15, 16]. The model was subsequently employed in the interpretation of the behaviour of the material observed during the laboratory experimentation phase.

2 BCV bentonite

The Czech DGR concept is based on the use of bentonites extracted from Czech bentonite deposits. BCV (Bentonite Černý Vrch) is a Ca/Mg bentonite extracted from the Černý vrch bentonite deposit located in the České Středohoří Mts. in the NW of the Czech Republic. BCV bentonite was chosen as a suitable representative of Czech bentonites [9] and was first subjected to testing in 2017. Following the pilot characterisation of BCV (Červinka et al. [3]), this bentonite was used in a number of laboratory [22] and Baryla et al. [1] and in situ projects [11] and Svoboda et al. [19].

BCV is produced industrially by Keramost a.s. at their Obrnice plant. The bentonite treatment process commences with the sieving of the coarse material employing a sieve with a 20 × 20 cm mesh. The bentonite is then homogenised in a roller mill from where it is transferred to a rotary oven where the material is dried (average temperature of 110 °C) for 45 min. The drying process ensures a water content of around 10% and results in the preparation of the material for final milling and air sieving. The processing of the BCV material leads to a mixture where 1% of the total weight of the grains can be larger than 0.315 mm and at least 70% of the grains are smaller than 0.063 mm. The material is supplied in 48 kg bags, larger bags or tanks [22].

BCV bentonite (see Tables 1 and 2) exhibits a high proportion of minerals from the smectite group (Ca/Mg montmorillonite of over 60%), while other clay minerals (kaolinite, illite) are present to a lesser extent. With respect to the accessory phases, the presence of genesis-related Fe-carbonates (siderite, ankerite) and Fe oxides (mainly goethite) is of particular interest [9] and [14].

Table 1 Mineralogical composition of BCV bentonite (determined using X-ray diffraction, calculated via the Rietveld method) [14]

Table 2 Results of the silicate analysis of BCV bentonite [14]

It is the proportion of iron-rich phases and the iron-enrichment of the smectite in octahedral positions [7] that differentiates Czech bentonites from international standards and the Ca-bentonites extracted from the majority of European deposits.

The cation exchange capacity of BCV bentonite is 63.7 ± 2.2 meq/100 g and the major exchangeable cations consist of magnesium (42.0 ± 0.6 meq/100 g) and calcium (15.1 ± 1.8 meq/100 g). The density of the solid particles is 2.76 ± 0.02 g/cm³. The total specific surface area of BCV bentonite (employing EGME) is 438 ± 6 m²/g (Červinka et al. [3]).

The liquid limit according to the ČSN EN ISO 17892–12 standard [4] is 130% (according to Laufek et. al. [14]) and 139% (according to Červinka et. al. [3], Hausmannová et. al. [9]).

This study involved the investigation of a BCV bentonite powder and a uniaxially compacted powder. The batch of the material that was subjected to experimentation was named BCV_2017; for more detailed information, see Laufek et al. [14].

3 Laboratory investigation of the hydromechanical properties

3.1 Swelling pressure (constant volume)

The swelling pressure was measured using a constant volume cell apparatus that allowed for the combined investigation of the water permeability and the total pressure. The cells allowed for bottom-up saturation and the continuous monitoring of total pressure at the top or both at the top and bottom, depending on the type of test. Generally, only the top total measurement approach is used for the determination of the swelling pressure. Measurement on both sides is applied only in selected tests aimed at obtaining more accurate data for model calibration purposes.

The top and bottom of the samples were fitted with sintered steel permeable plates so as to prevent the leaching (“mobilisation”) of the material. The piston and the force sensor for the measurement of the total (or swelling) pressure of the bentonite were positioned on the top side between the flange of the chamber and the surface of the sample. A force sensor was connected to a central data logger.

The bentonite was uniaxially compacted into the hollow steel cylinder that formed the central part of the cell. Two laboratories were responsible for the investigation of the swelling pressure and permeability—the Czech Technical University (CTU) and Charles University (CU) laboratories. This allowed for the crosschecking of the results and procedures.

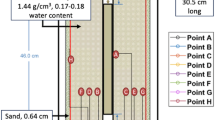
The setup used at the Charles University is shown in Fig. 2. Bentonite samples of 50 mm in diameter were compacted directly into the cells using 36 g of bentonite powder (hygroscopic water content of 11%). The height of the samples varied in the range 9–13 mm depending on the required initial dry density. The samples were saturated with distilled water through the bottom base. The water was not pressurised during the saturation process (Fig. 2a). The increase in the swelling pressure was monitored until a constant value was attained. Pressure and volume controllers were connected to both bases for the measurement of the hydraulic conductivity (Fig. 2b), and a constant pressure gradient was applied. The hydraulic conductivity was measured once a constant flow rate had been attained.

Fig. 2

Configuration of the constant volume cells for the measurement of the swelling pressure (a) and the hydraulic conductivity (b) at the Charles University

The setup used by the Czech Technical University team is shown in Fig. 3. Bentonite samples of 30 mm in diameter and heights of 20 mm were compacted directly into the cell rings. Distilled water was used as the saturation medium, which was propelled by compressed argon, typically at a pressure of 1 MPa. The saturation pressure applied does not influence the measured values provided the saturation pressure is lower than the swelling pressure of the sample [8]. The water flow was determined manually using a graded capillary tube-based flow meter in the inflow part. Testing continued until the flow and the total pressure stabilised (see the example in Fig. 4). The water flow over at least the four latest consecutive intervals was used for the determination of the coefficient of permeability (average of the four results). The water pressure source was subsequently disconnected so as to allow for the determination of the swelling pressure (Laufek et al. [14]).

Fig. 3

Configuration of the constant volume cells for the measurement of the swelling pressure and the hydraulic conductivity at the Czech Technical University

Fig. 4

Measurement of the permeability and total pressure (BCV ρ_d = 1597 kg/m³)

Figure 5 illustrates the dependency of the swelling pressure on the dry density as recorded by the two laboratories; the data is taken from Laufek et al. [14]. Figure 6 shows the dependency of the hydraulic conductivity on the dry density, again, as determined by the CTU and the CU.

Fig. 5

Swelling pressure of the BCV 2017 (Laufek et al. [14])

Fig. 6

Hydraulic conductivity of the BCV 2017

Figure 7 illustrates the temporal saturation evolution for a dry density of approximately 1600 kg/m³. A series of samples with a dry density of ~ 1600 kg/m³ was saturated followed by dismantling at predetermined intervals. During dismantling, the samples were cut into slices of a thickness of approximately 2 mm and the water content of each slice was determined by means of the gravimetric method. This allowed for the determination of the water saturation distribution in the samples. Note that the final sample (dismantled at 333.78 h) was found to be fully saturated—the change in the water content along the top of the sample was caused by the change in the dry density which, in turn, was caused by swelling during the saturation process (which led to density changes).

Fig. 7

Saturation development of the BCV 2017 over time (BEACON deliverable D4.1)

3.2 Swelling under a constant load (oedometric tests)

The hydromechanical behaviour of the BCV 2017 was investigated via the conducting of oedometric tests. A sample with a diameter of 120 mm and a height of 30 mm was placed in a cylindrical brass cell fitted with porous stone at the top and the bottom to allow for the saturation/desaturation of the sample. The sample was allowed to deform uniaxially (compaction/swelling) via the movement of a piston positioned on the top of the sample. The test was pressure controlled and with free deformation. The selected uniaxial load was transferred to the sample via the piston, while the sample deformation was monitored via the movement of the piston.

This setup enabled the investigation of the stress path dependence and hysteresis, as well as the influence of saturation via the alteration of the load scenario and the water regime.

Three main scenarios were investigated:

• Initial saturation without loading (Scenario I)—compacted samples were saturated at minimum loading (the weight of the piston of the apparatus) then loaded incrementally up to 700 kPa with free access to water, and subsequently incrementally unloaded with free access to water.

• Saturation without loading after a dry cycle (Scenario II)—samples with natural water contents were loaded incrementally up to 700 kPa, unloaded incrementally, saturated at minimum loading (the weight of the piston of the apparatus) and loaded incrementally up to 700 kPa with free access to water.

• Saturation under loading (Scenario III)—samples with natural water contents were loaded incrementally up to 700 kPa, saturated at 700 kPa, unloaded incrementally with free access to water, and loaded incrementally up to 700 kPa with free access to water.

Figure 8 illustrates the results of Scenario I, Fig. 9 those of Scenario II and Fig. 10 those of Scenario III. The results clearly indicate the presence of path dependence especially in the initial stage. However, once the samples have become fully saturated and fully loaded, they converge to form very similar curves.

Fig. 8

Scenario I - immediate saturation at zero loading

Fig. 9

Scenario II - saturation following a dry loading cycle

Fig. 10

Scenario III - saturation at full loading (after dry loading cycle)

3.3 Swelling pressure at a constant volume versus free swelling at constant loading

The incrementally loaded oedometric test revealed the importance of the stress path on the evolution of pressure. Further research was subsequently conducted aimed at the investigation of the influence of the stress path on the swelling pressure.

A series of single-stage free swelling under constant load tests were also conducted. Compacted samples (three initial densities were considered) were positioned in the oedometer, loading was applied (up to 7 different loads) and saturation initiated. The final density was determined once the deformation process had stabilised.

Figure 11 presents a comparison of the results of the constant volume cell testing (shown in red in the figure; data taken from Fig. 5) and the measurements obtained for free swelling under loading (shown in green in the figure). The arrows commence at the initial dry density and end at the final dry density (the blue arrows represent the relevant saturation phase from the oedometric tests described in the previous subchapter).

Fig. 11

Comparison of the swelling pressure - Urestricted swelling under constant load vs Swelling pressure at constant volume

The data clearly indicates a significant systematic difference between the values of the attained swelling pressure. If deformation is allowed during saturation and swelling, the swelling pressure is lower than the constant volume for the same final dry density. Mathematical material models need to take this factor into account.

4 THM hypoplastic double-structure model for bentonite

The BCV dataset discussed in the previous section was adopted for the evaluation of a THM hypoplastic double-structure model for bentonite. The model was developed by Mašín [16] via the hierarchical enhancement of an earlier model by Mašín [15] that did not consider the effects of temperature. The earlier model comprised, in turn, the double-structure enhancement of earlier hypoplastic models for unsaturated and saturated soils. Interested readers are urged to refer to these references for details of the creation of the models. In contrast to the model version of Mašín [16], an additional enhancement that replaced the original bi-linear form of the water retention curve by a smooth formulation was introduced to the latest model. For reasons of conciseness, the reader is referred to Mašín [16] for the complete model formulation. Here, only the changes in the formulation of the model from Mašín [16] are introduced. For the sake of clarity, however, Table 3 presents the model parameters and their physical meanings.

Table 3 Hypoplastic model parameters and their physical meanings

An improvement to the WRC equation concerned the reformulation of the macrostructural water retention model. The basic model by Mašín [16], which follows on from Mašín [15] and Wong and Mašín [24], uses the bi-linear formulation of the water retention curve according to Brooks and Corey [2]. The resulting water retention curve is shown in Fig. 12. It is clear that the water retention curve is C-0 continuous only, which means that the derivatives $\partial {S}_{r}^{M}/\partial s$ change abruptly at the intersection of the main wetting/drying curves with the scanning curve and at the air entry/expulsion suction value. These discontinuities comprise by-products of a simplification adopted while defining the model equations, since real soil does indeed evince the non-linear dependency of ${S}_{r}^{M}$ on suction. In addition, they lead to problems in terms of the numerical performance of the model. Finally, this bi-linear formulation, which resembles the response of the elasto-plastic constitutive model, contrasts with the general formulation of the THM constitutive model, which is hypoplastic and, thus, inherently non-linear.

Fig. 12

Hysteretic water retention macrostructure model adapted from a hypoplastic THM model for expansive soils

When redefining the water retention curve to be C-1 continuous, we adopted with advantage the ${r}_{\lambda }$ formulation proposed by Wong and Mašín [15]. Using this approach, it was possible to define the complete bi-linear water retention curve (not only the main wetting and drying curves) applying:

$${S}_{r}^{M}=\left\{\begin{array}{c}1\\ {\left(\frac{{s}_{e}}{s}\right)}^{{\lambda }_{p}}\end{array}\right.\begin{array}{c}\mathrm{ for}\quad s\le {a}_{e}{s}_{en}\\ \mathrm{for}\quad s>{a}_{e}{s}_{en}\end{array}$$

(1)

where ${a}_{e}$ is the parameter and the meaning of variable ${s}_{e}$ is clear from Fig. 12. It is calculated using:

$${s}_{e}={s}_{en}\left({a}_{e}+{a}_{scan}+{a}_{e}{a}_{scan}\right)$$

(2)

where ${a}_{scan}$ defines the position of the current state along the scanning curve such that ${a}_{scan}=1$ on the main drying curve and ${a}_{scan}=0$ on the main wetting curve:

$${a}_{scan}=\frac{s-{s}_{W}}{{s}_D-{s}_{W}}$$

(3)

For the meanings of ${s}_{W}$ and ${s}_{D}$, see Fig. 12. The rate of the variable ${a}_{scan}$ is given by:

$${\dot{a}}_{scan}=\frac{1-{r}_{\lambda }}{{s}_{D}(1-{a}_{e})}\dot{s}$$

(4)

where ${r}_{\lambda }$ represents the ratio of the scanning curve slope (in the $\mathrm{ln}s$ vs. $\mathrm{ln}{S}_{r}$ plane) and the slope of the main drying and wetting curves. For the original model, this ratio was given by:

$${r}_{\lambda }=\left\{\begin{array}{cc}1& \mathrm{for}\,s={s}_{D}\,\mathrm{and}\,\dot{s}>0\\ 1& \mathrm{for}\,s={{a}_{e}s}_{D}\,\mathrm{and}\,\dot{s}<0\\ \frac{{\lambda }_{pscan}}{{\lambda }_{p}}=0.1& \mathrm{otherwise}\end{array}\right.$$

(5)

The slopes ${\lambda }_{p}$ and ${\lambda }_{pscan}$ are model parameters and they are indicated in Fig. 12.

The discrete value of ${r}_{\lambda }$ from Eq. (5) was modified in the improved model so that the slope of the scanning curve varied smoothly between the main drying and wetting curves. The modification employs three parameters that are intended to be internal (i.e. hidden from the user and hard-coded in the implementation of the model) so that the parameters of the complete THM model, in terms of user-calibration, are identical for the two formulations; thus, no recalibration is required of the already calibrated original model for the new model. These internal parameters are denoted ${p}_{scan}=3$, ${S}_{lim}=0.75$ and ${p}_{wett}=1.1$. A new factor ${f}_{scan}$ is used in the formulation, defined as:

Fig. 13

Comparison of the predicted water retention curves with the original and modified macrostructural WRC formulations (a), the effect of internal model constants on the shape of water retention curves (b)

$${f}_{scan}=\left\{\begin{array}{c}{a}_{scan}\\ 1-{a}_{scan}\end{array}\right.\begin{array}{c}\mathrm{for}\quad \dot{s}>0\\ \mathrm{for}\quad \dot{s}<0\end{array}$$

(6)

A smoothed WRC formulation is then attained by redefining ${r}_{\lambda }$ from Eq. (5) to

$${r}_{\lambda }=\left\{\begin{array}{cc}0& \mathrm{for}\,s<{a}_{e}{s}_{en}\,\mathrm{and}\,\dot{s}>0\\ {\left(\frac{1-{S}_{r}^{M}}{1-{S}_{lim}}\right)}^{{p}_{wett}}& \mathrm{for}\,{S}_{r}^{M}>{S}_{lim}\,\mathrm{and}\,\dot{s}<0\\ {\left({f}_{scan}\right)}^{{p}_{scan}}& \mathrm{otherwise}\end{array}\right.$$

(7)

A comparison of the predicted water retention curves with those of the original and redefined models is provided in Fig. 13 a (note that the complete WRC is shown in terms of the global ${S}_{r}$, thus including the microstructural contribution). The effect of the internal parameters that control the shape of the WRC smoothing function is shown in Fig. 13b. Clearly, the updated model produces a smooth WRC curve while maintaining the main reference wetting and drying curves as asymptotic targets. Subsequently, Fig. 14 shows the results of the constant volume cyclic wetting–drying test expressed in terms of the degree of saturation (in this case, the global ${S}_{r}$ is also shown). Figure 14 demonstrates that apart from acting to smooth the formulation of the WRC, the other properties of the model (e.g. an irreversible change in ${S}_{r}$ during the cycles) are not compromised.

Fig. 14

Evolution of the degree of saturation in the THM hypoplastic model during the cyclic water retention test. Comparison of the original bi-linear logarithmic formulation (right) with the new smooth formulation (left)

5 Simulations of laboratory experiments on BCV bentonite

The THM hypoplastic model was calibrated and validated according to the comprehensive set of experimental data on BCV bentonite presented in Sect. 3.

When quantifying the degree of saturation from the experimentally measured mass water content, and when calculating the mass water content from the degree of saturation and the void ratio calculated by the model, a solid particle density of 2760 kg/m³ was adopted with a water density of 1150 kg/m³. The latter value was determined via the reverse-calculation of the experimental data from the constant volume water retention tests, via which the known mass water content, solid mass and specimen volume values can be used for the quantification of the degree of saturation. With a dry density of less than 1150 kg/m³, the calculated water content exceeded the value of 1 at low values of suction. A water density of more than 1000 kg/m³ is consistent with Jacinto et al. [10].

Figure 15 (left) presents predictions of the oedometric loading–unloading experiments conducted on saturated BCV bentonite performed at the CU; they demonstrate the good level of representation of the loading–unloading behaviour. The samples were prepared by means of the compaction of the bentonite powder to a dry density of 1270 kg/m³, which swelled under oedometric conditions at a constant load of 10 kPa and was subsequently subjected to oedometric loading–unloading. In this case, only the saturated loading–unloading phase was simulated (a comparison of the predictions of the swelling-loading–unloading oedometric tests with various path combinations is presented later in Fig. 23; the figure shows the void ratio e with respect to the vertical stress σ_v). Although initially highly pre-consolidated, the samples almost immediately attained normal compression lines, thus demonstrating that the swelling process led to a decrease in the apparent pre-consolidation. The model provided a good representation of both the loading and unloading stiffness.

Fig. 15

Predictions of the oedometric loading–unloading testing of saturated BCV bentonite (left) and the uniaxial loading experiments on unsaturated compacted B75 bentonite at a water content of 6% (right)

Figure 15 (right) shows the predictions of the uniaxial compression experiments conducted on unsaturated compacted bentonite. In this case, since no data was available for BCV bentonite, the experimental results for B75 bentonite tested at the CTU were simulated. It was assumed that the unconfined compression strength of the two types of bentonite (extracted from the same deposit) would not differ substantially. Cylindrical samples with aspect ratios of 1:1 were tested at various dry densities and an initial water content of 6%, corresponding to a suction of 100 MPa for the B75 bentonite. The experiments were simulated using the BCV parameters and an initial suction value of 100 MPa. It should be stressed that while the model considers the strength parameter critical state friction angle ${\varphi }_{c}$, the assumed effective stress for the macrostructure, calculated using the following Eq. (8), is key to the uniaxial compressive strength calculation:

$${{\varvec{\upsigma}}}^{M}={{\varvec{\upsigma}}}^{net}-1{S}_{r}^{M}s$$

(8)

The unconfined strength evinced a good level of representation for the lower dry density sample, whereas it was slightly underestimated for the higher dry density samples. The reasonably good uniaxial compressive strength predictions thus indicate the suitability of the adopted effective stress formulation.

The accurate prediction of the high uniaxial compressive strength can be explained with the assistance of the predictions of the water retention curves. Compacted bentonite with three differing initial dry densities (1200, 1600 and 1900 kg/m³) was tested under constant volume (Fig. 16) and unconfined (Fig. 17) conditions. Note that the unconfined WRC curves were calculated with a higher parameter N (see Table 3 for the definition thereof) value of 1.67, since the original value of 1.62 led to divergence. While under the unconfined conditions, the model slightly underpredicted the water content and the degree of saturation, the trends concerning the effect of dry density were well predicted, including a lower water content at low suctions for the high dry density samples than for the other two tests. Less satisfactory predictions were, however, produced by the free swelling experiments; although the drying curves were represented reasonably well, the water content was significantly underestimated in the wetting curves. The reason for this discrepancy is as follows. Since the macrostructural water content was relatively low (Fig. 18), the behaviour was predominantly affected by that of the microstructure and, since the microstructure was considered to be fully saturated, the water retention curves were primarily affected by the microstructural void ratio. Since the microstructural response was considered to be reversible in the model, the water retention curves should have exhibited a low degree of hysteresis, i.e. from the macrostructural part only (Fig. 18). However, since BCV is a highly swelling bentonite, the slope of the microstructural swelling line is in fact close to that of the normal compression line. Moreover, since the macrostructural effective stress is non-negligible so as to ensure the correct prediction of the uniaxial compression strength (Fig. 15), the state approaches the normal compression line during the wetting process (which is considered to be the boundary of the microstructural swelling in the model), thus breaching the reversibility of the microstructural deformation. This is demonstrated in Fig. 19, which shows the value of the state variable relative void ratio r_e, where a value of 1 indicates that the normal compression line state has been attained. It is important to note that the prediction of irreversible microstructural deformation was a consequence of the high swelling properties of BCV bentonite, a factor that was not so pronounced in the calibration of the model for other bentonites. However, it has not been physically substantiated and should be corrected in future versions of the model.

Fig. 16

Predictions of the water retention tests for compacted BCV bentonite under constant volume conditions at three differing initial dry densities of 1200, 1600 and 1900 kg/m³

Fig. 17

Predictions of the water retention tests for compacted BCV bentonite under free swelling conditions at three differing initial dry densities of 1200, 1600 and 1900 kg/m³ (calculated applying N = 1.67)

Fig. 18

Predictions of the macrostructural quantities (macrostructural water content and macrostructural degree of saturation) for the water retention testing of compacted BCV bentonite under free swelling conditions at three differing initial dry densities of 1200, 1600 and 1900 kg/m³ (calculated applying N = 1.67)

Fig. 19

Predictions of the relative void ratio for the water retention testing of compacted BCV bentonite under free swelling conditions at three differing initial dry densities of 1200, 1600 and 1900 kg/m³ (calculated applying N = 1.67)

A further indicator considered in the model concerned the macrostructural effective stress. The Bishop effective stress equation was adopted in the model for the macrostructure with a factor χ equal to the macrostructural degree of saturation ${S}_{r}^{M}$. As already mentioned, in order to predict the high uniaxial compressive strength of compacted bentonite, ${S}_{r}^{M}$ must be assigned a non-negligible (albeit low) value even for high suction values (see Fig. 18). This non-negligible effective stress contributes to the irreversibility of the microstructural void ratio (the enhanced effective stress shifts the state towards the normal compression line, which subsequently limits the microstructural swelling) and, moreover, limits the swelling potential, which is predicted reasonably well by the model (Fig. 20). It should be noted at this point that the experimental evidence indicated a dry macrostructure for higher suction values, which was clear from both the ESEM images [18] and from the fact that the water content of bentonite at higher suctions is known to be independent of the dry density (e.g. [17]. Thus, relating the high strength of compacted bentonite with the macrostructural degree of saturation ${S}_{r}^{M}$ (a concept that originated from the idea that the matric suction strengthens the inter-aggregate contacts through water menisci) appears to be a simplification of reality, since other physico-chemical phenomena also play a role at the inter-aggregate contact points. These model components should, therefore, be carefully reconsidered in future versions of the model.

Fig. 20

Predictions of the swelling pressure tests (left) and the oedometric swelling under constant load experiments at three differing initial dry densities (right) of the unsaturated compacted BCV bentonite

The model swelling characteristics were very well predicted (Fig. 20), as is also clear from Fig. 21, which shows the results of both types of experiment plotted on the same graph. The model, in line with the experimental data, predicted constant load swelling test results that were consistently lower in the pressure versus dry density graph than those of the constant volume swelling pressure tests.

Fig. 21

Comparison of the predictions of the swelling pressure tests and oedometric swelling under constant load experiments for unsaturated compacted BCV bentonite according to the model and the experiment

The reason for the predictive capability is demonstrated in Fig. 22 for selected tests as marked with a yellow circle in Fig. 21. Figure 22 (left) illustrates the evolution of the radial and axial stresses. They are obviously identical for the swelling pressure tests since the inherent anisotropy was not considered in the model. Conversely, with respect to the swelling under constant load test, the radial stresses developed substantially above the axial stress, which remained constant, defined by the boundary conditions of the experiment. Consequently, the swelling under constant load test proceeded at a high stress obliquity, i.e. the state boundary surface was reached much earlier than in the swelling pressure tests (see Fig. 22 (right), which graphically illustrates the value of the mean stress normalised by the mean stress at the state boundary surface for a given stress ratio). As discussed above, the swelling process is limited once the state boundary surface is reached, which explains the observed differences between the swelling pressure and the swelling under constant load results. Further, the swelling pressures in the graphs in Fig. 21 would be higher if the radial stress or mean stress were plotted rather than the vertical stress; nevertheless, this would still not have been sufficient to yield identical results for the two types of test.

Fig. 22

Comparison of the predictions of the selected swelling pressure tests and the oedometric swelling experiments for the constant load test. The tests selected are indicated by yellow circles in Fig. 21

Figure 23 illustrates a particularly interesting experimental data set for a model assessment conducted at the CTU involving the performance of oedometric swelling-loading–unloading tests applying various path combinations. The graphs indicate a trend line that runs through the experimentally obtained swelling pressure test results. It is clear that this trend line indicates the limit for the loading parts of the tests (thus, it coincides with the normal compression line), which is reasonably well predicted by the models even though the limit stress is somewhat overestimated. The model also predicted other important phenomena such as the high swelling potential of the sample at low load compared to the much lower swelling potential of the loaded sample. Moreover, the model relatively accurately predicted the significantly higher loading stiffness of the unsaturated sample compared to the saturated sample.

Fig. 23

Swelling-loading–unloading oedometric tests for various path combinations

In contrast to the experiment, the model predicted high swelling during the final unloading phase. In addition, it failed to distinguish between the swelling potential of the pre-loaded and unloaded samples when compared directly with the swelled sample. These experimental results were unexpected and more tests will be needed before the results can be confirmed.

The final tests to be predicted involved the swelling pressure testing of samples with three differing dry densities; the samples were 20 mm in height and were subjected to an elevated bottom pore water pressure of approx. 1 MPa with free drainage at the top. The tests were accompanied by the monitoring of the evolution of the pore water pressure over time as the water infiltrated into the samples. In addition, the experiment conducted at a dry density of 1600 kg/m³ was repeated several times; the samples were dismantled after various time periods and the distribution of the water content was investigated across the heights of the samples. In order to be able to predict this test, it was necessary to simulate the experiments as boundary value problems applying the finite element method. The models were processed in the CTU’s SIFEL finite element code [12]. The wall friction was not considered in the simulations.

The time evolution of the swelling pressure is shown in Fig. 24, which also shows the swelling pressure values as obtained using element test simulations (that is, simulations that assume constant state variable fields inside the sample, including constant suction and degree of saturation) of the swelling pressure tests. Consistent with Fig. 20, the swelling pressures were very well predicted. However, the model overpredicted the initial rate of the increase in the swelling pressure, which may have been due to having adopted a constant suction independent permeability.

Fig. 24

Experimental and predicted evolution of the swelling pressure in swelling pressure tests conducted with elevated bottom water pressures of approx. 1 MPa

The evolution of the water content in the sample at several time intervals following the commencement of the test is shown in Fig. 25 for the experiment with a dry density of 1597 kg/m³ (the experimental data was obtained for several samples with a target dry density of 1600 kg/m³). Although the water content was overpredicted at the start of the test, the trends concerning the water content distribution and evolution were predicted correctly.

Fig. 25

Water content distribution across a sample for several time intervals following the commencement of the test

It is interesting to note that the water content was not homogeneous across the sample at the 334 h time point, at which time the sample was practically fully saturated. In addition, Fig. 24 illustrates that the swelling pressures predicted by the finite element model are in fact lower than those predicted by the single element program (note that the bottom water pressure adds to the swelling pressure, the swelling pressure itself is thus directly measured only if water pressure is reduced to zero, which happened in 1306 kg/m³ and 1597 kg/m³ samples just before the end of the test). Both these observations can be explained with the aid of Fig. 26 which shows the void ratio and the degree of saturation distribution for the simulations from Fig. 25. It is clear that the sample had become fully saturated by the 334 h time point; however, the void ratio is not uniform across the sample, which implies the non-uniform distribution of the water content. The non-uniform distribution of the void ratio, which originated at the beginning of the test and did not change substantially thereafter (all the void ratio curves in Fig. 26 practically coincide), implies that the sample was not homogeneous. This indicates that adopting the single element approach to the swelling pressure calculation and model calibration, which has been adopted by most researchers in the field, is in fact not exactly correct.

Fig. 26

The void ratio and degree of saturation distribution across a sample for several time intervals following the start of the test

Aimed at the investigation of whether the observation described above of a non-uniform state within the samples tested for swelling pressure was caused by the elevated bottom water pressure of approx. 1 MPa, the simulations were repeated with a low water pressure of 1 kPa, the results of which are shown in Fig. 27. The lower saturation pressure resulted in a slower increase in the swelling pressure (Fig. 27 left), while the final swelling pressure was still lower than that calculated applying the element test (constant fields of state variables) assumption. The distribution of the void ratio (Fig. 27 right) was practically identical for the bottom water pressure.

Fig. 27

Swelling pressure experiment at a dry density of 1597 kg/m³ from Fig. 24 compared with an identical experiment with a bottom saturation pressure of 1 kPa

A summary of the model parameters adopted for the BCV simulations in this section is provided in Table 4. The simulations were performed with dry density dependent intrinsic permeabilities of 3 × 10^–20 m² for ρ_d = 1306 kg/m³, 1 × 10^–20 m² for ρ_d = 1508 kg/m³ and 8 × 10^–21 m² for ρ_d = 1597 kg/m³.

Table 4 Values of the parameters of the THM hypoplastic model for BCV bentonite

6 Conclusion

This article provides a complex H-M characterisation of BCV bentonite, which comprises the reference research material in the ongoing development of the Czech DGR concept. A complex data set was created for mathematical models of divalent bentonites. The BCV data set was created using the same batch of material, which is often not the case for bentonite datasets provided in the literature.

The laboratory results showed that the hydromechanical behaviour of BCV bentonite is highly dependent on the stress path taken. The state at which water is introduced is also very important in this respect. These factors indicate that the micro- and macrostructures of bentonite evolve on a continuous basis. This exerts a significant impact on the determination of the material properties considered in, and the development of mathematical models of the behaviour of bentonite.

It was demonstrated that the swelling pressures recorded applying the constant volume test attained higher values than the results of the oedometric swelling test at a constant load with deformation allowed. This was represented well by the constitutive model, which allowed for the interpretation of this observation. It was demonstrated that the main reason for the discrepancy comprised the radial stresses that developed during swelling in the constant load test under oedometric conditions, which differed from the stresses that developed during the constant volume swelling pressure test. Moreover, due to the comprehensive change in the void ratio, which is possible in the swelling under constant load test, the relative proportion of microstructural and macrostructural void ratios differs between the swelling pressure and swelling under constant load tests. Consequently, the results of the two tests do not follow an identical line when expressed in the form of a final dry density versus vertical stress graph. It was also demonstrated that the swelling pressure tests, although typically considered to be element tests (with a constant field of variables across the sample) when employed by researchers for the calibration of constitutive models, do not in fact constitute element tests. Due to the gradual progression of the wetting front from the wetting source, the void ratio is redistributed across the sample in a non-uniform manner (although the average sample void ratio is, from the test definition, constant). Consequently, the swelling pressures determined via the simulation of the test that applied the finite element method were lower than the swelling pressure predicted through the assumption of constant values of variables across the sample.

In summary, the experimental results indicate that BCV bentonite evinces all the hydro-mechanical characteristics that enable its use as a reference research material in the development of the Czech deep geological repository concept. These characteristics were well represented by the adopted hypoplastic constitutive model, thus proving its suitability for the numerical modelling required for the development of the Czech DGR concept.