1 Introduction

Extending the lifespan of civil engineering structures, including rockfall protection structures, is an important task in the construction industry. The damage caused by rockfalls has increased because of the deterioration of slopes due to age. The rise in heavy rainfall events due to climate change has led to larger sediment runoff frequencies on slope surfaces, which has resulted in more frequent rockfalls. Therefore, it is crucial to evaluate the performance of existing rockfall protection structures and increase their lifespan.

A granular cushion can be set on the slab of a rock shed to mitigate the direct damage caused by a rockfall. The typical materials of the granular cushion are sand and gravel, which have a high cushioning performance despite being natural mixtures. However, the collision between rocks and granular cushion is a complex phenomenon accompanied by large deformation and scattering, even for loading times of tens of milliseconds. Figure 1 shows that when a mass falls on a sand cushion, the maximum transmitted impact force, Ft, that acts on the slab of the rock shed through the cushion is larger than the impact force, Ff, that acts on the falling mass [6]. This phenomenon has been mentioned by other research groups [8, 11]. In the one-dimensional wave transmission problem for elastic waves, the stress is doubled at a fixed end boundary. However, the impact force ratio (Ft/Ff) has been experimentally observed to vary from 1 to 2; this has not yet been explained.

Fig. 1
figure 1

Relationship between maximum impact force of falling mass and maximum transmitted impact force [6]

Full size image

Several studies have shown that numerical analysis results can reproduce the impact force or penetration depth of a falling mass depending on the layer thickness of a cushioning material and falling conditions, e.g. [3, 4, 19, 20]. Our research group has previously examined the impact force propagation in a granular layer [10, 13]. We have shown that the discrete element method (DEM) [5] can reproduce not only the impact force but also the change in the density of a cushioning material after impact, which is observed in a large-scale falling-weight impact experiment [14]. However, the reason for the variation in the impact force ratio (Ft/Ff) from 1 to 2 has not yet been clearly explained. If the propagation mechanism of impact force, where Ft/Ff changes by a factor of 1 to 2, can be clarified, an economical method of cushioning layer installation and maintenance that appropriately controls the transmitted impact force acting on the structure and amount of penetration of the falling mass can be proposed by devising the selection of ground materials, their combination, and degree of compaction.

As a numerical study using the discrete element method, the impact of a falling mass on a coarse granular layer corresponding to rockfall events was investigated with a different falling mass and granular characteristics (falling mass size and shape, layer thickness, etc.) [1]. These simulations revealed the phenomena involved in energy exchanges between the falling mass and the granular layer. The energy propagation within the impacted granular layer and the bouncing of the falling mass were also investigated [27]. Over time, the energy propagation processes were investigated by analysing the spatial distribution of kinetic energy, elastic strain energy and energy dissipation within the granular layer. Finally, relations between the bouncing of the falling mass and the response of the granular layer were discussed.

A previous study has shown that the maximum value and duration of the impact force waveform of a falling mass are significant factors for generating the maximum transmitted impact force [12]. In addition, the shape of the collision surface of the falling mass strongly affects the impact force waveform. For example, the ascending part of the impact force waveform of a falling mass with a flat base is steeper than that of a falling mass with a rounded base [22]. Recent studies have investigated the influence of the shape of a falling mass on its impact force waveform [2, 23, 24]. However, the control factors for the generation of the impact force waveform have not been clarified. In a previous study, the impact posture and velocity of a falling mass were simulated, and correlations between the impact velocity and maximum impact force, between impact velocity and stress acting on a part of the bottom of the cushioning layer, and between the maximum impact force of the falling mass and stress acting on a part of the bottom of the cushioning layer were found. However, predicting the maximum impact force for an arbitrary shape of a falling mass is not possible only with the results obtained so far without DEM simulation. Further studies are needed to propose a calculation equation for the impact force waveform of an arbitrary falling mass shape.

These control factors were investigated in this study through a two-dimensional (2D) DEM analysis. In DEM simulations, a falling mass with a flat base and various diameters was used to simplify the impact condition between the falling mass and granular layer. Based on the simulation results, this study proposed a simple method of predicting the impact force waveform of the falling mass. The validity of the proposed method and control factors estimated through simulations was confirmed by comparing the results obtained using the proposed method with 2D DEM simulation results and experimental results.

2 DEM simulation model for rockfall impact on granular cushion

2.1 Contact model used in DEM

The contact model employed in this study was proposed by Cundall and Strack [5]. The contact model in the normal direction of the contact surface consisted of an elastic spring, dashpot, and no-tension divider, as shown in Fig. 2a, and that in the tangential direction of the contact surface consisted of an elastic spring, dashpot, slider, and no-tension divider, as shown in Fig. 2b. A linear spring was used in this study [5]. Figure 2c shows a magnified view of the noncircular particle model of the sand cushion model, where the centres of three circular particles with the same diameter form a regular triangle. Multiple circular particles are calculated as one rigid particle such that the relative displacement between each circular particle becomes zero. When noncircular particles are used, the shear strength of soil and the difference between the maximum and minimum void ratios of the sand cushion model increase, thereby improving soil compressibility and reproducibility. It is essential to express the sand cushioning material model as noncircular particles to reproduce the change in the sand density under impact loading. The viscous damping model used in DEM introduces normal and shear dashpots at each contact. The viscous damping force is proportional to the relative velocity between particles. The damping force is added to the contact force of which the normal and shear components. The numerical simulations presented in this paper are carried out with the commercial software Particle Flow Code in two dimensions (PFC2D).

Fig. 2
figure 2

Contact models: a normal direction, b tangential direction, and c rigid particle

Full size image

2.2 Analytical conditions

Figure 3a shows a schematic of the 2D DEM simulation model of a granular cushion with the x and y axes. This condition of granular cushions has been used in multiple large-scale falling-weight impact experiments, e.g. [7, 20]. Figure 3a shows that noncircular particles were arranged and fixed in a line, with no gap on the boundary at the bottom or either side of the sand cushion model. The granular cushion thickness, T, was set as 0.9, as recommended by the Rockfall Countermeasures Manual [6]. The cushion width, W, was set as 5.0 m because the effects of the lateral boundaries were negligible when the width was approximately four times the diameter of the falling mass [10]. The sand cushions were examined under the loosely packed condition, unless otherwise specified.

Fig. 3
figure 3

Schematic of the two-dimensional (2D) DEM simulation model: a model of granular cushion and falling mass; b mesh used in model

Full size image

As shown in Fig. 3a, the bottom of the falling mass was flat (type 1) or convex (type 2 and type 3). The falling mass of type 2 has been used in multiple large-scale falling-weight impact experiments, e.g. [7, 20]. The radius of curvature of this falling mass was 0.8 m, and the height of the convex part was 0.175 m. The spring coefficient, damping coefficient, and interparticle friction angle on the falling mass surface were set assigned same value as that used in the sand cushion parameters. In addition, the density of the elements that constituted the falling mass was adjusted according to the predetermined total mass [9, 25]. As shown in Fig. 3b, the granular cushion was divided into a mesh consisting of cells with dimensions of 0.1 m × 0.1 m for analysing the impact behaviour of granular materials. In this study, the uppermost cells in the mesh are excluded from analysis as they may be subject to variations in calculated stresses. This occurs because the number of cushioning layer particles in the uppermost mesh cells decreases as part of the mesh area is occupied by the falling mass immediately after the collision. The results for the area where the penetration depth exceeds 0.1 m are included for reference only as the number of cushioning particles in the observation mesh area decreases due to occupying part of the mesh area by the falling mass.

2.3 Method of calculating impact force and stress

The impact force of the falling mass was defined as the sum of the contact forces acting on the falling mass. The transmitted impact force, which is an important type of force incorporated into the design of structures such as rock sheds, was defined as the sum of the contact forces acting on the particles at the bottom boundary of the sand cushion. The maximum impact force was defined as the maximum value of the impact force waveform. The output time interval of the impact force was 0.5 ms, and the impact force waveform was calculated using the moving average process with a width of 1 ms.

The DEM provides the contact force between particles. However, stress is frequently used in the design and mechanical studies of rock sheds. Therefore, as shown in Fig. 4a, the stress acting on a particle was obtained using the divergence theorem to calculate the average contact force acting on each particle [15, 16, 18]. The mean principal stress, \({\sigma }_{ij}^{(p)}\), of a particle is calculated as follows:

$$ \sigma_{ij}^{\left( p \right)} = - \frac{1}{{V^{\left( p \right) } }}\mathop \sum \limits_{{N_{c} }} x_{i}^{\left( c \right)} F_{j}^{\left( c \right)} $$
Fig. 4
figure 4

Region for calculation of stress: a particle; b microregion

Full size image

where \({V}^{(p)}\) is the area (volume) of the particle, \({N}_{c}\) is the number of contact points, \({x}_{i}^{(c)}\) is the location of a contact point, and \({F}_{j}^{(c)}\) is the contact force.

Figure 4b shows the magnified view of a cell (microregion) in the mesh. The stress in the microregion was obtained by calculating the average stress acting on the particles in the microregion [18]. The average stress in the microregion (mesh) is given by

$$ \sigma_{ij}^{\left( r \right)} = \frac{1}{{V^{\left( r \right) } }}\mathop \sum \limits_{{N_{p} }} \sigma_{ij}^{\left( p \right)} V^{\left( p \right)} $$

where \({V}^{(r)}\) is the area (volume) of the region and \({N}_{p}\) is the number of particles in the region.

2.4 Analytical parameters

The 2D DEM simulation parameters are listed in Table 1.

Table 1 Two-dimensional (2D) DEM simulation parameters used in sand cushion model
Full size table

The maximum impact force decreased with the size of the particles that constituted the sand cushion, i.e. the relative falling mass diameter (Df/Dmax) increased, where Df is the diameter of the falling mass, and Dmax is the maximum particle diameter. The maximum impact force converged to a constant value when Df/Dmax was more than 10–20. Thus, the sand particle size can be set to be larger than the actual size when simulating the impact force on the sand cushion. Particle sizes were generated with a certain probability between Dmax and minimum particle diameter (Dmin).

In a previous study [14], the maximum and minimum void ratio of the cushioning layer were e = 0.23 and e = 0.13, respectively, obtained by adjusting the interparticle friction angle during packing under the same particle parameters and cushioning layer size as in the present analysis. Consequently, the unit volumetric mass of the unit depth corresponding to the maximum void ratio in this 2D DEM simulation model was γd = 2145 kg/m3.

A critical damping value of h = 1.0 is frequently used to ensure the stability of numerical calculations. This value may correspond to the state in which the plastic deformation in a contact region or the energy loss due to the breakage of the corner region of a complex particle is simulated using a circular particle.

Rowe [21] measured approximately 10 types of interparticle friction angles and revealed that this angle depends on the particle size and has a range of 22°–30°. Therefore, an interparticle friction coefficient of tanϕμ = 0.466 (ϕμ = 25°) was used in this study.

The spring coefficient was set such that the stress propagation velocity in the DEM simulation was the same as that in an actual sand cushion. As shown in Fig. 5, the stress propagation velocity, Vσ, was obtained by dividing the interval, tp, between the time of impact of the mass on the sand cushion and the time when transmitted impact force reached 1 kN for the initial thickness of the sand cushion layer, T (1 kN was the threshold at which transmitted impact force clearly increased). In a falling-weight impact experiment [7], the stress propagation velocity in a loosely packed sand cushion with a layer thickness of T = 0.9 m was approximately 100 m/s. When a spring coefficient of approximately 2 × 107 N/m was used, the stress propagation velocity in the 2D DEM simulation was approximately 100 m/s.

Fig. 5
figure 5

Diagram of stress wave velocity

Full size image

The time step in the simulation was Δt = 2.0 × 10 −5 s, which completely satisfied the Courant–Friedrichs–Lewy condition [17].

The methods used to determine the parameters are described in a previous paper [14]. The comparison of the parameters used in this simulation with those in the previous study [1] follows. The density of the particles and the friction coefficient between the particles are approximately the same. The ratio of the radius of the falling mass to the average radius of the particles constituting the granular layer in the present simulation is about 33, which is classified as the case where the falling mass size is sufficiently large in relation to the diameter of the particles constituting the cushioning layer that is the third impact regime in the previous study. Furthermore, the ratio corresponds to the condition where the falling mass bounces due to its interaction with a thin granular layer. Moreover, since the present simulation models sand with a finer grain layer than in the previous study, the particle size relative to the layer thickness is smaller than in the previous study, and the stress wave velocity is also smaller than that in the previous study.

The validity of this 2D DEM simulation model was confirmed by comparison with large-scale impact experimental results of three-dimensional (3D) real phenomena, the following conclusions being obtained [14]. In the experiment, a falling mass of diameter Df 1.0 m and weight M f 5000 kg was dropped onto a sand cushion (of width and depth 5.0 × 5.0 m, and layer thicknesses T 0.3, 0.5, 0.7, and 0.9 m) from a height H of 1.0–20.0 m. In the large-scale impact experiment, both the waveforms of the impact force of the falling mass and the transmitted impact force consisted of two half-sine waveforms. In the experiment, the maximum impact force and momentum (mv) of the first wave were more than twice as large as those of the second wave, so the first wave being the primary wave caused by the falling mass impact. In the 2D DEM simulation results, the first waves of the impact forces were mostly reproduced. In addition, the penetration depth of the falling mass was mostly reproduced until the end of the first wave. However, the simulation results did not reproduce the impact force and penetration depth corresponding to the time region of the second wave. The possible reasons why the first wave could be reproduced in the simulations, but the second wave could not be reproduced are as follows: the movement of soil particles was restricted unlike in the real world as the simulation was limited to two dimensions, the compression trend immediately below the falling mass being larger in the simulations. Therefore, even after the impact force of the falling mass reached its maximum, the duration was slightly longer, and a rebound tendency was observed.

Although the 2D DEM simulation did not completely reproduce the results of large-scale 3D impact experiments, the simulation reproduced the maximum value of the impact force of falling mass and the transmitted impact force with a precision of approximately ± 20% under different cushioning layer thicknesses and falling heights. In addition, the simulation reproduced the impact force and penetration depth corresponding to the time region of the first wave which is the primary wave of this impact phenomenon. Consequently, a 2D DEM simulation model was used in this study.

3 Influence of diameters of falling mass on stress of granular assemblies

3.1 Conditions of DEM simulation

DEM simulations were performed to investigate the control factors for the generation of the impact force waveform of the falling mass. A falling mass of type 1 with various diameters was used to simplify the impact condition between the falling mass and granular layer. The diameters of the falling mass, Df, were set as 0.5, 1.0, 1.5, and 2.0 m. The weight of the falling mass, W, was set as 3000 kg, and the free-fall height, H, as 30.0 m. The cushion conditions are described in Sect. 2.

3.2 Results of DEM simulation

Figure 6 shows the simulation results obtained for different values of Df. This figure shows the time history of the impact force (Ff), penetration depth (S), velocity (Vf) of the falling mass, and the mean principal stress (σm) of particles in the observation region and impact stress (σf) of the falling mass (the impact force of the falling mass divided by the diameter of the falling mass). At a certain time, as Df increased, the penetration depth, velocity, the mean principal stress, and the impact stress of the falling mass decreased.

Fig. 6
figure 6

Time history of response waveforms: a impact force of falling mass; b penetration depth; c velocity of falling mass; d mean principal stress; e impact stress of falling mass

Full size image

Figure 7 shows the velocity of the falling mass and the mean principal stress, σm, of particles at a penetration depth of S = 0.1 m. A linear relationship between the loading velocity and σm was observed. Figure 7 also shows the velocity of the falling mass and the impact stress of the falling mass σf, at a penetration depth of S = 0.09, 0.10, 0.11 m. A linear relationship between the loading velocity and σm is also observed. In the case of the flat bottom falling mass, such as type 1, if the void ratio of the granular assemblies just below the falling mass is assumed to be uniform, then Fig. 7 indicates that it is possible to define the value of σ immediately below the falling mass using the loading velocity, Vf. It is also possible to obtain the impact force, Ff, by multiplying σ and the contact area between the falling mass and granular cushion. The above assumption does not hold if the diameter of the falling mass is not sufficiently large compared to the sand particles.

Fig. 7
figure 7

Mean principal stress of particles and impact stress of falling mass vs. velocity of falling mass

Full size image

4 Influence of loading velocity of falling mass on impact force of falling mass

4.1 Conditions of DEM simulation

This section describes the simulations performed to examine the dependence of the loading velocity on the impact force of the falling mass. Two types of simulations were performed using the falling mass of type 2 with Df = 1.0 m. In the first type, the falling mass was continuously cast onto a sand cushion at a constant loading velocity V0 = 2.0, 4.0, 6.0, 8.0, 10.0, 12.0, 14.0, 16.0, 18.0, and 19.8 m/s. In the second type, the free-fall impact of the falling mass on the sand cushion was simulated. The weight of the falling mass (W) and the free-fall height (H) were set as 2000 kg and 20.0 m, respectively. The cushion conditions were the same as those described in Sect. 2.

4.2 Results of DEM simulation

Figure 8 shows the simulation results. The solid lines represent the relationship between the loading force and the penetration depth at a constant loading velocity [13]. The loading force rapidly increased immediately after collision and then remained almost constant. The penetration region where the loading force increased (0 ≤ S ≤ 0.15 m) was almost consistent with the height of the convex bottom of the collision mass (0.175 m). The loading force at an arbitrary penetration depth increased with the loading velocity until the contact area reached the maximum value. In the region of the impact velocity of the falling mass (0–20 m/s) for which the numerical analysis was performed in this paper, there was a univocal relationship between the loading force and loading velocity.

Fig. 8
figure 8

Loading force and loading velocity vs. penetration depth: a loading force; b loading velocity

Full size image

The oblique lines in Fig. 8a indicate another region in which the loading force increased. The cause of the increase was examined on the basis of the stress propagation behaviour in the sand cushion at V0 = 16.0 m/s. A reflected wave from the bottom of the sand cushion propagated to the collision mass close to S = 0.35 m. The loading force increased again at this point. Similar tendencies were observed at other loading velocities. A similar phenomenon has already been described for two-dimensional [1] and three-dimensional granular media [27]. This indicate that the reflected wave acted on the collision mass in the region depicted by the oblique lines.

The solid line with dots in Fig. 8 represents the relationship between the impact force of the falling mass and penetration depth under free-fall impact. Figure 8b shows that the velocity of the falling mass decreased as the penetration depth increased. Until approximately S = 0.2 m, the loading force waveform in the case of free-fall impact was formed following the curve of the loading force vs. the penetration depth obtained at a constant loading velocity. This result shows that the impact force of the falling mass depends only on the loading velocity for an arbitrary penetration depth, regardless of the loading history.

5 Simple method for predicting impact force of falling mass

5.1 Method of calculating impact force waveform

This section proposes a simple method of obtaining the impact force waveform of a falling mass using the concept of dynamic stress, based on the simulation results described in Sects. 3 and 4.

First, we provide a simple explanation for the impact stress induced by a one-dimensional wave equation using an example of a stress wave created by impact with an elastic rod. As shown in Fig. 9, we assume that a rigid body collides with the left side of an elastic rod at a constant penetration rate, v, creating a compression λ, which is the deformation due to a contact surface moving at velocity v (m/s) at time t. During time t, the stress wave propagates through the elastic rod with velocity c (m/s), resulting in compression deformation, which is given by ct. The change in momentum due to impact force is expressed as

$$ F = \frac{d}{dt}\left( {\rho Actv} \right) = \rho Acv $$
Fig. 9
figure 9

Stress wave generated by the collision of a rigid body with a one-dimensional elastic rod

Full size image

where F is impact force, ρ is the density of the elastic rod (kg/m3), and A is the cross-sectional area of the elastic rod (m2). Stress is expressed as follows:

$$ \sigma = \frac{F}{A} = \frac{\rho Acv}{A} = \rho cv $$

The stress, σ, generated in this compression range is expressed as ρcv (Pa), which can be derived from the one-dimensional wave equation. However, this stress definition is only valid under the condition that the velocity of the rigid body is constant during a duration of time t. Therefore, based on the results obtained in the simulations of Figs. 6, 7, and 8 in Sect. 3, we propose a method to calculate the time history waveform of the impact force of the falling mass, assuming that the equation for the relevant stress proportional to the velocity of the rigid body is valid even when the velocity of the rigid body decreases.

We assumed ρ as the density of the cushioning material (γd, kg/m3), c as the stress propagation velocity (Vσ, m/s), and v as the velocity of the falling mass (Vf, m/s). Stress was calculated using the weight and velocity of the falling mass, contact area of the falling mass expressed using a penetration function, and contact angle of the falling mass.

Figure 10 shows the flow chart of the calculation of the impact force of the falling mass. The time interval for each calculation step was δt = 0.05 ms. In step (i), the velocity of the falling mass, v(i), was obtained from the momentum, I(i − 1), of the falling mass at the (i − 1)th step. v(i) was used to calculated stress σ(i), penetration depth S(i), area of horizontal projection A’(i), which is in consideration of the contact angle of the falling mass. The penetration depth S is the vertical distance from the Initial cushion surface to the bottom of the falling mass. Then, the impact force of the falling mass F (i) was obtained from the area of horizontal projection, A’(i), which was subjected to stress σ (i). Furthermore, we obtained the impulse on the falling mass at time increments δt and F(i). Then, the momentum, I(i), of the falling mass was updated. The calculations consisted of 2000 steps (t = 100 ms). As shown in Fig. 11, the contact angle, θ, was defined as the tangential gradient at penetration depth S(i). As shown in Fig. 12, the contact angle was assumed to make an angle θ with the horizontal plane. In addition, it was assumed that only normal force acted on the contact surface (a) and only the upward vertical force was the impact force of the falling mass (b). In this manner, as shown in Fig. 12, the vertically upward response force corresponding to the inclination angle of contact surface was calculated. Figure 13 shows the calculation results of A(i) and A’(i) for the type 2 falling mass. In view of the application of this calculation method to large-scale impact experiments of real world 3D phenomena in Sect. 5.3, Fig. 13 also shows an example of the calculation of the horizontal projection area of the 3D falling mass used in the experiments.

Fig. 10
figure 10

Flow chart of method for calculating the impact force of a falling mass

Full size image
Fig. 11
figure 11

Diagram of the contact angle of a falling mass

Full size image
Fig. 12
figure 12

Diagram of the forces acting on a falling mass

Full size image
Fig. 13
figure 13

Relationship between area of horizontal projection and penetration depth

Full size image

5.2 DEM simulations for validation of the proposed method

5.2.1 Simulation conditions

The impact force of the falling mass was calculated using DEM simulations and the proposed method described in Sect. 5.1. The cushion conditions used in the simulation are described in Sect. 2. The specifications of the sand cushion were as follows: loose packing with density γd = 2145 kg/m3, which is a two-dimensional area multiplied by a depth of one metre, and stress propagation velocity Vσ = 98.3 m/s. The diameter (Df) and weight (Mf) of the falling mass were 1.0 m and 2000 kg, respectively. The falling height was H = 40.0 m. (The collision velocity was set as the terminal velocity, Vf = 28.0 m/s, as listed in the Rockfall Countermeasures Manual [6].) The falling masses of type 1, type 2, and type 3 were considered.

However, as the square falling mass in the simulation was modelled by rigidly connecting circular particles, the contact area was increased according to the curvature of the circle up to a penetration depth of 0.025 m; thereafter, a constant contact area was applied.

5.2.2 Comparison of the proposed method and simulation results

Figure 14 shows the impact force of the falling mass obtained using the proposed method and DEM simulations. The waveforms of the first wave, i.e. the main wave, were accurately estimated for the impact forces. A second wave was observed in the DEM simulation results; this wave was caused by the impact of the wave reflected from the base of the cushioning material [10]. The second wave was not observed in the results of the proposed method because the impact of the reflected stress wave was not considered by the proposed method.

Fig. 14
figure 14

Impact force of falling mass obtained using DEM simulations and analytical method: a type 1; b type 2; c type 3

Full size image

5.3 Large-scale cushion impact experiments for validation of the proposed method

5.3.1 Experimental conditions

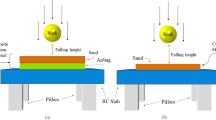
A large-scale impact experiment was performed using the experimental apparatus shown in Fig. 15 [20]. Yamaguchi et al. presented only certain results of the large-scale impact experiment, whereas we reproduced the impact experiment using the proposed method. Two falling masses were used in the experiment; the shapes of these masses are shown in Fig. 16. Sand and gravel were used as cushioning materials. Table 2 lists the experimental conditions. Figure 17 shows the relationship between the relative density and stress propagation velocity and their regression lines. The modified stress wave velocity, Vσmod, was calculated from the regression lines and relative density measured in the experiment. Vσmod was used for calculations in the proposed method.

Table 2 Experimental conditions
Full size table
Fig. 15
figure 15

Experimental apparatus with steel reinforced concrete

Full size image
Fig. 16
figure 16

Shapes of falling mass used in the experiments

Full size image
Fig. 17
figure 17

Relationship between the initial relative density of the granular cushion and stress wave velocity

Full size image
Fig. 18
figure 18

Results obtained from impact experiment and analytical method

Full size image
Fig. 19
figure 19

Maximum impact force obtained using analytical method vs. maximum impact force obtained in the experiment

Full size image

5.3.2 Comparison of the proposed method and experimental results

Figure 18 shows the results obtained from the impact experiment and the proposed method. The first wave (main wave) of the waveform was correctly estimated in almost all cases. Figure 19 shows the maximum impact force obtained using the proposed method and impact experiment. The proposed method reproduced the maximum impact force and the outline of the impact force waveform for different cushioning materials, relative densities, weights of the falling mass, and falling heights. These results confirm the validity of the proposed algorithm, suggesting that the stress of particles immediately below the falling mass is proportional to the loading velocity, and the impact force of the falling mass is likely to be expressed as the product of the stress of particles and the contact area considering the contact angle.

However, there are two problems in using the proposed method. The first is similar to the observations made from Fig. 14, i.e. the second wave of the waveform of the impact force of the falling mass cannot be reproduced. The second is that the rising gradient of the waveforms obtained in the experiment is smaller than that using the proposed method in Fig. 18. The reason for this discrepancy is assumed to be as follows: as sand spreads around the falling mass at the time of collision with the cushioning material, the contact area between the cushioning material and falling mass decreases in the actual phenomenon. In the two-dimensional DEM simulation, the movement of soil particles associated with the penetration of the falling mass is limited to two directions. Thus, unlike in the actual phenomenon, the cushioning material is deformed to a denser state. This phenomenon can be explained by the evolution of chain forces in the granular layer [1, 26]. The displacement of particles belonging to a chain force may reduce the force conveyed and occur in different directions in the 3D case. Consequently, strong chain forces are more stable in 2D than in 3D, resulting in a higher stiffness. This likely suppresses the differences in the rising gradient in the impact waveform in the comparison with two-dimensional DEM simulation, as shown in Fig. 14. In three-dimensional penetration behaviour, the movement of soil particles in the depth direction is considered. Therefore, it is presumed that gaps may form between the falling mass and cushioning material, thereby reducing the rising gradient of the impact waveform.

6 Conclusion

We investigated the control factors for the generation of the impact force waveform of a falling mass through DEM analysis. On the basis of DEM simulation results, a simple method for predicting the impact force waveform of a falling mass was proposed. The results can be summarised as follows:

  1. 1)

    At a certain weight and falling height of the falling mass with a flat base, the impact force of the falling mass and stress of particles increased with the diameter of the falling mass. In addition, the penetration depth and velocity of the falling mass decreased.

  2. 2)

    The stress of particles immediately below the falling mass was proportional to the loading velocity of the falling mass.

  3. 3)

    The impact force of the falling mass depended only on the loading rate for an arbitrary penetration depth, regardless of the loading history.

  4. 4)

    Based on the simulation results, we proposed a simple method for calculating the impact force waveform of the falling mass. In the proposed method, stress was proportional to the loading velocity, stress propagation velocity of cushioning layer, and the density. Additionally, the impact force could be obtained by multiplying particle stress and the contact area between the falling mass and granular cushion considering the contact angle.

  5. 5)

    The proposed method could reproduce the maximum value of the impact force and the outline of the impact force waveform even for different cushion materials, relative densities, weights of the falling mass, and falling heights.

The results of this study can help elucidate the mechanism of the generation of the impact force waveform of a falling mass. This can contribute to the rational design and performance evaluation of a rock shed intended for rockfall protection and the development of a new rational countermeasure. Furthermore, this study provides basic knowledge related to the soil deformation mechanism under high-speed loading.