Mechanical properties and stress–dilatancy relationships of unsaturated soil under various cyclic loading conditions

Abstract

Most studies investigating the effect of cyclic loading on soil properties have been conducted for saturated soils. Embankments such as fill dams, roads and railways are usually constructed by unsaturated geo-materials and retained under unsaturated conditions during their in-service periods. Then when the stabilities of the embankments against dynamic motions such as earthquakes and traffic loads are evaluated, it is necessary to account for the cyclic properties of unsaturated soils. However, there are few studies investigating mechanical properties of unsaturated soils under cyclic loadings. There are two objectives in this paper. One objective is to investigate cyclic properties of an unsaturated silt under various cyclic loading conditions, while the other is to investigate the stress–dilatancy relationships; the relation of plastic strain increment ratio,  − dε^p_v/dγ^p, versus stress ratio, q/p′; and to derive the plastic potential function of the unsaturated silt. Cyclic triaxial compression tests under various loading conditions were performed using the unsaturated silt. The material used is an artificial silty soil named DL clay. It was found from the series of the tests that the stiffness of the soil increased with an increase in suction and the number of cyclic loadings. The total volume reductions in the specimens decreased with an increase in suction. When the numbers of cyclic loadings and suction increased, the dilation also increased. Each unique stress–dilatancy relationship could be found in both loading and unloading processes. The relationships were similar to those of saturated soils under cyclic loadings. A unique plastic potential function could also be derived from the stress–dilatancy relationships.

1 Introduction

It is necessary to predict permanent deformations when the stability of fill dams for level 2 earthquakes is addressed. The level 2 earthquakes, defined as motions with huge magnitude but low frequency, should be incorporated in the performance-based design in which the performance of embankments may normally be evaluated by the permanent deformation of embankments. Moreover, the long-term stability of embankments for roads and railways under traffic loads has also been one of the most important research works in modern geotechnical engineering. Soil structures such as embankments are generally constructed by compacting geo-materials (soils and rocks). These materials usually exist under unsaturated conditions. In order to predict its permanent deformation, mechanical properties of unsaturated soils under cyclic loadings should be known. Especially for fill dams, while some parts of the embankments in upstream exist under nearly saturated condition, the others in downstream exist in unsaturated condition. Therefore, the seismic behavior of the embankments may be very complex, and unexpected damages may be induced during a level 2 earthquake due to different seismic properties between saturated and unsaturated soils.

When a saturated soil was subjected to monotonic loading under a drained condition, Rowe [21] experimentally found that there was a unique relationship between the stress ratio and the dilatancy ratio, namely the strain increment ratio, as is usually called the stress–dilatancy relationship. Many studies have used triaxial, plane strain and torsional shear loading tests for saturated soils to obtain the stress–dilatancy relationships [15, 16, 22, 23, 29, etc.].

Some experimental cyclic loading tests were conducted to obtain the stress–dilatancy relationship under cyclic loading for saturated soils. Pradhan et al. [19] performed various cyclic tests using saturated Toyoura sand. A unique stress–dilatancy relationship during loading and unloading was obtained in terms of the ratio of the plastic shear strain increment dγ^p and the plastic volumetric strain increment dε^p_v as − dε^p_v/dγ^p. The relationship was expressed by two lines corresponding to a loading line and an unloading line, respectively. Pradhan and Tatsuoka [20] modified the stress–dilatancy relationships on the basis of (1) the sliding block theory, (2) the Rowe’s theory, (3) the Roscoe’s energy dissipation theory and (4) the Taylor’s energy dissipation theory to extend them to cyclic loading conditions. De Silva et al. [3] experimentally investigated the relationships during cyclic torsional shear loading for saturated Toyoura sand and then proposed a bilinear stress–dilatancy model for subsequent loadings, except for the first loadings. Moreover, many studies have been conducted for the cyclic loading tests of saturated soils to obtain stress–dilatancy relationships [25, 26, 32, etc.].

For unsaturated soils, the potential for liquefaction has been investigated [e.g., 30, 31, 33]. Kimoto et al. [7] conducted cyclic triaxial tests for unsaturated sandy soil under drained and undrained conditions to investigate the effects of the initial suction, the confining pressure and the degree of compaction. The higher initial suction was provided, and the larger deviator stress, the smaller volumetric strain and axial strain were generated for the cyclic loading under drained condition.

Although investigating the behavior of unsaturated soils under cyclic loading is important for clarifying the mechanism of embankments’ permanent deformation as mentioned above, few reports have been published especially concerned with stress–dilatancy relationships for unsaturated soils under cyclic loading. Khalili et al. [6], Kohgo et al. [9, 12] and Oka et al. [17] have proposed elastoplastic models for unsaturated soils based on the cyclic plasticity theory, but so as to accomplish more accurate estimations especially of the cyclic stress–strain relationships, the stress–dilatancy relationships have to be investigated. Therefore, in this study, several series of cyclic triaxial shear loading tests were conducted to investigate mechanical properties and stress–dilatancy relationships under cyclic loadings for an unsaturated silt. A unique plastic potential function was derived from the stress–dilatancy relationships of the unsaturated silt.

2 Apparatus, material and testing procedures

The procedure of the experimental tests is presented in details below. A cyclic triaxial compression apparatus designed for unsaturated soils was used in this study. This apparatus had a ceramic disk, whose air entry value was 100 kPa, installed in the pedestal and a water-repellent filter installed in the top cap. These filters enable pore water pressure u_w and pore air pressure u_a to be separately measured and applied from the bottom and the top, respectively. Three pressure transducers were installed to measure the cell pressure, pore air pressure and pore water pressure. Suction can be applied to triaxial specimens by using the axis translation technique, i.e., pore air pressure was controlled to apply the assumed suction value, whereas the pore water pressure was maintained constant at atmospheric pressure with the burette in order not to occur cavitation. The apparatus adopting a double-cell system: inner and outer cells, was used in order to measure volume change of a specimen. Both cells were filled with de-aired water. The volume change was estimated by measuring the water level in the inner cell with a gap sensor mounted in the inner cell. This gap sensor can detect the water level changes of the inner cell upward and downward within 9 mm. This gap sensor was used for measuring the outer volume change of the specimens. The volume changed was calculated by multiplying the detected water level changed and the effective cross-sectional area, 29.29 cm², so its capacity is 26.36 cm³. The accuracy of the volume change measurement with the gap sensor had been carefully calibrated before the experiment and it was confirmed fully accurate by measuring the amount of water flowing in or out of the saturated soil specimen (CA00), as shown in Fig. 1. The volume change measured by the gap sensor was almost linear with the drainage amount of the saturated soil in all the loading and unloading cycles. An axial load cell (LP200) was installed above the top cap connected with the axis rod so that compression (loading) and extension (unloading) were applicable. This axial load cell has its capacity of the axial load of 2 kN for compression and extension under constant shearing rate. A LVDT displacement transducer was used for measuring the vertical displacement of the specimens by the 50 mm/10,000 με.

Fig. 1

Relationship of volume change measured by gap sensor and drainage amount

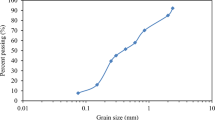
A silty soil named DL clay was used as the test material under a series of drained cyclic triaxial shear loading tests. The grading curve and physical properties of DL clay are shown in Fig. 2 and Table 1. Sand, silt and clay contents are 0.1, 90.4 and 9.5%, respectively. The soil was non-plastic silt. The soil–water retention curve (SWRC) of DL clay at the end of consolidation, which was conducted under prescribed constant confining pressures and suction values, is shown in Fig. 3 [11]. The tangential model [10, 13] was used to express the soil water retention characteristics. It is found from Fig. 3 that the air entry suction of the silt was around 10 kPa.

Fig. 2

Grading curve of DL clay

Table 1 Physical properties of specimen (DL clay)

Fig. 3

Soil water retention curve of DL clay after consolidation

The sample was adjusted 17% of the water content and to be left for 24 h or more to reach the equilibrium state. Each soil specimen was compacted with ρ_d = 1.3 g/cm³ and the degree of compaction [= ρ_d/ρ_dmax; ρ_d: dry density, ρ_dmax: the maximum dry density obtained from the standard compaction test (JGS 0711-2009)] = 85.5%. The specimens were compacted on the dry side of the optimum water content under loose conditions in order to make them deform not just in shear band but homogeneously. The compaction was carried out in five equal layers by using a push rod in the split mold with the dimension of 5 cm in diameter and 10 cm in height. All the specimens were compacted in the same way to get the same initial conditions in every test. The initial conditions of the specimens and the applied suction are summarized in Table 2. The capital characters in the second column of this table represent the loading condition, and the number means the applied suction value, for example, CS60 means CS series and its applied suction was 60 kPa. The tests were performed under the single net confining pressure σ_3net = σ₃ – u_a = 100 kPa and five different values of the constant suction s = 0, 10, 30, 60 and 90 kPa. At first, the suction was increased to the prescribed value and then the net confining pressure was raised up to 100 kPa. After the prescribed pressures have been reached, the consolidation process, in which both suction and net stress consolidations are included, was continued for at least 24 h. This consolidated time was confirmed enough by investigating the relationship between time and amounts of drainage according to JGS 0522-2009. This consolidation time was also employed by Zhou et al. [34], where a similar silty soil was used. During the consolidation process, the drainage water and volume change of the specimen were measured. Water absorption into specimens occurred when the applied suction was lower than the initial suction, s = 20 kPa. However, when the specimens were tested under the suction which were higher than the initial suction, s = 20 kPa, the specimens expelled water.

Table 2 Initial conditions of specimens and applied suction

After the consolidation, the shear process was progressed. During the shear processes, the cyclic loadings were conducted under three different stress conditions: constant stress ratio (CS series), constant axial strain (CA series) and increased shear strain (SS series). In the CS series, the amplitude of the stress ratio ($q/p^{\prime}$) during the cyclic loadings was 0.7 for compression and 1.0 for extension, respectively. In the CA series, the amplitude of the axial strain during the cyclic loadings was set to ± 1.5%, while the shear strain was increased progressively in an order of ± 0.5, 1.0, 2.0 and 4.0% in the SS series. The details of the experimental conditions are summarized in Table 3. The back pressure of 200 kPa was applied only to the saturated specimens. In all the tests, the cyclic loadings were applied under a constant shear axial strain rate of 0.05%/min. Oka et al. [18] also used the same shear axial strain rate of 0.05%/min for these unsaturated DL clay soil specimens under drained triaxial compression tests. After the cyclic shear loading was finished, the shearing continued until 15% of the axial strain in all the tests. During the shearing process, the net confining pressure and the suction values were kept constant.

Table 3 Experimental conditions

3 Test results

3.1 Evaluation of stress and strain

In this paper, the stresses and strains are defined positive for compression. There are some equations concerned with effective stresses of unsaturated soils. Bishop’s equation [2] is the most popular, and the equation in which the parameter χ in Bishop’s equation replaced S_r may be convenient and useful [4]. Here we used the effective stress equation proposed by Kohgo et al. [8, 14]. Kohgo et al. [8] discussed at first retentive situations of pore water and defined three saturation conditions: insular air, fuzzy and pendular saturations, in real soils. The pore water pressures act as neutral stresses in the pores whose situations are like the insular air saturation (the first suction effect), while pore water pressures may induce capillary forces in the pores whose situations are like the pendular saturation (the second suction effect).

The first effect is the same as one used in Terzaghi’s definition of effective stress [28]. The capillary forces confine the relative movements between soil particle, namely they induce a kind of internal confinement. As all the internal confinements disappear at the critical state [1, 5], the first suction effect may only remain there. Then the first suction effect may be identified. Equations (1) to (5) are introduced based on the approach described above.

$$\sigma^{\prime} = \sigma - u_{{\text{eq}}} ,$$

(1)

$$u_{{\text{eq}}} = u_{\text{a}} - s \qquad \left( {s \le s_{\text{e}} } \right),$$

(2)

$$u_{{\text{eq}}} = u_{\text{a}} - \left( {s_{\text{e}} + \frac{{a_{\text{e}} s^{*}}}{{s^{*} + a_{\text{e}} }}} \right)\quad \left({s > s_{\text{e}} } \right),$$

(3)

$$s^{*} = \left\langle {s - s_{\text{e}} } \right\rangle ,$$

(4)

$$s = u_{\text{a}} - u_{\text{w}} ,$$

(5)

where $\sigma^{\prime}$ is the effective stress, $\sigma$ is the total stress, u_eq is the equivalent pore pressure, a_e is the material parameter, s* is the effective suction, s_e is the air entry suction, s is the matric suction, u_a is the pore air pressure, u_w is the pore water pressure and the brackets <> denote the operation $\left\langle z \right\rangle = 0$ at z < 0 and $\left\langle z \right\rangle = z$ at $z \ge 0$.

Here, incremental Eq. (6), which is similar to the Bishop’s effective stress equation [2], may be derived from Eqs. (1) to (5), and where parameter χ is a function of effective suction s*.

$${\text{d}}\sigma^{\prime} = {\text{d}}\sigma - {\text{d}}u_{a}+ \chi\, {\text{d}}s$$

(6)

$$\chi = \left( {\frac{{a_{\text{e}} }}{{s^{*} + a_{\text{e}} }}} \right)^{2}$$

(7)

Stress invariants are the mean effective principal stress $p^{\prime} = \left( {\sigma^{\prime}_{\text{a}} + 2\sigma^{\prime}_{\text{r}} } \right)/3$ and the deviator stress q = $\left( {\sigma^{\prime}_{\text{a}} - \sigma^{\prime}_{\text{r}} } \right)$, where $\sigma^{\prime}_{\text{a}}$ and $\sigma^{\prime}_{\text{r}}$ are the effective axial stress and the effective radial stress, respectively. They are evaluated by Eqs. (1) to (5). The volumetric and shear strains were identified by $\varepsilon_{\text{v}} = \varepsilon_{\text{a}} + 2\varepsilon_{\text{r}}$ and $\gamma = \varepsilon_{\text{a}} - \varepsilon_{\text{r}}$, where $\varepsilon_{\text{a}}$ and $\varepsilon_{\text{r}}$ are the axial and radial strain, respectively.

The dilatancy ratio ($- {\text{d}}\varepsilon_{\text{v}}^{\text{p}} / {\text{d}}\gamma^{\text{p}}$) is defined as the ratio of the plastic volumetric strain increment to the plastic shear strain increment in this study. The volumetric strain increment dε_v consists of the plastic volumetric strain increment dε^p_v and the elastic volumetric strain increment dε^e_v. The plastic volumetric strain increment can be evaluated as follows,

$${\text{d}}\varepsilon_{\text{v}}^{\text{p}} = {\text{d}}\varepsilon_{\text{v}} - {\text{d}}\varepsilon_{\text{v}}^{\text{e}} ,$$

(8)

$${\text{d}}\varepsilon_{\text{v}}^{\text{e}} = \frac{{\kappa \, {\text{d}}p^{\prime}}}{{2.3\left( {1 + e_{\text{c}} } \right)p^{\prime}}},$$

(9)

where $\kappa$ is the slope of $e - \ln p^{\prime}$ curve during unloading and e_c is the void ratio after consolidation.

The plastic shear strain increment can be evaluated by

$${\text{d}}\gamma^{\text{p}} = \frac{3}{2}{\text{d}}\varepsilon_{\text{s}}^{\text{p}} = {\text{d}}\gamma - {\text{d}}\gamma^{\text{e}} ,$$

(10)

$${\text{d}}\gamma^{\text{e}} = \frac{{{\text{d}}q}}{{G_{\text{i}} }},$$

(11)

where ${\text{d}}\varepsilon_{s}^{p}$ is the plastic deviator strain increment, ${\text{d}}\gamma^{\text{e}}$ is the elastic shear strain increment that may be evaluated from the appropriate deviator stress increment dq and the initial tangential shear modulus G_i estimated at each loading and unloading as Eq. (11).

In this series of tests, the parameters that are used to evaluate the effective stresses and the elastic strains were a_e = 33.3 kPa, $\kappa$ = 0.020 and s_e = 10 kPa.

3.2 Cyclic stress–strain behavior of unsaturated DL clay

In this series, the shearing loads with the constant stress ratio amplitude of 0.7 for compression and 1.0 for extension were applied. The number of shearing cycles was ten, and the shearing was conducted under drained condition. The experimental results of the relationships between the stress ratio and the shear strain are shown in Fig. 4. The relationships in CS00 and CS10 specimens largely moved to negative sides at the first unloading. After a few loading cycles, the hysteresis loops approached almost a unique one. The hysteresis loops in the specimens with high suction values (see CS60 and CS90 specimens) formed almost a unique loop at the third cycle. The slopes of the hysteresis loops became steeper with an increase in suction.

Fig. 4

Stress–strain relationship for constant stress ratio amplitude

Table 4 shows the shear strain increment for each hysteresis loop of CS series. The shear strain increment in each suction value decreased with an increase in numbers of loading cycle. The amount of shear strain increment reduced with an increase in suction in each reloading and unloading cycles. So the application of higher suction values inhibited the plastic deformations. These phenomena are consistent with those derived from the second suction effect that an increase in suction increases both the yield stress and the stiffness of soil skeleton against plastic deformations as pointed out by Kohgo et at. [8, 9].

Table 4 Shear strain increment for each hysteresis loop of CS series

In the CA series, the constant axial strain amplitude of 1.5% for both compression and extension was applied. While the number of shearing cycles was four, the shearing was conducted under drained condition. Figure 5 shows the relationships between the stress ratio and the axial strain. It can be seen from these figures that the stress ratios slightly increased with cyclic times. The inclines of the reloading lines increased with cyclic times. The cyclic time at which the hysteresis loop became unique decreased with an increase in suction. The shapes of the hysteresis loops of CA30, CA60 and CA90 specimens were taller than those of the CA00 and CA10 specimens. Little plastic deformation induced by the cyclic loadings grew in all the cases.

Fig. 5

Stress–strain relationship for constant strain amplitude

In the SS series, the shear strain amplitudes were sequentially increased up to 0.5, 1.0, 2.0 and 4.0% during the cyclic loadings. The relationships of the stress ratio and the shear strain obtained from this series of tests are shown in Fig. 6. The stress ratios increased with the cyclic times and the suction. The slopes of the hysteresis loops became steeper with an increase in suction. An increase in suction indeed enhanced stiffness of the soil.

Fig. 6

Stress–strain relationship for increasing shear strain amplitude

The relationships between the plastic volumetric strain ε^p_v and the shear strain γ or ε^p_v and the axial strain ε_a obtained from three series of tests are shown in Figs. 7, 8 and 9. Figure 7 shows the relationships of the CS series. The plastic volumetric strains largely accumulated for CS00 and CS10 specimens. In the CS00 and CS10 cases, as the volume reductions occurred at both the first loading and unloading but not in subsequent progresses of loadings, the behavior in unloading changed from compression to expansion (dilation). In CS30, 60 and 90 cases, the expansion appeared even at the first unloading. The amounts of the volume reduction decreased with an increase in suction. In all the cases, the volume reductions occurred during loadings but the amounts of the volume reductions at each step decreased with an increase in cyclic times. The total volumetric strains after 10 cyclic shearing loadings reached 6.6, 6.0, 3.0, 1.6 and 1.2% for the cases CS00, CS10, CS30, CS60 and CS90, respectively.

Fig. 7

Volume change behavior for constant stress ratio amplitude

Fig. 8

Volume change behavior for constant strain amplitude

Fig. 9

Volume change behavior for increasing shear strain amplitude

Figure 8 shows the relationships of the CA series. The volumetric strains (compression) were accumulated in all the cases. As the loading processes, the volume reductions for all the cases occurred but the amounts of reductions decreased with an increase in cyclic times and suction. During the unloading processes, while the volume changes for CA00 and CA10 specimens expressed compression at first, it changed to dilation after the second cycle. However, for all the unloading processes, the CA30, CA60 and CA90 specimens expressed dilation. The amounts of dilation increased with cyclic times for all the cases. The behaviors of the specimens with high suction values (CA60 and CA90) were more dilative than those of the specimens with low suction values (CA00 and CA10) for all the loading cycles. The total volume reductions for CA00, 10, 30, 60 and 90 after four cycles were 5.4, 5.2, 3.6, 2.8 and 2.3%, respectively. Thus, the volume reductions due to cyclic loadings decreased with an increase in suction. The volume changes for both CA00 and CA10 were quite similar because the suction values were smaller than the air entry value s_e, which was about 10 kPa for DL clay as shown in Fig. 3. The conditions were both in insular saturation, in which Terzaghi’s effective stress equation was valid [8]. In addition, as the densities of both specimens were low, the both conditions are almost under the normal consolidation state.

The results of the SS series are shown in Fig. 9. Contractive volume change behavior could be seen at the first loading and unloading for all the specimens. The behavior progressively changed to be dilative with the cyclic times. The compression in each loading and unloading step became larger in all the cases as the shear strain amplitude increased. The total volume reductions for SS00, SS10, SS30, SS60 and SS90 specimens were 5.3, 5.4, 3.5, 3.0 and 2.4%, respectively. The smallest total volume reduction was found for the SS90 specimen, which was subject to the highest suction. The dilative behavior during the unloading stages started from the third unloading stage for the SS00 and SS10 specimens, while it started at the second unloading stage for the SS30, SS60 and SS90 specimens.

The deformation behavior of the unsaturated silt under cyclic loadings observed in this section can be summarized as: (1) when the suction s is equal to or smaller than the air entry suction s_e, the behavior was similar to that of the saturated soil, and (2) when s > s_e, the stiffnesses and the volume change were affected by the suction as an increase in suction increased the stiffness and reduced the volume reduction. These properties might be induced by the concept of two suction effects [3] that is (1) an increase in suction increases effective stresses and (2) an increase in suction enhances yield stresses and affects resistance to plastic deformations.

3.3 Stress–dilatancy relationships

It is very important to know the stress–dilatancy relationships of the unsaturated soils to evaluate permanent deformations due to cyclic loadings. Figures 10, 11 and 12 show the relationships of the stress ratio and the dilatancy ratio, i.e., the ratio of the plastic volumetric strain increment ${\text{d}}\varepsilon_{\text{v}}^{\text{p}}$ to the plastic shear strain increment dγ^p, for the CS, CA and SS test series, respectively. In the CS series shown in Fig. 10, while the black and yellow open circles depict the relationships obtained from the first loading and unloading cycle, the blue and red closed circles depict those obtained from the subsequent loading and unloading cycles, respectively. The stress–dilatancy relationship for the first cycle was slightly different from others, which was also pointed out by De Silva et al. [3]. One reason why there was a difference between the first and the subsequent relationships may be that the amplitude of the stress ratios ($q/p^{\prime}$) during cyclic loadings was 0.7 for compression and 1.0 for extension which were not adequate (may be too large) for the series of the cyclic tests. The stress–dilatancy relationships at both loading and unloading stages except for the first loading cycle seemed to be almost linear in all the specimens. The best fitting lines are shown as the solid lines, while the dashed lines are drawn from extended Taylor’s theory [27] where the net plastic work is assumed to be only dissipated in friction. They have the incline = 1.5 and $\phi^{\prime}_{{\text{pt}}}$ = 26 degrees. The value of $\phi^{\prime}_{{\text{pt}}}$ is the phase transformation angle with respect to effective stresses. Then the relationship estimated by the dashed lines derives the similar plastic yield function of the Cam-clay model [24] (see Appendix).

Fig.10

Stress–dilatancy relationship for constant stress ratio amplitude

Fig. 11

Stress–dilatancy relationship for constant strain amplitude

Fig. 12

Stress–dilatancy relationship for increasing shear strain amplitude

Figure 11 shows the stress–dilatancy relationships of the CA series. The stress–dilatancy relationships obtained from all the loading and unloading cycles appeared to be almost linear for all the cases. The best fitting lines are shown as the solid lines, while the dashed lines are the same as those plotted in Fig. 10. The difference between both estimates by solid and dashed lines was small.

Figure 12 shows the results of the SS series. The stress–dilatancy relationships obtained from all the loading and unloading cycles appeared to be almost linear as well as those of the CS and CA series. The best fitting lines are shown as the solid lines, while the dashed lines are the same as those plotted in Fig. 10. The estimates by both solid and dashed lines are also reasonable.

Figure 13a–c shows the comparison of stress–dilatancy relationship between different suction values under the same loading condition for CS, CA and SS series, respectively. In CS series, the stress–dilatancy relationship at the loading stages was overlapped as a linear line except for the first loading while in unloading stages, they look like almost linear, but the relationships moved a little bit upward with suction increased. The stress–dilatancy relationships obtained from different suctions appeared to be a same straight line at all the loading and unloading stages in CA and SS series. Figure 14 shows the comparison of stress–dilatancy relationship between different loadings under the same suction for s = 0, 10, 30, 60 and 90 kPa. All stress–dilatancy relationships seemed to be almost linear at each loading and unloading stages for different loading conditions under the same suction except for the first loading of CS series in all the suction. All the dashed lines in Figs. 13 and 14 are also the same as those plotted in Fig. 10. All these estimation lines are reasonable whether the suction values and cyclic shear loading conditions were changed in all the cases.

Fig. 13

Comparison of stress–dilatancy relationship between different suction values under the same loading condition

Fig. 14

Comparison of stress–dilatancy relationship between different loading conditions under the same suction

For all the specimens of three series, the dashed lines may be individually identified during loading and unloading. Each line is assumed to be the same for all the cases. Each line of the stress–dilatancy relationships for loading and unloading may be expressed as a unique one regardless of saturated and unsaturated conditions if the first suction effect: An increase in suction increases effective stress, is taken into account. Then the stress–dilatancy relationships may be expressed as:

$$\frac{q}{{p^{\prime}}} = - \frac{3}{2}\frac{{{\text{d}}\varepsilon_{\text{v}}^{\text{p}} }}{{{\text{d}}\gamma^{\text{p}} }} + M,$$

(12)

where M is given by the following equations,

$$M = M_{\text{c}} = \frac{{6\sin \phi^{\prime}_{{\text{pt}}} }}{{\left( {3 - \sin \phi^{\prime}_{{\text{pt}}} } \right)}}\; {\text{for}}\;{\text{compression}},$$

(13)

$$M = M_{\text{e}} = \frac{{6\sin \phi^{\prime}_{{\text{pt}}} }}{{\left( {3 + \sin \phi^{\prime}_{{\text{pt}}} } \right)}} \;{\text{for}}\;{\text{extension}}.$$

(14)

The solid lines shown in Figs. 9, 10 and 11 are given as:

$$\frac{q}{{p^{\prime}}} = - a\frac{{{\text{d}}\varepsilon_{\text{v}}^{\text{p}} }}{{{\text{d}}\gamma^{\text{p}} }} + M,$$

(15)

where a is the empirical parameter.

4 Plastic potential function

From the test results described in Chapter 3, the stress ratio q/p′ and dilatancy ratio − dε^p_v/dγ^p relationship may be expressed by Eq. (15). The following plastic potential function $\psi$ may be then derived from Eq. (15) as shown in “Appendix”.

$$\psi = \eta + M\ln \frac{{p^{\prime}}}{{p^{\prime}_{{\text{pt}}} }} - M = 0 \qquad \left( {a^{*} \,= \, 1} \right),$$

(16)

$$\psi = \ln \left( {\frac{\eta - \beta }{M - \beta }} \right) - \frac{1}{\alpha }\ln \frac{{p^{\prime}}}{{p^{\prime}_{{\text{p}{\text{t}}}} }} = 0 \quad \left( {a^{*} \ne 1} \right),$$

(17)

where the stress ratio $\eta \text{ = }{q \mathord{\left/ {\vphantom {q {p^{\prime}}}} \right. \kern-0pt} {p^{\prime}}}$, $p^{\prime} = p^{\prime}_{{\text{pt}}}$ on the phase transformation line, $\alpha = \frac{a^{*}}{{\left( {1 - a^{*}} \right)}}$, $\beta = \frac{M}{{\left( {1 - a^{*}} \right)}}$ and $a^{*} = \frac{2}{3}a$.

Figure 15 shows the potential functions of the SS series derived from Eqs. (16) and (17). The orange, gray, green and blue colors are the potential functions for a* = 0.7, 0.8, 0.9 and 1.0, respectively. The black line is the phase transformation line. The functions were enhanced with an increase in suction. When $p^{\prime} \le p^{\prime}_{{\text{pt}}}$, the difference due to parameter a* is small. When a* is greater than 0.7 and less than 1.0, we may select a* = 1.0, always using Eq. (16).

Fig. 15

Plastic potential function for increasing shear strain amplitude

5 Conclusions

Cyclic triaxial compression shear loading tests with constant five different suctions and a net constant confining stress were performed under drained conditions using an unsaturated artificial silt, named DL clay. The following major conclusions were obtained from the tests with three different cyclic loading conditions.

The stiffness of the soil increased with an increase in suction and the number of loadings. The application of higher suction values inhibited the plastic deformation under cyclic loading, namely the inclinations and the sizes of the hysteresis loops of the stress–strain relationships became steeper and thinner with higher suction, respectively.

Volume reduction occurred just after the loading direction was reversed in all the specimens under cyclic loading. The amount of volume reduction due to cyclic loading decreased with an increase in suction. The shear strains and volume changes induced by the cyclic loadings decreased with an increase in suction for CS series.

The shear behavior of both specimens with suction s = 0 and 10 kPa was almost the same, since the applied suction values were smaller than the air entry value, s_e = 10 kPa. The dilation due to the cyclic loading tended to increase with an increase in suction. The deformation of this silt under the cyclic loadings could be interpreted by the two suction effects concepts: (1) An increase in suction increases effective stresses, and (2) An increase in suction enhances yield stresses and affects resistance to plastic deformations, proposed by Kohgo et al. [8].

Unique stress–dilatancy relationship at loading and unloading stages could be obtained for all the cases. The stress–dilatancy relationships obtained for the unsaturated soil were almost linear and the same as those of saturated soils if effective stresses are evaluated by Eqs. (1) to (5). Uniqueness of the stress–dilatancy relationships was almost independent of the suction values and cyclic shear loading conditions. The plastic potential functions could be derived from the stress–dilatancy relationships as Eqs. (16) and (17) for the unsaturated soil. The plastic potential functions were enhanced with an increase in suction. The proposed plastic potential functions will be used in the estimation of permanent deformation of embankments.

Appendix

Assuming the plastic potential function ψ, the plastic strains are obtained by adopting the normality rule

$${\text{d}}\varepsilon_{\text{s}}^{\text{p}} = \frac{2}{3}{\text{d}}\gamma^{\text{p}} = \lambda \frac{\partial \psi }{\partial q} ,$$

(18)

$${\text{d}}\varepsilon_{\text{v}}^{\text{p}} = - \lambda \frac{\partial \psi }{{\partial p^{\prime}}} .$$

(19)

From Eqs. (18) and (19), we may obtain the strain increment ratio as:

$$- \frac{{{\text{d}}\varepsilon_{\text{v}}^{\text{p}} }}{{{\text{d}}\gamma^{\text{p}} }} = - \frac{2}{3}\frac{{{\text{d}}\varepsilon_{\text{v}}^{\text{p}} }}{{{\text{d}}\varepsilon_{\text{s}}^{\text{p}} }} = \frac{2}{3}\left( {\frac{{\lambda \frac{\partial \psi }{{\partial p^{\prime}}}}}{{\lambda \frac{\partial \psi }{\partial q}}}} \right) = \frac{2}{3}\frac{{{\text{d}}q}}{{{\text{d}}p^{\prime}}} .$$

(20)

Substituting Eq. (20) into Eq. (15), we obtain

$$\frac{q}{{p^{\prime}}} = \frac{2a}{3}\frac{{{\text{d}}q}}{{{\text{d}}p^{\prime}}} + M .$$

(21)

Supposing the stress ratio $\eta \text{ = }{q \mathord{\left/ {\vphantom {q {p^{\prime}}}} \right. \kern-0pt} {p^{\prime}}}$, then $q\text{ = }\eta \, p^{\prime}$.

Therefore,

$$\frac{{{\text{d}}q}}{{{\text{d}}p^{\prime}}} = \frac{\text{d}}{{{\text{d}}p^{\prime}}}\left( {\eta \,p^{\prime}} \right) = \eta + p^{\prime}\frac{{{\text{d}}\eta }}{{{\text{d}}p^{\prime}}} .$$

(22)

Now, substituting Eq. (22) into (21),

$$\eta = a^{*}\left( {\eta + p^{\prime}\frac{d\eta }{{{\text{d}}p^{\prime}}}} \right) + M ,$$

(23)

where $a^{*} = 2a/3$.

When $a^{*} = 1$, Eq. (23) is

$$p^{\prime}\frac{{{\text{d}}\eta }}{{{\text{d}}p^{\prime}}} + M = 0 ,$$

(24)

$$\int {{\text{d}}\eta } = \int {\frac{ - M}{{p^{\prime}}}{\text{d}}p^{\prime}} \qquad\therefore \, \eta\ + M\ln p^{\prime} + C = 0 .$$

(25)

When $p^{\prime} = p^{\prime}_{{\text{pt}}}$, η = M. Then C = − M − M ln $p^{\prime}_{{\text{pt}}}$

$$\psi = \eta + M\ln \frac{{p^{\prime}}}{{p^{\prime}_{{\text{pt}}} }} - M = 0 .$$

(26)

Equation (26), which is similar to the yield function of Cam-clay model, is the plastic potential function at $a^{*} = 1$.

If $a^{*} \ne 1$, Eq. (23) may be rewritten as:

$$\eta = \frac{a^{*}}{{\left( {1 - a^{*}} \right)}}p^{\prime}\frac{{{\text{d}}\eta }}{{{\text{d}}p^{\prime}}} + \frac{M}{{\left( {1 - a^{*}} \right)}} .$$

(27)

Supposing $\alpha = \frac{a^{*}}{{\left( {1 - a^{*}} \right)}}$ and $\beta = \frac{M}{{\left( {1 - a^{*}} \right)}}$, Eq. (27) is

$$\eta = \alpha \,p^{\prime}\frac{{{\text{d}}\eta }}{{{\text{d}}p^{\prime}}} + \beta ,$$

(28)

$$\int {\frac{{{\text{d}}\eta }}{{\left( {\eta - \beta } \right)}}} = \frac{1}{\alpha }\int {\frac{{{\text{d}}p^{\prime}}}{{p^{\prime}}}}\qquad\therefore \ln \left( {\eta - \beta } \right) = \frac{1}{\alpha }\ln p^{\prime} + C .$$

(29)

When $p^{\prime} = p^{\prime}_{{\text{pt}}}$, η = M. Then $C = \ln \left( {{\rm M} - \beta } \right) - \frac{1}{\alpha }\ln p^{\prime}_{{\text{pt}}}$.

$$\psi = \ln \left( {\frac{\eta - \beta }{M - \beta }} \right) - \frac{1}{\alpha }\ln \frac{{p^{\prime}}}{{p^{\prime}_{{\text{p}t}} }} = 0 .$$

(30)