Skip to main content
SpringerLink
Log in

Hyperbolic structure and stickiness effect: A case of a 2D area-preserving twist mapping

  • Article
  • Published:
Science China Physics, Mechanics & Astronomy Aims and scope Submit manuscript

Abstract

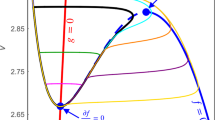
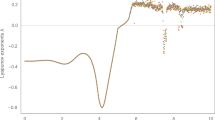
The stickiness effect suffered by chaotic orbits diffusing in the phase space of a dynamical system is studied in this paper. Previous works have shown that the hyperbolic structures in the phase space play an essential role in causing the stickiness effect. We present in this paper the relationship between the stickiness effect and the geometric property of hyperbolic structures. Using a two-dimensional area-preserving twist mapping as the model, we develop the numerical algorithms for computing the positions of the hyperbolic periodic orbits and for calculating the angle between the stable and unstable manifolds of the hyperbolic periodic orbit. We show how the stickiness effect and the orbital diffusion speed are related to the angle.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Karney C F, Rechester A B, White R B. Effect of noise on the standard mapping. Phys D, 1982, 4: 425–438

    Article  MATH  MathSciNet  Google Scholar 

  2. Karney C F. Long-time correlations in the stochastic regime. Phys D, 1983, 8: 360–380

    Article  MathSciNet  Google Scholar 

  3. Zaslavsky G M, Edelman M, Niyazov B A. Self-similarity, renormalization, and phase space nonuniformity of Hamiltonian chaotic dynamics. Chaos, 1997, 7: 159–181

    Article  ADS  MATH  MathSciNet  Google Scholar 

  4. Zaslavsky G M. Chaos, fractional kinetics, and anomalous transport. Phys Rep, 2002, 371: 461–580

    Article  ADS  MATH  MathSciNet  Google Scholar 

  5. Barash O, Dana I. Type specification of stability islands and chaotic stickiness. Phys Rev E, 2005, 71: 036222

    Article  ADS  MathSciNet  Google Scholar 

  6. Abdullaev S S. Chaotic transport in Hamiltonian systems perturbed by a weak turbulent wave field. Phys Rev E, 2011, 84: 026204

    Article  ADS  Google Scholar 

  7. Custódio M S, Beims M W. Intrinsic stickiness and chaos in open integrable billiards: Tiny border effects. Phys Rev E, 2011, 83: 056201

    Article  ADS  Google Scholar 

  8. Jaffé C, Ross S D, Lo M W, et al. Statistical theory of asteroid escape rates. Phys Rev Lett, 2002, 89: 011101

    Article  ADS  Google Scholar 

  9. Karne C F, Bers A. Stochastic ion heating by a perpendicularly propagating electrostatic wave. Phys Rev Lett, 1977, 39: 550–554

    Article  ADS  Google Scholar 

  10. Beloshapkin V V, Chernikov A A, Natenzon MI, et al. Chaotic streamlines in pre-turbulent states. Nature, 1989, 337: 133–137

    Article  ADS  Google Scholar 

  11. Chia P K, Schmitz L, Conn R W. Stochastic ion behaviour in subharmonic and superharmonic electrostatic waves. Phys Plas, 1996, 3: 1545–1568

    Article  ADS  Google Scholar 

  12. Fromhold T M, Patane A, Bujkiewicz S, et al. Chaotic electron diffusion through stochastic webs enhances current flow in super lattices. Nature, 2004, 428: 726–730

    Article  ADS  Google Scholar 

  13. Varga I, Pollner P, Eckhardt B. Quantum localization near bifurcations in classically chaotic systems. Annal Phys, 1999, 8: 265–268

    Google Scholar 

  14. Kalapotharakos C, Voglis N, Contopoulos G. Chaos and secular evolution of triaxial N-body galactic models due to an imposed central mass. Astron Astrophys, 2004, 428: 905–923

    Article  ADS  MATH  Google Scholar 

  15. Chirikov B, Shepelyansky D L. Correlation properties of dynamical chaos in Hamiltonian systems. Phys D, 1984, 13: 395–400

    Article  MATH  MathSciNet  Google Scholar 

  16. Meiss J D, Ott E. Markov-tree model of intrinsic transport in Hamiltonian systems. Phys Rev Lett, 1985, 55: 2741–2744

    Article  ADS  Google Scholar 

  17. Lai Y C, Ding M C, Grebogi C, et al. Algebraic decay and fluctuations of the decay exponent in Hamiltonian systems. Phys Rev A, 1992, 46: 4661–4669

    Article  ADS  Google Scholar 

  18. Perry A D, Wiggins S. KAM tori are very sticky: Rigorous lower bounds on the time to move away from an invariant Lagrangian torus with linear flow. Phys D, 1994, 71: 102–121

    Article  MATH  MathSciNet  Google Scholar 

  19. Contopoulos G, Voglis N, Efthymiopoulos C, et al. Transition spectra of dynamical systems. Celest Mech Dyn Astron, 1997, 67: 293–317

    Article  ADS  MATH  MathSciNet  Google Scholar 

  20. Froeschlé C, Lega E. Modeling mappings: An aim and a tool for the study of dynamical systems. In: Benest D, Froeschlé Cl, eds. Analysis and Modeling of Discrete Dynamical Systems. Netherland: Overseas Publishers Association, 1998. 3–54

    Google Scholar 

  21. Sun Y S, Fu Y N. Diffusion character in four-dimensional volume preserving map. Celest Mech Dyn Astron, 1999, 73: 249–258

    Article  ADS  MATH  MathSciNet  Google Scholar 

  22. Contopoulos G, Harsoula M, Voglis N, et al. Destruction of islands of stability. J Phys A-Math Gen, 1999, 32: 5213–5232

    Article  ADS  MATH  MathSciNet  Google Scholar 

  23. Contopoulos M, Harsoula M. Stickiness effects in chaos. Celest Mech Dyn Astron, 2010, 107: 77–92

    Article  ADS  MATH  MathSciNet  Google Scholar 

  24. Efthymiopoulos C, Contopoulos G, Voglis N. Cantori, islands and asymptotic curves in the stickiness region. Celest Mech Dyn Astron, 1999, 73: 221–230

    Article  ADS  MATH  MathSciNet  Google Scholar 

  25. Sun Y S, Zhou L Y, Zhou J L. The role of hyperbolic invariant sets in stickiness effects. Celest Mech Dyn Astron, 2005, 92: 257–272

    Article  ADS  MATH  MathSciNet  Google Scholar 

  26. Sun Y S, Zhou L Y. Stickiness in three-dimensional volume preserving mappings. Celest Mech Dyn Astron, 2009, 103: 119–131

    Article  ADS  MATH  MathSciNet  Google Scholar 

  27. Morbidelli A, Giorgilli A. Superexponential stability of KAM tori. J Stat Phys, 1995, 78: 1607–1617

    Article  ADS  MATH  MathSciNet  Google Scholar 

  28. Howard J E, Humpherys J. Nonmonotonic twist maps. Phys D, 1995, 80: 256–276

    Article  MATH  MathSciNet  Google Scholar 

  29. Chirikov R V. A universal instability of many-dimensional oscillator systems. Phys Rep, 1979, 52: 263–379

    Article  ADS  MathSciNet  Google Scholar 

  30. Cheng J, Sun Y S. Stable and unstable properties of the standard-liked map. Random Comput Dyn, 1996, 4: 73–85

    MATH  MathSciNet  Google Scholar 

  31. Siegel C L, Moser J K. Lectures on Celestial Mechanics. Berlin: Springer-Verlag, 1971. 225–256

    Book  MATH  Google Scholar 

  32. Bangert V. Mather sets for twist maps and geodesics on tori. Dyn Rep, 1988, 1: 1–56

    Article  MathSciNet  Google Scholar 

  33. Cheng J. Variational approach to homoclinic orbits in twist maps and an application to billiard systems. Z Angew Math Phys, 2004, 55: 400–419

    Article  MATH  MathSciNet  Google Scholar 

  34. Greene J M. A method for determining a stochastic transition. J Math Phys, 1979, 20: 1183–1201

    Article  ADS  Google Scholar 

  35. Zhou J L, Zhou L Y, Sun Y S. Hyperbolic structures and the stickiness effect. Chin Phys Lett, 2002, 19: 1254–1256

    Article  ADS  Google Scholar 

  36. Benegeroles R. Universality of algebraic laws in Hamiltonian systems. Phys Rev Lett, 2009, 102: 064101

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Astronomy and Space Sciences, Nanjing University, Nanjing, 210093, China

    LiYong Zhou, Jian Li & YiSui Sun

  2. Key Laboratory of Modern Astronomy and Astrophysics in Ministry of Education, Nanjing University, Nanjing, 210093, China

    LiYong Zhou, Jian Li & YiSui Sun

  3. Department of Mathematics, Nanjing University, Nanjing, 210093, China

    Jian Cheng

Authors
  1. LiYong Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jian Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jian Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. YiSui Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to YiSui Sun.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhou, L., Li, J., Cheng, J. et al. Hyperbolic structure and stickiness effect: A case of a 2D area-preserving twist mapping. Sci. China Phys. Mech. Astron. 57, 1737–1750 (2014). https://doi.org/10.1007/s11433-013-5299-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11433-013-5299-7

Keywords

Search

Navigation