Skip to main content
SpringerLink
Log in

Multi-domain physics-informed neural network for solving heat conduction and conjugate natural convection with discontinuity of temperature gradient on interface

  • Article
  • Published:
Science China Technological Sciences Aims and scope Submit manuscript

Abstract

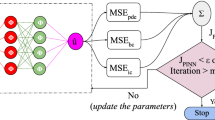
Deep learning has been increasingly recognized as a promising tool in solving kinds of physical problems beyond powerful approximations. A multi-domain physics-informed neural network (mPINN) is proposed to solve the non-uniform heat conduction and conjugate natural convection with the discontinuity of temperature gradient on the interface. Local radial basis function method (LRBF) is applied to compute the case without the analytical solution and is regarded as the benchmark solver. Each physical domain matches a private neural network and all neural networks are connected by the shared information of temperature and heat flux on the interface. Joint training and separate training are utilized to minimize the loss function, which usually consists of the residual of boundary conditions, interface conditions and governing equations. Joint training minimizes the sum of all losses from neural networks with one shared optimizer, while separate training owns its private optimizer. Local adaptive activation function (LAAF) is used to accelerate the convergence and acquire a lower loss value when compared with its fixed counterpart. The numerical experiments on three types of residual points, uniform, Gauss-Lobatto and random, are conducted and it can be concluded that the uniform residual points can obtain the most accurate solution than the random and Gauss-Lobatto. Joint training is more accurate than the separate training when the number of residual points is relatively small, while the separate training performs better than the joint training for the large number of residual points. Numerous test cases on multi-domain heat transfer and fluid flow show the accuracy of the proposed mPINN. Local and global heat transfer rates show good agreements with the results from LRBF. Excepting the forward problems, the thermal conductivity ratio, the constant source and the characteristic parameters of natural convection are accurately learned from sparsely distributed data points.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Dissanayake M W M G, Phan-Thien N. Neural-network-based approximations for solving partial differential equations. Commun Numer Meth Engng, 1994, 10: 195–201

    Article  MATH  Google Scholar 

  2. González-García R, Rico-Martínez R, Kevrekidis I G. Identification of distributed parameter systems: A neural net based approach. Comput Chem Eng, 1998, 22: S965–S968

    Article  Google Scholar 

  3. Lagaris I E, Likas A, Fotiadis D I. Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans Neural Netw, 1998, 9: 987–1000

    Article  Google Scholar 

  4. Hornik K, Stinchcombe M, White H. Multilayer feedforward networks are universal approximators. Neural Networks, 1989, 2: 359–366

    Article  MATH  Google Scholar 

  5. Chen T P, Chen H. Universal approximation to nonlinear operators by neural networks with arbitrary activation functions and its application to dynamical systems. IEEE Trans Neural Netw, 1995, 6: 911–917

    Article  Google Scholar 

  6. Mall S, Chakraverty S. Application of legendre neural network for solving ordinary differential equations. Appl Soft Comput, 2016, 43: 347–356

    Article  Google Scholar 

  7. Panghal S, Kumar M. Optimization free neural network approach for solving ordinary and partial differential equations. Eng Comput, 2020, 37: 2989–3002

    Article  Google Scholar 

  8. Yang Y, Hou M, Luo J. A novel improved extreme learning machine algorithm in solving ordinary differential equations by Legendre neural network methods. Adv Differ Equ, 2018, 2018: 469

    Article  MathSciNet  MATH  Google Scholar 

  9. Lorin E. Derivation and analysis of parallel-in-time neural ordinary differential equations. Ann Math Artif Intell, 2020, 88: 1035–1059

    Article  MathSciNet  MATH  Google Scholar 

  10. Mao Z, Jagtap A D, Karniadakis G E. Physics-informed neural networks for high-speed flows. Comput Methods Appl Mech Eng, 2020, 360: 112789

    Article  MathSciNet  MATH  Google Scholar 

  11. Baydin A G, Pearlmutter B A, Radul A A, et al. Automatic differentiation in machine learning. J Mach Learn Res, 2017, 18: 5595–5637

    MathSciNet  Google Scholar 

  12. Lu L, Meng X, Mao Z, et al. DeepXDE: A deep learning library for solving differential equations. SIAM Rev, 2021, 63: 208–228

    Article  MathSciNet  MATH  Google Scholar 

  13. Poggio T, Mhaskar H, Rosasco L, et al. Why and when can deep-but not shallow-networks avoid the curse of dimensionality: A review. Int J Autom Comput, 2017, 14: 503–519

    Article  Google Scholar 

  14. Cai S, Mao Z, Wang Z, et al. Physics-informed neural networks (PINNs) for fluid mechanics: A review. Acta Mech Sin, 2021, 37: 1727–1738

    Article  MathSciNet  Google Scholar 

  15. Raissi M, Perdikaris P, Karniadakis G E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comput Phys, 2019, 378: 686–707

    Article  MathSciNet  MATH  Google Scholar 

  16. Pang G, Lu L, Karniadakis G E. fPINNs: Fractional physics-informed neural networks. Siam J Sci Comput, 2019, 41: A2603–A2626

    Article  MathSciNet  MATH  Google Scholar 

  17. Zhang D, Lu L, Guo L, et al. Quantifying total uncertainty in physics-informed neural networks for solving forward and inverse stochastic problems. J Comput Phys, 2019, 397: 108850

    Article  MathSciNet  MATH  Google Scholar 

  18. Zhang D, Guo L, Karniadakis G E. Learning in modal space: Solving time-dependent stochastic PDEs using physics-informed neural networks. Siam J Sci Comput, 2020, 42: A639–A665

    Article  MathSciNet  MATH  Google Scholar 

  19. Jin X, Cai S, Li H, et al. NSFnets (Navier-Stokes flow nets): Physics-informed neural networks for the incompressible Navier-Stokes equations. J Comput Phys, 2021, 426: 109951

    Article  MathSciNet  MATH  Google Scholar 

  20. Jagtap A D, Kharazmi E, Karniadakis G E. Conservative physics-informed neural networks on discrete domains for conservation laws: Applications to forward and inverse problems. Comput Methods Appl Mech Eng, 2020, 365: 113028

    Article  MathSciNet  MATH  Google Scholar 

  21. Jagtap A D, Karniadakis G E. Extended physics-informed neural networks (XPINNs): A generalized space-time domain decomposition based deep learning framework for nonlinear partial differential equations. Commun Comput Phys, 2020, 28: 2002–2041

    Article  MathSciNet  MATH  Google Scholar 

  22. Raissi M, Yazdani A, Karniadakis G E. Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. Science, 2020, 367: 1026–1030

    Article  MathSciNet  MATH  Google Scholar 

  23. Rao C, Sun H, Liu Y. Physics-informed deep learning for incompressible laminar flows. Theor Appl Mech Lett, 2020, 10: 207–212

    Article  Google Scholar 

  24. Zhang R, Liu Y, Sun H. Physics-informed multi-LSTM networks for metamodeling of nonlinear structures. Comput Methods Appl Mech Eng, 2020, 369: 113226

    Article  MathSciNet  MATH  Google Scholar 

  25. Meng X, Li Z, Zhang D, et al. PPINN: Parareal physics-informed neural network for time-dependent PDEs. Comput Methods Appl Mech Eng, 2020, 370: 113250

    Article  MathSciNet  MATH  Google Scholar 

  26. Wang S, Teng Y, Perdikaris P. Understanding and mitigating gradient flow pathologies in physics-informed neural networks. Siam J Sci Comput, 2021, 43: A3055–A3081

    Article  MathSciNet  MATH  Google Scholar 

  27. Wang S, Yu X, Perdikaris P. When and why PINNs fail to train: A neural tangent kernel perspective. J Comput Phys, 2022, 449: 110768

    Article  MathSciNet  MATH  Google Scholar 

  28. Xiang Z, Peng W, Zheng X, et al. Self-adaptive loss balanced physics-informed neural networks for the incompressible Navier-Stokes equations. arXiv: 2104.06217

  29. Moseley B, Markham A, Nissen-Meyer T. Solving the wave equation with physics-informed deep learning. arXiv: 2006.11894

  30. Jagtap A D, Kawaguchi K, Em Karniadakis G. Locally adaptive activation functions with slope recovery for deep and physics-informed neural networks. Proc R Soc A, 2020, 476: 2239

    Article  MathSciNet  MATH  Google Scholar 

  31. Jagtap A D, Kawaguchi K, Karniadakis G E. Adaptive activation functions accelerate convergence in deep and physics-informed neural networks. J Comput Phys, 2020, 404: 109136

    Article  MathSciNet  MATH  Google Scholar 

  32. Sukumar N, Srivastava A. Exact imposition of boundary conditions with distance functions in physics-informed deep neural networks. Comput Methods Appl Mech Eng, 2022, 389: 114333

    Article  MathSciNet  MATH  Google Scholar 

  33. Lagari P L, Tsoukalas L H, Safarkhani S, et al. Systematic construction of neural forms for solving partial differential equations inside rectangular domains, subject to initial, boundary and interface conditions. Int J Artif Intell Tools, 2020, 29: 2050009

    Article  Google Scholar 

  34. Wang T, Huang Z, Sun Z, et al. Reconstruction of natural convection within an enclosure using deep neural network. Int J Heat Mass Transfer, 2021, 164: 120626

    Article  Google Scholar 

  35. Patel R G, Manickam I, Trask N A, et al. Thermodynamically consistent physics-informed neural networks for hyperbolic systems. J Comput Phys, 2022, 449: 110754

    Article  MathSciNet  MATH  Google Scholar 

  36. Fuks O, Tchelepi H A. Limitations of physics informed machine learning for nonlinear two-phase transport in porous media. J Machine Learn Model Comput, 2020, 1: 19–37

    Article  Google Scholar 

  37. Yu J, Lu L, Meng X, et al. Gradient-enhanced physics-informed neural networks for forward and inverse PDE problems. Comput Methods Appl Mech Eng, 2022, 393: 114823

    Article  MathSciNet  MATH  Google Scholar 

  38. Lou Q, Meng X, Karniadakis G E. Physics-informed neural networks for solving forward and inverse flow problems via the Boltzmann-BGK formulation. J Comput Phys, 2021, 447: 110676

    Article  MathSciNet  MATH  Google Scholar 

  39. Ruder S. An overview of gradient descent optimization algorithms. arXiv: 1609.04747

  40. Wang T, Huang Z, Sun Z, et al. Numerical simulation of mixed flow past an inclined square cylinder using a local radial basis function method. In: Proceedings of the ASME-JSME-KSME 2019 8th Joint Fluids Engineering Conference, AJKFluids, 2019. American Society of Mechanical Engineers (ASME). San Francisco, 2019

    Book  Google Scholar 

  41. Wang T, Huang Z, Xi G. Entropy generation for mixed convection in a square cavity containing a rotating circular cylinder using a local radial basis function method. Int J Heat Mass Transfer, 2017, 106: 1063–1073

    Article  Google Scholar 

  42. Wang T, Wang Z, Xi G, et al. Periodic unsteady mixed convection in square enclosure induced by inner rotating circular cylinder with time-periodic pulsating temperature. Int J Heat Mass Transfer, 2017, 111: 1250–1259

    Article  Google Scholar 

  43. Kansa E J. Multiquadrics—A scattered data approximation scheme with applications to computational fluid-dynamics—II solutions to parabolic, hyperbolic and elliptic partial differential equations. Comput Math Appl, 1990, 19: 147–161

    Article  MathSciNet  MATH  Google Scholar 

  44. Kansa E J. Multiquadrics—A scattered data approximation scheme with applications to computational fluid-dynamics—I surface approximations and partial derivative estimates. Comput Math Appl, 1990, 19: 127–145

    Article  MathSciNet  MATH  Google Scholar 

  45. Ha M Y, Jung M J. A numerical study on three-dimensional conjugate heat transfer of natural convection and conduction in a differentially heated cubic enclosure with a heat-generating cubic conducting body. Int J Heat Mass Transfer, 2000, 43: 4229–4248

    Article  MATH  Google Scholar 

  46. Zhao F Y, Liu D, Tang G F. Determining boundary heat flux profiles in an enclosure containing solid conducting block. Int J Heat Mass Transfer, 2010, 53: 1269–1282

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an, 710049, China

    TongSheng Wang, ZhiHeng Wang, Zhu Huang & Guang Xi

Authors
  1. TongSheng Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. ZhiHeng Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhu Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Guang Xi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Guang Xi.

Additional information

This work was supported by the National Natural Science Foundation of China (Grant Nos. 12102331 and 52130603).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, T., Wang, Z., Huang, Z. et al. Multi-domain physics-informed neural network for solving heat conduction and conjugate natural convection with discontinuity of temperature gradient on interface. Sci. China Technol. Sci. 65, 2442–2461 (2022). https://doi.org/10.1007/s11431-022-2118-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11431-022-2118-9

Keywords

Search

Navigation