Skip to main content
SpringerLink
Log in

Vapor-liquid equilibria of CH4, CO2 and their binary system CH4 + CO2: A comparison between the molecular simulation and equation of state

  • Article
  • Published:
Science China Technological Sciences Aims and scope Submit manuscript

Abstract

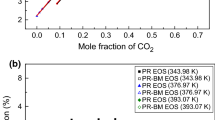
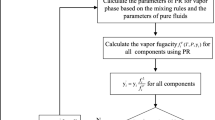
An accurate knowledge about phase behaviors of CH4, CO2 and their binary mixture is crucial in fields of natural gas liquefaction and refrigeration applications. In this work, two all-atom force fields of TraPPE-EH and EMP2 were used for the components CH4 and CO2, respectively. Then the vapor-liquid equilibria (VLE) of CH4, CO2 and their binary system were calculated via the NVT- and NpT Gibbs Ensemble Monte Carlo Simulations. Meanwhile the traditional method using Equation of State (EoS) to correlate the VLE properties was also investigated. The EoSs considered in this work were three classic cubic RK, SRK, PR and another advanced molecular-based PC-SAFT equations. For pure components, both molecular simulations and the PC-SAFT EoS could obtain satisfactory predictions for all the saturated properties. However, the saturated liquid densities calculated by the cubic EoSs were not so good. It was also observed that the TraPPE-EH force field had a good representation for CH4 molecule, while the EMP2 force field was not enough accurate to represent CO2 molecules. For the mixture CH4 + CO2, SRK and PR showed the best predictions for the saturated pressure-component property, while good results were also obtained via molecular simulations and PC-SAFT EoS. It was suggested that special combining rules or binary interaction parameters were important to obtain enough accurate prediction of the mixed phase behavior. Compared with the cubic EoS, the PC-SAFT and molecular simulation method showed better adaptabilities for both the pure and mixture systems. Besides, the accurate molecular parameters used in the PC-SAFT and molecular simulations could bring about direct and deep understanding about the molecular characteristics.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Kosseim A. New development in gas purification for LNG plants. In: Tenth International Conference & Exhibition on Liquefied Natural Gas, 1992

    Google Scholar 

  2. Cao W S. Study on natural gas purification and liquefaction process of small scale LNG project. Dissertation of Doctor Degree. Shanghai: Shanghai Jiaotong University, 2008

    Google Scholar 

  3. Oldenburg C M, Pruess K, Benson S M. Process modeling of CO2 injection into natural gas reservoirs for carbon sequestration and enhanced gas recovery. Energy Fuels, 2001, 15: 293–298

    Article  Google Scholar 

  4. Class H, Ebigbo A, Helmig R, et al. A benchmark study on problems related to CO2 storage in geologic formations. Comput Geosci, 2009, 13: 409–434

    Article  MATH  Google Scholar 

  5. Han C, Zhang P, Ye T H, et al. Numerical study of methane/air jet flame in vitiated co-flow using tabulated detailed chemistry. Sci China Tech Sci, 2014, 57: 1750–1760

    Article  Google Scholar 

  6. Yu J, Meng H. A numerical study of counterflow diffusion flames of methane/air at various pressures. Sci China Tech Sci, 2014, 57: 615–624

    Article  Google Scholar 

  7. Kvenvolden K A. Gas hydrates-geological perspective and global change. Rev Geophys, 1993, 31: 173–187

    Article  Google Scholar 

  8. Deusner C, Bigalke N, Kossel E, et al. Methane production from gas hydrate deposits through injection of supercritical CO2. Energies, 2012, 5: 2112–2140

    Article  Google Scholar 

  9. Kanoğlu M. Exergy analysis of multistage cascade refrigeration cycle used for natural gas liquefaction. Int J Energ Res, 2002, 26: 763–774

    Article  Google Scholar 

  10. Lim W, Choi K, Moon I. Current status and perspectives of liquefied natural gas (LNG) plant design. Ind Eng Chem Res, 2013, 52: 3065–3088

    Article  Google Scholar 

  11. Redlich O, Kwong J N S. On the thermodynamics of solutions. V. An equation of state. Fugacities of gaseous solutions. Chem Rev, 1949, 44: 233–244

    Article  Google Scholar 

  12. Soave, G. Equilibrium constants from a modified Redlich-Kwong equation of state. Chem Eng Sci, 1972, 27: 1197–1203

    Article  Google Scholar 

  13. Peng D Y, Robinson D B. A new two-constant equation of state. Ind Eng Chem Fundam, 1976, 15: 59–64

    Article  MATH  Google Scholar 

  14. Chapman W G, Gubbins K E, Jackson G, et al. SAFT: Equation-of-state solution model for associating fluids. Fluid Phase Equilib, 1989, 52: 31–38

    Article  Google Scholar 

  15. Huang S H, Radosz M. Equation of state for small, large, polydisperse, and associating molecules. Ind Eng Chem Res, 1990, 29: 2284–2294

    Article  Google Scholar 

  16. Gross J, Sadowski G. Perturbed-chain SAFT: An equation of state based on a perturbation theory for chain molecules. Ind Eng Chem Res, 2001, 40: 1244–1260

    Article  Google Scholar 

  17. Panagiotopoulos A Z. Direct determination of fluid phase equilibria by simulation in the Gibbs ensemble: A review. Mol Sim, 1992, 9: 1–23

    Article  Google Scholar 

  18. Skvorova M, Smith W R. Molecular-level simulation of bubble and dew points of fluid mixtures and application to refrigerant cycle design. Int J Refrig, 2014, 42: 1–7

    Article  Google Scholar 

  19. Smith W R, Figueroa-Gerstenmaier S, Skvorova M. Molecular simulation for thermodynamic properties and process modeling of refrigerants. J Chem Engin Data, 2014, 59: 3258–3271

    Article  Google Scholar 

  20. Figueroa-Gerstenmaier S, Lísal M, Nezbeda I, et al. Prediction of isoenthalps, Joule-Thomson Coefficients and Joule-Thomson inversion curves of refrigerants by molecular simulation Fluid Phase Equilibr, 2014, 375: 143–151

    Article  Google Scholar 

  21. Vinš V, Hrubý J. Solubility of nitrogen in one-component refrigerants: Prediction by PC-SAFT EoS and a correlation of Henry’s law constants. Int J Refrig, 2011, 34: 2109–2117

    Article  Google Scholar 

  22. Marcelino Neto M A, Barbosa Jr J R. Prediction of refrigerant-lubricant viscosity using the general PC-SAFT friction theory. Int J Refrig, 2014, 45: 92–99

    Article  Google Scholar 

  23. Polishuk I, Assor E, Cohen N, et al. Implementation of PC-SAFT and SAFT+ Cubic for modeling thermodynamic properties of haloalkanes. II. 7 Haloethanes and their mixtures. Int J Refrig, 2013, 36: 980–991

    Article  Google Scholar 

  24. Liu Y, Panagiotopoulos A Z, Debenedetti P G. Monte carlo simulations of high-pressure phase equilibria of CO2-H2O mixtures. J Phys Chem B, 2011, 115: 6629–6635

    Article  Google Scholar 

  25. Lin W, Yang Q, Zhong C. Molecular simulation of vapor-liquid equilibria of toxic gases. Fluid Phase Equilibr, 2004, 220: 1–6

    Article  Google Scholar 

  26. Do H, Wheatley R J, Hirst J D. Microscopic structure of liquid 1-1-1-2-tetrafluoroethane (R134a) from Monte Carlo simulation. Phys Chem Chem Phys, 2010, 12: 13266–13272

    Article  Google Scholar 

  27. Yamakov V, Wolf D, Phillpot S R, et al. Deformation-mechanism map for nanocrystalline metals by molecular-dynamics simulation. Nat Mater, 2003, 3: 43–47

    Article  Google Scholar 

  28. Vrabec J, Fischer J. Vapor-liquid equilibria of binary mixtures containing methane, ethane, and carbon dioxide from molecular simulation. Int J Thermophys, 1996, 17: 889–908

    Article  Google Scholar 

  29. Liu A, Beck T L. Vapor-liquid equilibria of binary and ternary mixtures containing methane, ethane, and carbon dioxide from Gibbs ensemble simulations. J Phys Chem B, 1998, 102: 7627–7631

    Article  Google Scholar 

  30. Peguin R P S, Kamath G, Potoff J J, et al. All-atom force field for the prediction of vapor-liquid equilibria and interfacial properties of HFA134a. J Phys Chem B, 2008, 113: 178–187

    Article  Google Scholar 

  31. Raabe G, Maginn E J. A force field for 3, 3, 3-fluoro-1-propenes, including HFO-1234yf. J Phys Chem B, 2010, 114: 10133–10142

    Article  Google Scholar 

  32. Raabe G. Molecular simulation studies on the vapor-liquid phase equilibria of binary mixtures of R-1234yf and R-1234ze (E) with R-32 and CO2. J Chem Engin Data, 2013, 58: 1867–1873

    Article  Google Scholar 

  33. Chen B, Siepmann J I. Transferable potentials for phase equilibria. 3. Explicit-hydrogen description of normal alkanes. J Phys Chem B, 1999, 103: 5370–5379

    Article  Google Scholar 

  34. Harris J G, Yung K H. Carbon dioxide’s liquid-vapor coexistence curve and critical properties as predicted by a simple molecular model. J Phys Chem, 1995, 99: 12021–12024

    Article  Google Scholar 

  35. Daridon J L, Saint-Guirons H, La Courette B, et al. A generalized process for phase equilibrium calculation with cubic equations of state. Int J Thermophys, 1993, 14: 1101–1108

    Article  Google Scholar 

  36. Grandjean L, de Hemptinne J C, Lugo R. Application of GC-PPC-SAFT EoS to ammonia and its mixtures. Fluid Phase Equilibr, 2014, 367: 159–172

    Article  Google Scholar 

  37. NguyenHuynh D, Passarello J P, Tobaly P, et al. Application of GC-SAFT EOS to polar systems using a segment approach. Fluid Phase Equilibr, 2008, 264: 62–75

    Article  Google Scholar 

  38. Gross J, Sadowski G. Application of the perturbed-chain SAFT equation of state to associating systems. Ind Eng Chem Res, 2002, 41: 5510–5515

    Article  Google Scholar 

  39. Diamantonis N I, Economou I G. Evaluation of statistical associating fluid theory (SAFT) and perturbed Chain-SAFT equations of state for the calculation of thermodynamic derivative properties of fluids related to carbon capture and sequestration. Energy Fuels, 2011, 25: 3334–3343

    Article  Google Scholar 

  40. Cornell W D, Cieplak P, Bayly C I, et al. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J Am Chem Soc, 1995, 117: 5179–5197

    Article  Google Scholar 

  41. MacKerell A D, Bashford D, Bellott M, et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B, 1998, 102: 3586–3616

    Article  Google Scholar 

  42. Jorgensen W L, Maxwell D S, Tirado-Rives J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J Am Chem Soc, 1996, 118: 11225–11236

    Article  Google Scholar 

  43. Panagiotopoulos A Z. Direct determination of phase coexistence properties of fluids by Monte Carlo simulation in a new ensemble. Mol Phys, 1987, 61: 813–826

    Article  Google Scholar 

  44. Kofke D A. Direct evaluation of phase coexistence by molecular simulation via integration along the saturation line. J Chem Phys, 1993, 98: 4149–4162

    Article  Google Scholar 

  45. Vrabec J, Stoll J, Hasse H. A set of molecular models for symmetric quadrupolar fluids. J Phys Chem B, 2001, 105: 12126–12133

    Article  Google Scholar 

  46. Potoff J J, Panagiotopoulos A Z. Critical point and phase behavior of the pure fluid and a Lennard-Jones mixture. J Chem Phys, 1998, 109: 10914–10920

    Article  Google Scholar 

  47. Allen M P, Tildesley D J. Computer Simulation of Liquids. Oxford: Clarendon, 1987

    MATH  Google Scholar 

  48. Kleinrahm R, Wagner W. Measurement and correlation of the equilibrium liquid and vapour densities and the vapour pressure along the coexistence curve of methane. J Chem Thermodyn, 1986, 18: 739–760

    Article  Google Scholar 

  49. Lemmon E W, Huber M L, McLinden M O. 2007, NIST Reference Fluid Thermodynamic and Transport Properties-REFPROP, NIST Standard Reference Database 23-Version 8.0

    Google Scholar 

  50. Duschek W, Kleinrahm R, Wagner W. Measurement and correlation of the (pressure, density, temperature) relation of carbon dioxide II. Saturated-liquid and saturated-vapour densities and the vapour pressure along the entire coexistence curve. J Chem Thermodyn, 1990, 22: 841–864

    Article  Google Scholar 

  51. Rowlinson J S, Swinton F L. Liquids and Liquid Mixtures. 3rd ed. London: Butterworth, 1982

    Google Scholar 

  52. Rowlinson J S, Widom B. Molecular Theory of Capillarity. Oxford: Clarendon Press, 1982

    Google Scholar 

  53. Davalos J, Anderson W R, Phelps R E, et al. Liquid-vapor equilibria at 250.00. deg. K for systems containing methane, ethane, and carbon dioxide. J Chem Eng Data, 1976, 21: 81–84

    Article  Google Scholar 

  54. Wei M S W, Brown T S, Kidnay A J, et al. Vapor+ liquid equilibria for the ternary system methane+ ethane+ carbon dioxide at 230 K and its constituent binaries at temperatures from 207 to 270 K. J Chem Eng Data, 1995, 40: 726–731

    Article  Google Scholar 

  55. Vrabec J, Stoll J, Hasse H. Molecular models of unlike interactions in fluid mixtures. Mol Sim, 2005, 31: 215–221

    Article  Google Scholar 

  56. Schnabel T, Vrabec J, Hasse H. Unlike Lennard-Jones parameters for vapor-liquid equilibria. Mol Liq, 2007, 135: 170–178

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Key Laboratory of Cryogenics, Technical Institute of Physics and Chemistry, Chinese Academy of Sciences, Beijing, 100190, China

    Zhi Yang, MaoQiong Gong, Yuan Zhou, XueQiang Dong, HuiYa Li & JianFeng Wu

  2. University of Chinese Academy of Sciences, Beijing, 100049, China

    Zhi Yang

  3. School of Energy and Power Engineering, Beihang University, Beijing, 100191, China

    XiaoDong Li

Authors
  1. Zhi Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. MaoQiong Gong
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yuan Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. XueQiang Dong
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. XiaoDong Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. HuiYa Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. JianFeng Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to MaoQiong Gong.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, Z., Gong, M., Zhou, Y. et al. Vapor-liquid equilibria of CH4, CO2 and their binary system CH4 + CO2: A comparison between the molecular simulation and equation of state. Sci. China Technol. Sci. 58, 650–658 (2015). https://doi.org/10.1007/s11431-015-5785-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11431-015-5785-4

Keywords

Search

Navigation