1 Introduction

Soil erosion and sedimentation are recognized globally as a critical problem (Pimentel 2006). On-site impacts of soil erosion include the degradation of soil structure (Zhang et al. 2007), depletion in soil carbon and nutrients (Bashagaluke et al. 2018), and a reduction in agricultural productivity (Bakker et al. 2007). However, off-site impacts (e.g., sedimentation) can be equally detrimental, leading to pollution and eutrophication of fresh and ocean waters (Zamparas and Zacharias 2014). The accurate identification and apportionment of sediment sources is necessary for developing targeted and effective sediment mitigation strategies to ensure the long-term sustainability of aquatic ecosystems and land resources (Collins and Walling 2004; Walling 2005; Owens et al. 2016).

The sediment fingerprinting method uses various characteristics of the soil and sediment to fingerprint possible sources, tracking back to potential land-uses, vegetation cover, or geological bedrock. However, classic fingerprinting approaches using geochemical (Batista et al. 2019) or fallout radionuclide tracers (Evrard et al. 2013) are often not suitable to provide information on land-use-specific sources. Compound specific stable isotopes (CSSI) of long chain fatty acids (LCFA) and alkanes have been used to apportion the relative contribution of different land-uses (Gibbs 2008; Alewell et al. 2016; Upadhayay et al. 2018a, b; Lavrieux et al. 2019).

The linear relationship between 13C depletion and LCFA elongation during biosynthesis occurs similarly in all land-uses, often causing multiple δ13C LCFA tracers to have co-linearity, resulting in a problematic one-dimensional mixing line (Alewell et al. 2016; Lavrieux et al. 2019; Cox et al. 2023). In particular, Cox et al. (2023) demonstrated that one-dimensional mixing lines have the potential to cause inaccurate apportionment estimates due to the misclassification of contributions of the central source(s) as contributions from sources at either endpoint. Additionally, Cox et al. (2023) demonstrated that additional co-linear tracers decrease the performance of the un-mixing model. Lavrieux et al. (2019) clearly illustrated the problematic mixing line when using δ13C values of LCFA (C24-C28) as tracers at Lake Baldegg (Canton Luzern, central Switzerland). The δ13C LCFA one-dimensional mixing line prevented meaningful sediment source estimates with the δ13C LCFA of forest and grassland source fingerprints plotting at either endpoint of a mixing line, with orchards and arable sources plotting on a line in between these two endmember sources. Furthermore, sediment δ13C FA24,26 values were found to be extremely depleted in 13C and outside the range of the source values potentially indicative of an unknown source.

Lavrieux et al. (2019) hypothesized that the missing source was of aquatic origins. The δ13C FA28 values of source soils bracketed all sediment δ13C FA28 values except 1956 and 1965. 1956 coincided with evidence of large turbidites in Lake Baldegg (Lotter et al. 1997), and 1965 had the highest TOC and TN levels over the 130-year record suggesting primary production was at its maximum (Lotter et al. 1997). Considering the remaining sediments are within the δ13C FA28 value source range, Lavrieux et al. (2019) presumed that the unknown source did not significantly contribute to the δ13C FA28 sediment fingerprint for the majority of years. Nonetheless, for accurate land-use-specific source apportionment in Lake Baldegg, it is evident that the incorporation of an additional non-aquatic and land-use-specific tracer is necessary to expand the mixing line into a suitable mixing polygon. In this context, we propose the incorporation of δ13C values of lignin-derived methoxy groups (δ13C LMeO) as a promising novel tracer.

Lignin and its copper oxidation products have been employed to discriminate sediment sources (angiosperms vs gymnosperms, terrestrial vs marine, and land-uses) (Goñi et al. 1998; Goñi et al. 2000; Kuzyk et al. 2008; Rezende et al. 2010). However, the application of lignin copper oxidation products has limitations. These include reduced source discrimination (Thevenot et al. 2010), modifications to the monomer composition during degradation (Dümig et al. 2009), and fractionation occurring during soil phase transitions (Hernes et al. 2007). Methoxy groups (MeO, molecular formular: CH3O) comprise approximately 10–25% of lignin monomers and 2.5% of the total carbon content in the terrestrial biosphere (Galbally and Kirstine 2002). MeO predominantly originate from lignin (ether bound MeO groups) and pectin (ester bound MeO groups). While pectin, a polysaccharide, can be found in some algae species (Domozych et al. 2014), lignin is exclusively found in higher terrestrial plants (Boerjan et al. 2003). The selective removal of ester bound pectin MeO by alkaline hydrolysis allows for the analysis of the remaining terrestrial derived lignin MeO (LMeO) through the conversion of the residual LMeO groups to methyl iodide (MeI) using the Zeisel method (Zeisel 1885).

Two prerequisites are required for a successful fingerprinting tracer: the ability to discriminate between land-uses (e.g., forest, arable, pasture), and secondly, to have predictable or no modification of tracer signature from source to sink (e.g., conservative behavior) (Motha et al. 2002; Koiter et al. 2013; Belmont et al. 2014; García-Comendador et al. 2023). LMeO display not only large 13C discrimination between C3, C4, and CAM plants (Keppler et al. 2004), but are potentially appropriate for land-use-specific source discrimination between C3 vegetation. The conservativeness of LMeO has yet to be explored fully for fingerprinting applications. Litter bag experiments in soils measuring bulk δ13C MeO (pectin and lignin MeO) indicated small isotopic fractionation during degradation (Anhäuser et al. 2015); however, this was reasoned to be due to the preferential degradation of pectin. Analysis of the MeO δ13C values from wood to coal indicated significant fractionation during degradation, with Rayleigh coefficients of − 15‰ being calculated. Considering we would not expect LMeO degradation on the same scale as the wood-to-coal continuum (remaining MeO fraction in coal ca. 10−4) (Lloyd et al. 2021), we would expect isotopic fractionation to be minimal within LMeO concentrations in soil and sediments.

The utilization of CSSI tracers to apportion sediment sources has the implicit assumption that the sediment isotopic fingerprint originates from the input and mixing of the isotopic fingerprint of the possible terrestrial source soils (i.e., mineral horizons). However, this presupposes the absence of CSSI tracers from additional sources present in the sediment. While lake sediments are largely comprised of clastic materials (i.e., clay, silt and sand), they also contain an organic fraction in the form of mineral-associated organic matter (MAOM), plant debris (terrestrial particulate organic matter- POMterr), and particulate organic matter from aquatic sources (POMaq). Since the primary goal of sediment fingerprinting is to provide information for soil erosion mitigation policies, the main aim of using CSSI tracers is the apportionment of the tracers in the MAOM fraction and the subsequent conversion to soil proportions using concentration dependency. Thus, any contribution of the sediment CSSI signal from POMterr or POMaq will result in erroneous MAOM sediment source attribution.

POMaq is known to be an important factor in lacustrine biochemical cycles and contributes to sediment organic matter (Xu et al. 2019; Wynants et al. 2021). However, to accurately apportion sediment soil sources, tracers are specifically used which are not substantially present in POMaq (e.g., LCFA and LMeO). However, non-MAOM sources of carbon (and CSSIs) such as POMterr, can enter the watercourses through aeolian transport, leaching, and surface wash-off during rain events. As suggested by Wiltshire et al. (2022), the inclusion of POMterr in the sediment isotopic fingerprint might cause the overestimation of forest sediment input. While the physical separation of POM and MAOM has been achieved previously by density centrifugation (Cui et al. 2016), relatively large amounts of sample are required (5 g). Distinguishing between MAOM and POMterr as separate endmembers using δ13C LCFA is difficult due to the small isotopic difference (Wiltshire et al. 2022). Compared to LCFAs, LMeO have a much larger δ13C discrimination between woody material and leaves (ca. − 20‰) (Keppler et al. 2004), potentially resulting in a larger difference of δ13C between MAOM and POMterr. Although multiple studies utilize proxies, ratios and tracers to determine the POMaq and POMterr contribution to the sediment (Derrien et al. 2017), there are currently no studies attempting to disentangle the POMterr and MAOM contribution and the subsequent land-use-specific apportionment of MAOM.

Currently in sediment fingerprinting research, there is extensive literature dedicated to tracer selection (Laceby et al. 2015; Smith et al. 2018; Batista et al. 2019; Vale et al. 2022; Cox et al. 2023). Despite the wealth of information surrounding this initial stage, the subsequent tracer selection steps often follow a reductionist approach, systematically eliminating tracers through a series of selection tests. Beyond whether to choose CSSI, geochemical or radionuclides tracers, there appears to be a lack of literature on additive tracer selection in which tracers are added for targeted discrimination. We propose a paradigm shift towards a more purpose-oriented tracer selection strategy, in which tracers are intentionally incorporated to serve a specific discrimination objective (Cox et al. 2023). Here, we use the average alkane chain length (ACL, 21–33 C odd alkanes). While the ACL may not be able to discriminate between specific land-uses (Wiltshire et al. 2022), ACL can be used as an additional tracer to enhance the discrimination of POMterr and MAOM in the sediment. Moreover, the extraction and analysis of alkanes often coincide with CSSI analysis, providing readily available data for retrospective and future studies.

The use of CSSI δ13C tracers for historical sediment apportionment requires Suess correction (i.e., correcting the isotopic values for the changing atmospheric δ13CO2 composition), during the last 100 years due to anthropogenic fossil fuel burning (Verburg 2007; Gibbs et al. 2014). However, in sediment fingerprinting, Suess corrections are often either omitted under the assumption that variability induced by the Suess effect is negligible when compared to the source uncertainty (Brandt et al. 2018), or a single mean residence time (MRT) is used (Bravo-Linares et al. 2020). To accurately model the possible Suess effect on isotopic tracers, a range of MRTs should be assessed. The MRTs of FAs varies from decades to millennia (Lützow et al. 2006; Wiesenberg et al. 2010). While the MRT of LMeO has not been investigated, the MRT of lignin has been estimated to be comparatively shorter than FAs (5–26 years for pasture, 9–38 years for arable soils) (Heim and Schmidt 2007). As the exact MRT for each isotopic tracer is dependent on the soil ecosystem and soil properties (Schmidt et al. 2011), to accurately model the possible Suess effects, three MRTs (10 years, 30 years, and 100 years) were considered.

Point in polygon/mixing space tests (e.g., range/bracket tests) are a standard procedure in sediment fingerprinting (Collins et al. 2020). Polygons (mixing spaces) are drawn around the sources to identify sediment values which are located outside the mixing space. Sediment fingerprints outside the polygon then indicate that with the current sources (presuming no modification of the tracer), the mixture is highly implausible or even impossible. However, the sediment isotopic fingerprint is known to be impacted not only by the proportions of each source and the sources isotopic value, but also the concentration of the CSSI in each source (Upadhayay et al. 2018a, b) and as such, this should be reflected in the possible mixing space.

In this study, first, we test the accuracy and precision of δ13C LMeO, ACL, and δ13C FA28 as a tracer set using mathematical mixtures. Second, the sediment contribution from the main land-uses was then estimated for the last 130 years for a sediment core from Lake Baldegg. Third, we explore the impact of MRTs on Suess corrections, by comparing three different MRTs for both isotopic tracers. Fourth, we test the hypothesis that high forest contribution in sediment fingerprinting might be a result of the misclassification of POMterr, if POMterr is not considered as a separate source. For this, we group forest and POMterr into a single source to simulate tracers which cannot discriminate between these sources and compare against the ungrouped results.

The objective of this study is to advance our understanding of CSSI sediment fingerprinting by addressing the challenges associated with these tracers, including the presence of one-dimensional mixing lines, aquatic and POMterr sources of organic tracers, accounting for tracer MRTs when applying Suess corrections, and the improbable high contribution of forest soils to sediment. This study aims to enhance the accuracy of land-use specific mixing models and ultimately facilitate better techniques for monitoring sediment erosion mitigation strategies. This will be accomplished by (i) introducing an additional land-use-specific tracer, (ii) incorporating multiple Suess effects, and (iii) investigating the influence of POMterr on apportionment estimates. This study aims to improve land-use specific sediment source apportionment using CSSI tracers to aid targeted sediment management interventions. This approach is particularly valuable for ensuring the maintenance of both soil health and water quality and can be applied to regions of similar temperate climate and agricultural practices.

2 Methods

2.1 Study site

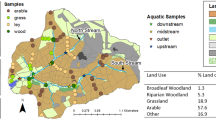
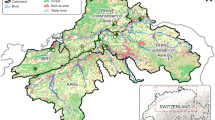
Lake Baldegg is a glacial lake located in the central Swiss plateau situated 463 m above sea level (coordinates: 47°1200 00 N, 8°1,504,000 E) (Fig. 1). It extends from north to south with a maximum depth of 66 m and mean depth of 33 m. The lake covers a surface area of 5.2 km2 and holds a volume of 0.173 km3. The water residence time of Lake Baldegg has been estimated to be 4.3 years, with the outflow located at its northern end. The catchment area surrounding the lake, excluding the lake surface area, spans 68.2 km2 (Wehrli et al. 1997). On the year of source sampling (2016), 77% of the catchment was being used for agriculture and 12% was covered by forest and 5% urbanized (Lavrieux et al. 2019).

Fig. 1
figure 1

Connectivity and land-use of the Lake Baldegg (Canton Luzern; Central Switzerland) catchment with source soils and sediment coring sampling sites from Lavrieux et al. (2019) marked with the “O” symbol

Full size image

Over the last century, Lake Baldegg has shown an extensive history of eutrophication (Lotter et al. 1997). Since the beginning of the twentieth century, the discharge of untreated waste and agricultural runoff into the lake has increased due to population growth and the intensification of agriculture. The rise of nutrients led to an increase in primary production from 1885 to 1970. The geographical setting of Lake Baldegg prevents water column mixing and resulted in permanent anoxic conditions in the hypolimnion. The anoxic conditions prohibited bioturbation and resulted in seasonal material being preserved in laminated varved layers which have been used for core dating (Lotter et al. 1997; Wehrli et al. 1997). Additionally, the sediment core contained multiple turbidites. Most turbidites which originate in the Baldegg catchment are transported into the lake during heavy rainfall or flood events (Lotter et al. 1997).

2.2 Sampling

In this study, we reanalyzed source samples presented in Lavrieux et al. (2019) and POMterr (leaves, pine needles, and the Oi organic horizon) from Hirave et al. (2020). Samples were stored dry at 4 °C in a sample archive (Department of Environmental Sciences, University of Basel). Using a modified sediment connectivity index (Borselli et al. 2008), Lavrieux et al. (2019) selected source sample locations based on high connectivity and representing the main land-uses in the catchment (arable lands, permanent grasslands, temporary grasslands, forests, orchards). Importantly, only A horizons (mineral soil) were collected from each source sample location and sieved to 2 mm. In the case of forest samples, plant debris was removed from source samples.

Subsamples from the sediment core Ba-09–03 (Lavrieux et al. 2019) were reanalyzed. As described in Lavrieux et al. (2019), the varved sediment allowed seasonal bi-annual dating back to 1885. Subsamples had a 3-cm thickness (Table S2) and the mean age is reported throughout. For further core sub sampling information, see Lavrieux et al. (2019). Details on sampling the sediment core, as well as the full core age–depth model can be found in van Raden (2012) and Kind (2012).

Usually, sediment source attributions are limited to relative source contributions. To convert these relative contributions to absolute sediment accumulated from each source, the mean sediment accumulation rate (SAR) from the sediment cores BA93-C and BA93-BA were extracted from Lotter et al. (1997). Lotter et al. (1997) determined SAR by varve counting and measuring the thickness of sediment deposit annually. The SAR was then used to convert source proportions to annually deposited sediment.

For improved source discrimination, temporary and permanent grassland were grouped into one pasture source. Although at the time of sampling, orchards represented only 1% of the catchment; aerial photographs demonstrate orchards to be a more significant land cover in the catchment since 1950. However, orchard source samples taken by Lavrieux et al. (2019) are from modern orchard plantations, which consist of highly dense fruit trees in rows. Historically, fruit trees have been grown in pastures or meadow fields at low density and have isotopic signatures that are similar to pastures or meadows. As such, the orchard source samples taken by Lavrieux et al. (2019) are not representative of the orchard land cover for the last 130 years and therefore have not been included as a sediment source.

2.3 Laboratory analysis

2.3.1 Sample preparation

Adapting the method of Greule and Keppler (2011), ester bound MeO groups (predominantly of pectin origin) were removed from the sediment and source soils by the conversion to methanol by alkaline hydrolysis. Briefly, 1 ml of 1 M NaOH was added to approximately 150 mg of soil/sediment in 1.5-ml vials; samples were capped and heated at 90 °C for 4 h. Samples were then uncapped and dried at 60 °C in a sand bath. To ensure hydroiodic acid (HI) is not used up by the neutralization of NaOH or the removal carbonates, 100 µl deionized water was added to each sample followed by acid fumigation for 24 h in 37% fuming hydrochloric acid (HCl). Samples were then dried again at 60 °C in a sand bath. Residual LMeO groups (ether bound) were converted to MeI by the addition of 500 µl HI 57% (Sigma Aldrich, Stabilized) and heated for 1 h at 130 °C. Samples were left to equilibrate at room temperature for 1 h before GC-FID and GC-IRMS analysis (Greule et al. 2009).

2.3.2 Lignin methoxy concentration

The analysis of MeI was conducted using static headspace analysis, adapting the procedure outlined in Greule et al. (2009). A headspace volume of 10–90 µl was manually injected (Hamilton, 100 µl, gas tight, side-port) into the Trace Ultra gas chromatograph (GC) with a flame ionization detector system (FID; Thermo Scientific, Waltham, MA 02451, USA). Conditions of the GC-FID were set at; 200 °C inlet temperature, 1.8 ml/ min He flow rate, and an isothermal oven temperature at 65 °C resulting in an approximate elution time of 4 min. The MeI analyte was quantified using an external calibration curve generated from compounds with known MeO concentrations (i.e., Vanillin, (Sigma Aldrich, 99%) and HUGB3 (Greule et al. 2020)). The concentration of source samples was analyzed with triplicate samples with single injection. Due to minimal sediment sample availability (ca. 200 mg), the concentration of sediment samples was analyzed by triplicate injection of a single sample.

The calibration of MeO quantification ranged from 0.001 to 0.5 mg MeO, with a r2 > 0.97 (Pearson’s correlation) for all analysis. Deviation from a linear relationship was not found between analyte content and instrument response using static headspace injection as reported by Lee et al. (2019) and as such, we found injection of head space a simple and effective methodology of quantification for soil content of LMeO.

2.3.3 Lignin methoxy isotopic values

The δ13C isotopic composition of MeI was determined using a Trace Ultra GC instrument interfaced online through a GC-Isolink to a Conflo IV and Delta V Advantage isotope ratio mass spectrometer (Thermo Scientific, Waltham, MA 02451, USA) via an oxidation reactor. A reduction stage was fitted to remove potential corrosive contamination (Feakins et al. 2013) (see Fig. S1 for instrument schematic). The inlet temperature was set to 200 °C; the column flow rate (He) was 1.8 ml min−1. The initial oven temperature was set to 30 °C for 3.8 min, ramp at 30 °C per minute until 100 °C.

In this paper, all stable carbon isotope ratios are expressed in the conventional “delta” δ notation, meaning the relative difference of the isotope ratio of a substance compared to the standard substance Vienna Peedee Belemnite (VPDB). Reference materials HUGB1 (δ13CV-PDB =  − 50.17 ± 0.08‰) and HUGB4 (δ13CV-PDB =  − 30.07 ± 0.10‰) were used for the normalization of sample isotopic ratios (Greule et al. 2019, 2020). HUGB3 (δ13CV-PDB =  − 29.30 ± 0.10‰) was treated identically to samples and used as a quality control sample throughout the run.

Triplicate injections of MeI were used to determine the instrumental uncertainty of isotopic analysis. We found the mean instrumental precision (1 SD) to be 0.16‰ over all sequences. Single injection of triplicate source samples had a mean SD of 0.3‰. Using a two-point calibration of HUGB1 and HUGB4, and HUGB3 as a quality control sample throughout, HUGB3 was shown to have a RSME of 0.4‰. For information on the FA and ACL method and analytical precision, see Hirave et al. (2020) and Lavrieux et al. (2019).

2.4 Suess corrections

To account for a time lag between atmospheric changes and changes in the soil, different MRTs were compared (10 years, 30 years, and 100 years). Following an identical methodology to Lavrieux et al. (2019), isotopic values of both sources and sediments were corrected using the atmospheric CO2 curve of Verburg (2007) for multiple MRTs. Equation (1) was applied to correct isotopic values to the pre-industrial era (1840).

$$\delta {}^{13}C{ Soil}_{ \left(t+1\right)}=\left(1-\frac{1}{R} \right)\delta {}^{13}C {Soil}_{\left(t\right)}+\frac{1}{R}(\delta {}^{13}C {Soil}_{\left(t0\right) }+(\delta {}^{13}C {Atmosphere}_{\left(t+1\right)}-\delta {}^{13}C {Atmosphere}_{\left(t0\right)} ))$$
(1)

We assigned the variable “t” as the year of observation, with “t0” corresponding to the year 1840. “R” represents the MRT of the isotopic tracer in years (10 years, 30 years, and 100 years). We assumed that there were only marginal changes in the δ13C values of atmospheric CO2 prior to 1840. The calculated change in δ13C values after 1840 is based on the atmospheric data from Verburg (2007). We also maintained the assumption of stability in the soil organic carbon pool size over time and no changes in the isotopic fractionation during CO2 uptake due to increased atmospheric CO2 concentrations.

2.5 Defining a mixing space and sediment classification

Point in polygon/ mixing space tests (e.g., range/bracket tests) are standard practice in sediment fingerprinting (Collins et al. 2020). They are designed to identify mixtures which are located outside of the possible mixing space of the sources, which suggests the mixture is not possible from the current sources and will result in erroneous unmixing. Although point in polygon tests are standard practices, they have yet to be adapted to concentration dependent tracers (e.g., CSSI). To define a concentration dependent mixing space, the open-source python script of Cox et al. (2023) was used to generate mathematical mixtures. For each Suess correction, 300 concentration dependent mathematical mixtures were created by weighting the mean source isotopic tracer values by their respective mean concentrations and multiplying by 300 randomly selected proportions with the condition that all proportions must sum to one.

A limitation of using the methodology of Cox et al. (2023) is that the source variation is not incorporated. We attempted to incorporate the source variation by expanding the mixing space to include all source samples. While MixSIAR uses the mean and SD, we suggest that even though highly improbable, sediment could be derived from an outlying source sample outside the SD of source value. As MixSIAR incorporates source variance, the mixing space is diffused and lacks a precisely defined boundary. Whether a sediment is within the mixing space is probability based, and as such is non-binary. The position of the sediment fingerprint may be around the diffuse boundary of the possible mixing space (mixing horizon). Mixing horizons can be defined as the boundary in which the unmixing results are sensical. Beyond this horizon (in a three-source model of sources X, Y and Z), the model’s calculation is dominated by a reduction in contribution X, leading to imputation of Y and Z source contributions to satisfy the condition that the sum of contributions should equal 1. Importantly, this is the case even when the sediment moves away from the mixing space and the X, Y, and Z sources. This must be taken into consideration when interpreting unmixing results with the comparison of bi-plots.

Using bi-plots, we classified sediment values into three classes: (A) inside the mixing space, (B) located around the mixing space horizon in the expanded mixing space, and (C) outside the expanded mixing space. Sediments are classified on their lowest class in all bi-plots (A → B → C). Class C sediments are excluded from interpretation due to a high probability of erroneous mixing results. The coherence of the apportionment of sediments in Class B is tested using a range test. The range test consists of determining if the sediment apportionment is within the range of the Class A sediments on either side (the years before and after). This method of evaluating coherence relies on the assumption that the transition of sediment sources occurs gradually, and the sediment being evaluated exhibits comparable source contributions to the bracketing samples which may not hold true for all cases. Sediment apportionments which show non-coherence are interpreted with caution and potentially excluded from interpretation.

2.6 Unmixing

Source apportionments were estimated using the open-source R package, MixSIAR (Stock et al. 2018). Using δ13C of FA28, LMeO and the ratio ACL (alkanes 21–31 C) as a tracer set, MixSIAR was run with concentration dependency (mean concentrations of each source) and uninformative priors. As demonstrated by Lavrieux et al. (2019) only δ13C FA28 source values bracketed all sediment values (except 1965 and 1956), as such δ13C FA24,26 were excluded from the tracer set. Additionally, source soils in the Baldegg catchment displayed δ13C FA co-linearities. The use of multiple tracers with co-linearities has been demonstrated to decrease model performance (Cox et al. 2023). Given that ACL represents a ratio, the ACL concentration was set to value of 1 for all sources to remove its concentration dependency. All MixSIAR runs used the same model parameters: chains = 3, chain length = 3,000,000, thin = 500, burn = 2,700,000 with a “very long” run time. The convergence of the mixing model was assessed by using the Gelman-Rubin diagnostic, with model output being rejected if variables scored > 1.05. Due to minimal amount of sediment core samples available (ca. 200 mg), a single mixture of each sample is unmixed using the “process only” error structure, in which the variation in the mixtures is assumed to be fully dependent on the weighted source variation.

There are some often overlooked limitations when running the “process only” error structure in MixSIAR. Bayesian mixing models incorporate probability distributions for both sources and mixtures. In this study, only a single sediment replicate was available to represent the mixture; as such, we cannot empirically determine a probability distribution for each layer in a sediment core. In such cases, MixSIAR users rely on the “process only” error structure, where the model derives the probability distribution for the mixture from the variance of the sources (Smith et al. 2018). The intricate nature of complex mixing systems inevitably yields disparities in both source and mixture variances, and as such, the “process only” error structure has limitations in incorporating the natural variation in the sediment samples. Nevertheless, the “process only” error structure is frequently applied due to lack of sediment replicates or the need for higher resolution apportionment estimates.

2.7 Evaluation of unmixing performance

To evaluate the accuracy and precision of the model, mathematical mixtures previously created to determine the mixing space were unmixed in identical manner to sediment samples. Results of the estimated proportions of mathematical mixtures were then compared to the known mixture proportions. As advocated by Batista et al. (2022a, b), the evaluation of MixSIAR’s probabilistic output should be probabilistic rather than deterministic. As such, we use the continuously ranked probability score (CRPS) (Matheson and Winkler 1976). Model comparisons between tracer sets were evaluated using the continuously ranked probability skill score (CRP skill score) (Pedro et al. 2018; Cox et al. 2023).

2.8 Removal of the POMterr fingerprint from sediment

Source apportionments were converted into g cm−2 y−1 deposited by mineral sources using Eq. (2). First, source proportions were corrected to reflect contribution from only mineral sources (i.e., the removal of the POMterr fraction) by converting mean MAOM source estimates to the percentage of the total MAOM fraction (MAOM fraction = Forest % + arable % + pasture %). To determine the sediment accumulated per year by each source, the MAOM apportionments were then multiplied by the mean SAR extracted from Lotter et al. (1997). The uncertainty of the sediment accumulated per source was calculated by the standard deviation (SD) of the MixSIAR outputs being treated identically to the apportionment estimates using Eq. (3). Furthermore, it is essential to note that the exclusion of POMterr was carried out using mean values, potentially introducing an unquantified source of additional uncertainty.

$$Sediment\ accumulated\ per\ year\ by\ source = (s\mathrm{\%}/( F\mathrm{\% }+A\mathrm{\%}+P\mathrm{\%}))* SAR$$
(2)
$$SD\ of\ sediment\ accumulated\ per\ year\ by\ source= (sSD /( FSD +ASD+PSD))* SAR$$
(3)

In this context, “s%” is the model estimates for either forest, arable, or pasture (the source undergoing transformation). F%, A%, and P% denote the model estimates for MAOM sources. SAR is extrapolated from Lotter et al. (1997). Since SAR were only available from 1885 to 1990, source apportionment estimates were only converted into g cm−2 y−1 between these years.

3 Results and discussion

3.1 Isotopic fingerprints of soils, POMterr, and sediments

Mean soil δ13C LMeO values ranged from − 39.2 to − 47.8‰. Arable LMeO had the highest 13C content (δ13C, − 41.7‰; SD, 1.9‰) followed by forest (δ13C, − 43.2‰; SD, 0.54‰) then pasture (δ13C, − 44.1‰; SD, 2.0‰) (Table 1). Similar to Lavrieux et al. (2019) discussing δ13C FA enrichment in arable soils, we suggest the 13C enriched LMeO arable signature can be reasoned to be a result of rotational crop system in Switzerland, with a legacy maize (C4) signal contributing to the arable fingerprint. The observed similarities between forest and pasture can be explained by the dominance of C3 species in both sources. This suggests that the δ13C variance between C3 plants in LMeO may be less than in FA. In general, δ13C LMeO values of the sediment fall within the sources isotopic range (min–max ± SD) (Fig. 2, Table 1). However, sediment from the years 1971 and 1958 are enriched in 13C LMeO compared to the sources and outside the mixing space (Fig. 2). In these years, large turbidites are recorded in the sediment core representing a flood or earthquake event. Such events may trigger subsurface erosion of older deep soils potentially containing isotopically enriched LMeO. The δ13C LMeO of POMterr had a mean value of − 52.5‰ (SD, 5.9‰), with maple leaves being 13C depleted in comparison to the rest of the POMterr. δ13C LMeO values of  POMterr are within range of leaves previously reported by Keppler et al. (2004). The δ13C LMeO values of soils are novel and not available in the current literature. Our results report the δ13C LMeO values of soil was between wood (− 25 to − 28‰) and tree leaves (mean ~  − 60‰, ranging from − 40 to − 77‰ including C3 and C4 plants) (Keppler et al. 2004; Greule et al. 2009, 2020). Considering that soil organic carbon is a mixture of both woody (roots and above ground woody material) and leaf material, our findings of soil δ13C LMeO values of − 39.2 to − 47.8‰ are within a reasonable range.

Table 1 Summary of δ13C values and concentrations of LMeO and FA28 of sources and sediment (see Table S1 for the full ungrouped dataset and Fig. S2 for PCA)
Full size table
Fig. 2
figure 2

Isotopic values of δ13C LMeO (this study) and δ13C FA28 and ACL (from Hirave et al. (2021) and Lavrieux et al. (2019)) of source soils, POMterr, and sediment. The boxes represent 25, 50, and 75% quantiles with whiskers showing a 1.5 interquartile range

Full size image

The δ13C FA28 values of source soils bracket all sediment values apart from 1965 and 1958 (min–max ± SD). The inclusion of POMterr expanded the range to bracket 1958, with only 1965 to not be within range. 1965 has been suggested to be the peak of eutrophication (Lotter et al. 1997), and as such may contain non-terrestrial derived FA28 which have been hypothesized to be produced in hyper-eutrophic lakes (Van Bree et al. 2018; Lavrieux et al. 2019). The large discrimination of POMterr and MAOM using ACL indicates that ACL hold significant potential as a proficient tracer to aid with the estimation of POMterr contribution. Although only a fraction of the source samples was analyzed for alkanes by Lavrieux et al. (2019) (Table 1), ACL from source soils presented here agree with ACL reported in literature (Cooper et al. 2015; Chen et al. 2016; Wiltshire et al. 2023).

3.2 Defining a mixing space and Suess-corrected sediment classification

Fingerprinting with δ13C FA tracers often present a one-dimensional mixing line leading to potentially inaccurate sediment apportionment estimates. In our findings, incorporating δ13C LMeO values as an additional tracer expands the FA mixing line presented in Lavrieux et al. (2019), creating a more suitable mixing space (Fig. 3). This expansion of the mixing space allows for the use of mixing models with significantly reduced misclassification of the central source as contribution from source(s) from either end point (Cox et al. 2023).

Fig. 3
figure 3

Bi-plots of soil sources, POMterr, and sediment fingerprints illustrating the expansion of the mixing space using ACL and δ13C LMeO tracers of non-Suess corrected values. Error bars are shown on the mean source values and calculated as 1 SD of the source variation

Full size image

Concentration dependent mathematical mixtures were used to define the mixing space and identify sediment samples outside the mixing space. The fingerprints of mathematical mixtures illustrated on Fig. 4 demonstrate how the mathematical mixtures are highly weighted by the concentration dependency of δ13C LMeO values. Interestingly, the mixing space (green polygon-defined by the mathematical mixtures) is not limited to the convex hull of source means, suggesting traditional tests of conservatism should be questioned when concentration dependency is involved. Considering only the mean source values were used to generate the mixtures, we would assume the incorporation of source variation in the generation of mathematical mixtures would increase the mixing space (yellow polygon) and provide a more accurate mixing space of possible sediment fingerprints.

Fig. 4
figure 4

Bi-plots of sources before and after Suess correction using three different MRTs (10, 30, and 100 years). The mean mixing space is defined as the area around the location of the mathematical mixtures (green polygon). The green mixing space is then expanded to incorperate all source samples (yellow polygon). Full labeled bi-plots are available in supplementary (Figs. S3, S4, S5, and S6)

Full size image

Isotopic fingerprints of source soils, POMterr, and sediment were corrected for the Suess effect using thee different MRTs (Table S2 and S3). Suess-corrected sediment samples are classsifed into the following groups: sediments are within the mathmatical mixture mixing space (Class A, green), located around the mixing horizon (Class B, orange), or outside the expanded mixing space (Class C, red) (Fig. 5). Without any Suess correction,14% (1945, 1951, and 1977) are in Class B (around the mixing horizon) and 24% of sediment values are in Class C (outside the mixing space, Fig. 5). Results of the 10-year MRT show 14% of sediments in Class B and a higher number of sediment values in Class C (38%). The 30-year MRT-corrected sediments had 19% of samples in Class B and 24% in Class C. The 100-year MRT corrections have a higher number of sediment values within the mixing space with 29% in Class B and only 14% being in Class C, and all Suess corrections depict the 1971, 1965, and 1958 to be outside the mixing space (Class C). 1970 and 1958 coincide with high SAR (Lotter et al. 1997). 1965 was suggested to be the peak of eutrophication and as such may contain significant concentrations of non-terrestrial material (Lotter et al. 1997).

Fig. 5
figure 5

The identification of Suess-corrected sediment samples which are within the mixing space (Class A, green), located around the mixing horizon (Class B, orange), and outside the expanded mixing space (Class C, red)

Full size image

Particle size is another possible area of uncertainty and reasoning for Class C sediments; the particle size distribution was not assessed by Lavrieux et al. (2019). The depleted isotope tracers of sediment years associated with turbidites were speculated to arise from the sediment originating from subsurface erosion. However, it may also be a result of particle size selectivity during these events (Laceby et al. 2017). As there was insufficient material available to assess for particle size or subsurface contribution analysis, future research will have to assess these potential areas of uncertainty.

While multiple MRT were applied to accurately model the effect of different Suess corrections, here, we used the same MRT for both FA and LMeO and for each source; however, in reality, this is unlikely. To improve the accuracy of modelling the Suess effect on historical records, multiple iterations of the different MRT for all tracers and sources separately could be applied. However, we find our approach as an appropriate starting point for using multiple MRT Suess corrections for CSSI fingerprinting. While we have modelled the Suess effect by applying a wide range of mean residency times, sediment which is outside the mixing space might also arise from an overcorrection using a MRT of 10 years. Additionally, it is important to acknowledge the relatively low number of samples associated sediment apportionment using CSSI tracers may impede capturing the full source variance or even missing sources.

3.3 Assessment of model and tracer selection performance

As suggested by Cox et al. (2023), concentration dependent mathematical mixtures (n = 300) (Fig. 4) were used to test performance of the model and tracer suites. Considering mathematical mixtures are generated from only source values, Suess corrections do not significantly affect the mixing space (illustrated in Fig. 4), and as such, we find the evaluation of the non-Suess-corrected mathematical mixtures applicable to all MRTs. Figure 6A shows the estimated proportions vs the known proportions of the mathematical mixtures using the δ13C FA28 and δ13C LMeO tracer set, with the 1:1 line indicating a perfect fit. Results show the overestimation of arable contribution (until ca. 50% contribution), consequently causing an underestimation in forest and pasture contribution estimates. POMterr has a relatively accurate and highly certain estimate at lower contributions, while the performance of estimates slightly decreases with increasing POMterr contribution. Extremely low known proportions of POMterr of two mixtures appears to have highly inaccurate estimates, both mixtures contain almost 0% contribution from POM. Using CRPS, the performance of the model was evaluated and forest, pasture, and POMterr had similar performances, with a median CRPS of 0.06, 0.05, and 0.05, respectively. Arable was demonstrated to have the lowest performance (CRPS 0.11), demonstrating the effect of a lower source discrimination. The higher CRPS score of arable can be attributed to more centralized position and reduced source discrimination between the other source (PCA supplied in Fig. S2), causing a higher likelihood for misclassification. The reduced source discrimination may be result of the legacy isotopic signal of forest present after the deforestation and conversion to arable fields.

Fig. 6
figure 6

Estimated proportions vs known mixture proportion for different tracer sets, with no Suess correction being applied. The solid line indicating perfect fit (estimated proportion = known proportion). A δ13C LMeO and δ13C FA28. B δ13C LMeO, δ13C FA28, and ACL. The model performance is denoted by the CRPS value

Full size image

The inclusion of ACL improves the model performance (Fig. 6B) (Forest CRPS, 0.04; arable, 0.06; pasture, 0.03; and POMterr, 0.03). Using the CRP skill score, the inclusion of ACL improved the average model performance by 39% (Forest CRP skill score, 38%; arable, 43%; pasture, 37%; POMterr, 39%). Additionally, the higher sensitivity of the arable estimates to changing source contributions is illustrated in Fig. 6B. However, arable estimates still displayed an overestimation and underestimation of lower and higher known contributions, respectively. Apart from two extremely low POMterr contribution mixtures, POMterr estimates are very accurate. Results of unmixing the mathematical mixtures had no non-sensical results caused by mixtures being outside of the “traditional” convex hull mixing space, demonstrating the need to reassess the current approach to the frequently used point in polygon tests for concentration dependent tracers.

One of the options when using the MixSIAR model is the flexible Bayesian framework incorporating adaptable error structures. The “process error” structure is often used in the sediment fingerprinting literature, where the variation in the mixtures is only dependent on variation in the sources, while not incorporating the variation in the mixture (e.g., target sediment) (Smith et al. 2018). While this error structure may not be optimal for accounting for variation in sediment core samples, the use of mathematical mixtures allows for the evaluation of the errors associated with the apportionment and how much confidence should be applied to the model results. Although both mathematical mixtures and sediments are unmixed identically, the omission of sediment variance limits the capability of the MixSIAR model to propagate the inherent variance within the sediment samples to the posterior distributions in the model outputs. For catchment sediment systems, the “residual error only” structure is preferable since it better represents erosion and sediment transport processes (Smith et al. 2018). Here, the “process only” error structure was selected due to limited sediment sample availability, which is a frequent issue for sediment cores due to their limited sample mass. Considering the potential implications of not incorporating the variation in the sediment mixtures, future sediment core fingerprinting approaches should incorporate multiple sediment mixtures either by (i) sampling multiple cores, (ii) increasing the number of samples per core sample, or (iii) grouping core sections by their age and/or depth. Future work testing different error structures using mathematical mixtures that incorporate both sediment and source variance could significantly aid in improving the fingerprinting method.

3.4 Relative proportion of POMterr to sediment

Here, we used the δ13C LMeO, δ13C FA28, and ACL tracer set to determine the relative contribution of POMterr to the sediment record. To determine the relative contribution of POMterr to the sediment, mineral source soils and POMterr were unmixed simultaneously using MixSIAR. Three different MRT scenarios are used to model the possible Suess effect on the apportionment estimates. Class B sediments are checked for coherence with the assumption that they should fit within the range of years bracketing (Table S4). Furthermore, sediment values which are Class C (Fig. 5) are not considered in Fig. 7A in our interpretation of historical POMterr trends.

Fig. 7
figure 7

A Estimated proportion of POMterr to the sediment core before and after three different Suess corrections (10, 30, and 100 years). Sediment samples in Class C are removed from the figure. SD of POMterr contributions are shown as error band B SAR extracted from Lotter et al. (1997)

Full size image

All MRTs show a similar trend of relatively high contributions of POMterr from 1885 to 1909 (Fig. 7A). The comparison to the high SAR (Fig. 7B) indicates this may be a result of flood events eroding the forest floor of debris. There is a gradual decline in POMterr from 1909 to 1939 in all models with the exception of 10-year MRT model where the Suess-corrected POMterr contribution appears to further decline until 1951. For the other three models, the year 1939 demonstrates an increased contribution of POMterr. Around this time, the Wahlen plan (a Swiss self-sufficiency plan) entered into force, deforesting large areas in Switzerland and around Lake Baldegg to increase agricultural production (Federal Statistical Office 1949). This may have caused an increase in sediment input from forest soils, but also eroding and washing off formerly forest humus layers and POMterr. The interpretation of POMterr contributions from the 1951 to 1971 is hindered by the exclusion of samples lying outside the mixing space. These exclusions are suggested to arise from subsurface erosion events during periods of elevated SAR, as illustrated in Fig. 7B. Additionally, in the case of 1965, the detected signal may be influenced by the peak of eutrophication, potentially incorporating contributions from algae.

For all models apart from 10-year MRT, the shift in the estimated historical POMterr contribution matches with aerial photographs and pollen records (Van Der Knaap et al. 2000). These records illustrate the increase in trees and shrubs around the lake shore and stream banks from 1940 onwards. The misalignment of the 10-year MRT with the catchment’s historical trends suggests errors when applying a 10-year MRT correction to the isotopic tracers. 1977 appears to be another notable time in which POMterr drastically increases for all Suess-corrected models; this increase in POMterr coincides with an increase in pollen from trees in the sediment record (Van Der Knaap et al. 2000). Despite the relatively low percentage of POMterr introduced, the depleted 13C LMeO values and to a lesser extent, the depleted 13C FA values from POMterr can potentially have a substantial effect on the isotopic record in the sediment. Consequently, this could result in the apportionment of organic carbon rather than soil if the POMterr source is not grouped separately. While the exact cause for increased POMterr is somewhat speculative, the use of mathematical mixtures allows for the evaluation of the model and can help determine how much confidence we should have in the model output. Results of the model evaluation in Fig. 6 illustrate the increase in uncertainty with increasing POMterr contribution, which corroborates with Fig. 7A, adding evidence to suggest mathematical mixtures are a valuable and representative tool of sediment unmixing. Additionally, Fig. 6 illustrates an underestimation of predicted POMterr contribution (ca. < 5%); as such, we would assume our estimates of POMterr in the sediment are also slightly underestimated.

Apart from the non-Suess-corrected sediment of 1951, all sediments that are classified as Class B (Fig. 5, Table S4) displayed non-outlying apportionments (i.e., the estimated sediment apportionment is within the range of the Class A POMterr estimates either side of the class B sediment) suggesting coherent results and confidence can be applied the apportionment estimates. Interestingly, the non-Suess-corrected sediment of 1951 suggests a high contribution of POM, although bi-plots illustrate 1951 being located on the opposite side from the POMterr source. The high contribution of sediment from 1951 is erroneous and a result of the sediment being out of the mixing space. As such, we hypothesize that as the sediments move away from the arable, pasture, and forest sources (in the direction away from the mixing space) in the bi-plots, the model overcompensates and solves the model by increasing the estimated POMterr contribution. While this method of determining non-coherent results has limitations, we suggest that the identification of sediment with outlying results using the concentration dependent mixing space is evidence for the need to reevaluate concentration dependent point in polygon tests.

3.5 Improved sediment source apportionment by including POMterr discrimination

When using δ13C LMeO, δ13C FA, and ACL as a tracer set, all source apportionment estimates of mathematical mixtures, apart from arable, are shown to be highly reliable (Fig. 6) and can be interpreted with confidence. Arable estimates can be seen as less reliable, with potential under and overestimation for high and low contributions, respectively. Considering arable contributions are minimal until 1940, taking over/underestimation into account, would not drastically change pre-1940 arable contributions. However, mathematical mixtures indicate that arable apportionment might be underestimated after 1940, as arable land increases its dominance as a sediment source. Apportionment of Class B sediments (Table S5) shows no outlying results, except for 1951 POMterr (Table S4), suggesting no additional erroneous results.

SAR were not available in the years post-1990 and pre-1885, and therefore cannot be converted to sediment deposited by each land-use. Additionally, it is important to recognize that the removal of POMterr was accomplished using mean values, potentially introducing an additional uncertainty that was not incorporated. Nonetheless, the unmixing of the mineral soil sources demonstrates similar trends for all Suess corrections (Fig. 8, see Table S5 for values of sediment delivered by land-use). For all Suess corrections, the end of the nineteenth century is dominated by high forest input. While these years are not identified as turbidites by Lotter et al. (1997), the high SAR suggest high flow events likely resulting in large amounts of POMterr (Fig. 7) and forest soil potentially being transported into the lake (Alewell et al. 2016). Although all models show an increase in pasture until around 1945, land-use statistics display no significant change in the relative proportion of productive land cover (arable and pasture) in the surrounding catchment in the years 1912 and 1923 (Federal Statistical Office 1912, 1924). The high pasture contribution can then be reasoned to be a result of two possible scenarios: pasture fields being converted temporally or permanently to arable fields, with the legacy pasture signal being dominant. However, if this was true, the legacy effect of pasture would decrease proportionally to the increase in arable contribution, but this is not the case. Another rationale is the intensification of the harvesting of pasture fields for silage, hay, and barn feeding during World War I, as farming resources were diverted to support the war effort.

Fig. 8
figure 8

Estimated sediment delivered by each land-use source after POMterr correction, before and after using three different Suess corrections (10, 30, and 100 years), and the SAR extracted from Lotter et al. (1997)

Full size image

Sediment from 1920 shows a notable change of apportionment using different MRTs, demonstrating the sensitivity of δ13C tracers to the Suess corrections. The sensitivity of apportionment result to the varying MRT Suess corrections can be suggested to be dependent on source discrimination. All models except the 10-year MRT depict a peak in forest contributions around 1939. This can be credited to the enforcement of the Wahlen plan, leading to a 3.6-fold increase in open land in the Baldegg catchment (Federal Statistical Office 1949). Contributions of arable sources appear to be low and stable until 1939, at which point arable becomes the dominant source. The timing of the arable dominance coincides with the introduction of maize in the catchment in the 1940s (Federal Statistical Office 1949; Van Der Knaap et al. 2000). The sediment record then potentially indicates maize cultivation as the main sediment source after the 1940s. Another explanation of increased arable contribution might be due to the increasing use of agricultural machinery as well as the increased connectivity of sources to the watercourse (e.g., land consolidation, removal of linear landscape features, improvements in drainage systems). Connectivity models of the Baldegg catchment indicated linear landscape features, especially roads, are important regulators of sediment transport (Batista et al. 2022a, b). Additionally, it is important to acknowledge that while sediment samples potentially associated with subsurface erosion and outside the mixing space were removed from the historic interpretation, subsurface/channel bank erosion is ubiquitous in sediment transport. As such, our estimations of sediment delivery by each source may be overestimated due to the exclusion of channel bank erosion as a potential source.

3.6 Sediment source apportionment of sediment without POMterr discrimination

The difference in the historical sediment source trend when merging forest and POMterr is illustrated in Fig. 9. The difference between the three and four source model was calculated by subtracting the mean apportionment of the three-source model (Table S6) from the four-source model (Table S5, see Table S7 for differences and Fig. S7 for sediment deposition). The 10-year MRT Suess corrected sediments are illustrated to be highly affected by the merging of forest and POMterr and depict an inconsistent outcome to other MRT corrections. Again, we suggest that this is a result of the 10-year MRT being a less accurate representation of the MRT of the tracers. The 30-year MRT, 100-year MRT, and non-Suess-corrected sediment contributions demonstrate similar forest sedimentation rates when in comparison with the three-source model, with relatively minor difference between the three and four source model until 1945 (mean difference, − 5%). From 1945 to 1990, the three-source model then estimates a higher sediment contribution of forest (mean, 0.0133 g cm−2 y−1 difference; 37%), and a lower contribution of arable (mean, − 0.014 g cm−2 y−1; − 29%), and pasture (mean, − 0.002 g cm−2 y−1; − 12%). The lower contribution of arable can be reasoned to be a result of a reduced source discrimination between forest and arable (Fig. S2).

Fig. 9
figure 9

The difference in the mean estimated sediment delivered using the three or four source model before and after three different Suess corrections (10-year, 30-year, and 100-year MRT) (three-source model − four-source model = difference)

Full size image

Sediment fingerprinting using CSSI tracers is a semi-empirical method to determine the relative contribution of different land-uses. Interestingly, results regularly report forest as a major source of sediment (Alewell et al. 2016; Chen et al. 2016; Upadhayay et al. 2020; Wiltshire et al. 2022). While this may be true in specific cases, in general, this appears to contradict our current understanding of the mechanistic process involved in soil erosion as well as soil erosion modelling (Borrelli et al. 2021; Wiltshire et al. 2022). In general, forests should be less susceptible to soil erosion due to the tree canopy cover with additional understory or ground vegetation and a humus layer cover (Blanco-Canqui and Lal 2010).

As stated previously, aerial images since 1940 show an increase in trees and shrubs along the stream bank. Without the separation of POMterr and forest, apportionments suggest a higher sediment contribution from forests. A more coherent explanation for the increase in forest contribution since 1945 can be contributed to the fact that POMterr from newly planted trees around the lake shore could have the potential to contribute to the sediment isotopic fingerprint. Without the source separation of forest and POMterr, the POMterr contribution is then mistakenly identified as forest input.

In the Baldegg catchment, our initial hypothesis suggests that the misclassification of POMterr as forest contribution would result in forest being the dominant source; this was not supported. However, we demonstrated the separation of POMterr improves the model performance by reducing the overestimation of forest (37%). While our hypothesis was not supported in the Baldegg catchment, it is possible that for catchments that are dominated with forests and/or increased connectivity of POMterr sources to the watercourse, there could be an increased potential for erroneous source apportionment results. In any case, this hypothesis does require more testing. Although the dominant source of sediment did not significantly change (Forest, pre-1990; Pasture, 1910–1940; Arable, post-1940), we recommend the inclusion of the POMterr as a separate source of CSSI tracers as being fundamental to helping ensure accurate and representative sediment apportionments.

4 Conclusion

The use of δ13C LMeO values as an additional land-use-specific tracer is highly effective at improving source discrimination and subsequent expansion of the mixing space. While the results of the historic apportionment are highly credible and fit well with land-use history, the conservativeness of δ13C LMeO during transport and deposition requires further investigation. Furthermore, the use of two different types of CSSI tracers increases the representativeness of the soil and reduces the potential bias associated with specific tracers. The preparation of samples for δ13C FA analysis is a time and organic solvent-consuming procedure. In contrast, the preparation of samples for δ13C LMeO analysis is a relatively rapid but also a solvent free method, allowing for higher sample throughput and the subsequent increase in source heterogeneity testing, all while being more environmentally friendly. Furthermore, the minimal sample mass required for LMeO analysis enables the replication of sediment analysis, facilitating the empirical determination of mixture variance. Consequently, this method can be used in the future to enhance the conclusiveness of the mixing model by directly accounting for mixture variance, rather than being estimated by source variance.

A range of MRTs are used to model the possible Suess effect on CSSI fingerprints and should be applied as a standard protocol for historical use of CSSI tracers. Mathematical mixtures are an effective tool to define a concentration dependent mixing space, and identify sediment values which may give erroneous results. Additionally, they allow for the evaluation of the degree of confidence which should be put in the model output. Although the exact explanation for historical sediment trends remains speculative, the overall story of sediment contribution becomes significantly more credible when using POMterr-corrected apportionments. Although our hypothesis was not supported, as the merging of POMterr and forest did not result in a change of forest being the dominant source, our results did demonstrate the possibility of an overestimation of forest contributions in the literature. Therefore, we suggest the discrimination of POMterr and forest is important to enhance the accuracy of sediment fingerprinting applications when using CSSIs or other organic tracers in order to enable future policies to be based on the most reliable data available.

By determining the past historic trends of sediment sources, we gain insight into the causes of soil erosion. Additionally, land-use specific apportionments allow the discrimination between natural and anthropogenic events leading to soil erosion. While this study was focused on Lake Baldegg, we find it applicable to other temperate regions with similar intensive agricultural practices. However, limitations may be present when using CSSI tracers for regions dominated by subsurface erosion. Nonetheless, this information is vital for effectively evaluating soil erosion models and consequently their use in designing or evaluating sediment mitigation strategies. Improving the accuracy of land-use specific apportionment estimates is therefore of the utmost importance to prevent the negative consequences of soil erosion and sedimentation.