A study on the two-level allocation of carbon emission quotas in China at the provincial level

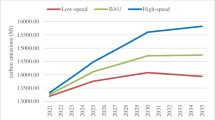
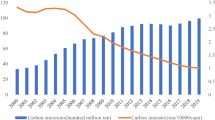
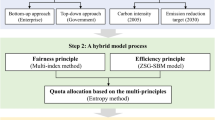
Abstract

Carbon emission reduction is an essential means to achieve the "double carbon goal," and the scientific and reasonable allocation of carbon emission quotas (CEQ) is the basis for promoting carbon emission reduction. In this study, the first level was based on the entropy TOPSIS scores of provinces under the principles of fairness, efficiency, sustainability, and feasibility and used the K-mean clustering method to cluster the 30 provinces and allocate the CEQ to each zone group; the second level consolidated the impacts of the four principles and the marginal abatement costs of CO₂ to allocate CEQ to the provinces within the zone group. Finally, each province's initial spatial balance of CEQ (ISBQ) is classified and evaluated. The study shows that the most quotas are for Guangdong, Zhejiang, and Inner Mongolia, and the least for Ningxia, Shanxi, and Guizhou. This study compares the results of CEQ allocation with the current carbon emission scale and finds that 11 provinces, such as Shandong and Hebei, show a deficit in future carbon emission space, and 19 provinces, such as Hainan and Beijing, show a surplus in carbon emission space. Given each province's different emission reduction tasks and pressures, differentiated emission control policies are the key to achieving China's "2030 target".

Appendix

Sensitivity analysis

When the entropy weight method is used for the calculation, the data of each province in 2020 is used. In order to ensure the stability of the results of calculating the weights of the indicators, we collected data from 2018 and 2019 in each province to calculate the weights of the indicators separately. The descriptive statistics of the data we collected for 2018 and 2019 for each indicator are shown in the Tables 9 and 10.

Table 9 Descriptive statistics for 2018 indicator data

Table 10 Descriptive statistics for 2019 indicator data

According to Eq. (1) to (6), the weights of the indicators of each province under the entropy weighting method can be found, and the weights of the indicators in 2018 and 2019 are shown in the Table 11.

Table 11 Comparison of indicator weights for 2018, 2019 and 2020

Comparison of the weights of the indicators at three different time scales reveals that, except for indicator C3, the deviation between the weight values of the other indicators at different time scales does not exceed 2%, as shown in Fig. 11. 

Fig. 11

Descriptive statistics for 2018 indicator data

This result indicates that the influence of different time scale data on the results of entropy weighting method is relatively small. The significant difference in the weights of indicator C3 in different time scales is because there is no data on the average wind power density of land at 100-m altitude in the annual bulletin of China's wind and solar energy resources in 2018 and 2019, so the percentage of the area with a large annual average wind power density of 70-m altitude of the land is used, and the calculation, therefore, produces a slight deviation in the results. Generally speaking, the entropy weighting method is used to calculate the weights, and the stability of the results is better.

Proportion of CEQ allocated within zone groups

The proportions of CEQs allocated within regional groups are detailed in Tables 12, 13, and 14.

Table 12 Shadow price of CO₂ as a percentage of provinces within the zone groups

Table 13 Percentage of the four principle scores for each province within the regional grouping

Table 14 Proportion of CEQ allocated to each province within the regional grouping

Natural breaks

The category "natural breaks" is based on natural groupings inherent in the data. Classification intervals will be identified so that similar values can be most appropriately grouped and differences between classes can be maximized. Elements will be divided into classes, and for these classes, boundaries will be set at locations where the differences in data values are relatively significant. The calculation steps are shown below:

• (1) Calculate the sum of squares of deviations from the mean of the array.

  $$aver=\left(a+b+c+d\right)/n$$

  (28)
  $$SDAM={\left(a-aver\right)}^{2}+{\left(b-aver\right)}^{2}+{\left(c-aver\right)}^{2}+{\left(d-aver\right)}^{2}$$

  (29)

  where n is the number of elements in the array.

• (2) Iterate over each combination of ranges, calculate the "sum of squared deviations from the category mean squared," and find the smallest value.

  For the first group: $A=\left[a\right];B=\left[b,c,d\right]$.

  $$SDCM\_ALL=\left(a-aver\_A\right)^2+\left(b-aver\_B\right)^2+\left(c-aver\_B\right)^2+\left(d-aver\_B\right)^2$$

  (30)

  where $aver\_A$ is the mean value of the elements of the array A, $aver\_B$ is the mean value of the elements of the array B.

  For the second group: $C=\left[a,b\right];D=\left[c,d\right]$.

  $$SDCM\_ALL=\left(a-aver\_C\right)^2+\left(b-aver\_C\right)^2+\left(c-aver\_D\right)^2+\left(d-aver\_D\right)^2$$

  (31)

  where $aver\_C$ is the mean value of the elements of the array C, $aver\_D$ is the mean value of the elements of the array D.

  For the third group: $E=\left[a,b,c\right];F=\left[d\right]$.

  $$SDCM\_ALL={\left(a-aver\_E\right)}^{2}+{\left(b-aver\_E\right)}^{2}+{\left(c-aver\_E\right)}^{2}+{\left(d-aver\_F\right)}^{2}$$

  (32)

  where $aver\_E$ is the mean value of the elements of the array C, $aver\_F$ is the mean value of the elements of the array D.

  Finally find the minimum of the sum of squared deviations of squares of the category means.

• (3) Calculate the variance goodness-of-fit.

  $$GVF=\left(SDAM-SCDM\right)/SDAM$$

  (33)

  The value of GVF is between 0 and 1, with 1 indicating an excellent fit and 0 indicating an inferior poor fit.

Explanation of the four principles

• (1) Principle of fairness

  The principle of fairness refers to the reasonable and unbiased distribution of CEQ to provinces and regions, reflecting the right of everyone to enjoy carbon emissions. In this study, six indicators, including historical cumulative carbon emissions, cumulative carbon emissions per capita, population size, province area, GDP per capita, and the Gini coefficient, are chosen as decomposition indicators representing the principle of fairness.

  Historical cumulative carbon emissions (A1): historical cumulative carbon emissions are the sum of the accumulated carbon emissions of each country over a while in history, and this study selects the carbon emissions from 2010 to 2020. Regions with higher historical cumulative carbon emissions should bear more responsibility for reducing emissions, so the CEQ allocated to them should be smaller, emphasizing the attribution of historical responsibility, so historical cumulative carbon emissions are a negative indicator. The following equation can usually calculate this indicator:

  $${HCE}_{i}\sum_{k=2010}^{2020}{CE}_{ik},i=\mathrm{1,2},\dots ,n$$

  (34)

  where HCE_i denotes the historical cumulative carbon emissions of the ith province and CE_ik denotes the carbon emissions of the ith province in year k.

  Cumulative carbon emissions per capita (A2): cumulative carbon emissions per capita is the sum of the accumulated carbon emissions of each country over a while in history, the historical accumulated carbon emissions divided by China's current (2020) population. The larger the cumulative carbon emissions per capita, the smaller the carbon emission rights allocated to the region in theory, emphasizing the intergenerational equality of carbon emissions in terms of stock and better guaranteeing the development rights and interests of the less developed regions, so the cumulative carbon emissions per capita is a negative indicator. The following equation can usually calculate this indicator:

  $${PCE}_{i}=\frac{{HCE}_{i}}{{NP}_{i2020}},i=\mathrm{1,2},\dots ,n$$

  (35)

  where PCE_i and HCE_i denote the per capita cumulative carbon emissions and historical cumulative carbon emissions of the ith province, respectively. NP_ik denotes the population size of the ith province at the end of 2020.

  Population size (A3): population size refers to the quantitative prescriptive nature of the population, which indicates the degree of existence and change of the population in terms of quantity, and this paper adopts the population size at the end of the year to measure this indicator. The larger the population size, the larger the CEQ allocated to the region should be, reflecting the per capita equality in the allocation of CEQ. Hence, the population size is a positive indicator.

  Province area (A4): provincial area refers to the total land area of each province. The larger the provincial area, the larger the CEQ allocated to that region should be, reflecting per capita equality in the allocation of CEQ, so the provincial area is a positive indicator.

  GDP per capita (A5): GDP per capita is calculated by comparing the GDP realized during a country's accounting period (usually one year) with the country's resident population (or household population) to obtain GDP per capita, which measures people's living standards in various countries. The studies using GDP per capita for provincial CEQ allocation all follow the rule that the CEQ of each province is inversely proportional to its GDP per capita. Since GDP per capita is a valid indicator representing the economic capacity of a region, the higher the GDP per capita, the stronger the economic capacity of the region, the more it can carry out emission reduction. Therefore, the smaller the CEQ are, and thus, the GDP per capita is a negative indicator.

  Gini coefficient (A6): the Gini coefficient is one of the common indicators used internationally to measure the income disparity among residents of a country or region. The maximum Gini coefficient is "1", and the minimum equals "0". The closer to 0 indicates that the income distribution tends to be equal. It is used as a positive indicator to measure the distribution of CEQ, and the larger the Gini coefficient, the more significant the gap between the residents' income is. The greater the CEQ are allocated to them. The larger the Gini coefficient, the greater the income disparity and the greater the CEQ allocated to residents. It is a dimensionless indicator.

• (2) Principle of efficiency

  The principle of efficiency refers to the fact that CEQ, as a kind of scarce resource, must be optimally allocated so that limited inputs can obtain the maximum output as far as possible. It is necessary to consider the differences between different regions in five aspects: energy consumption per unit of GDP, electricity consumption per unit of GDP, carbon productivity, R&D investment intensity, and the energy consumption elasticity coefficient.

  Energy consumption per unit of GDP (B1): energy consumption per unit of GDP is the primary indicator reflecting the level of energy consumption and the status of energy conservation and consumption reduction, and the ratio of total primary energy consumption to GDP is an indicator of energy use efficiency. This indicator illustrates the degree of energy utilization in the economic activities of a country (region), reflecting the changes in economic structure and energy utilization efficiency; the higher the intensity, the higher the energy consumption and the lower the energy utilization efficiency, so the energy consumption per unit of GDP is a negative indicator. The following equation can usually calculate this indicator:

  $${EP}_{i}=\frac{{EC}_{i}}{{GDP}_{i}},i=\mathrm{1,2},\dots ,n$$

  (36)

  where EP_i, EC_i, and GDP_i denote the energy consumption per unit of GDP, total energy consumption, and GDP of the ith province, respectively.

  Electricity consumption per unit of GDP (B2): electricity consumption per unit of GDP is the amount consumed per unit of gross domestic (regional) product produced in a country (region) over a given period, emphasizing the efficiency of using electrical energy and, therefore, a negative indicator. The indicator can usually be calculated using the following equation:

  $${PP}_{i}=\frac{{PC}_{i}}{{GDP}_{i}},i=\mathrm{1,2},\dots ,n$$

  (37)

  where PP_i, PC_i, and GDP_i denote the electricity consumption per unit of GDP, total electricity consumption, and GDP of the ith province, respectively.

  Carbon productivity (B3): Carbon productivity refers to the economic contribution per unit of carbon emissions, and a rise in carbon productivity leads to a more efficient output of quantitative substances and energy, the desire to invest less energy to maximize desired outputs, making carbon productivity a positive indicator. This indicator can usually be calculated using the following equation:

  $${CP}_{i}=\frac{{GDP}_{i}}{{CE}_{i2020}},i=\mathrm{1,2},\dots ,n$$

  (38)

  where CP_i and GDP_i denote the carbon productivity and GDP of the ith province, respectively. CE_ik denotes the carbon emissions of the ith province in 2020.

  R&D investment intensity (B4): R&D investment intensity is represented by the proportion of science and technology R&D expenditure to GDP. When the R&D investment intensity is higher, the R&D expenditure per unit of regional GDP is higher. In contrast, the R&D efficiency is lower, so fewer CEQ are allocated to it, and thus it is a negative indicator.

  Energy consumption elasticity coefficient (B5): The elasticity coefficient of energy consumption is a technical and economic indicator of the relationship between energy and the development of the national economy. It refers to the ratio of the average growth rate of energy consumption in a certain period to the average growth rate of the gross national product in the same period. The larger the elasticity coefficient of energy consumption is, the faster the growth of energy consumption is compared with the growth rate of the national economy, which reflects that at this point, the energy use technology of the region is relatively backward and that the efficiency of the use of energy is at a relatively low level. The energy consumption elasticity coefficient is, therefore, a negative indicator. The following equation can usually calculate this indicator:

  $${ECE}_{i}=\frac{{ECG}_{i}}{{GDPG}_{i}},i=\mathrm{1,2},..,n$$

  (39)
  $${ECG}_{i}=\frac{{EC}_{i2020}-{EC}_{i2019}}{{EC}_{i2019}},i=\mathrm{1,2},\dots ,n$$

  (40)
  $${GDPG}_{i}=\frac{{GDP}_{i2020}-{GDP}_{i2019}}{{GDP}_{i2019}},i=\mathrm{1,2},\dots ,n$$

  (41)

  where ECE_i, ECG_i, and GDPG_i denote the elasticity coefficient of energy consumption, the growth rate of energy consumption, and the growth rate of GDP of the ith province, respectively. EC_ik and GDP_ik denote the carbon emissions and GDP of the ith province in year k, respectively.

• (3) Principle of sustainability

  The principle of sustainability should consider whether the economic, social, and environmental conditions of the main body of emission reduction can bear the cost of emission reduction and achieve sustainable development. Carbon emission reduction is a long-term endeavor, and the allocation of CEQ needs to be based on a long-term perspective and follow the concept of sustainable development while considering the survival needs of the present and future generations. In this study, six indicators are selected to measure the principle of sustainability, including the renewable energy consumption, share of new energy power generation, wind energy resources, solar resources, urbanization rate, and forest cover.

  Renewable energy consumption (C1): the more renewable energy is consumed, the greater the share of renewable energy consumption in electricity consumption, thus indicating that the regional energy transition to cleaner and lower carbon is more successful, in line with the concept of sustainable development, and is, therefore, a positive indicator.

  Share of new energy power generation (C2): the share of new energy power generation is the proportion of new energy power generation to total electricity consumption, of which, in this paper, there are three types of new energy power generation: nuclear power, wind power, and solar power. New energy generation is not only environmentally friendly but also meets the electricity demand, following the concept of sustainable development, and thus is also a positive indicator. The following equation can usually calculate this indicator:

  $${NE}_{i}=\frac{{NP}_{i}+{WP}_{i}+{SP}_{i}}{{PC}_{i}},i=\mathrm{1,2},\dots ,n$$

  (42)

  where NE_i, NP_i, WP_i, and SP_i denote the proportion of new energy power generation, nuclear power generation, wind power generation, and solar power generation in the ith province, respectively.

  Wind energy resources (C3): this study measures the abundance of wind energy resources by the average wind power density at 100 m height in each province; the more prosperous the wind energy resources, the better the conditions and prospects for sustainable development in the region, so the wind energy resources are a positive indicator.

  Solar resources (C4): this study measures the abundance of solar resources by the number of hours of sunshine in each province. The more abundant solar resources, the better the conditions and prospects for sustainable development in the region, so solar resources are a positive indicator.

  Urbanization rate (C5): the urbanization rate is a general demographic measure—the proportion of the urban population to the total population. The ecological damage caused by urbanization affects the sustainable development of the urban economy and poses a severe threat to the sustainable development of social resources. Therefore, the urbanization rate is a negative indicator.

  Forest cover (C6): forest cover refers to the ratio of forest area to total land area. It is an important indicator reflecting the actual level of forest resources and forest land occupation in a country (or region), generally expressed as a percentage. In actual production, photosynthesis produced in the process of forest growth can absorb a large amount of CO₂ in the air, and the larger the cover, the stronger the carbon absorption capacity, which not only ensures the sustainability of the ecosystem but also effectively resolves the potential hazards triggered by carbon emissions, so the forest cover is a positive indicator.

• (4) Feasibility principle

The feasibility principle emphasizes whether provinces and regions can fulfill the stipulated CEQ, taking into account the state of economic and social development, including the economic level, industrial structure, energy structure, and other factors, i.e., the cost of emission reduction should be within the affordable range, and the emission reduction target should be achieved without compromising the basic living standard of the people. Therefore, CEQ should be more inclined to be allocated to regions with more advanced technological means and significant emission reduction potential. This study selects five indicators to quantify the feasibility principle, including tertiary industry share, technology level, Share of end-use coal consumption, General public budget, and crops sowing area.

Tertiary industry share (D1): tertiary industry share is the proportion of GDP accounted for by various types of services or businesses. A higher proportion of tertiary industry means a better industrial structure. However, the space and potential for emission reduction will gradually become smaller, and therefore, fewer CEQ need to be allocated, so the proportion of tertiary industry is a negative indicator.

Technology level (D2): the number of authorised domestic patent applications is a reasonable indicator of the technology level. The more authorised domestic patent applications, the higher the scientific and technological level of a province or region, and the more capable it is to achieve technological emission reductions in high-carbon industries, with a greater potential for emission reductions, and therefore more CEQ can be allocated to it, so the level of science and technology is a positive indicator.

Share of end-use coal consumption (D3): Share of end-use coal consumption refers to the proportion of end-use coal consumption in total energy consumption, which can reflect regional energy consumption more realistically. Achieving the carbon peak and carbon neutrality goal requires significant clean substitution of end-use energy, which has always been dominated by coal. The lower the share of end-use coal consumption, the more the energy structure is gradually optimized. However, the space for emission reduction is gradually becoming smaller and, therefore, needs to be accompanied by fewer CEQ. Hence, the share of end-use coal consumption is a negative indicator. The following equation can usually calculate this indicator:

$${CCR}_{i}=\frac{{CC}_{i}}{{EC}_{i}},i=\mathrm{1,2},\dots ,n$$

(43)

where CCR_i and CC_i denote the share of terminal coal consumption and terminal coal consumption of the ith province, respectively.

General public budget (D4): general public budget revenues refer to the actual tax revenues (after deducting the tax revenues attributed to the center and provinces) and non-tax revenues of the region. The higher general public budget revenue reflects the higher level of regional revenue, the more capable of paying for the cost of regional emission reduction, and the lower the potential for emission reduction, paired with fewer CEQ, so it is a negative indicator.

Crops sowing area (D5): In actual production, photosynthesis produced during crop growth can absorb a large amount of CO₂ in the air and play a carbon offsetting role; the more significant the crop sowing area is, the stronger its carbon sink capacity is, the more effective it can be in resolving potential hazards triggered by carbon emissions. The region has a more significant potential for emission reduction, so it is a positive indicator.