Skip to main content
SpringerLink
Log in

Long-lead streamflow forecasting using computational intelligence methods while considering uncertainty issue

  • Research Article
  • Published:
Environmental Science and Pollution Research Aims and scope Submit manuscript

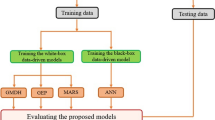
Abstract

While some robust artificial intelligence (AI) techniques such as Gene-Expression Programming (GEP), Model Tree (MT), and Multivariate Adaptive Regression Spline (MARS) have been frequently employed in the field of water resources, documents aimed to explore their uncertainty levels are few and far between. Meanwhile, uncertainty determination of these AI models in practical applications is highly important especially when we aimed to use the AI models for streamflow forecast due to the repercussions of poorly managed water resources. With the aid of a global daily streamflow dataset, understanding the uncertainty of GEP, MT, and MARS for forecasting streamflow of natural rivers was studied. The efficiency of uncertainty analysis was quantified by two statistical indicators: 95% Percent Prediction Uncertainty (95%PPU) and R-factor. The results demonstrated that MT had lower uncertainty (95%PPU=0.59 and R-factor=1.67) in comparison with MARS (95%PPU=0.61 and R-factor=1.92) and GEP (95%PPU=0.64 and R-factor=2.03). Overall, although the confidence interval bands of uncertainty for the AI models almost captured the mean streamflow measurements, wide bands of uncertainty were obtained and consequently remarkable uncertainty in the calculation of monthly streamflow values was met.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data Availability

Some or all data, models, or codes that support the findings of this study are available from the corresponding author upon reasonable request.

Abbreviations

a 0 :

Bias term of multivariate linear equation

a 1, a 2, a 3 :

Weighting coefficients of multivariate linear equation

ACF :

Auto-Correlation Function

ANFIS :

Adaptive Neuro-Fuzzy Inference System

AI :

Artifiucuial Intelligence

AR :

Auto-Regression

ARMA :

Auto-Regression Moving Average

ARIMA :

Auto-Regression Integrated Moving Average

BF :

Basis Function

CC :

Correlation of Coefficient, R.

CM :

Conventional Model

\(\overline d\) :

Average distance between the lower and upper 95PPU band

EPR :

Evolutionary Polynomial Regression

FFNN :

Feed Forward Neural Network

GA :

Genetic Algorithm

GEP :

Gene-Expression Programming

GLUE :

Genetalized Likelihood Uncertainty Estimation

GMDH :

Group Method of Data Handling

KNN :

K-Nearest Neighbor

KELM :

Kernel Extreme Learning Machine

MARS :

Multivariate Adaptive Regression Spline

MCS :

Monte-Carlo Simulation

MSE :

Mean Square Error

MT :

Model Tree

NBF :

Number of Basis Function

P-factor :

The key element for quantifying the uncertainty of AI models performance

PACF :

Partial Auto-Correlation Function

PSO :

Particle Swarm Optimization

Q :

Monthly or dialy streamflow discharge

RE :

Relative Error

R-factor :

The key elements for quantifying the uncertainty of AI models performance

RC :

Coefficient of Correlation

RMSE :

Root Mean Square Error

SF :

Streamflow

SHDI :

Standardized Hydrological Drought Index

SOI :

Southern Oscillation Index

STD :

Standard Deviation

SVM :

Support Vector Machine

t :

Time

t−1,  t−2,  t−3:

Lag times of streamflow discharge

TF :

Thomas-Fiering method

WRM :

Water Resources Management

x U :

Upper limit of 95PPU

x L :

Lower limit of 95PPU

ψ 0 :

Bias term of MARS model

ψ i :

Weigthing coefficients of MARS model

95PPU :

95 Percent Prediction Uncertainty

References

  • Al-Sudani ZA, Salih SQ, Sharafati A, Yaseen ZM (2019) Development of multivariate adaptive regression spline integrated with differential evolution model for streamflow simulation. J Hydrol 573:1–12

    Google Scholar 

  • Abbaspour KC (2008) SWAT-CUP user manual. Federal Institute of Aquatic Science and Technology (Eawag), Swiss

    Google Scholar 

  • Abbaspour KC, Yang J, Maximov I, Siber R, Bogner K, Mieleitner J, Srinivasan R (2007) Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J Hydrol 333(2-4):413–430

    Google Scholar 

  • Adnan RM, Liang Z, Heddam S, Zounemat-Kermani M, Kisi O, Li B (2020) Least square support vector machine and multivariate adaptive regression splines for streamflow prediction in mountainous basin using hydro-meteorological data as inputs. J Hydrol 586:124371

    Google Scholar 

  • Adeloye AJ (2012) Hydrological sizing of water supply reservoir. In: Bengtsson L, Herschy RW, Fairbridge RW (eds) Encyclopedia of lakes and reservoirs. Springer, Dordrecht, pp 346–355

    Google Scholar 

  • Afkhami M, Shariat M, Jaafarzadeh N, Ghadiri H, Nabizadeh R (2007) Developing a water quality management model for Karoon and Dez Rivers. J Environ Health Sci Eng 4(2):99–106

    Google Scholar 

  • Amininia K, Saghebian SM (2021) Uncertainty analysis of monthly river flow modeling in consecutive hydrometric stations using integrated data-driven models. J Hydroinf 23(4):897–913

    Google Scholar 

  • Anvari S, Rashedi E, Lotfi S (2022) A Coupled Metaheuristic Algorithm and Artificial Intelligence for LongLead Stream Flow Forecasting. International Journal of Optimization in Civil Engineering 12(1):91–104

    Google Scholar 

  • Anvari S, Mousavi SJ, Morid S (2014) Sampling/stochastic dynamic programming for optimal operation of multi-purpose reservoirs using artificial neural network-based ensemble streamflow predictions. J Hydroinf 16(4):907–921

    Google Scholar 

  • Aqil M, Kita I, Yano A, Nishiyama S (2007) A comparative study of artificial neural networks and neuro-fuzzy in continuous modeling of the daily and hourly behaviour of runoff. J Hydrol 337:22–34

    Google Scholar 

  • Bayazit M (2015) Nonstationarity of hydrological records and recent trends in trend analysis: a state-of-the-art review. Environ Process 2(3):527–542

    Google Scholar 

  • Bazartseren B, Hildebrandt G, Holz KP (2003) Short-term water level prediction using neural networks and neuro-fuzzy approach. Neurocomputing 55:439–450 (can be deleted)

    Google Scholar 

  • Bensoussan A, Farhi N (2010) Uncertainties and Risks in Water Resources Management. In: The economics of sustainable development (Chapter: Uncertainties and Risks in Water Resources Management). Publisher: Economica

    Google Scholar 

  • Cheng CT, Feng ZK, Niu WJ, Liao SL (2015) Heuristic methods for reservoir monthly inflow forecasting: A case study of Xinfengjiang Reservoir in Pearl River, China. Water 7(8):4477–4495

    Google Scholar 

  • Coulibaly P, Anctil F, Bobée B (2000) Daily reservoir inflow forecasting using artificial neural networks with stopped training approach. J Hydrol 230:244–257

    Google Scholar 

  • Cui Q, Wang X, Li C, Cai Y, Liang P (2016) Improved Thomas-Fiering and Wavelet Neural Network Models for Cumulative Error Reduction in Reservoir Inflow Forecast. J HydroEnvironment Res 13:134–143

    Google Scholar 

  • Diomede T, Marsigli C, Nerozzi F, Paccagnella T, Montani A (2006) Quantifying the discharge forecast uncertainty by different approaches to probabilistic quantitative precipitation forecast. Adv Geosci 7:189–191

    Google Scholar 

  • Dehghani M, Saghafian B, Nasiri Saleh F, Farokhnia A, Noori R (2014) Uncertainty analysis of streamflow drought forecast using artificial neural networks and Monte-Carlo simulation. Int J Climatol 34(4):1169–1180

    Google Scholar 

  • Di Baldassarre G, Montanari A (2009) Uncertainty in river discharge observations: a quantitative analysis. Hydrol Earth Syst Sci Discuss 6:39–61

    Google Scholar 

  • El-Shafie A, Noureldin A (2011) Generalized versus non-generalized neural network model for multi-lead inflow forecasting at Aswan High Dam. Hydrol Earth Syst Sci 15(3):841–858

    Google Scholar 

  • Etemad-Shahidi A, Bali M (2012) Stability of rubble-mound breakwater using H50 wave height parameter. Coast Eng 59(1):38–47

    Google Scholar 

  • Ferreira C (2001) Gene expression programming: A new adaptive algorithm for solving problems. Complex Systems 13:87–129

    Google Scholar 

  • Ferreira C (2006) Gene Expression Programming, 2nd edn. Springer-Verlag, Berlin Heidelberg, The Netherlands

    Google Scholar 

  • Friedman JH (1991) Multivariate adaptive regression splines. Ann Stat 19:1–67

    Google Scholar 

  • He Z, Wen X, Liu H, Du J (2014) A comparative study of artificial neural network, adaptive neuro fuzzy inference system and support vector machine for forecasting river flow in the semiarid mountain region. J Hydrol 509:379–386

    Google Scholar 

  • Heddam S, Kisi O (2018) Modelling daily dissolved oxygen concentration using least square support vector machine, multivariate adaptive regression splines and M5 model tree. J Hydrol 559:499–509

    CAS  Google Scholar 

  • Hussain D, Khan AA (2020) Machine learning techniques for monthly river flow forecasting of Hunza River, Pakistan. Earth Sci Inform 13:939–949

    Google Scholar 

  • Kisi O (2005) Daily river flow forecasting using artificial neural networks and auto-regressive models. Turk J Eng Environ Sci 29:9–20

    Google Scholar 

  • Kroese DP, Brereton T, Taimre T, Botev ZI (2014) Why the Monte Carlo method is so important today. Wiley Interdiscip Rev Comput Stat 6(6):386–392

    Google Scholar 

  • Leandro J, Bander A, Beg MNA, Bhola P, Konnerth I, Willems W, Carvalho R, Disse M (2019) Forecasting upper and lower uncertainty bands of river flood discharges with high predictive skill. J Hydrol 576:749–763

    Google Scholar 

  • McMahon TA, Adeloye AJ (2005) Water Resources Yield. Water Resources Publications, Littleton, CO, USA

    Google Scholar 

  • Moosavi V, Gheissori Fard Z, Vafakhah M (2022) Which one is more important in daily runoff forecasting using data driven models: Input data, model type, preprocessing or data length? J Hydrol 606:127429

    Google Scholar 

  • Marcé R, Comerma M, García JC, Armengol J (2004) A neuro-fuzzy modeling tool to estimate fluvial nutrient loads in watersheds under time-varying human impact. Limnol Oceanogr Methods 2(11):342–355

    Google Scholar 

  • Modaresi F, Araghinejad S, Ebrahimi K (2018) A comparative assessment of artificial neural network, generalized regression neural network. Least-Square support vector regression, and K-nearest neighbor regression for monthly Streamflow forecasting in linear and nonlinear conditions. Water Resour Manag 32(1):243–258

    Google Scholar 

  • Montanari A, Grossi G (2008) Estimating the uncertainty of hydrological forecasts: A statistical approach. Water Resour Res 44(12):W00B08

    Google Scholar 

  • Moghaddasi M, Anvari S, Akhondi N (2022) A trade-off analysis of adaptive and non-adaptive future optimized rule curves based on simulation algorithm and hedging rules. Theor Appl Climatol 148(1–2):65–78

    Google Scholar 

  • Narsimlu B, Gosain AK, Chahar BR, Singh SK, Srivastava PK (2015) SWAT model calibration and uncertainty analysis for streamflow prediction in the Kunwari River Basin, India, using sequential uncertainty fitting. Environ Process 2(1):79–95

    Google Scholar 

  • Nayak PC, Sudheer KP, Rangan DM, Ramasastri KS (2004) A neuro-fuzzy computing technique for modeling hydrological time series. J Hydrol 291:52–66

    Google Scholar 

  • Niu WJ, Feng ZK, Cheng CT, Zhou JZ (2018) Forecasting daily runoff by extreme learning machine based on quantum-behaved particle swarm optimization. J Hydrol Eng 23(3):04018002

    Google Scholar 

  • Noorbeh P, Roozbahani A, Moghaddam HK (2020) Annual and monthly dam inflow prediction using Bayesian networks. Water Resour Manag 34(9):2933–2951

    Google Scholar 

  • Noori R, Karbassi AR, Moghaddamnia A, Han D, Zokaei-Ashtiani MH, Farokhnia A, Gousheh MG (2011) Assessment of input variables determination on the SVM model performance using PCA, Gamma test, and forward selection techniques for monthly stream flow prediction. J Hydrol 401(3-4):177–189

    Google Scholar 

  • Noori R, Khakpour A, Omidvar B, Farokhnia A (2010) Comparison of ANN and principal component analysis-multivariate linear regression models for predicting the river flow based on developed discrepancy ratio statistic. Expert Syst Appl 37(8):5856–5862

    Google Scholar 

  • Pham T (2011) Tracking the uncertainty in streamflow prediction through a hydrological forecasting system, M.Sc Thesis. University of Twente

    Google Scholar 

  • Pablo AM, McPhee J, Vargas X (2012) Uncertainty in flood forecasting: A distributed modeling approach in a sparse data catchment. Water Resour Res 48(9):W09532

    Google Scholar 

  • Poul AK, Shourian M, Ebrahimi H (2019) A comparative study of MLR, KNN, ANN and ANFIS models with wavelet transform in monthly stream flow prediction. Water Resour Manag 33(8):2907–2923

    Google Scholar 

  • Quinlan JR (1992) Learning with continuous classes. In: Proceedings of the 5th Australian Joint Conference on Artificial Intelligence (AI ’92). World Scientific, Singapore, pp 343–348

    Google Scholar 

  • Riahi-Madvar H, Dehghani M, Memarzadeh R, Gharabaghi B (2021) Short to long-term forecasting of river flows by heuristic optimization algorithms hybridized with ANFIS. Water Resour Manag 35(4):1149–1166

    Google Scholar 

  • Rubinstein RY, Kroese DP (2016) Simulation and the Monte Carlo method. John Wiley & Sons

    Google Scholar 

  • Singh A, Imtiyaz M, Isaac RK, Denis DM (2014) Assessing the performance and uncertainty analysis of the SWAT and RBNN models for simulation of sediment yield in the Nagwa watershed, India. Hydrol Sci J 59(2):351–364

    Google Scholar 

  • Shahabi S, Azarpira F (2021) Evaluating the capability of hybrid data-driven approaches to forecast monthly streamflow using hydrometric and meteorological variables. J Hydroinf 23(6):1165–1181

    Google Scholar 

  • Steenbergen NV, Willems P (2015) Uncertainty decomposition and reduction in river flood forecasting: Belgian case study. Flood Risk Manag 8(3):263–275

    Google Scholar 

  • Saghafian B, Anvari S, Morid S (2013) Effect of Southern Oscillation Index and spatially distributed climate data on improving the accuracy of Artificial Neural Network, Adaptive Neuro-Fuzzy Inference System and K-Nearest Neighbour streamflow forecasting models. Expert Syst 30(4):367–380

    Google Scholar 

  • Schnier S, Cai XM (2014) Prediction of regional streamflow frequency using model tree ensembles. J Hydrol 517:298–309

    Google Scholar 

  • Setegn SG, Srinivasan R, Melesse AM, Dargahi B (2010) SWAT model application and prediction uncertainty analysis in the Lake Tana Basin, Ethiopia. Hydrol Process 24(3):357–367

    Google Scholar 

  • Shiri J (2018) Improving the performance of the mass transfer-based reference evapotranspiration estimation approaches through a coupled wavelet-random forest methodology. J Hydrol 561:737–750

    Google Scholar 

  • Soundharajan BS, Adeloye AJ, Remesan R (2016) Evaluating the variability in surface water reservoir planning characteristics during climate change impacts assessment. J Hydrol 538:625–639

    Google Scholar 

  • Solomatine DP, Xue Y (2004) M5 Model Trees and Neural Networks: Application to Flood Forecasting in the Upper Reach of the Huai River in China. J Hydrol Eng 9(6):491–501

    Google Scholar 

  • Talebizadeh M, Morid S, Ayyoubzadeh SA, Ghasemzadeh M (2010) Uncertainty analysis in sediment load modeling using ANN and SWAT model. Water Resour Manag 24(9):1747–1761

    Google Scholar 

  • Tikhamarine Y, Souag-Gamane D, Ahmed AN, Kisi O, El-Shafie A (2020) Improving artificial intelligence models accuracy for monthly streamflow forecasting using grey Wolf optimization (GWO) algorithm. J Hydrol 582:124435

    Google Scholar 

  • Wanger T, Gupta H, Yatheendradas S, Goodrich D, Unkrich C, Schaffner M (2007) Understanding sources of uncertainty in flashflood forecasting for semi-arid regions. Quantification and Reduction of Predictive Uncertainty for Sustainable Water Resources Management. In: Proceedings of Symposium HS2004 at IUGG2007, Perugia. IAHS Publication

    Google Scholar 

  • Yu P-S, Tseng T-Y (1996) A model to forecast flow with uncertainty analysis. Hydrol Sci J 41(3):327–344

    Google Scholar 

  • Yang T, Asanjan AA, Welles E, Gao X, Sorooshian S, Liu X (2017) Developing reservoir monthly inflow forecasts using artificial intelligence and climate phenomenon information. Water Resour Res 53(4):2786–2812

    Google Scholar 

  • Yang J, Reichert P, Abbaspour KC, Xia J, Yang H (2008) Comparing uncertainty analysis techniques for a SWAT application to the Chaohe Basin in China. J Hydrol 358:1–23

    Google Scholar 

  • Yaseen ZM, Naganna SR, Sa’adi, Z, Samui, P., Ghorbani, M.A., Salih, S.Q., Shahid, S. (2020) Hourly river flow forecasting: application of emotional neural network versus multiple machine learning paradigms. Water Resour Manag 34:1075–1091

    Google Scholar 

  • Yaseen ZM, El-Shafie A, O., Jaafar, H. Afan, A., Sayl. M. N. (2015) Artificial intelligence based models for stream-flow forecasting: 2000-2015. J Hydrol 530:829–844

    Google Scholar 

  • Yan J, Lio G-Y, Gebremichael M, Shedd R, Vallee DR (2012) Characterizing the uncertainty in river stage forecasts conditional on point forecast values. Water Resour Res 48(12):W12509

    Google Scholar 

  • Zhang X, Liang F, Srinivasan R, Van Liew M (2009) Estimating uncertainty of streamflow simulation using Bayesian neural networks. Water Resour Res 45(2):W02403

    Google Scholar 

  • Zealand CM, Burn DH, Simonovic SP (1999) Short term streamflow forecasting using artificial neural networks. J Hydrol 214(1-4):32–48

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Water Engineering, Faculty of Civil and Surveying Engineering, Graduate University of Advanced Technology, P.O. Box 76315117, Kerman, Iran

    Mohammad Najafzadeh

  2. Department of Ecology, Institute of Science and High Technology and Environmental Sciences, Graduate University of Advanced Technology, P.O. Box 76315117, Kerman, Iran

    Sedigheh Anvari

Authors
  1. Mohammad Najafzadeh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sedigheh Anvari
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Mohammad Najafzadeh: providing computer programming codes for AI models, performing Artificial Intelligence models for stream flow forecast, writing analysis of AI models results, improving introduction, and writing literature review, abstract, conclusion, and comparisons sections. Sedigheh Anvari: writing introduction, data analysis, case study, describing uncertainty descriptions, and performing uncertainty analysis of AI models, and providing figures and tables.

Corresponding author

Correspondence to Mohammad Najafzadeh.

Ethics declarations

Ethical approval

All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards.

Consent to participate

Informed consent was obtained from all individual participants included in the study.

Consent for publication

All the authors give the publisher the permission of the authors to publish the research work.

Competing interests

The authors declare no competing interests.

Additional information

Responsible Editor: Marcus Schulz

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Najafzadeh, M., Anvari, S. Long-lead streamflow forecasting using computational intelligence methods while considering uncertainty issue. Environ Sci Pollut Res 30, 84474–84490 (2023). https://doi.org/10.1007/s11356-023-28236-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11356-023-28236-y

Keywords

Search

Navigation