Carbon emission reduction cooperation of three-echelon supply chain under consumer environmental awareness and cap-and-trade regulation

Abstract

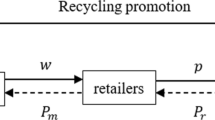
Considering that both the manufacturer’s production process and the transporter’s freight process produce carbon emissions, this paper constructed a three-echelon supply chain composed of a manufacturer, a transporter, and a retailer. This article studies the cooperative carbon emission reduction among the supply chain members under the carbon cap-and-trade policy and consumer environmental awareness. We used the Stackelberg game to explore four scenarios as follows: (1) in the non-cooperative decision model, no cooperation takes place among all supply chain members; (2) in the local cooperation decision of the manufacturer and the transporter alliance model, the manufacturer and the transporter work together to make decisions reducing carbon emissions, but each member of the supply chain makes its own pricing decisions; (3) in the local cooperation decision of the retailer-transporter alliance model, there is no cooperation except that the retailer and the transporter cooperate with each other to determine the selling price of the product; and (4) in the overall-cooperative decision model, there is complete cooperation among the members of the supply chain, who collectively decide on carbon emission reduction and the selling price of the product. Then, using the backward induction method, we derived and compared the equilibrium solutions and the profits of the supply chain system. The results showed that the scenario of complete cooperation among all supply chain members had the best performance in carbon emission reduction, market equilibrium quantity, and the supply chain system’s profit, but the selling price of the product was likely to be higher than other scenarios. Two contracts have been proposed to coordinate the supply chain system. The cost-sharing contract is effective but imperfect under limited constraints. The two-part tariff contract can realize perfect coordination of the supply chain. Finally, we obtained several interesting conclusions from the numerical example and provide managerial insights and policy implications from the analytical results.

Appendices

Appendix A

Proof of Theorem 1

Taking the second-order partial derivatives of ${\Pi}_M^N$ and ${\Pi}_T^N$ with respect to e_m and e_t, we have the following:

$$ \frac{\partial^2{\Pi}_M^N}{\partial {e}_m^2}=\frac{{\left(\eta +{bp}_0\right)}^2}{8b}-2{k}_1,\frac{\partial^2{\Pi}_T^N}{\partial {e}_t^2}=\frac{{\left(\eta +{bp}_0\right)}^2}{16b}-2{k}_2. $$

Let’s make ${\partial}^2{\Pi}_M^N/\partial {e}_m^2$ and ${\partial}^2{\Pi}_T^N/\partial {e}_t^2$ less than zero, and we get $\eta <4\sqrt{bk_1}-{bp}_0$ and $\eta <4\sqrt{2{bk}_2}-{bp}_0$. At this time, the manufacturer’s profit function, ${\Pi}_M^N$, is concave in e_m, and the transporter’s profit function, ${\Pi}_T^N$, is concave in e_t. Letting the first-order conditions of the profit function be zero, that is $\partial {\Pi}_M^N/\partial {e}_m=0$ and $\partial {\Pi}_T^N/\partial {e}_t=0$, and simultaneously solving the two equations, then the final carbon emissions from the manufacturer and the transporter are given, respectively, by

$$ \left\{{\displaystyle \begin{array}{c}{e}_m^N=\frac{32b{k}_1{k}_2{e}_{m0}-\left({k}_1{e}_{m0}-2{k}_2{e}_{t0}\right){\left(\eta +{bp}_0\right)}^2-2{k}_2\left(\eta +{bp}_0\right)\left.\left(a- bc- bv- Mb{p}_0\right)\right)}{32b{k}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +b{p}_0\right)}^2}\\ {}{e}_t^N=\frac{32b{k}_1{k}_2{e}_{t0}-\left(2{k}_2{e}_{t0}-{k}_1{e}_{m0}\right){\left(\eta +{bp}_0\right)}^2-{k}_1\left(\eta +{bp}_0\right)\left.\left(a- bc- bv- Mb{p}_0\right)\right)}{32b{k}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +b{p}_0\right)}^2}\end{array}}\right. $$

Thus, the carbon emission reduction of the supply chain system is expressed as follows:

$$ \Delta {e}_{SC}^N=\left({e}_{m0}-{e}_m^N\right)+\left({e}_{t0}-{e}_t^N\right)=\frac{\left({k}_1+2{k}_2\right)\left(\eta +{bp}_0\right)\left(a- bc- bv+{Mbp}_0-\left(\eta +{bp}_0\right)\left({e}_{m0}+{e}_{t0}\right)\right)}{32{bk}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +{bp}_0\right)}^2}. $$

Appendix B

Proof of Theorem 2

Substituting the equations of ${e}_m^N$ and ${e}_t^N$ into p(e_m, e_t), t(e_m, e_t), andw(e_m, e_t), it’s easy to get the expression of p^N, t^N, and w^N. Substituting the expressions of p^N, t^N, and w^N into Eq. (1) and the market demand function q(p, e_m, e_t), we can easily obtain ${\Pi}_M^N$, ${\Pi}_T^N$, ${\Pi}_R^N$, and q^N. Therefore, the profit of the supply chain system is expressed by ${\varPi}_{SC}^N={\varPi}_M^N+{\varPi}_T^N+{\varPi}_R^N=\frac{k_1{k}_2\left(112b{k}_1{k}_2-\left({k}_1+4{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)\left(a- bc- bv+ bM{p}_0-{\left(\eta +{bp}_0\right)}^2\left({e}_{m0}+{e}_{t0}\right)\right)}{32b{k}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +b{p}_0\right)}^2}$

Appendix C

Proof of Corollary 1

Taking the first-order derivatives of $\Delta {e}_{SC}^N$ with respect to η, we have the following:

$$ \frac{\partial \Delta {e}_{SC}^N}{\partial \eta }=\frac{\left({k}_1+2{k}_2\right)\left(\left({k}_1+2{k}_2\right)\left(a- bc- bv+ Mb{p}_0\right){\left(\eta +{bp}_0\right)}^2-64b{k}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)\left(\eta +{bp}_0\right)+32b{k}_1{k}_2\left(a- bc- bv+ Mb{p}_0\right)\right)}{{\left(32b{k}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +b{p}_0\right)}^2\right)}^2} $$

To simplify the discussion, we denote ${f}_1^N\left(\eta +{bp}_0\right)=\left({k}_1+2{k}_2\right)\left(a- bc- bv-{Mbp}_0\right){\left(\eta +{bp}_0\right)}^2-64{bk}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)\left(\eta +{bp}_0\right)+32{bk}_1{k}_2\left(a- bc- bv+{Mbp}_0\right)$, then we know that ${f}_1^N\left(\eta +{bp}_0\right)$ has the same monotonicity as $\mathrm{\partial \Delta }{e}_{SC}^N/\partial \eta$. Obviously, ${f}_1^N\left(\eta +{bp}_0\right)$ is a quadratic function with a parabola going upwards, and its discriminant is given by

$$ {\Delta}_{f_1^N\left(\eta +{bp}_0\right)}=128{bk}_1{k}_2\left(32{bk}_1{k}_2{\left({e}_{m0}+{e}_{t0}\right)}^2-\left({k}_1+2{k}_2\right){\left(a- bc- bv+{Mbp}_0\right)}^2\right). $$

We can see that when the initial carbon emissions of the supply chain system meet ${e}_{m0}+{e}_{t0}>\left(a- bc- bv+{Mbp}_0\right)\sqrt{\frac{k_1+2{k}_2}{32{bk}_1{k}_2}}$, then it satisfies ${\Delta}_{f_1^N\left(\eta +{bp}_0\right)}>0$. At this point, $f^N_1(\eta+bp_0)$ has two intersections with the horizontal axis, represented by

$$ {\displaystyle \begin{array}{*{20}c}{\eta}_1^N+{bp}_0=\frac{32{bk}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)+\sqrt{32{bk}_1{k}_2\left(32{bk}_1{k}_2{\left({e}_{m0}+{e}_{t0}\right)}^2-\left({k}_1+2{k}_2\right){\left(a- bc- bv+{Mbp}_0\right)}^2\right)}}{\left({k}_1+2{k}_2\right)\left(a- bc- bv+{Mbp}_0\right)},\\ {}{\eta}_2^N+{bp}_0=\frac{32{bk}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)-\sqrt{32{bk}_1{k}_2\left(32{bk}_1{k}_2{\left({e}_{m0}+{e}_{t0}\right)}^2-\left({k}_1+2{k}_2\right){\left(a- bc- bv+{Mbp}_0\right)}^2\right)}}{\left({k}_1+2{k}_2\right)\left(a- bc- bv+{Mbp}_0\right)}.\end{array}} $$

Based on the given assumption $0<{e}_{m0}+{e}_{t0}<\frac{a- bc- bv+{Mbp}_0}{\eta +{bp}_0}$, we know that $\eta +{bp}_0<\frac{a- bc- bv+{Mbp}_0}{e_{m0}+{e}_{t0}}$, so there is $\eta +{bp}_0<\sqrt{\frac{32{bk}_1{k}_2}{k_1+2{k}_2}}$. Owing to ${\eta}_1^N+{bp}_0>\frac{32{bk}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)}{\left({k}_1+2{k}_2\right)\left(a- bc- bv+{Mbp}_0\right)}>\sqrt{\frac{32{bk}_1{k}_2}{k_1+2{k}_2}}$, the point ${\eta}_1^N+{bp}_0$ does not suit the assumption, so it will not be discussed. The above analysis shows that if $0<\eta <{\eta}_1^N$, then ${f}_1^N\left(\eta +{bp}_0\right)>0$, that is $\mathrm{\partial \Delta }{e}_{SC}^N/\partial \eta >0$; and if ${\eta}_1^N<\eta <\sqrt{\frac{32{bk}_1{k}_2}{k_1+2{k}_2}}-{bp}_0$, then ${f}_1^N\left(\eta +{bp}_0\right)<0$, that is $\mathrm{\partial \Delta }{e}_{SC}^N/\partial \eta <0$. In addition, if the initial carbon emissions of the supply chain system meet ${e}_{m0}+{e}_{t0}<\left(a- bc- bv+{Mbp}_0\right)\sqrt{\frac{k_1+2{k}_2}{32{bk}_1{k}_2}}$, the result of ${\Delta}_{f_1^N\left(\eta +{bp}_0\right)}<0$ happens, and ${f}_1^N\left(\eta +{bp}_0\right)$ has no intersection with the horizontal axis. Hence, as long as it meets $0<\eta <\sqrt{\frac{32{bk}_1{k}_2}{k_1+2{k}_2}}-{bp}_0$, then there is ${f}_1^N\left(\eta +{bp}_0\right)>0$, that is $\mathrm{\partial \Delta }{e}_{SC}^N/\partial \eta >0$.

Appendix D

Proof of Theorem 3

Taking the second-order partial derivatives of ${\Pi}_{M+T}^S$ with respect to e_m and e_t, we have the Hessian matrix:

$$ H=\left(\begin{array}{*{20}c}\kern-4pt\frac{3{\left(\eta +{bp}_0\right)}^2}{16b}-2{k}_1 \kern14pt \frac{3{\left(\eta +{bp}_0\right)}^2}{16b}\\ \kern9pt {}\frac{3{\left(\eta +{bp}_0\right)}^2}{16b} \kern49pt \kern-37pt \frac{3{\left(\eta +{bp}_0\right)}^2}{16b}-2{k}_2\end{array}\right) $$

Let’s make $\frac{3{\left(\eta +{bp}_0\right)}^2}{16b}-2{k}_1<0$ and $\left|\mathrm{H}\right|=\frac{3\left({k}_1+{k}_2\right)}{8b}{\left(\eta +{bp}_0\right)}^2-4{k}_1{k}_2<0$, that is $0<\eta <\sqrt{\frac{32{bk}_1{k}_2}{3\left({k}_1+{k}_2\right)}}-{bp}_0$, then ${\Pi}_{M+T}^S$ is a strictly jointly concave function on e_m and e_t. Therefore, the optimal solutions of this optimization problem exist. Taking the first-order conditions of ${\Pi}_{M+T}^S$ with respect to e_m and e_t be zero, that is $\partial {\Pi}_{M+T}^S/\partial {e}_m=0$ and $\partial {\Pi}_{M+T}^S/\partial {e}_t=0$, and simultaneously solving the two equations, then the final carbon emissions from the manufacturer and the transporter are given, respectively, by

$$ \Big\{{\displaystyle \begin{array}{*{20}c}{e}_m^S=\frac{32b{k}_1{k}_2{e}_{m0}-3\left({k}_1{e}_{m0}-{k}_2{e}_{t0}\right){\left(\eta +b{p}_0\right)}^2-3{k}_2\left(\eta +b{p}_0\right)\left(a- bc- bv+ bM{p}_0\right)}{32b{k}_1{k}_2-3\left({k}_1+{k}_2\right){\left(\eta +b{p}_0\right)}^2}\\ {}{e}_t^S=\frac{32b{k}_1{k}_2{e}_{t0}-3\left({k}_2{e}_{t0}-{k}_1{e}_{m0}\right){\left(\eta +b{p}_0\right)}^2-3{k}_1\left(\eta +b{p}_0\right)\left(a- bc- bv+ bM{p}_0\right)}{32b{k}_1{k}_2-3\left({k}_1+{k}_2\right){\left(\eta +b{p}_0\right)}^2}\end{array}} $$

Thus, the carbon emission reduction of the supply chain system is expressed as follows:

$$ \Delta {e}_{SC}^S=\left({e}_{m0}-{e}_m^S\right)+\left({e}_{t0}-{e}_t^S\right)=\frac{3\left({k}_1+{k}_2\right)\left(\eta +{bp}_0\right)\left(a- bc- bv+{bMp}_0-\left(\eta +{bp}_0\right)\left({e}_{m0}+{e}_{t0}\right)\right)}{32{bk}_1{k}_2-3\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2}. $$

Appendix E

Proof of Theorem 4

Substituting the equations of ${e}_m^S$ and ${e}_t^S$ into p(e_m, e_t), t(e_m, e_t), andw(e_m, e_t), we can obtain the expression of p^S, t^S, andw^S. Then, substituting the expressions of p^S, t^S, and w^S into Eq. (1) and the market demand function q(p, e_m, e_t), we can easily get $\Pi^S_M$, $\Pi^C_T$, $\Pi^C_R$, and q^S. Hence, The profit of the supply chain system is expressed by

$$ {\Pi}_{SC}^S={\Pi}_M^S+{\Pi}_T^S+{\Pi}_R^S=\frac{k_1{k}_2\left(112{bk}_1{k}_2-9\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)\left(a- bc- bv+{Mbp}_0-{\left(\eta +{bp}_0\right)}^2\left({e}_{m0}+{e}_{t0}\right)\right)}{32{bk}_1{k}_2-3\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2}. $$

Appendix F

Proof of Corollary 2

Taking the first-order derivatives of $\Delta {e}_{SC}^S$ with respect to η, we have the following:

$$ \frac{\partial \varDelta {e}_{SC}^S}{\partial \eta }=\frac{3\left({k}_1+{k}_2\right)\left(3\left({k}_1+{k}_2\right)\left(a- bc- bv+ bM{p}_0\right){\left(\eta +b{p}_0\right)}^2-64b{k}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)\left(\eta +b{p}_0\right)+32b{k}_1{k}_2\left(a- bc- bv+ bM{p}_0\right)\right)}{{\left(32b{k}_1{k}_2-3\left({k}_1+{k}_2\right){\left(\eta +b{p}_0\right)}^2\right)}^2}. $$

To simplify discussion, we denote $f^S_1(\eta+bp_0)=3x(k_1+k_2)(a-bc-bv+bMp_0)(\eta+bp_o)^2-64bk_1k_2(e_{m0}+e_{t0})(\eta+bp_0)+32bk_1k_2(a-bc-bv+bMp_0)$, then we know that ${f}_1^S\left(\eta +{bp}_0\right)$ has the same monotonicity as $\mathrm{\partial \Delta }{e}_{SC}^S/\partial \eta$. Obviously, ${f}_1^S\left(\eta +{bp}_0\right)$ is a quadratic function with a parabola going upwards, and its discriminant is given by

$$ {\Delta}_{f_1^S\left(\eta +{bp}_0\right)}=128{bk}_1{k}_2\left(32{bk}_1{k}_2{\left({e}_{m0}+{e}_{t0}\right)}^2-3\left({k}_1+{k}_2\right){\left(a- bc- bv+{bMp}_0\right)}^2\right). $$

We can see that when the initial carbon emissions of the supply chain system meet ${e}_{m0}+{e}_{t0}>\left(a- bc- bv+{bMp}_0\right)\sqrt{\frac{3\left({k}_1+{k}_2\right)}{32{bk}_1{k}_2}}$, then it satisfies ${\Delta}_{f_1^S\left(\eta +{bp}_0\right)}>0$. At this point, $f^S_1(\eta+bp_0)$ has two intersections with the horizontal axis, represented by

$$ {\displaystyle \begin{array}{*{20}c}{\eta}_1^S=\frac{32{bk}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)+\sqrt{32{bk}_1{k}_2\left(32{bk}_1{k}_2{\left({e}_{m0}+{e}_{t0}\right)}^2-3\left({k}_1+{k}_2\right){\left(a- bc- bv+{bMp}_0\right)}^2\right)}}{3\left({k}_1+{k}_2\right)\left(a- bc- bv+{bMp}_0\right)}-{bp}_0,\\ {}{\eta}_2^S=\frac{32{bk}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)-\sqrt{32{bk}_1{k}_2\left(32{bk}_1{k}_2{\left({e}_{m0}+{e}_{t0}\right)}^2-3\left({k}_1+{k}_2\right){\left(a- bc- bv+{bMp}_0\right)}^2\right)}}{3\left({k}_1+{k}_2\right)\left(a- bc- bv+{bMp}_0\right)}-{bp}_0.\end{array}} $$

Based on the given assumption $0<{e}_{m0}+{e}_{t0}<\frac{a- bc- bv+{bMp}_0}{\eta +{bp}_0}$, we know that $\eta +{bp}_0<\frac{a- bc- bv+{bMp}_0}{e_{m0}+{e}_{t0}}$, so there is $\eta +{bp}_0<\sqrt{\frac{32{bk}_1{k}_2}{3\left({k}_1+{k}_2\right)}}$. Owing to ${\eta}_1^S+{bp}_0>\frac{32{bk}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)}{3\left({k}_1+{k}_2\right)\left(a- bc- bv+{bMp}_0\right)}>\sqrt{\frac{32{bk}_1{k}_2}{3\left({k}_1+{k}_2\right)}}$, the point ${\eta}_1^S+{bp}_0$ does not suit the assumption, so it will not be discussed. The above analysis shows that of $0<\eta <{\eta}_1^S$, then ${f}_1^S\left(\eta +{bp}_0\right)>0$, that is $\mathrm{\partial \Delta }{e}_{SC}^S/\partial \eta >0$; and if ${\eta}_1^S<\eta <\sqrt{\frac{32{bk}_1{k}_2}{3\left({k}_1+{k}_2\right)}}-{bp}_0$, then ${f}_1^S\left(\eta +{bp}_0\right)<0$, that is $\mathrm{\partial \Delta }{e}_{SC}^S/\partial \eta <0$. In addition, if the initial carbon emissions of the supply chain system meet ${e}_{m0}+{e}_{t0}<\left(a- bc- bv+{bMp}_0\right)\sqrt{\frac{3\left({k}_1+{k}_2\right)}{32{bk}_1{k}_2}}$, the result of ${\Delta}_{f_1^S\left(\eta +{bp}_0\right)}<0$ happens, and ${f}_1^S\left(\eta +{bp}_0\right)$ has no intersection with the horizontal axis. Hence, as long as it meets $0<\eta <\sqrt{\frac{32{bk}_1{k}_2}{3\left({k}_1+{k}_2\right)}}$, then there is ${f}_1^S\left(\eta +{bp}_0\right)>0$, that is $\mathrm{\partial \Delta }{e}_{SC}^S/\partial \eta >0$.

Appendix G

Proof of Theorem 5

Taking the second-order partial derivatives of ${\Pi}_M^L$ and ${\Pi}_{T+R}^L$ with respect to e_m and e_t, we have the following:

$$ \frac{\partial^2{\Pi}_M^L}{\partial {e}_m^2}=\frac{{\left(\eta +{bp}_0\right)}^2}{4b}-2{k}_1,\frac{\partial^2{\Pi}_{T+R}^L}{\partial {e}_t^2}=\frac{{\left(\eta +{bp}_0\right)}^2}{8b}-2{k}_2. $$

Let’s make ${\partial}^2{\Pi}_M^L/\partial {e}_m^2$ and ${\partial}^2{\Pi}_{T+R}^L/\partial {e}_t^2$ less than zero, and we get $\eta <2\sqrt{2{bk}_1}-{bp}_0$ and $\eta <4\sqrt{bk_2}-{bp}_0$. At that moment, the manufacturer’s profit function, ${\Pi}_M^L$, is concave in e_m, and the transporter-retailer alliance’s profit function, ${\Pi}_{T+R}^L$, is concave in e_t. Letting the first-order conditions of the profit function be zero, that is $\partial {\Pi}_M^L/\partial {e}_m=0$ and $\partial {\Pi}_{T+R}^L/\partial {e}_t=0$, and simultaneously solving the two equations, then the final carbon emissions from the manufacturer and the transporter-retailer alliance are given, respectively, by

$$ \left\{\begin{array}{*{20}c}{e}_m^L=\frac{16b{k}_1{k}_2{e}_{m0}-\left({k}_1{e}_{m0}-2{k}_2{e}_{t0}\right){\left(\eta +b{p}_0\right)}^2-2{k}_2\left(\eta +b{p}_0\right)\left(a- bc- bv+ bM{p}_0\right)}{16b{k}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +b{p}_0\right)}^2}\\ {}{e}_t^L=\frac{16b{k}_1{k}_2{e}_{t0}-\left(2{k}_2{e}_{t0}-{k}_1{e}_{m0}\right){\left(\eta +b{p}_0\right)}^2-{k}_1\left(\eta +b{p}_0\right)\left(a- bc- bv+ bM{p}_0\right)}{16b{k}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +b{p}_0\right)}^2}\end{array}\right. $$

Thus, the carbon emission reduction of the supply chain system is expressed as follows:

$$ \Delta {e}_{SC}^L=\left({e}_{m0}-{e}_m^L\right)+\left({e}_{t0}-{e}_t^L\right)=\frac{\left({k}_1+2{k}_2\right)\left(\eta +{bp}_0\right)\left(a- bc- bv+{bMp}_0-\left(\eta +{bp}_0\right)\left({e}_{m0}+{e}_{t0}\right)\right)}{16{bk}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +{bp}_0\right)}^2}. $$

Appendix H

Proof of Theorem 6

Substitute the equations of ${e}_m^L$ and ${e}_t^L$ into p(e_m, e_t) and w(e_m, e_t), it’s easy to gain the expression of p^L and w^L. Subsequently, continuing to substituting the expressions of p^L and w^L into Eq. (9) and the market demand function q(p, e_m, e_t), we can easily obtain ${\Pi}_M^L$, ${\Pi}_{T+R}^L$, and q^L. Therefore, the profit function of the supply chain system is expressed by ${\Pi}_{SC}^L={\Pi}_M^L+{\Pi}_{T+R}^L=\frac{k_1{k}_2\left(48{bk}_1{k}_2-\left({k}_1+4{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)\left(a- bc- bv+{Mbp}_0-{\left(\eta +{bp}_0\right)}^2\left({e}_{m0}+{e}_{t0}\right)\right)}{16{bk}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +{bp}_0\right)}^2}$.

Appendix I

Proof of Corollary 3

Taking the first-order derivatives of $\Delta {e}_{SC}^L$ with respect to η, we have the following:

$$ \frac{\mathrm{\partial \Delta }{e}_{SC}^L}{\partial \eta }=\frac{\left({k}_1+2{k}_2\right)\left(\left({k}_1+2{k}_2\right)\left(a- bc- bv+{bMp}_0\right){\left(\eta +{bp}_0\right)}^2-32{bk}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)\left(\eta +{bp}_0\right)+16{bk}_1{k}_2\left(a- bc- bv+{bMp}_0\right)\right)}{{\left(16{bk}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)}^2}. $$

To simplify the discussion, we denote ${f}_1^L\left(\eta +{bp}_0\right)=\left({k}_1+2{k}_2\right)\left(a- bc- bv+{bMp}_0\right){\left(\eta +{bp}_0\right)}^2-32{bk}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)\left(\eta +{bp}_0\right)$ +16bk₁k₂(a − bc − bv + bMp₀), then we know that ${f}_1^L\left(\eta +{bp}_0\right)$ has the same monotonicity an $\mathrm{\partial \Delta }{e}_{SC}^L/\partial \eta$. Apparently, ${f}_1^L\left(\eta +{bp}_0\right)$ is a quadratic function with a parabola going upwards, and its discriminant is given by

$$ {\Delta}_{f_1^L\left(\eta +{bp}_0\right)}=64{bk}_1{k}_2\left(16{bk}_1{k}_2{\left({e}_{m0}+{e}_{t0}\right)}^2-\left({k}_1+2{k}_2\right){\left(a- bc- bv+{bMp}_0\right)}^2\right). $$

We can see that when the initial carbon emissions of the supply chain system meet ${e}_{m0}+{e}_{t0}>\left(a- bc- bv+{bMp}_0\right)\sqrt{\frac{k_1+2{k}_2}{16{bk}_1{k}_2}}$, then it satisfies ${\Delta}_{f_1^L\left(\eta +{bp}_0\right)}>0$. At this point, $f^L_1(\eta+bp_0)$ has two intersections with the horizontal axis, represented by

$$ {\displaystyle \begin{array}{*{20}c}{\eta}_1^L+{bp}_0=\frac{16{bk}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)+\sqrt{16{bk}_1{k}_2\left(16{bk}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)-\left({k}_1+2{k}_2\right){\left(a- bc- bv+{bMp}_0\right)}^2\right)}}{\left({k}_1+2{k}_2\right)\left(a- bc- bv+{bMp}_0\right)},\\ {}{\eta}_2^L+{bp}_0=\frac{16{bk}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)-\sqrt{16{bk}_1{k}_2\left(16{bk}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)-\left({k}_1+2{k}_2\right){\left(a- bc- bv+{bMp}_0\right)}^2\right)}}{\left({k}_1+2{k}_2\right)\left(a- bc- bv+{bMp}_0\right)}.\end{array}} $$

Based on the given assumption $0<{e}_{m0}+{e}_{t0}<\frac{a- bc- bv+{bMp}_0}{\eta +{bp}_0}$, we know that $\eta +{bp}_0<\frac{a- bc- bv+{bMp}_0}{e_{m0}+{e}_{t0}}$, so there is $\eta +{bp}_0<\sqrt{\frac{16{bk}_1{k}_2}{k_1+2{k}_2}}$. Owing to ${\eta}_1^L+{bp}_0>\frac{16{bk}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)}{\left({k}_1+2{k}_2\right)\left(a- bc- bv+{bMp}_0\right)}>\sqrt{\frac{16{bk}_1{k}_2}{k_1+2{k}_2}}$, the point ${\eta}_1^L+{bp}_0$ does not suit the assumption, so it will not be discussed. The above analysis shows that if $0<\eta <{\eta}_1^L$, then ${f}_1^L\left(\eta +{bp}_0\right)>0$, that is $\mathrm{\partial \Delta }{e}_{SC}^L/\partial \eta >0$; and if ${\eta}_1^L<\eta <\sqrt{\frac{16{bk}_1{k}_2}{k_1+2{k}_2}}-{bp}_0$, then ${f}_1^L\left(\eta +{bp}_0\right)<0$, that is $\mathrm{\partial \Delta }{e}_{SC}^L/\partial \eta <0$. In addition, if the initial carbon emissions of the supply chain system meet ${e}_{m0}+{e}_{t0}<\left(a- bc- bv+{bMp}_0\right)\sqrt{\frac{k_1+2{k}_2}{16{bk}_1{k}_2}}$, the result of ${\Delta}_{f_1^L\left(\eta +{bp}_0\right)}<0$ happens, and ${f}_1^L\left(\eta +{bp}_0\right)$ has no intersection with the horizontal axis. Hence, as long as it meets $0<\eta <\sqrt{\frac{16{bk}_1{k}_2}{k_1+2{k}_2}}-{bp}_0$, then there is ${f}_1^L\left(\eta +{bp}_0\right)>0$, that is $\mathrm{\partial \Delta }{e}_{SC}^L/\partial \eta >0$.

Appendix J

Proof of Theorem 7

Taking the second-order partial derivatives of ${\Pi}_{SC}^D$ with respect to e_m and e_t, we have the Hessian matrix as follows:

$$ H=\left(\begin{array}{*{20}c}\frac{{\left(\eta +{bp}_0\right)}^2}{2b}-2{k}_1 \kern34pt \frac{{\left(\eta +{bp}_0\right)}^2}{2b}\\ {}\frac{{\left(\eta +{bp}_0\right)}^2}{2b} \kern34pt \frac{{\left(\eta +{bp}_0\right)}^2}{2b}-2{k}_2\end{array}\right) $$

Let’s make $\frac{{\left(\eta +{bp}_0\right)}^2}{2b}-2{k}_1<0$ and $\left|\mathrm{H}\right|=\frac{\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2}{b}-4{k}_1{k}_2<0$, that is $0<\eta <\sqrt{\frac{4{bk}_1{k}_2}{k_1+{k}_2}}-{bp}_0$, then ${\Pi}_{SC}^D$ is a strictly jointly concave function on e_m and e_t. Therefore, the optimal solutions to this optimization problem exist. Taking the first-order conditions of ${\Pi}_{SC}^D$ with respect to e_m and e_t be zero, that is $\partial {\Pi}_{SC}^D/\partial {e}_m=0$ and $\partial {\Pi}_{SC}^D/\partial {e}_t=0$, and simultaneously solving the two equations, then the final carbon emissions from the manufacturer and the transporter are given, respectively, by

$$ \Big\{{\displaystyle \begin{array}{*{20}c}{e}_m^D=\frac{4b{k}_1{k}_2{e}_{m0}-\left({k}_1{e}_{m0}-{k}_2{e}_{t0}\right){\left(\eta +b{p}_0\right)}^2-{k}_2\left(\eta +b{p}_0\right)\left(a- bc- bv+ bM{p}_0\right)}{4b{k}_1{k}_2-\left({k}_1+{k}_2\right){\left(\eta +b{p}_0\right)}^2}\\ {}{e}_t^D=\frac{4b{k}_1{k}_2{e}_{t0}-\left({k}_2{e}_{t0}-{k}_1{e}_{m0}\right){\left(\eta +b{p}_0\right)}^2-{k}_1\left(\eta +b{p}_0\right)\left(a- bc- bv+ bM{p}_0\right)}{4b{k}_1{k}_2-\left({k}_1+{k}_2\right){\left(\eta +b{p}_0\right)}^2}\end{array}} $$

Thus, the carbon emission reduction of the supply chain system is expressed as follows:

$$ \Delta {e}_{SC}^D=\left({e}_{m0}-{e}_m^D\right)+\left({e}_{t0}-{e}_t^D\right)=\frac{\left({k}_1+{k}_2\right)\left(\eta +{bp}_0\right)\left(a- bc- bv+{bMp}_0-\left(\eta +{bp}_0\right)\left({e}_{m0}+{e}_{t0}\right)\right)}{4{bk}_1{k}_2-\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2}. $$

Appendix K

Proof of Theorem 8

Substituting the equations of ${e}_m^D$ and ${e}_t^D$ into p(e_m, e_t), we can obtain the expression of p^D. Next, substituting the expression of p^D into Eq. (14) and it’s easy to obtain the profit of the supply chain system, simplified as ${\varPi}_{SC}^D{}_{SC}{}^{D\kern0.5em }=\frac{k_1{k}_2{\left(a- bc- bv+{bMp}_0-\left(\eta +{bp}_0\right)\left({e}_{m0}+{e}_{t0}\right)\right)}^2}{4{bk}_1{k}_2-\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2}.$

Appendix L

Proof of Corollary 4

Taking the first-order derivatives of $\Delta {e}_{SC}^D$ with respect to η, we have the following:

$$ \frac{\mathrm{\partial \Delta }{e}_{SC}^D}{\partial \eta }=\frac{\left({k}_1+{k}_2\right)\left(\left({k}_1+{k}_2\right)\left(a- bc- bv+{bMp}_0\right){\left(\eta +{bp}_0\right)}^2-8{bk}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)\left(\eta +{bp}_0\right)+4{bk}_1{k}_2\left(a- bc- bv+{bMp}_0\right)\right)}{{\left(4{bk}_1{k}_2-\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)}^2}. $$

To simplify discussion, we denote ${f}_1^D\left(\eta +{bp}_0\right)=\left({k}_1+{k}_2\right)\left(a- bc- bv+{bMp}_0\right){\left(\eta +{bp}_0\right)}^2-8{bk}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)\left(\eta +{bp}_0\right)$ +4bk₁k₂(a − bc − bv + bMp₀), then we know that ${f}_1^D\left(\eta +{bp}_0\right)$ has the same monotonicity as $\mathrm{\partial \Delta }{e}_{SC}^D/\partial \eta$. Obviously, ${f}_1^D\left(\eta +{bp}_0\right)$ is a quadratic function with a parabola going upwards, and its discriminant is given by

$$ {\Delta}_{f_1^D\left(\eta +{bp}_0\right)}=16{bk}_1{k}_2\left(4{bk}_1{k}_2{\left({e}_{m0}+{e}_{t0}\right)}^2-\left({k}_1+{k}_2\right){\left(a- bc- bv+{bMp}_0\right)}^2\right). $$

We can see that when the initial carbon emissions of the supply chain system meet ${e}_{m0}+{e}_{t0}>\left(a- bc- bv+{bMp}_0\right)\sqrt{\frac{k_1+{k}_2}{4{bk}_1{k}_2}}$, then it satisfies ${\Delta}_{f_1^D\left(\eta +{bp}_0\right)}>0$. At this point, $f^D_1(\eta+bp_0)$ has two intersections with the horizontal axis, represented by

$$ {\displaystyle \begin{array}{*{20}c}{\eta}_1^D+{bp}_0=\frac{4{bk}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)+\sqrt{4{bk}_1{k}_2\left(4{bk}_1{k}_2{\left({e}_{m0}+{e}_{t0}\right)}^2-\left({k}_1+{k}_2\right){\left(a- bc- bv+{bMp}_0\right)}^2\right)}}{\left({k}_1+{k}_2\right)\left(a- bc- bv+{bMp}_0\right)},\\ {}{\eta}_2^D+{bp}_0=\frac{4{bk}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)-\sqrt{4{bk}_1{k}_2\left(4{bk}_1{k}_2{\left({e}_{m0}+{e}_{t0}\right)}^2-\left({k}_1+{k}_2\right){\left(a- bc- bv+{bMp}_0\right)}^2\right)}}{\left({k}_1+{k}_2\right)\left(a- bc- bv+{bMp}_0\right)}.\end{array}} $$

Based on the given assumption $0<{e}_{m0}+{e}_{t0}<\frac{a- bc- bv+{bMp}_0}{\eta +{bp}_0}$, we know that $\eta +{bp}_0<\frac{a- bc- bv+{bMp}_0}{e_{m0}+{e}_{t0}}$, so there is $\eta +{bp}_0<\sqrt{\frac{4{bk}_1{k}_2}{k_1+{k}_2}}$. Owing to ${\eta}_1^D+{bp}_0>\frac{4{bk}_1{k}_2\left({e}_{m0}+{e}_{t0}\right)}{\left({k}_1+{k}_2\right)\left(a- bc- bv+{bMp}_0\right)}>\sqrt{\frac{4{bk}_1{k}_2}{k_1+{k}_2}}$, the point ${\eta}_1^D+{bp}_0$ does not suit the assumption, so it will not be discussed. The above analysis shows that if $0<\eta <{\eta}_1^D$, then ${f}_1^D\left(\eta +{bp}_0\right)>0$, that is $\mathrm{\partial \Delta }{e}_{SC}^D/\partial \eta >0$; and if ${\eta}_1^D<\eta <\sqrt{\frac{4{bk}_1{k}_2}{k_1+{k}_2}}-{bp}_0$, then ${f}_1^D\left(\eta +{bp}_0\right)<0$, $\mathrm{\partial \Delta }{e}_{SC}^D/\partial \eta <0$. In addition, if the initial carbon emissions of the supply chain system meet ${e}_{m0}+{e}_{t0}<\left(a- bc- bv+{bMp}_0\right)\sqrt{\frac{k_1+{k}_2}{4{bk}_1{k}_2}}$, the result of ${\Delta}_{f_1^D\left(\eta +{bp}_0\right)}<0$ happens, and ${f}_1^D\left(\eta +{bp}_0\right)$ has no intersection with the horizontal axis. Hence, as long as it meets $0<\eta <\sqrt{\frac{4{bk}_1{k}_2}{k_1+{k}_2}}-{bp}_0$, there is ${f}_1^D\left(\eta +{bp}_0\right)>0$, that is $\mathrm{\partial \Delta }{e}_{SC}^D/\partial \eta >0$.

Appendix M

Proof of Corollary 5

Comparing the carbon emission reductions of the NCD and LCDM models, we have the following:

$$ \frac{\Delta {e}_{SC}^S}{\Delta {e}_{SC}^N}=\frac{3\left({k}_1+{k}_2\right)\left(32{bk}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)}{\left({k}_1+2{k}_2\right)\left(32{bk}_1{k}_2-3\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)}>1. $$

Thus, there is $\Delta {e}_{SC}^S>\Delta {e}_{SC}^N$.

Comparing the selling price of the NCD and LCDM models, we have the following:

$$ {p}^S-{p}^N=\frac{4{k}_1{k}_2\left(2{k}_1+{k}_2\right)\left(\eta +{bp}_0\right)\left(7\eta -{bp}_0\right)\left(a- bc- bv+{bMp}_0-\left({e}_{m0}+{e}_{t0}\right)\left(\eta +{bp}_0\right)\right)}{\left(32{bk}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)\left(32{bk}_1{k}_2-3\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)}. $$

If it meets $0<\eta <\frac{1}{7}{bp}_0$, then there is p^S < p^N; if it meets $\frac{bp_0}{7}<\eta <\sqrt{\frac{32{bk}_1{k}_2}{3\left({k}_1+{k}_2\right)}}-{bp}_0$, then there is p^S > p^N.

Comparing the market demand of the NCD and LCDM models, we have the following:

$$ \frac{q^S}{q^N}=\frac{32{bk}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +{bp}_0\right)}^2}{32{bk}_1{k}_2-3\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2}>1. $$

Thus, there is q^S > q^N.

Comparing the supply chain system’s profit of the NCD and LCDM models, we have the following:

$$ \frac{\varPi_{SC}^S}{\varPi_{SC}^N}=\frac{{\left(32{bk}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)}^2\left(112{bk}_1{k}_2-9\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)}{{\left(32{bk}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)}^2\left(112{bk}_1{k}_2-\left({k}_1+4{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)}. $$

Letting x = (η + bp₀)², y = 32bk₁k₂/3, then there is y > (k₁ + k₂)x. We know that, ${\left(32{bk}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)}^2\big(112{bk}_1{k}_2-9\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2-{\left(32{bk}_1{k}_2-3\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)}^2{\left(112{bk}_1{k}_2-\left({k}_1+4{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)}^2={\left(3y-\left({k}_1+2{k}_2\right)x\right)}^2\left(\frac{21y}{2}-9\left({k}_1+{k}_2\right)x\right)-{\left(3y-3\left({k}_1+{k}_2\right)x\right)}^2\left(\frac{21y}{2}-\left({k}_1+4{k}_2\right)x\right)=\frac{21y}{2}{\left(3y-\left({k}_1+2{k}_2\right)x\right)}^2-9\left({k}_1+{k}_2\right)x{\left(3y-\left(k+2k\right)x\right)}^2-\frac{21y}{2}{\left(3y-3\left({k}_1+{k}_2\right)x\right)}^2+\left({k}_1+4{k}_2\right)x{\left(3y-3\left({k}_1+{k}_2\right)x\right)}^2=\frac{21y}{2}\left({\left(3y-\left({k}_1+2{k}_2\right)x\right)}^2-{\left(3y-3\left({k}_1+{k}_2\right)x\right)}^2\right)-9\left({k}_1+{k}_2\right)x\left(9{y}^2-6 xy\left({k}_1+2{k}_2\right)+{\left({k}_1+2{k}_2\right)}^2{x}^2\right)+\left({k}_1+4{k}_2\right)x\left(9{y}^2-18 xy\left({k}_1+{k}_2\right)+9\left({k}_1+{k}_2\right){x}^2\right)=\frac{21y}{2}\left(6y-\left(4{k}_1+5{k}_2\right)x\right)\left(2{k}_1+{k}_2\right)x-9{xy}^2\left(8{k}_1+5{k}_2\right)+36{x}^2y{\left({k}_1+{k}_2\right)}^2+9{x}^3{k}_1{k}_2\left({k}_1+{k}_2\right)=63{xy}^2\left(2{k}_1+{k}_2\right)-\frac{21}{2}{x}^2y\left(2{k}_1+{k}_2\right)\left(4{k}_1+5{k}_2\right)-9{xy}^2\left(8{k}_1+5{k}_2\right)+36{x}^2y{\left({k}_1+{k}_2\right)}^2+9{x}^3{k}_1{k}_2\left({k}_1+{k}_2\right)= xy\left(63y\left(2{k}_1+{k}_2\right)-9y\left(8{k}_1+5{k}_2\right)+36x{\left({k}_1+{k}_2\right)}^2-\frac{21}{2}x\left(2{k}_1+{k}_2\right)\left(4{k}_1+5{k}_2\right)\right)+9{x}^3{k}_1{k}_2\left({k}_1+{k}_2\right)= xy\left(18y\left(3{k}_1+{k}_2\right)-x\left(48{k}_1^2+75{k}_1{k}_2+\frac{33}{2}{k}_2^2\right)\right)+9{x}^3{k}_1{k}_2\left({k}_1+{k}_2\right)> xy\left(18x\left({k}_1+{k}_2\right)\left(3{k}_1+{k}_2\right)-x\left(48{k}_1^2+75{k}_1{k}_2+\frac{33}{2}{k}_2^2\right)\right)+9{x}^3{k}_1{k}_2\left({k}_1+{k}_2\right)= xy\left(6{k}_1^2-3{k}_1{k}_2+\frac{3}{2}{k}_2^2\right)+9{x}^3{k}_1{k}_2\left({k}_1+{k}_2\right)>{x}^3\left(6{k}_1^2-3{k}_1{k}_2+\frac{3}{2}{k}_2^2\right)\left({k}_1+{k}_2\right)+9{x}^3{k}_1{k}_2\left({k}_1+{k}_2\right)={x}^3\left(6{k}_1^2+6{k}_1{k}_2+\frac{3}{2}{k}_2^2\right)\left({k}_1+{k}_2\right)>0$, then there is ${\Pi}_{SC}^S>{\Pi}_{SC}^N$.

Appendix N

Proof of Corollary 6

Comparing the carbon emission reductions of the NCD and LCDR models, we have the following:

$$ \frac{\Delta {e}_{SC}^L}{\Delta {e}_{SC}^N}=\frac{32{bk}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +{bp}_0\right)}^2}{16{bk}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +{bp}_0\right)}^2}>1. $$

Thus, there is $\Delta {e}_{SC}^L>\Delta {e}_{SC}^N$.

Comparing the selling price of the NCD and LCDR models, we have the following:

$$ {p}^L-{p}^N=\frac{16{k}_1{k}_2\left(a- bc- bv+ bM{p}_0-\left({e}_{m0}+{e}_{t0}\right)\left(\eta +b{p}_0\right)\right)\left(\left({k}_1+2{k}_2\right)\eta \left(\eta +b{p}_0\right)-4b{k}_1{k}_2\right)}{\left(32b{k}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +b{p}_0\right)}^2\right)\left(16b{k}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +b{p}_0\right)}^2\right)}. $$

We know that, If it meets (k₁ + 2k₂)η(η + bp₀) − 4bk₁k₂ > 0, that is $\sqrt{\frac{\left({k}_1+2{k}_2\right){\left({bp}_0\right)}^2+16{bk}_1{k}_2}{4\left({k}_1+2{k}_2\right)}}-\frac{bp_0}{2}<\eta <\sqrt{\frac{16{bk}_1{k}_2}{k_1+2{k}_2}}-{bp}_0$, then there is p^L > p^N; and when $0<\eta <\sqrt{\frac{\left({k}_1+2{k}_2\right){\left({bp}_0\right)}^2+16{bk}_1{k}_2}{4\left({k}_1+2{k}_2\right)}}-\frac{bp_0}{2}$, then there is p^L < p^N.

Comparing the market demand of the NCD and LCR models, we have the following:

$$ \frac{q^L}{q^N}=\frac{32{bk}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +{bp}_0\right)}^2}{16{bk}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +{bp}_0\right)}^2}>1. $$

Thus, there is q^L > q^N.

Comparing the supply chain system’s profit of the NCD and LCDR models, we have the following:

$$ \frac{\varPi_{SC}^L}{\varPi_{SC}^N}=\frac{\left(48{bk}_1{k}_2-\left({k}_1+4{k}_2\right){\left(\eta +{bp}_0\right)}^2\right){\left(32{bk}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)}^2}{{\left(16{bk}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)}^2\left(112{bk}_1{k}_2-\left({k}_1+4{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)}. $$

Letting x = (η + bp₀)², y = 16bk₁k₂, then there is y > (k₁ + 2k₂)x. We know that (48bk₁k₂ − (k₁ + 4k₂)(η + bp₀)²)(32bk₁k₂ − (k₁ + 2k₂)(η + bp₀)²)² − (16bk₁k₂ − (k₁ + 2k₂)(η + bp₀)²)²(112bk₁k₂ − (k₁ + 4k₂)(η + bp₀)²) = (3y − (k₁ + 4k₂)x)(2y − (k₁ + 2k₂)x)² − (y − (k₁ + 2k₂)x)²(7y − (k₁ + 4k₂)x) = 3y(2y − (k₁ + 2k₂)x)² − 7y(y − (k₁ + 2k₂)x)² − (k₁ + 4k₂)x(2y − (k₁ + 2k₂)x)² − (k₁ + 4k₂)x ⋅ (y − (k₁ + 2k₂)x)² = y(3(2y − (k₁ + 2k₂)x)² − 7(y − (k₁ + 2k₂)x)²) − (k₁ + 4k₂)x((2y − (k₁ + 2k₂)x)² − (y − (k₁ + 2k₂)x)²) = y(5y² + 2xy(k₁ + 2k₂) + 4x²(k₁ + 2k₂)² − xy(k₁ + 4k₂)(3y − 2(k₁ + 2k₂)x) = y(5y² + 2xy(k₁ + 2k₂) − 4x²(k₁ + 2k₂)² − 3xy(k₁ + 4k₂) + 2x²(k₁ + 2k₂)(k₁ + 4k₂) = y(5y² − xy(k₁ + 8k₂) − 2x²k₁(k₁ + 2k₂)) = y(y(5y − x(k₁ + 8k₂)) − 2x²k₁(k₁ + 2k₂)) > y(y(5x(k₁ + 2k₂) − x(k₁ + 8k₂)) − 2x²k₁(k₁ + 2k₂)) = y(2xy(2k₁ + k₂) − 2x²k₁(k₁ + 2k₂)) = 2xy(y(2k₁ + k₂) − xk₁(k₁ + 2k₂)) > 2xy(x(k₁ + 2k₂)(2k₁ + k₂) − xk₁(k₁ + 2k₂)) = 2x²y(k₁ + 2k₂)(k₁ + k₂) > 0, then there is ${\Pi}_{SC}^L>{\Pi}_{SC}^N$.

Appendix O

Proof of Corollary 7

Comparing the carbon emission reductions of the LCDM and OCD models, we have the following:

$$ \frac{\Delta {e}_{SC}^D}{\Delta {e}_{SC}^S}=\frac{32{bk}_1{k}_2-3\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2}{12{bk}_1{k}_2-3\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2}>1. $$

Thus, there is $\Delta {e}_{SC}^D>\Delta {e}_{SC}^S$.

Comparing the selling price of the LCDM and OCD models, we have the following:

$$ {p}^D-{p}^S=\frac{2{k}_1{k}_2\left(a- bc- bv+ bM{p}_0-\left({e}_{m0}+{e}_{t0}\right)\left(\eta +b{p}_0\right)\right)\left(\left({k}_1+{k}_2\right)\left(\eta +b{p}_0\right)\left(11\eta +b{p}_0\right)-24b{k}_1{k}_2\right)}{\left(4b{k}_1{k}_2-\left({k}_1+{k}_2\right){\left(\eta +b{p}_0\right)}^2\right)\left(32b{k}_1{k}_2-3\left({k}_1+{k}_2\right){\left(\eta +b{p}_0\right)}^2\right)}. $$

We know that, if it meets (k₁ + k₂)(η + bp₀)(11η + bp₀) − 24bk₁k₂ > 0, that is $\sqrt{\frac{25\left({k}_1+{k}_2\right){\left({bp}_0\right)}^2+264{bk}_1{k}_2}{121\left({k}_1+{k}_2\right)}}-\frac{6{bp}_0}{11}<\eta$ $<\sqrt{\frac{4{bk}_1{k}_2}{k_1+{k}_2}}-{bp}_0$, then there is p^D > p^S; and when $0<\eta <\sqrt{\frac{25\left({k}_1+{k}_2\right){\left({bp}_0\right)}^2+264{bk}_1{k}_2}{121\left({k}_1+{k}_2\right)}}-\frac{6{bp}_0}{11}$, then there is p^D < p^S.

Comparing the market demand of the LCDM and OCD models, we have the following:

$$ \frac{q^D}{q^S}=\frac{32{bk}_1{k}_2-3\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2}{8{bk}_1{k}_2-2\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2}>\frac{32{bk}_1{k}_2-3\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2}{12{bk}_1{k}_2-3\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2}>1. $$

Thus, there is q^D > q^S.

Comparing the supply chain system’s profit of the LCDM and OCD models, we have the following:

$$ \frac{\varPi_{SC}^D}{\varPi_{SC}^S}=\frac{{\left(32{bk}_1{k}_2-3\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)}^2}{\left(4{bk}_1{k}_2-\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)\left(112{bk}_1{k}_2-9\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)}. $$

Letting x = (η + bp₀)², y = 4bk₁k₂, then there is y > (k₁ + k₂)x. We know that (32bk₁k₂ − 3(k₁ + k₂)(η + bp₀)²)² − (4bk₁k₂ − (k₁ + k₂)(η + bp₀)²)(112bk₁k₂ − 9(k₁ + k₂)(η + bp₀)²) = (8y − 3(k₁ + k₂)x)² − (y − (k₁ + k₂)x)(28y − 9(k₁ + k₂)x) = 36y² − 11xy(k₁ + k₂) > y(36x(k₁ + k₂) − 11x(k₁ + k₂)) = 25xy(k₁ + k₂) > 0, then there is ${\Pi}_{SC}^D>{\Pi}_{SC}^S$.

Appendix P

Proof of Corollary 8

Comparing the carbon emission reductions of the LCDR and OCD models, we have the following:

$$ \frac{\Delta {e}_{SC}^D}{\Delta {e}_{SC}^L}=\frac{16{bk}_1{k}_2\left({k}_1+{k}_2\right)-\left({k}_1+{k}_2\right)\left({k}_1+2{k}_2\right){\left(\eta +{bp}_0\right)}^2}{4{bk}_1{k}_2\left({k}_1+2{k}_2\right)-\left({k}_1+{k}_2\right)\left({k}_1+2{k}_2\right){\left(\eta +{bp}_0\right)}^2}>1. $$

Thus, there is $\Delta {e}_{SC}^D>\Delta {e}_{SC}^L$.

Comparing the selling price of the LCDR and OCD models, we have the following:

$$ {p}^D-{p}^L=\frac{2{k}_1{k}_2\left(a- bc- bv+ bM{p}_0-\left({e}_{m0}+{e}_{t0}\right)\left(\eta +b{p}_0\right)\right)\left(\left(\eta +b{p}_0\right)\left(4{k}_2\eta +{k}_1\left(5\eta -b{p}_0\right)\right)-8{bk}_1{k}_2\right)}{\left(16{bk}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +b{p}_0\right)}^2\right)\left(4{bk}_1{k}_2-\left({k}_1+{k}_2\right){\left(\eta +b{p}_0\right)}^2\right)} $$

We know that, if it meets (η + bp₀)(4k₂η + k₁(5η − bp₀)) − 8bk₁k₂ > 0, that is $\frac{\sqrt{\left(9{k}_1^2+12{k}_1{k}_2+4{k}_2^2\right){\left({bp}_0\right)}^2+8{bk}_1{k}_2\left(5{k}_1+4{k}_2\right)}}{5{k}_1+4{k}_2}$ $-\frac{2\left({k}_1+{k}_2\right){bp}_0}{5{k}_1+4{k}_2}<\eta <\sqrt{\frac{4{bk}_1{k}_2}{k_1+{k}_2}}-{bp}_0$, then there is p^D > p^L; and when $0<\eta <\frac{\sqrt{\left(9{k}_1^2+12{k}_1{k}_2+4{k}_2^2\right){\left({bp}_0\right)}^2+8{bk}_1{k}_2\left(5{k}_1+4{k}_2\right)}}{5{k}_1+4{k}_2}$ $-\frac{2\left({k}_1+{k}_2\right){bp}_0}{5{k}_1+4{k}_2}$, then there is p^D < p^L.

Comparing the market demand of the LCDR and OCD models, we have the following:

$$ \frac{q^D}{q^L}=\frac{16{bk}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +{bp}_0\right)}^2}{8{bk}_1{k}_2-2\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2}>1. $$

Thus, there is q^D > q^L.

Comparing the supply chain system’s profit of the LCDR and OCD models, we have the following:

$$ \frac{\varPi_{SC}^D}{\varPi_{SC}^L}=\frac{{\left(16{bk}_1{k}_2-\left({k}_1+2{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)}^2}{\left(4{bk}_1{k}_2-\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)\left(48{bk}_1{k}_2-\left({k}_1+4{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)}. $$

Letting x = (η + bp₀)², y = 4bk₁k₂, then there is y > (k₁ + k₂)x. We know that (16bk₁k₂ − (k₁ + 2k₂)(η + bp₀)²)² − (4bk₁k₂ − (k₁ + k₂)(η + bp₀)²)(48bk₁k₂ − (k₁ + 4k₂)(η + bp₀)²) = (4y − (k₁ + 2k₂)x)² − (y − (k₁ + k₂)x)(12y − (k₁ + 4k₂)x) = 16y² − 8xy(k₁ + 2k₂) + (k₁ + 2k₂)²x² − (12y² − xy(k₁ + 4k₂) − 12xy(k₁ + k₂) + (k₁ + k₂)(k₁ + 4k₂)x²) = 4y² + 5xyk₁ − k₁k₂x² = 4y² + k₁x(5y − k₂x) > 4y² + xk₁(5(k₁ + k₂)x − k₂x) = 4y² + xk₁(5k₁ + 4k₂) > 0, then there is ${\Pi}_{SC}^D>{\Pi}_{SC}^L$.

Appendix Q

Proof of Theorem 9

Taking the second-order partial derivatives of ${\Pi}_M^C$ and ${\Pi}_{T+R}^C$ with respect to e_m and e_t, we can obtain

$$ \frac{\partial^2{\Pi}_M^C}{\partial {e}_m^2}=\frac{{\left(\eta +{bp}_0\right)}^2}{4b}-2{k}_1t,\frac{\partial^2{\Pi}_{T+R}^C}{\partial {e}_t^2}=\frac{{\left(\eta +{bp}_0\right)}^2}{8b}-2{k}_2t. $$

Let’s make ${\partial^2\Pi^C_M/\partial{e}_{m}}^2$ and ${\partial^2\Pi^C_{T+R}/\partial{e}_t}^2$ less than zero, and we get $\eta <2\sqrt{2{bk}_1t}-{bp}_0$ and $\eta <4\sqrt{bk_2t}-{bp}_0$. At this time, the manufacturer’s profit function, ${\Pi}_M^C$, is concave in e_m, and the retailer-transporter alliance’s profit function, ${\Pi}_{T+R}^C$, is concave in e_t. Letting the first-order conditions of the profit function be zero, that is $\partial\Pi^C_M/\partial{e}_m=0$ and $\partial\Pi^C_{T+R}/\partial{e}_t=0$, and simultaneously solving the two equations, then the final carbon emission from the manufacturer and the retailer-transporter alliance are given, respectively, by

$$ \left\{\begin{array}{*{20}c}{e}_m^C=\frac{16 bt{k}_1{k}_2{e}_{m0}-\left({k}_1{e}_{m0}-2t{k}_2{e}_{t0}\right){\left(\eta +b{p}_0\right)}^2-2t{k}_2\left(\eta +b{p}_0\right)\left(a- bc- bv+ bM{p}_0\right)}{16 bt{k}_1{k}_2-\left({k}_1+2t{k}_2\right){\left(\eta +b{p}_0\right)}^2}\\ {}{e}_t^C=\frac{16 bt{k}_1{k}_2{e}_{t0}-\left(2t{k}_2{e}_{t0}-{k}_1{e}_{m0}\right){\left(\eta +b{p}_0\right)}^2-{k}_1\left(\eta +b{p}_0\right)\left(a- bc- bv+ bM{p}_0\right)}{16 bt{k}_1{k}_2-\left({k}_1+2t{k}_2\right){\left(\eta +b{p}_0\right)}^2}\end{array}\right. $$

Then, the carbon emission reduction of the supply chain system is expressed as

$$ \Delta {e}_{SC}^C=\left({e}_{m0}-{e}_m^C\right)+\left({e}_{t0}-{e}_t^C\right)=\frac{\left({k}_1+2{tk}_2\right)\left(\eta +{bp}_0\right)\left(a- bc- bv+{bMp}_0-\left(\eta +{bp}_0\right)\left({e}_{m0}+{e}_{t0}\right)\right)}{16{btk}_1{k}_2-\left({k}_1+2{tk}_2\right){\left(\eta +{bp}_0\right)}^2}. $$

Appendix R

Proof of Theorem 10

Substituting the values of ${e}_m^C$ and ${e}_t^C$ into p(e_m, e_t) and w(e_m, e_t), it is not difficult to get the expression of p^C and w^C. Substituting the values of p^C and w^C into Equation (21) and the market demand function q(p, e_m, e_t), we can easily obtain ${\Pi}_M^C$, ${\Pi}_{T+R}^C$, and q^C. The profit of the supply chain system is expressed as

$$\Pi^C_M=\Pi^C_M+\Pi^C_{T+R}=\frac{k_1k_2(48t^2bk_1k_2-(k_1+4t^2k_2)(\eta+bp_0)^2)(a-bc-bv+bMp_0-(\eta+bp_0)(e_{m0}+e_{t0}))^2}{16tbk_1k_2-(k_1+2tk_2)(\eta+bp_0)^2)^2}$$

Appendix S

Proof of Corollary 9

To simplify the discussion, we denote x = k₁(η + bp₀)², y = 2k₂(η + bp₀)², and z = 16bk₁k₂, then there is z > x + y.

Firstly, we analyze the value range of t when the cost-sharing contract is valid for the manufacturer. We have the following:

$$\Pi^C_M-\Pi^L_M=\frac{32t^2bk_1k_2-((1-t)k_1+4t^2k_2)(\eta+bp_0)^2)A}{(16tbk_1k_2-(k_1+2tk_2)(\eta+bp_0)^2)^2}-\frac{(32bk_1k_2-4k_2(\eta+bp_0)^2)A}{(16bk_1k_2-(k_1+2k_2)(\eta+bp_0)^2)^2}$$

Letting $g(t)=\frac{\Pi_M^C-{\Pi}_M^L}{A}$, then we have $G(t)=\frac{2\left(z-y\right){t}^2-\left(1-t\right)x}{{\left(\left(z-y\right)t-x\right)}^2}-\frac{2\left(z-y\right)}{{\left(z-x-y\right)}^2}=\frac{x\left(t-1\right)\left({x}^2-\left(4t-1\right){\left(y-z\right)}^2+2 tx\left(z-y\right)\right)}{{\left(\left(z-y\right)t-x\right)}^2{\left(z-x-y\right)}^2}=\frac{x\left(\left(2x\left(z-y\right)-4{\left(z-y\right)}^2\right){t}^2+\left({x}^2+5{\left(z-y\right)}^2-2x\left(z-y\right)\right)t-\left({x}^2+{\left(z-y\right)}^2\right)\right)}{{\left(\left(z-y\right)t-x\right)}^2{\left(z-x-y\right)}^2}$. We denote (t) = (2x(z − y) − 4(z − y)²)t² + (x² +5(z − y)² − 2x(z − y))t − (x² + (z − y)²), then it is not difficult to find that g(t) is a quadratic function with a parabola going downwards, and its discriminant is given by Δ_g(t) = x²(z − x − y)²(3z + x − 3y)². We know that it meets z > x + y, then there is Δ_g(t) > 0. Therefore, g(t) has two intersections with the horizontal axis, represented by ${t}_M^1=\frac{x^2+{\left(z-y\right)}^2}{2\left(2z-x-2y\right)\left(z-y\right)}$ and ${t}_M^2=1$. Due to (x² + (z − y)²) − 2(2z − x − 2y)(z − y) =  − (z − x − y)(3z + x − 3y) < 0, then there is ${t}_M^2<{t}_M^1$. From the above, we obtain ${t}_M^1=\frac{x^2+{\left(z-y\right)}^2}{2\left(2z-x-2y\right)\left(z-y\right)}\le t\le 1={t}_M^2$.

Secondly, we analyze the value range of t when the cost-sharing contract is valid for the transporter-retailer alliance. We have the following:

$$\Pi^C_{T+R}-\Pi^L_{T+R}=\frac{(16t^2bk_1k_2-tk_1(\eta+bp_0)^2)A}{(16tbk_1k_2-(k_1+k_2t2k_2)(\eta+bp_0)^2)^2}-\frac{16bk_1k_2-k_1(\eta+bp_0)^2A}{(16bk_1k_2-(k_1+2k_2)(\eta+bp_0)^2)^2}$$

Letting $H(t)=\frac{\Pi_{T+R}^C-{\Pi}_{T+R}^L}{A}$, then we have $H(t)=\frac{zt^2- tx}{{\left( zt-\left(x+ yt\right)\right)}^2}-\frac{z-x}{{\left(z-\left(x+y\right)\right)}^2}=\frac{\left({zt}^2- tx\right){\left(z-\left(x+y\right)\right)}^2-\left(z-x\right){\left( zt-\left(x+ yt\right)\right)}^2}{{\left( zt-\left(x+ yt\right)\right)}^2{\left(z-\left(x+y\right)\right)}^2}$ $=\frac{x\left(\left({y}^2-z\left(z-x\right)\right){t}^2+\left({z}^2-{x}^2-{y}^2\right)t-x\left(z-x\right)\right)}{{\left( zt-\left(x+ yt\right)\right)}^2{\left(z-\left(x+y\right)\right)}^2}$. We denote h(t) = (y² − z(z − x))t² + (z² − x² − y²)t − x(z − x), then it is not difficult to find that h(t) is a quadratic function with a parabola going downwards, and its discriminant is given by Δ_h(t) = x²(z − x − y)²(z − x + y)². We know that it meets z > x + y, then there is Δ_h(t) > 0. Therefore, h(t) has two intersections with the horizontal axis, represented by ${t}_{T+R}^1=\frac{x\left(z-x\right)}{z\left(z-x\right)-{y}^2}$ and ${t}_{T+R}^2=1$. Due to (z − x) − (z(z − x) − y²) = − (z − x − y)(z − x + y) < 0, then there is ${t}_{T+R}^2<{t}_{T+R}^1$. From the above, we obtain ${t}_{T+R}^1=\frac{x\left(z-x\right)}{z\left(z-x\right)-{y}^2}\le t\le 1={t}_{T+R}^2$.

By comparing ${t}_M^1$ and ${t}_{T+R}^1$, we find that it is difficult to determine their size relationship, so the value range of t is expressed by $\mathit{\max}\left\{{t}_M^1,{t}_{T+R}^1\right\}\le t\le 1$.

Appendix T

Proof of Corollary 10

Comparing the supply chain system’s profit of the cost-sharing contract model and the OCD model, we have the following:

$$ \frac{\varPi_{SC}^D}{\varPi_{SC}^C}=\frac{{\left(16t{bk}_1{k}_2-\left({k}_1+2{tk}_2\right){\left(\eta +{bp}_0\right)}^2\right)}^2}{\left(4b{k}_1{k}_2-\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)\left(48{t}^2b{k}_1{k}_2-\left({k}_1+4{t}^2{k}_2\right){\left(\eta +{bp}_0\right)}^2\right)}. $$

To simplify the discussion, we denote x = k₁(η + bp₀)², y = k₂(η + bp₀)², and z = 4bk₁k₂, then there is z > x + y. Letting Ψ(t) =(16tbk₁k₂ − (k₁ + 2tk₂)(η + bp₀)²)² − (4bk₁k₂ − (k₁ + k₂)(η + bp₀)²)(48t²bk₁k₂ − (k₁ + 4tk₂)(η + bp₀)²) = (4zt − (x + 2yt))² − (z − x − y)(12zt² − (x + 4yt²) = (4(2z − y)² − (z − x − y)(12z − 4y))t² − 4x(2z − y)t + x(z − y). It is not difficult to find that Ψ(t) is a quadratic function with a parabola going upwards, and its discriminant is given by Δ_Ψ(t) =  − 16xz(z − x − y) < 0, then we know that Ψ(t) has no intersection with the horizontal axis. In other words, no matter what t is, Ψ(t) is always greater than zero, that is ${\Pi}_{SC}^D>{\Pi}_{SC}^C$.

Appendix U

Proof of Theorem 11

Substituting the equations of ${e}_m^D$ and ${e}_t^D$ into p(e_m, e_t) and w(e_m, e_t), we can obtain the expression of p^T and w^T. Then, Substituting the expressions of p^T and w^T into Eqs. (22) and (23) and the market demand function q(p, e_m, e_t), we can easily get $\Pi^T_M$, $\Pi^T_{T+R}$, and q^T. Hence, the profit of the supply chain system is expressed by

$$ {\varPi}_{SC}^T={\varPi}_M^T+{\varPi}_{T+R}^T=\frac{k_1{k}_2{\left(a- bc- bv+ bM{p}_0-\left(\eta +{bp}_0\right)\left({e}_{m0}+{e}_{t0}\right)\right)}^2}{4b{k}_1{k}_2-\left({k}_1+{k}_2\right){\left(\eta +{bp}_0\right)}^2}. $$