Reaching Large Strains During Simple Shear Experiments Thanks to Sequential Re-Machining of the Free Edges

Abstract

Background

The simple shear experiment is widely used for the calibration of plasticity models due to straightforward post processing. The specimen can be as simple as a rectangular strip of sheet metal, but the maximum strain is limited by early initiation of fractures from the free edges. Avoiding this drawback has been a major motivation for the development of new specimens with optimized edge geometries or the in-plane torsion test, but at the cost of a more complex analysis of the test and often a reduction of the gauge section.

Objective

The objective of the present work is to overcome the initiation of fracture from the free edges during simple shear experiments. Our goal is to double the achievable maximum strain, while keeping the size of the specimen and the post processing simplicity of a standard simple shear test.

Methods

A sequential single shear test is proposed, consisting of several two steps sequences on a notched geometry. First, an interrupted shear test is performed up to a specified displacement value. Then, the damaged free edges of the specimen are removed through milling. The specimen is then ready for the following sequence of shear and re-machining.

Results

Experiments are performed on three engineering materials, with up to five loading-machining sequences. The maximum attained effective strain is up to two times the one reached during a monotonic experiment. Numerical simulations are used to validate the shear stress and strain calculations from experimental measurements. Practical recommendations are derived for the choice of the displacement step size and Digital Image Correlation analysis.

Conclusion

It is found that the maximum strain attained before the undesired failure of the specimen during simple shear test can be substantially extended through repeated re-machining of the specimen boundaries, enabling behavior identification at larger strains.

Introduction

The accuracy of numerical simulations for sheet metal forming relies on the selection and calibration of an appropriate material behavior model. The demand for robust models is increased due to the use of advanced steels and aluminum alloys in industrial applications, which can exhibit high local strains, see [1,2,3,4,5] for examples . The first simple shear test set-ups were presented in the 80’s by Miyauchi [6] and G’Sell et al. [7]. Twenty years later, Bouvier et al. [8] and An et al. [9], have demonstrated the effectiveness of the simple shear test in evaluating the mechanical behavior of sheet metal.

Shear techniques can be classified into two categories based on whether the shear is induced by a translation or a rotation displacement, as shown in Fig. 1(a)–(d). A second classification can be performed from the presence or absence of free edges, i.e. without slits in the case of in-plane torsion, as shown in Fig. 1(d). In this case, circular groove is typically machined on the specimen surface to localize the strain on a narrow circular band. It should be noted that material anisotropy can cause stress state and strain heterogeneity during in-plane torsion experiments of slit-free specimens, see Grolleau et al. [10].

Fig. 1

Different categories of shear tests, inspired from [11, 12]

Free edges, such as in Fig. 1(a)–(c), introduce a heterogeneous stress state, which becomes prominent as the gauge section length becomes shorter for a given width. As a result, accurate determination of the plastic behavior may require a hybrid numerical and experimental analysis, especially for gauge sections with small length to width ratio, e.g. Fig. 1(b) and (c), and Tarigopula et al. [13], Reyne et al. [12], and Yin et al. [14]. Obtaining a homogeneous stress state, suitability for dynamic testing and prevention of premature specimen failure due to edge effects motivated the optimization of the geometry of ASTM B831 or Peirs’s type of shear specimens Fig. 1(b), see Peirs et al. [15]. This type of geometry has found many applications for strain to fracture determination, see for example Rahmaan et al. [16], Roth and Mohr [17] and Tarigopula et al. [13] for Peirs’s type, Yin et al. [14] and Kim et al. [18] for in-plane torsion test type. Note that in the case of Peirs’s type of specimen, the distance from the clamping area to the shear gauge section prevents any possibility of reverse loading. For the systematic investigation of stress-state dependent fracture of sheet metals, it is also possible to superpose a lateral loading using cross-type specimens and bi-axial tensile machines, see the H-specimens presented by Gerke et al. [19] and Brünig et al. [20].

Fig. 2

Different geometries of simple shear specimens

Nonetheless, simple shear testing, as illustrated in Figs. 1 and 2, remains a widely-used method for characterizing the shear behavior of materials and has not been replaced by Peirs’s or in-plane torsion tests. A wide variety of geometries have been proposed for the simple shear specimen. Some of these are illustrated in Fig. 2. In the present study, the specimen features circular notch roots as presented in Fig. 2(a), see [14], and more recently [21] for examples. The classical rectangular specimen Fig.2(b) is compared to the notched specimen (e) by An et al. [9]. Miyauchi [6] used rectangular notch roots, (c), and Reyne at al. [12] compared various geometries including partial circular notch roots (d). This widespread use can be explained by the fact that, for shear gauge section length L to width h ratio above 10, $L/h>10$, see Fig. 2, and shear gauge width to sheet thickness t ratio below 5, $h/t<5$, a direct estimation of the stress-strain curve can be established based on load and strain/displacement measurements up to a maximum shear strain, see [8]. Moreover, in quantitative terms, the homogeneity is better by up to an order of magnitude for simple shear tests when compared to ASTM B831 type of specimen, see [12].

The simplest shear stress estimate is the average shear stress $\sigma _{eng}$, the ratio of the shear load F to the section area of the specimen $S=L \cdot t$, yielding $\sigma _{eng}=F/S$. In the context of Digital Image Correlation DIC analysis for strain calculation, the shear strain is calculated from the average value over a designated area on the specimen surface, the so-called Region Of Interest ROI, see Weiss et al. fro example [22]. Whatever the geometry, the specimen’s center is the area of the specimen that is in the stress and strain states closest to simple shear, see for example [8, 9, 12, 22].

Our goal is to determine the best estimates of the shear strain and the shear stress of the specimen’s center from the measurable quantities of the test, i.e. the geometry, the displacement field, and the load. The validity of each estimation heavily depends on the homogeneity of the strain and the stress along the shear gauge section, which is affected by the geometry of the slit root and the specimen dimensions see An et al. [9], Reyne at al. [12], and Yin et al. [14]. It is important to emphasize that the issue caused by heterogeneity of the deformation field can be circumvented by calculating the strains in a specific ROI. However, in the case of stress estimation, the global force is the only one measured information available during the test, without the possibility of circumventing a possible non-homogeneity in the stress field. Thus, the accuracy of the stress and strain estimations needs to be checked for each geometry to be used and geometries leading to the best stress homogeneity should be preferred.

The maximum shear strain is typically limited by the occurrence of fracture along the free edges of the specimen and tearing from the clamping jaws as revealed by Bouvier et al. [8]. These limitations restrict the maximum attainable shear strain, and, consequently, the strain range usable for precise selection of a hardening model and its parameter identification may be insufficient.

The objective of the present work is to overcome the initiation of fracture from the free edges during simple shear tests, aiming at doubling the achievable maximum strain, while keeping the size of the specimen and the post-processing simplicity of a standard simple shear test. A sequential simple shear test is proposed, consisting of the repetition of two steps sequences of machining or re-machining of the free edges of the specimen, and, interrupted shearing of the specimen.

After the presentation of the experimental set-up in “Experimental Set-Up”, followed by theoretical developments in “Theory”, the validity of the stress and strain calculations is presented in “Numerical Study of the Test, Validation of the Stress and Strain Estimations”. Experimental results on three materials are presented in  “Experimental Results”.

Experimental Set-Up

The principle of the sequential shear machining is presented in Fig. 3 where three sequences are depicted. The specimen geometry features a gauge section length of $76\ mm$, a width of $4\ mm$, and two circular notches of $1.7\ mm$ radius. Each sequence (i) starts with the machining, or re-machining, of the specimen’s edges, step 1 in order to remove damaged areas located on the slit’s roots. After machining, the slit’s roots are back to their initial circular shape. In the second step of each sequence, step 2, a shearing displacement $u_i$ is applied to the specimen, the test is interrupted and next sequence can start over. The gauge length is kept in the $[40; 80]\ mm$ range in order to respect the shape ratio $L/h>10$, see [8].

Fig. 3

Scheme of the sequential shear for three sequences. Step 1, machining of the free edges leading to a reduced gauge length by $2\times delta$; step 2, simple shear test up to a limited displacement value u

A detailed view of the shear device is presented in Fig. 4(b). It is composed of two frames with a prismatic mechanical joint, labeled 1 and 2 in Fig. 4(b). Prior to testing, the specimen (label 8 in the right zoom, where the right jaw is removed to allow for the specimen’s shoulder to be seen) is affixed to the frames with jaws (label 6) and screws (label 7). The four screws (label 7) are tightened to a material-dependent torque level, aiming to achieve a balance between preventing slippage and preventing damage to the specimen’s shoulder, see [23, 24].

Fig. 4

(a) Specimen’s design with an initial gauge length of $76\ mm$. (b) Experimental set-up in the universal testing machine. (1) movable jaw, (2) fixed jaw, (3) camera, (4) lights, (5) universal tensile machine, (6) clamping jaws, (7) clamping screws, (8) shear specimen. (c) Machining set-up showing the milling cutter and the simple shear device clamped to the vertical milling machine table

The test is performed in an universal testing machine Instron 5969 equipped with a 50 kN load cell, at a displacement speed of $0.5\ mm/min$, in order to ensure a strain rate of about $10^{-3}\ /s$. The load and the displacement are measured using the machine’s load cell and displacement sensor.

Digital image correlation is used to evaluate the displacements of a speckle pattern painted on specimen’s surface. Images are recorded with a Basler camera (label 3 in Fig. 4(b); 5 Mpx 2448 x 2048 px) equipped with a 35mm f1.9 Fujinon lens, at a frequency of 1 Hz and spatial resolution of $35\mu m/px$. Two LED spots (label 4 in Fig. 4(b)) are used as illumination sources. Post-processing of the specimen’s images is performed using VIC 2D-7, (Correlated solutions). A square subset size of 15 px and step size of 3 to 5 px is selected for displacement calculation while a 5 points Gaussian weight filter size is used for Hencky strain field calculations, leading to a floor noise mean value in effective strain about 0.0028 with a standard deviation value about 0.0043 for a central area of $5\times 2\ mm$ and a virtual strain gauge size value $L_{VSG}\approx \ 800\mu m$ [25]. These subset parameters make it possible to calculate the strain at the center on a small area of $1\times 1\ mm$. Whatever the sequence, the same reference image is used for DIC analysis, i.e. the first image of first sequence. Finally, the effective strain is determined from the surface major $\varepsilon _I$ and minor $\varepsilon _{II}$ strains by the equation:

$$\begin{aligned} \bar{\varepsilon }_{eff} = \frac{2}{\sqrt{3}} \sqrt{\varepsilon _I^2 + \varepsilon _{II}^2 + \varepsilon _I\varepsilon _{II}} \end{aligned}$$

(1)

During each shear step, a crosshead displacement $u_i$ is applied to the moving frame. This displacement is evaluated from an initial monotonic shear test performed up to the maximum displacement $u_{max}$ leading to fracture from the edges or specimen tearing from the jaws. After some trial and error campaigns, limiting the crosshead shear displacement of each sequence $u_i$ to a value between 1/3 and 1/2 of the maximum displacement $u_{max}$ appears to be a good compromise avoiding both excessive number of sequences and damage to the edges.

After reaching the prescribed displacement, the load is reduced to zero, and the relative displacement of the two frames is blocked using two lateral screws avoiding any spurious loading of the specimen during the machining step. The device is then moved to the milling machine.

During the re-machining of the specimen’s edges, the specimen along with the shear clamping device are positioned on the table of a vertical milling machine. Edges are re-machined using a $3.4\ mm$ diameter micro-grain carbide, four-flutes, square end mill, on a manual vertical milling machine. The cutting movement is a simple translation in the longitudinal direction of the specimen. Cutting parameters are similar to that of the CNC operation reported by Roth and Mohr [26], a machining affected depth as small as $2 \mu m$ is expected on the edges, without cracks. Note that a crack would generate a strain concentration that would be detected during the DIC analysis process. The gauge section is shortened by $\delta \approx 3\pm 0.5\ mm$. This uncertainty doesn’t allow the stress to be estimated accurately. Consequently, we systematically measure the length of the ligament after machining, using a digital caliper. This caliper features modified jaws, with $3\ mm$ diameter cylindrical contact surfaces, enabling precise measurement of the ligament length with an accuracy of about $\pm 0.04\ mm$, leading to a relative uncertainty of the length lower than $\pm 0.1\%$ regardless of the step.

Experiments are performed on three engineering sheet materials: a $0.8\ mm$ thick DP450 dual phase steel, a $1.0\ mm$ thick DC01 deep drawing steel and a $1.1\ mm$ thick AA6014-T4 aluminum alloy. The specimens are extracted using water jet cutting.

Theory

Considering simple shear in the reference frame $\mathcal {R}\ \{\underline{e}_X, \underline{e}_Y\}$, the deformation gradient is represented by:

$$\begin{aligned} \varvec{F} = \varvec{1} + \gamma \underline{e}_X \otimes \underline{e}_Y = \varvec{RU} \end{aligned}$$

(2)

With $\gamma$ the engineering shear strain, which we also refer to as shear ratio, $\varvec{U}$ the right stretch tensor and $\varvec{R}$ the rotation tensor. The Hencky strain $\varepsilon ^L=log(\varvec{U})$ has two opposite eigenvalues $\varepsilon _{I,II}^{SH}$, which lead to the theoretical simple shear logarithmic effective strain $\bar{\varepsilon }_{eff}^{SH}$, see [10] for example:

$$\begin{aligned} \varepsilon _{I,II}^{SH} =\pm asinh(\gamma /2) \end{aligned}$$

(3)

$$\begin{aligned} \bar{\varepsilon }_{eff}^{SH} = \frac{2}{\sqrt{3}} \vert asinh(\gamma /2) \vert \end{aligned}$$

(4)

Considering Levy von Mises plasticity, the cumulated work conjugate equivalent strain $\bar{\varepsilon }_{vM}$ differs from the effective strain, see Butcher and Abedini [27]:

$$\begin{aligned} \bar{\varepsilon }_{vM} = \frac{\vert \gamma \vert }{\sqrt{3}} \end{aligned}$$

(5)

The effective strain $\bar{\varepsilon }_{eff}$ and the von Mises equivalent strain $\bar{\varepsilon }_{vM}$ differ only by $1\%$ at a shear ratio of 0.5, and $2.5\%$ only at a shear ratio of 0.8, but the difference increases with the strain ratio.

From a practical point of view, calculating a shear ratio from the experiment is the unique necessary scalar value to describe the strain level during simple shear test. Calculating the shear ratio also enables for elastic correction to calculate plastic shear ratio $\gamma ^p$ for plasticity model identification which reads:

$$\begin{aligned} \gamma ^p=\gamma -\gamma ^e=\gamma -\sigma _{XY}/G \end{aligned}$$

(6)

with $\gamma ^e$ the elastic strain, $\sigma _{XY}$ the shear stress, and G the elastic shear modulus.

DIC enables to calculate the Hencky strain eigenvalues and the effective strain. Assuming a simple shear kinematic, equations (3) and (4) enable to calculate the shear ratio value from three different strains, i.e. the major, the minor and the effective strains. These values will be considered later in the experimental result section.

Numerical Study of the Test, Validation of the Stress and Strain Estimations

Finite element analysis is used to determine the optimal dimensions of the device and verify the accuracy of the stress and strain estimation technique. The LS-Dyna R11 commercial solver is utilized to simulate the experiment with implicit time integration. The mesh is composed of single-integration-point Belytschko-Tsay shell elements. A study of the mesh size influence led to choosing a maximum mesh size of $0.1\ mm$, i.e. a minimum of 40 elements across the width gauge section. This choice ensures the independence of both stress at the central element and the strain field from the mesh size. Three numerical models are considered, they are depicted in Fig. 5: (i) a notched shear specimen with standard boundary conditions, (ii) a rectangular specimen with standard boundary conditions and (iii) a notched shear specimen with shoulder modeling. The standard boundary condition considers one side of the gauge section entirely fixed, while on the other side, a longitudinal rigid body translation displacement u is applied. In model (ii), the specimen doesn’t feature any cutout. In model (iii) the shoulders of the specimen and jaws are meshed, $4\ mm$ width, using the same element size with a normal pressure applied to simulate clamping, with Coulomb’s friction between the specimen and the jaws. Gauge section lengths $L\in [40;76]\ mm$ are considered. Five different lengths were used for the numerical study. The evolution of the results has consistently shown a monotonic evolution with respect to the ligament length. Therefore, to streamline the presentation of results, we will generally limit the presentation to only the extreme dimensions, i.e., 40 and 76 mm. In order to avoid excessive distortion of the mesh, the displacement is limited to about $2.5\ mm$, leading to a maximum engineering shear strain about 0.65.

Fig. 5

View of the mesh used for the simulation. (a) Zoom on the free edge, (b) zoom on the center, (c) specimen and boundary conditions of the standard model, (d) specimen and boundary conditions of the rectangular model, (e) view of the full-model, including jaws, the red arrows visualize the clamping force. X direction is aligned with the gauge length, Y direction is aligned with gauge width

To gain a thorough understanding of the mechanical fields, a variety of engineering materials behaviors, ranging from soft aluminum alloys to high-strength steels, are investigated. The set of hardening uses Swift, Voce, linear, and mixed Swift-Voce laws equation (7), where $\bar{\varepsilon }^p$ reads for the work equivalent plastic strain and other letters are material constants. Parameters of the hardening laws are given on Table 1. The sensitivity of the test to a change in the material behavior is studied using generic virtual materials labeled Voce, Swift, and Linear hardening. Three more sets of parameters are based on the literature, corresponding to DP450 steel, DC01 steel, and AA2024-T3 aluminum alloy. These behavior law parameters have been identified using a hybrid experimental-numerical method from uniaxial tension experiments of dog-bone and notched specimens, see [28] (DP450 steel and AA2024-T3 aluminum alloy), and [10] (DC01 steel) for details. The numerical material model is the Levy von Mises elasto-plastic piecewise plasticity MAT123 of LS-Dyna R11. The corresponding stress-strain curves are presented in Fig. 6, where the label ’Re+400MPa’ refers to Swift and Voce behaviors given Table 1 with a yield stress increased by $400\ MPa$. These behaviors are used in the “Numerical Study of the Test, Validation of the Stress and Strain Estimations”, i.e. ’Numerical Study of the test’.

The comparison of the experimental results obtained from sequential shear tests to numerical results requires the use of a behavior law already validated at large strains. This is the case for the two steels DC01 and DP450. Their sets of experiments used for the hybrid experimental-numerical identification method comprised in-plane torsion tests (DC01) and bulge tests (DP450). In the case of the DP450 steel, a better accuracy at large strains is obtained using the hardening law along with the anisotropic Hill’s 48 non-associated flow rule proposed by Mohr et al. [3]. The reader is referred to [28] for details on their experimental validation. In this case, the numerical material model is the MAT260B of LS-Dyna R11. The DC01 and the DP450 Hill’48 behaviors are used for experimental to numerical comparisons in “Experimental Results” and “Conclusion”.

$$\begin{aligned} \begin{aligned} \sigma _{mixed}&= \alpha \sigma _{Swift} + (1-\alpha ) \sigma _{Voce} \\&= \alpha K(\bar{\varepsilon }^p + \varepsilon _0)^n + (1-\alpha )[\sigma _0+ Q(1-e^{ -b\bar{\varepsilon }^p})] \end{aligned} \end{aligned}$$

(7)

Table 1 Behavior law parameters

Fig. 6

Stress strain evolution of the hardening laws. The dotted line correspond to Voce and Swift hardening with increased yield stresses Re+400 MPa

To streamline the presentation, only the principal outcomes of the numerical investigation are presented hereafter, and illustrated with results obtained using the DP450 material behavior.

The main goal of the numerical study is to evaluate the estimation accuracy of the shear stress, referred as $\sigma _{XY-center}$ hereafter, and the shear strain at the center of the specimen using the load F, the gauge section $S=L\cdot t$, and the specimen’s surface strain field.

Figure 7 shows the major and minor surface strains of the central element as a function of the crosshead displacement in the case of the DP450 steel behavior and a $40\ mm$ gauge length. The corresponding effective strain at specimen’s center is displayed on the secondary x-axis, with a maximum value of 0.36 for a displacement value about $2.5\ mm$. In accordance with simple shear kinematics, the two in-plane strain eigenvalues are opposite. Notably, identical strain measurements were obtained by averaging strain values over a rectangular area of $5 \times 2\ mm$ centered on the central element, $\varepsilon _{eff.ROI}$, but would differ for larger areas close to the full gauge area due to inhomogeneity of the mechanical fields.

Fig. 7

Major (green) and minor (purple) strain evolution as a function of the crosshead displacement. Central element strains are presented in solid line with full circular dots, $5\times 2\ mm$ ROI averaged values are presented in solid line with empty circular dots. The corresponding effective strain at specimen center is displayed on the secondary x-axis

Figure 8 displays the shear stress and the effective strain along the gauge section for the two extreme values, i.e. $40\ mm$ and $70\ mm$, and the mean value of the gauge length, i.e. $55\ mm$. Both stress and effective strain exhibit a homogeneous plateau value at the center of the specimen, with almost symmetric peaks toward the edges. The shapes of the curves appear to be independent of the gauge length. In the case of the $40\ mm$ gauge length, the effective strain (shear stress resp.) increases by $1\%$ from the central value at a distance from the center of about $10\ mm$ ($13 \ mm$ resp.). Note that the slight non-symmetry is caused by the fact that the elements are not perfectly located in the center of the sample after deformation. The stress state evolves along the gauge section, transitioning from simple shear at the central region to a state of uniaxial tension in the immediate vicinity of the edges. While the peak values in effective strain increase by almost $40\%$, the peak values in stress increase by only $6\%$ compared to their values at the center, before dropping down. This is also illustrated in Fig. 9 at an effective strain value at the center of 0.15. The peak amplitudes appear to be independent of the gauge length but depend on mean strain level.

Fig. 8

Effective strain (green line) and shear stress (purple line) along the shear gauge when the effective strain at center is about 0.15, for $76\ mm$ gauge length (dashed lines), 55 mm gauge length (dashed-dot lines) and $40\ mm$ gauge length (solid lines)

Fig. 9

Effective strain (left) and shear stress (right) fields from numerical simulation of a $40\ mm$ gauge length specimen, at a central effective strain value of 0.15

To illustrate this point, Fig. 10(a) shows normalized effective strain and shear stress values with respect to the central element value for four central element strain levels and two gauge lengths. In the case of the DP450 hardening law, we found that the relative difference in strain and stress decreases with increasing shear strain. While the relative difference in stress is less than $8\%$ and decreases to below $5\%$ when the center strain level is above 0.15, the peak value in strain is as high as $40\%$ for a plateau value of approximately 0.05 in the center, and decreases to only about $17\%$ for the highest strain levels. The evolution of the peak strain values as a function of the shear strain level is found to be weakly dependent on the hardening law. On the contrary, the evolution of the peak stress value depends on the hardening law. This is illustrated in Fig. 10(a)–(c) showing the normalized effective shear stress values for a saturating (Voce 2) and a linear hardening (Lin. hard.). The peak value of the relative difference in stress decreases with the shear strain level in the case of the saturating hardening, while it is almost constant for a linear hardening.

Fig. 10

(a) Normalized effective strain (green line, left side) and shear stress (purple line, right side) along the shear gauge with respect to the central element value ($\frac{\varepsilon _{eff}}{\varepsilon _{central}}$ and $\frac{\sigma _{xy}}{\sigma _{central}}$), for various central effective strain levels of 0.05, 0.15, 0.25 and 0.35. The in-view zoom highlights the stress values below and above the central one for both geometries. Focus on the evolution of the normalized shear stress in the case of saturating Voce 2 (b) and linear hardening laws (c)

These results indicate that using an average strain value calculated over the entire gauge surface would lead to significant errors in strain estimation. Instead, the average strain must be calculated at the center of the specimen, over a symmetric window of approximately $\pm 10\ mm$.

In line with An et al. [9], a relative error in stress is calculated quantifying the error between shear stress estimation and shear stress of the central element:

$$\begin{aligned} RE_{shear\ stress} = \left( \frac{\sigma _{eng}}{\sigma _{XY-center}} -1 \right) \cdot 100 \end{aligned}$$

(8)

In the case of DP450 steel, the evolution of the shear stress at specimen center $\sigma _{XY-center}$ and the estimated shear stress $\sigma _{eng}$ are plotted in Fig. 11, along with the relative error as function of the crosshead displacement u. A maximum relative error in stress about $0.4\%$ only is observed.

Fig. 11

Stress evolution as a function of the crosshead displacement. Shear stress at the specimen center $\sigma _{XY-center}$ (purple with circle dot), estimated shear stress $\sigma _{eng}$ (green with crosses). The shear stress relative error $RE_{shear\ stress}$ (solid red line). The corresponding effective strain at specimen center is displayed on the secondary x-axis

The relative error in stress is dependent on the material behavior and the geometry of the specimen. Fig. 12 shows the evolution of the relative error in stress with respect to the crosshead displacement for a chosen set of behaviors and gauge lengths, which produces the highest and lowest error values. For comparison, the results obtained using the DP450 hardening parameters are included. The upper and lower curves of the graph represent the maximum and minimum errors, respectively, that could be obtained through any of the behaviors and lengths combinations for each crosshead displacement value. The relative error in stress ranges from $-0.5\%$ to $1\%$ for all the tested configurations. It appears that the material with the lowest hardening in combination with smallest shear gauge length leads to largest relative error about $1~\%$, while the minimum error value about $0.2~\%$ is obtained for the Swift+400 hardening law and a 76 mm gauge length. The numerical simulations notably show that whatever the tested configuration, the gauge section area remains within $0.6~\%$ of the initial area. The accuracy of the central shear stress approximation $\sigma _{eng}$ can be explained by the fact that the global force corresponds to the integral of the shear stress over the sheared section, which takes advantage of the peak values to compensate for the final drop of the shear stress close to the edge. This is illustrated in Fig. 10(a) where values below and above the central ones are highlighted with $(-)$ and $(+)$ signs.

Performing a similar study on rectangular notched free specimen with $40\ mm$ gauge length, see Fig. 2(b) , it is noticeable that the error in stress can be up to $-3\%$, whatever the strain level, due to the monotonic decrease of the stress value along the gauge length, from the center to the edges, see Fig. 10(a). Contrarily, the strain plateau is longer in the longitudinal direction compared to the notched specimen, as already presented by An et al. [9] and more recently by Rossi et al. [2]. Both effective strain and shear stress have a plateau value at the center of the specimen and drop toward the edges, without any peak. For example, in the case of the $0.8\ mm$ thick DP450, at an effective strain value of 0.15 in the center, the central shear stress is 330 MPa. At the same strain level, the load of a rectangular specimen is $10.3\ kN$, i.e. $\sigma ^{rect.}_{F/S}=322\ MPa$ an underestimation by about $-2.5\ \%$. For the notched specimen, the load is $10.56\ kN$, i.e. $\sigma ^{notched}_{F/S}=331\ MPa$. The impossibility to circumvent the issue caused by the non-homogeneity of the stress field motivated us to privilege notched shear specimens.

Fig. 12

Shear stress relative error range vs. crosshead displacement for all the tested configuration of behaviors and gauge lengths of 40 and $76\ mm$. The envelope curves correspond to the following configurations (behavior law, length): (DC01 steel, 76 mm, solid turquoise line), (DP450 law, 40 mm and 76 mm, dotted purple line and solid purple line), (Voce 2 law, 40 mm and 76 mm, dotted green line and solid green line), and (Swift Re+400 MPa law, 76 mm, solid orange line)

Finally, the numerical results are post-processed as experiments, with the proposed stress and strain estimations. The shear stress estimation is classically calculated as the engineering shear stress $\sigma _{eng}$. The shear plastic ratio $\gamma ^p(\bar{\varepsilon }_{eff})$ is calculated using equations (1), (4), and (6) based on the average value of the effective strain over a $5\times 2 \ mm$ ROI. Figure 13 illustrates the shear stress plotted against the plastic shear strain for the initial material model (solid lines) and the estimation (symbols) for three material behaviors, with a negligible difference between the curves of maximum $1\%$.

Fig. 13

Shear stress vs. Effective plastic strain for DP450 steel (green), DC01 steel (purple) and AA2024-T3 aluminum (red). Theoretical shear stress-strain behavior laws with solid lines, and shear stress-strain values at the center element with triangle solid symbols

Experimental Results

Experimental Validation

Sequential and monotonic shear test were carried out on three materials. Figure 14 shows a DP450 steel specimen at the end of the first, second and fifth sequences. Due to sequential machining, the length of the shear gauge section is decreasing with sequence number, while the shoulder relative displacement is increasing due to the machining of the specimen. In order to emphasize the shear strain, straight lines are initially drawn across the gauge section. On both sides of the shear gauge section, the footprints of the jaw’s teeth are clearly visible, and no massive longitudinal slipping or tearing from the jaws is visible. The sequential machining results in a reduction of the gauge length, and thus a force drop from sequence to sequence. This is illustrated in Fig. 15 where the evolution of the force as a function of the effective strain is plotted for a monotonic test, a sequential shear test composed of five sequences, and the numerical simulation of the monotonic test. During all the experiments, the gauge length is aligned with the transverse direction of the sheet. Monotonic tests are performed on $76\ mm$ long notched shear specimens. The numerical simulation is based on the DP450 Hill’48 behavior model.

Fig. 14

DP450 steel specimen images after one (a), two (b) and five (c) machining-shear sequences

Fig. 15

Evolution of the force as a function of the effective strain during a 5 sequences shear-machining test (solid purple line) and a monotonic shear test on DP450 steel (solid black line), and numerical results of the monotonic test simulation (empty blue circles)

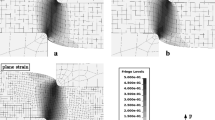
The final effective strain field of each of the five sequences is plotted in Fig. 16. For each sequence, the minimum and the maximum values of the effective strain are reported, along with the average value from the central $5\times 2\ mm$ ROI. The color map ranges from minimum to maximum of each sequence, which enables to highlight the peak values of the strain toward the edges. The inhomogeneity of the strain field is depicted Figs. 17 and 18 showing the evolution of the effective strain as a function of the position along and across the shear gauge section respectively. The purple solid lines curves refer to the effective strain at the final stage of each sequence, the blue and green lines refers to major and minor surface strains. As predicted from numerical simulation, see Fig. 9, the strain field is characterized by a plateau value at the center along the longitudinal direction, and increased values toward the edges, see Fig. 17 ; while an almost constant value can be observed across the gauge section at mid-length, see Fig. 18. Major and minor strains have almost the same value on the specimen surface, the difference is about the order of magnitude of the floor noise at the specimen center, see Figs. 17 and 18, and slowly increases toward the edges to reach a value of about 0.03, see Fig. 17. Consequently, the calculation of the shear ratio from the major, minor or effective strain leads to extremely close values. In the following, the engineering shear ratio is calculated from the surface effective strain equation (4).

Fig. 16

Strain fields calculated at the end of the shearing cycle of 5 sequences on a DP450 steel. The central ROI 5x2 mm is highlighted with a white rectangle

Fig. 17

Strain evolution along the shear gauge section for DP450 steel. Effective strain is displayed with solid purple line, minus minor strain with solid green line and major strain with solid blue line

Fig. 18

Strain evolution across the shear gauge section for DP450 steel. Effective strain is displayed with solid purple line, minus minor strain with solid green line and major strain with solid blue line

A comparison of the numerical and the experimental evolution of the effective strain vs. longitudinal position on the shear gauge is presented in Fig. 19 for a central effective strain about 0.14. The model with standard boundary conditions and shoulder modeling are considered. In the case of the standard model, without jaws, represented by a purple line, the size of the plateau region where the strain remains almost constant is larger in the numerical simulation than in the experimental data represented by a black line. Additionally, the peaks in the numerical model are lower in amplitude when compared to the experimental results. To address this discrepancy, shoulder modeling is considered, represented by a green line. The use of the full model, with a constant friction coefficient, reduced the error by a factor of two. A better agreement can be obtained using a non constant friction coefficient along the specimen’s shoulder, but for the cost of using arbitrary evolution of the friction coefficient values. But it is assumed that such a model will never be able to reproduce accurately the local indentation process of the teeth in the specimen’s shoulder as depicted in Fig. 14(c).

Fig. 19

Effective strain evolution along the ligament for numerical simulation with clamped boundary condition (solid purple line), with friction boundary condition (solid green line) and experimental result (solid black line)

This result suggests that longitudinal slipping of the specimen within the jaws at the border of the clamping area enhances the strain field’s inhomogeneity. Still, the central plateau, where the local values differs from the central one by less than $1\%$, is $35\ mm$ long. This led to a full experimental study of the strain field’s inhomogeneity at large strains, focusing on determining the appropriate size of the ROI (region of interest) that should be used for strain averaging. Considering a reference $2 \times 2\ mm$ ROI, the Fig. 20 depicts the evolution of the relative error between various ROI sizes as a function of the reference strain. Two ROI widths of 1 and $2\ mm$ are considered, and three different lengths: the full gauge length, 25, and $5\ mm$ length. As predicted from the numerical simulation, the error is almost independent from the ROI width, and decreasing for a decreasing length of the ROI. Note that this calculation is performed all along the five sequences already presented for the DP450 steel. This explains the non monotonic evolution of the relative error when the ROI length is the full length of the specimen, i.e. changing value at each sequence. When the ROI length is lower than $5\ mm$, the relative error is below $\pm 0.5\ \%$, up to strain level value of about 0.9. The same holds true in the case of the DC01 steel and the two first sequences in the case of the AA6014-T4 aluminum alloy. For the latter, a maximum local error close to $1\%$ was observed during the third sequence, while the loading force was already decreasing, so it was concluded that the material was already too much damaged to invalidate the proposed protocol.

Fig. 20

Evolution of the relative error in strain for a $2\ mm$ width ROI (solid lines) and a $1\ mm$ width ROI (dotted line) and three ROI lengths: full specimen length (blue), $25\times 2\ mm$ ROI (green) and $5\times 2\ mm$ ROI (purple). The reference strain is calculated using a $2\times 2\ mm$ ROI at specimen center

Application

Sequential machining and simple shear experiments have been performed on three materials. The Figs. 15 and 21 show the force as a function of the effective strain curves of the five sequences performed on the two steels, and the three sequences performed on the aluminum alloy. The experimental and the numerical results of monotonic tests are presented in the case of the DP450 and DC01 steels, showing a good agreement for these behavior models leading to an error in force lower than $4\%$, similar to previously published results, see [17, 26, 29] for examples.

Fig. 21

Evolution of the force as a function of the effective strain during sequential shear (solid green line) and monotonic (solid black line) shear test of the DC01 steel, and sequential shear of AA6014-T4 aluminum alloy (solid red line). Numerical results of the monotonic shear simulation of the DC01 is plotted using orange empty circles

The shear stress estimation $\sigma _{eng}$ was calculated, as well as the effective strain $\bar{\varepsilon }_{eff}$ on a $5\times 2\ mm$ ROI in order to plot the shear stress as a function of the effective strain for each test. Fig. 22 depicts these results in the case of the DP450 steel for two sequential shear tests and one monotonic test. The maximum load value during the monotonic test was obtained at an effective strain about 0.33, this point is highlighted with a red circle in Fig. 22. The sequential tests have been performed using various values of the shear displacement increment. The monotonic and sequential tests match up to the maximum load of the monotonic test, whether the sequential test was made of 2 or 3 sequences. This shows the safety of the repetition of the machining of the edges on the shear test results. At larger strains, the application of various shear strain increment sizes seems not to affect the reproductibility of the results. which can be appreciated in the two insets (a) and (b) in Fig. 22 where a maximum discrepancy value of less than $5\ MPa$ can be observed between the curves. The maximum effective strains obtained after five sequences were 0.77 and 0.87, more than twice the maximum strain obtained during monotonic simple shear test.

Fig. 22

Shear stress vs. effective strain curves of a monotonic (black solid line) and two sequential (purple and green solid line) shear tests of the DP450 steel up to final effective strains of 0.77 and 0.85 respectively. The end of the monotonic test is highlighted with a red circle at an effective strain value of 0.33. Two zoomed in-view of sections of the curves are presented in (a) and (b) with local scales. Note that the unloading-reloading of the curves are truncated for improved visibility

The same results are presented in Fig. 23 in the case of the DC01 steel and the AA6014-T4 aluminum alloy. For the latter, three tests are presented, with maximum strains of 0.14, using one sequence, 0.33 (2 seq.) and 0.51 (3 seq.). As presented in Fig. 21, during the third shear step, the force started to decrease slightly, which is attributed to damage or tearing of the specimen from the jaws, even not detectable from post-mortem observation. In the case of the DC01 steel, three sequential tests are presented and compared to one monotonic test. Again, the reproductibility error in stress is limited to a value about $10\ MPa$, representing less a $3\%$ error.

The results of the sequential shear test with re-machining of the edges are also compared to an in-plane torsion test, without free edge as presented Fig. 1(d). For detailed description of the test, readers should refer to the article by Grolleau et al. [10] presenting the in-plane torsion of DC01 steel. The specimen is a simple disc, fully clamped on its outer ring $60<diam.<80\ mm$ while a driving rotation is imposed to the inner clamping ring up to a diameter of $40\ mm$ at a rotation speed of 0.025°/s, leading to a strain rate about 0.001/s. The torque is transmitted to the specimen thanks to a set of 90 teeth-grooves pairs acting on the inner clamping area of the specimen. A circular groove is machined from one side, at a mean diameter of $2.R_g=47\ mm$ in order to reduce the thickness of the sheet from $1.5\ mm$ down to a minimum value of about $0.75\ mm$ at radius $R_g$ and localize the strain away from the clamping area. A DIC speckle pattern is applied to the flat surface of the specimen allowing for strain calculations ($25\ Mpx$ camera, $10\ \mu m/px$ pixel size, subset and step sizes of 31 and $7\ px$), while a load cell enables for torque measurement T. The shear stress is calculated as the mean stress $T/(S.R_g)$ where S is the sheared section at radius $R_g$. The effective strain is calculated as the average value calculated at radius $R_g$. Contrary to in-plane torsion test results, a decreasing shear stress with shear strain is clearly visible in the case of the monotonic test when the effective strain is above 0.5. When compared to the sequential shear and monotonic shear test results, a clear agreement is obtained up to an effective strain value about 0.8.

Fig. 23

Shear stress versus strain curves of sequential machining and simple shear test of DC01 steel and AA6014-T4 aluminum alloy. Stress versus strain curve of the monotonic (black solid line) and the in-plane torsion experiments (dashed black line) of the DC01 steel

Figure 24 shows the evolution of the shear stress as a function of the effective strain for sequential shear tests conducted on DP450 and DC01 steels. These results are compared to the theoretical shear behaviors predicted by the corresponding material models, i.e. DP450 Hill’48 and DC01 models, see Table 1. This analysis was conducted using a single element subjected to simple shear kinematics. In both cases, the stress error remains below $4\%$, which is comparable to the error level achieved in the comparison between numerical and experimental results through an inverse procedure for behavior law parameter identification, see [24, 26, 28, 30] for examples. This suggests that the sequential shear test could be used for the identification of material hardening parameters at large strains, completing or replacing notched tension tests, bulge test or in-plane torsion test.

Fig. 24

Shear stress versus effective strain curves of sequential shear machining tests (solid lines) and simple shear numerical simulation of a single element (empty circles) for DC01 and DP450 steels

Conclusion

In an attempt to extend the achievable range of strain of the simple shear test, we propose an experimental protocol involving sequential steps of re-machining of the semi-circular sample edges and interrupted simple shear. To determine stress and strain at the center of the specimen, the shear stress estimate is calculated as the ratio of the loading force to the sheared gauge section, while engineering shear strain is quantified through Digital Image Correlation in a central Region Of Interest area of the gauge section. This methodology results in a twofold increase in the maximum strain attainable compared to a single simple shear test.

To gain a comprehensive insight into the mechanical fields, a large span of hardening laws has been considered in a numerical study of the shear tests. The comparison of rectangular and notched specimens of varying dimensions reveals that circular notched specimens yield the most accurate stress estimates. Conversely, notched geometry produces smaller central areas with homogeneous strain values in comparison to rectangular specimens. A length-to-shear width ratio value above 10 was maintained for all the geometries. For a $4\ mm$ width gauge section and gauge lengths ranging from 76 to $40\ mm$, a $5\times 2\ mm$ central ROI and the shear stress estimate enable the recovery of theoretical stress-strain curves with a maximum error of $1\%$.

The experiments conducted on DP450 steel, DC01 steel, and AA6014 aluminum alloy validate the numerical findings regarding the strain field. This field exhibits a central plateau and peak values toward the edges along the ligament, with relatively constant values across the gauge section.

Monotonic and sequential shear tests employing various displacement step values during the interrupted shear have been performed. These experiments demonstrate that repeated machining does not impact the results. From a practical point of view, the displacement step for each sequence can be chosen as 1/3 to 1/2 of the maximum displacement observed in a monotonic test without affecting the final results of the sequential test.

A final comparison of the experimental stress-strain curves obtained from sequential shear of DP450 and DC01 with published results reveals maximum errors of $4\%$ in stress, for effective strains up to 0.8. Additionally, a comparison with edge-free in-plane torsion testing shows that the sequential shear test yields the same results for DC01 steel.

These findings suggest that the sequential shear test holds promise for identifying material hardening parameters at large strains, potentially complementing or replacing notched tension tests, bulge tests, or in-plane torsion tests in practical operations.