Skip to main content
SpringerLink
Log in

Simulation of Infinite Boundaries When Evaluating Hole-Drilling Calibration Data

  • Sp Iss: Advances in Residual Stress Technology
  • Published:
Experimental Mechanics Aims and scope Submit manuscript

Abstract

Background

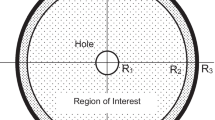
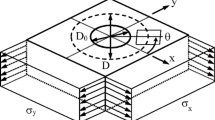
Effective use of the hole-drilling method for measuring residual stresses depends on the availability of accurate calibration data. A challenge arises when doing finite element modeling because the hole is conceptually drilled into an "infinite" material, while any practical model must have a finite far boundary. The use of a very distant far boundary provides a better simulation, but makes the required finite element model large and computationally burdensome.

Objective

The objective is to develop the practical use of an outer ring surrounding the target area of interest that can simulate an infinite far boundary and so allow the use of a more compact and computationally efficient finite element model.

Methods

Mathematical formulas were developed that specify the material properties of the needed outer ring. These apply to calibration calculations using both the hole loading and thermal loading methods.

Results

Isotropic loading models work directly for all finite element types and reproduce theoretical expectations to within 0.05%. Deviatoric loading models require some adjustment to fit the finite element model used, after which they can reproduce theoretical expectations to within 0.4%.

Conlusions

The use of a boundary ring is effective in simulating an “infinite” boundary when modeling the deformations around a stressed hole. This is useful when computing the calibration coefficients required when making hole-drilling residual stress measurements.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Notes

  1. Equation (1) is a general equation that describes the deformations around a circular hole in a stressed infinite material. For a hole-drilling measurement R would refer to the radius R1 of the drilled hole. This is the source of the “Theory” lines that subsequently appear in Figs. 4 and 5. Alternatively, R could refer to the radius of the "hole" formed when the "Area of Interest" shown in Fig. 1 is removed so as to focus on the properties of the surrounding material that extends to infinity. This latter interpretation of R is used when evaluating the elastic properties of the boundary ring that will make it elastically equivalent to the "infinite" surrounding material.

References

  1. Schajer GS, Whitehead PS (2018) Hole-Drilling Method for Measuring Residual Stress. Morgan & Claypool, Vermont, USA. 186pp

  2. Grant PV, Lord JD, Whitehead PS (2002) The Measurement of Residual Stresses by the Incremental Hole Drilling Technique. Measurement Good Practice Guide No.53, National Physical Laboratory, Teddington, UK

  3. Ajovalasit A, Scafidi M, Zuccarello B, Beghini M, Bertini L, Santus C, Valentini E, Benincasa A, Bertelli L (2010) The Hole-drilling Strain Gauge Method for the Measurement of Uniform or Non-Uniform Residual Stresses." AIAS–TR01:2010, Associazione Italiana per l'Analisi delle Sollecitazione, Rome, Italy, 70pp. https://doi.org/10.5772/intechopen.90392

  4. ASTM (2020) Determining Residual Stresses by the Hole-Drilling Strain-Gage Method. Standard Test Method E837–20. American Society for Testing and Materials, West Conshohocken, PA

  5. Rendler NJ, Vigness I (1966) Hole-drilling strain-gage method of measuring residual stresses. Exp Mech 6(12):577–586. https://doi.org/10.1007/BF02326825

    Article  Google Scholar 

  6. Steinzig M, Ponslet E (2003) Residual stress measurement using the hole drilling method and laser speckle interferometry: part i. Exp Tech 27(3):43–46. https://doi.org/10.1111/j.1747-1567.2003.tb00114.x

    Article  Google Scholar 

  7. Nelson DV, Makino A, Schmidt T (2006) Residual stress determination using hole drilling and 3d image correlation. Exp Mech 46(1):31–38. https://doi.org/10.1007/s11340-006-5859-0

    Article  Google Scholar 

  8. Beghini M, Bertini L (2000) Analytical expressions of the influence functions for accuracy and versatility improvement in the hole drilling method. J Strain Anal 35(2):125–135. https://doi.org/10.1243/0309324001514071

    Article  Google Scholar 

  9. Blödorn R, Bonomo LA, Viotti MR, Schroeter RB, Albertazzi A (2017) Calibration coefficients determination through fem simulations for the hole-drilling method considering the real hole geometry. Exp Tech 41(1):37–44. https://doi.org/10.1007/s11340-021-00719-4

    Article  Google Scholar 

  10. Held E, Gibmeier J (2015) Application of the incremental hole-drilling method on thick film systems—an approximate evaluation approach. Exp Mech 55(3):499–507. https://doi.org/10.1007/s11340-014-9962-3

    Article  Google Scholar 

  11. Nau A, von Mirbach D, Scholtes B (2013) Improved calibration coefficients for the hole-drilling method considering the influence of the poisson ratio. Exp Mech 53(8):1371–1381. https://doi.org/10.1007/s11340-013-9740-7

    Article  Google Scholar 

  12. Beer G, Watson JO (1989) Infinite boundary elements. Int J Numer Methods Eng 28(6):1233–1247

    Article  Google Scholar 

  13. Baldi A (2017) Far-Field boundary conditions for calculation of hole drilling residual stress calibration coefficients. Exp Mech 57(4):659–664. https://doi.org/10.1007/s11340-016-0235-1

    Article  Google Scholar 

  14. Schajer GS (2016) Personal communication to A. Baldi, June 6, 2016

  15. Schajer GS (1988) Measurement of non-uniform residual stresses using the hole-drilling method, Part I. J Eng Mater Technol 110(4):338–343. https://doi.org/10.1115/1.3226059

    Article  Google Scholar 

  16. Richards R (2000) Principles of Solid Mechanics. CRC Press, Boca Raton, FL

    Book  Google Scholar 

  17. Schajer GS (1981) Application of finite element calculations to residual stress measurements. J Eng Mater Technol 103(2):157–163. https://doi.org/10.1115/1.3224988

    Article  Google Scholar 

Download references

Acknowledgements

Thanks are due to Prof. Antonio Baldi for his insightful discussions and for his interest and support in the pursuit of this topic. The work was financially supported by the Natural Sciences and Engineering Research Council of Canada (NSERC).

Author information

Authors and Affiliations

  1. Dept. Mechanical Engineering, University of British Columbia, Vancouver, Canada

    G. S. Schajer & L. To

Authors
  1. G. S. Schajer
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. L. To
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to G. S. Schajer.

Ethics declarations

Conflict of Interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Schajer, G.S., To, L. Simulation of Infinite Boundaries When Evaluating Hole-Drilling Calibration Data. Exp Mech 62, 1247–1255 (2022). https://doi.org/10.1007/s11340-022-00834-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11340-022-00834-w

Keywords

Search

Navigation