A Mixed Stochastic Approximation EM (MSAEM) Algorithm for the Estimation of the Four-Parameter Normal Ogive Model

Abstract

In recent years, the four-parameter model (4PM) has received increasing attention in item response theory. The purpose of this article is to provide more efficient and more reliable computational tools for fitting the 4PM. In particular, this article focuses on the four-parameter normal ogive model (4PNO) model and develops efficient stochastic approximation expectation maximization (SAEM) algorithms to compute the marginalized maximum a posteriori estimator. First, a data augmentation scheme is used for the 4PNO model, which makes the complete data model be an exponential family, and then, a basic SAEM algorithm is developed for the 4PNO model. Second, to overcome the drawback of the SAEM algorithm, we develop an improved SAEM algorithm for the 4PNO model, which is called the mixed SAEM (MSAEM). Results from simulation studies demonstrate that: (1) the MSAEM provides more accurate or comparable estimates as compared with the other estimation methods, while computationally more efficient; (2) the MSAEM is more robust to the choices of initial values and the priors for item parameters, which is a valuable property for practice use. Finally, a real data set is analyzed to show the good performance of the proposed methods.

Appendix: The Simulation Result on the Recovery Accuracy of the 4PL Model

In this simulation, the 4PL is the data-generating model,

$$\begin{aligned} P_{i}(\theta _j)=P(U_{ij}=1|\theta _i,\pmb {\xi }_j)=c_j+(d_j-c_j)\frac{\exp [D(a_j\theta _i+b_j)]}{1+\exp [D(a_j\theta _i+b_j)]}, \end{aligned}$$

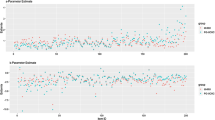
where $D=1.702$ is the scale constant. To keep comparability with the results shown in Tables 2, 3 and 4, the testing conditions as well as the true values of $a_j, b_j, c_j$ and $d_j$ are the same as that of “Study 2”. The MMAP estimate of the 4PL model is computed by the EM algorithm implemented in the R package of “mirt” and the EM algorithm proposed by Meng et al. (2020) separately.

The prior for $(a_j,b_j)$ is $(\ln a_j, b_j)'\sim N_2 (\mu _{0}, \Sigma _{0}),$ which is different from that for the 4PNO model, since the above two EM algorithms are implemented under a lognormal prior for $a_j$. The prior for $(c_j,d_j)$ is the same as that of the 4PNO, which is a bivariate Beta distribution given in Eq. 20.

Following the design of “Study 2”, the MMAP estimate of the 4PL model is computed under the four different priors, please see Table 8. Note that the variance of $\ln a_j$ is 1, which is to make the prior information close to the truncated normal distribution in Eq. 19 with the variance is 2. The same as that of “Study 2”, the simulation study generated 200 replications, and the parameter recovery is assessed by computing the three criteria (ARMSE, ACor and AIRF) across the 200 replications. The obtained results are given in Tables 9 and 10.