Partial Identification of Latent Correlations with Binary Data

Abstract

The tetrachoric correlation is a popular measure of association for binary data and estimates the correlation of an underlying normal latent vector. However, when the underlying vector is not normal, the tetrachoric correlation will be different from the underlying correlation. Since assuming underlying normality is often done on pragmatic and not substantial grounds, the estimated tetrachoric correlation may therefore be quite different from the true underlying correlation that is modeled in structural equation modeling. This motivates studying the range of latent correlations that are compatible with given binary data, when the distribution of the latent vector is partly or completely unknown. We show that nothing can be said about the latent correlations unless we know more than what can be derived from the data. We identify an interval constituting all latent correlations compatible with observed data when the marginals of the latent variables are known. Also, we quantify how partial knowledge of the dependence structure of the latent variables affect the range of compatible latent correlations. Implications for tests of underlying normality are briefly discussed.

Appendix A. Technical Proofs and Further Numerical Illustrations

1.1 A.1. Further Numerical Illustrations for Given Marginals

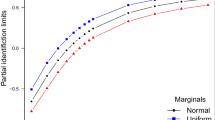
We here give further numerical illustrations of the bounds. Since there is a bijection between $2 \times 2$ tables and the dichotomization of standard normal distributions with free correlations and free thresholds $\tau _0, \tau _1$, we generate $2 \times 2$ tables from proportions of a normal latent variable with varying correlations and chosen threshold parameters. For each table, we compute the bounds from Proposition 1 with standard normal marginals, as well as the bound from Proposition 2. Recall that the bound from Proposition 2 is actually the bound from Proposition 1 with uniform marginals. The lengths of the resulting intervals are shown in Figs. 4 and 5. Full computational details are given in the accompanying R scripts. In Fig. 4, we have $\tau _1 = \tau _2 = 0$, which is a best case scenario. Figure 5 shows a more typical situation, where the length of all bounds are close to the maximal length of such an interval, namely 2. Figure 5 incidentally also illustrates that the bound for the Pearson correlation with standard normal marginals does not always contain the bound for Spearman’s rho. In both Fig. 4 and Fig. 5, points close or at the endpoints $\rho = \pm 1$ are not included, as different numerical techniques are needed in this region, as done in an attached R file found in the online supplementary material. It is here found that minimum lengths are attained at $\rho = \pm 1$ and $\tau _1 = \tau _2 = 0$, with a length of 0.67 for normal marginals and 0.5 for uniform marginals. In our analysis, we use the R (2020) packages copula (Yan and Others 2007), cubature (Narasimhan, Johnson, Hahn, Bouvier, and Kiêu 2020), and copBasic (Asquith 2020).

Fig. 4

Length of bounds for $\tau _1 = 0, \tau _2=0$ based on normal or uniform marginal assumptions. The graph does not cover points close to $\rho = \pm 1$

Fig. 5

Length of bounds for $\tau _1 = 1.2, \tau _2=1.2$ based on normal or uniform marginal assumptions. The graph does not cover points close to $\rho = \pm 1$

1.2 A.2. Proofs for Section 2

We will sometimes use the following principle of duality, as observed by Tankov (2011, Appendix). The usual matrix of probabilities is

$$\begin{aligned} P=\left[ \begin{array}{cc} p_{00} &{} p_{01} \\ p_{10} &{} p_{11}\\ \end{array}\right] . \end{aligned}$$

The swapped matrix is

$$\begin{aligned} P^{\star }=\left[ \begin{array}{cc} p_{01} &{} p_{00} \\ p_{11} &{} p_{10} \end{array}\right] . \end{aligned}$$

This matrix has will have the same upper bound as the negative lower bound of P; this is because it corresponds to the discretized distribution of $\left( -X,Y\right)$. Hence we may compute, say, a lower bound via an upper bound by using this duality. Some of the upcoming arguments apply this technique when convenient.

Proof of Theorem 1

We show that $|\rho | \ne 1$ by contradiction. Suppose $|\rho | = 1$. By the Cauchy-Schwarz inequality, $Z_1 = a + b Z_2$ for some numbers a, b. For any thresholds $\tau _1, \tau _2$, the probabilities of X equals the probability of observing $Z$ in one of the quadrants $x> \tau _1, y > \tau _2$ or $x< \tau _1, y < \tau _2$ or $x > \tau _1, y < \tau _2$ or $x < \tau _1, y > \tau _2$. Since any two straight lines intersect at either one or zero points, one quadrant will have zero probability, therefore contradicting our assumption that none of the cell probabilities are zero. Therefore, $|\rho | = 1$ is incompatible with the distribution of X.

Now we show that any $\rho \in (0,1)$ is compatible with X. To do this, let $a,b>0$ be two positive real numbers and define the random variable

$$\begin{aligned} Z(a,b)\mid X={\left\{ \begin{array}{ll} (a,a) &{} X=(1,1),\\ (b,-b) &{} X=(1,0),\\ (-a,-a) &{} X=(0,0),\\ (-b,b) &{} X=(0,1). \end{array}\right. } \end{aligned}$$

Then $\text {pr}[Z(a,b)\in A_{ij}]=\text {pr}[X=(i,j)]=p_{ij}$ when $A_{ij}$ are the quadrants $A_{00}=[-\infty ,0]\times [-\infty ,0]$, $A_{01}=[0,\infty ]\times [-\infty ,0]$, $A_{10}=[-\infty ,0]\times [0,\infty ]$, and $A_{11}=[0,\infty ]\times [0,\infty ]$. Thus Z(a, b) induces X through discretization when $\tau _{1}=\tau _{2}=0$. We now let $a = 1/b$. When $b \rightarrow 0^+$, we get a correlation converging to 1. When $b \rightarrow \infty$, we get a correlation converging to $-1$. This is visually obvious, as the points get closer and closer to a straight line, and is confirmed algebraically in the online appendix accompanying this paper. At the end of the online appendix, we also show that any intermediate value is possible, which is a consequence of the continuity of the correlation of Z as a function of b.

Proof of Proposition 1

Theorem 3.2.3 of Nelsen (2007, p. 70) shows that all copulas C that fulfil eq. (5) fulfil $W_p(u,v) \le C(u,v) \le M_p(u,v)$ and that $W_p,M_p$ are copulas fulfilling the constraint in eq. (5). The Höffding representation in eq. (4) therefore implies $\rho (W_p[F_1,F_2]) \le \rho (F) \le \rho (M_p[F_1,F_2])$. Since $W_p,M_p$ are copulas, this bound cannot be improved. We now show that the interval with limits as in the bound for $\rho (F)$ equals $\rho (\mathcal {P}, p)$. We use an argument that goes back to Fréchet (1958), (see Nelsen 2007, p. 15, exercise 2.4).

Let $\rho _L= \rho (W_p[F_1,F_2])$ and $\rho _U = \rho (M_p[F_1,F_2])$. Suppose $\rho \in [\rho _L, \rho _U]$. Then there is an $0 \le \alpha \le 1$ such that

$$\begin{aligned} \alpha \rho _L + (1-\alpha ) \rho _U = \rho . \end{aligned}$$

(8)

Let $C_\alpha (u,v) = \alpha W_p(u,v) + (1 - \alpha ) M_P(u,v)$ which is a convex combination of copulas, and hence a copula (Nelsen 2007, Exercise 2.3 and 2.4). Let $H_\alpha (x_1,x_2) = C_\alpha (F_1(x_1), F_2(x_2))$. By the second half of Sklar’s theorem, $H_\alpha$ is a distribution function with marginals $F_1,F_2$. Since $F_1(\tau _1) = p_{01} + p_{00}$ and $F_2(\tau _2) = p_{10} + p_{00}$, and $p_{00} = H_\alpha (\tau _1,\tau _2) = C_\alpha (F_1(\tau _1), F_2(\tau _2)) = C_\alpha (p_{01} + p_{00})$ the copula $C_\alpha$ fulfils eq. (5). Therefore, $H_\alpha \in \mathcal {P}$. We now show that $\rho (H_\alpha ) = \rho$ using the Höffding representation from eq. (4) in Sect. 2.

Firstly, we have $F_1(x_1) F_2(x_2) = \alpha F_1(x_1) F_2(x_2) + (1 - \alpha ) F_1(x_1) F_2(x_2)$, and so by the Höffding representation eq. (4), the covariance of $H_\alpha$ equals

$$\begin{aligned} \rho (H_\alpha ) =&{\text {sd}} (F_1)^ {-1} {\text {sd}} (F_2)^ {-1} \int \limits _{-\infty }^{\infty } \int \limits _{-\infty }^{\infty } C_\alpha (F_1(x_1), F_2(x_2)) - F_1(x_1) F_2(x_2) \, \mathrm{d}x_1 \mathrm{d}x_2 \\&= {\text {sd}} (F_1)^ {-1} {\text {sd}} (F_2)^ {-1} \int \limits _{-\infty }^{\infty } \int \limits _{-\infty }^{\infty } \alpha C_L(F_1(x_1), F_2(x_2)) - \alpha F_1(x_1) F_2(x_2) \\&\quad + {\text {sd}} (F_1)^ {-1} {\text {sd}} (F_2)^ {-1} \int \limits _{-\infty }^{\infty } \int \limits _{-\infty }^{\infty } (1 - \alpha ) C_U(F_1(x_1), F_2(x_2)) \\&\quad - (1 - \alpha ) F_1(x_1) F_2(x_2) \, \mathrm{d}x_1 \mathrm{d}x_2 \\&= \alpha \rho (W_p[F_1,F_2]) + (1 - \alpha ) \rho (M_p[F_1,F_2]) \\&= \rho \end{aligned}$$

using eq. (8). $\square$

Proof of Proposition 2

Define $a=p_{00}$, $b=p_{00}+p_{01},$ $c=p_{00}+p_{10}$ and $d=c+b-a$. We will calculate the integral $\int _{[0,1]^2} C_{U}\left( u,v\right) \mathrm{d}u \mathrm{d}v.$ Define the set $A_{F}=\left[ a,d\right] \times \left[ a,d\right]$. Then

$$\begin{aligned} \int _{[0,1]^2} C_{U}\left( u,v\right) \mathrm{d}u \mathrm{d}v= & {} \int _{A_{F}}C_{U}\left( u,v\right) \mathrm{d}u \mathrm{d}v+\int _{A_{F}^{C}}C_{U}\left( u,v\right) \mathrm{d}u \mathrm{d}v. \end{aligned}$$

(9)

On $A_{F}^{C}$ it holds that $C_{U}\left( u,v\right) =\min \left( u,v\right)$. Since $\int _{[0,1]^2}\min \left( u,v\right) \mathrm{d}u \mathrm{d}v=1/3$ and

$$\begin{aligned} \int _{a}^{d}\int _{a}^{d}\min \left( u,v\right) \mathrm{d}u \mathrm{d}v= & {} \frac{1}{3}\left( a+b+c\right) \left( a+b-2c\right) \end{aligned}$$

the second integral in (9) equals

$$\begin{aligned} \int _{A_{F}^{c}}C_{U}\left( u,v\right) \mathrm{d}u \mathrm{d}v=\frac{1}{3}-\frac{1}{3}\left( b-a\right) \left( c-a\right) \left( b+c\right) . \end{aligned}$$

The next part is $\int _{A_{F}}C_{U}\left( u,v\right) \mathrm{d}u \mathrm{d}v$. It is handy to divide $A_{F}$ into four rectangles

$$\begin{aligned} A_{BL}= & {} \left[ a,b\right] \times \left[ a,c\right] ,\\ A_{TR}= & {} \left[ b,d\right] \times \left[ c,d\right] ,\\ A_{TL}= & {} \left[ a,b\right] \times \left[ c,d\right] ,\\ A_{BR}= & {} \left[ b,d\right] \times \left[ a,c\right] . \end{aligned}$$

At $A_{BL}$ we have $C_{U}\left( u,v\right) =a$ and

$$\begin{aligned} \int _{A_{BL}}C_{U}\left( u,v\right) \mathrm{d}u \mathrm{d}v=a\left( b-a\right) \left( c-a\right) . \end{aligned}$$

At $A_{TR}$, $C_{U}\left( u,v\right) =-d+u+v$ and its integral is

$$\begin{aligned} \int _{A_{TR}}C_{U}\left( u,v\right) \mathrm{d}u \mathrm{d}v= & {} \frac{1}{2}\left( b-a\right) \left( c-a\right) \left( b+c\right) . \end{aligned}$$

At $A_{TL}$, $C_{U}\left( u,v\right) =\min \left( u,a-c+v\right)$ and the integral equals

$$\begin{aligned} \int _{A_{TL}}C_{U}\left( u,v\right) \mathrm{d}u \mathrm{d}v= & {} \frac{1}{3}\left( b-a\right) ^{2}\left( 2a+b\right) , \end{aligned}$$

and at $A_{BR}$, $C_{U}\left( u,v\right) =\min \left( v,a-b+u\right)$ the integral is

$$\begin{aligned} \int _{A_{BR}}C_{U}\left( u,v\right) \mathrm{d}u \mathrm{d}v= & {} \frac{1}{3}\left( c-a\right) ^{2}\left( 2a+c\right) . \end{aligned}$$

Add all the expressions together, make the substitutions $b=p_{01}+p_{00}$, $a=p_{10}+p_{00}$ and simplify to get

$$\begin{aligned} \int _{[0,1]^2} C_{U}\left( u,v\right) \mathrm{d}u \mathrm{d}v=\frac{1}{6}\left( 2-3p_{01}p_{10}\left( p_{01}+p_{10}\right) \right) \end{aligned}$$

hence

$$\begin{aligned} 12\int _{[0,1]^2} C_{U}\left( u,v\right) \mathrm{d}u \mathrm{d}v-3=1-6p_{01}p_{10}\left( p_{01}+p_{10}\right) \end{aligned}$$

as claimed. The lower bound follows by duality.

The reasoning behind the decomposition can be seen in Fig. 6, where each colour correspond to a continuous part of the piece-wise continuous function $C_U(u,v)$.

Fig. 6

Colour-coded graph of the bound copula. Each colour correspond to a continuous part of the piece-wise continuous function $C_U(u,v)$

1.3 A.3. Proofs for Section 2.5

Proof of Proposition 3

We follow the structure of the argument of Proposition 1. To help simplify the argument, we structure the argument in a series of lemmas. For easy reference, these lemmas are stated inside the present proof. The proofs of these supporting lemmas follow after the present proof is complete.

Firstly, let us identify what can be said of C when knowing the distribution of X, which is given by the function $p(x_1, y) = {\text {P}}( X_1 = x_1, Z_2 \le y)$, for $x_1 = 0,1$ and y a real number. We have that $p(0, y) = {\text {P}}(X_1 = 0 , Z_2 \le y) = {\text {P}}(Z_1 \le \tau _1, Z_2 \le y) = C(F_1(\tau _1), F_2(y)).$ Since $p(0,y) + p(1,y) = F_2(y)$, and therefore $p(1,y) = F_2(y) - p(0,y)$, we do not get new knowledge from similarly expressing p(1, y) in terms of the copula C. Our knowledge of C is therefore that

$$\begin{aligned} C(u,v) = p(0, F_2^ {-1} (v)) \quad \left( (u,v) \in \mathcal {U} = \{ (u,v) \mid u = F_1(\tau _1), 0 \le v \le 1 \}\right) . \end{aligned}$$

(10)

We now use a constrained Fréchet–Höffding bound found in Tankov (2011) to take into account this knowledge.

Lemma 1

Any copula C that satisfies eq. (10) also satisfies

$$\begin{aligned} C_{L,\mathcal {U}}(u,v) \le C(u,v) \le C_{L,\mathcal {U}}, \end{aligned}$$

where $C_{L,\mathcal {L}}$ and $C_{U,\mathcal {U}}$ are

$$\begin{aligned} C_{U,\mathcal {U}}(u,v)&= \min (u,v, \min _b [C(F_1(\tau _1), b) + (u - F_1(\tau _1))^+ + (v - b)^+]), \end{aligned}$$

(11)

$$\begin{aligned} C_{L,\mathcal {U}}(u,v)&= \max (0,u+v-1, \max _b [ C(F_1(\tau _1), b) - (F_1(\tau _1) - u)^+ - (b - v)^+]). \end{aligned}$$

(12)

Moreover, both $C_{L,\mathcal {U}}$ and $C_{U,\mathcal {U}}$ are copulas that satisfy eq. (10).

Let us now simplify the expressions for $C_L, C_U$ through identifying the inner minimum or maximum in $C_L, C_U$ respectively. This will show that they are equal to the expressions in the statement of the result. This is achieved in the following lemma.

Lemma 2

The copulas $C_{L,\mathcal {U}}$ and $C_{U,\mathcal {U}}$ are equal respectively to $W_p, M_p$ from the statement of Proposition 3. That is,

$$\begin{aligned} C_{U,\mathcal {U}}(u,v)&= \min (u,v,\min _{b\in [0,1]}[C(F_{1}(\tau _{1}),b)+(u-F_{1}(\tau _{1}))^{+}+(v-b)^{+}])\nonumber \\&= \min (u,v,C(F_{1}(\tau _{1}),v)+(u-F_{1}(\tau _{1}))^{+}), \end{aligned}$$

(13)

and

$$\begin{aligned} C_{U,\mathcal {U}}(u,v)&= \max (u,u+v-1,\max _{b\in [0,1]}[C(F_{1}(\tau _{1}),b)-(F_{1}(\tau _{1})-u)^{+}-(b-v)^{+}]),\nonumber \\&= \max (0,u+v-1,C(F_{1}(\tau _{1}),v)-(F_{1}(\tau _{1})-u)^{+}). \end{aligned}$$

(14)

From this, the Höffding representation from eq. (3) in Sect. 2 gives for any $F \in \mathcal {P}$ which is compatible with p that $\rho (W[F_1,F_2; p]) \le \rho (F) \le \rho (M[F_1,F_2; p])]$. We now show that any values within this interval can be attained as correlations in $\rho (\mathcal {P}, p)$.

As in the proof of Proposition 1, we study convex combinations of $W_p$ and $M_p$. For $0 \le \alpha \le 1$, we study $C_\rho (u,v) =\alpha W_p + (1 - \alpha ) M_p$. That this class induces all correlation values in the stated interval follows exactly as in the proof of Proposition 1. What is left to show is that the convex combination also fulfil the restriction in eq. (10). Now from Lemma 1, we have that both $W_p$ and $M_p$ fulfil eq. (10), i.e., that $W_p(F_1(\tau _1),v) = M_p(F_1(\tau _1),v) = p(0, F_2^ {-1} (v))$. Therefore, we also have $C_\rho (F_1(\tau _1),v) =\alpha C_{L,\mathcal {U}}(F_1(\tau _1),v) + (1 - \alpha ) C_{U,\mathcal {U}}(F_1(\tau _1),v) = \alpha p(0, F_2^ {-1} (v)) + (1-\alpha ) p(0, F_2^ {-1} (v)) = p(0, F_2^ {-1} (v))$. $\square$

We now prove the two lemmas stated within the proof of Proposition 3.

Proof of Lemma 1

Since $\mathcal {U}$ is compact, Theorem 1 (i) of Tankov (2011) shows the claimed bound, and that $C_{L,\mathcal {U}}$ and $C_{U,\mathcal {U}}$ fulfil eq. (10).

We now check the conditions of Theorem 1 (ii) of Tankov (2011) which shows that $C_{L,\mathcal {U}}$ and $C_{U,\mathcal {U}}$ are actually copulas. What is required is that $\mathcal {U}$ is both a increasing and a so-called decreasing set, as defined in Tankov (2011, Sect. 2, bottom of p. 390) : A set $S \subset [0,1]^2$ is increasing if for all $(a_1, b_1), (a_2, b_2) \in S$ we have either (i) $a_1 \le a_2$ and $b_1 \le b_2$ or (ii) $a_1\ge a_2$ and $b_1 \ge b_2$. For $S = \mathcal {U}$ this is trivially fulfilled, since if $(a_1, b_1), (a_2, b_2) \in \mathcal {U}$ we have $a_1 = a_2 = F_1(\tau _1)$ as we only have one possible element in the first coordinate, and therefore we trivially also have that either $b_1 \le b_2$ or $b_1 \ge b_2$ by tautology.

Similarly, recall that a set $S \subseteq [0,1]^2$ is decreasing if for all $(a_1, b_1), (a_2, b_2) \in S$ we have either (i) $a_1 \le a_2$ and $b_1 \ge b_2$ or (ii) $a_1\ge a_2$ and $b_1 \le b_2$. This is again trivially fulfilled.

For the proof of Lemma 2, we need the following technical result.

Lemma 3

Let C be a bivariate copula distribution function and $0\le a\le 1$. Then $C(a, v) - v$ is decreasing in v when $0\le v \le 1$.

Proof

By definition (Nelsen 2007, p. 8), a bivariate copula satifies $C(1,v)=v$ when $0\le v\le 1$ and

$$\begin{aligned} C(u_{1},v_{1})-C(u_{2},v_{1})\ge C(u_{1},v_{2})-C(u_{2},v_{2}) \end{aligned}$$

when $0\le u_{1}\le u_{2}\le 1$ and $0\le v_{1}\le v_{2}\le 1$. Now choose $u_{1}=a$ and $u_{2}=1$, and $C(a,v_{1})-v_{1}\ge C(a,v_{2})-v_{2}$ when $0\le v_{1}\le v_{2}\le 1$, as claimed. $\square$

Proof of Lemma 2

We start with $C_{U,\mathcal {U}}.$ We must show that

$$\begin{aligned} C_{U,\mathcal {U}}(u,v)= & {} \min (u,v,\min _{b\in [0,1]}[C(F_{1}(\tau _{1}),b)+(u-F_{1}(\tau _{1}))^{+}+(v-b)^{+}]), \nonumber \\= & {} \min (u,v,C(F_{1}(\tau _{1}),v)+(u-F_{1}(\tau _{1}))^{+}), \end{aligned}$$

where the first equality is from Lemma 1 while the second line is the definition of $M_{p}(u,v)$ from Proposition 3. The second equality holds if, and only if,

$$\begin{aligned} \min _{b\in [0,1]}[C(F_{1}(\tau _{1}),b)+(v-b)^{+}]=C(F_{1}(\tau _{1}),v), \end{aligned}$$

which is true if and only if $C(F_{1}(\tau _{1}),b)+(u-F_{1}(\tau _{1}))^{+}+(v-b)^{+}$ is minimized when $b=v$. Now we show this is indeed the case. For $b \le v$, we have $0 \le v-b$, and so $h(b) = C(F_1(\tau _1),b) + v-b$, which is decreasing by Lemma 3 (p. 20). For $b > v$, we have $v-b < 0$, and so $h(b) = C(F_1(\tau _1),b)$, which is increasing. The minimum is therefore attained at $b=v$ and

$$\begin{aligned} \min _{b\in [0,1]}[C(F_{1}(\tau _{1}),b)+(v-b)^{+}]=C(F_{1}(\tau _{1}),v), \end{aligned}$$

as claimed.

The case of $C_{L,\mathcal {U}}$ is similar, as we have to show that

$$\begin{aligned} C_{U,\mathcal {U}}(u,v)= & {} \max (u,u+v-1,\max _{b\in [0,1]}[C(F_{1}(\tau _{1}),b)-(F_{1}(\tau _{1})-u)^{+}-(b-v)^{+}]), \\= & {} \max (0,u+v-1,C(F_{1}(\tau _{1}),v)-(F_{1}(\tau _{1})-u)^{+}). \end{aligned}$$

Again, the first line is from Lemma 1 and second line is the definition of $W_{p}$ from Proposition 3. The second equality holds if, and only if,

$$\begin{aligned} \max _{b\in [0,1]}[C(F_{1}(\tau _{1}),b)-(b-v)^{+}]=C(F_{1}(\tau _{1}),v). \end{aligned}$$

This equality is true by the same reasoning as above. For $b \le v$, we have $b-v \le 0$ and so $g(b) = C(F_1(\tau _1),b)$, which is increasing. For $b > v$, we have $b-v > 0$ and so $g(b) = C(F_1(\tau _1),b)-b+v$, which is decreasing by Lemma 3 (p. 20). Therefore, the maximum is attained at $b=v$, and

$$\begin{aligned} \max _{b\in [0,1]}[C(F_{1}(\tau _{1}),b)-(b-v)^{+}]=C(F_{1}(\tau _{1}),v). \end{aligned}$$

as claimed.

1.4 A.4. Proof for Section 3.2

Let $S=\left( \Omega ,\Sigma \right)$ be a measure space. We assume S is an uncountable standard Borel space, i.e., it can be identified with the Borel space over the real numbers. We also assume that S is a rich Borel space, meaning it supports an independent uniform random variable that can be used as a randomization device (Kallenberg 2006, p.112). This assumption can be made with practically no loss of generality.

Proof of Theorem 2

The inclusion $\gamma \left( P_{X,Y}\right) \subseteq \gamma \left( P_{X}\right)$ is true for any Z and S. Choose a $P_{X}$, a $P_{X,Y}$ compatible with $P_X$, and a $P_{Z}\in \gamma \left( P_{X}\right)$. We must show $P_{Z}\in \gamma \left( P_{X,Y}\right)$, or $P_{f_{\theta }\left( Z\right) ,Y}=P_{X,Y}$ for some $\theta \in \Theta$. As a candidate $\theta$ choose one of the witnesses of $P_{f_{\theta }\left( Z\right) }=P_{X}$. By assumption there are two variables X, Y in S with distribution $P_{X,Y}$ such that X is distributed as $f_{\theta }\left( Z\right)$ when Z is distributed according to $P_{Z}$. By Corollary 6.11 of Kallenberg (2006), there is a variable $Z'$ in S such that $X=f_{\theta }\left( Z'\right)$ and $P_Z = P_Z'$. But then $P_{f_{\theta }\left( Z'\right) ,Y}=P_{X,Y}$ and we are done.

1.5 A.5. Computational Simplifications when Applying Proposition 1

The integrals defining the end points of $\rho (\mathcal {P}, p)$ in Proposition 1 can be calculated directly via numerical integration. However, this approach is computationally intensive, as we integrate functions with jumps. We here simplify the integrals in Proposition 1 by splitting the integrals into regions without jumps. This considerably reduces the computational burden of numerical integration. The analysis is analogous to the proof in Proposition 2, except that the integrals at $A_{BR}$ and $A_{TR}$ must be divided in two.

We only treat the upper bound. The lower bound can be found by duality. In the following argument, we assume that $F_1, F_2$ have variance one, an assumption made without loss of generality, as it can be achieved by re-scaling.

Define

$$\begin{aligned} g\left( u,v\right) =M[F_1,F_2;p]\left( F_1\left( u\right) ,F_2\left( v\right) \right) -\min \left( F_1\left( u\right) ,F_2\left( v\right) \right) . \end{aligned}$$

By the Höffding formula for covariance, we have

$$\begin{aligned} \rho (M[F_1,F_2;p])&= \int _{\mathbb {R}^2} M[F_1,F_2;p]\left( F_1\left( u\right) ,F_2\left( v\right) \right) -F_1\left( u\right) F_2\left( v\right) \mathrm{d}u \mathrm{d}v \\&= J_1 +\int _{\mathbb {R}^2} g\left( u,v\right) \mathrm{d}u \mathrm{d}v \end{aligned}$$

where

$$\begin{aligned} J_1 = \int _{\mathbb {R}^2} \min \left( F_1\left( u\right) ,F_2\left( v\right) \right) -F_1\left( u\right) F_2\left( v\right) \mathrm{d}u \mathrm{d}v. \end{aligned}$$

Here, $J_1$ is the covariance of the distribution with the Fréchet–Höffding upper bound copula and marginals $F_1,F_2$. The integral $J_1$ is seen to be finite by the Cauchy-Schwarz inequality, since it is a covariance where the marginals are assumed to have finite variance. The integral $\int _{\mathbb {R}^2} g\left( u,v\right) \mathrm{d}u \mathrm{d}v$ can be calculated using a similar decomposition as the one used in Proposition 2. We see that $\rho (M[F_1,F_2;p]) = \sum _{i=1}^8 J_i$ where

$$\begin{aligned} J_{2}= & {} -\int _{B}\min \left( F_1\left( u\right) ,F_2\left( v\right) \right) \mathrm{d}u \mathrm{d}v,\\ J_{3}= & {} \int _{A_{BL}}M[F_1,F_2;p]\left( F_1\left( u\right) ,F_2\left( v\right) \right) \mathrm{d}u \mathrm{d}v,\\ J_{4}= & {} \int _{A_{TR}}M[F_1,F_2;p]\left( F_1\left( u\right) ,F_2\left( v\right) \right) \mathrm{d}u \mathrm{d}v,\\ J_{5}= & {} \int _{T_{TL1}}M[F_1,F_2;p]\left( F_1\left( u\right) ,F_2\left( v\right) \right) \mathrm{d}u \mathrm{d}v,\\ J_{6}= & {} \int _{T_{TL1}}M[F_1,F_2;p]\left( F_1\left( u\right) ,F_2\left( v\right) \right) \mathrm{d}u \mathrm{d}v,\\ J_{7}= & {} \int _{T_{BR1}}M[F_1,F_2;p]\left( F_1\left( u\right) ,F_2\left( v\right) \right) \mathrm{d}u \mathrm{d}v,\\ J_{8}= & {} \int _{T_{BR2}}M[F_1,F_2;p]\left( F_1\left( u\right) ,F_2\left( v\right) \right) \mathrm{d}u \mathrm{d}v. \end{aligned}$$

The domains of integration can be seen in Fig. 6. Here $R_{BL}$ is the bottom-left rectangle, $T_{TL1}$ the first top-left triangle, et cetera.

When the marginals are normal, concrete formulas for the integrals over $J_{3}$ and $J_{4}$ are possible to derive by using well-known results for normal integrals (Owen 1980). A simple algebraic formula such as that given in Proposition 2 seems out of reach in this case, as the integrals $J_{5},J_{6},J_{7},J_{8}$ are too complicated.

In our numerical implementation, we assume that $F_1, F_2$ are equal, and are capable of supporting perfect correlations of $\pm 1$, as is well known to hold for normal marginals. As shown in Sect. 2, the maximum possible correlation with marginals $F_1,F_2$ equals $J_1$, and so this assumption amounts to $J_1 = 1$.