Compensation and Amplification of Attenuation Bias in Causal Effect Estimates

Abstract

Covariate-adjusted treatment effects are commonly estimated in non-randomized studies. It has been shown that measurement error in covariates can bias treatment effect estimates when not appropriately accounted for. So far, these delineations primarily assumed a true data generating model that included just one single covariate. It is, however, more plausible that the true model consists of more than one covariate. We evaluate when a further covariate may reduce bias due to measurement error in another covariate and in which cases it is not recommended to include a further covariate. We analytically derive the amount of bias related to the fallible covariate’s reliability and systematically disentangle bias compensation and amplification due to an additional covariate. With a fallible covariate, it is not always beneficial to include an additional covariate for adjustment, as the additional covariate can extensively increase the bias. The mechanisms for an increased bias due to an additional covariate can be complex, even in a simple setting of just two covariates. A high reliability of the fallible covariate or a high correlation between the covariates cannot in general prevent from substantial bias. We show distorting effects of a fallible covariate in an empirical example and discuss adjustment for latent covariates as a possible solution.

Appendix: Proof that W is an Irrelevant Covariate in 1a, 1b, 1c, 1d

We are interested in $\beta _X ={\text {ATE}}$ that is the regression coefficient of treatment X in the outcome regression $E\left( {Y{|}X,\xi ,W} \right) =\beta _0 +\beta _X \cdot X+\beta _\xi \cdot \xi +\beta _W \cdot W$. Omitting W and using the outcome regression $E\left( {Y{|}X,\xi } \right) =\beta _0^\xi +\beta _X^\xi \cdot X+\beta _\xi ^\xi \cdot \xi$ for ATE estimation results in the ATE estimate $\beta _X^\xi =\frac{\rho _{XY} -\rho _{X\xi } \rho _{Y\xi } }{1-(\rho _{X\xi })^{2}}$, with the bivariate correlations of X, Y,  and $\xi$. The bias in this ATE estimate can be quantified in our formal framework according to Steiner & Kim (2016) as

$$\begin{aligned} \beta _X^\xi -\beta _X =\alpha _W \beta _W \cdot \left( {1-\left( {\rho _{\xi W} } \right) ^{2}} \right) \cdot \frac{1}{1-\left( {\alpha _\xi +\alpha _W \rho _{\xi W} } \right) ^{2}}. \end{aligned}$$

(A1)

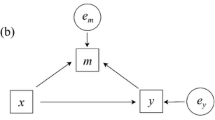
In 1a, 1b, 1c, 1d the bias is always zero, because either $\alpha _W$, $\beta _W$, or both parameters are fixed to zero. Thus, using $E\left( {Y{|}X,\xi } \right)$ instead of $E\left( {Y{|}X,\xi ,W} \right)$ obtains the same ATE estimate. W has no impact on ATE estimation in addition to $\xi$. This is not the case in 2a and 2b, where using $E\left( {Y{|}X,\xi } \right)$ instead of $E\left( {Y{|}X,\xi ,W} \right)$ can result in different ATE estimates. Note, different causal frameworks provide more general conditions [backdoor criterion (Pearl 2009), strong ignorability condition (Rubin 2005), causality conditions in the theory of causal effects (Steyer et al. 2014)] which result in the same conclusions for the relevance of W in addition to $\xi$.