Achievable Spectral Efficiency of Line-of-Sight MIMO Fixed Links with Compact Planar Antenna Arrays and Power Amplifier Limitations

Abstract

Fixed Point-to-Point microwave wireless systems with high spectral efficiency are needed to meet the pervasive and increasing demand for capacity in back-haul networks of mobile radio systems. In this context, spatially multiplexed LoS-MIMO (Line-of-Sight Multiple Input Multiple Output) systems have been studied for about twenty years, particularly in the millimeter wave frequency bands (above 15 GHz). However, their deployment in real networks has been really limited, to the authors’ knowledge. This has been due to several factors, i.e. the practical possibility of using extremely high-level modulation formats (nowadays up to 8192-QAM), the joint use of co-channel dual polarization, and the availability of wider channel bands in the new high frequency ranges (e.g. E-Band). In addition, a crucial reason has been the difficulty of installing multiple antennas spaced apart in order to maximize the MIMO spatial multiplexing so providing the maximum capacity gain. This optimal antenna separation, even for the classical MIMO $M \times N$ with M = 2 antennas at the receiver and N = 2 antennas at the transmitter, can be several meters, e.g. 5.71 m at 23 GHz on a 5 km link. In this article, we analyze the performance of LoS-MIMO systems where antenna separation is highly sub-optimal, for limiting the array size, and a satisfactory performance is made possible by the exploitation of specific bit loading and power allocation strategies and the setting of the working region of the RF transmitter power amplifiers to operate at a given Signal-to-Inter Modulation Distortion Ratio (SIMDR). The result is an overview of the advantages and drawbacks of compact LoS-MIMO from a wider perspective than in the existing literature, including fundamental aspects for the practical implementation of these systems. Performance is discussed in many cases of interest and compared with the state of the art SISO (Single Input Single Output) system.

1 Introduction

In transport networks, commonly referred to as backhaul networks, fixed point-to-point microwave links are a valid choice w.r.t. wired links in terms of installation costs, rapidity of deployment and flexibility in urban, rural environments and in geographically challenging areas. Microwave transmission carried out in the conventional radio frequency (RF) licensed bands (from 15 GHz to the E-Band) should occur in Line-of-Sight (LoS) conditions to support the capacity and reliability targets. LoS-MIMO (Multiple Input Multiple Output) systems have been studied for about twenty years and the potential high multiplexing gain of these systems has stimulated the study in the context of rectangular arrays and also circular arrays, massive MIMO, and Terahertz LoS communications. However, the practical deployment of LoS-MIMO in real networks has been limited so far. This is due to several factors, among which we can mention the possibility of using higher modulation formats (nowadays up to 8192-QAM), the use of double polarization transmission, and the availability of wider channel bandwidths (125 MHz, 250 MHz, 500 MHz) at the high frequency carriers (e.g. E-Band). Nevertheless, one major limiting factor for the implementation of LoS-MIMO systems has been the difficulty of installing antennas spaced apart in order to maximize the capacity. Such an optimal antenna separation is dependent on the frequency f and the link length L and can reach several meters even in the simplest LoS-MIMO $M \times N$ system, i.e. M = 2 antennas at the receiver (Rx) and N = 2 antennas at the transmitter (Tx); for instance, the optimal antenna separation is 5.71 m at $f = 23$ GHz on link of length $L = 5$ km.

In the literature, the optimization of antenna array design in LoS-MIMO systems has been widely treated for different structures of the arrays and different applications. In [1] the optimal design for the antenna arrangement is derived for the LoS-MIMO $4 \times 4$ as a function of frequency and distance focusing on the characteristics of the channel matrix, in particular on the ratio between the highest to the lowest eigenvalue, i.e. the condition number. In [2] and [3] a general geometrical model for Uniform Rectangular Arrays (URAs), comprising Uniform Linear Arrays (ULAs) as a special case, is introduced to derive the formula of the optimal antenna separation as a function of the wavelength $\lambda$, the link length L, the number of antenna elements on the two dimensions and the array orientation; in addition it is also investigated how a non-optimal design affects the eigenvalues of the channel matrix. More recently, in [4] the analysis is extended to LoS-MIMO systems with multiple panel arrays, dealing with the optimization of the antennas locations to mitigate the impact of sub-optimal array size varying the link length. In [5], the optimal array antenna separation is derived for LoS-MIMO $2 \times 2$ and $3 \times 3$ circular arc arrays for short-range communication in non-scattering environments, returning the best choices of the model parameters, i.e. array element spacing, wavelength, and link length. The very short link lengths for the considered frequencies, till to $f = 28$ GHz, return antenna separation values below one meter. In [6] the objective is to find an array structure that maximizes the minimum capacity for a LoS-MIMO $4\times 4$ array system that has to operate in a range around the optimum for a given link length. The application of interest is the short-range E-band, with $f = 80$ GHz and link length in the range [15, 200] and the proposed solution is an adaptive aperiodic-switched array. Nevertheless, to the best of our knowledge, there are not works that face the problem of the achievable spectral efficiency in a practical fixed microwave Point-to-Point LoS-MIMO with stringent constraints on the arrays size evaluating the performance of different Tx and Rx structures and taking into account the setting of the power amplifiers at the Tx antennas.

In a MIMO $M \times N$ system, when the condition on the optimal antenna separation is met at both Tx and Rx arrays, the spatial multiplexing gain is maximized and the transmission occurs through min(M, N) orthogonal parallel Single Input Single Output (SISO) sub-channels with the same gain. This well-established result comes from the Singular Value Decomposition (SVD) of the full rank channel matrix ${\textbf {H}}$. Practical receiver schemes of a LoS-MIMO system, which provide similar Bit Error Rates (BER) at high Signal-to Noise-Ratio (SNR) and with optimal array design, are based on the SVD decomposition with uniform power distribution among the sub-channels at the transmitter, and the well-known Zero Forcing (ZF) equalization.

When the separation of the antennas is reduced w.r.t. the optimum, e.g. to fulfill practical installation constraints, the performance deteriorates for both detection schemes (SVD and ZF) in terms of capacity and BER. The SVD analysis shows that the sub-channel gains diverge substantially, so penalizing the theoretical capacity if there is not a smart power and bit loading distribution among the sub-channels. We will show how the SVD performance can be improved significantly adopting appropriate power allocation and bit loading in the sub-channels. On the other hand, the ZF receiver scheme will suffer from noise enhancement when the array antenna separation is not optimal, even if it remains a simple benchmark scheme for the high SNR values that characterize these LoS links. In [7], this issue is investigated for the LoS-MIMO $2\times 2$ with sub-optimal antenna separation array, highlighting how the SVD-based precoding and receiver scheme with uniform power distribution on the sub-channels has worse performance than the ZF receiver. In [8], in presence of sub-optimal antenna separations it is proposed the decomposition of the LoS-MIMO channel matrix into a free-space propagation and a phase shifting part, which can be modulated by exploiting a dielectric material with adjustable depth. In [9], the same authors present some measurement results for LoS-MIMO $2 \times 2$ and $3 \times 3$ array configurations operating at 60 GHz on very short link distances, till to 60 m; the experimental results confirm that the estimated condition numbers (i.e. the ratio between the maximum and the minimum eigenvalue) of the measured channel, which are a measure of the spatial multiplexing capability of the channel matrix, are in good agreement with the theory for various link lengths and antenna setups. In [10], the results from a two-years measurement campaign of a LoS-MIMO $2 \times 2$ link with link length around $L = 7$ km and frequency $f = 32$ GHz are investigated in order to study the channel variations due to atmospheric disturbances, and verify the impact of antenna separation on the system throughput for the ZF based receiver. The measurements show that the system can achieve still about $50\%$ of the data throughput improvement expected with optimal array design even at $33\%$ of the optimal antenna separation. Finally, in [11] it is provided a deep analysis of the LoS-MIMO channel eigenvalues at certain system settings and their asymptotic behavior for increasing antenna numbers and transmission distance; finally, it is defined and discussed an effective multiplexing distance of the E-band channel as the distance at which the channel can support a certain number of simultaneous spatial streams at a given SNR.

We will show that overcoming, at least partially, the degradation experienced by SVD-based detection when sub-optimal antenna arrays are deployed, is possible by appropriate power and/or bit loading smart allocation techniques. In the literature, several algorithms for power allocation and bit loading can be found, from the classical water filling algorithm to more complex ones specifically designed for the wireless applications. The study in [12] provides simulated performance validation in the LoS-MIMO $2 \times 2$ case. Here, starting from the algorithm proposed in [13], we propose an improved version of it and verify that it provides better performance in terms of Bit Error Rate (BER). Focused on the practical implementation of microwave radio links, this work can be seen as a continuation of [14], where the LoS-MIMO $2 \times 2$ system is investigated in the context of generalized adaptivity.

In this work, we consider a single-polarized LoS-MIMO $M \times N$ link of length L with broadside Uniform Rectangular Arrays (URAs) where $M = M_1 \times M_2$ and $N = N_1 \times N_2$ antennas respectively at the Rx and Tx sides, as sketched in Fig. 1. The URAs under investigation are square, i.e. $M_1 = M_2$ and $N_1 = N_2$ and, independently from the values of $M_1$ and $N_1$ (in our analysis from 1 to 4), have a fixed side of length d. Obviously, the Uniform Linear Array (ULA) arrangement can be seen as a special case of URA, when one dimension (e.g., $M_1$ or $N_1$) is unitary and, in this case, d is the length of the array. We denote as $d_{\text{opt}}$ the optimal antenna separation for LoS-MIMO $(1 \times 2) \times (1 \times 2)$ at $f=23$ GHz and link length $L=5$ km and express the side d through the factor SQF (SQueeze Factor) as $d = d_{\text{opt}} \cdot SQF$. The SQF value, when less than 1, represents the compactness degree of the arrays since a lower SQF corresponds to a smaller side d of the square arrays. Given the link structure in Fig. 1, we analyze the performance of the LoS-MIMO $(M_1 \times M_2) \times (N_1 \times N_2)$ system with single polarization varying the number of antennas fixed the side d of the arrays, or varying SQF, fixed the number of antennas. The different array deployments under investigation are shown in Fig. 2. The simulated BER performance obtained by the ZF or SVD-based detection with the aid of specific power and bit loading algorithms and amplifiers settings is compared with the state of the art SISO system operating at 8192-QAM.

We summarize the contributions of this work in the following points:

• the evaluation of the theoretical spectral efficiency achievable in point-to-point radio system with LoS-MIMO systems and compact antenna arrays, i.e. arrays with sub-optimal size. The detection methods are the SVD-based detection, which requires a precoding matrix, and the ZF equalizer without precoding.

• The modification of the bit loading algorithm in [13], which maximizes the sub-channels SNRs and improves the total rate on the link in the SVD-based precoding and detection scheme (Sect. 4.1).

• The simulated BER performance comparison between ZF detection method and the method based on SVD decomposition with the modified bit and power loading algorithms for different arrays configurations, taking into account the impact of the working regions of the RF Tx power amplifiers. In fact, RF technology must support stringent constraints in terms of linearity, which depend on the modulation, the precoding matrix and the corresponding Peak-to-Average Power Ratio. The different settings of the power amplifiers in the LoS-SISO and Los-MIMO schemes have been taken into account to define an effective Tx power guaranteeing the appropriate value of the Signal-to-InterModulation Distortion Ratio (SIMDR) (Sect. 4.2).

In the sequel, Sect. 2 presents the system model and Sect. 3 introduces the receiver architectures of SVD based and ZF detection methods. In Sect. 4, the application of the proposed power allocation and bit loading algorithm on SVD-based detection method and the constraints deriving from an appropriate use of the RF Power amplifier are discussed. Then, in Sect. 5 and in Sect. 6 the theoretical spectral efficiencies and the BER performance results obtained by simulations are reported and commented for different LoS-MIMO $(M_1\times M_2) \times (N_1 \times N_2)$ array configurations. Finally, Sect. 7 summarizes the main outcomes of the work.

Fig. 1

General broadside antenna definitions and link arrangement

2 System Model

The channel model of a single polarized LoS-MIMO $M \times N$ link operating in non frequency-selective propagation conditions is described by a ($M \times N$) matrix ${\textbf {H}}$ with scalar entries $h_{ij}$, which represent the complex channel gains between each transmit ($j=1,2,...,N$) and receive antenna ($i=1,2,..,M$). Denoting

$$\begin{aligned} {\textbf {s}}= & {} \left[ \begin{array}{cccc} s_{1}&s_{2}&...&s_{N} \end{array}\right] ^T, \end{aligned}$$

(1)

$$\begin{aligned} {\textbf {r}}= & {} \left[ \begin{array}{cccc} r_{1}&r_{2}&...&r_{M} \end{array}\right] ^T, \end{aligned}$$

(2)

$$\begin{aligned} {\textbf {n}}= & {} \left[ \begin{array}{cccc} n_{1}&n_{2}&...&n_{M} \end{array}\right] ^T, \end{aligned}$$

(3)

the transmit signal vector, received signal vector and additive Gaussian noise vector with variance $\sigma ^2$ respectively, the system input–output relation is given by

$$\begin{aligned} {\textbf {r}}={\textbf {H}}{} {\textbf {s}}+{\textbf {n}}. \end{aligned}$$

(4)

In a pure LoS environment, the elements of the channel matrix ${\textbf {H}}$ are usually modeled with unitary amplitudes and phases depending on the wavelength $\lambda$ and link length $l_{ij}$ between $j^{\text {th}}$ antenna at the Tx and $i^{\text {th}}$ antenna at Rx, i.e.

$$\begin{aligned} h_{ij}=e^{(-\frac{j2\pi }{\lambda })l_{ij}}, \end{aligned}$$

(5)

that can be determined exploiting the array geometrical construction procedure similar to [3]. In [2, 3] the authors derive the optimal array design that guarantees the maximum spatial multiplexing gain by the Shannon capacity formula (see also Sect. 5). For a LoS-MIMO $(M_1 \times M_2) \times (N_1 \times N_2)$ link and two broadside antenna arrays, for each array (at Tx or Rx), the relation for the optimal values of the antenna separations $d_1$ and $d_2$ on the two spatial directions (Fig. 1) are (from [3] the formula for Tx)

$$\begin{aligned} (d_{1,\text{opt}})^2=\frac{\lambda \cdot L}{N_{1}}, \hspace{0.5 cm} (d_{2,\text{opt}})^2=\frac{\lambda \cdot L}{N_{2}}. \end{aligned}$$

(6)

Our analysis considers systems operating at frequency bands above 15 GHz and, in particular, at $f = 23$ GHz with a reference link length $L = 5$ km (nevertheless, the results can be easily adapted to other frequency bands and link lengths) and broadside URA arrays at Tx and Rx with square shape, i.e. $d_1 = d_2 = d$, with only one dimension when ULA is considered. Independently from the number of antennas considered in the different configurations, in our analysis we fix the size of the array d (see Fig. 2). The Eq. (6), applied to the URA array ($2 \times 2$), or to the ULA one ($1 \times 2$), provides the optimal array size, denoted as $d_{\text{opt}} = 5.71$ m, which can be impractical in a real installation.

Fig. 2

ULA and URA antenna array configurations considered in our analysis, with $d=d_{\text{opt}}\cdot SQF$. ULA arrays have size d, URA arrays are inscribed in a square $d\times d$

3 Receiver Architectures

Let us summarize the two reference architectures for the receiver, the linear ZF equalizer and the SVD-based linear decoder. These well-known schemes, shared with most of the literature contributions, are exploited for showing the impact of the reduced size and of the loading strategies (Sect. 4). Notice that here the LoS-MIMO array configurations $M \times N$ have $M\ge N$ without loss of generality.

3.1 Zero Forcing Equalizer

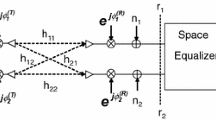
The equalizer in the ZF form is sketched in Fig. 3 (bottom). Assuming that the receiver has perfect knowledge of the channel H, it multiplies the received signal by the inverse of the channel ${\textbf {H}}^{-1}$ if $M=N$ or by the pseudo-inverse ${\textbf {H}}^{+}$ if $M > N$. This equalization is equivalent to the Minimum Mean Square Error (MMSE) formulation at high SNR, which is the typical working region for LoS microwaves links. The signals at the output of the equalizer are expressed by the vector ${\textbf {y}}=\left[ y_{1},y_{2},...,y_{N}\right] ^T$,

$$\begin{aligned} {\textbf {y}}={\textbf {H}}^{-1}{} {\textbf {r}} = {\textbf {s}}+{\textbf {H}}^{-1}{} {\textbf {n}}, \end{aligned}$$

(7)

if $M = N$, otherwise ${\textbf {H}}^{-1}$ is replaced by ${\textbf {H}}^{+}$ if $M>N$. Defining as $SNR_0 = \frac{P_{rx}}{P_n}$ the SNR of the LoS-SISO system with a total received signal power $P_{rx}$ and additive Gaussian noise power $P_n$, we express the SNR of the $i{\text{th}}$ sub-channel of the ZF LoS-MIMO $M \times N$ system as

$$\begin{aligned} SNR_{i, ZF}=\frac{P_{rx}}{N \cdot P_n\cdot \sum _{j=1}^{M} \vert {q_{i,j}}\vert ^{2}}=\frac{SNR_0}{N \cdot \sum _{j=1}^{M} \vert {q_{i,j}}\vert ^{2}}, \end{aligned}$$

(8)

where $q_{i,j}$ is the element at $i{\text{th}}$ row and $j{\text{th}}$ column of the matrix ${\textbf {Q}}= {\textbf {H}}^{-1}$ or ${\textbf {Q}}= {\textbf {H}}^{+}$ for $N=M$ or $N<M$ respectively.

3.2 Singular Value Decomposition

The detection by means of the SVD of the channel matrix ${\textbf {H}}$ assumes that not only the receiver but also the transmitter has perfect knowledge of the channel.

Through the application of the SVD theorem, ${\textbf {H}}$ can be written as

$$\begin{aligned} {\textbf {H}}= {\textbf {UDV}}^{H} \end{aligned}$$

(9)

where ${\textbf {D}}$ is an $M\times N$ non-negative and diagonal matrix, ${\textbf {U}}$ and ${\textbf {V}}$ are $M\times M$ and $N\times N$ unitary matrices, respectively. The N (with $N\le M$) diagonal entries of ${\textbf {D}}$ are the singular values $\sqrt{\lambda _i}$ of the matrix ${\textbf {H}}$, with $i=1,2,...N$, i.e. the square roots of the eigenvalues of the matrix ${\textbf {HH}}^{H}$. Furthermore, the columns of ${\textbf {U}}$ are the eigenvectors of ${\textbf {HH}}^{H}$ and the columns of ${\textbf {V}}$ are the eigenvectors of ${\textbf {H}}^{H} {\textbf {H}}$.

In the SVD-based scheme (Fig. 3 top), the transmit precoding matrix is constituted by the matrix ${\textbf {V}}$ and the receiver matrix by ${\textbf {U}}^H$, realizing the decomposition of the channel into N parallel orthogonal sub-channels with gains equal to the singular values of ${\textbf {H}}$. It is important to notice that the precoding matrix affects the PAPR (Peak-to-Average-Power-Ratio) of the transmitted signals.

Analogously to (8) we define the SNR of the $i{\text{th}}$ sub-channel using the unitary property of the matrix ${\textbf {U}}$, as

$$\begin{aligned} SNR_{i,SVD} = \frac{P_{rx} \cdot \lambda _{i}}{N \cdot P_n} = SNR_{0} \frac{\lambda _{i}}{N}, \end{aligned}$$

(10)

where the transmit power is equally distributed among the N input signals. In particular, the optimal antenna design makes orthogonal the N columns of ${\textbf {H}}$ and all the N eigenvalues are equal.

Fig. 3

Block diagram of a MIMO $M \times N$ system, based on SVD detection (top) and ZF equalized (bottom). The parameter pcf is the value of Power Correction Factor [dB] defined in 4.2, converted in linear units

4 Bit Loading Strategies and RF Power Amplifier Settings

In this Section, we develop the two main contributions of this work, which give a different insight on the potential of the practical implementation of LoS-MIMO links: in Sect. 4.1 we present the modified bit loading algorithm, able to capture a significant gain w.r.t. classical SVD approach with uniform distribution of the power and, in Sect. 4.2, we explain how to set the working point of RF amplifiers, keeping the SIMDR requirements under control, and capitalizing important advantages in the effective transmitted powers for some cases of interest.

4.1 Bit Loading Algorithm

When the LoS-MIMO arrangement is optimally designed, the power gains and the SNR of the N sub-channels, i.e. $\lambda _{i}$ and the $SNR_{i,SVD}$ $i = 1...N$, are all equal; therefore, the optimal resource allocation is uniform power and transmission rate for all the sub-channels. This is not the case when the singular values are different and, even more, when some eigenvalues are almost null; in these conditions, appropriate power allocation and bit loading algorithms can perform considerably better than the uniform power and rate allocation. In the simulations we adopt the loading algorithm that performs rate and power assignment to guarantee equal error rates to the parallel data streams [13]. Given the total rate to be transmitted $R_{t}$ and the maximum rate per sub-channel $R_{max}$, the allocation strategy, for integer transmission rates, follows the 4 fundamental steps:

• (1) The partition of the total rate $R_{t}$ into N $R_{i}$, $i=1...N$, assigned to the sub-channels, made iteratively according to the eigenvalues $\lambda _{i}$. Bad sub-channels, i.e. with gains close to zero, can be assigned $R_i = 0$.

• (2) The quantization of the rates to the nearest integer $R_{qi}$ with limitation to $R_{max}$.

• (3) A further adjustment of the rates $R_{qi}$ if their sum is greater than $R_{t}$.

• (4) The distribution of the total power $P_0$ on the $N_{active}$ sub-channels with $R_{qi} > 0$ in order to have the same BER on all the streams.

We have observed that sometimes, at step 2, sub-channels previously switched off are reactivated for the reassignment of the rate exceeding $R_{max}$ in the sub-channels with better gains; however, this usually requires a large amount of power and decreases the system efficiency. In order to mitigate this drawback, the step 2 of the algorithm has been modified as follows:

• (2a) If K sub-channels have been assigned rates $R_i$ greater than $R_{max}$, their rates are limited to $R_{max}$ and the residual rate $R_{res}=R_{t}-KR_{max}$ is allocated to the remaining channels, excluding those already allocated at previous iteration step 1). This process continues until no rate exceeds $R_{max}$.

• (2b) The rates $R_i$ are quantized to the nearest integer $R_{qi}$.

A flowchart of the modified algorithm is in Fig. 4, where the dashed blocks are the parts added to the original version. During the iterations the rates are assigned to the remaining channels respecting the criteria of equal probability of error and maximization of SNR. Finally the total power is distributed on the resulting complete set of active sub-channels. The numerical results show that this iterative bit loading, denoted in the sequel as Iterative Loading, achieves better performance especially for critical profiles of the eigenvalues since it tends to discard sub-channels with small eigenvalues.

Fig. 4

Flow chart of the modified bit loading algorithm (Iterative Loading)

4.2 RF Power Amplifier Setting

Here we introduce our approach for the setting of the RF Power Amplifiers (PAs), which turns out to be an important issue in the performance comparison between SISO and MIMO systems. The comparison between different systems is usually operated at the same average total transmitted power $P_{0}$, i.e. the same SNR defined as the ratio between the total received signal power and the noise power. Therefore, given $P_{0}$ and $P_{pk,0}$ the average power and the supported peak power in the SISO system for the 8192-QAM modulation, the average powers and the supported peak powers of the PAs in the MIMO system with N transmitters and same modulation format will be down-scaled by a factor N, i.e. equal to $P_{0}/N$ and $P_{pk,0}/N$, and provide the same inter-modulation distortion of the full-power SISO, but with cheaper devices. However, the working point of the PAs for the MIMO system can be modified according to the characteristics of the transmitted signals, i.e. the precoding matrix, the modulation formats and the powers assigned by the bit loading algorithm, in order to maintain the same $SIMDR_{ref}$ of the reference SISO system. In particular, given a certain BER, a level modulation format lower than 8192-QAM can accept a SIMDR lower than $SIMDR_{ref}$, as it requires a lower SNR ($-3$ dB per bit). To take into account this crucial point we introduce a Power Correction Factor (PCF), assumed common to all the antennas PAs, that is translated into an SNR Correction Factor for evaluating the practical performance of MIMO systems. The value of PCF is the sum (in dB) of two contributions:

• $PCF_{PEAK}$: the difference (in dB) between the down-scaled peak power of the SISO $P_{pk,0}/N$ and the effective peak power $P_{pk}$ measured on the antennas at the output of the precoder, if present. This factor realigns the maximum peak of the MIMO signals (worst case) to that of the reference SISO bringing back the inter-modulation products to the SISO level.

• $PCF_{IMD}$: the difference (in dB) between the $SIMDR_{ref}$ of the reference SISO with 8192-QAM modulation and the SIMDR for the signal transmitted with the highest modulation level in MIMO system, divided by 2. This formula derives from the SIMDR variation law in the case of two tones third order inter-modulation distortion products. A common high level system engineering assumption is to consider an “ideal” non-linearity of the 3rd order type for the PA (i.e. $y=a_{1}x+a_{3}x^{3}$): it turns out that, assuming that the average output power P of the PA is located within the linear region of its input/output characteristic, the output SIMDR can be expressed as [15]

  $$\begin{aligned} SIMDR=2\cdot (IP3-P), \end{aligned}$$

  (11)

  where IP3 is the third-order intercept point, i.e. the theoretical point where the desired signal and the third-order distortion have equal magnitudes, i.e. $SIMDR=0$ dB. The IP3 parameter is characteristic of any RF chain. For the purpose of this analysis we observe from (11) that an increase (decrease) of 1 dB of the output power P implies a decrease (increase) of 2 dB in the SIMDR as

  $$\begin{aligned} SIMDR_{ref}-SIMDR=2\cdot (P-P_{ref}), \end{aligned}$$

  (12)

  so that

  $$\begin{aligned} PCF_{IMD}=(P-P_{ref})=\frac{(SIMDR_{ref}-SIMDR)}{2}. \end{aligned}$$

  (13)

For the SVD case with bit loading, in the computation of $PCF_{IMD}$ we consider the worst case from the PA perspective, i.e. the highest level modulation actually transmitted, and not the "average" on the modulations of the active streams. The $PCF_{IMD}$, based on the measurement of the peak power of the various signals at the antennas, is calculated in the simulations on the discrete levels of the QAM signal. The practical peak power of the simulated signals was calculated as the power level exceeded with a certain probability ($10^{-3}$), instead of the instantaneous maximum peak value.¹ The approach described above allows a fair comparison among the different LoS-MIMO systems, i.e. with similar SIMDR targets, by quantifying the effects of the different settings of the PAs as a variation of the total average Tx power. Even if a more accurate analysis or simulation should include the effects of inter-modulation distortion to evaluate the role of power allocation in the bit loading algorithm for the SVD method, we are confident that this approach guarantees an acceptable approximation. In fact we have seen that SVD method tends to bring more power to the sub-channels with smaller singular values at the expense of the power to the channels with higher singular values. Therefore, a penalizing power imbalance could arise for the channels with the higher singular values (especially the best channel), which transport most of the total rate by means of higher level modulations. However, these configurations have a performance heavily penalized by the presence of thermal noise and are of limited interest.

5 LoS-MIMO Shannon Capacity

We can now calculate the theoretical performance of a LoS-MIMO $M \times N$ system in terms of Shannon capacity for various types of arrays, considering the two possible detection methods (ZF and SVD with uniform distribution of power on the N sub-channels, as a conservative result). The arrays that will be analyzed, here and in the following, are illustrated in Fig. 2. Let us remind that the reference system is the SISO one and all the formulas are expressed w.r.t. the received $SNR_0$ of the equivalent SISO system.

5.1 The SVD System

The computation for the SVD case follows the classical steps, which can be found in [16]. From (10) it follows that the Shannon spectral efficiency $\eta$ [bit/s/Hz] is

$$\begin{aligned} \eta _{SVD} = \sum _{i=1}^{N} \text{log}_{2}(1+SNR_{i,SVD})=\sum _{i=1}^{N} \text{log}_{2}\left( 1+SNR_0\frac{\lambda _{i}}{N} \right) , \end{aligned}$$

(14)

where $\sqrt{\lambda _i}$ are the singular values of ${\textbf {H}}$.

5.2 The ZF Receiver

In this case, from (8) we have the Shannon spectral efficiency $\eta$ [bit/s/Hz] for the ZF detection method as

$$\begin{aligned} \eta _{ZF} = \sum _{i=1}^{N} \text{log}_{2}(1+SNR_{i,ZF})=\sum _{i=1}^{N} \text{log}_{2} \left( 1+\frac{SNR_0}{N \cdot \sum _{j=1}^{M} \vert {q_{i,j}}\vert ^{2}} \right) . \end{aligned}$$

(15)

5.3 Capacity Results

Here we apply (14) and (15) to derive the capacities for the value $SNR_0=45$ dB, corresponding to $BER=10^{-4}$ in the reference SISO system with 8192-QAM modulation, different arrangements of the square arrays (Fig. 2), fixed the array side $d = d_{\text{opt}} \cdot SQF$ where $d_{\text{opt}} = 5.71m$ is the optimal array size for URA $2 \times 2$ at carrier frequency 23 GHz for link length $L = 5$ km and $SQF=0.25$, i.e. $d = d_{\text{opt}} \cdot 0.25=1.42$ m². Throughout the article, this SQF has been chosen as a reference value for a significant level of compactness, which leads to acceptable antenna array sizes in many installation for microwave back-hauling applications.³

Firstly, it has been verified that optimal array designs provide the theoretical multiplexing gain, multiplying the spectral efficiency of the reference SISO by the factor N. Table 1 reports the spectral efficiencies for compact arrays ($SQF = 0.25$) in the SVD case, confirming that this detection method maintains significant multiplexing gains, even if substantially reduced w.r.t. the multiplexing gain N of optimally designed arrays.

Table 1 Shannon capacity at $SNR_0=45$ dB for various LoS-MIMO configurations in the SVD case with $SQF=0.25$

A comparison between configuration $(1 \times 4) \times (1 \times 4)$ and $(2 \times 2) \times (2 \times 2)$ proves that, fixed the number $N=4$, LoS-MIMO based on URA arrays are clearly better than the system based on ULAs, passing from $\eta _{SVD} =34.24$ to $\eta _{SVD} =23.53$. From the analysis of the results in Table 1, it can also be seen that almost all the capacity is reached just with a MIMO $(2 \times 2) \times (2 \times 2)$. The spectral efficiency improvement obtainable by increasing the antenna elements, maintaining fixed the array size, does not justify the increased complexity. It is also significant to notice that configurations $(3 \times 3) \times (2 \times 2)$ and $(4 \times 4) \times (2 \times 2)$, both with $N=4$, have capacities slightly higher than $(3 \times 3) \times (3 \times 3)$, with $N=9$, and $(4 \times 4) \times (4 \times 4)$, with $N=16$. It is interesting to note that it appears not only useless but even counterproductive to increase the complexity and the costs for the deployment of a greater number of antennas, fixed the array size, as it does not change the number of the singular values significantly different from zero, which really contribute to the overall capacity. We report in Table 2 the singular values and the spectral efficiency of the corresponding sub-channels for the configuration $(2 \times 2) \times (2 \times 2)$ as a significant example.

Table 2 Singular values (SV) and capacities ($\eta$) at $SNR=45$ dB for LoS-MIMO $(2 \times 2) \times (2 \times 2)$

Table 2 does not report the results for ZF detection method as, due to the noise enhancement inherently present in ZF techniques, the ZF performance degrades heavily with sub-optimal antenna design. In this perspective, Fig. 5 shows the spectral efficiencies of ZF (dashed lines) and SVD (continuous lines) for different URA arrays as a function of the SQF value.

Fig. 5

Capacity at $SNR_0=45$ dB for LoS-MIMO with different URA type arrays vs SQF

The curves show that array configurations of LoS-MIMO with ZF receiver provide higher spectral efficiencies w.r.t. to SISO link, and still compeptitive w.r.t. SVD method, decreasing SQF from 1 till to 0.7, as long as there are 4 Tx antennas. For a greater number of Tx antennas (9 and 16) the performance tends to collapse even for higher SQF values and for $SQF<0.5$ the SVD scheme outperforms ZF. But, even if the ZF scheme would appear unfeasible for compact arrays from these results, as will be discussed later, its performance can be partially recovered taking into account the considerations on the RF amplifier setting. Coming back to Fig. 5, SVD configurations $(3 \times 3) \times (2 \times 2)$ and $(4 \times 4) \times (2 \times 2)$ always achieve slightly better results than $(2 \times 2) \times (2 \times 2)$, but, as already noted, not significantly better. SVD configurations $(3 \times 3) \times (3 \times 3)$ and $(4 \times 4) \times (4 \times 4)$ unfold their greatest potential starting from approximately $SQF=0.5$ and above. Finally it can be observed that configuration $(4 \times 4) \times (4 \times 4)$ is not better than the $(3 \times 3) \times (3 \times 3)$ even for $SQF=1$ and their multiplexing gain is significantly lower than N, respectively 16 and 9, as packing more antennas in a limited sized array with fixed side d the separation between antennas is very far from the optimum. Figure 6 shows the spectral efficiency of the configuration $(2 \times 2) \times (2 \times 2)$ fixed the array size $d=1.42$ m versus the link distance L m. It is obvious that the smaller L, the closer d is to the optimal separation $d_{\text{opt}}$ for the current link length L, as if we had an increasing effective SQF, shown by the dashed curve. At the distance $L=312.5$ m, $d=d_{opt}$ and $SQF = 1$, so the capacity reaches the theoretical maximum spatial multiplexing gain $N=4$.

Fig. 6

Capacity at $SNR_0=45$ dB for LoS-MIMO $(2 \times 2) \times (2 \times 2)$ at f=23 GHz vs link length L with $d=1.42$m, i.e. $SQF = 0.25$ w.r.t. reference link $L=5000$m. The effective SQF vs L is reported by the dashed black line

If we consider the poor performance of ZF detection for very compact arrays, including $SQF = 0.25$, we will show that ZF detection can provide still significant performance gain (albeit generally lower than the SVD method) by exploiting the "power reserve" that can be extracted from the RF amplifiers under the constraints of peak power and inter-modulation distortion that can be tolerated by the used modulation formats. From an engineering point of view, this aspect is of considerable importance. When $PCF>0$ dB, which occurs for ZF detection when streams are transmitted with a modulation format lower than 8192-QAM, the effective SNR increases by 1.5 dB for each bit reduction in the modulation order, according to the rules defined in 4.2. Consequently, the resulting higher spectral efficiency sometime leads to an acceptable performance even with the ZF receiver.

Figure 7 may help to explain what happens: the spectral efficiency $\eta$ and the total rate $R_{t}$ are shown vs the rate of the modulation format [bits/T] of the signal transmitted by each antenna. The figure also shows the two MIMO arrays arrangements $(1 \times 2) \times (1 \times 2)$ and $(2 \times 2) \times (2 \times 2)$ together with the increase of the effective SNR $\Delta SNR$ due to PCF rules ($\Delta SNR = 0$ corresponds to $SNR_0=45$ dB). The results in Fig. 7 highlight that:

• when the modulation rate is 13 bits/T and $\Delta SNR = 0$, $\eta < R_{t}$, so the full rates of 26 and 52 bits/T for the two MIMO arrangements cannot be reliably reached.

• By reducing the modulation format per antenna, the total target rate $R_{t}$ reduces accordingly. So it is possible to increase the Tx power (i.e. $\Delta SNR > 0$), according to PCF rules and $\eta$ increases.

• Starting from the crossing point between the respective $\eta$ and $R_{t}$ curves, $\eta$ becomes greater than $R_{t}$ and the reliable transmission of the corresponding $R_{t}$ becomes potentially achievable. Obviously, this should happen at a rate $R_{t}$ greater than the rate of the reference SISO (13 bits/T) and this is satisfied for both arrangements.

The results in Fig. 7 are coherent with the simulation results for these two MIMO configurations and ZF receiver, as it will be discussed in Sect. 6. It can be also seen that, the capacity of the MIMO $(2 \times 2) \times (2 \times 2)$ system is smaller than the MIMO $(1 \times 2) \times (1 \times 2)$ system till to a very high SNR, i.e. at very high $\Delta SNR$, and the MIMO $(2 \times 2) \times (2 \times 2)$ prevails. This can be explained by observing that the multiplicity of the streams is $N=4$ and $N=2$ respectively and the capacity grows, as the transmitted power increases, with a gain 4 instead of 2.

Fig. 7

Capacity $\eta$ and total target rate $R_t$ for ZF receiver vs the variation of the SNR due to PCF enabling. $SNR_0=45$ dB, $SQF=0.25$

6 Simulation Results

In this Section, the performance of LoS-MIMO array configurations are compared with the reference SISO through the average Bit Error Rate (BER) simulated by generating $1.5\cdot 10^{6}$ symbols per stream. The BER is simulated for each array configuration varying the total rate $R_t$ provided by the system measured in bits per symbol time T [bits/T]. Each figure in this Section reports in red the performance of the SISO system and in blue the performance of the LoS-MIMO array configurations closest to it. Moreover, the figures report the ZF detection performance with dashed lines and the performance obtained by SVD-based detection with power allocation and bit loading algorithm with continuous lines. Let us summarize the simulation assumptions:

• Our reference system is the uncoded SISO system with 8192-QAM modulation ($R_t =13$ bits/T), taken as the current state of the art for microwave links;

• The total transmitted power, common to all PAs, is fixed to  $P_0$, possibly modified by the PCF parameter;

• Given a value of the reference SISO $SNR_0$, the MIMO systems BERs are simulated for the ratio between the "nominal" total received signal power and the single antenna noise power $SNR=SNR_0$, where "nominal" means that the received power can vary according to the value of the PCF, as defined in Sect. 4.2;

• Unless otherwise indicated, the array arrangements refer to a compactness factor $SQF=0.25$ at frequency $f= 23$ GHz and link length $L = 5$ km (i.e. $d = 1.42$ m).

• The notation ’SVD’ refers to SVD detection using the proposed “iterative” bit loading algorithm. The notation ’SVD-Original’ denotes the original bit loading algorithm.

• The curves are parameterized according to the total rate $R_t$ [bits/T], i.e. the overall rate target: in the ZF case the total rate is divided equally among the transmitters, in the SVD case the iterative bit loading algorithm optimally distributes the rate and the power on the sub-channels in order to minimize the BER (equal on all the sub-channels) and to match the constraint on $R_t$. The algorithm can select rates (i.e. modulation formats) on the single sub-channel from $R_{max}=13$ bits/T (8192-QAM) down to 1 bits/T (BPSK).

Fig. 8

BER curves of LoS-MIMO $(1 \times 2) \times (1 \times 2)$ with $SQF=0.25$, unless otherwise specified, at different total rate $R_t$ [bits/T] with SVD (continuous lines), ZF (dashed lines) and PCF enabled. The blue color highlights the curves closest to SISO performance

Figure 8 reports the BER of the MIMO $(1 \times 2) \times (1 \times 2)$ case, with optimal antenna spacing $SQF = 1$ and sub-optimal $SQF = 0.25$. The curve with legend "26 bits/T SQF=1" means that the array size is optimized and the total rate $R_t$ is doubled w.r.t. the SISO rate. The ZF curves perfectly overlaps on the "SISO 13 bits/T" one, as expected, while the SVD method shows a degradation of about 2 dB, due to the presence of the precoding matrix, which modifies the PAPR at its output reducing the average power allowed to keep the peak within the Power Amplifier constraints. For the compact array with $SQF=0.25$ the results are reported for $R_{t} < 26$, namely 24, 22, 20, 18 and 16 bits/T. The figure allows a direct comparison with the reference SISO and between the two methods ZF and SVD, highlighting the performance degradation of compact MIMO schemes with respect to SISO. In general the performance of the scheme SVD is better than ZF at the same rate. Only with $R_t=26$ bits/T, ZF and SVD schemes have similar performance, but very poor for both and consequently of no interest. The combination 18 bits/T with SVD (blue curve) achieves a comparable performance with the reference SISO (13 bits/T) reaching $44 \%$ rate gain. On the other hand, we verified that the channel matrix has only two singular values (one very large and one very small). In general, it has been verified that for $SQF>0.5$, ZF is still competitive as it does not suffer from the power reduction due to the needed extra power peak, which affects the SVD method. On the contrary, for $SQF<0.5$, namely the $SQF<0.25$ of our examples, and when the capacity is lower than 26 bits/T, it benefits from the extra power made possible by the use of lower modulations on both streams, and the consequent lower sensitivity to the Inter-Modulation Distortion, reaching an acceptable performance in some cases.

Fig. 9

BER curves of LoS-MIMO $(1 \times 4) \times (1 \times 4)$ with $SQF=0.25$ at different total rate $R_t$ [bits/T] with SVD (continuous lines), SVD-Original ( dashed lines) and PCF enabled. The blue color highlights the curves closest to SISO performance

Figure 9 shows the results for another ULA arrays configuration, i.e. $(1 \times 4) \times (1 \times 4)$. This case is particularly interesting for highlighting the limits of the bit loading algorithm [13] compared to the proposed iterative bit loading one. The two algorithms have equivalent performance only at total rate 16 bits/T (the curves are overlapping in the figure). The achievable spectral efficiency that approaches the SISO BER performances is again about 18 bits/T, and consequently there is no substantial increase w.r.t. the previous case with only two antennas per array, as already observed from the Shannon’s theoretical capacity. Likewise, it can be concluded that ULA arrays with more than two antennas are unable of providing further increases in spectral efficiency with these compact array sizes. ZF curves are not shown, as their performance is poor even at 16 bits/T: in this case the power recovery due to the PCF is not sufficient to provide a satisfactory performance.

Fig. 10

BER curves of LoS-MIMO $(2 \times 2) \times (2 \times 2)$ with $SQF=0.25$ at different total rate $R_t$ [bits/T] with SVD (continuous lines) detection, ZF (dashed lines) equalization and PCF enabled. The blue color highlights the curves closest to SISO performance

Figure 10 shows the BER results for the $(2 \times 2) \times (2 \times 2)$ arrangement, which outperforms the $(1 \times 4) \times (1 \times 4)$ configuration, as already seen. In this case, given the profile of the eigenvalues, the original and the iterative loading algorithms are almost equivalent, with the exception of the 28 bits/T case. The curve for 28 bits/T ’SVD-Original’ has been reported here to highlight how the original bit loading algorithm [13] performs worse than the proposed iterative one for some combinations of eigenvalues and total required rate. The $(2 \times 2) \times (2 \times 2)$ SVD with the proposed iterative bit loading algorithm provides $R_t = 25$ bits/T at the SISO BER performance. As the number of elements in the arrays increases, better results are obtained as already observed from the Shannon theoretical capacities. The practical results, as resulting from the simulations, show differences with respect to the theoretical behavior: as an example, the MIMO (4×4)×(4×4) performs better than MIMO (4×4)×(2×2), differently from the Shannon capacity calculation. The explanation is that the bit loading algorithm, namely the quantization effects on the available rates, and the transmitted power correction (PCF) may be more or less beneficial according to each specific case.

Fig. 11

BER curves of LoS-MIMO $(3 \times 3) \times (3 \times 3)$ (dashed lines) and $(4 \times 4) \times (4 \times 4)$ (continuous lines) with $SQF=0.25$, for SVD detection at different total rate $R_t$ [bits/T] with PCF enabled. The blue color highlights the curves closest to SISO performance

Fig. 12

BER curves of LoS-MIMO $(3 \times 3) \times (2 \times 2)$ (dashed lines) and $(4 \times 4) \times (2 \times 2)$ (continuous lines) with $SQF=0.25$, for SVD detection at different total rate $R_t$ [bits/T] with PCF enabled. The blue color highlights the curves closest to SISO performance

The results are shown in Fig. 11 for SVD detection: looking at the blue curves, which approach the SISO BER performance, we can observe that, compared to $(2 \times 2) \times (2 \times 2)$ array arrangements, the $(4 \times 4) \times (4 \times 4)$ scheme gains about 4 bits/T, and $(3 \times 3) \times (3 \times 3)$ about 2 bits/T. It is interesting to notice also that the performance with only 4 transmitters at the external vertices of the arrays, i.e the cases $(3 \times 3) \times (2 \times 2)$ and $(4 \times 4) \times (2 \times 2)$ (Fig. 12), is close to the performance achievable with more antennas at the transmitter, i.e. $(3 \times 3) \times (3 \times 3)$ and $(4 \times 4) \times (4 \times 4)$, except in the 36 bits/T case, which is a case with huge BER degradation and consequently of no interest. This latter result is coherent with the Shannon capacity computations (Table 1), while the former is due again to the bit loading quantization and PCF impacts. We remark that this is an interesting result from a practical point of view, since the reduction of the number of RF transmitters has a clear positive impact on costs and complexity.

Finally, the impact of the PCF is variable: in general, in the presence of precoding with SVD detection, the power may be reduced up to $2-4$ dB if the maximum modulation assigned to at least one stream is equal to the reference SISO one. Conversely, with ZF detection there is a power increase of 1.5 dB each time the modulation format is reduced by one bit/T starting from the 13 bits/T SISO rate.

7 Conclusions

In this article we have studied LoS-MIMO $M \times N$ schemes with an emphasis on the practical applicability of such systems in real microwave radio links. Therefore, we focused on a series of very compact antenna arrays with square shape and side d, after identifying the size of the arrays as the determining factor for the limited diffusion of such systems. The compactness factor has been chosen as $SQF=0.25$, one fourth of the optimal design for the classical MIMO $2 \times 2$ at $f=23$ GHz for $L=5$ km link length, i.e. $d =1.42$ m. The performance in terms of spectral efficiency on a single polarization is compared with a state-of-the-art SISO system, characterized by 8192-QAM modulation format (total rate $R_t=13$ bits/T). We derived the theoretical capacities for two detection methods, Zero Forcing and the one based on Singular Value Decomposition, concluding that the latter is the viable way for justifying the greater complexity of a MIMO system. Moving towards the practical application of the SVD method, for a channel matrix with high condition number, i.e. great variability in the eigenvalues as in compact arrays, we propose a smart algorithm for bit loading and power sharing. Another relevant aspect of the study is the inclusion of the impact of RF power amplifiers settings, characterized by constraints regarding both the Inter-Modulation Distortion level of the underlying modulation as the Peak to Average Power Ratio at the output of the precoding matrix, for SVD detection. The detection based on ZF has shown a particular benefit from the Power Correction Factor provided by the Power Amplifier working point, while the detection based on SVD and bit loading algorithm is generally penalized. Finally, comparing the achievable spectral efficiencies in the most promising MIMO schemes, identified as those with the same level of availability of the reference SISO rate, we have conservatively achieved the results summarized in Table 3. The scheme $(2 \times 2) \times (2 \times 2)$ is confirmed as the best candidate for LoS-MIMO systems even with a reduced array size, thanks to its improved spectral efficiency and its reasonable complexity. In a future study, a more in-depth analysis of the effects of inter-modulation distortion noise could be interesting in order to quantify more accurately the degradation due to PA limitations.

Table 3 Achievable Spectral Efficiencies in LoS-MIMO links: 23 GHz, $L=5000$ m, $SQF=0.25$, $d = d_{\text{opt}}\cdot SQF=1.42$ m