1 Introduction

Densification of base stations (BSs) is a promising approach towards achieving the goals of 5G as it enhances the capacity of the network and improves link quality, since the distance between users and BSs is decreased. However, this densification increases the level of inter-cell interference. To mitigate inter-cell interference, 3GPP introduced the concept of coordinated multipoint transmission (CoMP) in Release 11 for the 4th generation (4G) wireless networks. Basically, CoMP can be divided into two different categories: joint transmission CoMP (JT-CoMP) and coordinated scheduling/beamforming CoMP. This work focuses on JT-CoMP where a user equipment (UE) is connected to multiple BSs. The strength of JT-CoMP is not only the elimination of the strong interfering signal(s) but also the conversion of interfering signal(s) into useful signals. This powerful feature of JT-CoMP helps to mitigate inter-cell interference, while improving the signal to interference plus noise ratio (SINR) and cell-edge throughput. 5G networks are expected to implement JT-CoMP since it can play a crucial role in tackling inter-cell interference which is a key concern in dense 5G and beyond wireless cellular systems [1].

The purpose of this paper is to develop a user-centric JT-CoMP clustering approach that can enhance the SINR gain without wasting radio resources and also to develop a multi-cell resource allocation scheme that can support JT-CoMP networks. Joint user-centric clustering and allocation of radio resources are performed in two phases. In the first phase, the cluster of each user is identified by the traditional PLD scheme or the proposed algorithm. Based on the obtained clustering results, resources from multiple BSs are assigned. This work aims to enhance edge throughput without reducing the total network throughput.

The following lists the main contributions of this work:

  1. (1)

    A novel user-centric clustering approach that can provide an effective balance between SINR improvement and bandwidth wastage is proposed. Besides providing this balance, the developed user-centric clustering approach can be used to find the maximum user-centric cluster size.

  2. (2)

    A novel multi-cell JT-CoMP radio resource management scheme is developed. The proposed resource allocation scheme solves the JT-CoMP mismatching resources problem where one BS has a higher number of resource blocks (RBs) for the CoMP region than a cooperating BS by letting the two cooperating BSs negotiate and agree on the number of RBs that they can provide for their CoMP region. It also describes how the total available bandwidth can be divided among CoMP and non-CoMP regions.

  3. (3)

    Evaluation of the effect of assigning different portions of bandwidth to CoMP users on the performance of CoMP and non-CoMP users.

The rest of the paper is organised as follows. A literature review on the recent advances on JT-CoMP is presented in Sect. 2. Section 3 describes the system model. In Sect. 4, the traditional and the proposed user-centric JT-CoMP clustering algorithms are presented. Section 5 provides the proposed multi-cell radio resource management scheme. Simulation results are presented in Sect. 6. Finally, Sect. 7concludes this work.

2 Related Work

The existing JT-CoMP research has shown the ability of JT-CoMP to improve the coverage area significantly [2,3,4,5]; nevertheless, JT-CoMP reduces the availability of RBs since a CoMP UE must be assigned identical PRB(s) from all of its cooperating BSs to transmit the same data, meaning that cooperating BSs are not allowed to reuse these PRB(s). Thus, it is essential to consider resource allocation when investigating the performance of JT-CoMP.

This work considers user-centric JT-CoMP clustering where each user is associated with a number of cooperating BSs. The work in [6] [7] has proved that the user-centric clustering approach achieves better average and cell edge throughput compared with static clustering. Significant user-centric JT-CoMP research has been carried out to find an optimal or near-optimal user-centric cluster size and to allocate radio resources efficiently in CoMP networks. However, the majority of the research work has addressed these two issues separately [6,7,8,9].

In [6], a user-centric clustering algorithm is developed to enhance the cell-edge throughput. This work developed optimal and low complex sub-optimal algorithms and it compared their average and cell-edge throughput performance with the static clustering scheme. Results showed that the proposed user-centric CoMP clustering algorithms are more efficient than static clustering in enhancing the average throughput and the throughput of cell-edge users. The authors in [7] proposed a user-centric clustering algorithm in a one-tier network in order to address inter-cell interference. The idea of the developed scheme is to let each UE measure the average path loss and decide its potential serving BSs. After this measurement, a UE forms its own cluster according to a given objective function that optimises the normalised goodput. Results proved that the proposed user-centric approach performs better than the static clustering approach. In [8], a user-centric CoMP clustering algorithm is proposed where a UE is served by the CoMP technique only if the second strongest power it receives is close in value to the power it receives from the strongest BS. The work in [9] developed a user-centric clustering approach to maximise energy efficiency in heterogeneous networks. In [10], JT-CoMP is applied to enhance the energy efficiency and overall throughput. The CoMP cluster of a UE is formed by choosing the two BSs that can achieve the maximum SINR. Results have demonstrated that cooperation can achieve up to 26% energy savings.

The work in [11] applied non-coherent JT-CoMP to reduce inter-cell interference in ultra dense heterogeneous networks where macro BSs are distributed hexagonally and small cell BSs are distributed based on Poisson Point Process (PPP). The authors analysed the coverage performance in the hexagonal-PPP network and it was proved that the JT-CoMP coverage probability decreases exponentially as the number of small cell BSs rises. Considering non-coherent transmission in PPP networks, the authors in [12] proposed a location-dependent cooperation approach where cell centre users, cell edge users, and cell corner users are connected to the strongest one, two, and three BSs, respectively. The sizes of the three areas are controlled by a cooperation level parameter \(n\) in the range of [0,1] where a value of 1 indicates full cooperation and a value of 0 indicates no cooperation. The results have shown that a moderate \(n\) value can enhance the signal-to-interference ratio (SIR) performance. The performance of user-centric clustering in vehicular networks is investigated in [13] where results have demonstrated that the implementation of user-centric clustering can significantly enhance connectivity. To mitigate interference in mmWave networks, user-centric clustering is implemented in [14] to allow users to connect to multiple BSs. As an analytical tool, stochastic geometry is utilized to analyse the average spectral efficiency as well as the coverage probability. Results have shown that user-centric clustering achieves better performance compared with static clustering and single BS association.

Besides the cell-centric approach, user-centric clustering has been applied in various wireless networks such as C-RAN [15, 16] and cell-free [17, 18] [19] wireless architectures. In [15], user-centric clustering is applied in a CoMP C-RAN network where results have shown the strength of CoMP in improving the performance of cell-edge users. Considering low latency and high spectral efficiency, a user-centric clustering algorithm is implemented in a C-RAN network where a user selects its own remote radio heads (RRHs) according to its specific delay requirements [16].

A cell-free network consists of a number of access points connected by front haul connections to central processing units (CPUs). Although a cell-free architecture has shown its superiority over the conventional cellular systems, it is impractical since it assumes that all BSs communicate and transmit data to all users. In practice, a user receives strong signal only from a sub-set of BSs in the network while the strength of the received signals from the rest of base stations is poor. As a result, it is crucial to develop efficient user-centric cell-free clustering approach where only a carefully selected number of base stations that promise to provide significant benefits to a user should be involved to serve this user. Recently, the authors in [17] proposed a deep reinforcement learning approach to simultaneously optimize the beamforming vectors of users and BS clustering in multiple access cell-free networks. Following the work in [20], base stations are divided into several clusters where each cluster forms an independent cell-free network. Based on the maximum long-term average received power, a Voronoi-based user-centric clustering approach is proposed in dense cell-less networks [18]. In [19], user-centric clustering is implemented in a multiuser cell-free network with the objective of optimizing power allocation, user scheduling and beamforming. In the proposed work, a user is associated with a RRH if the RRH provides an average channel power above a predefined threshold.

Though most of the research in the state-of-the-art has tackled user-centric clustering and radio resource assignment separately, some research has attempted to jointly address this clustering and radio resource assignment problem [21,22,23,24,25]. The authors in [21] proposed a two-step joint clustering/scheduling algorithm with the aim of balancing the load in multi-tier networks. The first step of the proposed algorithm utilises game theory to design a load-aware clustering approach. According to the clustering results obtained from the first step, the second step implements graph colouring to optimise utilisation of radio resources. The performance of joint user-centric JT-CoMP clustering and resource allocation in a single-tier network has been recently investigated in [24]. The main focus on the work in [24] was to investigate the influence of choosing a power level difference (PLD) value on the performance of CoMP and non-CoMP users. The results showed that choosing a proper PLD value as well as allocating radio resources efficiently can significantly improve the throughput of CoMP and non-CoMP users. Another recent work that has dealt with joint user-centric CoMP clustering and resource allocation is presented in [26]. In [26], JT-CoMP is applied in a control/data decoupled cell-less architecture where a macro BS handles control signaling whereas small cell BSs provide data. The authors in [23] applied JT-CoMP in control/data decoupled architecture with the objective of balancing the load. Following the work in [23, 27] developed a load balancing algorithm with the aim of reducing the number of users that obtain less than a certain data rate threshold.

Recently, the authors in [25] addressed joint user-centric clustering and resource assignment using graph coloring with the aim of maximising spectral efficiency. With the help of graph coloring, the user-centric clustering and resource allocation are solved independently. First, a user-centric clustering is constructed in three stages: anchoring, exploration, and confirmation. After the construction of the user-centric clusters, a two-stage graph-based resource assignment approach is developed. To reduce the interference at the cell expansion area in heterogeneous networks with biased user association, JT-CoMP has been applied in [28] to allow the two strongest BSs in terms of average received power to serve users located at the cell range expansion area. Results have shown that JT-CoMP can significantly improve the overall throughput and the throughput of cell range expansion users. Table 1 presents the notation that is used in this paper.

Table 1 Notation
Full size table

The following summarises the recent advances in JT-CoMP:

  • The work in [6,7,8,9] evaluated the user-centric CoMP clustering performance without considering the management of radio resources.

  • The majority of the research on JT-CoMP identifies CoMP users based on PLD [5, 6, 8, 23, 24, 26, 28].

  • Recent research [5, 23, 24, 26, 28] has considered joint user-centric clustering and radio resource assignment where identifying CoMP users is still based on PLD.

3 System Model

A downlink cellular network that consists of \(M\) macro base stations and \(U\) users is considered in this work. UEs and BSs are considered to be equipped with single antenna. UEs are distributed randomly in the region. Two modes of operations are considered: without CoMP and with JT-CoMP. In the no CoMP case, all UEs are connected to one BS only. In the JT-CoMP case, user-centric clustering is implemented where UEs decide whether they should operate in no-CoMP or CoMP mode. In the no-CoMP mode, a UE is connected to the BS that offers the strongest received power. If a UE decides to operate with CoMP, then it is connected to the \(m\) strongest BSs where \(m\) is the maximum cluster size. In this work, the maximum cluster size is limited to two because allowing more than two BSs to cooperate would require a very large SINR gain to achieve a rate gain that compensates for bandwidth wastage, as shown in Fig. 2. This work considers non-coherent joint transmission: cooperating BSs simultaneously transmit the same data to a particular UE without ensuring coherent combination at the user [29]. At the user side, the non-coherent signals are added resulting in received power gain. Non-coherent JT-CoMP is used because it eliminates the process of channel state information (CSI) exchange and its associated overhead. Implementing JT-CoMP without the knowledge of CSI restricts multi-user MIMO communications as well as distributed precoding; however, JT-CoMP can benefit from diversity gain [30,31,32,33]. Also, we have considered round robin scheduling algorithm which is channel independent. Round robin scheduling is a common resource allocation algorithm that is widely used by the wireless research community [34,35,36] as well as by 3GPP in its standardizations [37, 38].

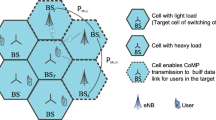
The downlink JT-CoMP system model is presented in Fig. 1. In this work, both the hexagonal deployment and the random deployment formed by the PPP modelling are considered. Although some work [8, 39] has assumed that the locations of macro BSs can be modelled as a PPP network, in practice, operators deploy macro BSs after careful planning [40, 41] with some restrictions due to geographical limitations [42]. In [40,41,42], it is argued that it is more practical to assume hexagonal deployment of macro BSs. This argument is also consistent with what 3GPP recommends [37].

Fig. 1
figure 1

System model

Full size image

Though pure PPP can capture the randomness in the deployment of macro BSs that may exist due to geographical factors, it is unrealistic since a number of macro BSs may be located close to each other. To consider a more realistic deployment which takes into account the correlation that exists during the network planning phase, the parent homogenous PPP is modified by implementing the repulsive dependent thinning resulting in a new PPP known as type II Matern Hard-core Point Process (MHPP) with a repulsion distance \(d\) [43].Compared with pure PPP, the work in [44] has demonstrated that MHPP is a more accurate spatial model that can represent the actual deployments of BSs.

The SINR that is received by \(UE_{k} { }\) is calculated as follows [23]:

$$ SINR_{u} = \frac{{P_{Tx} \mathop \sum \nolimits_{{i \in {\mathcal{C}}_{M}^{u} }} \left| {g_{ui} } \right|^{2} }}{{P_{Tx} \mathop \sum \nolimits_{{i \in {\mathcal{M} / \mathcal{C}}_{M}^{u} }} \left| {g_{uj} } \right|^{2} + \sigma^{2} }} $$
(1)

where \(P_{Tx}\) is the transmission power of BS \(i\), \({\mathcal{C}}_{M}^{u}\) is the cluster of UE \(u\), \(g_{ui}\) is the channel gain between UE \(u\) and BS \(j\) which is composed of path loss and shadowing, \(\sigma^{2}\) is the noise power. Long term received power levels are used to make clustering decisions; thus, fast fading averages out [23]. The SINR of a UE in (1) clearly depends on its cluster size. If a UE decides to operate as a CoMP UE with a cluster size larger than 1, then the dominant interference signal will be eliminated and converted into a useful signal resulting in a significant SINR gain.

Using Shannon’s equation, the achievable throughput is given as follows:

$$ T = B{\text{log}}_{2} \left( {1 + SINR} \right) $$
(2)

The outage probability is the probability where a UE’s SINR is below a specific threshold \(\theta \). It is mathematically expressed as follows:

$$ P(SINR < \theta ) $$
(3)

4 User-Centric Clustering

4.1 Traditional User-Centric Approach

In the traditional user-centric clustering scheme, a UE forms its own cooperative set of BSs relying on the average power it receives from neighboring BSs. If the second strongest received power, third strongest received power,…, \({m}^{th}\) strongest received power are comparable with the strongest received power, then a UE selects the \(m\) strongest BSs as its own cluster. The following illustrates the steps that a UE performs to choose its cluster when the maximum cluster size 2 (a similar approach has been used in [23]):

  1. (1)

    Each UE records the average received power from neighbouring macro BSs based on the following:

    $$ P_{um}^{rx} = P_{um}^{tx} \left| {g_{um} } \right|^{2} , m \in {\mathcal{M}} $$
    (4)

    where \(P_{um}^{rx}\) is the average received power of \(UE_{u}\) from \(BS_{m}\), \(P_{um}^{tx}\) is the power transmitted by \(BS_{m}\) to \(UE_{u}\), \(g_{um}\) is the channel gain between \(UE_{u}\) and \(BS_{m}\) which includes path loss and shadowing.

  2. (2)

    The set of average received powers of a UE are sorted as follows:

    $$ P_{u1}^{rx} > P_{u2}^{rx} > \ldots P_{uM}^{rx} $$
    (5)

    where \(P_{u1}^{rx}\) is the strongest power received by \(UE_{u}\), \(P_{u2}^{rx}\) is the second strongest power received by \(UE_{u}\) and so on.

  3. (3)

    Each UE compares its second strongest received power with its strongest received power. If its second strongest received power is close in value with the strongest received power, then a UE selects the strongest and second strongest BSs as its own cluster, otherwise a UE is connected only to the strongest BS. This received power comparison is known as PLD and it is mathematically written as follows:

    $$ \frac{{P_{u1}^{rx} }}{{P_{u2}^{rx} }} < \beta $$
    (6)

where \(\beta\) is the PLD value that identifies whether a UE should implement CoMP or not. The power level \(\beta\) is a threshold of choice between CoMP and non-CoMP mode because it can determine the relative strength between the strongest and second strongest received power. The power level \(\beta\) prevents users with marginal SINR gain from operating in CoMP mode which saves the available bandwidth from being wasted. This restriction enables efficient use of the bandwidth and as a result improves the capacity of the system. It is clear that a high PLD value allows more UEs to implement CoMP and vice versa. The selection of an effective PLD value is crucial as a small PLD value restricts some cell-edge UEs to be served only by the strongest BS though the second strongest BS can still cause harmful interference to these UEs. On the contrary, a large PLD value admits UEs that may not significantly improve their SINR if they operated in CoMP mode since the power they receive from the second strongest BS is negligible in comparison with the strongest BS. Moreover, allowing UEs with marginal SINR improvement to operate in CoMP mode would waste the bandwidth and as a consequence non-CoMP UEs would be left with fewer radio resources. This illustrates that it is crucial to choose an effective PLD threshold that can help to achieve SINR improvement without wasting bandwidth.

4.2 Proposed User-Centric Clustering Approach

A new user-centric clustering algorithm for JT-CoMP is proposed to achieve SINR improvement without wasting bandwidth. In the proposed user-centric algorithm, a UE forms its own cluster by comparing its SINR with and without CoMP. Throughout this work, we denote the SINR with CoMP and SINR with no CoMP as \(SINR^{CoMP}\),\( SINR^{nonCoMP}\), respectively. In \(SINR^{CoMP}\), the most dominant interfering signal caused by the second strongest BS becomes a useful signal. To guarantee an effective balance between SINR improvement and bandwidth wastage, the reduction in radio resources caused by implementing JT-CoMP must be compensated for by the \(SINR^{CoMP}\) gain. In other words, the rate that a UE achieves when it operates in CoMP mode must be at least equal to \(\gamma\) times the rate it achieves with no CoMP. This is mathematically expressed as follows:

$$ {\text{log}}_{2} \left( {1 + SINR_{u}^{CoMP} } \right) \ge \gamma {\text{log}}_{2} \left( {1 + SINR_{u}^{nonCoMP} } \right) $$
(7)

where \(\gamma\) is the rate gain that can be achieved when a UE operates in the CoMP mode. \(\gamma\) can also represent the user-centric cluster size as a UE that is served by \(\gamma\) cooperative BSs must at least achieve \(\gamma\) rate gain to balance the SINR improvement and loss of bandwidth. The system performance will degrade if a UE is served by \(\gamma\) BSs and the resultant rate gain is less than \(\gamma\). The value for parameter gamma is set based on the cluster size. If we limit the maximum cluster size to be 2, the value for parameter gamma is then set to be 2 as well. This is because when a user is served by two BSs, it must at least achieve two times the rate when it operates in CoMP mode.

By using (7), the minimum \(SINR^{CoMP}\) that can achieve \(\gamma\) rate gain can be found as follows:

$$ 2^{{log_{2} \left( {1 + {\text{SINR}}_{u}^{CoMP} } \right)}} \ge 2^{{\gamma log_{2} \left( {1 + {\text{SINR}}_{u}^{nonCoMP} } \right)}} $$
(8)
$$ {\text{ SINR}}_{u}^{CoMP} \ge \left( {1 + {\text{SINR}}_{u}^{nonCoMP} } \right)^{\gamma } - 1 $$
(9)

Figure 2 shows the minimum \(SINR^{CoMP}\) values that can satisfy the requirement in (9) in order to achieve different rate gains ranging from 2 to 8. Allowing a UE to be served by 8 BSs as in [7, 21, 23, 29] can result in significant SINR gain; however this SINR gain may still not compensate the loss of bandwidth since 8 BSs will have to reserve identical RBs to serve this particular UE. As seen from Fig. 2, if the SINR with no CoMP of a UE is 0 dB, its SINR with CoMP must be at least 4.8 dB, 11.8 dB, 18 dB, and 24 dB in order to achieve rate gains of 2, 4, 6, and 8 respectively. It is clear that allowing more than 2 BSs to cooperate requires extreme SINR gain in order to achieve a rate gain that can compensate the loss of bandwidth. It is also observed that a UE must achieve higher than 25 dB when it operates in CoMP mode in order to achieve 2, 4, 6, and 8 rate gains if its SINR with no CoMP is higher than 12 dB, 6 dB, 2 dB, and 0 dB respectively.

Fig. 2
figure 2

Minimum \({\varvec{SINR}}^{{{\varvec{CoMP}}}}\) to achieve rate gains ranging from 2 to 8

Full size image

The proposed user-centric algorithm where a UE forms its own cluster of BSs is presented in Algorithm 1. The traditional and the proposed algorithms are user-centric algorithms where a user forms its set of BSs. Since a UE forms its own cluster by measuring the average received power, the cluster size changes according to the measurement of the average received power.

figure e

The computational complexity of the proposed user-centric clustering algorithm is compared with the traditional PLD algorithm. Since both algorithms include steps 2 and 3 in Algorithm 1, those steps are not considered in the computational complexity analysis. The complexity of the PLD approach and the proposed algorithm with a maximum cluster size of \(C\) can be computed as \(\mathcal{O}(UC)\) and \(\mathcal{O}(UC)\), respectively. When the maximum cluster size is restricted to 2, the complexity of the PLD approach and the proposed approach reduces to \(\mathcal{O}\left(2U\right)\) and \(\mathcal{O}\left(2U\right),\) respectively. This further reduces to \(\mathcal{O}\left(U\right)\) for both the PLD algorithm and the proposed algorithm when the maximum cluster size is 2. From the computational complexity analysis, it is clear that limiting the number of cooperating BSs to 2, as in this work, reduces the complexity. Also, the complexity of the proposed algorithm is comparable with the complexity of the traditional PLD algorithm.

5 Radio Resource Management

In a JT-CoMP system, a multi-cell radio resource management scheme is needed to satisfy not only CoMP users but also non-CoMP users. Effective schemes are not available up to now. Assigning a high proportion of bandwidth for CoMP UEs will boost their throughput; nevertheless, this will decrease the bandwidth for non-CoMP UEs causing their throughput to significantly drop. Moreover, assigning a high proportion of bandwidth for non-CoMP UEs will enhance their throughput; however, the throughput of CoMP UEs will clearly decrease. Thus, developing a multi-cell radio resource allocation technique that can support JT-CoMP UEs is required to balance resource assignment between no CoMP and CoMP UEs. One approach that attempts to provide this balance is to assign CoMP users half of the radio resources that a no CoMP UE would be assigned. We refer to this approach as a half bandwidth assignment. This assignment is considered quite fair for two reasons. The first is that it is anticipated that the SINR of CoMP users will significantly increase while the second is that a RB that is assigned to a CoMP UE by one of its cooperating BSs (strongest BS) is restricted from being reused by any other BS in its cluster (the second strongest BS). Although half bandwidth assignment appears to be reasonably fair, there is currently no proof that it is an optimal assignment. Therefore, it is important to investigate assigning different portions of bandwidth for CoMP users. For example, compared to the number of RBs that a no CoMP UE would obtain, a CoMP UE can be assigned a different fraction of RBs compared with the RBs assigned as a no CoMP UE, i.e. full bandwidth.

5.1 Challenges of Resource Allocation in User-Centric JT-CoMP

Multi-cell JT-CoMP radio resource management is a challenging task since it involves assigning radio resources from multiple BSs. This multi-cell assignment induces three resource allocation restrictions in user-centric JT-CoMP:

  1. (1)

    A resource block (RB) that is allocated to a UE by one BS of its cluster cannot be reused by any other BS in the same cluster. This restricts the usage of the same resource block from the cooperating BS to serve another user (not the intended user); however, two BSs can utilise the same resource block (JT-CoMP) to serve a typical user which is consistent with Eq. (1).

  2. (2)

    All BSs that form a UE’s cluster must reserve an identical number of RBs for this UE, in order for JT-CoMP to operate. In other words, a PRB that is used by one BS of a UE’s clusters cannot be reused by another BS in the same cluster. This reduces the frequency reuse to a factor of \(C\) where \(C\) is the cluster size. For example, if all users are allowed to operate with JT-CoMP and the maximum cluster size is set to be 5, then the frequency reuse reduces to 5. (This problem can be reduced by allowing only a certain percentage of users to operate in CoMP mode and also by assigning CoMP users fewer radio resources compared to those assigned to a non-CoMP user).

  3. (3)

    Due to load unevenness and the different numbers of CoMP regions a BS may have, one BS may have fewer radio resources to support a specific CoMP region while the other cooperating BSs supporting the same CoMP region have more radio resources. This resource mismatch clearly restricts the radio resources that can be used to support CoMP users. This problem must be addressed to enable all CoMP UEs to be supported.

5.2 Resource Matching Approach

This part focuses on addressing the resource mismatching problem that occurs when allocating resources from multiple BSs. An example that illustrates how the different loads of each BS and different CoMP regions of each BS cause a mismatch in the number of RBs that two cooperating BSs can provide for their CoMP region is shown in Fig. 3. Figure 3 shows that BS 1 and BS 2 have different loads (number of users) and different CoMP regions, thus the bandwidth that BS 1 can provide for its overlapping region with BS 2 is different from the bandwidth that BS 2 can provide for the same region. For CoMP region 1, the example shows that BS 1 is able to provide 40 RBs while BS 2 can only provide 25 RBs. This resource mismatching problem in the number of RBs that can be provided by two cooperating BSs for their CoMP region must be considered when implementing JT-CoMP.

Fig. 3
figure 3

An example of resource mismatching for CoMP regions

Full size image

To solve this mismatching issue, a resource matching approach is proposed where both BSs need to negotiate and agree on the amount of bandwidth that each BS should provide. Since one BS may have a smaller number of available RBs than its cooperating BS, both BSs should agree to provide a bandwidth that is equal to the minimum affordable bandwidth of both BSs. This is mathematically explained in Algorithm 2 from step 8 to step 15. This strategy will ensure that the two cooperating BSs have perfect matching in terms of the offered bandwidth allowing them to reserve identical RBs to support their CoMP region. Due to this proposed allocation, the BS that offers a larger bandwidth will be left with a portion of bandwidth that is not used to support the CoMP region. To efficiently utilise this unused portion of bandwidth, we allocate this bandwidth to non-CoMP users that belong to the BS with higher available bandwidth. To further illustrate this concept, an example is provided in Fig. 4. In Fig. 4, BS 1 and BS 2 are two cooperating BSs that jointly transmit data to some particular users located in their overlapping region. BS1 communicates with BS 2 informing it that it has 40 available RBs. Also, BS2 sends a message to BS1 informing that it has 25 RBs. Each BS then agrees to provide the minimum offered bandwidth of BS 1 and BS 2. In this particular example, BS 1 and BS 2 agree to provide 25 RBs each. Since BS 1 will be left with 15 unused RBs (40 RBs—25 RB), BS 1 allocates those RBs for its non-CoMP users.

Fig. 4
figure 4

An example solved by the resource matching approach

Full size image

The hardware complexity of the proposed multi-cell approach is similar to the complexity of the 3GPP Almost Blank Subframes (ABS) scheme since both techniques require cooperating base stations to communicate and exchange information. In ABS schemes, macro base stations communicate with small cells via × 2 interface informing them about the ABS pattern. A similar approach can be implemented in the proposed multi-cell scheme to allow communication between cooperating base stations to agree on the number of RBs that each base station can offer.

5.3 Bandwidth Allocation

This part explains how the total bandwidth can be used to support both no CoMP and CoMP UEs. When CoMP is implemented, each BS can have no-CoMP and CoMP UEs. No-CoMP UEs are typically UEs that belong to the cell-center area whereas the CoMP users are the UEs that are inside the overlapping area. The overlapping area can be identified either by the PLD approach or by the proposed user-centric clustering approach. In the PLD scheme, if a UE can satisfy the requirement in (6) then it belongs to the overlapping area (CoMP user) else it belongs to the cell-center area (non-CoMP user). This overlapping area identification is similar in the proposed user-centric clustering approach but users in the proposed approach need to satisfy the requirement in Eq. (9).

The following explains how each BS can identify its no-CoMP and CoMP UEs. Each BS considers all UEs in its overlapping regions as its CoMP users without taking into account if this BS provides the strongest or second strongest received power. Also, each BS considers the remaining UEs that are outside the overlapping regions as its non-CoMP UEs.

The bandwidth of \(BS_{m}\) is split into non-CoMP bandwidth \(B_{m}^{non - CoMP}\) and CoMP bandwidth \(B_{m}^{CoMP}\) as follows:

$$ BS_{m}^{non - CoMP} = \frac{{B_{m} }}{{\left( {\left| {{\mathcal{N}}_{U}^{m} } \right| + \left( {b\left| {{\mathcal{Q}}_{U}^{m} } \right|} \right)} \right)}}\left| {{\mathcal{N}}_{U}^{m} } \right| $$
(10)
$$ BS_{m}^{CoMP} = BS_{m} - BS_{m}^{non - CoMP} $$
(11)

where \(b\) is the proportion of resources a CoMP UE would be assigned when it operates in CoMP mode compared to those it obtains with no CoMP. For instance, with \(b = 0.5\), if a UE that operates with no CoMP is allocated 8 RBs, it would be assigned 4 RBs if it chooses to use CoMP. \(BS_{m}^{CoMP}\) is the CoMP bandwidth of \(BS_{m}\) that should support all the CoMP regions that \(BS_{m}\) is involved in. Thus, \(BS_{m}^{CoMP}\) is further split into \(L \) portions where \(L\) is the number of CoMP regions of \(BS_{m}\). The following expresses how the CoMP bandwidth of \(BS_{m}\) is divided among its CoMP regions:

$$ B_{ml}^{CoMP} = BS_{m}^{CoMP} \frac{{\left| {{\mathcal{D}}_{U}^{ml} } \right|}}{{\left| {{\mathcal{Q}}_{U}^{m} } \right|}} $$
(12)

Algorithm 2 illustrates the proposed multi-cell bandwidth allocation that can support JT-CoMP networks.

figure f

5.4 Impact of JT-CoMP on Load of BSs

The load per BS increases when JT-CoMP is implemented since each BS will serve not only the UEs it provides with the strongest received power as it does with no CoMP but it will also serve the UEs it provides with the second strongest received power. Figure 5 provides an example where it is shown how JT-CoMP increases the load per BS. To illustrate the influence of JT-CoMP on the load of BSs, some potential load distributions are presented in Fig. 5. In Fig. 5a, BS 1 and BS 2 have 6 and 4 UEs with no CoMP, respectively. When CoMP is applied, the load of BS 1 becomes 7 UEs since the UE that is served by BS 2 with no CoMP operates now in CoMP.

Fig. 5
figure 5

Some potential load distributions in JT-CoMP

Full size image

mode and it needs to be served jointly by BS 1 and BS 2. Similarly the load of BS 2 will increase from 4 UEs with no CoMP to 7 UEs with CoMP. It is clear that JT-CoMP has a direct influence on the load of BSs. Considering a full bandwidth assignment where a CoMP UE obtains the same amount of bandwidth as a non-CoMP UE and also considering the proposed resource matching approach described in section V(B), the non-CoMP UEs of BS 1 will obtain slightly fewer RBs since there is only one extra UE that needs to be served by BS 1. Although BS 2 needs help from BS 1 to jointly serve one of its UEs, BS 1 will require BS 2 to jointly serve 3 of its UEs. As a result, the non-CoMP UEs of BS 2 will be left with fewer radio resources. This scenario shows that both non-CoMP UEs of BS 1 and BS 2 need to sacrifice a certain amount of bandwidth to enhance the throughput of the CoMP UEs. Figure 5b shows the same scenario of load distribution as in Fig. 5a except that BS 1 has only one non-CoMP user. Since BS 1 can support a higher bandwidth for the CoMP region as it has fewer non-CoMP UEs compared with BS 2, it will have to match the bandwidth provided by BS 2 to support the CoMP region. After resource matching, the CoMP bandwidth that BS 1 did not utilise will be reallocated to the non-CoMP UE of BS 1. The non-CoMP user of BS 1 will achieve significantly higher throughput compared with that with no CoMP. In Fig. 5c, BS 2 can provide higher bandwidth for the CoMP region as it has fewer non-CoMP UEs compared with BS 1. Although BS 2 will reallocate the unused amount of CoMP bandwidth to its non-CoMP UE, this UE still achieves higher throughput with no CoMP as the unused CoMP bandwidth allocated for this UE is not large. In other words, the amount of bandwidth this UE is assigned when CoMP is implemented is less than the bandwidth it obtains with no CoMP, even if it still obtains a bandwidth bonus via the resource matching approach.

6 Results and Discussion

The performance of the proposed joint user-centric CoMP clustering and multi-cell radio resource management scheme is evaluated by performing snapshot simulation using MATLAB.

To compare the JT-CoMP performance against no CoMP, all UEs first operate without CoMP and then CoMP is applied for the same user set. This clearly allows the effect of the implementation of CoMP on UEs to be demonstrated. To obtain accurate statistical data, 100 snapshots are carried out.

We compare the performance of JT-CoMP in hexagonal and random deployments. In the first case, macro BSs are deployed hexagonally in an area 6 km × 6 km with an inter-site distance of 500 m. In the random deployment, we consider a repulsive PPP deployment with a hard core distance of 189 m. According to actual macro BS locations obtained from TELUS (one of the main Canadian operators [45, 46]), the nearest neighbour distance of macro BSs is 189 m. Following this real BS distribution, we consider the minimum separation distance between two BSs to be 189 m. For fair comparison, the density of BSs in the repulsive PPP deployment is 8 BSs/km2 which is equivalent to an inter-site distance of 500 m in hexagonal deployment located in an area 6 km × 6 km. UEs with a density of 120 users/km2 are randomly deployed over the same area. BSs and UEs are equipped with a single antenna. For JT-CoMP, non-coherent joint transmission is assumed. When JT-CoMP is implemented, the maximum user-centric cluster size is set to 2. There are two main reasons to limit the number of cooperating BSs to 2. First, as shown in Fig. 2, allowing more than two BSs to cooperate requires extremely high SINR gain in order to compensate for the bandwidth loss. From Fig. 2, if a user achieves a 5 dB SINR with no CoMP, it must achieve at least 18.5 dB when it operates with three ways CoMP in order to compensate for the bandwidth loss. This SINR gain is clearly hard to achieve. Another reason for not allowing three or more BSs to cooperate is because of the unevenness that happens due to load imbalance among BSs. This problem reduces the available bandwidth for CoMP users as all cooperating BSs except the BS with the minimum CoMP bandwidth cannot use their full CoMP bandwidth to support their overlapping CoMP region. The BS with the minimum CoMP bandwidth clearly restricts the benefit available from JT-CoMP. In the case of a cluster size of 2 and a significant load imbalance among cooperating BSs, a CoMP user might perform better if it were to operate in non-CoMP mode. Obviously, allowing more than two BSs to cooperate increases the load unevenness level which further restricts cooperating BSs from supporting their CoMP regions. Also, we set the PLD value to be 5 dB, 10 dB and 15 dB while the rate gain of the proposed user-centric clustering algorithm is set to be 2. The simulation parameters are summarised in Table 2.

Table 2 Simulation parameters
Full size table

The results comparing the performance of a hexagonal deployment and a random deployment for Figs. 6, 7, 8, 9, 10, 11, 12, 13 are performed; however, we include the results only for the hexagonal case to improve the readability of the Figures and to avoid repeating results that show almost the same performance behavior. Comments on the results obtained for the random case are provided. The results for Figs. 14 and 15 are included for both cases. According to the random deployment results obtained for Figs. 6, 7, 8, 9, 10, 11, 12, 13 which are not shown in the paper, the proposed approach still achieves better average throughput and cell-edge throughput compared with the traditional PLD scheme when a repulsive PPP network is considered. Also, the behavior of the traditional PLD approach and the proposed approach is the same as in the hexagonal deployment. The only difference is that JT-CoMP performs slightly better in random deployments. For instance, when b = 1, the proposed algorithm improves the throughput of 66% of users in random deployment while only 62% of users improve their throughput in the case of hexagonal deployment.

Fig. 6
figure 6

SINR of fixed cluster sizes including a cluster size of 1 (no CoMP) and cluster sizes of 2, 4, 6, and 8

Full size image
Fig. 7
figure 7

Percentage of non-CoMP and CoMP UEs for different PLD thresholds

Full size image
Fig. 8
figure 8

SINR with and without user-centric JT-CoMP for the traditional PLD approach and the proposed approach

Full size image
Fig. 9
figure 9

Percentage of no CoMP and CoMP UEs for different rate gain

Full size image
Fig. 10
figure 10

User throughput (\({\varvec{b}} = 0.5)\) without JT-CoMP, with JT-CoMP (PLD approach) and with JT-CoMP (proposed approach)

Full size image
Fig. 11
figure 11

Cell edge throughput (\({\varvec{b}} = 0.5)\) without JT-CoMP, with JT-CoMP (PLD approach) and with JT-CoMP (proposed approach)

Full size image
Fig. 12
figure 12

User throughput (\({\varvec{b}} = 1)\) without JT-CoMP, with JT-CoMP (PLD approach) and with JT-CoMP (proposed approach)

Full size image
Fig. 13
figure 13

Cell edge throughput (\(b = 1)\) without JT-CoMP, with JT-CoMP (PLD approach) and with JT-CoMP (proposed approach)

Full size image
Fig. 14
figure 14

Proportion of “winners” and “losers” as a percentage of the user population in hexagonal and random deployments, where a “winner” is a user that applies CoMP and achieves at least two times rate improvement

Full size image
Fig. 15
figure 15

Percentage of UEs that achieve a rate gain that is higher than the cluster size in hexagonal and random deployments

Full size image

Figure 6 shows the outage probability with fixed user-centric clustering CoMP and with no CoMP. In fixed user-centric clustering CoMP, all UEs operate in CoMP mode where each UE chooses the \(m\) strongest BSs, where \(m\) is the cluster size. As Fig. 6 shows, JT-CoMP can significantly improve the SINR. This is expected as JT-CoMP utilizes the dominant interfering signal as a useful signal. It is also obvious that higher SINR gain is achieved as the cluster size increases. Although allowing all UEs to work with CoMP results in significant SINR gain, the frequency reuse decreases from 1 to \(m\) where \(m\) is the cluster size.

To balance the SINR gain and loss of radio resources, only certain UEs should operate in CoMP mode. The UEs that should implement CoMP can be identified by using the traditional PLD approach or by the proposed user-centric clustering approach. Figure 7 illustrates the percentage of non-CoMP and CoMP UEs when the PLD is varied from 0 to 15 dB. When the PLD threshold is 0 dB, all UEs work with no CoMP. In this case, the system acts as a system with no CoMP. Increasing the PLD from 0 to 15 dB will decrease the number of no-CoMP UEs and the number of CoMP UEs will increase. This is because more UEs can meet the requirement in (6) when the PLD threshold is high. Figure 8 shows the outage probability with user-centric JT-CoMP clustering and with no CoMP. The outage probability of JT-CoMP in this case is different from that in Fig. 6 as UEs need to choose whether to operate with or without CoMP based on the PLD user-centric clustering approach or the proposed user-centric clustering approach. Figure 8 shows that 69% of UEs achieve an SINR greater than 0 dB with no CoMP. By utilizing JT-CoMP, a significant SINR gain is expected as JT-CoMP can convert harmful signal(s) into useful signal(s). As Fig. 8 illustrates 88%, 92%, and 92% of UEs can achieve an SINR higher than 0 dB when the PLD threshold is 5 dB, 10 dB, and 15 dB, respectively. For the proposed user-centric clustering algorithm with a rate gain of 2, the percentage of UEs that can attain an SINR greater than 0 dB is 82%. It is evident that implementing JT-CoMP significantly improves the SINR. A PLD threshold of 10 dB achieves higher SINR gain in comparison with a PLD threshold of 5 dB since this increases the percentage of JT-CoMP UEs. As shown in Fig. 7, the percentage of JT-CoMP UEs when the PLD threshold is 5 dB and 10 dB is 35% and 62%, respectively: 27% more UEs will benefit from operating in JT-CoMP mode in terms of SINR gain when the PLD threshold is 10 dB. Increasing the PLD threshold from 10 to 15 dB provides only minor improvement in SINR. This is because the UEs whom PLD threshold is between 10 and 15 dB (16% of UEs as shown in Fig. 7) are not significantly benefited by JT-CoMP, since their second strongest BS is relatively weak compared with their strongest BS. Generally, increasing the PLD value improves the SINR. In the proposed user-centric clustering algorithm, the percentage of UEs that can obtain higher than 0 dB is 82%. As Figs. 6 and 8 have shown, the SINR gain depends on the user-centric clustering size and it also depends on the user-centric clustering algorithm. In addition, the SINR gain is also dependent on the PLD value.

Figure 9 illustrates the percentage of no-CoMP and CoMP UEs when the proposed user-centric JT-CoMP clustering approach is applied. The rate gain \(\gamma \) that decides how many UEs should work with CoMP is varied from 1 to 5.5. When the rate gain is 1, all UEs in the system will implement CoMP. This is analogues to a system where all UEs are allowed to work with CoMP without the need to satisfy the PLD requirement in (6) or the proposed requirement in (9).

Increasing the rate gain will reduce the number of CoMP UEs and increase the number of non-CoMP UEs, because meeting the requirement in (9) to operate as a CoMP UE becomes difficult when the rate gain \(\gamma \) increases. Setting the rate gain to be 2, which is a typical value for half bandwidth assignment, will allow 30% of the total users to operate as CoMP UEs. Then the JT-CoMP rate of the 30% of UEs is twice the rate when they operate with no CoMP. From Fig. 9, it is clear that a few UEs can improve their rates by more than 3 times compared with their no CoMP rate. Those are the users that achieve extreme SINR gain as their second strongest received power is almost as strong as the strongest power they receive from the strongest BS. This means that the worst case UEs in the no CoMP system are those that benefit most from JT-CoMP. Figure 9 also shows that no UE can achieve higher than 5 rate gain.

Considering half bandwidth assignment (where a CoMP user gets only half of the RBs that a no-CoMP UE gets) i.e., \(b=0.5\), Fig. 10 compares the CDF of the throughput of all UEs when they operate with and without CoMP. As Fig. 10 shows, the percentage of UEs that get throughput lower than 1Mbps is 25% with no CoMP. When JT-CoMP is implemented, this percentage decreases to 26%, 32%, and 32% when the PLD threshold is 5 dB, 10 dB, and 15 dB, respectively. This throughput degradation occurs because the traditional PLD approach admits some UEs to work with CoMP even though their SINR improvement does not compensate the bandwidth wastage. It is clear that the proposed SINR user-centric clustering algorithm outperforms no CoMP and the traditional PLD clustering approach in terms of the overall throughput as the proposed algorithm reduces the percentage of users that get less than 1 Mbps to 22%.

From Fig. 10, it can be seen that JT-CoMP with a 5 dB PLD achieves better throughput compared with no CoMP, except for 30% of the users who get slightly lower throughput.

Increasing the PLD from 5 to 10 dB will allow 32% of users to achieve higher throughput compared with no CoMP while 68% of users will have to sacrifice a significant amount of throughput. In the case of 15 dB PLD, only 17% of UEs will significantly improve their throughput while the throughput of most of UEs (about 83%) will extremely decrease. This indicates that allowing too many UEs to operate as CoMP UEs, for example by setting the PLD to be 15 dB, will degrade the overall performance. The reason for this is that many of the CoMP UEs will achieve marginal SINR gain but at the same time they still consume the bandwidth as they need to be served by multiple BSs. Figure 10 shows that the proposed user-centric clustering approach outperforms no CoMP as well as the traditional PLD user-centric clustering approach. This is because it allows users to implement CoMP only if their SINR improvement can compensate the bandwidth wastage. Overall, the traditional PLD user-centric clustering approach can provide throughput improvement to some users but at the expense of other users. In other words, many users would enjoy more throughput if they operated with no CoMP especially when the PLD threshold is high.

Figures 11 and 13 show the CDF of the throughput of cell-edge UEs when \(b=0.5\) and \(b=1\), respectively. Cell-edge UEs can be defined as the 5th percentile of the distribution of user SINR with no CoMP and their throughput is defined as the cell-edge throughput. This definition may include a few users with extremely poor SINR due to heavy shadowing although they are not physically located in the cell-edge region. In Fig. 11, the CDF of cell-edge throughput when \(b=0.5\) is shown. Clearly, no CoMP achieves higher cell-edge throughput than the PLD CoMP. It is also clear that the performance of the proposed SINR clustering approach in terms of cell-edge throughput is better than the PLD approach and it has a similar performance to no CoMP. This performance occurs because CoMP UEs are assigned only half bandwidth and the SINR improvement of some PLD CoMP UEs does not compensate the bandwidth wastage. Also, another factor that affects the performance of the cell-edge throughput is the resource mismatching problem. Though a CoMP UE is initially assigned half bandwidth, it may obtain a smaller amount of bandwidth after performing the resource matching. For the proposed user-centric clustering approach, the SINR gain always compensates for the loss of bandwidth, thus the only limiting factor is the resource mismatching due to different loads.

Figure 12 shows the CDF of user throughput when \(b=1\). From the Figure, comparing no CoMP and 5 dB PLD, JT-CoMP with PLD of 5 dB enhances the throughput of 48% of users; however, about 52% of users lose significant throughput. When the PLD threshold is 10 dB, 38% of users will get slight throughput improvement while the throughput of 62% of users will significantly reduce. If the PLD is increased from 10 to 15 dB, the throughput of almost all users will decrease. The proposed user-centric clustering approach outperforms the traditional PLD approach for all the compared PLD values. Also, the proposed user-centric clustering algorithm can improve the throughput of more than 62% of users compared with no CoMP; nevertheless, about 36% of users would achieve higher throughput if they operated with no CoMP.

Figure 13 shows the CDF of cell-edge throughput when \(b=1\). The CDF shows that the traditional PLD approach can significantly enhance the throughput of cell-edge UEs. The cell-edge improvement becomes more significant when the PLD decreases from 15 to 5 dB. The proposed user-centric clustering approach also shows how it can significantly enhance the throughput of cell-edge UEs. Unlike the proposed user-centric clustering approach, this cell-edge improvement provided by the 5 dB PLD comes at the expense of the throughput of the rest of the users as shown in Fig. 12. This significant cell-edge throughput improvement is achieved because the cell-edge users are assigned full bandwidth. Since a CoMP UE is assigned a bandwidth that it would obtain if it operated with no CoMP, the cell-edge throughput improvement comes from the SINR gain. This full bandwidth assignment will enhance the throughput of almost all cell-edge UEs. Due to the resource mismatching problem, a cell-edge CoMP UE with slight SINR gain may perform better with no CoMP as shown in Fig. 13 when the PLD threshold is 10 dB and 15 dB.

The system performance is expected to be slightly different when it operates in bandwidths less than 20 MHz since such bandwidths have lower number of RBs which might cause shortage of radio resources for CoMP users in case half and full bandwidth assignment are used. To tackle this issue, double bandwidth assignment can be used where CoMP users are allocated twice the amount of RBs that non-CoMP users obtain.

Figure 14 shows the percentage of users that would gain or lose throughput when JT-CoMP is implemented in the hexagonal and random deployments. As shown in Fig. 14, the percentage of users associated with 2 or more BSs in the random deployment is slightly higher than the hexagonal deployment. This is because the irregular topology in the random deployment causes higher levels of interference and attracts more users to operate in CoMP mode. If a user can achieve at least twice the rate it achieves with no CoMP, then this user benefits, else it loses. This is helpful to evaluate the effectiveness of a given user-centric clustering algorithm. A good user-centric clustering algorithm should allow UEs to implement CoMP only if a user can guarantee significant improvement in their rate as failing to satisfy this requirement increases the number of CoMP UEs and reduces the resource availability. An optimal approach is an approach that can achieve at least \(\gamma \) rate improvement where \(\gamma \) is the user-centric cluster size. In Fig. 14, \(\gamma \) is set to 2 since this work limits the number of cooperative BSs to 2. As the proposed SINR approach will only allow a user to operate as a CoMP UE if its rate improvement is higher than \(\gamma \), then all CoMP UEs are winners. For the traditional PLD approach, a 5 dB PLD in both the hexagonal and random deployments includes almost all users that will achieve higher than \(\gamma \) rate improvement. However, a 5 dB PLD value will also include 14% and 12% of users who will achieve less than \(\gamma \) rate improvement in the hexagonal and random deployments, respectively. Allowing these UEs to implement CoMP will degrade the system performance since the SINR improvements of these UEs do not compensate the bandwidth wastage. When the PLD increases from 5 to 10 dB, the number of winners will slightly increase from 22 to 24% (hexagonal) and from 24 to 26% (random). This is because 2% of the UEs whose PLD is between 5 and 10 dB can still achieve at least \(\gamma \) rate improvement. The number of losers will significantly increase as most of the UEs with PLD higher than 5 dB and less than 10 dB fails to achieve higher than \(\gamma \) rate improvement. For a PLD of 15 dB, all UEs that can achieve at least \(\gamma \) rate improvement are included. However, the number of losers is extremely high (about 53% in hexagonal deployment and about 52% in random deployment).

Comparing hexagonal and random deployments, Fig. 15 shows the percentage of UEs that can achieve a rate gain \(\gamma \) that is higher than their user-centric cluster size \(\gamma \) provided that this rate gain has not been achieved by a lower user-centric cluster size. As shown in Fig. 15, there are about 26% and 27% of UEs that can achieve higher than 2 rate gain when the cluster size is set to 2 in the hexagonal and random deployments, respectively. With a cluster size of 3, only about 2% of UEs in the hexagonal case and 2.4% of UEs in the random case (excluding the UEs that have achieved higher than 3 rate gain when their cluster size was 2) can achieve a rate gain higher than 3. It is obvious from Fig. 15 that a negligible improvement is achieved if UEs are served by more than 2 BSs irrespective of the topology modelling. This negligible improvement happens because macro BSs in a hexagonal and a repulsive PPP network are separated with a minimum distance which makes the third, fourth BSs and so on far away from the served user. Thus, allowing more than two BSs to cooperate does not significantly help to reduce and exploit the interference coming from the third strongest BS and beyond. In pure PPP where BSs can be located close to each other, a user is expected to benefit significantly when served by three or four BSs; however, the deployment of pure PPP is unrealistic.

To validate the effectiveness of the proposed user-centric clustering approach, it is compared with three well-known user-centric clustering algorithms: PLD [23], average received signal strength (RSS) [47], and SINR level [4]. Since the PLD and SINR approaches are measured in dB while the RSS is in dBm, a parameter \(\rho \) ranging from 1 to 20 is used as a threshold representative for the three approaches. \(\rho =1\) represents a PLD of 1 dB, an RSS of −50 dBm, and an SINR of 1 dB whereas \(\rho =2\) represents a PLD of 2 dB, an RSS of −51 dBm, and an SINR of 2 dB, and so on.

As seen from Fig. 16, the PLD, RSS, and SINR approaches have a similar behaviour where the number of winners rises until a stable point is reached and then after a certain threshold, the number of winners starts to decrease. This is because the average received power from each BS other than the strongest BS that belong to the user’s cluster is strong due to the low value of the PLD (less than 8 dB). This helps to achieve a rate gain higher than the cluster size. For the PLD approach, the number of winners starts to increase when the PLD increases from 1 dB until it reaches 7 dB. PLD thresholds of 6 dB to 8 dB include 26.51%, 26.94%, and 26.78% of winners, respectively. However, 6 dB to 8 dB PLD thresholds will also include 14.42%, 19.19%, and 24.04% of losers, respectively. Allowing these users to operate as CoMP users will degrade the system performance since the SINR improvement of these UEs does not compensate the wastage of bandwidth. When the PLD and SINR thresholds goes beyond 7 dB and 5 dB and the RSS threshold goes below −59 dBm, the number of winners declines and the number of losers sharply rises. For the PLD, RSS, SINR approaches, the highest number of winners is 26.94%, 25.12%, and 25.21% achieved at thresholds of 7 dB, −59 dBm, and 5 dB, respectively. Although the PLD, RSS, and SINR approaches at these thresholds attempt to include all UEs that would benefit from CoMP, they also include 19.19%, 55.92%, and 34.81% of losers. For the proposed approach, the number of winners and losers are 27% and 0%, respectively.

Fig. 16
figure 16

A comparison between the proposed approach and PLD, RSS, and SINRlevel in terms of percentage of “winners” and “losers” where a “winner” is a user that applies CoMP and achieves at least two times rate improvement

Full size image

7 Conclusion

JT-CoMP faces two main constraints to maximising system capacity, which are operating with an effective user-centric clustering algorithm that can balance between SINR improvement and the wastage of bandwidth and operating an efficient multi-cell resource allocation scheme. To balance the SINR improvement and wastage of bandwidth, this paper has developed a new user-centric clustering algorithm where a UE implements CoMP only if it can achieve a given rate improvement. To solve the problem of resource mismatching between cooperative BSs that occurs due to load imbalance, a resource matching approach has been proposed where cooperative BSs need to agree on the amount of bandwidth that they can provide for JT-CoMP. Simulation results have been obtained of the performance of the joint user-centric JT-CoMP clustering and multi-cell resource allocation in a single-tier network with hexagonal and random deployment of BSs. To validate the effectiveness of the proposed user-centric clustering algorithm, it has been compared with the conventional PLD scheme, showing that the proposed approach outperforms than the traditional PLD approach and no CoMP in terms of overall throughput and cell-edge throughput. Results also show that the performance of JT-CoMP mainly depends on the user-centric clustering approach and the portion of bandwidth that is assigned to the CoMP region. In addition, JT-CoMP performs slightly better in repulsive PPP networks since JT-CoMP can help to reduce the increased levels of interference caused by the repulsive PPP irregular topology. Although the proposed user-centric multi-cell approach has shown promising performance particularly in improving cell-edge throughput, it introduces additional signalling to allow cooperating base stations to agree on the number of offered RBs. This additional complexity can be reduced in centralized wireless architectures such as cell-free and C-RAN networks. As future work, it would interesting to investigate the performance of the proposed approach in heterogeneous networks, cell-free networks, and C-RAN networks.