Resource Allocation Strategy of SWIPT Relay Under General Interference

Abstract

The interference often results in a low rate of the wireless relay systems. The recent research on radio frequency signal energy harvesting makes it possible to utilize the interference energy. Based on the widely applicable time switching relay operation strategy and decode-and-forward (DF) relay modes, this paper studies the resource allocation strategy of the simultaneous wireless information and power transfer relay system under the general interference. The h₂ method is proposed for resource allocation. It establishes a resource allocation coordinate system, and divides the energy harvesting area and the DF area by using the h₂ method. Through derivation, the relationship between the non-interruption probability of the system and the line h₂ is found. Aiming at maximizing the non-interruption probability, the golden splitting method is used to solve the optimal value. The numerical simulation results demonstrate that the h₂ method can effectively improve the non-interruption probability of the system.

Appendix

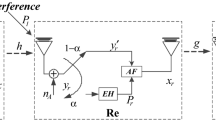
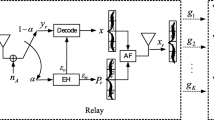
The meaning of the variables in the Fig. 10 is the same as above. The TS ratio is defined as $\alpha$ and $\alpha \in \left[ {0,1} \right)$. First, the communication process from the transmitter to the relay in Fig. 10 is considered. In a certain channel state, the received signal at the relay can be expressed as

Fig. 10

Schematic diagram of TS-DF-based SWIPT relay system model

$$ y_{R} = \sqrt {hP_{S} } x + n_{R} + i $$

(A1)

The signal-to-noise ratio (SNR) of the signal is

$$ \gamma_{SR} = \frac{{hP_{S} }}{{I + \sigma_{R}^{2} }} $$

(A2)

At this point, the instantaneous information rate from the transmitter to the relay can be expressed as

$$ R_{SR} = \left( {1 - \alpha } \right)\log_{2} \left( {1 + \frac{{hP_{S} }}{{I + \sigma_{R}^{2} }}} \right) $$

(A3)

We consider a delay limited transmission with a threshold of $r_{0}$. The threshold transmission rate $r_{0}$ is referred to as the interruption rate. According to [24], the outage probability of transmitter-to-relay can be expressed as

$$ p_{out} = P\left\{ {R_{SR} < r_{0} } \right\} = P\left\{ {\left( {1 - \alpha } \right)\log_{2} \left( {1 + \frac{{hP_{S} }}{{I + \sigma_{R}^{2} }}} \right) < r_{0} } \right\} $$

(A4)

The non-interruption probability of transmitter-to-relay is defined as $p_{1} = 1 - p_{out}$, and $p_{1}$ can be expressed as

$$ p_{1} = P\left\{ {\left( {1 - \alpha } \right)\log_{2} \left( {1 + \frac{{hP_{S} }}{{I + \sigma_{R}^{2} }}} \right) \ge r_{0} } \right\} $$

(A5)

Simplifying $\left( {1 - \alpha } \right)\log_{2} \left( {1 + {{hP_{S} } \mathord{\left/ {\vphantom {{hP_{S} } {\left( {I + \sigma_{R}^{2} } \right)}}} \right. \kern-0pt} {\left( {I + \sigma_{R}^{2} } \right)}}} \right) \ge r_{0}$, we obtain

$$ h \ge \frac{{\left( {2^{{\frac{{r_{0} }}{1 - \alpha }}} - 1} \right)\left( {I + \sigma_{R}^{2} } \right)}}{{P_{S} }} $$

(A6)

Let $h_{1} = {{\left( {2^{{\frac{{r_{0} }}{1 - \alpha }}} - 1} \right)\left( {I + \sigma_{R}^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {2^{{\frac{{r_{0} }}{1 - \alpha }}} - 1} \right)\left( {I + \sigma_{R}^{2} } \right)} {P_{S} }}} \right. \kern-0pt} {P_{S} }}$ ,and we can get

$$ p_{1} = \int_{0}^{\infty } {\int_{{h_{1} }}^{\infty } {f(h,I)} } dhdI $$

(A7)

where $f(h,I) = \frac{1}{{\theta_{I} }}e^{{ - \frac{I}{{\theta_{I} }}}} e^{ - h}$.

The relay energy harvesting power is

$$ E\left[ {P_{EH} } \right] = \int_{0}^{\infty } {\int_{0}^{\infty } {\alpha (hP_{S} + I)} } f(h,I)dhdI $$

(A8)

The relay provides the forwarding power $P_{R} = E\left[ {P_{EH} } \right] - P_{C}$.

Then, the communication process from the relay to the receiver is considered. In a certain channel state, the received signal at the receiver can be expressed as

$$ y_{D} = \sqrt g x_{R} + n_{D} $$

(A9)

Assuming that the relay can correctly decode the information, we obtain $x_{R} = \sqrt {P_{R} } x$, so the SNR of the received signal at the receiver is

$$ \gamma_{RD} = \frac{{gP_{R} }}{{\sigma_{D}^{2} }} $$

(A10)

The instantaneous information rate from the relay to the receiver can be expressed as

$$ R_{RD} = \log_{2} \left( {1 + \frac{{gP_{R} }}{{\sigma_{D}^{2} }}} \right) $$

(A11)

The non-interruption probability of relay-to-receiver is defined as $p_{2}$, and $p_{2}$ can be expressed as

$$ p_{2} = P\left( {\log_{2} \left( {1 + \frac{{gP_{R} }}{{\sigma_{D}^{2} }}} \right) \ge r_{0} } \right) $$

(A12)

Simplifying $\log_{2} \left( {1 + {{gP_{R} } \mathord{\left/ {\vphantom {{gP_{R} } {\sigma_{D}^{2} }}} \right. \kern-0pt} {\sigma_{D}^{2} }}} \right) \ge r_{0}$, we obtain

$$ g \ge \frac{{\left( {2^{{r_{0} }} - 1} \right)\sigma_{D}^{2} }}{{P_{S} }} $$

(A13)

Let $g_{1} = {{\left( {2^{{r_{0} }} - 1} \right)\sigma_{D}^{2} } \mathord{\left/ {\vphantom {{\left( {2^{{r_{0} }} - 1} \right)\sigma_{D}^{2} } {P_{S} }}} \right. \kern-0pt} {P_{S} }}$ ,and we can get

$$ p_{2} = \int_{{g_{1} }}^{\infty } {f(g)} dg $$

(A14)

where $f(g) = e^{ - g}$.

Finally, you can get non-interruption probability $p_{non}$ expressed as

$$ p_{non} = p_{1} p_{2} $$

(A15)

The optimization problem is established with the goal of maximizing non-interruption probability as follows:

$$ \begin{aligned} \mathop {\hbox{max} }\limits_{\alpha } \,\,\,\,\,\,p_{non} = p_{1} p_{2} \hfill \\ s.t. \,\,\,\,\,\,\,\alpha \in \left[ {0,1} \right] \hfill \\ \end{aligned} $$