Combined Inter-layer FEC and Hierarchical QAM for Stereoscopic 3D Video Transmission

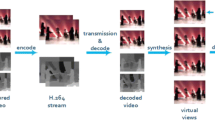
Abstract

We consider an inter-layer FEC (IL-FEC) technique combined with hierarchical QAM for an efficient and reliable transmission of stereoscopic 3D video. The transmit sources are left and right video streams, and one of them is considered a more important stream for guarantee of conventional 2D service. The source node transmits both left and right videos to a destination node by using the IL-FEC and hierarchical 16QAM schemes, in which video peak signal-to-noise ratio (PSNR) performance varies with the hierarchical value $(\alpha )$. In this paper, we present the suitable hierarchical values to achieve the target PSNR performances even in low SNR environment. Numerical simulation results show that the proposed system using IL-FEC and hierarchial 16QAM schemes with the suitable $\alpha$ value can gain about 7.3–9.3 dB in the average PSNR performance, compared with the system using IL-FEC and conventional 16QAM schemes.

Appendix

This appendix on the simplified LLR computation for hierarchical 16QAM is based on a study of [32]. Figure 3 shows the hierarchical 16QAM constellation, in which it is well known that the four bits in each constellation point can be considered as two bits each on independent 4PAM modulation on real-axis (I) and imaginary-axis (Q), respectively. The mapping for hierarchical is shown in Table 1, where $b_1={c_1^{(2{m_n} - 1)}}$ and $b_3={c_1^{2{m_n}}}$ denote HP codeword bits, and $b_2={c_{12}^{(2{m_n} - 1)}}$ and $b_4={c_{12}^{2{m_n}}}$ denote LP codeword bits. The m-th received symbol ${y_m} = {x_m} + {w_m}$, where ${x_m}$ is the m-th transmitted symbol and ${w_m}$ is the AWGN following the probability distribution function,

$$\begin{aligned} p({w_m}) = \frac{1}{{\sqrt{2\pi {\sigma ^2}} }}{e^{\frac{{ - {{({w_m} - \mu )}^2}}}{{2{\sigma ^2}}}}} \end{aligned}$$

(13)

where mean $\mu =0$ and variance $\sigma ^2=N_0/2$. For the hierarchical 16QAM de-mapper, the the probability that the bits $b_r\,(r=1,2,3,4)$ was transmitted when the received symbol vector ${y_m}$ is given, i.e. $P(b_r|{y_m})$. The probability can be rewritten by using Bayes rule as follows:

$$\begin{aligned} {P(b_r|{y_m})}=\frac{{P(b_r|{y_m})}{p(b_r)}}{p({y_m})} \end{aligned}$$

(14)

It is well known that maximizing ${P(b_r|{y_m})}$ is equivalent to maximizing $P({y_m}|b_r)$ because the probability of all constellation points is the same.

Table 1 Constellation mapping for hierarchical 16QAM

1.1 LLR Computation for HP bits

The bit mapping for the HP bits, i.e. $b_1$ and $b_3$, is shown in Fig. 8a. Since the mapping rules for $b_1$ and $b_3$ are the same, only the mapping for $b_1$ is considered. The likelihood ratio for $b_1$ is as follows:

$$\begin{aligned} \frac{{P\left( {y_m|{b_1} = 0} \right) }}{{P\left( {y_m|{b_1} = 1} \right) }} = \frac{{{e^{\frac{{ - {{\left( {y_m - \left( {{d_1} - {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}} + {e^{\frac{{ - {{\left( {y_m - \left( {{d_1} + {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}{{{e^{\frac{{ - {{\left( {y_m - \left( { - {d_1} - {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}} + {e^{\frac{{ - {{\left( {y_m - \left( { - {d_1} + {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}. \end{aligned}$$

(15)

Fig. 8

Hierarchical 16QAM constellation mapping for a HP bit and b LP bit

When $y_m < - {d_1}$, i.e. Region #1, we can assume that relative contribution by constellation $d_1+d_2$ in the numerator and $-d_1+d_2$ in the denominator is less. Therefore, these can be ignored, and be expressed as

$$\begin{aligned} \frac{{P\left( {y_m|{b_1} = 0} \right) }}{{P\left( {y_m|{b_1} = 1} \right) }} \approx \frac{{{e^{\frac{{ - {{\left( {y_m - \left( {{d_1} - {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}{{{e^{\frac{{ - {{\left( {y_m - \left( { - {d_1} - {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}. \end{aligned}$$

(16)

Taking logarithm on both side,

$$\begin{aligned}&\ln \left( {\frac{{P\left( {y_m|{b_1} = 0} \right) }}{{P\left( {y_m|{b_1} = 1} \right) }}} \right) \approx \ln \left( {\frac{{{e^{\frac{{ - {{\left( {y_m - \left( {{d_1} - {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}{{{e^{\frac{{ - {{\left( {y_m - \left( { - {d_1} - {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}} \right) \nonumber \\&\quad = \frac{1}{{2{\sigma ^2}}}\left\{ {{{\left( {y_m- \left( { - {d_1} - {d_2}} \right) } \right) }^2} - {{\left( {y_m - \left( { - {d_1} + {d_2}} \right) } \right) }^2}} \right\} \nonumber \\&\quad = \frac{1}{{{\sigma ^2}}}2{d_1}\left( {y_m + {d_2}} \right) \end{aligned}$$

(17)

When $- {d_1} \le y_m < +{d_1}$, i.e. Region #2 and #3, we can assume that relative contribution by constellation $d_1+d_2$ in the numerator and $-d_1-d_2$ in the denominator is less. Therefore, these can be ignored, and be expressed as

$$\begin{aligned} \frac{{P\left( {y_m|{b_1} = 0} \right) }}{{P\left( {y_m|{b_1} = 1} \right) }} \approx \frac{{{e^{\frac{{ - {{\left( {y_m - \left( {{d_1} - {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}{{{e^{\frac{{ - {{\left( {y_m - \left( { - {d_1} + {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}. \end{aligned}$$

(18)

Taking logarithm on both side,

$$\begin{aligned}&\ln \left( {\frac{{P\left( {y_m|{b_1} = 0} \right) }}{{P\left( {y_m|{b_1} = 1} \right) }}} \right) \approx \ln \left( {\frac{{{e^{\frac{{ - {{\left( {y_m - \left( {{d_1} - {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}{{{e^{\frac{{ - {{\left( {y_m - \left( { - {d_1} + {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}} \right) \nonumber \\&\quad = \frac{1}{{2{\sigma ^2}}}\left\{ {{{\left( {y_m - \left( { - {d_1} + {d_2}} \right) } \right) }^2} - {{\left( {y_m - \left( {{d_1} - {d_2}} \right) } \right) }^2}} \right\} \nonumber \\&\quad = \frac{1}{{{\sigma ^2}}}2y_m\left( {{d_1} - {d_2}} \right) \end{aligned}$$

(19)

When $y_m \ge + {d_1}$, i.e. Region #4, we can assume that relative contribution by constellation $d_1-d_2$ in the numerator and $-d_1-d_2$ in the denominator is less. Therefore, these can be ignored, and be expressed as

$$\begin{aligned} \frac{{P\left( {y_m|{b_1} = 0} \right) }}{{P\left( {y_m|{b_1} = 1} \right) }} \approx \frac{{{e^{\frac{{ - {{\left( {y_m - \left( {{d_1} + {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}{{{e^{\frac{{ - {{\left( {y_m - \left( { - {d_1} + {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}. \end{aligned}$$

(20)

Taking logarithm on both side,

$$\begin{aligned}&\ln \left( {\frac{{P\left( {y_m|{b_1} = 0} \right) }}{{P\left( {y_m|{b_1} = 1} \right) }}} \right) \approx \ln \left( {\frac{{{e^{\frac{{ - {{\left( {y_m - \left( {{d_1} + {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}{{{e^{\frac{{ - {{\left( {y_m - \left( { - {d_1} + {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}} \right) \nonumber \\&\quad = \frac{1}{{2{\sigma ^2}}}\left\{ {{{\left( {y_m - \left( { - {d_1} + {d_2}} \right) } \right) }^2} - {{\left( {y_m - \left( {{d_1} + {d_2}} \right) } \right) }^2}} \right\} \nonumber \\&\quad = \frac{1}{{{\sigma ^2}}}2{d_1}\left( {y_m - {d_2}} \right) \end{aligned}$$

(21)

1.2 LLR Computation for LP bits

The bit mapping for the LP bits, i.e. $b_2$ and $b_4$, is shown in Fig. 8b. Since the mapping rules for $b_2$ and $b_4$ are the same, only the mapping for $b_2$ is considered. The likelihood ratio for $b_2$ is as follows:

$$\begin{aligned} \frac{{P\left( {y_m|{b_2} = 0} \right) }}{{P\left( {y_m|{b_2} = 1} \right) }} = \frac{{{e^{\frac{{ - {{\left( {y_m - \left( {-{d_1} + {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}} + {e^{\frac{{ - {{\left( {y_m - \left( {{d_1} - {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}{{{e^{\frac{{ - {{\left( {y_m - \left( { - {d_1} - {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}} + {e^{\frac{{ - {{\left( {y_m - \left( { {d_1} + {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}. \end{aligned}$$

(22)

When $y_m < 0$, i.e. Region #1 and #2, we can assume that relative contribution by constellation $d_1+d_2$ in the numerator and $d_1-d_2$ in the denominator is less. Therefore, these can be ignored, and be expressed as

$$\begin{aligned} \frac{{P\left( {y_m|{b_1} = 0} \right) }}{{P\left( {y_m|{b_1} = 1} \right) }} \approx \frac{{{e^{\frac{{ - {{\left( {y_m - \left( {-{d_1} + {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}{{{e^{\frac{{ - {{\left( {y_m - \left( { - {d_1} - {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}. \end{aligned}$$

(23)

Taking logarithm on both side,

$$\begin{aligned}&\ln \left( {\frac{{P\left( {y_m|{b_1} = 0} \right) }}{{P\left( {y_m|{b_1} = 1} \right) }}} \right) \approx \ln \left( {\frac{{{e^{\frac{{ - {{\left( {y_m - \left( { - {d_1} + {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}{{{e^{\frac{{ - {{\left( {y_m - \left( { - {d_1} - {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}} \right) \nonumber \\&\quad = \frac{1}{{2{\sigma ^2}}}\left\{ {{{\left( {y_m - \left( { - {d_1} - {d_2}} \right) } \right) }^2} - {{\left( {y_m - \left( { - {d_1} + {d_2}} \right) } \right) }^2}} \right\} \nonumber \\&\quad = \frac{1}{{{\sigma ^2}}}2{d_2}\left( {y_m + {d_1}} \right) \end{aligned}$$

(24)

When $y_m \ge 0$, i.e. Region #3 and #4, we can assume that relative contribution by constellation $-d_1+d_2$ in the numerator and $-d_1-d_2$ in the denominator is less. Therefore, these can be ignored, and be expressed as

$$\begin{aligned} \frac{{P\left( {y_m|{b_1} = 0} \right) }}{{P\left( {y_m|{b_1} = 1} \right) }} \approx \frac{{{e^{\frac{{ - {{\left( {y_m - \left( {{d_1} - {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}{{{e^{\frac{{ - {{\left( {y_m - \left( { {d_1} + {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}. \end{aligned}$$

(25)

Taking logarithm on both side,

$$\begin{aligned}&\ln \left( {\frac{{P\left( {y_m|{b_1} = 0} \right) }}{{P\left( {y_m|{b_1} = 1} \right) }}} \right) \approx \ln \left( {\frac{{{e^{\frac{{ - {{\left( {y_m - \left( {{d_1} - {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}{{{e^{\frac{{ - {{\left( {y_m - \left( {{d_1} + {d_2}} \right) } \right) }^2}}}{{2{\sigma ^2}}}}}}}} \right) \nonumber \\&\quad = \frac{1}{{2{\sigma ^2}}}\left\{ {{{\left( {y_m - \left( {{d_1} + {d_2}} \right) } \right) }^2} - {{\left( {y_m - \left( {{d_1} - {d_2}} \right) } \right) }^2}} \right\} \nonumber \\&\quad = \frac{1}{{{\sigma ^2}}}2{d_2}\left( { - y_m + {d_1}} \right) \end{aligned}$$

(26)