Performance Analysis of Cross QAM with MRC Over Dual Correlated Nakagami-m, -n, and -q Channels

Abstract

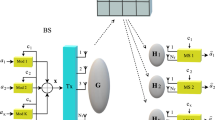
An approximation of the symbol error probability (SEP) of the cross QAM (XQAM) signal in a single-input multiple-output system over dual correlated Rayleigh, Nakagami-m, Nakagami-n (Rice) and Nakagami-q (Hoyt) fading channels is derived. The maximal-ratio combining is considered as the diversity technique, and the average SEP is obtained by using the moment generating function (MGF). Arbitrarily tight approximations for the Gaussian Q-function and the generalized Gaussian Q-function are obtained from the numerical analysis technique; the trapezoidal rule. The resulting expressions consist of a finite sum of MGF’s which are easily evaluated and accurate enough. In addition, a transformation technique is used to derive independent channels from the correlated channels which are then used in the analysis. The simulation results show excellent agreement with the derived approximation expressions.

Appendix

In a Nakagami-n fading channel the received signal from ith path is given by

$$ y_{i} = \sqrt {E_{s} } h_{i} x + n_{i} ,\quad i = 1,2 $$

(34)

where $h_{i} = (h_{i}^{I} + jh_{i}^{Q} ) + (h_{D}^{{I_{i} }} + jh_{D}^{{Q_{i} }} ).$

The transformation matrix $\varvec{T}$ is given by [25]

$$ \varvec{T} = \left[ {\begin{array}{*{20}c} {\frac{\sqrt 2 }{2}} & {\frac{\sqrt 2 }{2}} \\ { - \frac{\sqrt 2 }{2}} & {\frac{\sqrt 2 }{2}} \\ \end{array} } \right] $$

(35)

Then we define another two random variables as

$$ \left[ {\begin{array}{*{20}c} {y_{3} } \\ {y_{4} } \\ \end{array} } \right] = \varvec{T}\left[ {\begin{array}{*{20}c} {y_{1} } \\ {y_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{\sqrt 2 }{2}y_{1} + \frac{\sqrt 2 }{2}y_{2} } \\ { - \frac{\sqrt 2 }{2}y_{1} + \frac{\sqrt 2 }{2}y_{2} } \\ \end{array} } \right] $$

(36)

Based on (36) $y_{3}$ and $y_{4}$ are expressed as

$$ y_{3} = \left( {h_{3}^{I} + jh_{3}^{Q} } \right)x + n_{3} $$

(37)

$$ y_{4} = \left( {h_{4}^{I} + jh_{4}^{Q} } \right)x + n_{4} $$

(38)

where

$$ h_{3}^{I} = \sqrt {E_{s} } \left[ {\left( {\frac{\sqrt 2 }{2}h_{1}^{I} + \frac{\sqrt 2 }{2}h_{2}^{I} } \right) + \frac{\sqrt 2 }{2}\left( {h_{D}^{{I_{1} }} + h_{D}^{{I_{2} }} } \right)} \right] $$

(39a)

$$ h_{3}^{Q} = \sqrt {E_{s} } \left[ {\left( {\frac{\sqrt 2 }{2}h_{1}^{Q} + \frac{\sqrt 2 }{2}h_{2}^{Q} } \right) + \frac{\sqrt 2 }{2}\left( {h_{D}^{{Q_{1} }} + h_{D}^{{Q_{2} }} } \right)} \right] $$

(39b)

$$ h_{4}^{I} = \sqrt {E_{s} } \left[ {\left( { - \frac{\sqrt 2 }{2}h_{1}^{I} + \frac{\sqrt 2 }{2}h_{2}^{I} } \right) + \frac{\sqrt 2 }{2}\left( { - h_{D}^{{I_{1} }} + h_{D}^{{I_{2} }} } \right)} \right] $$

(39c)

$$ h_{4}^{Q} = \sqrt {E_{s} } \left[ {\left( { - \frac{\sqrt 2 }{2}h_{1}^{Q} + \frac{\sqrt 2 }{2}h_{2}^{Q} } \right) + \frac{\sqrt 2 }{2}\left( { - h_{D}^{{Q_{1} }} + h_{D}^{{Q_{2} }} } \right)} \right] $$

(39d)

$$ n_{3} = \frac{\sqrt 2 }{2}n_{1} + \frac{\sqrt 2 }{2}n_{2} $$

(39e)

$$ n_{4} = - \frac{\sqrt 2 }{2}n_{1} + \frac{\sqrt 2 }{2}n_{2} $$

(39f)

Since $E[h_{1}^{I} ] = E[h_{2}^{I} ] = 0$ and $E[(h_{1}^{I} )^{2} ] = E[(h_{2}^{I} )^{2} ] = \sigma^{2}$ the covariance of $h_{3}^{I}$ and $h_{4}^{I}$ can be calculated by

$$ C_{{h_{3}^{I} h_{4}^{I} }} = E\left[ {h_{3}^{I} h_{4}^{I} } \right] = 0 $$

(40)

The result of (40) indicates that $h_{3}^{I}$ and $h_{4}^{I}$ are uncorrelated and statistically independent. Similarly we can also prove that $h_{3}^{Q}$ and $h_{4}^{Q}$ are also uncorrelated and statistically independent. Since $E[h_{i}^{I} h_{j}^{Q} ] = 0,i = 1,2; j = 1,2$ we further can prove $E[h_{i}^{I} h_{j}^{Q} ] = 0,i = 3,4; j = 3,4$. $E[h_{i}^{I} h_{j}^{Q} ] = 0,i = 3,4; j = 3,4$, indicates that channel $h_{3}$ and $h_{4}$ are statistically independent. So the above transformation converts dual correlated Nakagami-n fading channel $h_{1}$ and $h_{2}$ into two independent fading channels, $h_{3}$ and $h_{4}$.

Without loss of generality we further assume $h_{D}^{{I_{2} }} = \beta h_{D}^{{I_{1} }}$ and $h_{D}^{{Q_{2} }} = \beta h_{D}^{{Q_{1} }}$. Then the mean values of $h_{3}^{I}$, $h_{3}^{Q}$,$h_{4}^{I}$ and $h_{4}^{Q}$ are derived as

$$ E\left[ {h_{3}^{I} } \right] = \frac{\sqrt 2 }{2}\left( {1 + \beta } \right)h_{D}^{{I_{1} }} $$

(41a)

$$ E\left[ {h_{3}^{Q} } \right] = \frac{\sqrt 2 }{2}\left( {1 + \beta } \right)h_{D}^{{Q_{1} }} $$

(41b)

$$ E\left[ {h_{4}^{I} } \right] = \frac{\sqrt 2 }{2}\left( {\beta - 1} \right)h_{D}^{{I_{1} }} $$

(41c)

$$ E\left[ {h_{4}^{Q} } \right] = \frac{\sqrt 2 }{2}\left( {\beta - 1} \right)h_{D}^{{Q_{1} }} $$

(41d)

The variances of $h_{3}^{I}$, $h_{3}^{Q}$, $h_{4}^{I}$, and $h_{4}^{Q}$ are also derived as

$$ E\left[ {\left( {h_{3}^{I} } \right)^{2} } \right] = E_{s} \left( {1 + \rho } \right)\sigma^{2} + 0.5\left( {1 + \beta } \right)^{2} E_{s} \left( {h_{D}^{{I_{1} }} } \right)^{2} $$

(42a)

$$ E\left[ {\left( {h_{3}^{Q} } \right)^{2} } \right] = E_{s} \left( {1 + \rho } \right)\sigma^{2} + 0.5\left( {1 + \beta } \right)^{2} E_{s} \left( {h_{D}^{{Q_{1} }} } \right)^{2} $$

(42b)

$$ E\left[ {\left( {h_{4}^{I} } \right)^{2} } \right] = E_{s} \left( {1 - \rho } \right)\sigma^{2} + 0.5\left( {1 - \beta } \right)^{2} E_{s} \left( {h_{D}^{{I_{1} }} } \right)^{2} $$

(42c)

$$ E\left[ {\left( {h_{4}^{Q} } \right)^{2} } \right] = E_{s} \left( {1 - \rho } \right)\sigma^{2} + 0.5\left( {1 - \beta } \right)^{2} E_{s} \left( {h_{D}^{{Q_{1} }} } \right)^{2} $$

(42d)

In general, the results of (41a)–(42d) indicate that the transformation proposed in [25] converts dual correlated Nakagami-n fading channel $h_{1}$ and $h_{2}$ with parameter $K_{1}$ and $K_{2}$ into two independent Nakagami-n fading channel $h_{3}$ and $h_{4}$ with $K_{3}$ and $K_{4}$ which are given by

$$ K_{3} = \frac{{\left( {1 + \beta } \right)^{2} }}{{4\left( {1 + \rho } \right)\sigma^{2} }}\left[ {\left( {h_{D}^{{I_{1} }} } \right)^{2} + \left( {h_{D}^{{Q_{1} }} } \right)^{2} } \right] $$

(43a)

$$ K_{4} = \frac{{\left( {1 - \beta } \right)^{2} }}{{4\left( {1 - \rho } \right)\sigma^{2} }}\left[ {\left( {h_{D}^{{I_{1} }} } \right)^{2} + \left( {h_{D}^{{Q_{1} }} } \right)^{2} } \right] $$

(43b)

Typically when $h_{D}^{{I_{1} }} = h_{D}^{{I_{2} }}$ and $h_{D}^{{Q_{1} }} = h_{D}^{{Q_{2} }}$ $(\beta = 1)$ the transformation converts dual correlated Nakagami-n fading channels with equal parameter $K_{1} = K_{2}$ into two independent fading channels, one is Rayleigh fading channel $(K_{4} = 0)$, another still is Nakagami-n with parameter $K_{3}$ which is given by

$$ K_{3} = \frac{{\left( {h_{D}^{{I_{1} }} } \right)^{2} + \left( {h_{D}^{{Q_{1} }} } \right)^{2} }}{{\left( {1 + \rho } \right)\sigma^{2} }} $$

(44)