Power Allocation and Transmission Period Selection for Device-to-Device Communication as an Underlay to Cellular Networks

Abstract

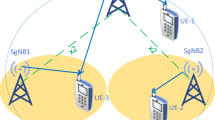
Efficient design of device-to-device (D2D) communication calls for D2D users to propose adaptive power allocation strategy and to establish reliable communication links while protecting the QoS of cellular communications. In this paper, we consider the D2D communication as an underlay to relay-assisted cellular networks. To maximize the ergodic capacity, we derive an optimal transmission power under an average power constraint. With the derived optimal transmission power, a transmission period selection strategy for D2D communication is firstly introduced to improve reliability. We derive the outage probability in closed forms and evaluate the ergodic capacity to show performances of the proposed system. Numerical results show that the D2D system can achieve high capacity gains by flexibly allocating transmission power based on channel state information and significantly enhance reliability by selecting a transmission period, while satisfying various QoS conditions for cellular communication.

Appendix

1.1 Solve (7) Under the KKT Conditions

The Lagrangian of (7) is

$$\begin{aligned} L&= E_{g_{12},g_{i2},g_{1j}}\bigg [\ln \bigg (1+\frac{g_{12}P_{T,1}(g_{12},g_{i2},g_{1j})}{\sigma ^{2}+g_{i2}P_{CT,i}^{min^{\dag }}}\bigg )\bigg ]\nonumber \\&-\lambda _{1}(E_{g_{12},g_{i2},g_{1j}}[g_{1j}P_{T,1}(g_{12},g_{i2},g_{1j})]-\overline{I}) +\lambda _{2}P_{T,1}(g_{12},g_{i2},g_{1j}) \end{aligned}$$

(28)

where $\lambda _{i,1}$ and $\lambda _{i,2}$ are the non-negative Lagrangian multipliers of the corresponding constraints. The KKT conditions of (28) are

$$\begin{aligned}&\displaystyle \frac{\partial {L}}{\partial {P_{T,1}}}\bigg |_{P_{T,1}=P_{T,1}^{*}}= E\bigg [\bigg (\frac{g_{12}}{\sigma ^{2}+g_{i2}P_{CT,i}^{min^{\dag }}+g_{1j}P_{T,1}}\bigg ) -\lambda _{1}g_{1j}\bigg ]+\lambda _{2} = 0,\nonumber \\&\displaystyle \lambda _{1}(E_{g_{12},g_{i2},g_{1j}}[g_{1j}P_{T,1}]-\overline{I})=0,\nonumber \\&\displaystyle \lambda _{2}P_{T,1}=0 \end{aligned}$$

(29)

where $(\cdot )^{*}$ refers to the optimal value. For brevity, we omit the variables in the transmission power $P_{T,1}(g_{12},g_{i2},g_{1j})$. To satisfy the KKT conditions, $\lambda _{2}$ should be zero since $P_{T,1}\ge 0$. Thus, we obtain the optimal transmission power $P_{T,1}^{*}$ as

$$\begin{aligned} P_{T,1}^{*}=\left\{ \begin{array}{cc} P_{T,1}^{*}(g_{12},g_{i2},g_{1j})=\bigg [\frac{\lambda _{1}^{f}}{g_{1j}}-\frac{\sigma ^{2}+g_{i2}P_{CT,i}^{min^{\dag }}}{g_{12}}\bigg ]^{+},\quad if\quad \frac{\lambda _{1}^{f}}{\sigma ^{2}+g_{i2}P_{CT,i}^{min^{\dag }}}\ge \frac{g_{1j}}{g_{12}}\\ \qquad \qquad \qquad \qquad \qquad \quad 0, \quad \mathrm {otherwise}\\ \end{array} \right. \end{aligned}$$

(30)

where $[\cdot ]^{+}$ represents $\max (\cdot ,0)$.

1.2 Derive the Distribution in (10)

We derive the distribution of $g_{1j}/g_{12}$ where $g_{1j}$ and $g_{12}$ have exponential distributions with the parameter $\zeta$ and $\nu$, respectively. Firstly, define two random variable $U$ and $V$ as,

$$\begin{aligned} U=\frac{g_{1j}}{g_{12}},\quad {V=g_{1j}+g_{12}} \end{aligned}$$

(31)

Then the Jacobian is calculated as

$$\begin{aligned} J=\bigg | \begin{array}{cc} -\frac{g_{1j}}{g_{12}^{2}} &{} \frac{1}{g_{12}} \\ 1 &{} 1 \\ \end{array} \bigg |=-\frac{g_{1j}+g_{12}}{g_{12}^{2}}=-\frac{(1+u)^{2}}{v}. \end{aligned}$$

(32)

With (31), a joint pdf of $U$ and $V$ is expressed as

$$\begin{aligned} f_{U,V}(u,v)=\zeta \nu {e^{-\frac{(\zeta {u}+\nu )v}{u+1}}}\frac{v}{(1+u)^{2}} \end{aligned}$$

(33)

where $\zeta =d_{1j}^{\alpha }$, $\nu =d_{12}^{\alpha }$, and the random variables $U$ and $V$ are independent. Thus, a marginal distribution of $U=\frac{g_{1j}}{g_{12}}$ can be obtained by integration of the joint pdf $f_{U,V}(u,v)$ with respect to $V$ as follow:

$$\begin{aligned} f_{U}(u)&= \int \limits _{0}^{\infty }\zeta \nu {e^{-\frac{(\zeta {u}+\nu )v}{u+1}}}\frac{v}{(1+u)^{2}}dv\nonumber \\&= \frac{\zeta \nu }{(\zeta {u}+\nu )^{2}}\underbrace{\int \limits _{0}^{\infty }te^{-t}dt}_{\varGamma (2)=1}\nonumber \\&= \frac{\varTheta _{j}}{(u+\varTheta _{j})^{2}} \end{aligned}$$

(34)

where $\varGamma (\cdot )$ is the gamma function and $\varTheta _{i}=\nu /\zeta =(d_{1j}/d_{12})^{-\alpha }$.

1.3 Derive the Equation in (12)

The reciprocal of Lagrangian multiplier $\lambda _{1}^{f}$ should satisfy the Eq. (12). The equation can be obtained as follow:

$$\begin{aligned} \overline{I}&= \int \limits _{0}^{\infty }\int \limits _{0}^{\frac{\lambda _{1}^{f}}{\sigma ^{2}(1+v)}}\{\lambda _{1}^{f}-\sigma ^{2}(1+v)u\}f_{U}(u)f_{V}(v)dudv\nonumber \\&= \int \limits _{0}^{\infty }\int \limits _{0}^{\frac{\lambda _{1}^{f}}{\sigma ^{2}(1+v)}}(\lambda _{1}^{f}-\sigma ^{2}(1+v)u)\frac{\varTheta _{i}}{(\varTheta _{i}+u)^{2}}f_{V}(v)dudv\nonumber \\&= \int \limits _{0}^{\infty }\bigg \{\lambda _{1}^{f}-\sigma ^{2}\varTheta _{j}(1+v)\ln \bigg [1+\frac{\lambda _{1}^{f}}{\varTheta _{j}\sigma ^{2}(1+v)}\bigg ]\bigg \}\mu _{i}{e}^{-\mu _{i}{v}}dv\nonumber \\&= \lambda _{1}^{f}-\frac{\mu _{i}e^{\mu _{i}}}{\varTheta _{j}\sigma ^{2}}\int \limits _{\varTheta _{j}\sigma ^{2}}^{\infty }t\{\ln (t+\lambda _{1}^{f})-\ln {t}\}e^{-\frac{t}{\varTheta {j}\sigma ^{2}/\mu _{i}}}dt. \end{aligned}$$

(35)

To have the closed-form equation, we firstly derive a general result of the last integral term. The last integral term can be rewritten as

$$\begin{aligned} \int \limits _{a}^{\infty }t\ln (t+b)e^{-\frac{t}{c}}dt \end{aligned}$$

(36)

where $a$, $b$, and $c$ are constants. Using integration by parts, we can generalize the result as

$$\begin{aligned}&\int \limits _{a}^{\infty }t\ln (t+b)e^{-\frac{t}{c}}dt\nonumber \\&\quad =-e^{-\frac{t}{c}}(c^{2}+ct)\ln (t+b)\bigg |_{a}^{\infty }+c\int \limits _{a}^{\infty }\frac{t+c}{t+b}e^{-\frac{t}{c}}dt\nonumber \\&\quad =ce^{-\frac{a}{c}}\bigg \{c+(a+c)\ln (a+b)+e^{\frac{a+b}{c}}(c-b)E_{1}\bigg (\frac{a+b}{c}\bigg )\bigg \}. \end{aligned}$$

(37)

Combining the result in (37) with (35), we can have the closed-form expression of the equation in (12) as

$$\begin{aligned} \overline{I}&= \lambda _{1}^{f}-\bigg \{\varTheta _{j}\sigma ^{2}\bigg (1+\frac{1}{\mu _{i}}\bigg )\ln \Big (1+\frac{\lambda _{1}^{f}}{\varTheta _{j}\sigma ^2}\Big )\nonumber \\&\qquad +\bigg (\frac{\varTheta _{j}\sigma ^{2}}{\mu _{i}}-\lambda _{1}^{f}\bigg )e^{\mu _{i}(1+\frac{\lambda _{i,1}^{f}}{\varTheta _{j}\sigma ^2})}E_{1}\bigg (\mu _{i}(1+\frac{\lambda _{i,1}^{f}}{\varTheta _{j}\sigma ^2})\bigg ) -\frac{\varTheta _{j}\sigma ^2}{\mu _{i}}e^{\mu _{i}}E_{1}(\mu _{i})\bigg \}.\quad \end{aligned}$$

(38)

1.4 Statistical Analysis Under the Peak Power Constraint

Distributions of the end-to-end SINR of the D2D communication under the peak constraint are derived in this section. In this case, the optimal transmission power is directly obtained as $P_{T,1}^{*,peak}(g_{1j})={(\kappa -1)\sigma ^{2}}/{g_{1j}}$ without further limitations in an allowable D2D transmission power. Thus, the received SINR is $\gamma _{12}^{l,peak}=\frac{g_{12}(\kappa -1)\sigma ^{2}}{(\sigma ^{2}+g_{i2}P_{CT,i}^{min^{\dag }})g_{1j}}$. Similar to (17) and its derivative with respect to $Z$, the exact distributions of the end-to-end SINR are derived as follow:

$$\begin{aligned} F_{\gamma _{12}^{l,peak}}(\gamma )&= 1-\frac{\mu _{i}\overline{Q}\varPhi _{j}}{\sigma ^{2}\gamma }\exp \bigg [\mu _{i}\bigg (1+\frac{\overline{Q}\varPhi _{j}}{\sigma ^{2}\gamma }\bigg )\bigg ] E_{1}\bigg (\mu _{i}\bigg (1+\frac{\overline{Q}\varPhi _{j}}{\sigma ^{2}\gamma }\bigg )\bigg )\end{aligned}$$

(39)

$$\begin{aligned} f_{\gamma _{12}^{l,peak}}(\gamma )&= \frac{\mu _{i}\overline{Q}\varPhi _{j}}{\sigma ^{2}\gamma }\bigg \{\Bigg (\frac{1}{\gamma }+\frac{\mu _{i}\overline{Q}\varPhi _{j}}{\sigma ^{2}\gamma ^{2}}\bigg )e^{\mu _{i}(1+\frac{\overline{Q}\varPhi _{j}}{\sigma ^{2}\gamma })}E_{1}(\mu _{i}(1+\frac{\overline{Q}\varPhi _{j}}{\sigma ^{2}\gamma })) -\frac{{\overline{Q}\varPhi _{j}}/{\sigma ^{2}\gamma }}{(\gamma +\frac{\lambda _{l,1}^{f}\varPhi _{j}}{\sigma ^{2}})}\Bigg \}\nonumber \\ \end{aligned}$$

(40)

where $\overline{Q}=(\kappa -1)\sigma ^{2}$. We use $\overline{Q}$ instead of $\overline{I}$ to distinguish two types of the power constraints in (5) and (6).