Collision resolving relay selection in large-scale blind relay networks

Abstract

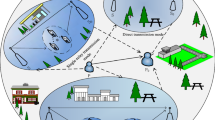
Optimal relay selection in large-scale networks is a difficult task since the network is usually considered as blind due to the high volume and collection difficulty of the relays’ information. In this paper, we develop a collision resolving relay selection (CReS) scheme that achieves the optimal relay from a random set of candidates without the previous knowledge of any individual relay. By introducing stochastic geometry based quality-of-service region, the relation between the distribution of the available relay number and the transmission request is established. Furthermore, the selection phase of the CReS scheme is divided into two sub-phases according to different distributions of the relay number in boundless and bounded regions. A switch rule is proposed when several relays collide in the first sub-phase, followed by the second sub-phase to resolve the collision with the splitting algorithm. The optimal solution that requires minimum selection slots for all sub-phases is derived. In addition, a sub-optimal solution is also explored to reduce the computational complexity. The scheme shows a better applicability than conventional information-based schemes in view of its little information requirement when dealing with large-scale relay allocation problems.

Appendices

Appendix 1: Derivation of formula (10)

When $n=1$, the resolution success probability $P^\mathbf{S2}(p_{_{{\mathbf{V}}_0}})$ is the probability that only 1 relay is available among $k_0$ colliding relays. Considering the relay number distribution of $K(|{\mathcal {S}}^{\mathrm{C}}_{{\mathbf{V}}_0}|)=k_0$ ($2 \le k_0 < \infty$) in (1), the expressions of $P^\mathbf{S2}(p_{_{{\mathbf{V}}_0}})$ and ${{\mathbf{V}}_0}$ are given by

$$\begin{aligned} \begin{aligned} \quad P^\mathbf{S2}(p_\phi )=\sum \limits _{{k_0} = 2}^\infty {{P_{{k_0}}}(\lambda )P_1^{{k_0}}(p_\phi )}\ ,\quad {{\mathbf{V}}_0}=\phi . \end{aligned} \end{aligned}$$

(20)

When $n=2$, the formula of $P^\mathbf{S2}(p_{_{{\mathbf{V}}_1}})$ depends on the resolution result in $n=1$. There are two possible results when $n=1$ fails: idle (0) or collision (1). If idle, all $k_0$ colliding relays in the first unit still collide in the second unit, resulting formula (21). Otherwise in a probability of $P_{k_1}^{k_0}(p_\phi ), k_1$ out of $k_0$ relays ($2 \le k_1 \le k_0$) collide and the expression is given in (22).

$$\begin{aligned}&\begin{aligned} P^\mathbf{S2}(p_{_{[0]}})=\sum \limits _{{k_0} = 2}^\infty {{P_{{k_0}}}(\lambda )P_0^{{k_0}}({p_{_\phi }})P_1^{{k_0}}({p_{_{[0]}}})}\ ,\quad {{\mathbf{V}}_1}=[0]. \end{aligned} \end{aligned}$$

(21)

$$\begin{aligned}&\begin{aligned} P^\mathbf{S2}(p_{_{[1]}})=\sum \limits _{{k_0} = 2}^\infty {{P_{{k_0}}}(\lambda )\sum \limits _{{k_1} = 2}^{{k_0}} {P_{{k_1}}^{{k_0}}({p_{_\phi }})} P_1^{{k_1}}({p_{[1]}})}\ ,\quad {{\mathbf{V}}_1}=[1]. \end{aligned} \end{aligned}$$

(22)

When $n=3$, similar to $n=2$, there are also two failure results for each situation in $n=2$, forming 4 results in all. The expression of $P^\mathbf{S2}(p_{_{{\mathbf{V}}_2}})$ when ${\mathbf{V}}_2=[0,0], [0,1], [1,0]$, and [1, 1] are given below, respectively.

$$\begin{aligned}&\begin{aligned} P^\mathbf{S2}(p_{_{[0,0]}})=\sum \limits _{{k_0} = 2}^\infty {{P_{{k_0}}}(\lambda )P_0^{{k_0}}({p_{_\phi }})P_0^{{k_0}}({p_{_{[0]}}})P_1^{{k_0}}({p_{_{[0,0]}}})},\quad {\mathbf{V}}_2=[0,0], \end{aligned} \end{aligned}$$

(23)

$$\begin{aligned}&\begin{aligned} P^\mathbf{S2}(p_{_{[0,1]}})=\sum \limits _{{k_0} = 2}^\infty {{P_{{k_0}}}(\lambda )P_0^{{k_0}}({p_{_\phi }})\sum \limits _{{k_1} = 2}^{{k_0}} {P_{k_1}^{{k_0}}({p_{_{[0]}}})} P_1^{{k_1}}({p_{_{[0,1]}}})},\quad {\mathbf{V}}_2=[0,1], \end{aligned}\end{aligned}$$

(24)

$$\begin{aligned}&\begin{aligned} P^\mathbf{S2}(p_{_{[1,0]}})=\sum \limits _{{k_0} = 2}^\infty {{P_{{k_0}}}(\lambda )\sum \limits _{{k_1} = 2}^{{k_0}} {P_{{k_1}}^{{k_0}}({p_{_\phi }})} P_0^{{k_1}}({p_{_{[1]}}})P_1^{{k_1}}({p_{_{[1,0]}}})},\quad {\mathbf{V}}_2=[1,0], \end{aligned} \end{aligned}$$

(25)

$$\begin{aligned}&\begin{aligned} P^\mathbf{S2}(p_{_{[1,1]}})=\sum \limits _{{k_0} = 2}^\infty {{P_{{k_0}}}(\lambda )\sum \limits _{{k_1} = 2}^{{k_0}} {P_{{k_1}}^{{k_0}}({p_{_\phi }})} \sum \limits _{{k_2} = 2}^{{k_1}} {P_{{k_2}}^{{k_1}}({p_{_{[1]}}})} P_1^{{k_2}}({p_{_{[1,1]}}})}, \quad {\mathbf{V}}_2=[1,1]. \end{aligned} \end{aligned}$$

(26)

Based on the formulas for $n=1,2,3\ldots$, we can conclude that there are $2^{n-1}$ forms of expression for $P^\mathbf{S2}(p_{_{{\mathbf{V}}_{n-1}}})$, which is directed by ${\mathbf{V}}_{n-1}$. A general expression for $P^\mathbf{S2}(p_{_{{\mathbf{V}}_{n-1}}})$ is therefore summarized in (10). Since the number of 1 in ${\mathbf{V}}_{n-1}$ expresses the collision time in S2 and only when a collision happens will the number of colliding relays changes, $M_{i-1}[{\mathbf{V}}_{n-1}]$ is therefore denoted as the collision time indicator and the subscripts for k. Also, due to the fact that the history vector of any previous unit is fixed when ${\mathbf{V}}_{n-1}$ for the nth unit is given, we denote $\mathbf{L}_{i-1}[{\mathbf{V}}_{n-1}]$ as the previous history vector and the subscript of p for the ith unit.

Appendix 2: Derivation of formulas (11) and (12)

When $n=1, {\mathbf{V}}_0=\phi$, the collision region ${\mathcal {S}}_\phi ^{\mathrm{C}}$ and blank region ${\mathcal {S}}_\phi ^{\mathrm{B}}$ are equal to the available region ${\mathcal {S}}_m ^{\mathrm{AR}}$ and blank region ${\mathcal {S}}_m ^{\mathrm{B}}$ in the last unit of S1, respectively. The expressions of $|{\mathcal {S}}_{\phi }^{\mathrm{AR}}|$ and $|{\mathcal {S}}_{\phi }^{\mathrm{B}}|$ are given as

$$\begin{aligned} \left| {\mathcal {S}}_\phi ^{\mathrm{AR}}\right|&= {p_\phi }\left| {\mathcal {S}}_\phi ^{\mathrm{C}}\right| \nonumber \\&= {p_\phi }|{\mathcal {S}}^{\mathrm{e}}|, \end{aligned}$$

(27a)

$$\begin{aligned} \left| {\mathcal {S}}_\phi ^{\mathrm{B}}\right|&=\left| {\mathcal {S}}_m ^{\mathrm{B}}\right| \nonumber \\&= (m - 1)|{{\mathcal {S}}^{\mathrm{e}}}|. \end{aligned}$$

(27b)

When $n=2$, if ${\mathbf{V}}_1=[0]$, there is no available relay in ${\mathcal {S}}_\phi ^{\mathrm{AR}}$ and it is added to blank region ${\mathcal {S}}_\phi ^{\mathrm{B}}$. ${\mathcal {S}}_{[0]}^{\mathrm{C}}$ is therefore the complementary region of ${\mathcal {S}}_\phi ^{\mathrm{AR}}$ in ${\mathcal {S}}_\phi ^{\mathrm{C}}$. The expressions of $|{\mathcal {S}}_{[0]}^{\mathrm{AR}}|$ and $|{\mathcal {S}}_{[0]}^{\mathrm{B}}|$ are given as

$$\begin{aligned} \left| {\mathcal {S}}_{[0]}^{\mathrm{AR}}\right|&= {p_{[0]}}\left| {\mathcal {S}}_{[0]}^{\mathrm{C}}\right| \nonumber \\&= {p_{[0]}}(1 - {p_\phi })|{\mathcal {S}}^{\mathrm{e}}|, \end{aligned}$$

(28a)

$$\begin{aligned} \left| {\mathcal {S}}_{[0]}^{\mathrm{B}}\right|&= \left| {\mathcal {S}}_\phi ^{\mathrm{B}}\right| + \left| {\mathcal {S}}_\phi ^{\mathrm{AR}}\right| \nonumber \\&=(m - 1)|{{\mathcal {S}}^{\mathrm{e}}}| + {p_\phi }|{{\mathcal {S}}^{\mathrm{e}}}|. \end{aligned}$$

(28b)

If ${\mathbf{V}}_1=[1]$, more than one available relay exists in ${\mathcal {S}}_\phi ^{\mathrm{AR}}$, making it the new collision region ${\mathcal {S}}_{[1]}^{\mathrm{C}}$. Thus ${\mathcal {S}}_{[1]}^{\mathrm{B}}$ remains unchanged. The expressions of $|{\mathcal {S}}_{[1]}^{\mathrm{AR}}|$ and $|{\mathcal {S}}_{[1]}^{\mathrm{B}}|$ are given as

$$\begin{aligned} \left| {\mathcal {S}}_{[1]}^{\mathrm{AR}}\right|&= {p_{[1]}}\left| {\mathcal {S}}_{[1]}^{\mathrm{C}}\right| \nonumber \\&= {p_{[1]}}{p_\phi }|{\mathcal {S}}^{\mathrm{e}}|, \end{aligned}$$

(29a)

$$\begin{aligned} \left| {\mathcal {S}}_{[1]}^{\mathrm{B}}\right|&= \left| {\mathcal {S}}_\phi ^{\mathrm{B}}\right| \nonumber \\&= (m - 1)|{\mathcal {S}}^{\mathrm{e}}|. \end{aligned}$$

(29b)

When $n=3$, the discussion is similar to $n=2$. The expressions for $|{\mathcal {S}}_{{\mathbf{V}}_2}^{\mathrm{AR}}|$ and $|{\mathcal {S}}_{{\mathbf{V}}_2}^{\mathrm{B}}|$ when ${\mathbf{V}}_2=[0,0], [0,1], [1,0]$, and [1, 1] are given below, respectively.

$$\begin{aligned} \left| {\mathcal {S}}_{[0,0]}^{\mathrm{AR}}\right|&= {p_{[0,0]}}\left| {\mathcal {S}}_{[0,0]}^{\mathrm{C}}\right| \nonumber \\&= {p_{[0,0]}}(1 - {p_{[0]}})(1 - {p_\phi })|{{\mathcal {S}}^{\mathrm{e}}}|, \end{aligned}$$

(30a)

$$\begin{aligned} \left| {\mathcal {S}}_{[0,0]}^{\mathrm{B}}\right|&= \left| {\mathcal {S}}_{[0]}^{\mathrm{B}}\right| + \left| {\mathcal {S}}_{[0]}^{\mathrm{AR}}\right| \nonumber \\&=(m - 1)|{{\mathcal {S}}^{\mathrm{e}}}| + {p_\phi }|{{\mathcal {S}}^\mathrm{e}}| + {p_{[0]}}(1 - {p_\phi })|{{\mathcal {S}}^{\mathrm{e}}}|, \end{aligned}$$

(30b)

$$\begin{aligned} \left| {\mathcal {S}}_{[0,1]}^{\mathrm{AR}}\right|&= {p_{[0,1]}}\left| {\mathcal {S}}_{[0,1]}^{\mathrm{C}}\right| \nonumber \\&= {p_{[0,1]}}{p_{[0]}}(1 - {p_\phi })|{{\mathcal {S}}^{\mathrm{e}}}|, \end{aligned}$$

(31a)

$$\begin{aligned} \left| {\mathcal {S}}_{[0,1]}^{\mathrm{B}}\right|&= \left| {\mathcal {S}}_{[0]}^{\mathrm{B}}\right| \nonumber \\&= (m - 1)|{{\mathcal {S}}_{\mathrm{e}}}| + {p_\phi }|{{\mathcal {S}}^\mathrm{e}}|, \end{aligned}$$

(31b)

$$\begin{aligned} \left| {\mathcal {S}}_{[1,0]}^{\mathrm{AR}}\right|&= {p_{[1,0]}}\left| {\mathcal {S}}_{[1,0]}^{\mathrm{C}}\right| \nonumber \\&= {p_{[1,0]}}(1 - {p_{[1]}}){p_\phi }|{{\mathcal {S}}^{\mathrm{e}}}|, \end{aligned}$$

(32a)

$$\begin{aligned} \left| {\mathcal {S}}_{[1,0]}^{\mathrm{B}}\right|&= \left| {\mathcal {S}}_{[1]}^{\mathrm{B}}\right| + \left| {\mathcal {S}}_{[1]}^{\mathrm{AR}}\right| \nonumber \\&=(m - 1)|{{\mathcal {S}}^{\mathrm{e}}}| + {p_{[1]}}{p_\phi }|{{\mathcal {S}}^{\mathrm{e}}}|, \end{aligned}$$

(32b)

$$\begin{aligned} \left| {\mathcal {S}}_{[1,1]}^{\mathrm{AR}}\right|&= {p_{[1,1]}}\left| {\mathcal {S}}_{[1,1]}^{\mathrm{C}}\right| \nonumber \\&= {p_{[1,1]}}{p_{[1]}}{p_\phi }|{{\mathcal {S}}^{\mathrm{e}}}|, \end{aligned}$$

(33a)

$$\begin{aligned} \left| {\mathcal {S}}_{[1,1]}^{\mathrm{B}}\right|&= \left| {\mathcal {S}}_{[1]}^{\mathrm{B}}\right| \nonumber \\&= (m - 1)|{{\mathcal {S}}^{\mathrm{e}}}|, \end{aligned}$$

(33b)

According to Algorithm 2, $|{\mathcal {S}}^{\mathrm{AR}}_{{\mathbf{V}}_{n-1}}|$ is influenced by all elements in ${\mathbf{V}}_{n-1}$. As ()–() shows, if collision occurs, $p_{_{{\mathbf{L}_{i-1}}[{{\mathbf{V}}_{n-1}}]}}$ will be multiplied to $|{\mathcal {S}}_{{\mathbf{L}_{i-1}}[{{\mathbf{V}}_{n-1}}]}^{\mathrm{C}}|$. Otherwise if idle occurs, $(1-p_{{_{{\mathbf{L}_{i-1}}[{{\mathbf{V}}_{n-1}}]}}})$ will be multiplied to $|{\mathcal {S}}_{{\mathbf{L}_{i-1}}[{{\mathbf{V}}_{n-1}}]}^{\mathrm{C}}|$. Given the history vector ${\mathbf{V}}_{n-1}$ and the corresponding set of $p_{{_{{\mathbf{L}_{i-1}}[{{\mathbf{V}}_{n-1}}]}}}$, the generalized expression of $|{\mathcal {S}}_{{\mathbf{V}}_{n-1}}^{\mathrm{AR}}|$ can be concluded as (11). Similarly, $|{\mathcal {S}}_{{{\mathbf{V}}_{n-1}}}^\mathrm{B}|$ increases only when idle occurs, its expression is concluded as

$$\begin{aligned} \begin{aligned} \left| {\mathcal {S}}_{{{\mathbf{V}}_{n-1}}}^{\mathrm{B}}\right| = (m - 1)|{{\mathcal {S}}^{\mathrm{e}}}| + \sum \limits _{i = 1}^{n - 1} {\left\{ {\left| {\mathcal {S}}_{{\mathbf{L}_{i - 1}}[{{\mathbf{V}}_{n - 1}}]}^{\mathrm{AR}}\right| \left[ {1 - {{\mathbf{V}}_{n - 1}}(i)} \right] } \right\} }. \end{aligned} \end{aligned}$$

(34)

The final area of the QoS region $|{\mathcal {S}}_{{{\mathbf{V}}_{n-1}}}|$ is the summation of $|{\mathcal {S}}_{{{\mathbf{V}}_{n-1}}}^{\mathrm{AR}}|$ and $|{\mathcal {S}}_{{{\mathbf{V}}_{n-1}}}^{\mathrm{B}}|$, and is obtained by (12).